Elementy liniowe układów automatyki

Elementy inercyjne wy szych rz dów

ELEMENTY INERCYJNE WY SZYCH RZ DÓW

W układach sterowania bardzo cz sto wyst puj elementy proporcjonalne

opisywane równaniami ró niczkowymi wy szego rz du.

t

k

0

X

t

k

0

1

2

3

Y

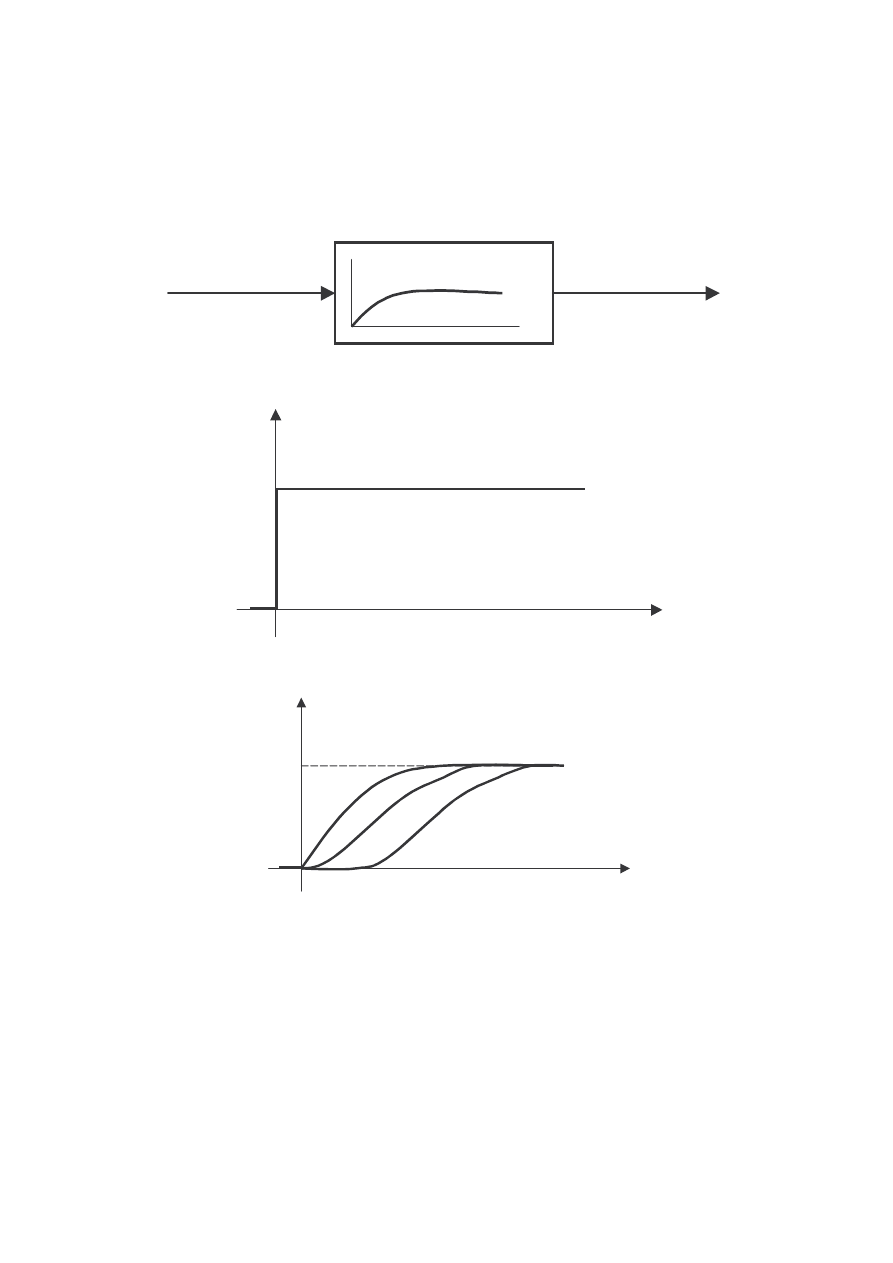
Odpowied skokowa elementu wieloinercyjnego:

a) symbol elementu wieloinercyjnego; b) wymuszenie skokowe;

c) odpowied na wymuszenie skokowe elementu: 1 - jednoinercyjnego, 2 -

oscylacyjnego tłumionego krytycznie, 3 - wieloinercyjnego

Elementy liniowe układów automatyki

Elementy inercyjne wy szych rz dów

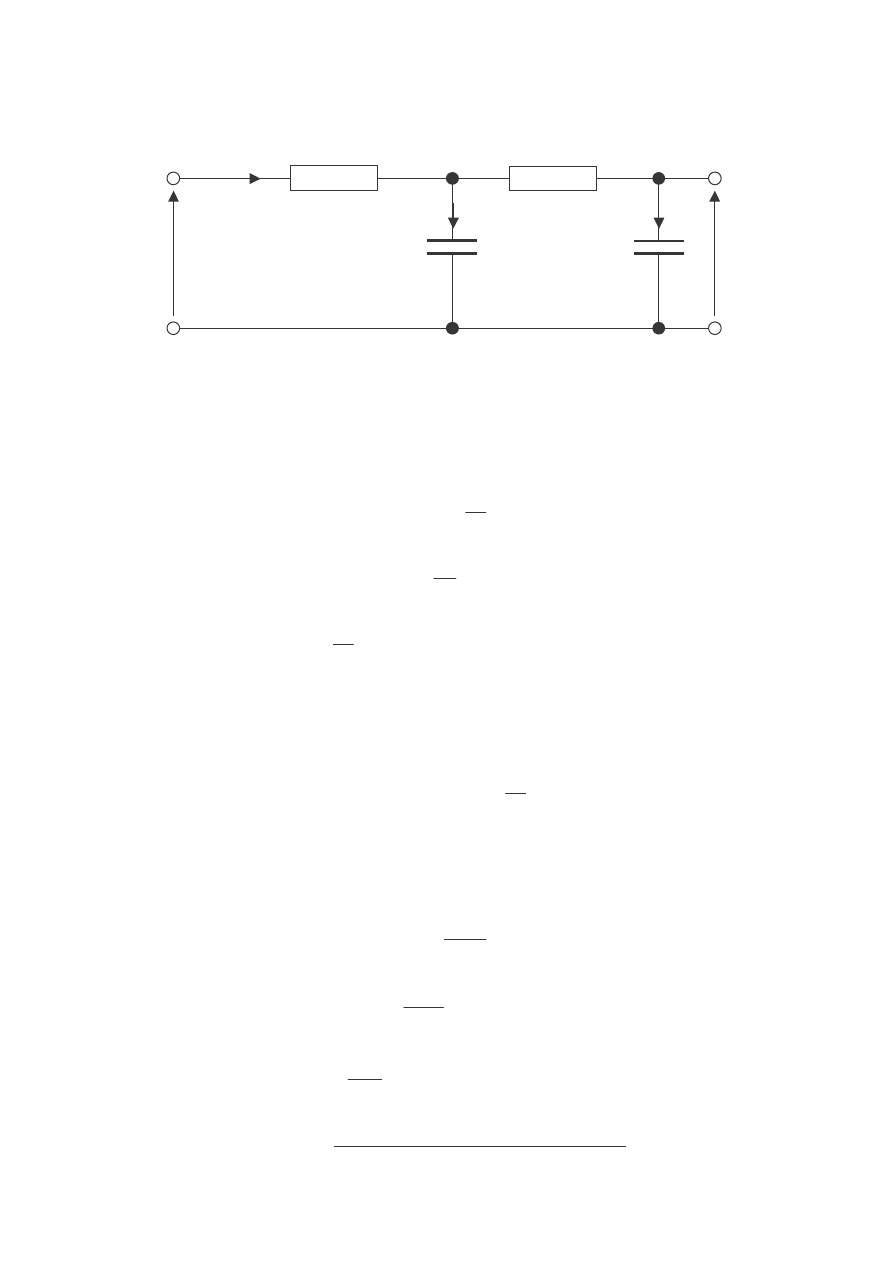
Czwórnik RC

C

1

U

we

(t)

U

wy

(t)

C

2

R

1

R

2

I(t)

I

1

(t)

I

2

(t)

Czwórnik RC

Dla nieobci onego czwórnika RC (przy zerowych warunkach pocz tkowych)

otrzymuje si równanie:

τ

τ

+

=

t

0

1

1

1

we

d

)

(

I

C

1

R

)

t

(

I

)

t

(

U

;

τ

τ

=

t

0

2

2

wy

d

)

(

I

C

1

)

t

(

U

;

)

t

(

I

R

)

t

(

U

d

)

(

I

C

1

2

2

wy

t

0

1

1

+

=

τ

τ

;

)

t

(

I

)

t

(

I

)

t

(

I

2

1

+

=

Po wyeliminowaniu pr du I(t) znajdujemy:

+

+

=

t

0

1

1

1

2

1

1

we

dt

)

t

(

I

C

1

R

)

t

(

I

R

)

t

(

I

)

t

(

U

;

W celu wyznaczenia transmitancji rozwa anego czwórnika wykonujemy

transformacj Laplace'a równa - przy zerowych warunkach pocz tkowych:

0

sC

)

s

(

I

)

t

(

U

2

2

wy

=

−

;

0

)

s

(

I

R

sC

)

s

(

I

)

s

(

U

2

2

1

1

wy

=

+

−

;

)

s

(

U

)

s

(

I

R

)

s

(

I

sC

1

R

we

2

1

1

2

1

=

+

+

;

1

s

)]

R

R

(

C

R

C

[

s

R

R

C

C

)

s

(

U

)

s

(

U

2

1

2

1

1

2

2

1

2

1

we

wy

+

+

+

+

=

Elementy liniowe układów automatyki

Elementy inercyjne wy szych rz dów

Po wprowadzeniu oznacze :

1

1

1

C

R

T

=

;

1

1

1

C

R

T

=

otrzymujemy

1

s

T

R

R

R

T

s

T

T

1

)

s

(

U

)

s

(

U

)

s

(

G

2

2

2

1

1

2

2

1

we

wy

+

+

+

+

=

=

Pierwiastki równania s rzeczywiste, poniewa :

=

−

+

+

=

−

+

+

2

1

2

2

2

1

2

1

2

1

2

2

2

2

1

1

T

T

4

T

R

R

T

T

T

T

4

T

R

R

R

T

=

−

+

+

+

+

=

2

1

2

2

2

1

2

1

2

2

1

2

2

1

T

T

4

T

R

R

R

R

T

)

T

T

(

2

)

T

T

(

0

T

R

R

R

R

T

)

T

T

(

2

)

T

T

(

2

2

2

1

2

1

2

2

1

2

2

1

>

+

+

+

+

=

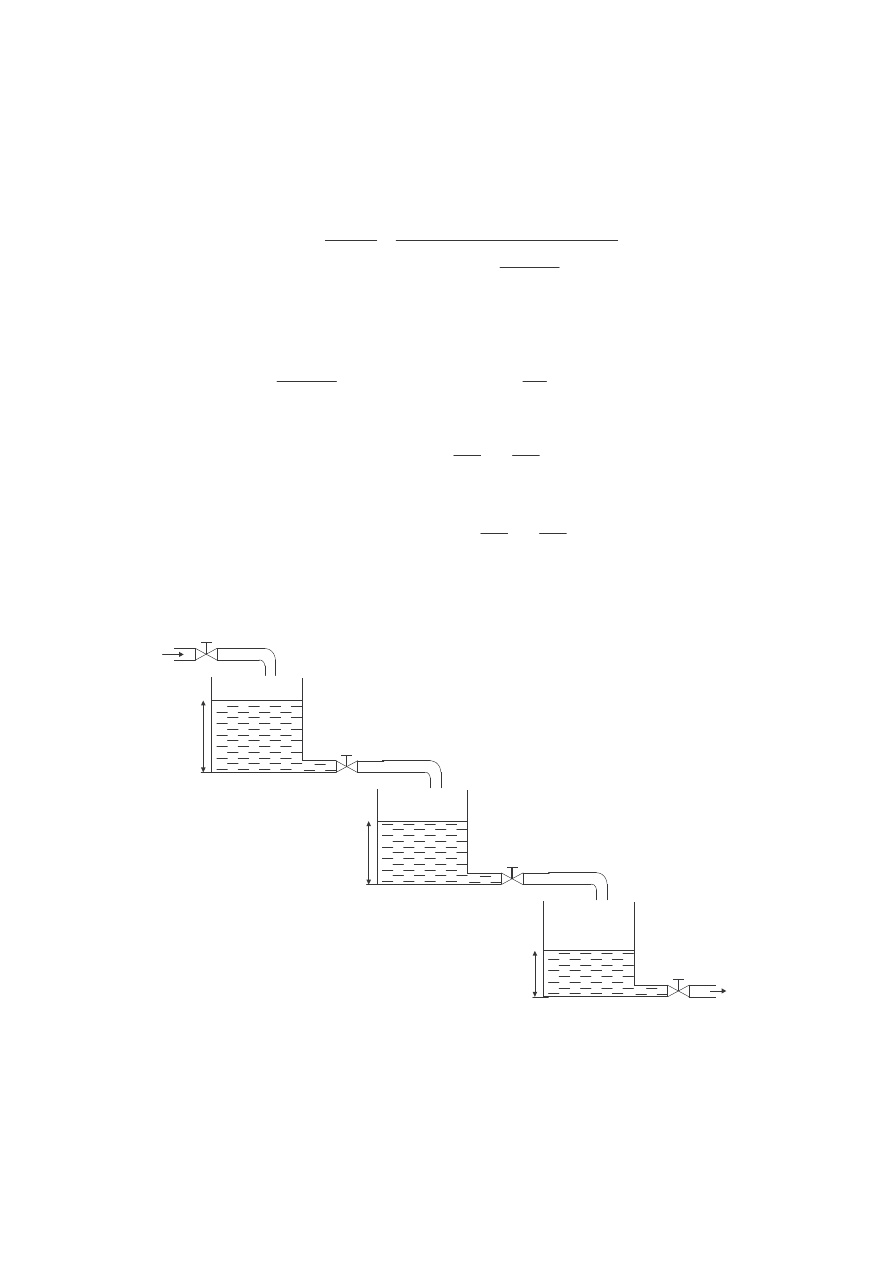
Układ trzech zbiorników poł czonych szeregowo

h

1

Q

1

Q

x

h

2

Q

2

h

3

Q

3

Układ trzech zbiorników poł czonych szeregowo