
1
CIĄGI I SZEREGI
Ciągiem nieskończonym nazywamy funkcję określoną na zbiorze liczb
naturalnych.
Jeżeli
n
a
n
f
=
)
(
dla n = 1, 2, ..., to ciąg zapisujemy symbolem {a
n
}, przy
czym liczbę a
n
nazywamy n-tym wyrazem tego ciągu.
Jeżeli wartości te są liczbami rzeczywistymi, to ciąg nazywamy ciągiem
liczbowym.

2
Metody określenia ciągów liczbowych
1.
podanie kilku wyrazów ciągu
2.
podanie wzoru na n-ty wyraz
3.
wzór rekurencyjny.

3
Ciągi monotoniczne
Ciąg liczbowy {a
n
} jest rosnący (niemalejący) wtedy i tylko wtedy, gdy
1
+
∈
<
∀
n
n
N
n
a
a
(
1
+
∈
≤
∀
n
n
N
n
a
a
).
Ciąg liczbowy {a
n
} jest malejący (nierosnący) wtedy i tylko wtedy, gdy
1
+
∈
>
∀
n
n
N
n
a
a
(
1
+
∈
≥
∀
n
n
N
n
a
a
).

4
Ciąg ograniczony
Ciąg liczbowy jest ograniczony z dołu, gdy zbiór jego wartości jest
ograniczony z dołu, tzn.
M
a
n
N
n
R
M
≥
∀
∃
∈
∈
.
Ciąg liczbowy jest ograniczony z góry, gdy zbiór jego wartości jest
ograniczony z góry, tzn.
M
a
n
N
n
R
M
≤
∀
∃
∈
∈
.
Ciąg jest ograniczony, gdy jest ograniczony z dołu i z góry,
M
a
n
N
n
R
M
≤
∀
∃
∈
∈
.

5
Granica ciągu
Liczbę
R
g
∈
nazywamy granicą ciągu {a
n
} i piszemy
g
a
n
n
=
∞
→
lim
(lub
∞
→
→
n
g
a
n
przy
), gdy
ε
δ
δ
ε
<
−
∀
∃
∀
>
>
g
a
n
n
0
.
ε
ε
<
−
<
−
g
a
n
ε
ε
+
<
<
−
g
a
g
n
Ciąg {a
n
} nazywamy zbieżnym, gdy istnieje
R
g
∈
takie, że
g
a
n
n
=
∞
→
lim
.
czyli:
Ciąg mający granicę nazywamy zbieżnym, ciąg niemający granicy
nazywamy rozbieżnym.
6
Twierdzenie
Jeżeli istnieją granice:
a
a
n
n
=
∞
→
lim
i
b
b
n
n
=
∞
→
lim
,
to istnieją również granice:
1.
c
a
c
a
c
a
n
n
n
n
±
=
±
=
±
∞
→
∞
→
)
(
lim
)
(
lim
dla stałej
R
c
∈
;
2.
a
c
a
c
n
n
⋅
=
⋅
∞
→
)
(
lim
dla stałej
R
c
∈
;
3.
b
a
b
a
n
n
n
±
=
±
∞
→
)
(
lim
;
4.
b
a
b
a
n
n
n
⋅
=
⋅
∞
→
)
(
lim
;
5.
0)
(b
lim
≠
=
∞
→
b
a
b
a
n
n
n
.
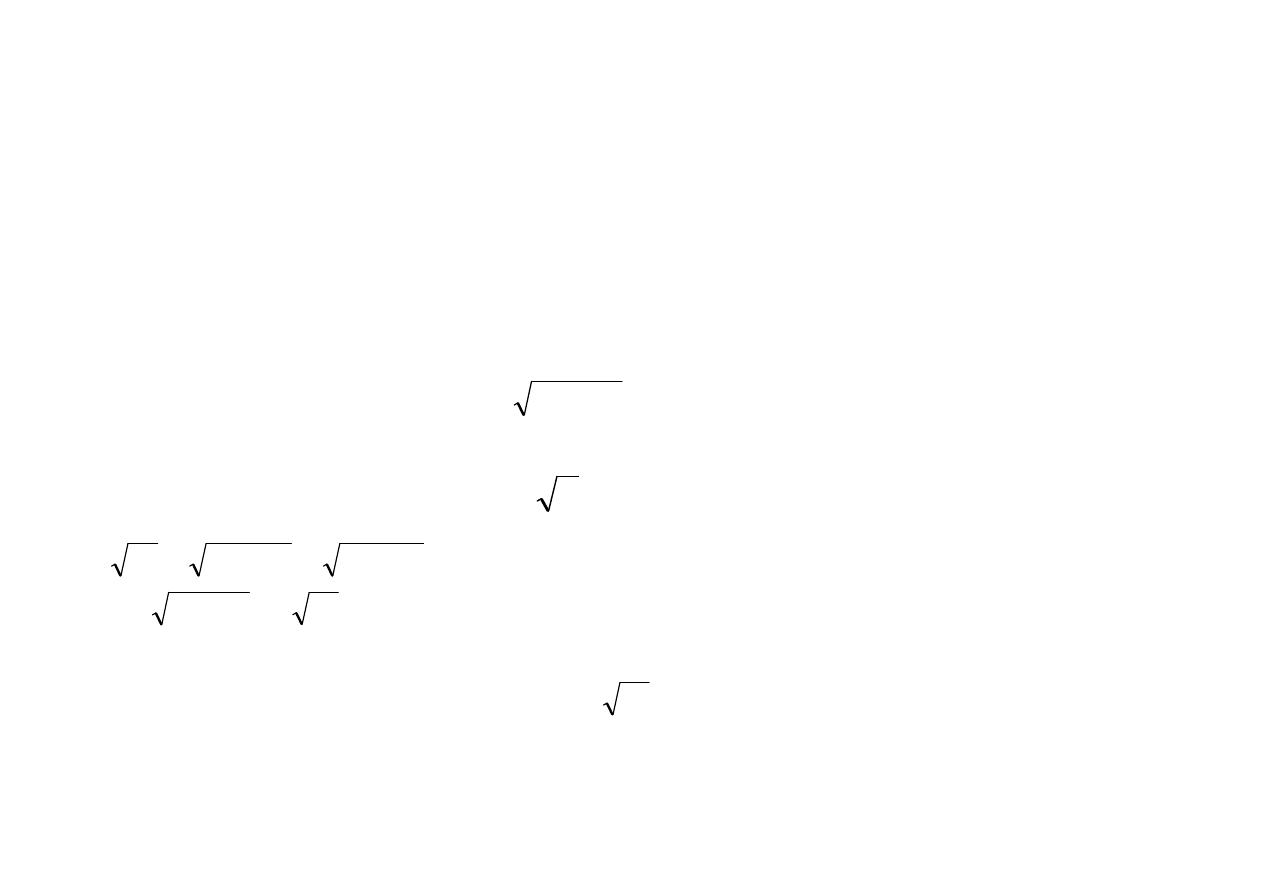
7
Twierdzenie (o trzech ciągach)
Jeżeli
g
c
a
n
n
n
n
=
=
∞
→
∞
→
lim
lim
oraz
n
n
n
k
n
N
k
c
b
a
≤
≤
∀
∃
≥
∈
, to
g
b
n
n
=
∞
→
lim
.
Przykład
Obliczyć granicę ciągu
n
n
n
n
a
3
2
+
=
.
Korzystając z tego, że
1
lim
=
∞
→
n
n
a
, gdy a > 1, oraz z nierówności
n
n
n
n
n
n
n
n
3
3
3
2
3
+
<
+
<
, prawdziwej dla każdego n, otrzymujemy
n
n
n
n
n
2
3
3
2
3
<
+
<
.
Ponieważ granicą ciągów {3}, {
n
n
2
3
} jest liczba 3, więc ciąg {a
n
} ma
również granicę 3.
8
Ciąg arytmetyczny
Ciągiem arytmetycznym nazywamy ciąg, w którym różnica między
dowolnym wyrazem ciągu (oprócz wyrazu pierwszego), a wyrazem
bezpośrednio go poprzedzającym jest stała. Różnicę tę nazywamy
różnicą ciągu arytmetycznego.
Niech {a
n
} będzie ciągiem arytmetycznym o różnicy d. Prawdziwe są
zdania:
d
n
a
a
n
N
n
)
1
(
1
−
+
=
∀
∈
,
)
(
2
1
1
1
}
1
{
\
+
−
∈
+
=
∀
n
n
n
N
n
a
a
a
,
n
a
a
a
a
a
S
n
n
n
N
n
⋅
+
=
+
+
+
=
∀
∈
)
(
2
1
...
1
2
1
.
Symbol S
n
oznacza n-tą sumę częściową ciągu.

9
Ciąg geometryczny
Ciągiem geometrycznym nazywamy ciąg, w którym stosunek
dowolnego wyrazu (oprócz pierwszego) do wyrazu bezpośrednio go
poprzedzającego jest stały. Wartość tego stosunku nazywamy ilorazem
ciągu geometrycznego.
Niech {a
n
} będzie ciągiem geometrycznym o ilorazie q. Wtedy
0
a
gdzie
,
1
1
1
≠
⋅
=
∀
−
∈
n
n
N
n
q
a
a
,
0
a
gdzie
,
1
1
1
2
}
1
{
\
≠
⋅
=
∀
+
−
∈
n
n
n
N
n
a
a
a
,
0
q
1
q
gdzie
,
1
1
...
1
2
1
≠
∧
≠
−
−
⋅
=
+
+
+
=
∀
∈
q
q
a
a
a
a
S
n
n
n
N
n
.
Symbol S
n
oznacza n-tą sumę częściową ciągu geometrycznego. Ciąg
{S
n
} ma wyrazy S
1
=a
1
, S
2
=a
1
+a
2
, ..., S
n
=a
1
+...+a
n
, ... i nazywamy go
ciągiem sum częściowych.

10
Suma nieskończonego ciągu geometrycznego
Jeżeli ciąg sum częściowych jest zbieżny, to jego granicę nazywamy
sumą nieskończonego ciągu geometrycznego i oznaczamy symbolem S,
czyli
n
n
S
S
∞
→
=
lim
.
Twierdzenie
Jeżeli |q|<1, to ciąg {S
n
} jest zbieżny oraz
q
a
S
−
=
1
1
.

11
Szeregi
Ciąg {S
n
} sum częściowych ciągu {a
n
} nazywamy szeregiem.
Szereg liczbowy {S
n
} nazywamy zbieżnym, gdy ciąg {S
n
} jego sum
częściowych
n
n
a
a
a
S
+
+
+
=
...
2
1
jest zbieżny.
W tym przypadku granicę
∑
∑
∞
=
=
∞
→
∞
→
=
=
=
1
1
lim
lim
k
k
n
k
k
n
n
n
a
a
S
S
nazywamy sumą
szeregu.
Szereg, który nie jest zbieżny, nazywamy rozbieżnym.

12
ZASTOSOWANIA W EKONOMII
Oprocentowanie proste i składane
Oprocentowanie proste polega na tym, że po każdym zakończonym
okresie oszczędzania odsetki są wypłacane. Kolejne odsetki obliczane są
znowu tylko od kwoty kapitału początkowego.
Jeżeli przyjmiemy oznaczenia: K
0
– kapitał początkowy, r – stopa
procentowa, n – liczba okresów oszczędzania, to kapitał w następnym
okresie będzie równy:
)
1
(
0
0
0
1
r
K
r
K
K
K
+
=
+
=

13
Kapitał w okresach następnych (przy założeniu, że odsetki z
wcześniejszych okresów nie zostały wydane, a jedynie przelane na
rachunek bieżący, nieoprocentowany) będzie wynosił:
)
2
1
(
0
0
0
0
2
r
K
r
K
r
K
K
K
+
=
+
+
=
,
.......................................................,
}
0
{
gdzie
),
1
(
0
∪
∈
+
=
N
n
nr
K
K
n
.
Oznacza to, że kapitał rośnie z roku na rok w tempie arytmetycznym o
różnicy d = K
0
r.
Przykład
Oblicz wartość posiadanych pieniędzy, jeżeli założyłeś roczną,
odnawialną lokatę 1000 zł, roczna stopa procentowa wynosi 5 %, czas
oszczędzania wynosi 3 lata, a odsetki po każdym roku przelewane są na
nieoprocentowany rachunek bieżący.
1150
)
05
,
0
3
1
(
1000
)
3
1
(
0
3
=
⋅
+
⋅
=
+
=
r
K
K
.

14
Oprocentowanie składane polega na tym, że po każdym zakończonym
okresie oszczędzania odsetki dopisywane są do kapitału, więc odsetki w
następnym okresie obliczane są od większej kwoty:
)
1
(
0
0
0
1
r
K
r
K
K
K
+
=
+
=
2
0
0
1
2
)
1
(
)
1
(
)
1
(
)
1
(
r
K
r
r
K
r
K
K
+
=
+
⋅
+
=
+
=
,
.......................................................,
W takim sposobie oprocentowania kwoty K
0
, K
1
, ..., K
n
tworzą ciąg
geometryczny o ilorazie q = 1 + r, czyli:
n
n
r
K
K
)
1
(
0
+
=
Przykład
Oblicz wartość posiadanych pieniędzy, jeżeli założyłeś roczną,
odnawialną lokatę 1000 zł, roczna stopa procentowa wynosi 5 %, czas
oszczędzania wynosi 3 lata, a odsetki po każdym roku dopisywane są do
kwoty kapitału zdeponowanego na lokacie.
62
,
1157
)
05
,
0
1
(
1000
)
1
(
3
3
0
3
=
+
⋅
=
+
=
r
K
K
.

15
Stopa procentowa podawana jest generalnie jako roczna nominalna
stopa procentowa, dlatego aby obliczyć stopę procentową dla danego
okresu należy podzielić roczną nominalną stopę procentową przez liczbę
okresów kapitalizacji w ciągu roku
m
n
m
n
m
r
K
K
⋅
⋅
+
=
)
1
(
0
.
Przykład
Oblicz ile otrzymasz pieniędzy po roku oszczędzania, jeżeli założyłeś
lokatę 10000 zł, o oprocentowaniu rocznym 8%, kapitalizowaną
kwartalnie.
32
,
10824
0824321
,
1
10000
)
4
08
,
0
1
(
10000
4
1
4
1
=
⋅
=
+
=
⋅
⋅
K
16
Kapitalizacja ciągła
W przypadku granicznym, gdy liczba okresów kapitalizacji zmierza do
nieskończoności (
∞
→
m
), otrzymujemy model kapitalizacji ciągłej.
Po t latach wartość lokaty K
0
będzie wynosić:
t
r
t
r
r
m
m
t
m
t
e
K
r
m
K
m
r
K
K
⋅
⋅
⋅
∞
→
⋅
=
+
⋅
=
+
=
0
0
0
1
1
lim
)
1
(
lim
,
gdzie e jest podstawą logarytmu naturalnego, korzystając ze wzoru
e
n
n
n
=
+
∞
→
1
1
lim
.

17
Spłata kredytu
Udzielony kredyt w wysokości L należy spłacić płatnościami P
1
, P
2
, ...,
P
n
na końcu okresów (lat, kwartałów, miesięcy). Wartości obecne obu
strumieni muszą być sobie równe. Jeżeli stopa procentowa kredytu za
jeden okres wynosi r, to
n
n
r
P
r
P
r
P
L
)
1
(
...
)
1
(
1
2
2
1
+
+
+
+
+
+
=
,
czyli
∑
=
+
=
n
k
k
k
r
P
L
1
)
1
(
.
Aby ustalić plan spłaty kredytu należy zdecydować czy stałe mają być
raty kapitałowe, czy kwoty płatności.

18
Spłata kredytu w równych kwotach płatności
Spłata kredytu w równych kwotach płatności następuje wtedy, gdy suma
raty kapitałowej za dany okres i odsetek za ten sam okres jest taka sama
w każdym okresie, tzn.
P = K
k
+R
k
, dla każdego k = 1, 2, ..., n,
gdzie n oznacza liczbę okresów płatności, K
k
– spłatę kapitału, R
k
– odsetki.
Jeżeli kwota kredytu równa jest L, to spłatę kredytu gwarantuje równość
∑
=
+
=
n
k
k
r
P
L
1
)
1
(
.
Składniki powyższej sumy tworzą ciąg geometryczny o wyrazie
pierwszym
r
P
a
+
=
1
1
oraz ilorazie
r
q
+
=
1
1
.

19
Zgodnie ze wzorem na sumę n wyrazów ciągu geometrycznego
r
r
r
P
L
n
+
−
+
−
⋅
+
=
1
1
1
1
1
1
1
,
a po przekształceniach
( )
n
n
r
r
r
P
L
)
1
(
1
1
+
⋅
−
+
⋅
=
.
Mając daną kwotę kredytu, stopę procentową oraz liczbę płatności,
można ustalić wysokość płatności
( )
1
)
1
(
1
−
+
+
⋅
⋅
=
n
n
r
r
r
L
P
.
Wyszukiwarka
Podobne podstrony:
ciagi i szeregi zespolone
24 ciagi i szeregi funkcyjne 6 3 szeregi fouriera
8 Ciągi i szeregi
22 ciagi i szeregi funkcyjne 6 1 ogolne wlasnosci ciagow i szeregow funkcyjnych
zagadnienia, punkt 12, XII Ciągi i szeregi funkcyjne - zbieżność punktowa i jednostajna
W 1 Funkcje ciągi szeregi
ciagi i szeregi
14 Rozdział 13 Ciągi i szeregi funkcji
ciagi i szeregi, geometryczne, algebraiczne, inne
ciagi i szeregi
23 ciagi i szeregi funkcyjne 6 2 szeregi potegowe
Koła dokoła, ciągle ciągi i szeregi całą dobę człowiek tyra, od tira, kurwa do tira
ciagi szeregi, Ściągi dla studentów, Matematyka
ciagi i szeregi zespolone
więcej podobnych podstron