Parcie na powierzchnie zakrzywioną 

 
 
 

Reakcję pomiędzy cieczą a ściankami naczynia w którym ciecz się znajduje nazywana jest 

parciem.  Parcie  jest  to  siła  [N].  Znajomość  wartości  parcia  jest  nieodzownym  elementem 
budownictwa wodnego, budownictwa ziemnego, budowy statków, ...   
 

Metoda obliczania wartości parcia na powierzchnie płaskie różnie się od metody obliczania 

parcia  na  powierzchnie  zakrzywione  dlatego  pomimo  wspólnych  podstaw  fizycznych  muszą  być 
omawiane oddzielnie. 
Parcie na powierzchnie zakrzywione rozkładamy na dwie składowe: poziomą, którą oznaczamy P

x

 

oraz pionową P

y

. Żeby to było możliwe ściankę zakrzywioną rzutujemy na płaszczyznę prostopadłą 

do zwierciadła wody. W wyniku tej operacji otrzymujemy płaski obraz ścianki, na którą obliczamy 
parcie. 
 
 

1. Wprowadzenie 

 

 

Przykładowy  rozkład  sił  parcia  na  składowe 
P

x

  i  P

y

  działającego  na  ściankę  zakrzywioną 

przestawiono na rys. 1. 

 

Rys. 1. Schemat działania składowych siły parcia 

 

Wartość 

wypadkowego 

parcia 

P  na 

powierzchnie  zakrzywione  obliczamy  ze 
wzoru: 
 

2

2

y

x

P

P

P

+

=

 

 

 

(1) 

gdzie:  Px – składowa pozioma parcia [N],  
 

Py – pionowa składowa parcia [N], 

 
Sposób obliczania poszczególnych składowych parcia przedstawia się następująco; 
 
Składowa pozioma P

x

 – ściankę zakrzywioną 

rzutujemy 

na 

płaszczyznę 

pionową 

– 

prostopadłą  do  zwierciadła  wody.  W  wyniku 
tej operacji otrzymujemy płaski obraz ścianki 
(Rys. 2).  
Zarówno  wzory  na  obliczenie  składowej 
poziomej  Px  jak  i  sama  procedura  obliczania 
są takie jak w przypadku obliczania parcia na 
ścianki  płaskie  P

x

=γFh.    Wykorzystanie  tego 

wzoru nie wymaga rysowania wykresu parcia.

 

 

 

Rys. 2. Rzut ścianki na płaszczyznę pionową - redukcja 

ścianki zakrzywionej do ścianki płaskiej  

W  przypadku  gdy  kształt  ścianki,  na  którą  obliczamy  parcie  jest  kwadratem  lub  prostokątem 
możemy  zastosować  wzór  P

x

=γAb.  We  wzorze  tym  A  jest  powierzchnią  wykresu  parcia  dlatego 

procedurę rozpoczynamy od wykonania wykresu parcia.  
 
Składowa pionowa P

y

 - wzór z którego liczymy wartość składowej pionowej ma postać: 

 

b

y

V

P

γ

=

 

 

 

 

 

 

(2) 

 
gdzie: 

V

b

 – bryła parcia; określana indywidualnie dla każdego przypadku. Bryła parcia ograniczona 

 

jest  płaszczyznami;  od  dołu  –  ścianką,  od  góry  –  zwierciadłem  wody  a  boki  są  to 

 

płaszczyzny łączące górę i dół bryły parcia i nazywane płaszczyznami tworzącymi. 

 

Kierunek  działania  wypadkowej  parcia  –  kąt  pod  jakim  wypadkowe  parcie  nachylone  jest  do 
poziomu 

α

α

α

tg

arc

P

P

tg

x

y

=

⇒

=

 

 

 

 

(3) 

 
Punkt  przyłożenia  wypadkowej  parcia  - 
punkt,  przez  który  przechodzi  kierunek 
działania  wypadkowej  parcia 

P

  znajduje  się 

na 

przecięciu 

kierunków 

działania 

składowych 

P

x

  i 

P

y

.  Wypadkowe  parcie 

nachylone  jest  do  poziomu  pod  obliczonym 
kątem 

α

.  Kierunki  działania  składowych 

parcia 

P

x

  i 

P

y

  przechodzą  przez  środki 

ciężkości brył parcia. 
Określenie  punktu  przyłożenia  wypadkowej 
parcia  w  przypadku  brył  symetrycznych  jest 
to  o  wiele  prostsze  niż  w  przypadku 
złożonych układów:   
-  ścianki  niesymetryczne  –  trzeba  określić 
przesunięcie  względem  środka  ciężkości 
zarówno w pionie jak i poziomie, 
- ścianki symetryczne – wystarczy określić  
 
 

przesunięcie w pionie ponieważ przesunięcie 
w poziomie 

η

=0 (Rys.3). 

Można to osiągnąć metodami analitycznymi 
lub w sposób graficzny (ścianki 
symetryczne). 
 

 

 

Rys. 3. Graficzne wyznaczenie punktu przyłożenia 

wypadkowej parcia 

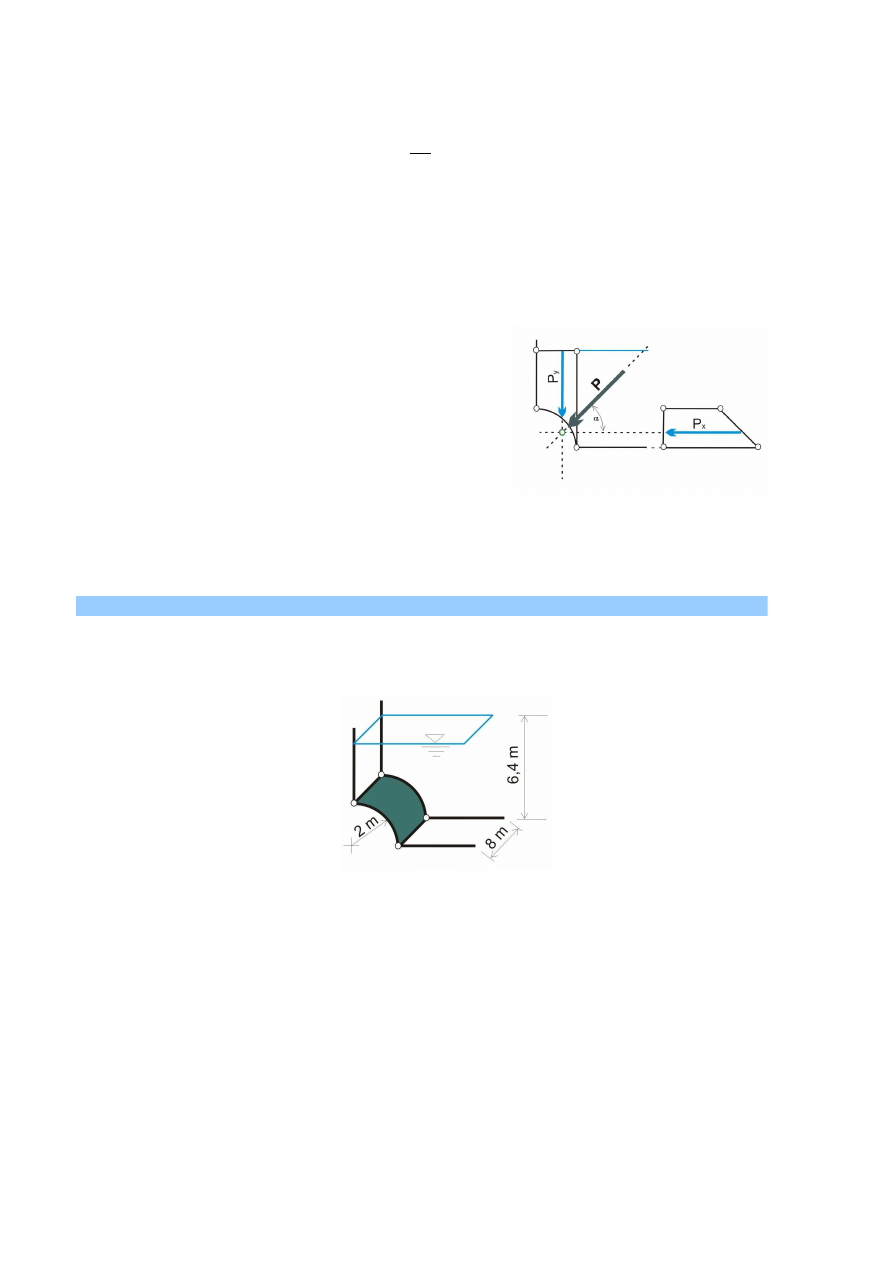
2. Przykład 

 
Obliczyć wartość parcia oraz określić kierunek działania wypadkowej parcia na ściankę pokazaną 
na rysunku 4. 
 

 

 

Rys. 4. Schemat obliczeniowy 

 
 
Obliczenia przeprowadzamy wg schematu: 

P

x

, 

P

y

 

→

 P, 

→

 

α

. 

 
W  pierwszej  kolejności  wykreślamy  wykresy  składowej  poziomej  i  pionowej  po  zrzutowaniu 
ścianki  na  płaszczyznę  pionową.  Wykres  parcia  w  układzie  trójwymiarowym  3D  i 
dwuwymiarowym  2D  przedstawiono  na  rys.  5.  Dodatkowo  zaznaczono  wypadkowe  parcia 
składowych poziomej i pionowej. 

 

 

Rys. 5. Wykres parcia w układzie 3D i 2D 

 
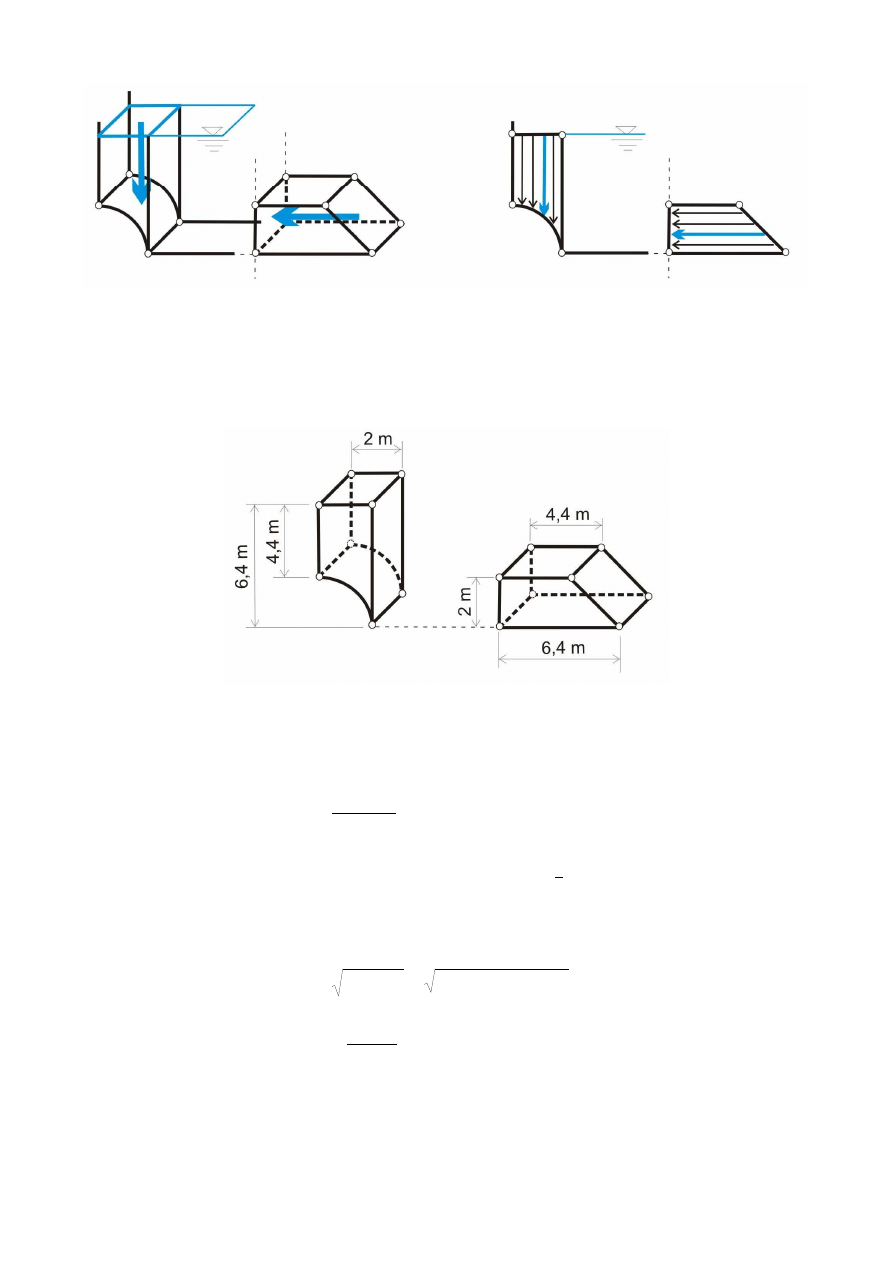
Zwymiarowane  bryły  parcia  przedstawiono  na  rys.  6.  Bryła  parcia  będąca  wykresem  składowej 
poziomej  ma  kształt  prostopadłościanu  ściętego  lub  innymi  słowami  graniastosłupa  o  podstawie 
trapezu. Składowa pionowa jest różnicą prostopadłościanu i ćwiartki walca.   
 

 

Rys. 6. Wymiary brył parcia

 

 
 
Składową poziomą obliczymy wykorzystując wzór 

b

A

P

x

γ

=

 (ścianka, na którą liczymy parcie ma 

kształt prostokąta): 

 

 

 

 

11

2

2

4

,

4

4

,

6

=

⋅

+

=

A

 m

2

, 

 

 

 

 

00

 

280,

 

863

8

11

9810

=

⋅

⋅

=

x

P

N 

Podstawa  bryły  parcia  składowej  pionowej  jest  równa 

9.66

2

2

4

,

6

2

4

1

=

−

⋅

π

m

2

  a  bryła  parcia  ma 

objętość 

77,27

8

9.66

=

⋅

=

b

V

m

3

. Wartość składowej pionowej wynosi: 

757991,81

27

,

77

9810

=

⋅

=

=

b

u

V

P

γ

N 

Wypadkowa parcia ma wartość: 

 

 

 

 

 

1148,83

99

,

757

28

,

863

2

2

2

2

=

+

=

+

=

y

x

P

P

P

kN 

Kierunek działania wypadkowej parcia: 

 

 

 

 

°

=

=

⇒

=

=

40

878

,

0

0,878

28

,

863

99

,

757

arc

tg

α

α

 

Punkt,  przez  który  przechodzi  kierunek  działania  wypadkowej  parcia  P  znajduje  się  na  przecięciu 
kierunków  działania  składowych  Px  i  Py.  Wypadkowe  parcie  działa  od  strony  wody  górnej  i 
nachylone jest do poziomu pod obliczonym kątem 

α.  

 
 

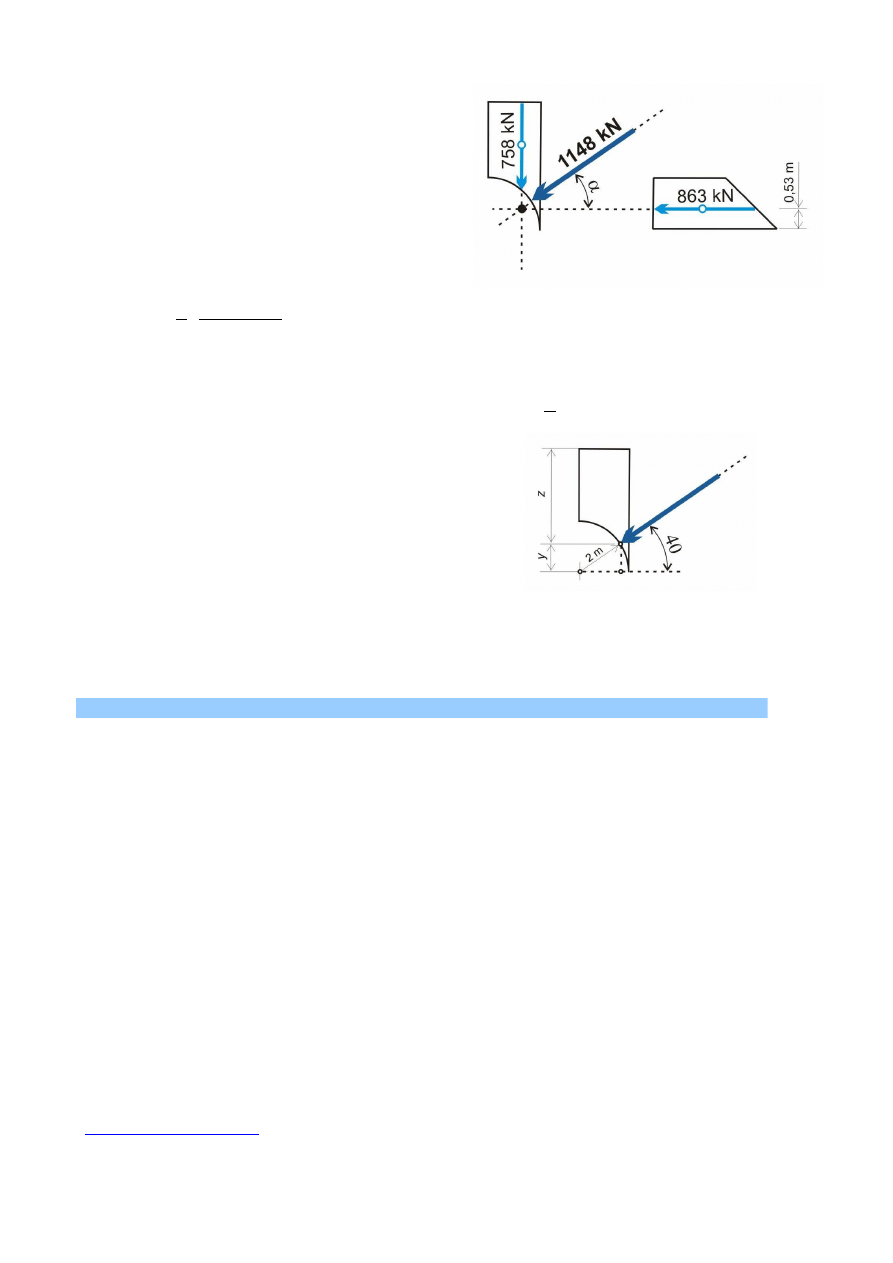
Środek  ciężkości  s

x

,  przez  który  przechodzi 

składowa 

P

x

  można  wyznaczyć  zarówno 

analitycznie  i  graficznie.  Metodę  graficzną 
wyznaczania 

środka 

ciężkości 

trapezu 

opisano  przy  omawianiu  podziału  parcia  na 
części  o  jednakowej  powierzchni.  Wartość 
rzędnej  środka  ciężkości  wynosi    (Rys.  7) 
[źródło: 

Kubrak 

J., 

1998, 

Hydraulika 

techniczna, Tab. 3.1, str. 58]: 
 

 

 

 

53

,

0

4

,

6

4

,

4

4

,

6

4

,

4

2

3

2

=













+

+

⋅

=

s

z

m 

 

 

Rys. 7. Wyznaczenie punktu przyłożenia wypadkowej parcia

 

 
W  przypadku  składowej  pionowej  osobno 
określamy  środki  ciężkości  fragmentów 
składających 

się 

na 

bryłę 

parcia: 

prostopadłościanu 

i 

wycinka 

będącego 

różnicą 

prostopadłościanu 

o 

podstawie 

kwadratu  i  ćwiartki  walca.  Dla  omawianego 
przypadku  jest  to  obliczenie  skomplikowane 
dlatego  postaramy  się  wyznaczyć  punkt 
przyłożenia  wypadkowej  parcia  z  funkcji 
trygonometrycznych. 

Punkt 

przyłożenia 

wypadkowej 

parcia 

z = 6,4 - y. 

Długość 

odcinka 

y 

wynika 

z 

funkcji 

trygonometrycznej:  

29

,

1

40

sin

2

2

40

sin

=

°

⋅

=

⇒

=

°

y

y

 m 

 

Rys. 8. Wyznaczenie punktu przyłożenia wypadkowej parcia

 

 
Zagłębienie punktu przyżenia punktu działania wypadkowej parcia wynosi 6,4 – 1, 29 = 5,01 m 
 
 

3. Odpowiedź 

 
Na  ściankę  działa  siła  parcia  wypadkowego  P  =1149  kN,  nachylona  do  poziomu  pod  kątem 

α  = 

40°. Punkt przyłożenia wypadkowej parcia znajduje się w połowie szerokości ścianki 8/2 = 4,0 m a 
jego zagłębienie wynosi z= 5,01 m.  
 
 
 

Literatura: 

 

Kubrak J.,1998, Hydraulika techniczna, Wyd. SGGW, Warszawa, 
Kubrak E., Kubrak J., 2004, Hydraulika techniczna, przykłady obliczeń, Wyd. SGGW, Warszawa, 
Podniesiński A., 1958, Zbiór zadań z hydrauliki, PWN, Łódź. 

 
 
 
 
 
 

Katedra  Inżynierii  Wodnej,  Wydział  Inżynierii  Środowiska  i  Geodezji,  Uniwersytet  Rolniczy  w 
Krakowie 

rmksiazek@cyf-kr.edu.pl