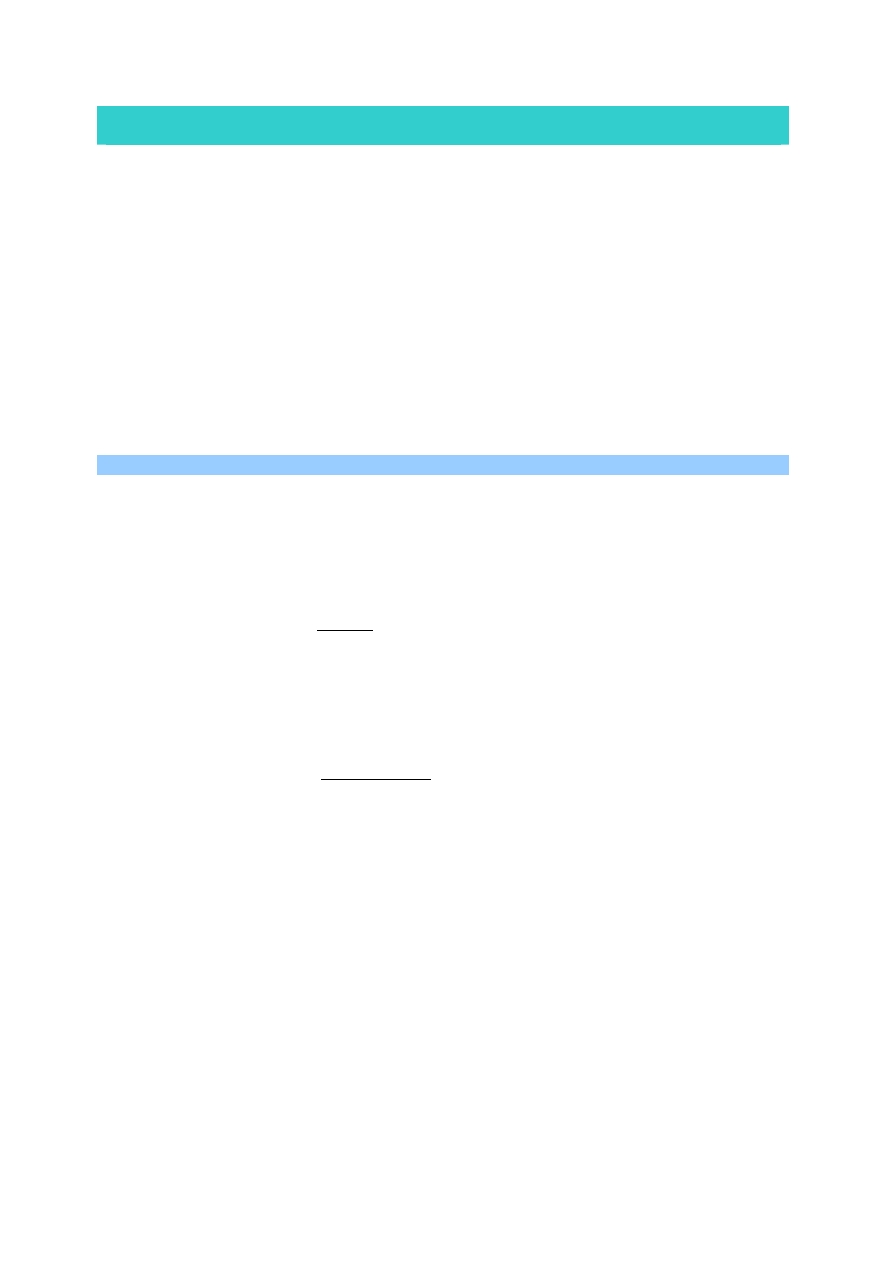
Parcie na powierzchnie płaską
Jednostką parcia jest [N]. Wynika z tego, że parcie jest to siła. Powtórzmy, parcie jest to siła.
Siła z jaką oddziaływuje ciecz na ścianki naczynia, w którym się znajduje. Znajomość
wartości parcia jest nieodzownym elementem budownictwa wodnego, budownictwa
ziemnego, budowy statków, ...
Metoda obliczania wartości parcia na powierzchnie płaskie różnie się od metody
obliczania parcia na powierzchnie zakrzywione dlatego pomimo wspólnych podstaw
fizycznych muszą być omawiane oddzielnie.
Wartość parcia na powierzchnie płaskie można obliczyć z dwóch wzorów: pierwszy
„uniwersalny” stosujemy do wszystkich rodzajów ścianek oraz „szczegółowy”, który
dedykowany jest tylko do ścianek o kształcie prostokąta (przypominam, że każdy kwadrat
jest prostokątem).
1. Wprowadzenie
Wartość parcia na powierzchnie płaskie obliczamy ze wzoru:
s
h
F
P
γ
=
(1)
gdzie: P – parcie [N],
rt
γ
- ciężar właściwy cieczy [Nm
-3
],
F – pole powierzchni ścianki, na którą działa parcie,
h
s
– zagłębienie środka ciężkości ścianki F (pionowo pod powierzchnią cieczy).
W przypadku ścianek, których kształt jest kwadratem lub prostokątem możemy stosować
wzór:
b
A
P
γ
=
(2)
gdzie: b – szerokość ścianki,
A – pole powierzchni wykresu parcia, wykres parcia jest graficznym przedstawieniem
hydrostatycznego rozkładu ciśnienia w cieczy będącej wyłącznie pad działaniem siły
ciężkości. Ciśnienie w dowolnym punkcie cieczy zależy od rodzaju cieczy j oraz
zagłębienia punktu (pod powierzchnią wody) h. Przykładowe wykresy parcia na
ściankę płaską przedstawiono na rys. 1a i b w układzie trójwymiarowym 3D i
dwuwymiarowym 2D.
W tym miejscu warto zwrócić uwagę na wyrażenie
Ab
[m
3
] we zworze (2). Jednostka
wskazuje, że jest to objętość. Bryłę tą, która jest widoczna na rys. 1 w układzie 3D
ograniczają ścianka, na którą działa parcie oraz płaszczyzny tworzące i nazywamy bryłą
parcia.
W zagadnieniach praktycznych ważne jest nie tylko określenie wartości parcia ale także
kierunku działania oraz punktu przyłożenia ponieważ parcie może wywoływać przesunięcie
obiektów i moment obrotowy. Wzór na określenie punktu przyłożenia wypadkowej parcia:
- w ściankach symetrycznych wystarczy określić przesunięcie w pionie
h
c
=
h
s
+
η
x
,
η
x
≠
0; ze
względu na symetryczność ścianki przesunięcie punktu przyłożenia wypadkowej parcia
względem osi pionowej wynosi
η
y
=0:
F
h
J
h
h
s
s
c
ξ
+
=
(3)
gdzie: h
s
– zagłębienie środka ciężkości,
J
ξ
- moment bezwładności ścianki względem osi x (poziomej) przechodzącej przez
środek ciężkości. Wzory na obliczanie momentów bezwładności zebrane są w
tabelkach a i uzależnione są od kształtu ścianki.
Rys. 1 Wykres parcia na ściankę płaską w układzie 3D i 2D: a) pionową, b) nachyloną do poziomu pod kątem 45°
- w przypadku ścianek niesymetrycznych obliczenia wymagają zarówno przesunięcia
η
x
≠
0
jak i
η
y
≠
0.
Podsumowując, jeżeli ścianka na którą liczymy parcie ma kształt np. koła to korzystamy ze
wzoru (1), gdy prostokąta mamy wybór. Ponadto wykorzystując wzór (2) konieczne jest
wykreślenie wykresu parcia podczas gdy w stosując wzór (1) należy określić głębokość
zagłębienia środka ścianki z czym mogą być nieraz trudności.
2. Przykład
Obliczyć parcie hydrostatyczne na ściankę boczną zapory EC (Rys. 2).
Dane:
H=6m,
H
1
=2m,
c=0,4m
e=12m -szerokość zapory
E
C
H1=2m
c=0,4m
H=6m
h
s=
(H-c)/2+H
1
e=12m
H
-c
Rys. 2. Przekrój przez budowlę hydrotechniczną
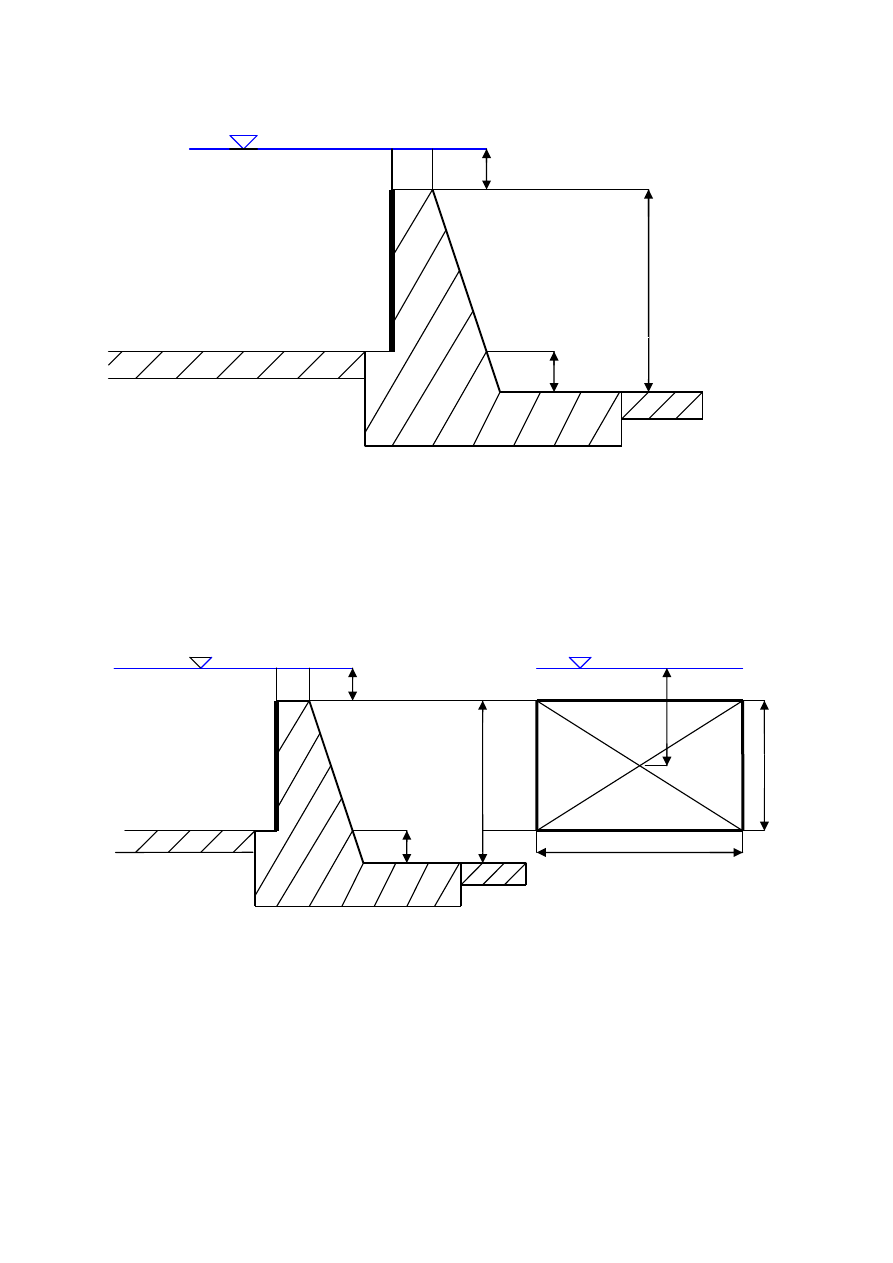
Parcie hydrostatyczne na ściankę EC możemy obliczyć dwoma metodami.
Metoda 1:
Rys. 3. Schemat do metody 1
s
h
F
P
γ
=
Zagłębienie środka ciężkości ścianki na którą działa parcie
h
s
. Słowo zagłębienie niesie w
sobie informacje, że chodzi o odległość punktu znajdującego się pod powierzchnią wody a
odległość ta liczona jest w pionie do zwierciadła (może też być pozorne zwierciadło wody).
E
C
H
1
=2m
H=6m
c=0,4m
e=12m
Środek ciężkość figur symetrycznych znajduje się na przecięciu środków boków lub
dwusiecznych kątów. W przypadku ścianek niesymetrycznych można korzystać z momentów
bezwładności.
W naszym przypadku (Rys. 3)
- zagłębienie środka ciężkości ścianki
)
(
2
1
1
c
H
H
h
s
−
+
=
- pole powierzchni ścianki
e
c
H
F
)
(
−
=
Po podstawieniu do wzoru otrzymujemy
)]
(
[
)
(
2
1
1
c
H
H
e
c
H
P
w
−
+
−
=
γ
Wartość wypadkowej parcia wynosi
MN
N
P
16
,
3
31643136
)
6
,
5
2
(
12
6
,
5
9810
2
1
≅
=
⋅
+
⋅
⋅
⋅
=
Metoda 2:
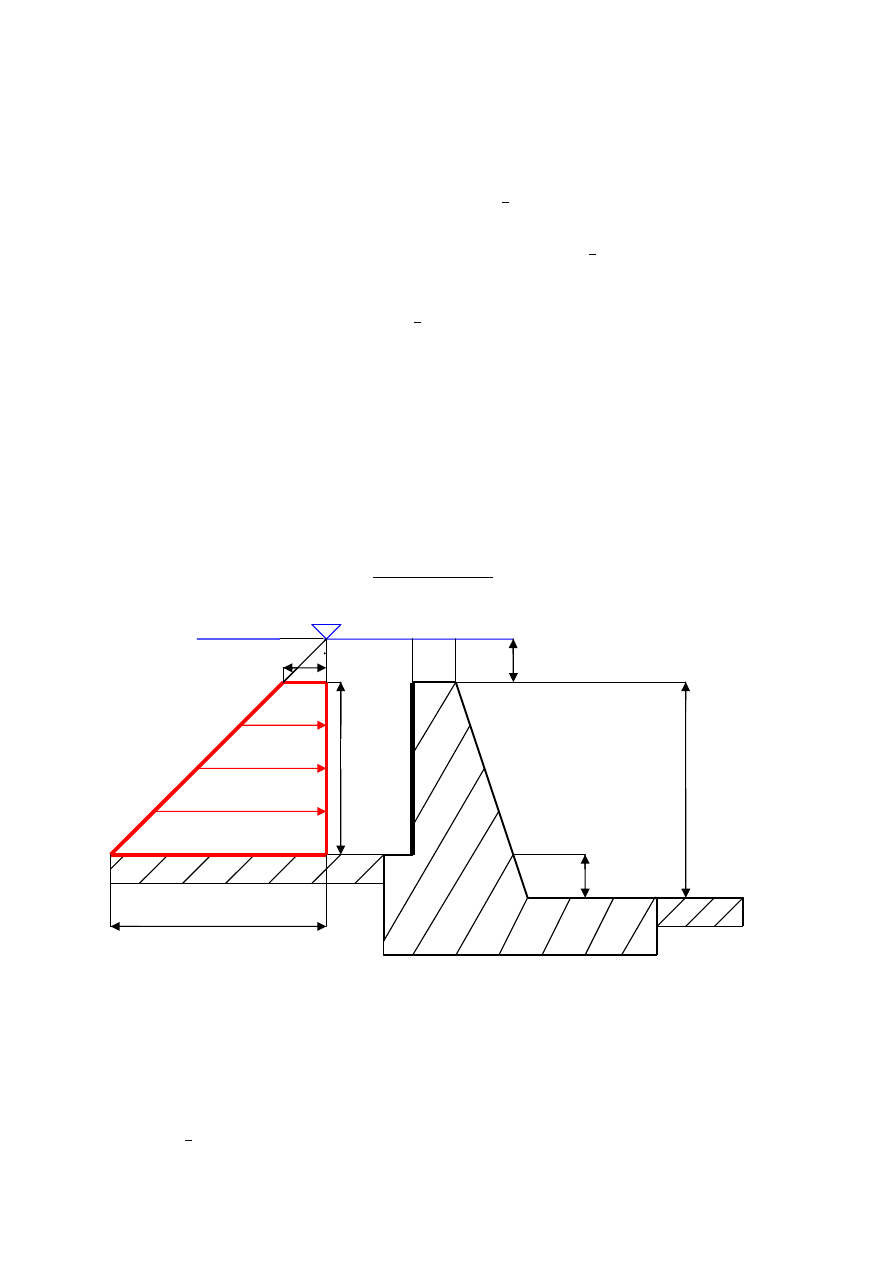
Rozpoczynamy od narysowania wykresu parcia. Wykres parcia na ściankę EC przedstawiono
kolorem czerwonym na Rys.4. Przekrój przez bryłę parcia ma kształt trapezu, którego
wymiary wynoszą:
- długość podstawy
c
H
H
a
−
+
=
1
- długość górnego boku
1
H
b =
- wysokość
c
H
h
−
=
Pole poweirzchni wykresu parcia wynosi zgodnie ze wzorem na pole powierzchni trapezu
)
(
2
1
1
c
H
H
c
H
H
A
−
+
−
+
=
Rys. 4. Wykres parcia na ściankę EC
Po podstawieniu wartości liczbowych otrzymujemy
MN
N
P
16
,
3
31643136
)
4
,
0
6
(
)
2
4
,
0
6
2
(
9810
2
1
≅
=
−
⋅
+
−
+
⋅
⋅
=
E
C
H1=2m
c=0,4m
H
1
+H-c
H-c
H=6m
H
1
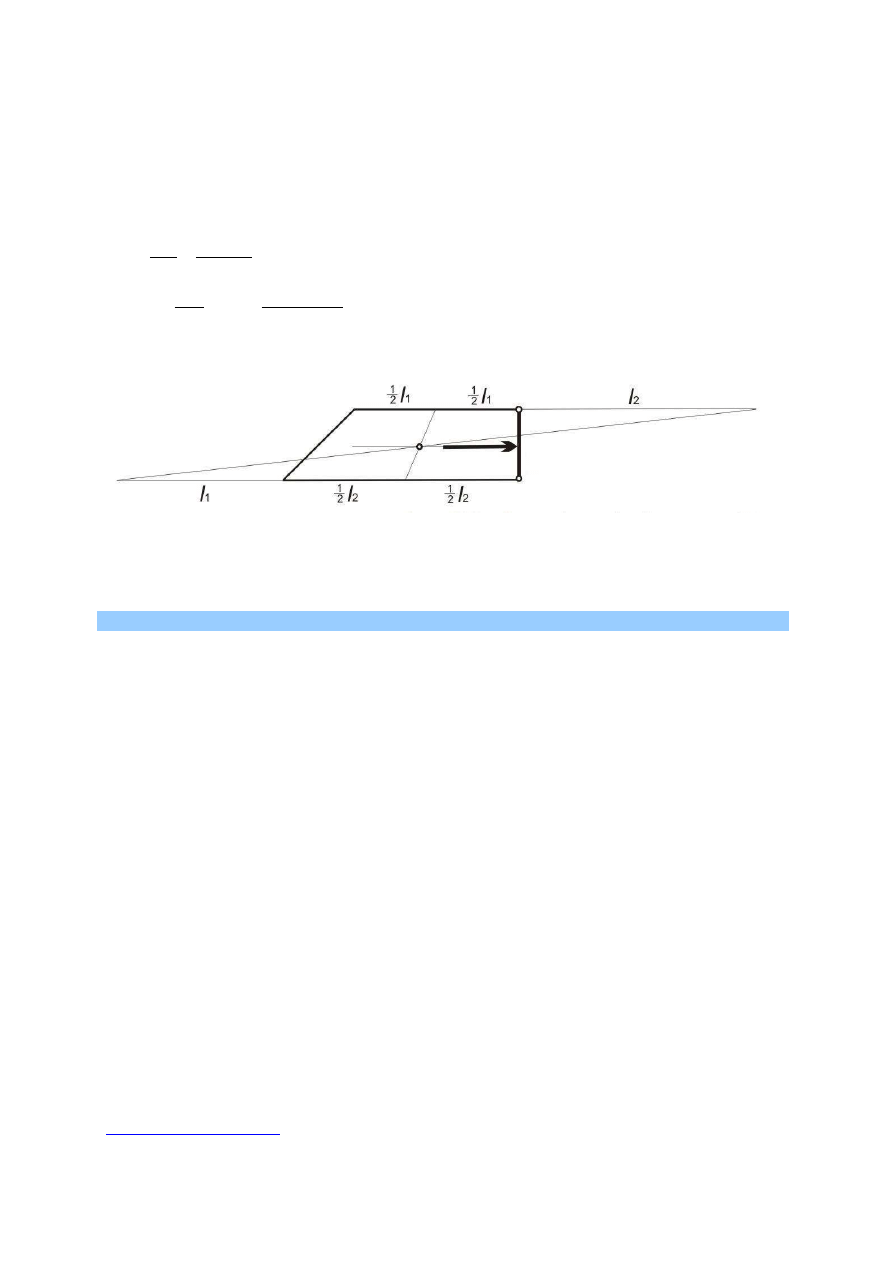
Punkt przyłożenie wypadkowej parcia
Metoda analityczna
Dla ścianki o kształcie prostokąta moment bezwładności względem osi poziomej
przechodzącej przez środek ciężkości:
12
6
,
5
12
12
3
3
⋅
=
=
bh
J
ξ
m
4,85
12
6
,
5
8
,
4
14,635
8
,
4
=
⋅
⋅
+
=
+
=
F
h
J
h
h
s
s
c
ξ
Metoda graficzna
Rys. 3. Kierunek działania wypadkowej parcia
3. Odpowiedź
Wartość parcia hydrostatycznego działającego na ściankę boczną zapory EC wynosi
3,16 MN. Punkt przyłożenie wypadkowej parcia znajduje się na głębokości 4,85 m, w
połowie szerokości ścianki. Parcie działa prostopadle do ściany bocznej zapory.
Literatura:
Kubrak J.,1998, Hydraulika techniczna, Wyd. SGGW, Warszawa,
Podniesiński A., 1958, Zbiór zadań z hydrauliki, PWN, Łódź.
Katedra Inżynierii Wodnej, Wydział Inżynierii Środowiska i Geodezji, Uniwersytet Rolniczy w
Krakowie
rmksiazek@cyf-kr.edu.pl