
Spis treści
8.ZAŁOŻENIA MODELU PŁYTOWEGO – PODAĆ SKŁADOWE NAPRĘŻEŃ .......................................... 5
UWZGLĘDNIENIE TŁUMIENIA? ODPOWIEDŹ ZILUSTRUJ ODPOWIEDNIM ..................................... 11
22.PODAĆ ZAGADNIENIA W KTÓRYCH NALEŻY ZASTOSOWAĆ NIELINIOWĄ ANALIZĘ.................. 11

METODY NUMERYCZNE ROZWIĄZYWANIA RÓWNAŃ NIELINIOWYCH ......................................... 13
36.NARYSUJ EFEKT ZAGĘSZCZENIA SIATKI PRZY UŻYCIU RÓŻNYCH TYPÓW ZAGĘSZCZEŃ ............ 17
1.Metody modelowania konstrukcji inżynierskich
Układy dyskretne – odpowiedź układu może być opisana przez skończoną liczbę zmiennych stanu.
Równania równowagi formułujemy dla poszczególnych stopni swobody. W wyniku przyjętej analizy
opisu otrzymujemy algebraiczny układ równań.
Układy ciągłe – opisujemy przy pomocy równań różniczkowych (lub całkowych). Rozwiązanie
dokładne równań różniczkowych przy zadanych warunkach brzegowych jest możliwe tylko dla
niewielu przypadków szczególnych. Z reguły do rozwiązania zadań praktyki inżynierskiej stosować
musimy procedury numeryczne. Procedury te w istocie swojej wymagają przedstawienia układu
ciągłego za pomocą idealizacji dyskretnej.
2.Podać kroki analizy układów dyskretnych
- idealizacja układu – układ przedstawiamy jako zespół elementów
-równowaga elementów–formułujemy wymagane warunki równowagi poszczególnych elementów w
opisie zmiennych stanu
- składanie elementów – rozpatrujemy oddziaływania pomiędzy elementami w celu ustalenia
(zapisania) układów równań z niewiadomymi zmiennymi stanu
- wyznaczenie odpowiedzi – rozwiązujemy układ równań czyli wyznaczamy nieznane zmienne
opisujące stan układu a następnie obliczamy odpowiedź każdego elementu
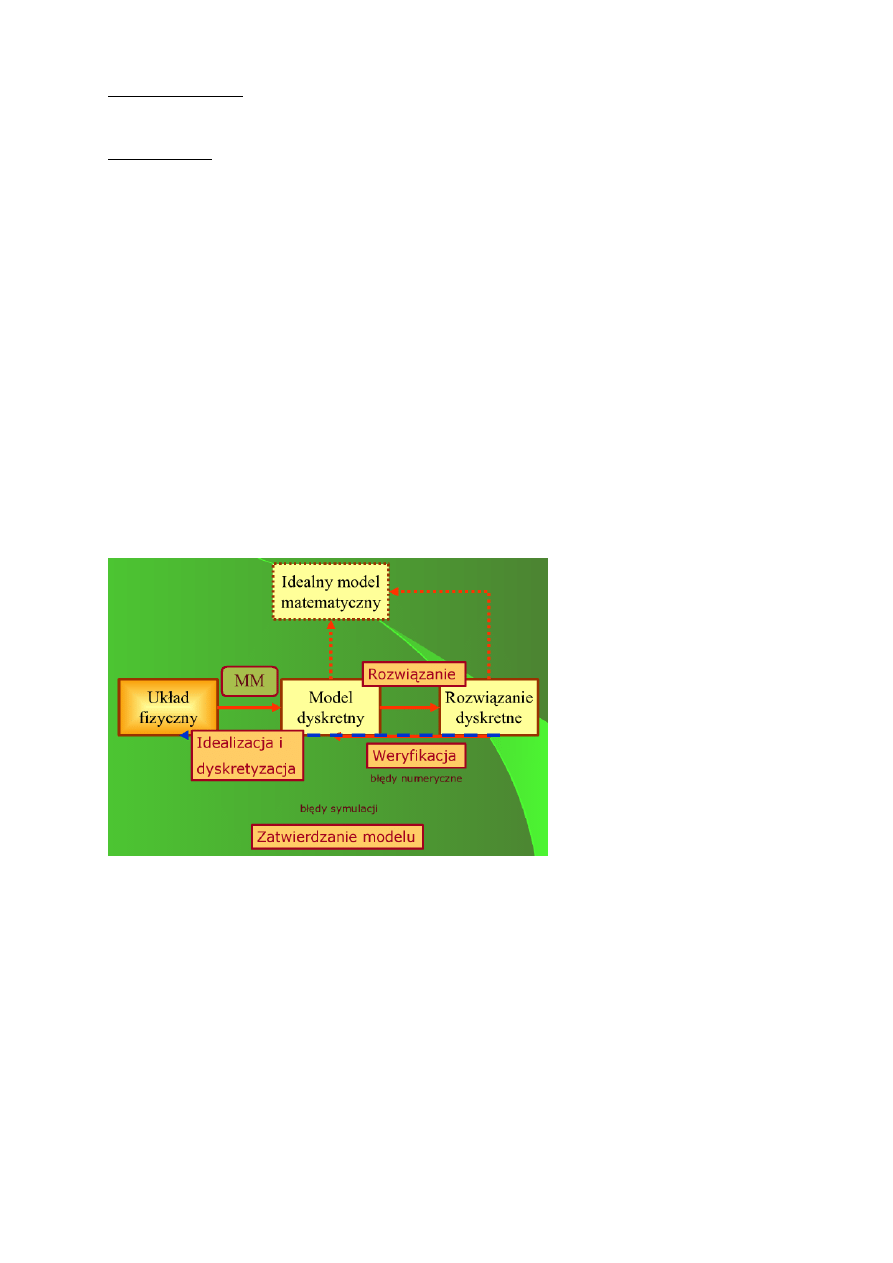
3.Omówić schematy budowy modelu dyskretnego
- schemat z modelu matematycznego
Przyjmujemy dowolny układ fizyczny w którym wykonujemy
idealizacje i dyskretyzacje, po czym za pomocą modeli
matematycznych otrzymujemy układ dyskretny. Po rozwiązaniu
modelu dyskretnego otrzymujemy rozwiązanie dyskretne czyli
idealny model matematyczny
- schemat modelu fizycznego
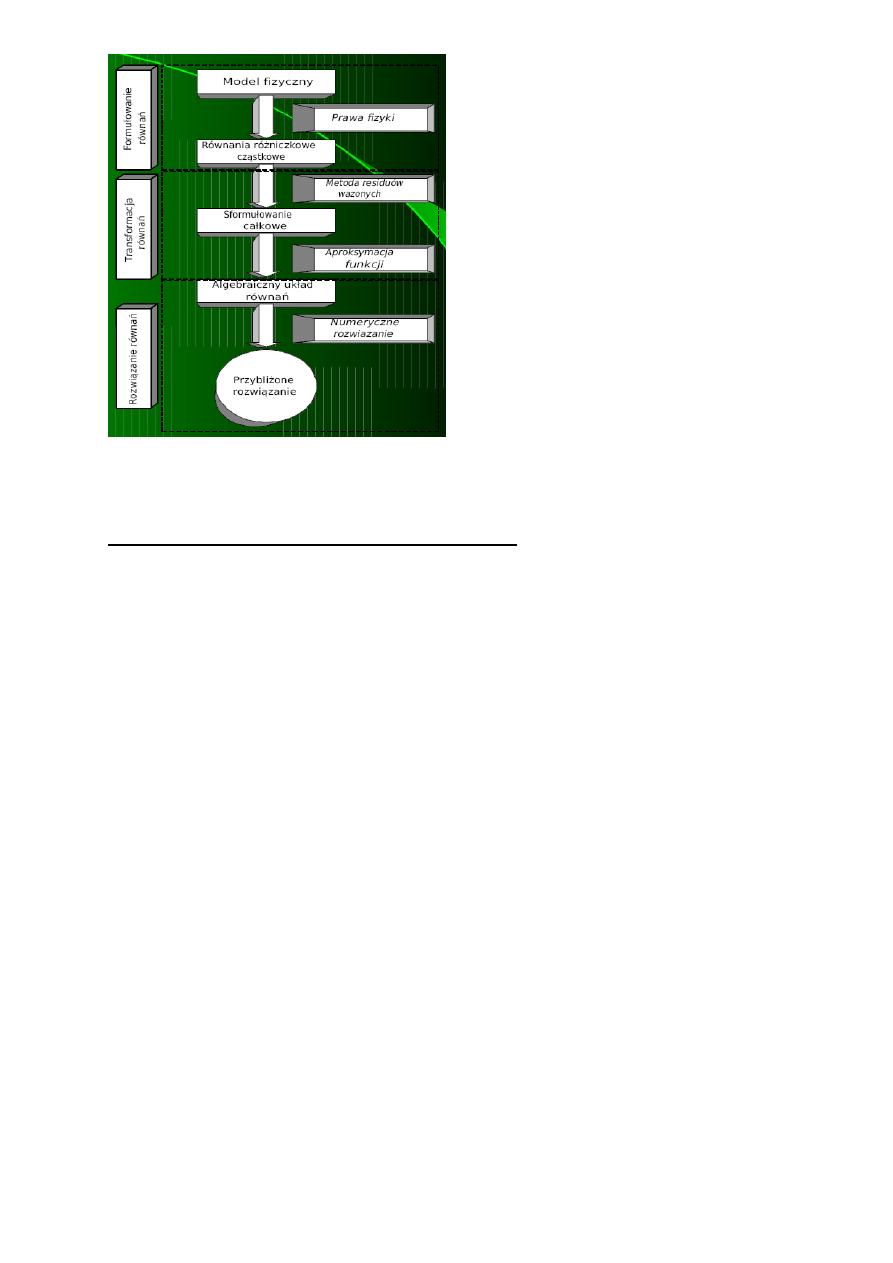
4.Idea metody elementów skończonych
Metoda rozwiązywania układów równań różniczkowych, opierająca się na podziale dziedziny
(dyskretyzacja) na skończone elementy, dla których rozwiązanie jest przybliżane, przez konkretne
funkcje i przeprowadzenie obliczeń tylko dla węzłów tego podziału.
IDEA METODY ELEMENTÓW SKOŃCZONYCH.
Główne założenie MES to podział modelu geometrycznego ciągłego na elementy skończone, łączące
się w tzw. węzłach, czego efektem jest utworzenie modelu geometrycznego dyskretnego. Należy
podkreślić, iż efektem dyskretyzacji jest
transformacja układu o nieskończonej liczbie stopni swobody (zdolności do zmiany wartości
określonej współrzędnej) do postaci układu o skończonej liczbie stopni swobody. Podczas obliczeń z
zastosowaniem MES dyskretyzacji ulegają również wszelkie inne wielkości fizyczne,
reprezentowane w układzie za pomocą funkcji ciągłych (np. obciążenia, utwierdzenia,
przemieszczenia, naprężenia). Podczas dyskretyzacji określonej wielkości fizycznej dąży się do
maksymalnego zbliżenia jej postaci dyskretnej i ciągłej z zastosowaniem metod aproksymujących.
5.Metody modelowania obiektów inżynierskich za pomocą MES
-metoda residuów ważonych-metoda Galerkina (jest ogólną metodą rozwiązywania w sposób
przybliżony zadań)
-funkcjonał wariacyjny problemu-metoda Rayleigha-Ritza (metody wariacyjne mogą być
wyprowadzone zgodnie z zasadą ekstremum (minimum))energii, znana też pod nazwą zasady
najmniejszego (minimum) działania, lub z metodą residuów ważonych.
6.Od czego zależy dokładność MES
Dokładność metody MES jest tym większa, im:
- złożone funkcje dokładniej opisują rzeczywisty rozkład pola elementu
- stopnia wielomianu
- podział na elementy jest bardziej gęsty (ten warunek nie jest wystarczający, kluczowy jest dobór
funkcji kształtu)
Przy właściwym odwzorowaniu wielkości fizycznych elementu, zmniejszenie obszarów elementów
(zwiększenie ich liczby) powoduje, że wartości węzłowe funkcji poszukiwanej, stanowiące
przybliżone rozwiązanie zadania, zbliżają się do rozwiązania dokładnego.
7.Co to są funkcje kształtu
Są to funkcje interpolacyjne opisujące stan odkształcenia w zależności od wartości przemieszczeń
węzłowych.
Maja gwarantować:
- ciągłość wewnątrz elementu
- zgodność na granicy podziału w elementach sąsiednich
- zapewnić możliwość dążenia wartości f-cji rozwiązującej do pewniej stałej
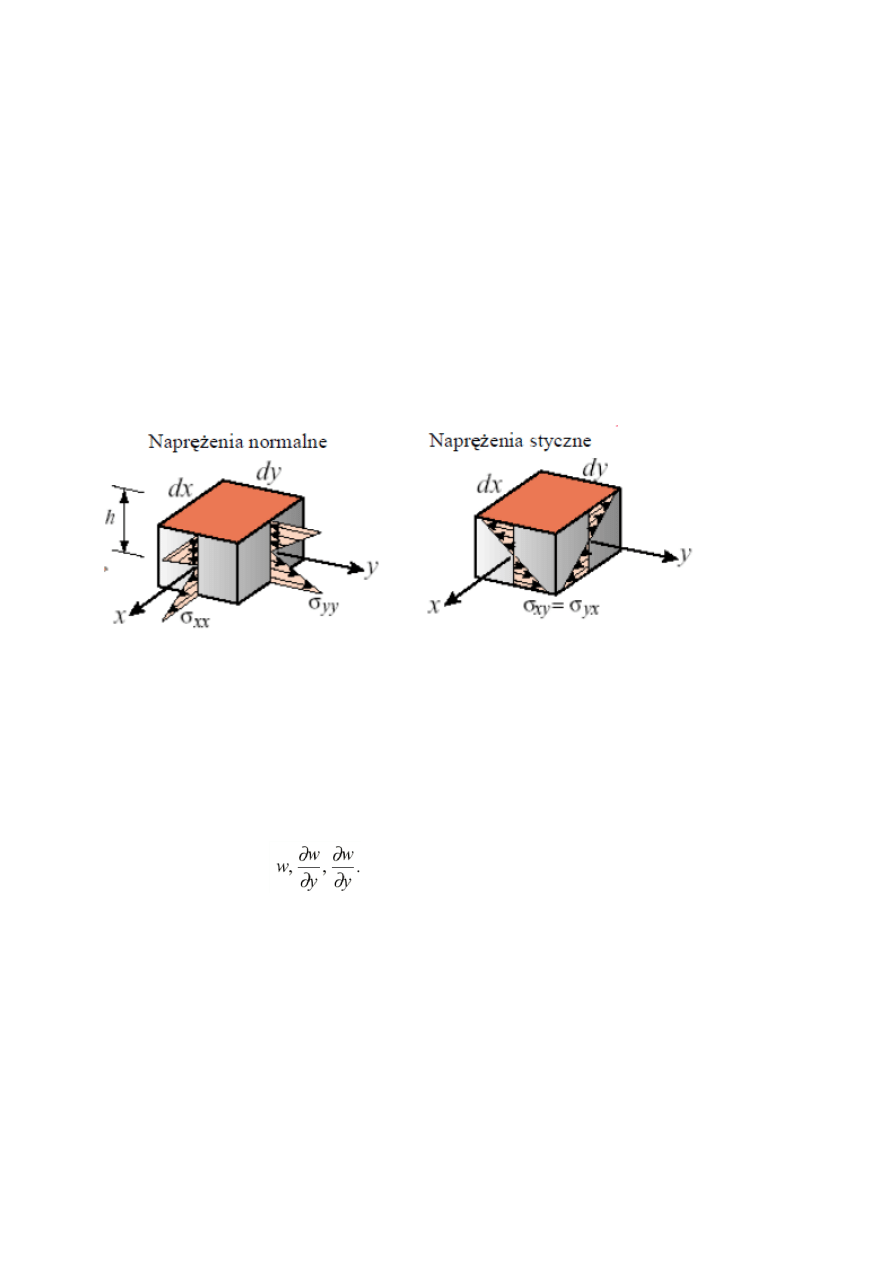
8.ZAŁOŻENIA MODELU PŁYTOWEGO – PODAĆ SKŁADOWE NAPRĘŻEŃ
UOGÓLNIONYCH.
- płaska płaszczyzna
- obciążenie prostopadłe do powierzchni płyty
- dominujący wpływ zginania
- ugięcie płyty jest małe w porównaniu z grubością
- płaszczyzna środkowa zmienia się w powierzchnię środkową bez zmiany długości elementów i
kątów między nimi
Naprężenia uogólnione:
9.Omówić element płytowy
Założenia modelu płyty
Płaska płaszczyzna
Obciążenie prostopadłe do powierzchni płyty
Dominujący wpływ zginania
Ugięcie płyty jest małe w porównaniu z grubością
Płaszczyzna środkowa zamienia się w powierzchnię środkową bez zmiany długości elementów i
kątów miedzy nimi.
Elementy skończone
Element 4-węzłowy
Stopnie swobody w węźle
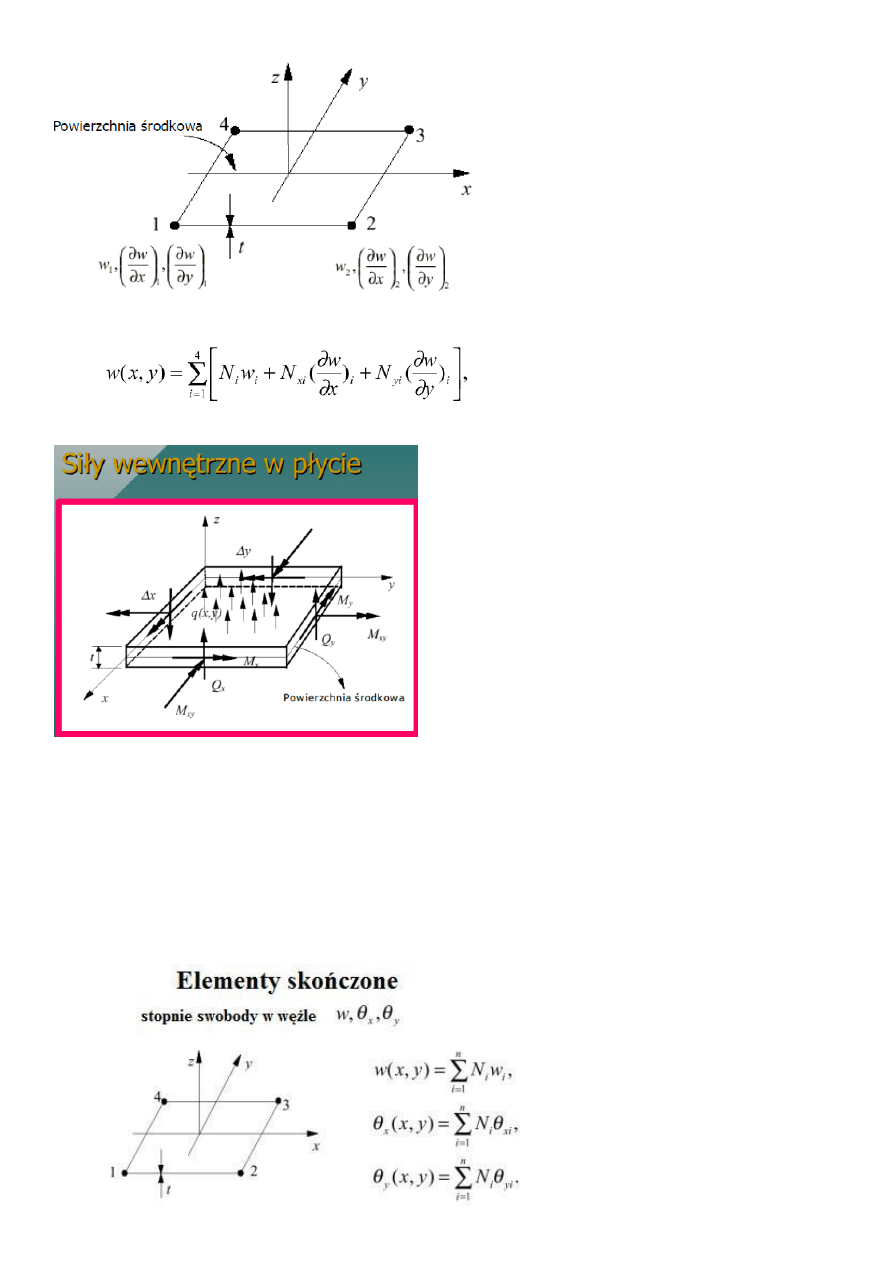
Funkcje kształtu dla elementu:
10.CO OZNACZA TERMIN „PŁYTA ŚREDNIEJ GRUBOŚCI”
Płytą o średniej grubości nazywamy ciało trójwymiarowe, które w stanie nieodkształconym
ograniczone jest dwiema równoległymi płaszczyznami leżącymi blisko siebie i dowolną
powierzchnią w kierunku prostopadłym do tych płaszczyzn. Wymiar grubości tego ciała jest mały w
stosunku do pozostałych wymiarów i wszystkie obciążenia działają prostopadle do płaszczyzny
środkowej.
Teoria płyt średniej grubości (Mindlina): t/L>1/10 . Ta teoria odrzuca hipotezę:
„Proste prostopadłe po płaszczyzny środkowej w nieodkształconej płycie, zostają po jej
odkształceniu proste i prostopadłe do powierzchni środkowej.” Wystąpi więc odkształcenie
postaciowe: γ
xz
≠0, γ
yz
≠0.
11.NA CZYM POLEGA I JAKIE SĄ WARUNKI STOSOWANIA OPCJI REDUKCJI SIŁĄ PRZY PODPORACH
(NAD SŁUPAMI I ŚCIANAMI) PRZY ANALIZIE USTROJÓW PŁYTOWYCH Z WYKORZYSTANIEM
PROGRAMU ROBOT?
Redukcja sił nad słupami i ścianami; jeśli ta opcja jest włączona, to dla elementów płytowych lub
powłokowych, które są podparte punktowo (przy pomocy dostępnych typów podpór lub słupów) lub
liniowo (przy pomocy panela ściany albo podpory liniowej ze zdefiniowanym wymiarem), wartości
momentów i naprężeń w okolicach punktów podparcia zostaną zastąpione średnią wartością z
otoczenia tych podpór/słupów/ścian.
Dla elementów płytowych i powłokowych, które są podparte punktowo lub liniowo (przy pomocy
dostępnych typów podpór, słupów lub ścian) wartości momentów i naprężeń w okolicach punktów
podparcia
mogą być znacznie
większe
niż w
pozostałych
punktach
płyty.
Może
to
powodować wyliczanie niepoprawnych zbrojeń w okolicach podpór i słupów; aby tego uniknąć,
można modelować takie połączenia przy pomocy dostępnych w programie połączeń sztywnych lub
wykorzystać opcję ‘Redukcja sił nad słupami i ścianami’. Redukcja wartości przy podporach polega
na zastąpieniu wartości wynikowych w okolicach podpór, słupów i ścian wartością zredukowaną z
otoczenia tych podpór.
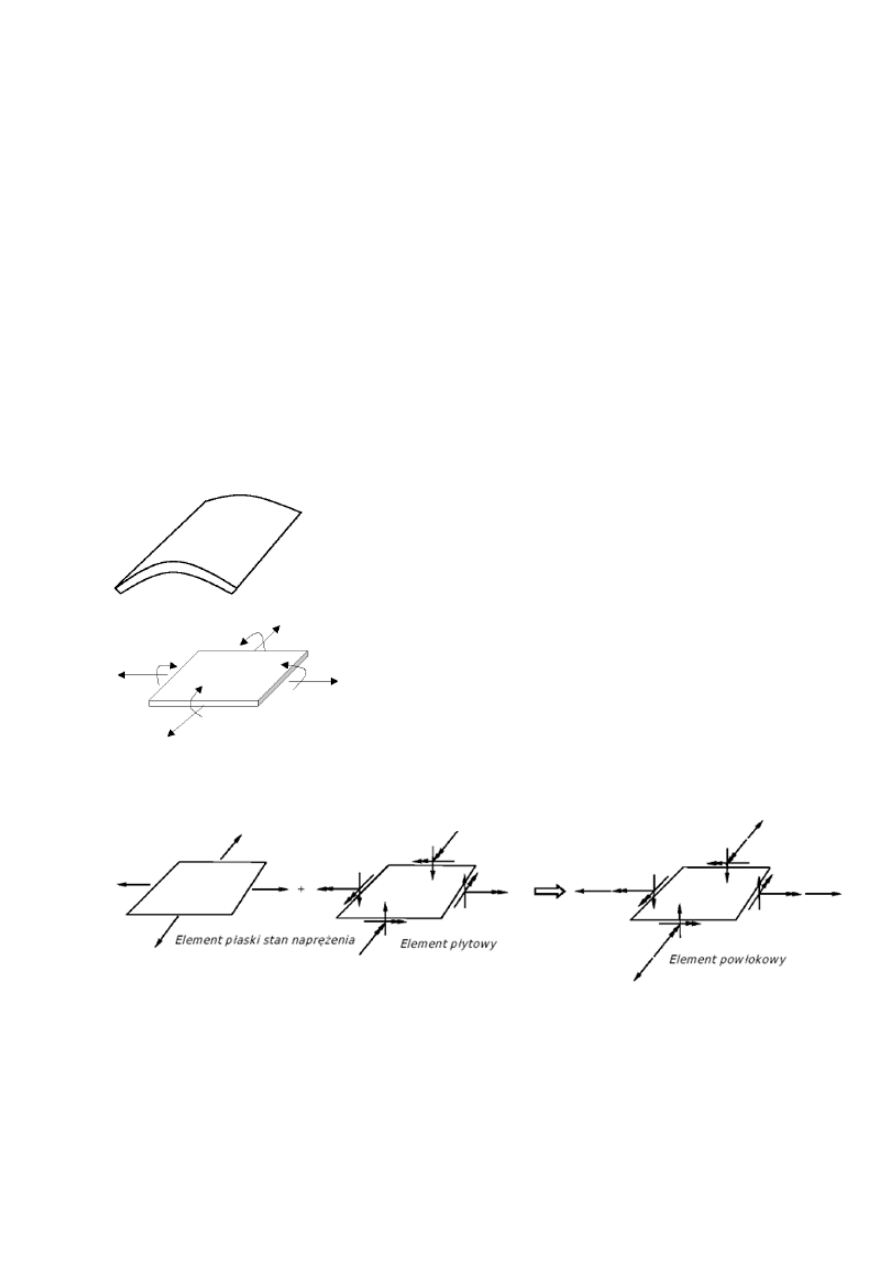
12.Omówić element powłokowy
Powłoka
Występują w niej siły membranowe oraz momentowe
Definicja elementu powłokowego:
Element powłokowy jest złożeniem elementu płytowego i płaskiego stanu naprężenia.
Element powłokowy posiada 6 stopni swobody 3 przesuwy plus 3 obroty względem osi x,y,z.
13.OMÓWIĆ RÓWNANIE RUCHU.
Kinematyczne równanie ruchu ciała jest bardzo wygodną metodą opisu ruchu. Pozwala ono na
proste obliczenie:
równania toru ciała(przez wyeliminowanie z równań parametru czasu t)
prędkości chwilowej ciała (jest ona pierwszą pochodną wektora położenia względem czasu)
przyspieszenia chwilowego ciała (jest ono drugą pochodną wektora położenia względem czasu)
Przykłady prostych równań ruchu

Ruch jednostajny prostoliniowy (x0 – położenie początkowe, v – prędkość)
Ruch prostoliniowy jednostajnie przyspieszony (x0 – położenie początkowe, v0 - prędkość
początkowa, a – przyspieszenie)
Rzut ukośny w górę przy osi OY skierowanej pionowo w górę ((x0,y0) – położenie początkowe, v0 -
prędkość początkowa, α – kąt wyrzucenia)
Ruch harmoniczny (A – amplituda, ω – częstość kołowa, φ0 – faza początkowa)
Ruch po elipsie może być opisany np. równaniami (a, b – długości półosi elipsy)
Gdy a = b jest to ruch po okręgu a ω jest prędkością kątową.
C*q’- Tłumienie; rozproszenie energii (np. podczas wyginania pręta następuje zmiana energii
sprężystej na energię termiczną na skutek tarcia wewnętrznego-energia się „rozchodzi”)
K- siła sprężystości
14.OMÓWIĆ ZAGADNIENIE WŁASNE W DYNAMICE
Zagadnienie własne jest to rozwiązanie liniowego jednorodnego układu równań postaci:
Zagadnienie własne liniowego układu dynamicznego bez tłumienia
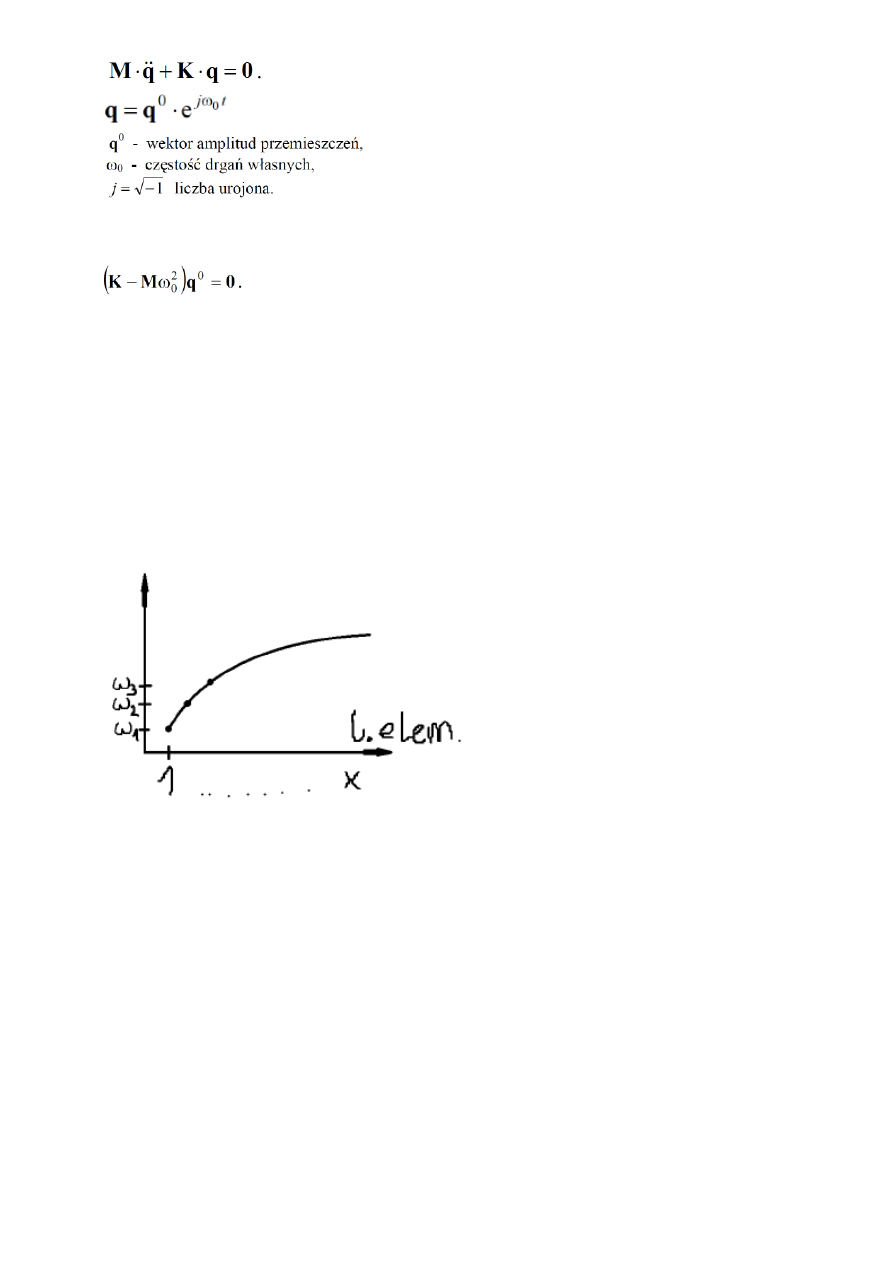
Uogólniony problem własny
Analiza zagadnień własnych opisuje drgania swobodne konstrukcji, rozważa problem rezonansu.
Znajomość form i częstości własnych pozwala na wykonanie analizy modalnej, tzn. rozseparowanie
zagadnienia względem tzw. współrzędnych modalnych. Z widma częstości drgań własnych możemy
wyciągnąć szereg wniosków co do zachowania sił konstrukcji pod wpływem obciążeń o charakterze
harmonicznym.
15.Jaki wpływ na obliczaną pierwszą częstotliwość drgań
własnych ma zwiększenie liczby stopni swobody/zagęszczenie
siatki MES? Odpowiedź zilustruj odpowiednim wykresem.
Wraz z zagęszczaniem siatki MES(dodawaniu stopni swobody). Wartość pierwszej częstotliwości
drgań maleje ponieważ jest to częstotliwość o najniższym poziomie energetycznym najczęściej
pojawiająca się.
16.OD CZEGO ZALEŻY LICZBA MOŻLIWYCH DO OBLICZENIA WARTOŚCI I
POSTACI DRGAŃ WŁASNYCH.
Liczba możliwych postaci zależy od SSD (stopni swobody dynamicznej) – możliwości ruchu mas w
określonych kierunkach.
A wartość zależy od parametrów geometrycznych i fizycznych np. EJ, m
17.JAKIE MODELE MAS MOŻNA STOSOWAĆ W OBLICZENIACH
DYNAMICZNYCH W ROBOCIE?
Masy używane w obliczeniach dynamicznych konstrukcji mogą być definiowane na podstawie:
-Ciężaru własnego konstrukcji
-Ciężaru własnego konstrukcji i skupionych mas dodanych
-Ciężarów pochodzących od sił – użytkownik może zmieniać wszystkie siły zdefiniowane wcześniej
na masy, które mogą być użyte w trakcie prowadzonej dynamicznej analizy konstrukcji. Na
przykład, gdy konstrukcja została obciążona siłami zewnętrznymi (np. ciężarem własnym), ciężary

wyznaczone na podstawie tych sił mogą być brane pod uwagę podczas obliczeń dynamicznych
konstrukcji.
18.Na czym polega całkowanie bezpośrednie równań ruchu.
Termin „całkowanie bezpośrednie” oznacza że równanie to nie jest przekształcane do innej postaci.
Istnieje wiele metod całkowania bezpośredniego równań ruchu, bazują one na następujących
założeniach:
-przedział czasu dzielimy na odcinki Δt, z reguły na odcinki stałe;
-równanie ruchu jest spełnione na granicach tych odcinków, czyli w punktach t=k• Δt (k=1,2,3...)
-zakłada się arbitralnie określoną zmienność przemieszczenia, prędkości i przyspieszenia na odcinku
czasu
Wśród metod jawnych możemy wymienić: metode róznic skończonych, Newmarka, modalną.
Tak dla zrozumienia o co chodzi
W metodach bezpośredniego całkowania równanie ruchu w postaci (9.5) jest całkowane krok po kroku. Termin
"całkowanie bezpośrednie" oznacza, że równanie to nie jest przekształcane do innej po-staci (w odróżnieniu od
metody superpozycji modalnej). Istotą metody całkowania bezpośredniego jest założenie, że równanie ruchu (9.5) ma
być spełnione w wybranych chwilach t, a nie w całym przedziale całkowania oraz założenie o charakterze zmienności
przemieszczeń, prędkości i przyspieszeń pomiędzy tymi chwilami.
19.OMÓW WPŁYW OBCIĄŻENIA NA CZĘSTOTLIWOŚCI WŁASNE
Obciążenia wpływają na charakterystykę modalną obiektu. Generalnie, obciążenia ściskające
zmniejszają częstotliwości rezonansowe, a obciążenia rozciągające zwiększają je. Można to łatwo
zaobserwować zmieniając napięcie struny w skrzypcach. Im wyższe napięcie, tym wyższa
częstotliwość (ton)
20.Podaj i omów trzy rodzaje obliczeń dynamicznych możliwych do przeprowadzenia w programie
ROBOT.
W programie użytkownik może przeprowadzić różne rodzaje obliczeń dynamicznych konstrukcji.
Analiza modalna
Podczas analizy modalnej konstrukcji wyznaczane są wszystkie podstawowe wielkości opisujące
postaci drgań własnych konstrukcji, tzn. wartości własne i wektory własne konstrukcji,
współczynniki udziału oraz masy udziału.
Liczba postaci wyznaczanych w trakcie analizy może być definiowana przez użytkownika lub można
ją określić poprzez podanie zakresu wartości niektórych wielkości opisujących drgania własne
konstrukcji.
Analiza czasowa (całkowanie równań ruchu)
Całkowanie równań ruchu jest to analiza pozwalająca otrzymać odpowiedź konstrukcji w wybranych
punktach czasowych na zadane wymuszenia w czasie (w przeciwieństwie do innych typów analiz
dostępnych w ROBOCIE, które dają odpowiedź w formie amplitud wyłącznie w jednej, ustalonej
chwili).
Istnieje wiele metod całkowania bezpośredniego równań ruchu.
Bazują one na założeniach:
- przedział czasu dzielimy na odcinki Δt – z reguły odcinki stałe
- równanie ruchu jest spełnione na granicach tych odcinków, czyli w punktach
𝑡 = 𝑘 ∙ ∆𝑡 (𝑘 =
1,2,3, … )
-zakłada się arbitralnie określoną zmienność: przemieszczenia, prędkości i przyspieszenia na odcinku
czasu
< (𝑘 − 1) ∙ ∆𝑡, 𝑘 ∙ ∆𝑡 >
Analiza harmoniczna
Użytkownik powinien zdefiniować geometrię konstrukcji i jej obciążenia jak dla przypadku statyki
liniowej. Przyłożone siły są w analizie harmonicznej interpretowane jako amplitudy sił
wymuszających. Ich częstość, kąt fazowy oraz okres są definiowane przez użytkownika.

21.JAKI WPŁYW NA WYNIKI OBLICZEŃ ANALIZY HARMONICZNEJ MA
UWZGLĘDNIENIE TŁUMIENIA? ODPOWIEDŹ ZILUSTRUJ ODPOWIEDNIM
WYKRESEM.
Jeżeli do układu dynamicznego zostaną zastosowane warunki początkowe, to układ drga z coraz
mniejszą amplitudą, aż do zatrzymania. Zjawisko to jest nazywane tłumieniem. Tłumienie jest
zjawiskiem złożonym, które polega na rozpraszaniu energii za pośrednictwem wielu mechanizmów,
jak np. tarcie wewnętrzne i zewnętrzne, efekty termiczne cyklicznego odkształcania materiałów
sprężystych na poziomie mikroskopowym oraz opór powietrza.
22.PODAĆ ZAGADNIENIA W KTÓRYCH NALEŻY ZASTOSOWAĆ NIELINIOWĄ ANALIZĘ.
W strukturach podlegających dużym przemieszczeniom mogą występować znaczne zmiany geometrii
spowodowane deformacjami wywołanymi obciążeniem, które mogą powodować nieliniową reakcję
struktury - bardziej sztywną lub bardziej miękką. Na przykład struktury kablowe generalnie wykazują
wzrost sztywności przy zwiększaniu stosowanych obciążeń, natomiast łuki mogą najpierw
wykazywać zmniejszenie sztywności, po czym wzrost sztywności - zachowanie znane powszechnie
jako wyboczenie z przeskokiem.
Nieliniowe zachowanie materiału może być spowodowane wieloma czynnikami. Zależność relacji
naprężenie-odkształcenie materiału od historii obciążenia (np. w problemach plastyczności), czas
trwania obciążenia (np. a analizie pełzania) oraz temperatura (np. termoplastyczność) to tylko
niektóre spośród tych czynników.
Szczególną klasą problemów nieliniowych jest sytuacja, gdy następuje zmiana natury warunków
brzegowych struktur uczestniczących w analizie podczas ruchu. Sytuacja ta występuje w analizie
problemów kontaktowych.
Uderzanie struktur, kontakt kół zębatych, problemy pasowania, połączenia gwintowe i zderzenia
obiektów to kilka przykładów wymagających oszacowania granic kontaktowych. Oszacowanie granic
kontaktowych (węzłów, linii lub powierzchni) można uzyskać używając elementów przerwy
(kontaktu) pomiędzy węzłami na przylegających granicach.
23.PODSTAWY ANALIZY NIELINIOWEJ.
Przyczyny nieliniowości:
a) geometryczne – wynikające z uwzględnienia konfiguracji początkowej i końcowej, z uwzględnienia
deformacji;
b) fizyczne – ze względu na przyjęty materiał ( nieliniowość stali czy betonu)
c) uwzględnienie tarcia
d) uwzględnienie zmieniających się warunków brzegowych
24.OMÓWIĆ CECHY ANALIZY NIELINIOWEJ.
Cechy nieliniowej analizy
-Zasada superpozycji nie obowiązuje
-Historia obciążenia wpływa na odpowiedź
-Wpływ stanu początkowego konstrukcji
-Analiza dla poszczególnych kroków czasowych
25.TYPY NIELINIOWOŚĆI
Gładkie:
-Nieliniowość geometryczna-Nieliniowość materiałowa
-Obciążenie śledzące
Ostre:
Więzy jednostronne ( punkt materialny może znajdować się na płaszczyżnie lub nad nią, to
płaszczyzna ta będzie stanowiła dla tego punktu więzy jednostronne f(x,y,z)
≥0)

26.NIELINIOWOŚĆ GEOMETRYCZNA
Źródła nieliniowości:
-duże przemieszczenia, duże gradienty przemieszczeń,
-duże odkształcenia.
W przypadku dużych przemieszczeń:
- obciążenie zachowawcze (potencjalne): nie zmienia swojej wielkości i orientacji na wskutek
przemieszczeń konstrukcji,
- obciążenie niezachowawcze (nie konserwatywne): zmienia swoją orientacje w zależności od
przemieszczeń konstrukcji, np. obciążenie śledzące, zawsze prostopadłe do aktualnej powierzchni
ciała
27.NIELINIOWOŚĆ MATERIAŁOWA
Nieliniowości materiałowe
-Plastyczność, uszkodzenie materiału i mechanizmy zniszczenia
-Zależność właściwości materiałów od temperatury, zmiennych stanu oraz zmiennych zależnych od
rozwiązań
28.Podać miary naprężeń i odkształceń
Miary naprężeń:
-Naprężenia fizyczne σ (Cauchy stress)
-Naprężenia nominalne P ( first Piola-Kirchhoff stress)
-Naprężenia drugiego stopnia S (secondo Piola-Kirchhoff stress)
Dla poszczególnych miar:
𝑛 𝜎 𝑑𝛤 = 𝑑𝑓 = 𝑡 𝑑𝛤
𝑛
𝑜
𝑃 𝑑𝛤
0
= 𝑑𝑓 = 𝑡
0
𝑑 𝛤
0
𝑛
𝑜
𝑆 𝑑𝛤
0
= 𝐹
−1
𝑑𝑓 = 𝐹
−1
𝑡
0
𝑑𝛤
0
Miary odkształceń:
-Tensor odkształceń inżynierskich P
𝑒
0
=
𝑙 − 𝑙
0
𝑙
0
-Tensor odkształceń Greena (Greena- Lagrangea) E
𝜀 =
1
2
∗ (
𝑙
2
−𝑙
0
2
𝑙
0
2
)
-Tensor odkształceń Almansiego A
𝜀
𝑎𝑙
=
1
2
∗ (
𝑙
2
− 𝑙
0
2
𝑙
2
)
-Tensor odkształceń logarytmicznych
𝑒
𝑥
= ∫
𝑑𝑙
𝑙
0
= ln
𝑙
𝑙
0
= ln (𝜆
𝑥
)
𝑙
𝑙
0
Naprężenie - odkształcenie
29.Co to są równania konstytutywne
Równania konstytutywne są związkami materiałowymi, definiujące materiał.
W procesach(zagadnieniach) mechanicznych takimi związkami są zależności pomiędzy tensorem
naprężenia a miarami deformacji(odkształcenia). W szczególności prawo Hooke’a jest związkiem
konstytuowanym ciał liniowo sprężystych.
Ogólna charakterystyka równań konstytuowanych:
-nie wynikają z ogólnych zasad, zachowania termodynamiki,
-mają charakter postulatywny
-nie ma uniwersalnych zasad konstruowania równań konstytutywnych
teoria równań konstytutywnych jest w ciągłym rozwoju i jest uzupełniana w miarę rozwoju inżynierii
materiałowej oraz bazy doświadczalnej.
Równania konstytutywne:
-Prawo Hooke’aσ=Eε
-Prawo Clapeyrona p=Rρθ
-Prawo dla naprężeń dyssypacyjnych(ciecz Newtona)
𝛕
𝐢𝐣=𝛍𝐕
𝐢;𝐣
30.ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH
METODY NUMERYCZNE ROZWIĄZYWANIA RÓWNAŃ NIELINIOWYCH
1. Metoda Bisekcji
2. Metoda „Regula falsi”
3. Metoda Siecznych
4. Metoda kolejnych przybliżeń
5. Metoda Stycznych (Newtona)

31.OMÓWIC ZAGADNIENIE PLASTYCZNOŚCI.
Plastyczność - zdolność do ulegania nieodwracalnym odkształceniom powstającym na skutek
działania na ciało stałych naprężeń mechanicznych, przekraczających zakres, w którym jest
ono zdolne do odkształceń sprężystych i jednocześnie na tyle małe, że nie powodują
zniszczenia ciągłości jego struktury. Naprężenie przy którym rozpoczyna się proces
plastyczny nazywane jest granicą plastyczności.
Dla złożonego stanu naprężenia niezbędne jest kryterium uplastycznienia (umożliwia
określenie czy materiał przekroczył granicę plastyczności). Geometrycznym przedstawieniem
opisującego kryterium uplastycznienia jest powierzchnia plastyczności. Najczęściej
stosowane warunki określające kryterium uplastycznienia:
-Tresca (
𝐹 = 2𝜎𝑐𝑜𝑠𝜑 − 𝑌(𝜅) = 0)
-Hubera–von Mises
-Mohr-Coulomb
-Drucker-Prager
Rys. Powierzchnie plastyczności
32.Co to jest ścieżka równowagi
Ścieżka równowagi – krzywa obrazująca model zachowania konstrukcji ( do stanu utraty
stateczności)
Przykłady ścieżek równowagi:
W teorii stateczności wyróżnia się dwa typy utraty stateczności (czyli obciążeń wywołujących te
stany: utrata stateczności przez osiągnięcie punktu granicznego (maksimum obciążenia) i utrata
stateczności przez wyboczenie bi-furkacyjne.
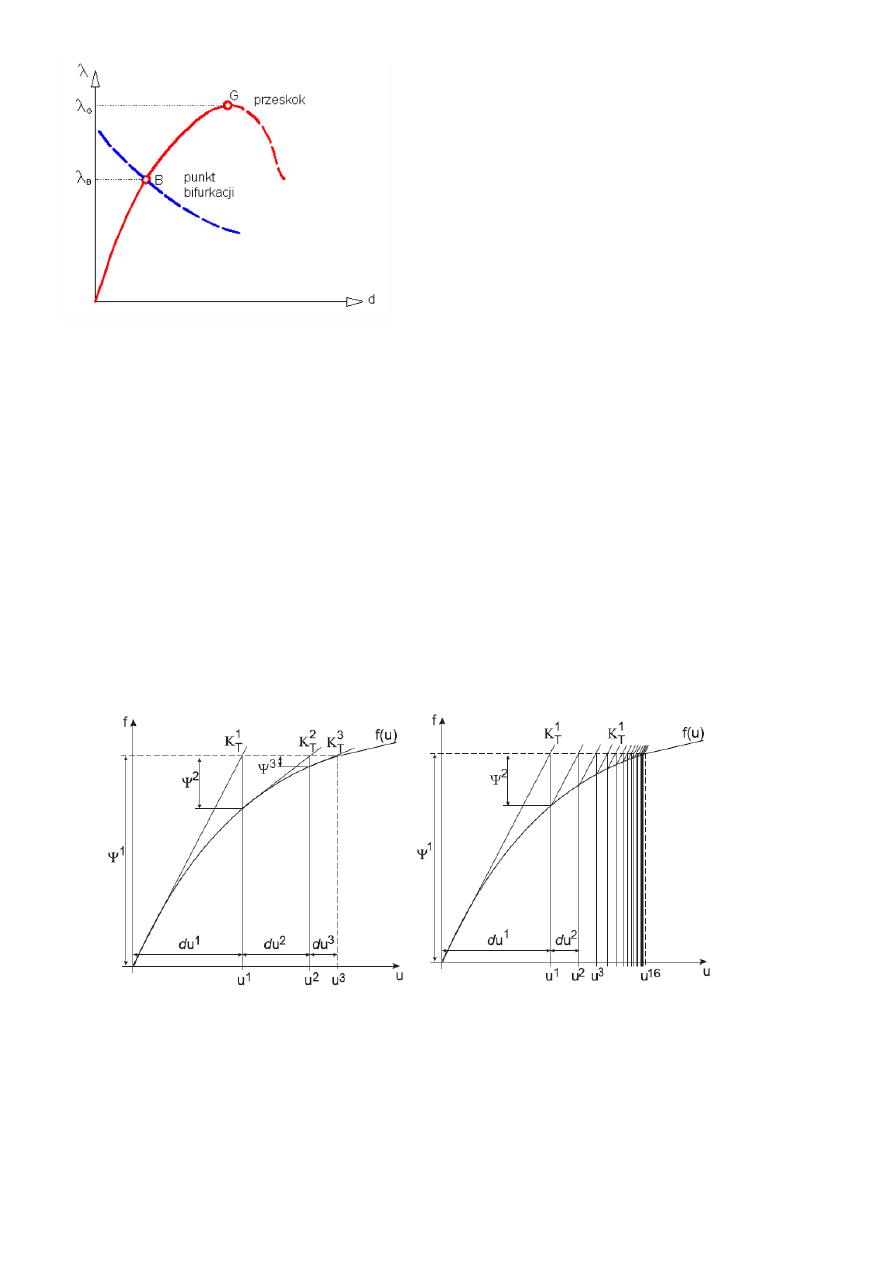
33.METODY ROZWIĄZYWANIA RÓWNAŃ NIELINIOWYCH.
- metoda Newtona-Raphsona
- zmodyfikowana metoda Newtona-Raphsona
- metoda Quasi-Newton
34.PODAĆ RÓŻNICE MIĘDZY METODĄ NEWTONA-RAPHSONA, ZMODYFIKOWANĄ METODĄ
NEWTONA-RAPHSONA A QUASI-NEWTONA.
Metoda Newtona – Raphsona
Dla typowych zadań jest metodą najszybciej zbieżną przy spełnieniu warunków :
– właściwie dobrany punkt początkowy (startu)
– macierz styczna nie jest osobliwa w obszarze iteracji
Rozwiązanie przykładowego zadania jednowymiarowego metodą
Newtona-Raphsona (na lewo)
Rozwiązanie przykładowego zadania jednowymiarowego modyfikowaną metodą Newtona-Raphsona
(na prawo)
Metoda modyfikowana Newtona-Raphsona jest zazwyczaj szybsza od metody
Newtona-Raphsona bez modyfikacji.
Metoda Quasi-Newtona - algorytm:
– start jak dla metody NR,
– dla kolejnych punktów iteracyjnych wyznacza się macierz lokalnie sieczną
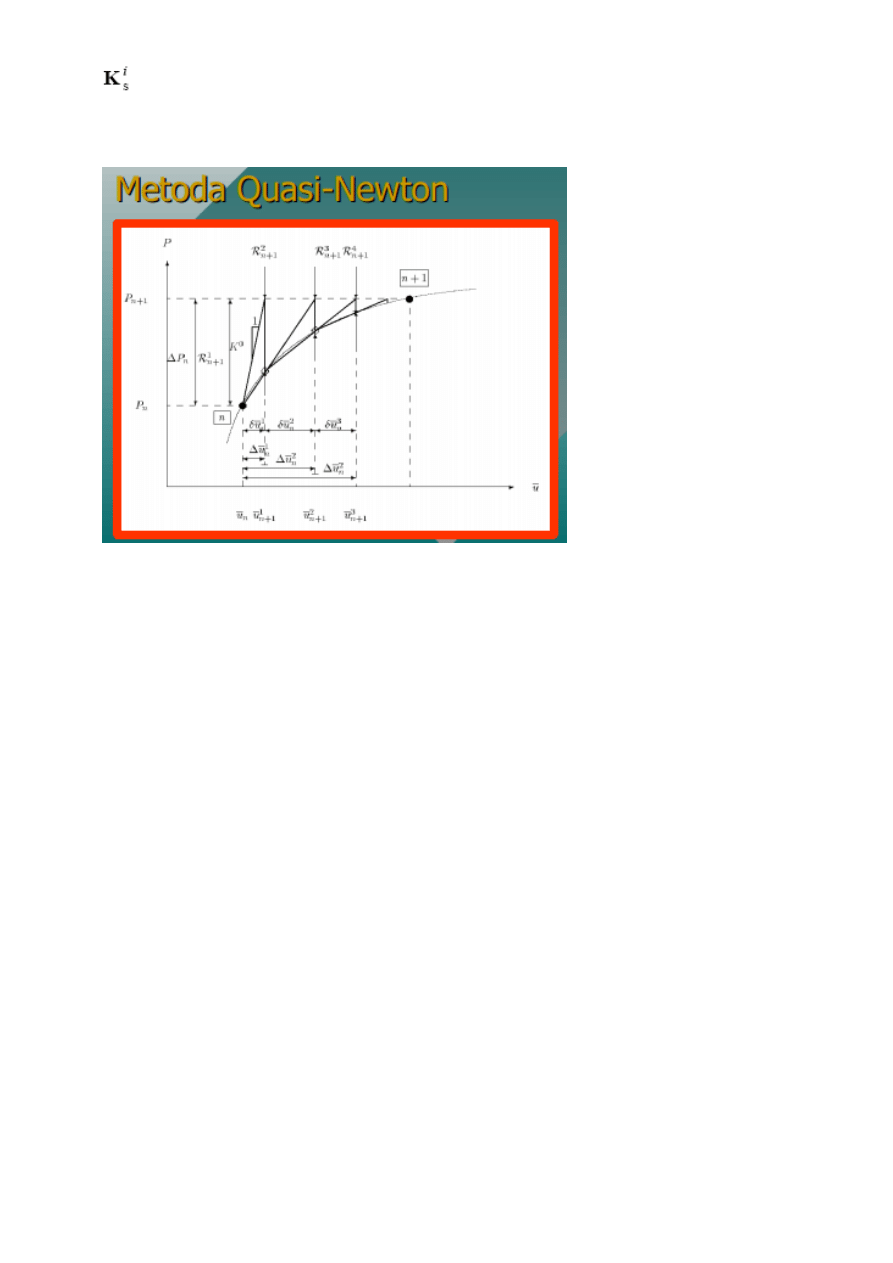
Metoda Quasi-Newtona może być używana, gdy obliczenie Hessianu (macierzy drugich pochodnych
funkcji) wymaganego przez metodę Newtona jest trudne lub czasochłonne. Idea metody polega na
przybliżeniu Hessianu lub jego odwrotności za pomocą pierwszych pochodnych.
35.Metody rozwiązywania zadań dynamiki.
- Zagadnienia dynamiczne liniowe (drgania liniowe) M,C,K są to stałe niezależne od
q ,q
- Zagadnienia dynamiczne liniowe (drgania liniowe parametryczne)
M(t),C(t),K(t) są jawnymi funkcjami czasu, niezależne od
q ,q
-Zagadnienia nieliniowe-drgania nieliniowe M,C,K zależą od czasu t,
q ,q
- Zagadnienie własne
b=0
-Normowanie wektora własnego
-Metoda Rayleigha-Ritza
)
,
,
(
)
,
(
)
,
,
(
)
,
,
(
t
q
q
b
q
t
q
q
K
q
t
q
q
C
q
t
q
q
M
0
q
K
q
C
q
M
)
(t
b
q
K
q
C
q
M
)
(
)
(
)
(
)
(
t
b
q
t
K
q
t
C
q
t
M
- Zagadnienia dynamiczne nieustalone:
Problem rozwiązania równania:
Mamy dwa sposoby rozwiązania:
-poprzez całkowanie numeryczne
-poprzez analizę modalną
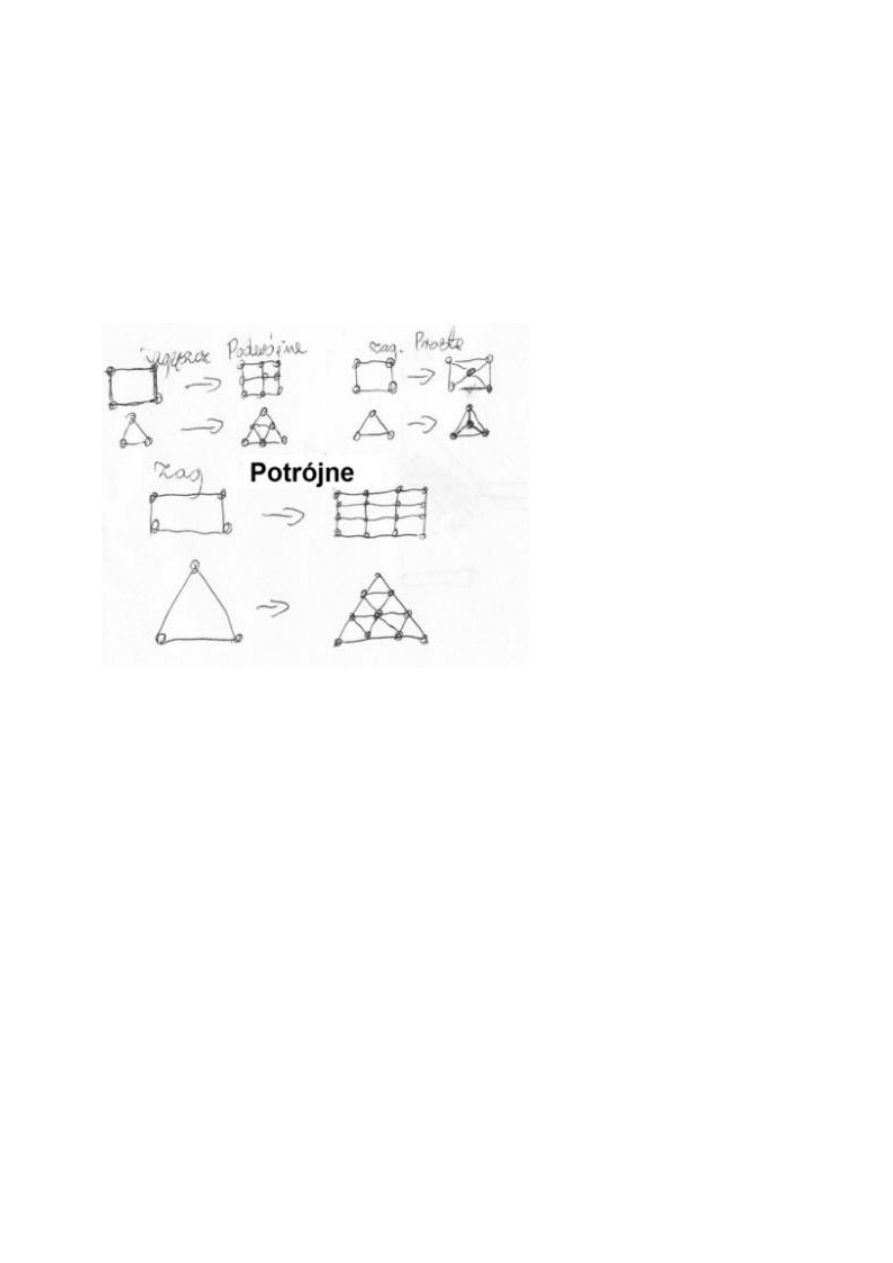
36.NARYSUJ EFEKT ZAGĘSZCZENIA SIATKI PRZY UŻYCIU RÓŻNYCH TYPÓW ZAGĘSZCZEŃ
b
q
K
q
C
q
M

Wyszukiwarka
Podobne podstrony:
METODY KOMPUTEROWE W MECHANICE 2
Metody komputerowe w inzynierii materiałowej 6
Metody Komputerowe i Numeryczne, Równania różniczkowe zwyczajne
Metody Komputerowe i Numeryczne, Równania nieliniowe
Metody komputerowe wykład 1
Metody Komputerowe, K-tar.wyn, ELEMENT NR 41
Metody Komputerowe, TARCZA.DAT
Metody komputerowe w inzynierii materiałowej 8
Metody komputerowe wykład 2
Metody Komputerowe i Numeryczne, Aproksymacja
Metody komputerowe, PAKO
ćwiczenie nr 2, Ćwiczenie nr 2 - Metody komputerowe w Inżynierii Materiałowej
Metody Komputerowe, Kub-tarcza.wyn, ELEMENT NR 41
METODY KOMPUTEROWE teoria (2)
więcej podobnych podstron