Aproksymacją nazywamy dział metod numerycznych służących do przybliżenia

wielkości dokładnej, inną wielkością, która poprawnie opisuje wielkość aproksymowaną.

Najczęściej wielkością aproksymowaną jest zbiór punktów opisujących zależność

funkcyjną, które zostały uzyskane z pomiarów pewnej wielkości fizycznej np. I (V). W
wyniku aproksymacji zostaje uzyskana prosta zależność analityczna.

Aproksymacja jest również narzędziem statystycznym służącym do wykluczania

wyników pomiarów obarczonych dużym błędem lub wykluczania funkcji danej wielkości
wokół wartości średniej. Przykładem zastosowania aproksymacji do wykluczania fluktuacji
jest opis za pomocą prostej zależności analitycznej zbioru punktów opisujących notowania
walorów na giełdzie papierów wartościowych.

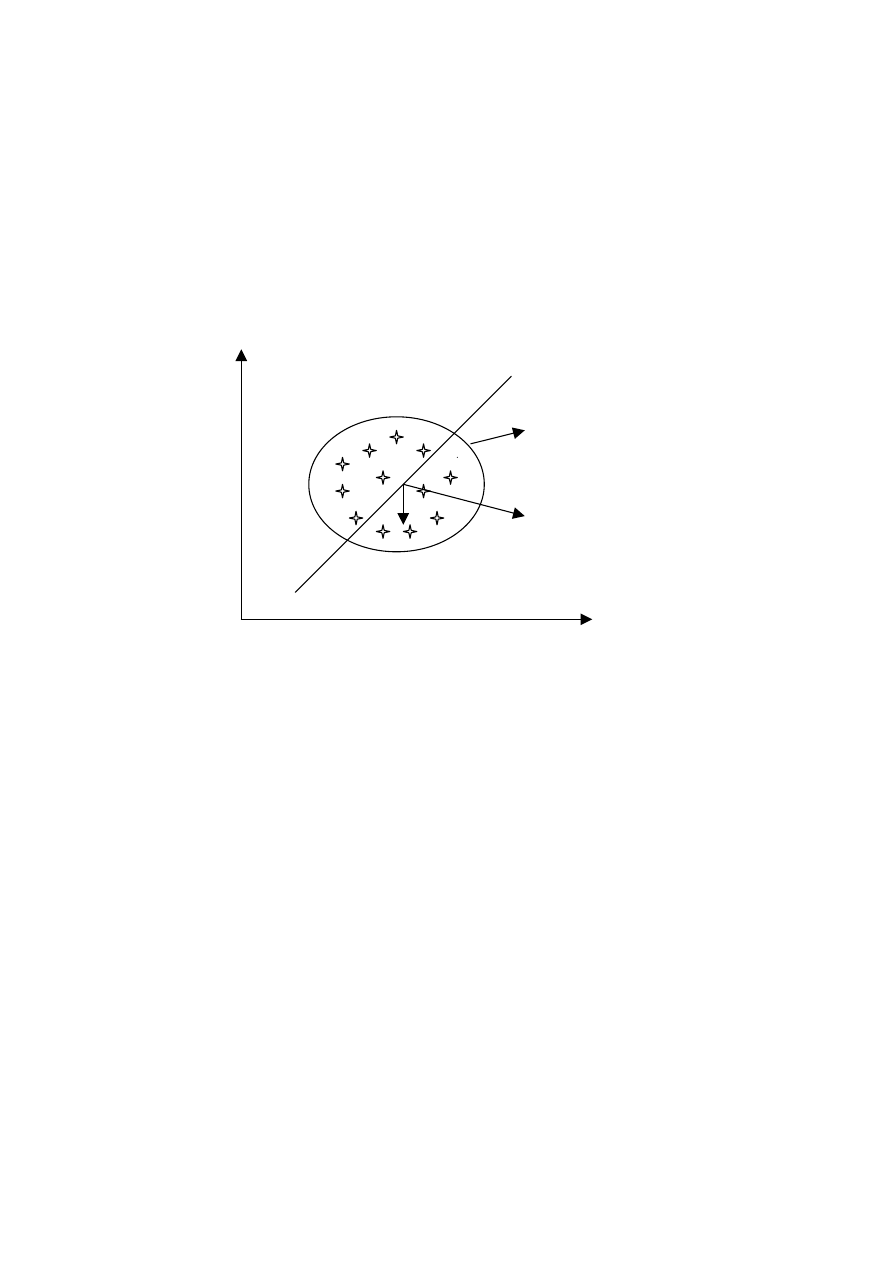
y = f(x) – funkcja aproksymująca

zbiór

)

,

(

y

x

m

i

i

dla i=1,...,n wielkość

aproksymowana

odległość pomiędzy punktem
pomiarowym i punktem
aproksymującym

Rys. 1 Wykres przedstawiający aproksymację zbioru punktów

(x , y ) dla i=1, ..., n funkcja y = f(x)

Istotnym zagadnieniem jest dobór prostej relacji analitycznej służącej do aproksymacji,
która jednocześnie dobrze opisuje punkty. Funkcje służące do aproksymacji powinny być
dobierane z grona prostych funkcji elementarnych lub ich kombinacji. W zależności od
zastosowanej funkcji aproksymującej mówi się o aproksymacji liniowej, kwadratowej lub na
przykład wykładniczej. Kwestia doboru funkcji aproksymującej powinna być oparta o analizę
rozkładu aproksymowanych punktów.

W drugim etapie należy zidentyfikować wartości współczynników występujących w

aproksymowanej funkcji, tak aby zminimalizować odległości pomiędzy punktami
pomiarowymi i punktami, które je aproksymują. Identyfikacja wartości współczynników
następuje poprzez minimalizację funkcjonatu błędu, określanego jako odległości pomiędzy
wartościami funkcji aproksymującej )

(

x

y

i

c

i

f

=

, a wartościami zmierzonymi 

y

m

i

dla i=1,...,n

gdzie n oznacza liczby pomiarów.

2

1

]

[

y

y

m

i

n

i

c

i

S

−

=

∑

=

 (1)

Przykład. Aproksymacja zbioru punktów pomiarowych 

)

,

(

y

x

i

i

 przy pomocy wielomianu

drugiego stopnia.

Funkcja aproksymująca :

=

)

(

2

x

w

a

x

a

x

a

0

1

1

2

2

+

+

(2)

Należy zidentyfikować wartości współczynników 

a

a

a

2

1

0

,

,

. W tym celu należy

zminimalizować funkcjonat błędu otrzymany poprzez podstawienie wielomianu (2) do
równania (1) za 

y

c

i

  .

2

0

1

1

2

1

2

)

(

y

a

x

a

x

a

m

i

n

i

S

−

+

+

=

∑

=

(3)

Funkcjonat może być traktowany jako funkcja trzech zmiennych 

).

,

,

(

2

1

0

a

a

a

S

Warunkiem

koniecznym I wystarczającym, aby funkcja osiągnęła minimum jest wyznaczenie miejsca
zerowego pochodnych cząstkowych funkcjonatu względem współczynników 

a

a

a

2

1

0

,

,

.

     

0

0

=

∂

∂

a

S

   ,                   

0

1

=

∂

∂

a

S

        ,               

0

2

=

∂

∂

a

S

        (4)

gdzie :

 

0

)

(

2

0

1

1

2

2

0

=

−

+

+

=

∂

∂

∑

=

y

a

x

a

x

a

x

a

i

i

n

i

i

i

S

=

∂

∂

a

S

1

0

)

(

2

0

1

1

2

2

=

−

+

+

∑

=

y

a

x

a

x

a

x

i

i

n

i

i

i

 (5)

=

∂

∂

a

S

2

0

)

(

2

0

1

1

2

2

=

−

+

+

∑

=

y

a

x

a

x

a

x

i

i

n

i

i

i

Problem wyznaczania wartości współczynników równania aproksymującego sprowadza się
do rozwiązania układu równań (5), które można zapisać w postaci macierzowej.





































=

























































∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

=

=

=

=

=

=

=

=

=

=

=

=

n

i

i

i

n

i

i

i

n

i

i

n

i

i

n

i

i

n

i

i

n

i

i

n

i

i

n

i

i

i

i

n

i

i

n

i

y

x

y

x

y

a

a

a

x

x

x

x

x

x

x

x

1

2

1

1

2

1

0

1

4

1

3

1

2

1

3

1

2

1

1

2

1

1

1

 

(6)