RÓŻNICZKOWANIE NUMERYCZNE

Podstawą wielu algorytmów rozwiązania równań różniczkowych zwyczajnych i

równań różniczkowych cząstkowych jest wyrażenie wartości pochodnej lub pochodnych
cząstkowych dla pewnego interesującego nas punktu przy pomocy wzorów pozwalających na
uzyskanie przybliżonej wartości. Wzory te zwane ilorazami różnicowymi wykorzystują
wartości funkcji podstawowej w kilku punktach wybranych z otoczenia tego punktu dla
którego jest wyznaczana pochodna .Najprostsze wzory tego typu można uzyskać przy
pomocy szeregu Taylora. Wzory bardziej zaawansowane można uzyskać poprzez
wprowadzenie wielomianu interpolacyjnego opartego na kilku punktach, poddanego w
dalszej kolejności operacji różniczkowania.

Wprowadźmy następujące oznaczenia:
h = x

i+1

-x

i

krok

y

i

= f(x

i

) wartość funkcji f w punkcie x

i

y’

i

= f

’

(x

i

)

wartość pochodnej funkcji f w punkcie x

i

i

indeks numerujący kolejne wartości zmiennych

W oparciu o szereg Teylora można uzyskać proste wzory wykorzystujące wartości funkcji w
dwóch punktach

h

y

y

y

i

i

i

−

=

+1

'

-iloraz różnicowy progresywny (przedni)

(2.1)

Wzór (2.1) można uzyskać przy użyciu rozwinięcia funkcji f w szereg Taylora w otoczeniu
punku x

i

. W szeregu należy opuścić wyrazy wyższego rzędu niż 1.

2

2

"

'

1

h

y

h

y

y

y

i

i

i

i

⋅

+

⋅

+

=

+

+ wyrazy wyższego rzędu

⇒

h

y

y

y

i

i

i

−

=

+1

'

h

y

y

y

i

i

i

1

'

−

−

=

-iloraz różnicowy regresywny (wsteczny)

(2.2)

Wzór (2.2) można uzyskać w podobny sposób jak wzór (2.1)

2

)

(

)

(

2

"

'

1

h

y

h

y

y

y

i

i

i

i

−

⋅

+

−

⋅

+

=

−

+ wyrazy wyższego rzędu

⇒

h

y

y

y

i

i

i

1

'

−

−

=

Wprowadzając do rozważań trzy punkty i odpowiedni wielomian interpolacyjny otrzymano
następujące wzory

h

y

y

y

y

i

i

i

i

2

4

3

2

1

'

+

+

−

+

−

=

-iloraz różnicowy przedni

(2.3)

h

y

y

y

i

i

i

2

1

1

'

+

−

+

−

=

-iloraz różnicowy centralny

(2.4)

h

y

y

y

y

i

i

i

i

2

3

4

1

2

'

+

−

=

−

−

-iloraz różnicowy wsteczny

(2.5)

Wzory (2.3), (2.4), (2.5) można uzyskać wprowadzając trzy punkty (x

0

, y

0

), (x

1

, y

1

), (x

2

, y

2

) i

przeprowadzając przez nie wielomian interpolacyjny Lagrange’a.

x

0

x

1

=x

0

+h

x

2

=x

0

+2h=x

1

+h

Wprowadzenie z wielomianu interpolacyjnego Lagrange’a.

)

)(

(

)

)(

(

)

)(

(

)

)(

(

)

)(

(

)

)(

(

)

(

1

2

0

2

1

0

2

2

1

0

1

2

0

1

2

0

1

0

2

1

0

2

x

x

x

x

x

x

x

x

y

x

x

x

x

x

x

x

x

y

x

x

x

x

x

x

x

x

y

x

L

−

−

−

−

+

−

−

−

−

+

−

−

−

−

=

-h

-2h

h

2h

-h

h

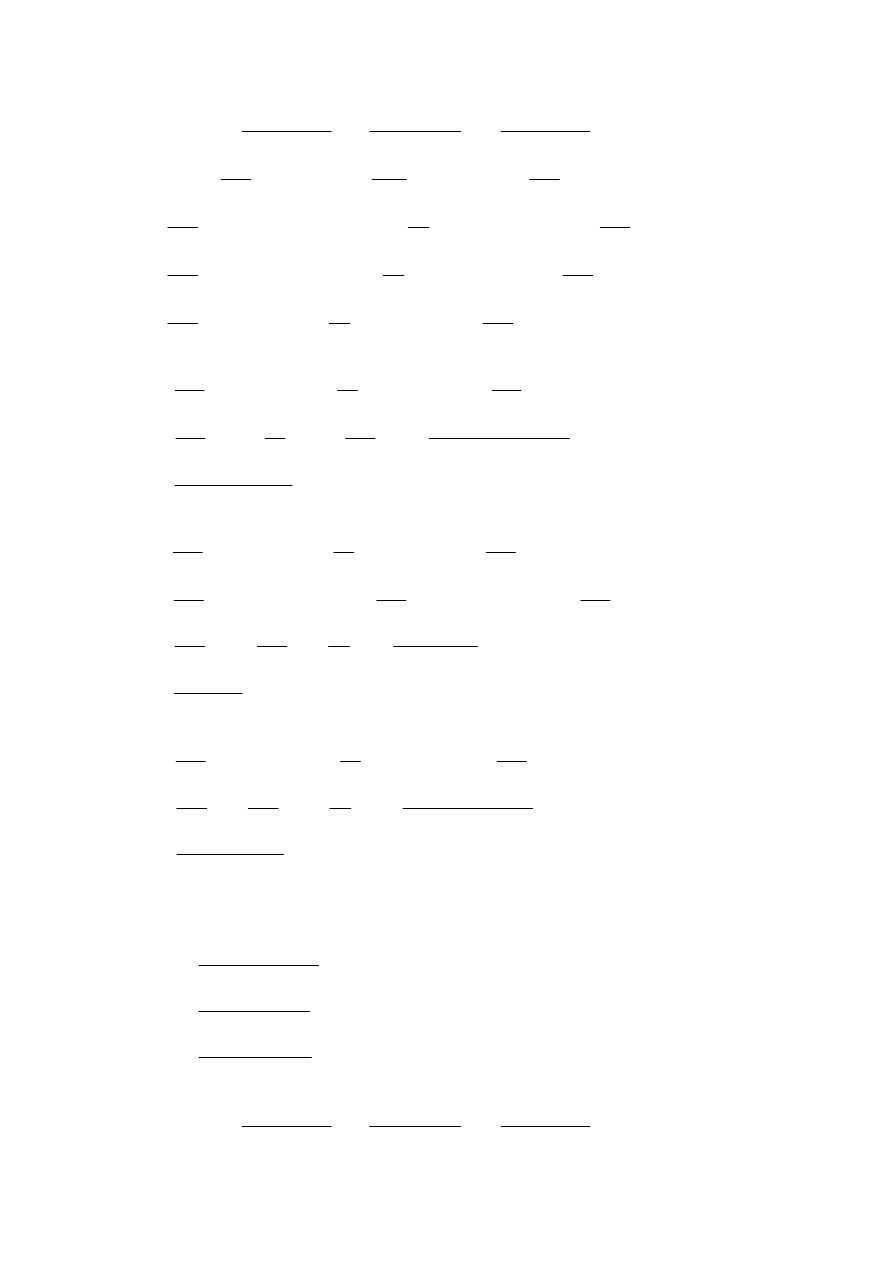
2

1

0

2

2

2

0

1

2

2

1

0

'

2

2

2

2

2

2

)

(

h

x

x

x

y

h

x

x

x

y

h

x

x

x

y

x

L

−

−

+

−

−

−

+

−

−

=

)

2

(

2

)

2

(

)

2

(

2

)

(

1

0

2

2

2

0

2

1

2

1

2

0

'

2

x

x

x

h

y

x

x

x

h

y

x

x

x

h

y

x

L

−

−

+

−

−

−

+

−

−

=

))

(

2

(

2

))

2

(

2

(

))

2

(

)

(

2

(

2

)

(

0

0

2

2

0

0

2

1

0

0

2

0

'

2

h

x

x

x

h

y

h

x

x

x

h

y

h

x

h

x

x

h

y

x

L

+

−

−

+

+

−

−

−

+

−

+

−

=

)

2

(

2

)

2

2

(

)

2

2

(

2

)

(

0

0

2

2

0

0

2

1

0

0

2

0

'

2

h

x

x

x

h

y

h

x

x

x

h

y

h

x

h

x

x

h

y

x

L

−

−

−

+

−

−

−

−

−

−

−

−

=

)

2

2

(

2

)

2

2

2

(

)

3

2

2

(

2

)

(

0

2

2

0

2

1

0

2

0

'

2

h

x

x

h

y

h

x

x

h

y

h

x

x

h

y

x

L

−

−

+

−

−

−

−

−

=

)

2

2

(

2

)

2

2

2

(

)

3

2

2

(

2

)

(

0

0

2

2

0

0

2

1

0

0

2

0

0

'

2

h

x

x

h

y

h

x

x

h

y

h

x

x

h

y

x

L

−

−

+

−

−

−

−

−

=

2

2

1

0

2

2

2

1

2

0

0

'

2

2

4

3

)

(

2

)

2

(

)

3

(

2

)

(

h

hy

hy

hy

h

h

y

h

h

y

h

h

y

x

L

−

+

−

=

−

+

−

−

−

=

h

y

y

y

x

L

2

4

3

)

(

2

1

0

0

'

2

−

+

−

=

progresywny iloraz różnicowy

)

2

2

(

2

)

2

2

2

(

)

3

2

2

(

2

)

(

0

1

2

2

0

1

2

1

0

1

2

0

1

'

2

h

x

x

h

y

h

x

x

h

y

h

x

x

h

y

x

L

−

−

+

−

−

−

−

−

=

)

2

)

(

2

(

2

)

2

2

)

(

2

(

2

2

)

3

2

)

(

2

(

2

)

(

0

0

2

2

0

0

2

1

0

0

2

0

1

'

2

h

x

h

x

h

y

h

x

h

x

h

y

h

x

h

x

h

y

x

L

−

−

+

+

−

−

+

−

−

−

+

=

2

2

0

2

2

1

2

0

1

'

2

2

)

(

2

)

0

(

2

2

)

(

2

)

(

h

hy

hy

h

h

y

h

y

h

h

y

x

L

+

−

=

+

−

−

=

h

y

y

x

L

2

)

(

2

0

1

'

2

+

−

=

centralny iloraz różnicowy

)

2

2

(

2

)

2

2

2

(

)

3

2

2

(

2

)

(

0

2

2

2

0

2

2

1

0

2

2

0

2

'

2

h

x

x

h

y

h

x

x

h

y

h

x

x

h

y

x

L

−

−

+

−

−

−

−

−

=

2

2

1

0

2

2

1

2

0

2

'

2

2

3

4

)

3

(

2

)

2

(

2

2

)

(

2

)

(

h

hy

h

y

hy

h

h

y

h

h

y

h

h

y

x

L

+

−

=

+

−

=

h

y

y

y

x

L

2

3

4

)

(

2

1

0

2

'

2

+

−

=

wsteczny iloraz różnicowy

Wyznaczając drugą pochodną wielomianu Lagrange’a można uzyskać wzory na przybliżoną
wartość drugiej pochodnej .

2

2

1

"

2

h

y

y

y

y

i

i

i

j

+

+

+

−

=

iloraz różnicowy przedni

(2.6)

2

1

1

"

2

h

y

y

y

y

i

i

i

j

+

−

+

−

=

iloraz różnicowy centralny

(2.7)

2

1

2

"

2

h

y

y

y

y

i

i

i

j

+

−

=

−

−

iloraz różnicowy wsteczny

(2.8)

Zatem:

2

1

0

2

2

2

0

1

2

2

1

0

'

2

2

2

2

2

2

)

(

h

x

x

x

y

h

x

x

x

y

h

x

x

x

y

x

L

−

−

+

−

−

−

+

−

−

=

2

2

1

0

2

2

2

1

2

0

"

2

2

2

2

2

2

2

)

(

h

y

y

y

h

y

h

y

h

y

x

L

+

−

=

+

−

+

=

)

(

)

(

)

(

2

"

2

1

"

2

0

"

2

x

L

x

L

x

L

=

=

Wprowadzając do rozważań 5 punktów (x

0

, y

0

), (x

1

, y

1

), (x

2

, y

2

), (x

3

, y

3

), (x

4

, y

4

) i badając

wielomian interpolacyjny stopnia 4 przechodzący przez te punkty można otrzymać
następujące wzory :

h

y

y

y

y

y

i

i

i

i

i

12

8

8

2

1

1

2

'

+

+

−

−

−

+

−

=

(2.9)

2

2

1

1

2

"

12

16

30

16

h

y

y

y

y

y

y

i

i

i

i

i

i

+

+

−

−

−

+

−

+

−

=

(2.10)

3

2

1

1

2

"

2

2

2

h

y

y

y

y

y

i

i

i

i

i

+

+

−

−

+

−

+

−

=

(2.11)

4

2

1

1

2

"

4

6

4

h

y

y

y

y

y

y

i

i

i

i

i

i

+

+

−

−

+

−

+

−

=

(2.12)

Wzory różniczkowania numerycznego są bardzo użyteczne w rozważaniach teoretycznych
dotyczących opracowania efektywnych procedur rozwiązania równań różniczkowych
zwyczajnych i cząstkowych. Do obliczania pochodnych funkcji, których postać jest znana i
posiada prostą budowę, należy stosować wzory analityczne.