OPTYMALIZACJA KONSTRUKCJI

1. Zapis konstrukcji

Model matematyczny konstrukcji – jest zapisem konstrukcji pozwalającym na komputerowe
wspomaganie procesu konstruowania

Zapis konstrukcji podlega ewolucji, problemom zapisu konstrukcji poświęcony jest przedmiot –
rysunek techniczny

Wymagania odnośnie zapisu konstrukcji:
- warunek jednoznaczności: zapis nie powinien wymagać dodatkowych wyjaśnień i przez
każdego odbiorcę powinien zostać odczytany identycznie
- warunek zupełności zapisu: odbiorca może stwierdzić, że przedstawiony zapis jest
wystarczającym i koniecznym przekazem
- liczba zastosowanych do zapisu znaków powinna być jak najmniejsza – ale wystarczająca
- rodzaj stosowanych znaków powinien odpowiadać celom wykonania zapisu
- zapis konstrukcji powinien być trwały i zabezpieczony przed nieupoważnionym dostępem

2. Matematyczny model konstrukcji

Istota konstruowania i zapisu konstrukcji polega na doborze i zapisie cech konstrukcyjnych
projektowanej maszyny.
Cechy geometryczne: kształt, powiązania elementów, wymiary i tolerancje, geometrię
powierzchni
Cechy materiałowe: informacja określająca strukturę wewnętrzną elementów maszyn: rodzaj
materiału, parametry obróbki cieplnej, własności wytrzymałościowe, własności chemiczne,
fizyczne
Cechy dynamiczne: informacja o naprężeniach wewnętrznych, obciążenia zewnętrzne i ich
charakterystyki

Powyższe cechy można zapisać liczbowo jaki układ N liczb lub funkcji

Przestrzeń konstrukcji:

K

N

E

X

X

X

∈

=

)

,....,

(

1

Do przestrzeni konstrukcji można zaliczyć wektor X, którego współrzędne określają cechy konstrukcji,
Jeżeli cechy są liczbami wówczas wektor X będzie należał do przestrzeni euklidesowej. Współrzędne
mogą być typu:
- parametry – stałe dla konstrukcji
- zmienne decyzyjne – wielkości dobierane w procesie konstruowania, w dalszym ciągu oznaczane
jako: x

1

, x

2

,….,x

n

Przestrzeń zmiennych decyzyjnych lub przestrzeń rozwiązań oznacza się symbolem E

x

, zatem:

x

n

E

x

x

x

∈

=

)

,...,

(

1

3. Matematyczne zapisy zasad konstrukcji

Konstruktor może przyjmować tylko pewne wartości zmiennych decyzyjnych co wynika z
ograniczeń nakładanych na konstrukcję

Zasada 1, ogólna: Konstrukcja powinna spełnić wszystkie ograniczenia w stopniu
niemniejszym: dla każdej zmiennej decyzyjnej x

i

można ustalić wstępnie zakres zmienności:

n

i

x

x

x

i

i

i

,...,

1

,

max

min

=

≤

≤

- zmienne decyzyjne przyjmują wartości:
a) ciągłe w pewnym zakresie

b) dyskretne, wynikające np. z normalizacji, liczba zębów jest całkowita w kole zębatym itd.

Zbiór wartości zmiennych decyzyjnych spełniających wszystkie ograniczenia nazywa się
zbiorem dopuszczalnym

Φ

x

E

x

⊂

Φ

=

Φ

)

(

Konstrukcja spełniająca zasadę 1 w zapisie matematycznym będzie miała postać:

x

E

x

⊂

Φ

∈

Zasady szczegółowe określają ograniczenia lub kryteria optymalizacyjne, można je zapisać
następująco:

))

(

),...,

(

(

)

(

1

x

q

x

q

x

Q

m

=

4. Optymalizacja i polioptymalizacja konstrukcji

Zadanie optymalizacji konstrukcji: wybór ze zbioru rozwiązań dopuszczalnych, rozwiązań,
dla których wartość funkcji celu, będącej kryterium optymalizacji, osiąga wartość
ekstremalną. Gdy występuje wiele kryteriów optymalizacji pojawia się zadanie
polioptymalizacji.

W przypadku minimalizacji funkcji celu rozwiązanie optymalne można zdefiniować
następująco:

)

(

)

(

)

(

:

)

(

opt

opt

x

Q

x

Q

x

x

≥

Φ

∈

∀

Φ

∈

a w przypadku maksymalizacji:

)

(

)

(

)

(

:

)

(

opt

opt

x

Q

x

Q

x

x

≤

Φ

∈

∀

Φ

∈

5. Przykład 1

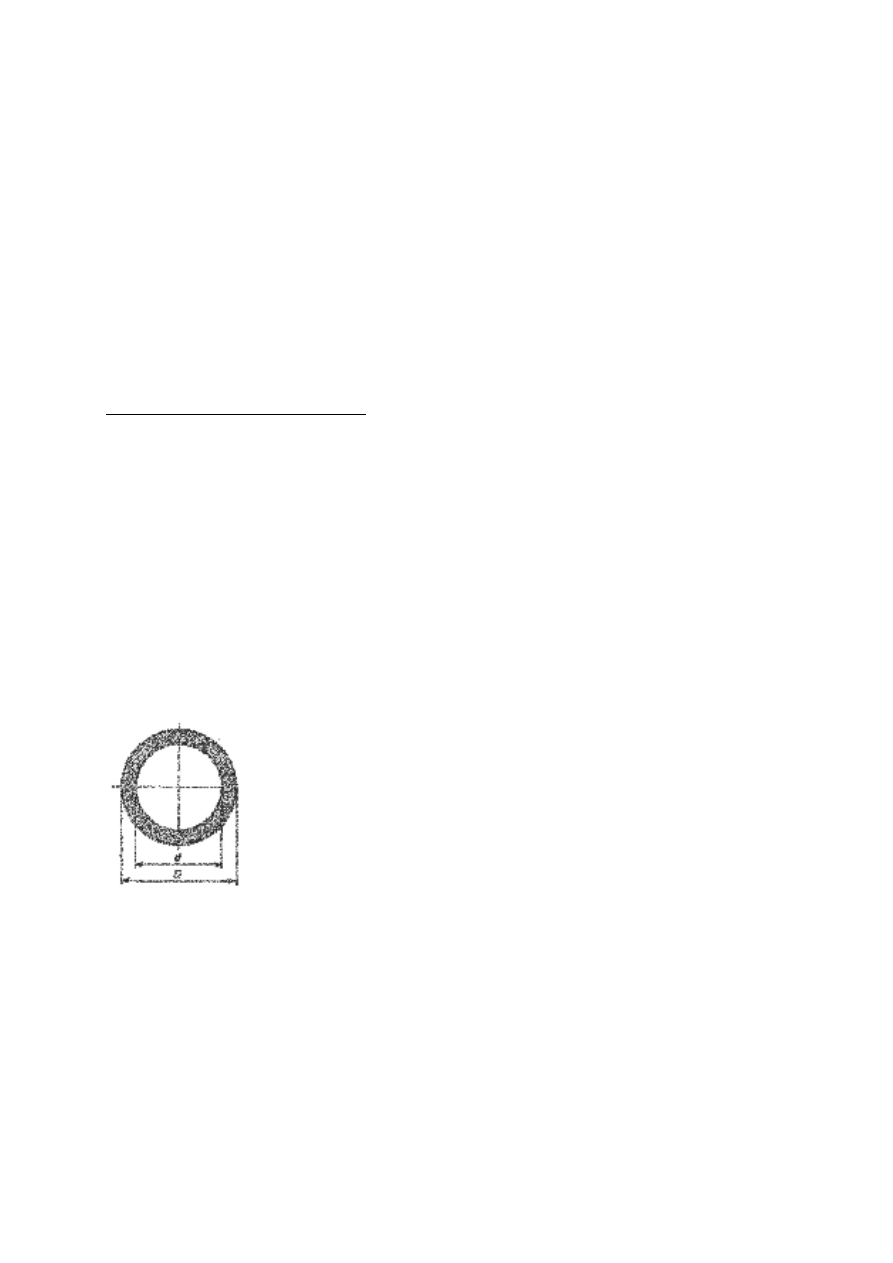
Należy zbudować model matematyczny wału drążonego (rys) przenoszącego
moment skrętny M=1000 Nm. Zadany jest materiał. Z którego wykonany jest wał
(stal C55), oraz dopuszczalne naprężenia na skręcanie k

s

=100 MPa. Ze

względów technologicznych powinien być spełniony warunek: a

1

<d/D<a

2

, a ze

względów konstrukcyjnych warunek D<b. Do obliczeń przyjąć: a

1

=0,2; a

2

=0,8;

b=0,05m

Rozwiązanie:

a) dobór zmiennych decyzyjnych i parametrów

zmienne decyzyjne: zewnętrzna i wewnętrzna średnica wału, czyli x=(d,D)
parametry: M=1000 Nm, ks=100MPa, a1=0,2, a2=08, b=0,05m

b) określenie zbioru dopuszczalnego

- są to wszystkie wartości zmiennych decyzyjnych: d, D, które spełniają warunek
wytrzymałościowy i pozostałe ograniczenia, d i D muszą być liczbami dodatnimi
- zapis matematyczny:

Warunek wytrzymałościowy

s

o

s

s

k

J

D

M

≤

=

2

τ

Po podstawieniach:

0

10

1

,

5

5

4

4

≥

⋅

−

−

−

D

d

D

Pozostałe ograniczenia:

0

,

0

,

,

,

2

1

>

>

<

<

>

D

d

b

D

D

a

d

D

a

d

Po podstawieniu danych liczbowych, zbiór dopuszczalny:

}

0

;

0

;

;

;

;

0

10

1

,

5

:

)

,

(

{

2

1

5

4

4

>

>

<

<

>

≥

⋅

−

−

=

=

Φ

−

D

d

b

D

D

a

d

D

a

d

D

d

D

D

d

x

c) kryterium optymalizacyjne: minimalizacja masy – czyli minimalizacja przekroju poprzecznego:

)

(

4

)

,

(

2

2

d

D

D

d

Q

−

=

π

- znaleźć takie wartości (d

opt

,D

opt

) aby wartość funkcji celu Q była minimalna

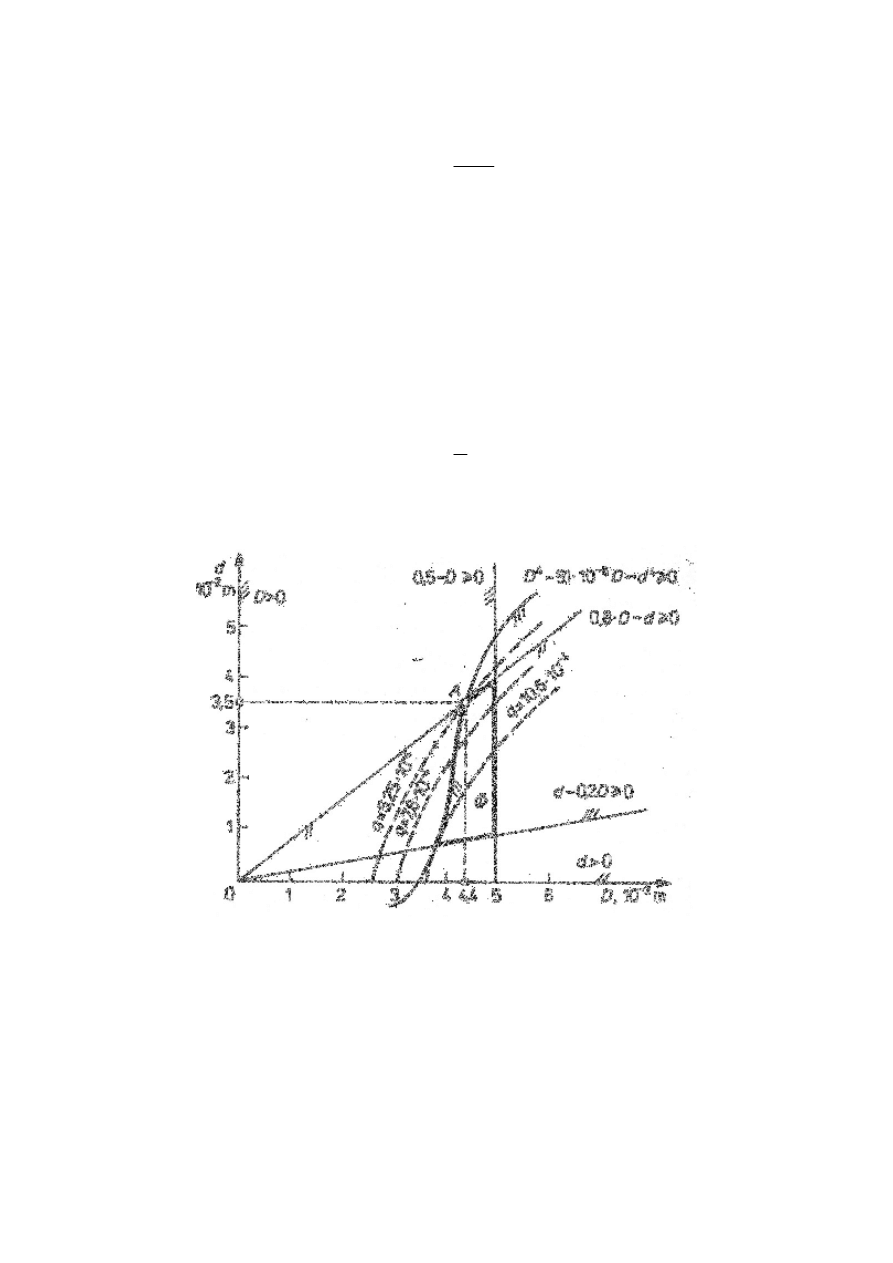
d) rozwiązanie graficzne
e)

f) rozwiązanie optymalne: punkt A

D

opt

=0,044 m; d

opt

=0,035 m; Q=0,000525 m

2