11. OPTYMALIZACJA KONSTRUKCJI

1

11.



11. OPTYMALIZACJA KONSTRUKCJI

11.1. Wprowadzenie

1. Optymalizacja potocznie i matematycznie

2. Przykład

3. Kryterium optymalizacji

4. Ograniczenia w zadaniach optymalizacji

5. Sformułowanie zadania optymalizacji

6. Podział zadania optymalizacji

7. Przykład zadania

8. Optymalizacja wymiarów

9. Optymalizacja kształtu

10.Optymalizacja topologii

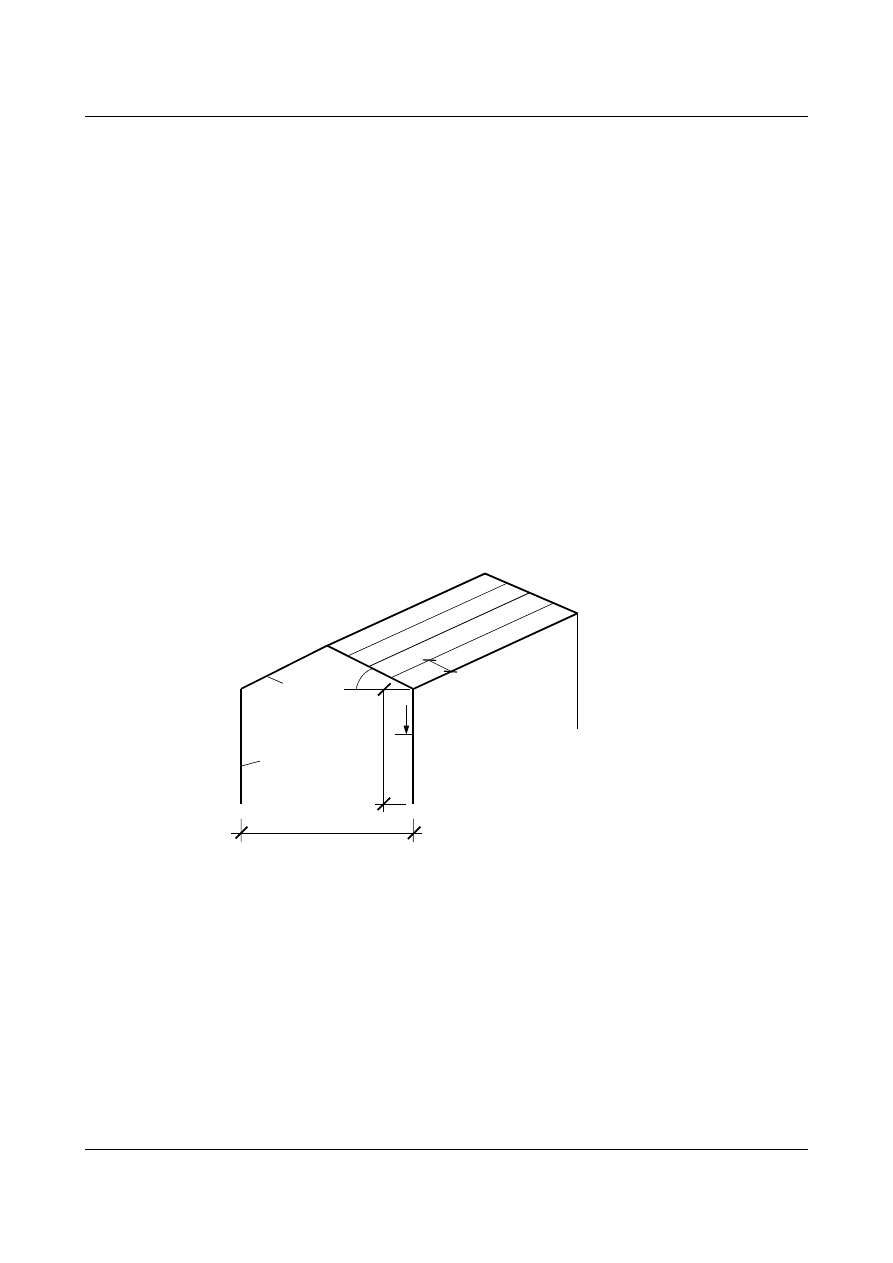
h

L

l

α

A

R

,I

R

A

S

,I

s

P

1. Rozwiązanie → liczba 1 np.12400zł (w zależności od parametrów L

1

,l

1

,I

1

,α

1

...)

2. Rozwiązanie → liczba 2 np.11700zł (w zależności od parametrów L

2

,l

2

,I

2

,α

2

...)

11.2. Kryteria optymalizacji

1. minimum kosztów,ciężaru lub objetości

Należy rozważyć czy cała konstrukcja wykonana będzie z tego samego materiału czy z różnych

materiałów o innych ciężarach. Proporcja wielkości M+R+S (gdzie M-materiał,R-robocizna,

S-sprzęt) może znacząco wpływać na optymalizację

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater

11. OPTYMALIZACJA KONSTRUKCJI

2

2. minimum energii:

•

potencjalnej

•

odkształcenia

•

sprężystej

3. maksimum sztywności(aby zapewnić jak najmniejszą odkształcalność konstrukcji)

4. minimum przemieszczeń

5. minimum odkształceń konfiguracji początkowej

6. maksimum siły krytycznej(np. przy dodwaniu do konstrukcji dodatkowych blach porównujemy

rozwiązania dla różnych przypadków ich miejsca przyłożenia i wybieramy to przy którym zmiana

wielkości siły krytycznej jest najoptymalniejsza)

7. maksimum częstości drgań własnych

ω

1

ω

ω

2

ω

3

max

Jeśli np. wielkość częstości drgań maszyny zamontowanej na konstrukcji zawiera się pomiędzy
pierwszą i drugą częstością drgań własnych należy rozważyć czy zmiana któregoś z parametrów
(np. wymiaru elementu) nie wpłynie korzystnie na rozsunięcie się przedziału między pierwszą i
druga częstością drgań własnych.

8. maksimum momentu bezwładności (np.w zależności od stounku boków prostokąta przy tym

samym polu mamy inne wartości momementów bezwładności danego przekroju).

9. maksimum niezawodności (niezawodność wyrażamy liczbami)

10.maksimum bezpieczeństwa

11.3. Parametry

1. Opisujące (O): h,b,L,E...(wymiary,charakterystyka materiału)

2. Wymuszające (W): P,q...(obciążenia)

3. Reakcje (R): u,ε,σ,R,M...

11.4. Ograniczenia występujące w optymalizacji konstrukcji.

1. Nieprzekraczanie wytężeń lub zapewnienie bezpieczeńtwa (dla wszystkichstanów obciążenia,np.

przy obciążeniu wiatrem należy rozważyć różne schematy przyłożenia tego obciążenia i wybrać
najniekorzystniejszy).

≪

M

≪M

(11.1)

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater

11. OPTYMALIZACJA KONSTRUKCJI

3

2. Nieprzekraczanie dopuszczalych wartości przemieszczeń

u

≪u

(11.2)

3. Nieprzekraczanie minimalnych i maksylanych dopuszczalnych wymiarów elementów (względy

użytkowe i technologiczne).

s

min

ss

max

(11.3)

Przy formułowaniu zadania optymalizacji należy zastanowić się i podjąć decyzję jakie jest główne
kryterium, jakie są ograniczenia i jakimi parametrami możemy sterować w celu zoptymalizowania
konstrukcji.

11.5. Sformułowanie zadania optymalizacji

1. Przyjęcie funkcji celu.

Funkcja ta ma być minimalna ze względu na parametry sterujące.

F

s min

(11.4)

2. Wybór zmiennej sterującej.

Możemy sterować tylko jednym parametrem a także zespołem parametrów,wektorem,tensorem.

3. Wprowadzenie ograniczeń równościowych g

s=0 lub nierównościowych g s≤0 oraz

określenie ograniczeń zmiennych decyzyjnych.

11.6. Przykład

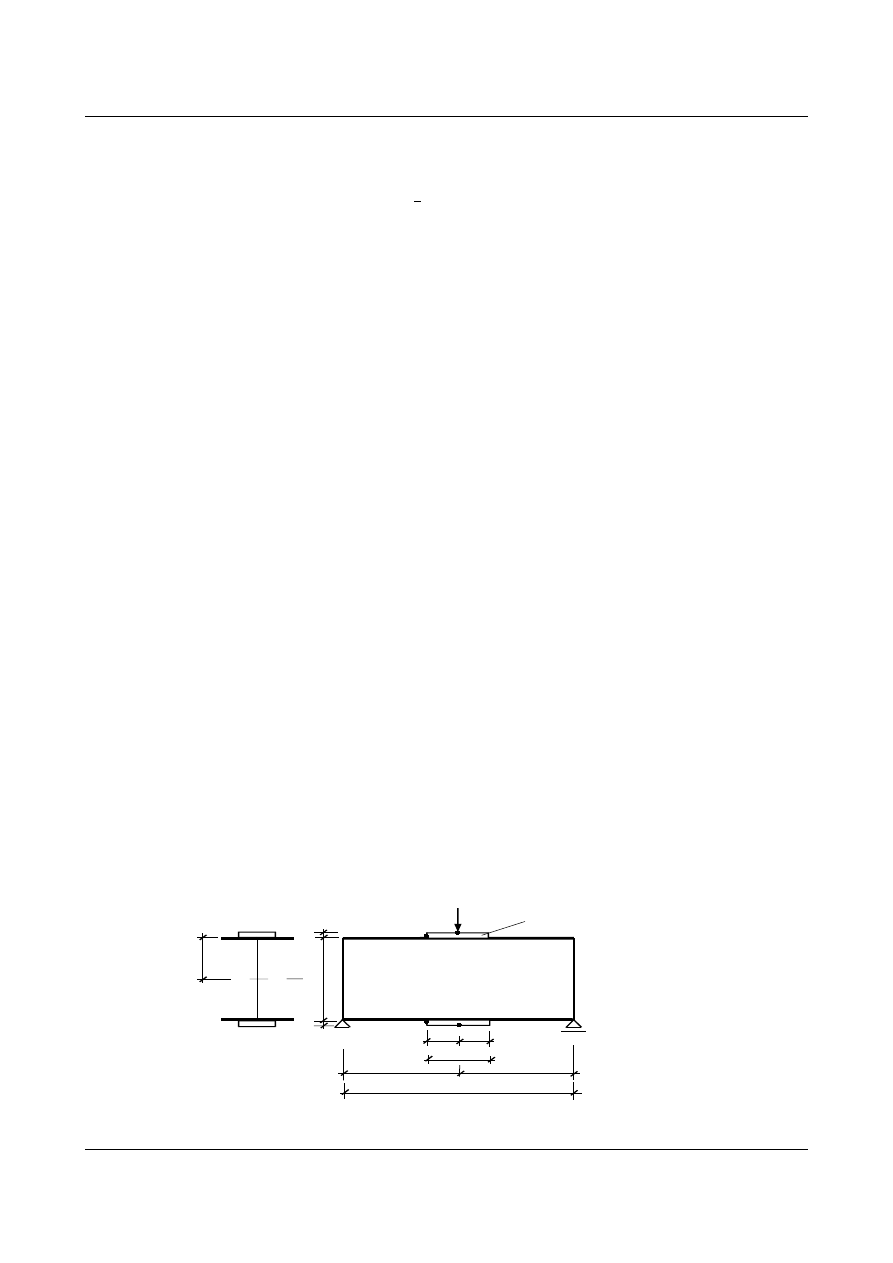
Dana jest belka swobodnie podparta,obciążona siłą skupioną P w połowie swej rozpietości. Pierwotny

przekrój dwuteowy jest niewstarczający ze względu na przekroczone naprężenia. W środkowej części

belki zaprojektować jako wzmocnienie przekroju optymalne nakładki.

g

2h

g

h

a

a

2a

1

2

nakładka

2l

l

l

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater

11. OPTYMALIZACJA KONSTRUKCJI

4

1. Opisujące (O) :{ l,a,h,I,g,b,R,E } (wymiary,charakterystyka materiału)

2. Wymuszające (W) :{P} (obciążenia)

3. Reakcje (R) : {R

A

,M,T,u,ε,σ}

1. Przyjęcie funkcji celu.

Minimalizacja ilości zastosowanego materiału

V

=4⋅a⋅g⋅b min ze względu na a i g

(11.5)

2. Wybór zmiennej sterującej.

s

=

{

a , g

}

(11.6)

3. Wprowadzenie ograniczeń

g

≥g

min

(11.7)



1

≤R



2

≤R

(11.8)

u

2

≤u

dop

(11.9)

Rozwiązanie:

1

2

I

1

=I

(11.10)

I

2

=I 2⋅b⋅g⋅h

2

(11.11)



1

=

P

2

⋅



l

−a



⋅h

I

≤R

(11.12)

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater

11. OPTYMALIZACJA KONSTRUKCJI

5



2

=

P

2

⋅l

I

2⋅b⋅g⋅h

2

⋅



h

g



≤R

(11.13)

∫

M

⋅M

E

⋅I

d

x

≤ f

dop

(11.14)

s

=

{

a

opt

, g

opt

}

(11.15)

g

a

g

min

σ

2

u

σ

1

F

1

F

2

l

a

opt

g

opt

11.7. Funkcje celu

Optymalizacja polega na wybraniu najlepszego rozwiązania ze wszystkich możliwych.

Funkcje celu mogą być funkcjami liniowymi. Zmienne sterujące funkcji liniowych występują w

pierwszej potędze. Tego typu zagadnienia możemy bez problemów rozwiązać przy pomocy programów
komputerowych. Przykładowa funkcja celu:

f

... , s min

g

... , sg

gr

(11.16)

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater

s

rozwiązania

dopuszczalne

rozwiązania

niedopuszczalne

linia ograniczeń

(s)

f

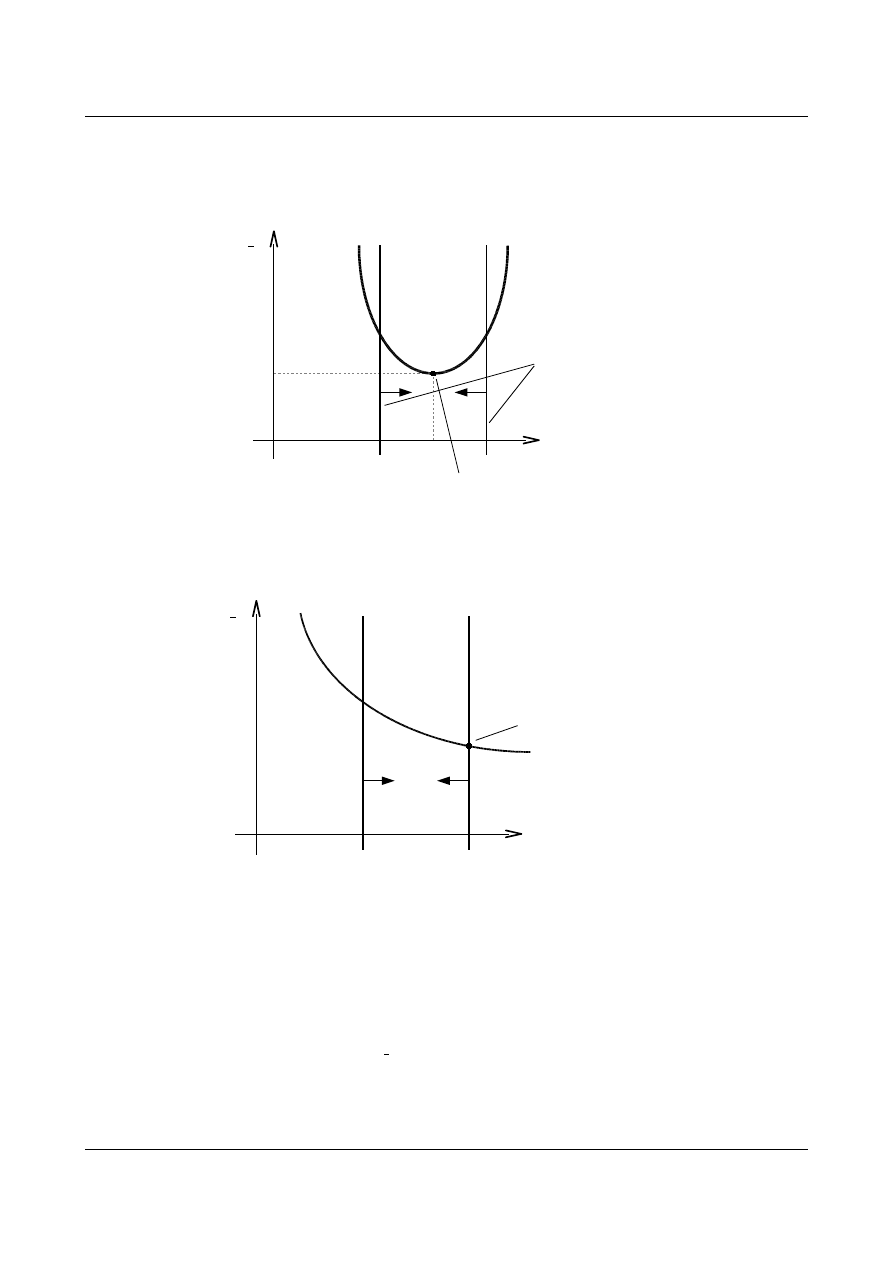
11. OPTYMALIZACJA KONSTRUKCJI

6

Funkcje celu mogą mieć także postać na przykład funkcji kwadratowych:

Rozwiązania optymalne bywają często blisko ograniczeń. W rozwiązaniach inżynierskich rozwiązanie

optymalne najczęściej znajduje się na ograniczeniu:

11.8. Obliczanie funkcjonału bez ograniczeń

Metody obliczania funkcjonału bez ograniczeń:

a) metoda gradientowa – jej przykładem może być twierdzenie o minimum całkowitej energii potencjalnej:

s=W −P

(11.17)

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater

s

rozwiązanie optymalne, najlepsze z możliwych

linie ograniczeń

(s)

f

s

rozwiązanie

optymalne na

ograniczeniu

(s)

f

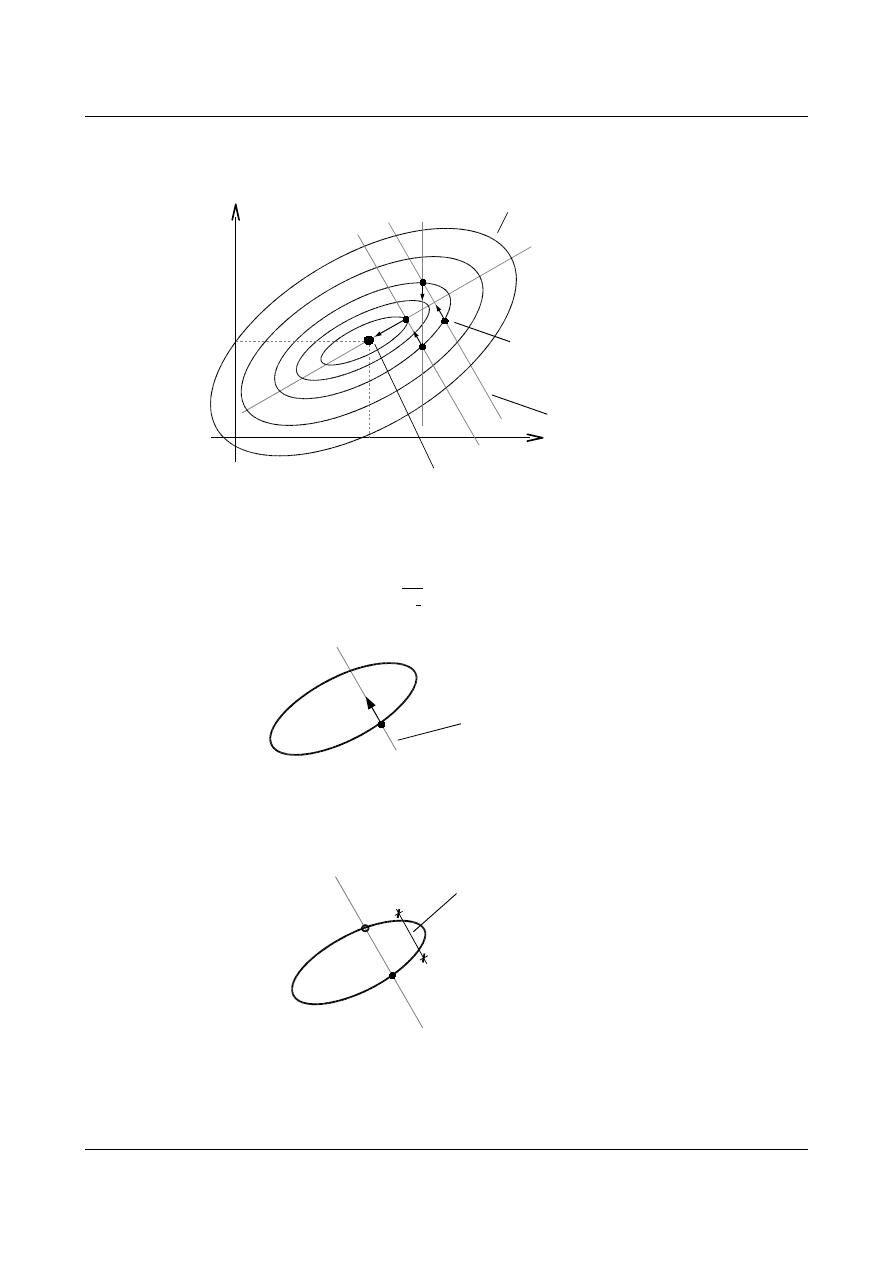
11. OPTYMALIZACJA KONSTRUKCJI

7

Wiemy, iż rozważany funkcjonał ma jedno ekstremum:

Szukanie wartości odbywa się w następujących etapach:

•

rozpoczynamy obierając gradient funkcji



 f

s

:

•

wykonujemy krok:

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater

szukanie wartości

izolinie

kierunek

największego

spadku – gradient

funkcji

jedno ekstremum, dla jednego zestawu

wartości funkcja minimalna

kierunek największego

spadku – gradient

funkcji

możemy wykonać

krok dowolnej

długości

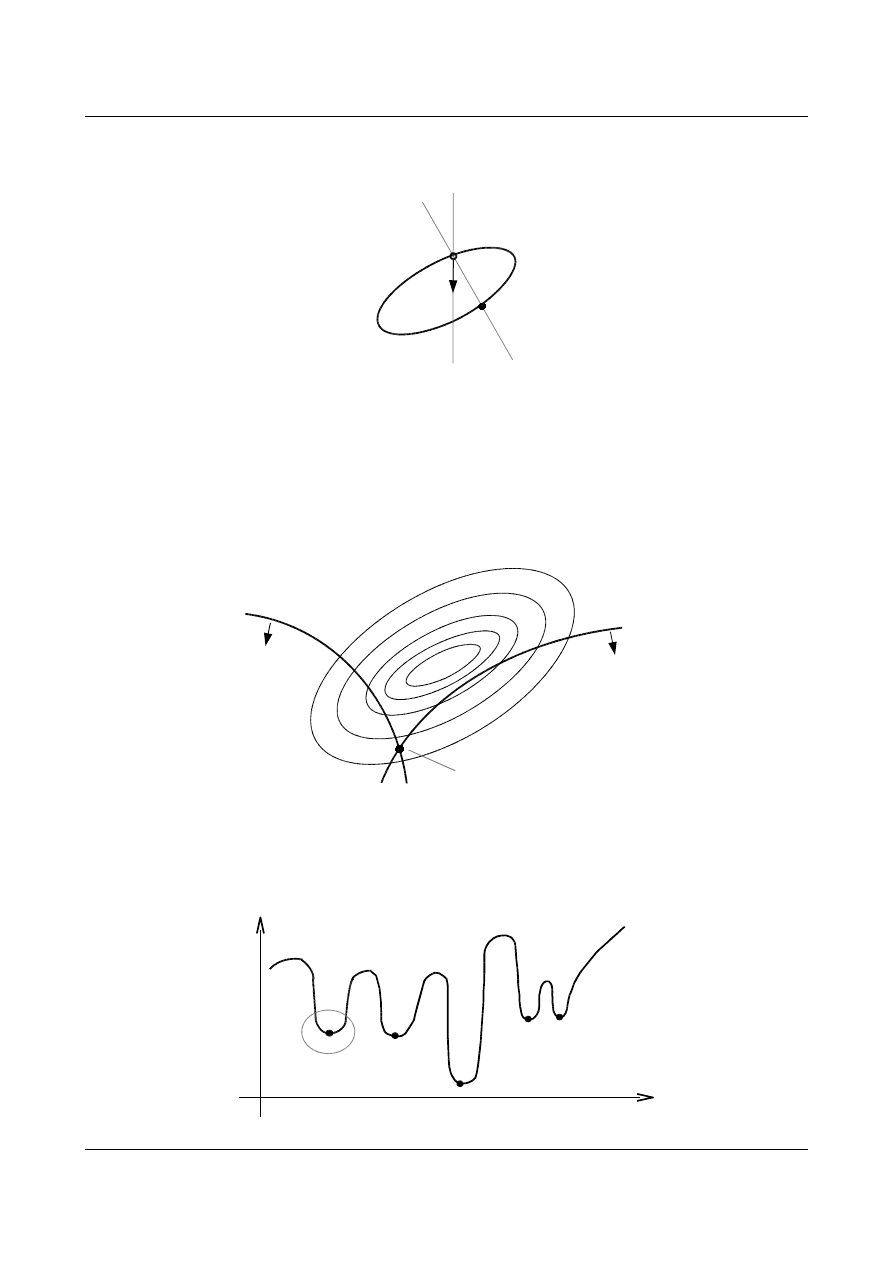
11. OPTYMALIZACJA KONSTRUKCJI

8

•

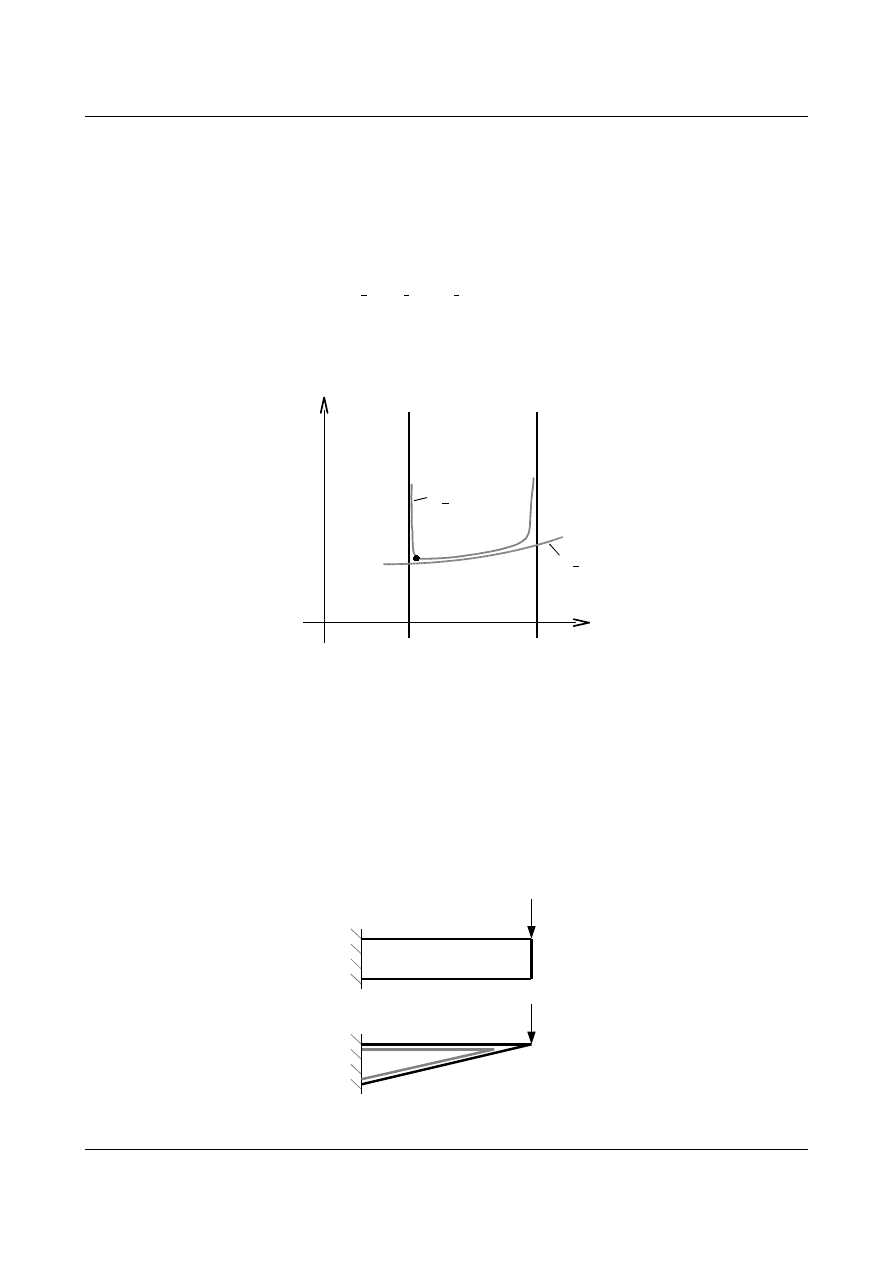
dostajemy kolejny kierunek gradientu:

Postępując dalej tym sposobem dochodzimy blisko do minimum. W omawianej metodzie można

policzyć gradienty analitycznie.

b) metoda bezgradientowa (metoda Powell'a).

Gradienty obliczamy numerycznie. Metodę bezgradientową stosujemy w sytuacjach, gdy nie

potrafimy obliczyć gradientu analitycznie.

W zadaniach inżynierskich występują ograniczenia:

Stosowane przez nas funkcje celu mogą być różnego kształtu:

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater

rozwiązania

dopuszczalne

rozwiązanie najmniejsze z możliwych

przy danych ograniczeniach

rozwiązania

dopuszczalne

11. OPTYMALIZACJA KONSTRUKCJI

9

Często okazuje się, że znalezione minimum (zakreślone na rysunku) jest tylko minimum lokalnym.

Nas natomiast interesuje minimum globalne. Celem staje się zatem udowodnienie, że wyszukana wartość
jest ekstremum globalnym, a nie lokalnym.

W zadaniach inżynierskich wygodnie jest poruszać się po ograniczeniach, gdyż tam często znajduje

się oczekiwane rozwiązanie. Szukamy minimum funkcjonału

F

s= f s g s

(11.18)

Funkcjonał ten wyprofiluje nam rozwiązanie:

Zadanie optymalizacji jest zadaniem syntezy. Rozwiązujemy je wielokrotnie, zakładając określone

parametry, sprawdzając, dokonując analiz. Mając wiele rozwiązań możemy wybrać rozwiązanie optymalne.

11.9. Optymalizacja kształtu

Działanie to jest często stosowane w przypadku konstrukcji, dla których przy sprawdzaniu naprężeń

dochodzimy do wniosku, że pewna część elementu jest niewykorzystana. W takim wypadku możemy
zoptymalizować kształt:

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater

(s)

f

(s)

F