Optymalizacja konstrukcji

 Przystępując do kształtowania

konstrukcyjnego, tj. nadania właściwych
cech przeszłej maszynie, należy określić z
jakiego punktu widzenia (wg jakiego
kryterium oceny) będą oceniane
alternatywne rozwiązania.

 Ścisłe (sformułowane matematycznie)

określenie punktu widzenia nazywa się
funkcją celu (funkcją jakości, funkcją
efektywności), zaś sam punkt oceny nazywa
się a kryterium optymalizacji.

 Uzyskanie funkcji celu wymaga zbudowania

odpowiedniego modelu matematycznego.

Optymalizacja to działalność, której

celem jest uzyskanie najlepszego
rezultatu w danych warunkach i dla
określonej funkcji celu.

Najlepszy z otrzymanych wyników

nazywa się optymalnym.

Załóżmy, że rozpatruje się trzy rodzaje

przekładni o tej samej mocy i przełożeniu :

• ślimakową,
• planetarną,
• walcową.
Załóżmy też, że kryterium optymalizacji są

najmniejsze gabaryty tej przekładni, które

można wyrazić w funkcji pozostałych cech

konstrukcyjnych.

Z punktu widzenia zadanego kryterium a

więc wymiarów gabarytowych, optymalnym

rozwiązaniem jest przekładnia planetarna.

Model matematyczny

konstrukcji

Zbudowanie funkcji celu, niezbędnej

w procesie optymalizacji konstrukcji,
wymaga zapisu cech konstrukcyjnych
maszyny (geometrycznych,
materiałowych i dynamicznych) w
postaci układu liczb i funkcji.

Uzyskany w ten sposób zapis nazywa

się modelem matematycznym
konstrukcji.

Dla potrzeb modelowania

matematycznego, konstrukcję

K

można

potraktować jako punkt w pewnej
przestrzeni

N

-wymiarowej czynnikowej,

co można zapisać następująco:

K = (C

1

,C

2

,...,C

N

)



R

N

gdzie:

K

- konstrukcja,

C

i

- cechy konstrukcji,

R

N

- przestrzeń konstrukcji.

Jeżeli wszystkie współrzędne wektora

K

są liczbami, to taki punkt można
traktować jako element

N

- wymiarowej

przestrzeni euklidesowej

E

N

:

K = (C

1

, C

2

,...,C

N

)



E

N

Wektor

K

należący do przestrzeni

konstrukcji jednoznacznie opisuje
konstrukcję.



p

D

z

D

D

w

d

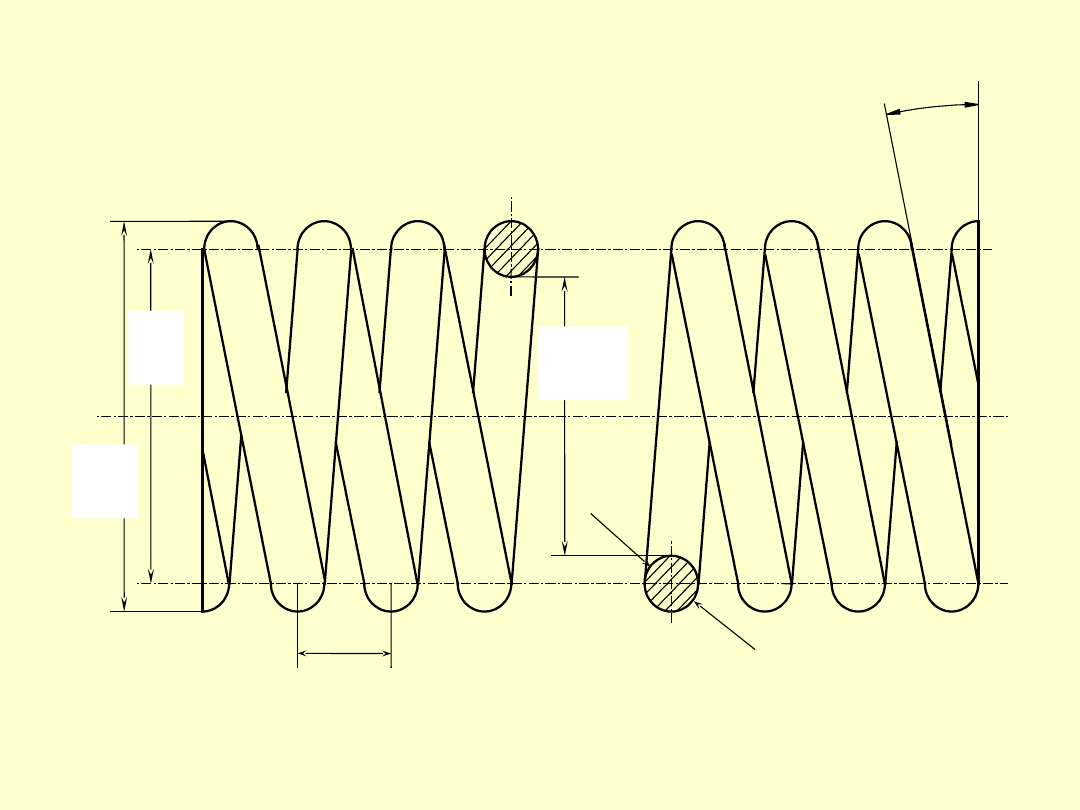
Niech opisywanym elementem będzie

śrubowa sprężyna naciskowa.

Umiejscowienie jej środka ciężkości w

maszynie można określić za pomocą
wartości liczbowych trzech
współrzędnych.

Następne współrzędne mogą opisywać,

np. średnicę drutu, średnicę nawinięcia
drutu, granicę plastyczności materiału
sprężyny, wartość siły napięcia
wstępnego, itp.

Wszystkie cechy opisujące konstrukcję

można podzielić na:

 parametry

P

 zmienne decyzyjne

X

.

Parametry

P

są zadane i ich wartość jest

niezmienna w procesie projektowania.

Natomiast zmienne decyzyjne

X

są

dobierane w procesie projektowania.

W przypadku rozpatrywanej sprężyny:
 parametrami

P

mogą być np.: wartość

siły napięcia wstępnego i wymiary
zewnętrzne sprężyny,

 zaś zmiennymi decyzyjnymi

X

, np.

średnica drutu, granica plastyczności
materiału

sprężyny

(materiał

sprężyny).

Biorąc pod uwagę podział cech konstrukcyjnych
na parametry

P

i zmienne decyzyjne

X

,

konstrukcje można formalnie zapisać

następująco:

K = (P

1

, P

2

,...,P

N

; X

1

,X

2

,...X

M

)



E

K

Z kolei zbiór zmiennych decyzyjnych

X

można

traktować jako punkt

x

w pewnej przestrzeni,

zwanej przestrzenia zmiennych decyzyjnych
(przestrzenia rozwiązań)

E

x

:

x = (x

1

, x

2

,…,x

n

)  E

x

Na złożoność modelu matematycznego

wpływa

głownie

liczba

zmiennych

decyzyjnych.

Im jest ona większa, tym trudniejsze i

kosztowniejsze jest prowadzenie obliczeń.

Z drugiej zaś strony, ograniczenie liczby

zmiennych decyzyjnych i ustalenie dużej
liczby

cech

konstrukcyjnych

jako

parametrów

zawęża

możliwości

poszukiwana najlepszych rozwiązań.

Matematyczne sformułowanie

szczegółowych i ogólnych zasad

konstrukcji

Konstruktor może przyjmować tylko

określone wartości zmiennych
decyzyjnych

X

.

Wynika to z ograniczeń narzuconych

na poszczególne zmienne decyzyjne i
na konstrukcję jako całość.

Ograniczenia te wynikają ze

szczegółowych zasad konstrukcji.

Zgodnie z pierwszą zasadą, konstrukcja

powinna spełniać wszystkie ograniczenia

wynikające ze szczegółowych zasad w

stopniu nie mniejszym od założonego.

Z matematycznego punktu widzenia,

ograniczenia te mogą mieć charakter

nierównościowy:

b

i

(x)= b

i

(x

1

,x

2

,...,x

n

)= 0; i = 1,2,...,m

g

j

(x)=g

j

( x

1

,x

2

,...,x

n

)=0; j=1,2,...,p

Dla każdej zmiennej decyzyjnej

x

i

można

ustalić wstępnie zakres jej zmienności:

x

imin

≤ x

i

≤ x

imax;

i = 1,...,n

Na skutek ograniczeń wynikających ze

szczegółowych zasad konstrukcji
przedział ten ulega zawężeniu.

Niektóre zmienne decyzyjne mogą

przyjmować dowolne wartości z ciągłego
przedziału [

x

imin

,

x

imax

], a inne mogą

przyjmować tylko wartości dyskretne.

Zmienne decyzyjne wynikające ze

względów fizycznych i
technologicznych, takie jak np.:

 wymiary,
 obciążenia,
 naprężenia., itp.

mają z reguły charakter ciągły.

Zmienne decyzyjne ściśle określone

przez normy, takie jak np.:

 moduły kół zębatych,
 wymiary łożysk tocznych,
 wymiary śrub, nitów, itp.,

mają charakter dyskretny i ich zakres

zawęża się do zbioru liczb dyskretnych.

Zmienne decyzyjne ściśle określone

przez normy, takie jak np.:

 moduły kół zębatych,
 wymiary łożysk tocznych,
 wymiary śrub, nitów, itp.,

mają charakter dyskretny i ich zakres

zawęża się do zbioru liczb dyskretnych.

Inne wartości zmiennych decyzyjnych

są dyskretne z założenia, np. liczba
zębów w kole zębatym.

Jednakże, zdecydowana większość

ograniczeń ma charakter
nierównościowy, np.:

 liczba zębów w kole zębatym nie

może być mniejsza niż graniczna liczba
zębów,

 obciążenie nie może wywoływać

naprężeń większych od dopuszczalnych,

 prędkość obwodowa czopa podczas

smarowania hydrodynamicznego musi
być większa od granicznej.

W procesie budowy modelu

matematycznego konstrukcji

K

wszystkie ograniczenia wynikające ze
szczegółowych zasad konstrukcji musza
być przedstawione w postaci
jednoznacznej matematycznie, tak aby
dla dowolnego wektora zmiennych
decyzyjnych

X

można było

jednoznacznie stwierdzić, czy należy on
do zbioru rozwiązań dopuszczalnych, a
więc czy są spełnione wszystkie
ograniczenia, czy też nie.

Zbiór punktów w przestrzeni zmiennych

decyzyjnych

X

, w których spełnione są

wszystkie ograniczenia narzucone przez
konstrukcję

K

, nazywa się zbiorem

dopuszczalnym lub zbiorem rozwiązań
dopuszczalnych:

Φ= Φ (x)



E

x

Konstrukcja spełniająca pierwszą ogólną

zasadę konstrukcji (a ściślej - wektor

zmiennych decyzyjnych

x

) musi należeć

do zbioru rozwiązań dopuszczalnych.

Matematyczny zapis tej zasady jest

następujący:

x  Φ E

x

Konstrukcja

K

należąca do zbioru

dopuszczalnego

Φ

jest poprawna

( dobra), a konstrukcja

K

nie należąca

do zbioru

Φ

jest niedobra.

W celu wyboru ze zbioru rozwiązań

dobrych

Φ

rozwiązania najlepszego,

konieczne jest ustalenie kryteriów
optymalizacji

Q

.

Druga ogólna zasada konstrukcji mówi,

że konstrukcja powinna być optymalna
(polioptymalna) w danych warunkach ze
względu na przyjęte kryterium
optymalizacji, np.:

 najmniejszy ciężar,
 największa wytrzymałość, itp.

Dobór kryteriów jest zadaniem bardzo

odpowiedzialnym i złożonym.

Zadanie optymalizacji można

przedstawić w kategoriach działania
praktycznego, tj. osiągnięcie:

– pożądanego efektu przy

najmniejszych nakładach,

– największego efektu przy

wykorzystaniu zadanych nakładów.

Reguły te maja charakter praw

ekonomicznych i już w tym podejściu
widać jak istotny jest dobór
kryteriów.

Szczególnie niebezpieczne jest

uleganie wyłącznie kryteriom
ekonomicznym.

Może to bowiem prowadzić do

niebezpiecznych skutków
ekologicznych, społecznych, a nawet
technicznych.

W procesie, projektowania należy

przede

wszystkim

uwzględniać

kryteria techniczne, nie zapominając
jednak o ekonomicznych.

Kryteria techniczne wynikają ze

szczegółowych zasad konstrukcji.

Są to kryteria funkcjonalności,

trwałości,

niezawodności,

sprawności,

lekkości,

taniości

i

dostępność materiałów, itp..

W projektowaniu wspomaganym

komputerowo należy każde kryterium

przedstawić jako funkcję zależną od
zmiennych decyzyjnych

X

.

Wówczas model matematyczny

konstrukcji, który składa się z wektora
zmiennych decyzyjnych

x

, zbioru

dopuszczalnego

Φ

i kryterium

optymalizacji

Q

, można zapisać

następująco:

x

= (x

1

,x

2

,...,x

n

) E

x

Φ

=

Φ

(x) E

x

Q

=

Q

(x

1

,x

2

,...,x

n

)

Istnieje wiele metod poszukiwania
rozwiązań optymalnych.
Ogólnie można je podzielić na
dwie zasadnicze grupy:

–

metody analityczne, np. metoda

pochodnych, metoda wariacyjna,
metoda wyznaczników Lagrange'a,

– metody numeryczne, np.

programowanie liniowe (metoda
simplex), programowanie
nieliniowe.

Przykład - zadanie

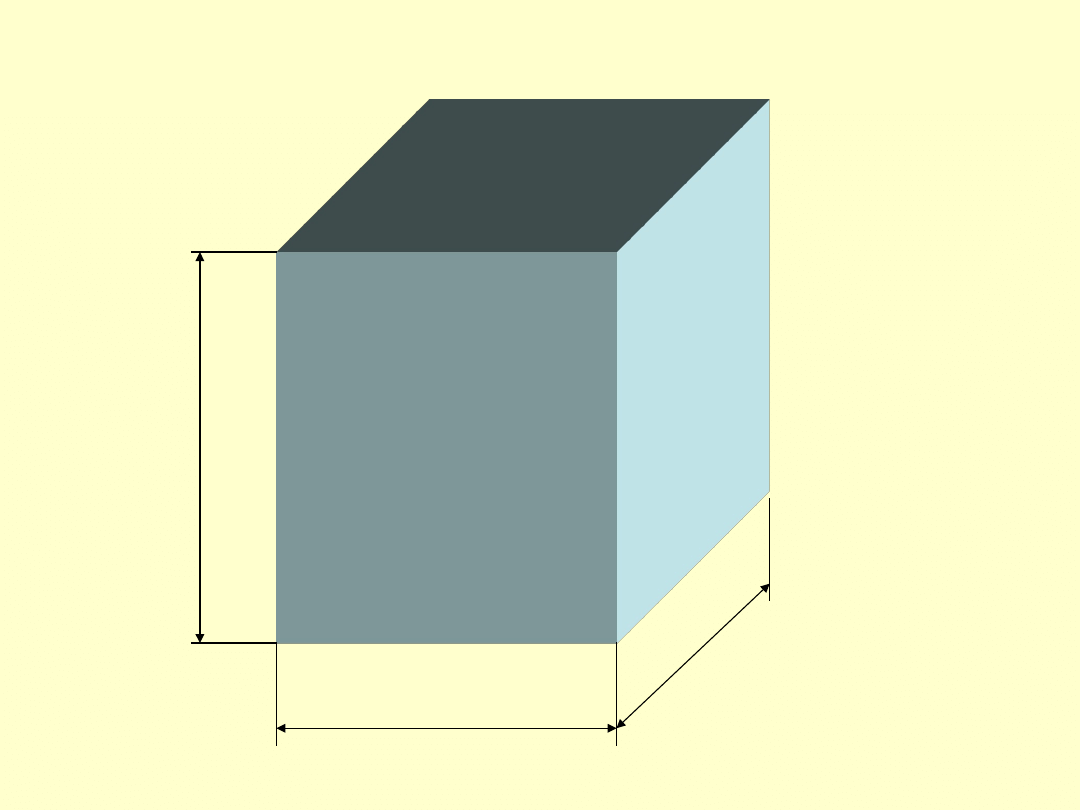
Przesyłki przewożone na statku mogą

być pakowane w skrzynie, których

suma wszystkich boków podstawy i

wysokości nie przekracza 240 cm, zaś

podstawa jest kwadratem.

W przeciwnym razie naliczane są

opłaty dodatkowe.

Obliczyć wymiary skrzyni

maksymalizujące jej objętość.

x

x

H

Metoda pochodnych

Metoda pochodnych zasadza się na wyznaczeniu

dwóch pochodnych w celu znalezienia wartości
ekstremalnych danej funkcji celu

Q

(

x

).

W pierwszym kroku, dla znalezienia wartości

ekstremalnych wyznacza się pierwszą pochodną
funkcji

Q

(

x

) i przyrównuję się ją do zera a następnie

oblicza się wartość zmiennej niezależnej

x

.

0

d

d



x

Q

Równanie to pozwala na wyznaczenie wartości
ekstremalnych.

W kroku drugim wyznacza się druga pochodną

funkcji

Q

(

x

). Jeśli wyznaczone wartości ekstremalne

są mniejsze od zera to funkcja osiąga maksimum,
jeśli większe od zera to funkcja osiąga minimum.

0

d

d

2

2



x

Q

funkcja

Q

(

x

) osiąga

maksimum

0

d

d

2

2



x

Q

funkcja

Q

(

x

) osiąga

minimum

Funkcja celu ma postać:

 

H

x

x

Q

2



Ograniczenie równościowe ma postać:

 

0

240

4









x

H

x

b

Wyznaczając H z poprzedniego równania:

240

4 



 x

H

i podstawiając do funkcji celu uzyskuje się:

 

2

3

240

4

x

x

x

Q







Pierwsza pochodna ma postać:

0

480

12

d

d

2









x

x

x

Q

Rozwiązaniem tego równania są
wartości:

x

1

= 0 oraz

x

2

= 40.

W celu upewnienia się czy funkcja

Q

(

x

)

osiąga maksimum przy

x

2

= 40,

wyznacza się drugą pochodną:

0

480

24

d

d

2

2









x

x

Q

i oblicza się jej wartość dla

x

2

= 40:

480

2

2

d

d

40

1







x

Q

x

Następnie oblicza się

H

z zależności na

ograniczenie równościowe:

cm

80

80

4

240

4

240













x

H

Wówczas największa pojemność skrzyni
wyniesie:

3

2

2

cm

128000

80

40











H

x

V