http://www.if.pwr.wroc.pl/~wozniak/

fizyka1.html

Dr hab. inż. Władysław Artur Woźniak

Instytut Fizyki Politechniki Wrocławskiej

Dr hab. inż. Władysław Artur Woźniak

Wykład FIZYKA I

10. Ruch drgający tłumiony i wymuszony

DRGANIA TŁUMIONE (GASNĄCE)



Siły oporu (tarcia) są zwykle proporcjonalne do prędkości ciała*:

Dr hab. inż. Władysław Artur Woźniak

dt

x

d

r

v

r

F

oporu

















Oscylator mechaniczny w

obecności sił tarcia (tłumienie):

kx

rv

ma









Obwód RLC (opór R odpowiada za tłumienie):

0







C

q

RI

dt

dI

L

* A przedtem

było (patrz wykład 3.), że do kwadratu prędkości! Nieoduczeni ci

wykładowcy, albo kłamią na wykładach…

DRGANIA TŁUMIONE (GASNĄCE)



Ogólne równanie drgań tłumionych (straty energii na oporze

ośrodka, proporcjonalne do pierwszej pochodnej zmiany położenia,
czyli

prędkości):

Dr hab. inż. Władysław Artur Woźniak

0

2

2

0







x

x

x











Dla oscylatora mechanicznego:

m

r

2





m

k



0



DRGANIA TŁUMIONE (GASNĄCE)



Ogólne rozwiązanie w postaci kombinacji liniowej rozwiązań

szczególnych:

Dr hab. inż. Władysław Artur Woźniak

 

 

 

t

x

N

t

x

N

t

x

2

2

1

1





gdzie:

 









t

A

t

x











2

0

2

2

,

1

2

,

1

exp







DRGANIA TŁUMIONE (GASNĄCE)

Dr hab. inż. Władysław Artur Woźniak

Rodzaje

rozwiązań:

1) dla

oba

pierwiastki

są

rzeczywiste

i

ujemne,

więc

rozwiązaniem

jest

aperiodyczne,

wykładnicze malenie x od A do zera;

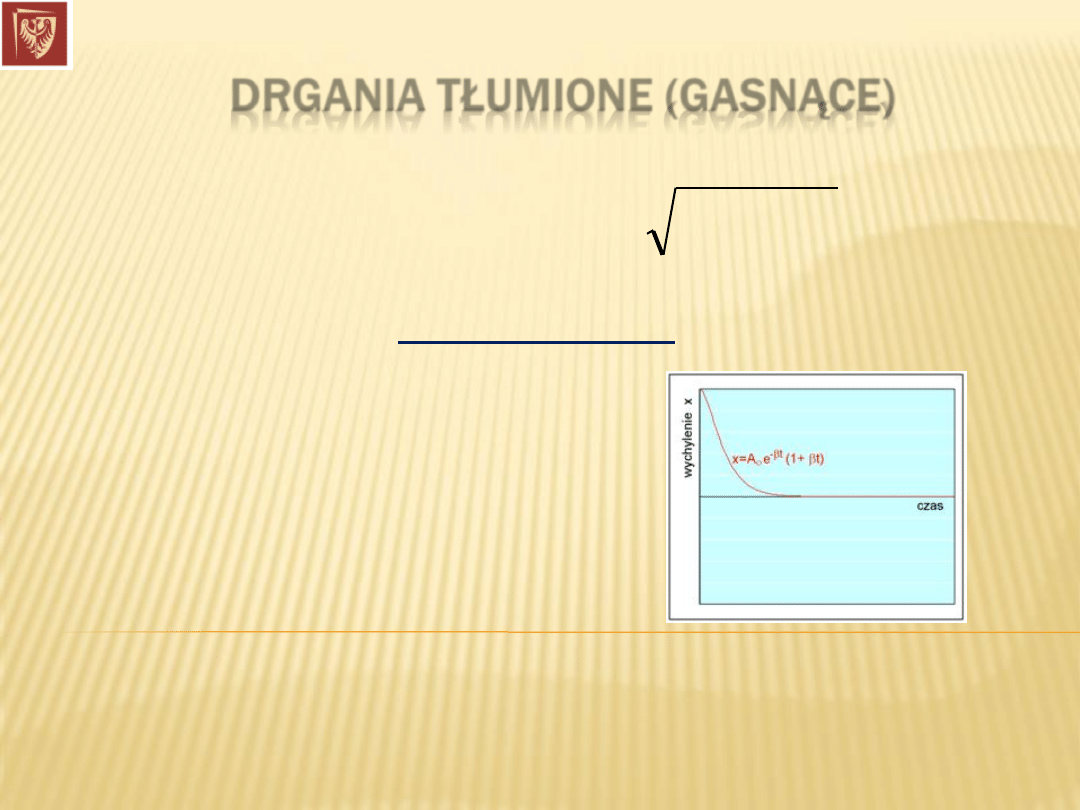
2) dla

występuje tzw. tłumienie krytyczne – jest to

minimalna

wartość tłumienia, przy której ruch jest aperiodyczny;

2

0

2







2

0

2







 









t

A

t

x











2

0

2

2

,

1

2

,

1

exp







DRGANIA TŁUMIONE (GASNĄCE)

Dr hab. inż. Władysław Artur Woźniak

Rodzaje

rozwiązań:

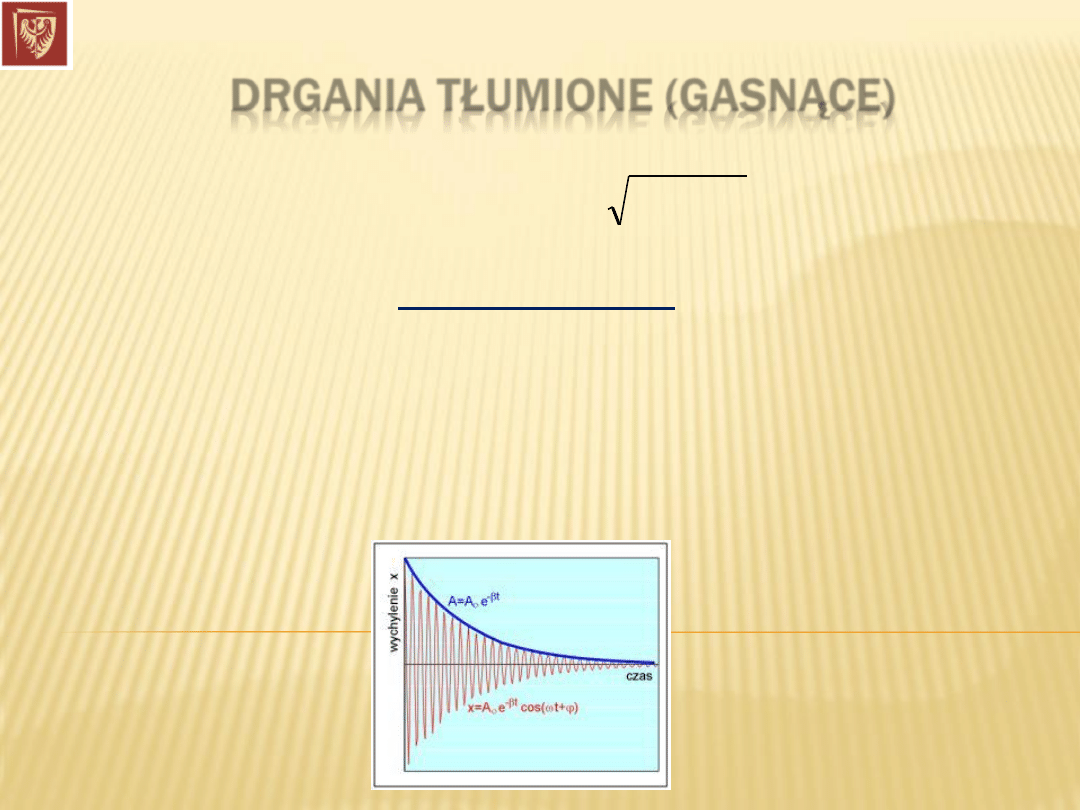
3) dla

mamy

drgania

gasnące

–

oscylacje

o

zanikającej amplitudzie:

2

0

2









 



t

i

t

A

x











exp

exp

0

2

,

1

 









t

A

t

x











2

0

2

2

,

1

2

,

1

exp







DRGANIA TŁUMIONE (GASNĄCE)



Ograniczając się do jednego rozwiązania (znak „plus” przy fazie) i

pisząc rozwiązanie w postaci funkcji harmonicznej:

Dr hab. inż. Władysław Artur Woźniak

 



 



0

0

sin

exp













t

t

A

t

x

 





t

A

t

A







exp

0

nazywamy

amplitudą drgań gasnących;

m

r

2





to

współczynnik tłumienia;

2

2

0











to

częstość własna drgań układu tłumionego;

m

k



0



to

częstość drgań swobodnych układu;

DRGANIA TŁUMIONE (GASNĄCE)



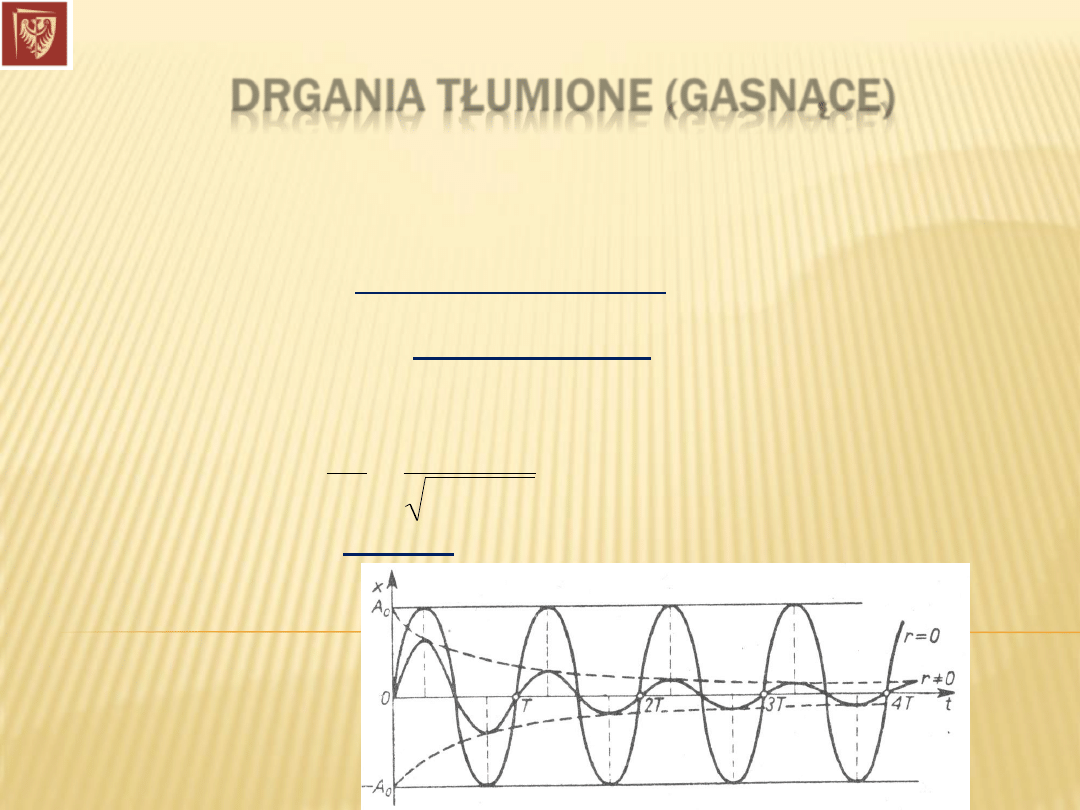
Drgania

gasnące są drganiami nieokreślonymi – nigdy nie powtarzają się

największe wartości wychylenia, prędkości, przyspieszenia. Dlatego

tylko

umownie

można nazwać

częstością kątową – w tym sensie, że wskazuje

ona, ile razy w

ciągu

sekund

drgający układ przechodzi przez położenie

równowagi!

Dr hab. inż. Władysław Artur Woźniak

 



 



0

0

sin

exp













t

t

A

t

x







Podobnie:

nazwiemy umownym okresem

drgań gasnących.

2

2

0

2

2

















T

DRGANIA TŁUMIONE (GASNĄCE)



Współczynnik tłumienia

:

mówi nam o stosunku kolejnych

amplitud

drgań gasnących:

Dr hab. inż. Władysław Artur Woźniak

m

r

2





 

T

A

A

n

n



exp

1







Logarytm naturalny stosunku amplitud

dwóch kolejnych wychyleń,

następujących po sobie w odstępie czasu

(umownego okresu)

nazywamy logarytmicznym dekrementem

tłumienia :

T



T

A

A

n

n











1

ln

DRGANIA TŁUMIONE (GASNĄCE)



Oznaczmy przez

odstęp czasu, w ciągu którego amplituda drgań

zmniejszy

się -krotnie. Wtedy:

Dr hab. inż. Władysław Artur Woźniak



e

1





albo:





1



czyli:

współczynnik tłumienia

jest

wielkością fizyczną równą

odwrotności odstępu czasu , w ciągu którego amplituda zmniejsza
się -razy. Czas

nazywamy czasem relaksacji.







e



Podobnie: gdy przez

oznaczymy

liczbę drgań, po wykonaniu

których amplituda zmaleje -razy, okaże się, że:

N

e

N

1





czyli: dekrement logarytmiczny

tłumienia

jest

wielkością równą

odwrotności liczby drgań, po upływie których amplituda zmniejszy
się

-razy.



e

DRGANIA WYMUSZONE



Oprócz siły sprężystej i siły oporu, działamy na układ dodatkową siłą

– okresową siłą wymuszającą :

Dr hab. inż. Władysław Artur Woźniak

F

 

 

t

F

t

F



cos

0





Ogólne równanie ruchu oscylatora mechanicznego przybiera

wtedy

postać:

 

t

F

kx

dt

dx

r

dt

x

d

m



cos

0

2

2







Jest to

równanie różniczkowe niejednorodne.

DRGANIA WYMUSZONE



Spodziewamy

się rozwiązania powyższego równania różniczkowego

w postaci drgania harmonicznego z

częstością

,

równą częstości

siły wymuszającej

, ale amplituda tych

drgań powinna „zawierać

informacje” o masie

,

tłumieniu

i

wielkości siły wymuszającej

a

także częstości własnej układu

:

Dr hab. inż. Władysław Artur Woźniak



F

m



0

F

0



 

t

F

kx

dt

dx

r

dt

x

d

m



cos

0

2

2







 





0

sin









t

A

t

x

m



0

F

0



?



?

0



DRGANIA WYMUSZONE



Można pokazać, że:

Dr hab. inż. Władysław Artur Woźniak





2

2

2

2

2

0

0

4















m

F

A

Amplituda

A

ustalonych

drgań wymuszonych

jest

wprost

proporcjonalna do amplitudy

siły wymuszającej F

0

i odwrotnie

proporcjonalna do masy m

układu oraz zmniejsza się wraz ze

wzrostem

współczynnika tłumienia



.



„Faza początkowa” ma teraz sens różnicy faz między amplitudą

drgań wymuszonych A i amplitudą siły wymuszającej F

0

(ściślej:

ponieważ użyliśmy funkcji „cosinus” do opisu siły wymuszającej i
funkcji

„sinus” do opisu drgania x(t), to szukaną różnicą faz będzie:

2

2

0

2

tan















2

0











DRGANIA WYMUSZONE



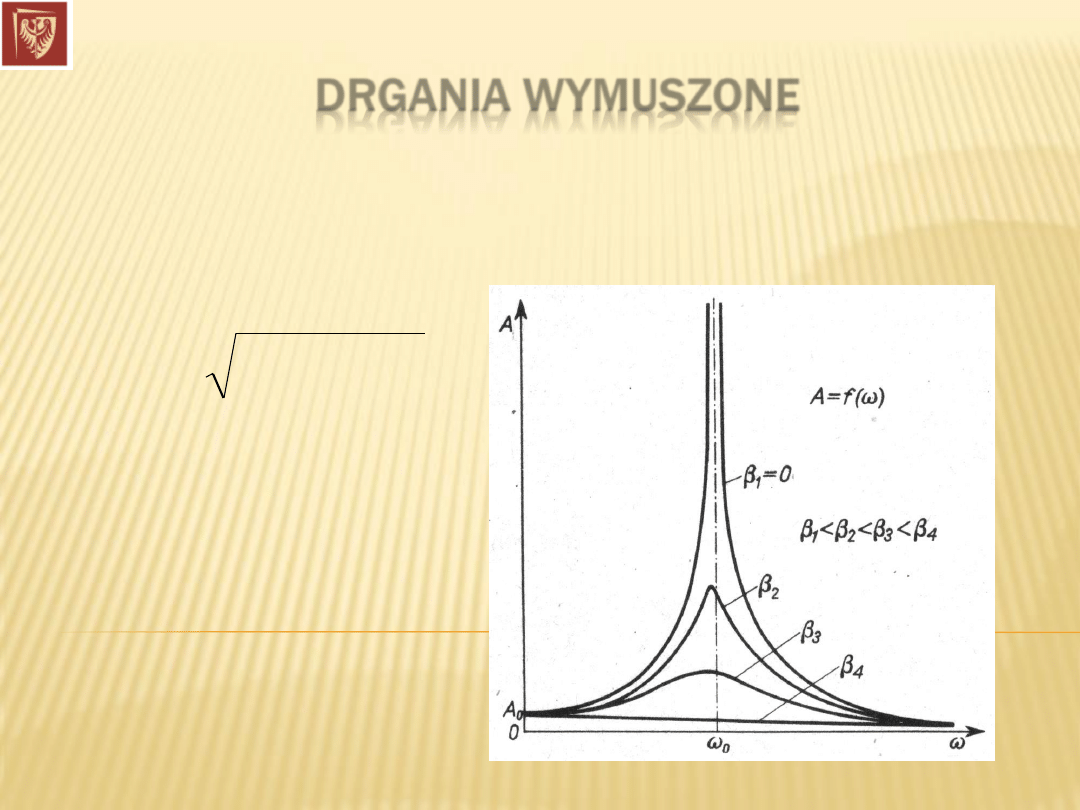
Analizując wyrażenie na amplitudę drgań wymuszonych:

Dr hab. inż. Władysław Artur Woźniak





2

2

2

2

2

0

0

4















m

F

A

możemy zauważyć, że w przypadku braku tłumienia (



=0), gdy

częstość



siły wymuszającej F równa jest częstości drgań

własnych układu



0

, amplituda ta

rośnie do nieskończoności!

DRGANIA WYMUSZONE



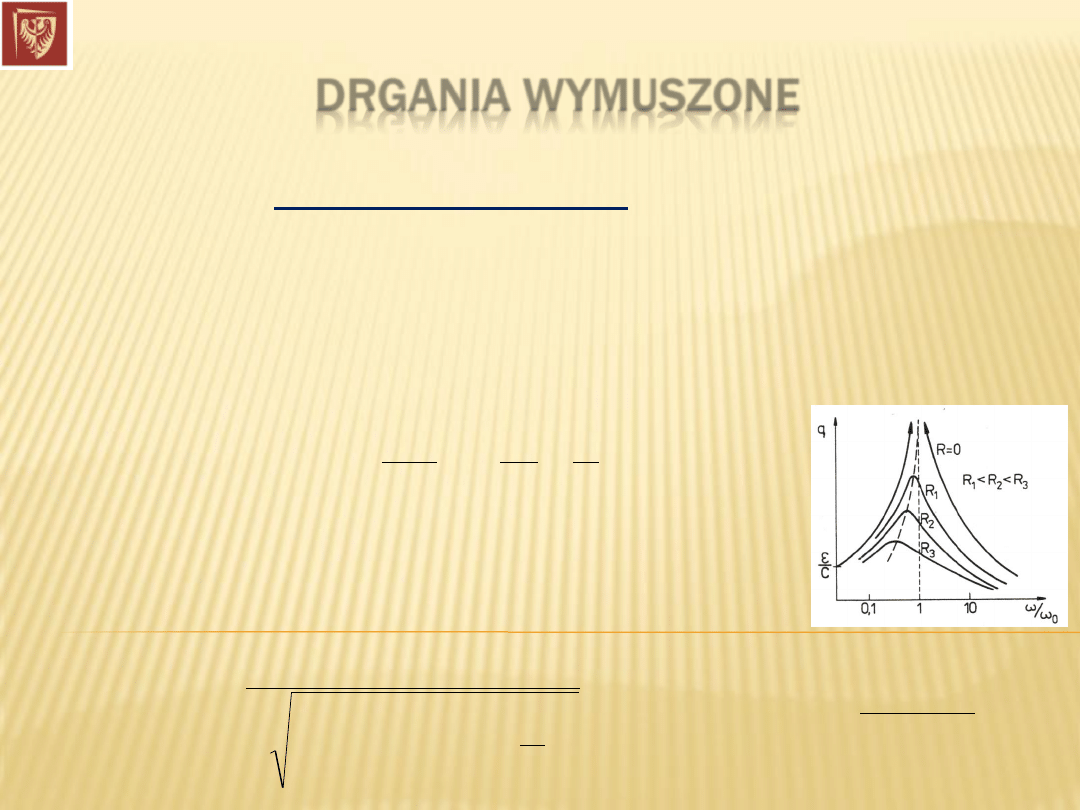
Natomiast w

obecności tłumienia

, maksimum

wyrażenia na

amplitudę A uzyskamy dla:

Dr hab. inż. Władysław Artur Woźniak

0





2

2

0

2











Zjawisko to nazywamy
rezonansem.

Ale

co

to

jest

rezonans?

Niedobry

wykładowca nie podał

definicji,

żeby ją na ściądze

zapisać…

DRGANIA WYMUSZONE



Przykład

obwodu

elektrycznego:

siła

elektromotoryczna,

wymuszająca drgania, jest równa:

Dr hab. inż. Władysław Artur Woźniak

 

 

t

i

t

E



exp

0





Wtedy:

równanie opisujące ruch ładunku elektrycznego w obwodzie

(=

prąd elektryczny!):

 

t

i

C

q

dt

dq

R

dt

q

d

L



exp

0

2

2









Rozwiązanie ogólne w postaci:

















t

i

q

q

exp

0





2

2

2

2

0

0

0





















L

R

L

q







gdzie:

2

2

0

/















L

R

tg