ANALIZA MATEMATYCZNA
Lista 2
1.Funkcja f(x) określona jest wzorem:
1
1
)
(
+
−
=
x
x
x
f
. Wyznaczyć f(2x), 2f(x), f(x2), [f(x)]2.
2. Funkcja f określona jest wzorem:
f x
x
x
x
x
x
x
( )
,
/ (
),
,
=
+
≤
−
< ≤
−
>
2
1
2
1
2 2
3
2
5
3
3
.
Obliczyć
).
2
(
),
8
(
),
2
(
5
f
f
f
3. Wyznaczyć dziedziny naturalne i zbiory wartości funkcji
).
1
(
log
)
(
)
,
2
1
)
(
)
,
6
1
)
(
)
3
2
x
x
f
c
x
x
x
f
b
x
x
x
f
a
+
=
−
−
=
−
+
−
=
4.Czy funkcja
1
)
(
2
−
=
x
x
f
ma funkcję odwrotną na
R; czy ma odwrotną na zbiorze (-∞,0]?
5. Wyznaczyć funkcje odwrotne do podanych:
.
1
1
)
(
)
,
0
,
1
)
(
)
,
27
3
3
)
(
)
3
2
2
3
−
+
=
≥
+
=
+
+
−
=
x
x
x
f
c
x
x
x
f
b
x
x
x
x
f
a
6. Określić, jeśli to możliwe,
))
(
(
)),
(
(
)),
(
(
)),
(
(
x
g
g
x
f
f
x
f
g
x
g
f
dla następujących funkcji:
a)
x
x
g
x
f
x
cos
)
(
,
2
)
(
=
=
, b)
x
x
g
x
x
f
sin
)
(
,
)
(
=
=
.
7.Mając dany wykres funkcji f(x) sporządzić wykres funkcji : f(x+c) , cf(x), f(x)+c, -f(x),
f(-x),
,
)
(x
f
)
( x
f
dla a)
],
1
,
1
[
,
)
(
3
−
∈
−
=
x
x
x
x
f
b)
x
x
f
=
)
(
.
8.Podać wzór funkcji liniowej, której wykres:
a) przechodzi przez punkty A(2,1), B(1,-1),
b) przechodzi przez punkt A(1,0) i tworzy z osią Ox kąt
6
π
,
c) przechodzi przez punkt A(1,0) i tworzy z osią Ox kąt
6
5
π
.
9. Narysować wykresy funkcji: a)
2
2
)
(
+
+
−
=
x
x
x
f
, b)
x
x
x
x
f
+
+
−
=
9
6
)
(
2
.
10. Wykorzystując wykres funkcji
x
x
f
3
)
(
=
sporządzić wykresy funkcji
x
x
f
3
2
)
(
−
=
,
,
3
2
)
(
x
x
f
−
=
x
x
f
3
2
)
(
−
=
.
11. Wykorzystując wykresy funkcji
x
x
f
2
1
log
)
(
=
sporządzić wykresy funkcji:
)
3
(
log
)
(
2
1
−
=
x
x
f
,
2
)
3
(
log
)
(
2
1
−
−
=
x
x
f
;
3
log
)
(
2
1
−
=
x
x
f
.
12. Znaleźć okresy funkcji i naszkicować ich wykresy:
x
x
f
d
x
tg
x
f
c
x
x
f
b
x
x
f
a
cos
)
(
)
,
2
)
(
)
,
2
cos
3
)
(
)
,
4
sin
5
)
(
)
=
=
=
=
13. Rozwiązać graficznie równania i nierówności trygonometryczne:
a)
2
1
)
4
sin(
=
+
π
x
, b)
3
3
2
−
=
x
ctg
, c)
2
1
)
2
3
cos(
−
≥
−
π
x
, d)
3
)
3
(
1
≤
−
≤
π
x
tg
.
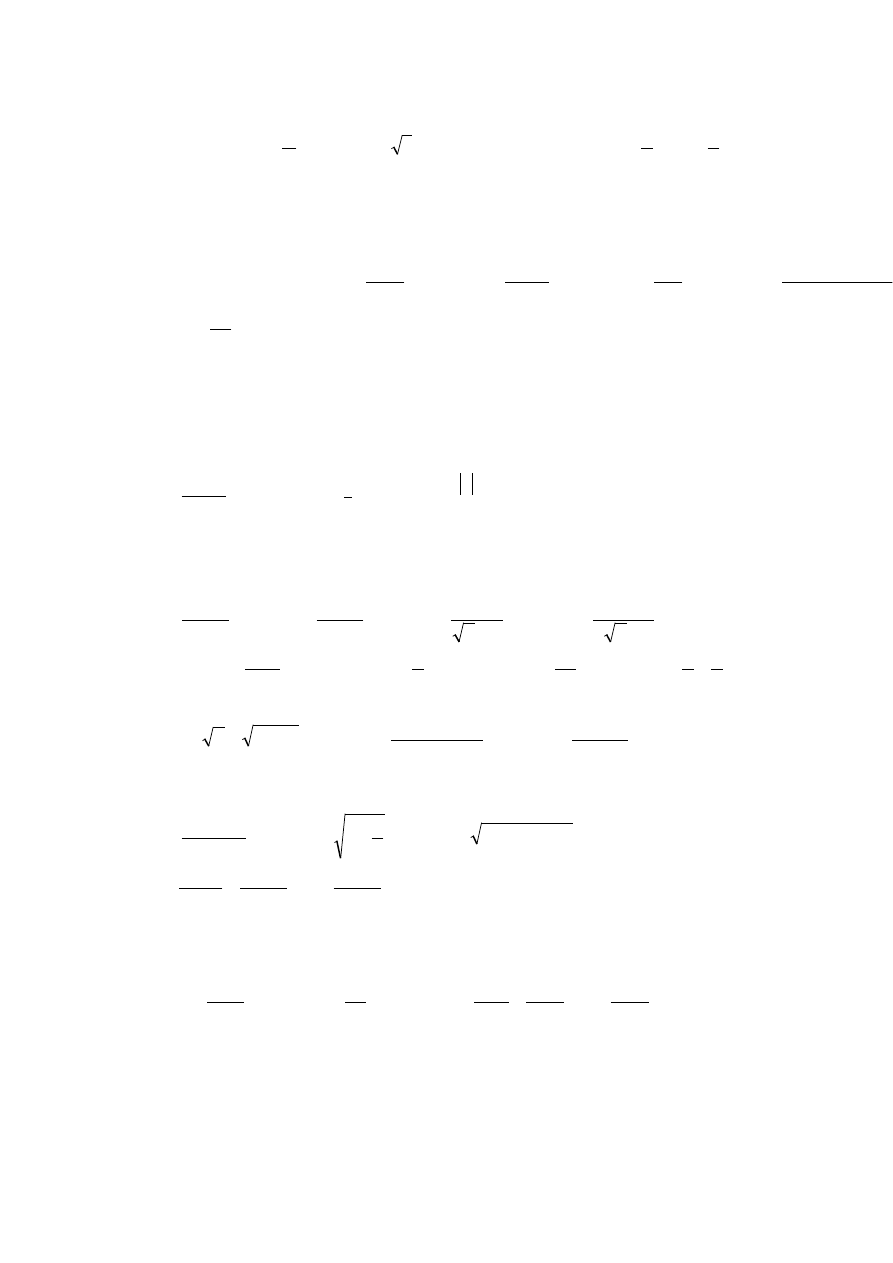
14. Dla funkcji okresowej
)
sin(
)
(
φ
ϖ
+
=
x
A
x
f
, stałą A nazywamy amplitudą , ω –
częstotliwością, a
φ
- fazą początkową. Wyznaczyć te trzy stałe oraz narysować
wykresy funkcji:
a)
)
3
3
sin(
4
)
(
π
+
=
x
x
f
, b)
x
x
x
f
2
cos
2
sin
3
)
(
−
=
, c)
2
cos
2
2
sin
2
)
(
x
x
x
f
+
=
.
LISTA 3
15. Zbadać, które z podanych ciągów są monotoniczne. Określić typ monotoniczności.
!
)
1
2
(
...
3
1
)
,
!
10
)
,
1
2
3
)
,
4
1
)
,
10
)
2
n
n
e
e
n
d
d
n
n
c
c
n
b
b
n
n
a
a
n
n
n
n
n
n
−
⋅
⋅
⋅
=
=
+
+
=
+
−
=
−
=
n
n
n
n
f
f
!
)
=
.
Czy ciągi te są ograniczone?
16. Wyznaczyć cztery początkowe wyrazy ciągu zadanego rekurencyjnie:
,
,
2
)
,
5
3
,
4
)
1
1
1
1
n
b
b
b
b
a
a
a
a
n
n
n
n
+
=
=
−
=
=
+
+
17. Korzystając z definicji granicy ciągu wykazać, że:
.
n
log
lim
)
c
,.
1
a
gdy
,
1
a
gdy
,
0
a
lim
)
b
.,
1
1
n
2
1
n
2
lim
)
a
5
.
0
n
n
n
n
−∞
=
>
∞
<
=
=
+
−
∞
→
∞
→
∞
→
18. Obliczyć granice:
,
2
1
lim
)
,
2
3
lim
)
,
3
2
4
lim
)
,
5
4
2
lim
)
2
+
+
+
+
+
−
+
−
∞
→
∞
→
∞
→
∞
→
n
n
n
d
n
n
c
n
n
b
n
n
a
n
n
n
n
n
n
n
n
n
n
n
n
n
h
n
g
n
f
n
e
)
1
2
1
(
lim
)
,
)
1
1
(
lim
)
,
)
2
1
(
lim
)
,
)
1
1
1
(
lim
)
2
+
−
+
+
−
∞
→
∞
→
∞
→
∞
→
19. Wykorzystując twierdzenie o trzech ciągach obliczyć granice:
20. Korzystając z twierdzenia o ciągu monotonicznym i ograniczonym, uzasadnić zbieżność
ciągów:
n
n
n
n
c
c
n
n
b
b
n
a
a
n
n
n
n
n
+
+
+
+
+
+
=
=
=
1
...
2
1
1
1
)
,
!
)
,
!
100
)
.
.
2
7
3
5
lim
)
,
1
...
3
2
lim
)
),
2
(
lim
)
2
3
n
n
n
n
n
n
n
k
n
n
j
n
n
n
i
−
−
−
+
+
+
−
−
∞
→
∞
→
∞
→
).
1
...
2
1
1
1
(
lim
2
4
7
lim
)
,
1
5
lim
)
,
2
3
cos
lim
)
2
2
2
n
n
n
n
c
n
b
n
n
n
a
n
n
n
n
n
n
n
n
n
n
+
+
+
+
+
+
−
+
+
−
+
∞
→
∞
→
∞
→
∞
→
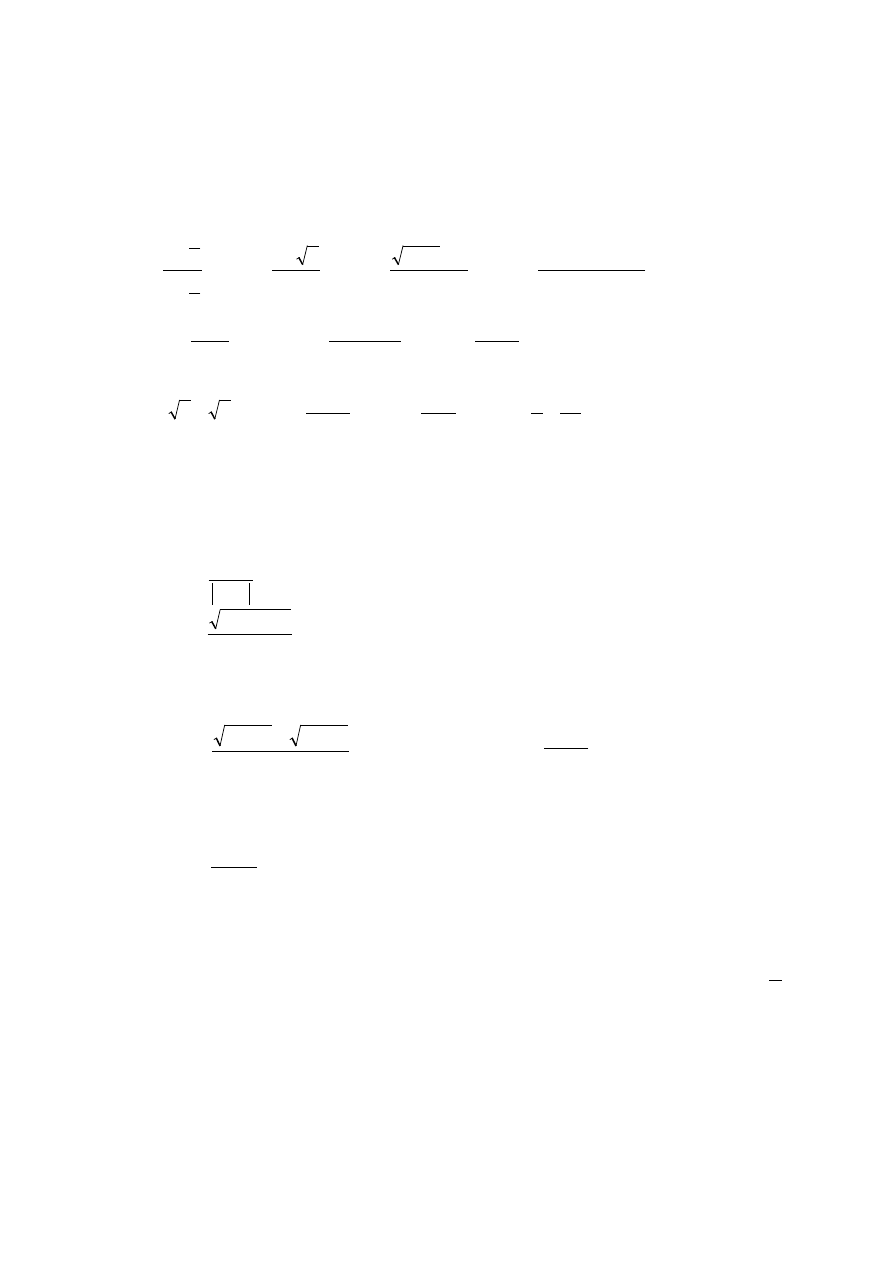
LISTA 4
21.Obliczyć granice funkcji:
.
)
1
2
1
2
(
lim
,
sin
2
cos
lim
,
)
2
1
1
(
lim
,
7
cos
3
cos
lim
,
6
2
2
lim
,
1
1
lim
,
3
sin
2
sin
lim
1
2
2
0
6
2
1
0
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
+
−
+
+
+
+
−
−
−
−
−
−
∞
→
∞
→
−
∞
→
→
→
→
→
22. Wyznaczyć jednostronne granice funkcji f(x) w podanym punkcie . Czy istnieje granica
f(x) w tym punkcie
a) f x
x
x
x
x
( )
,
,
=
−
+
≤
−
>
2
3
1
3
5
1
, w punkcie xo= 1.
b)
f x
x
x
( )
=
−
−
2
1
1
, w punkcie xo=1,
c)
f x
x
x
( )
cos
=
−
1
2
, w punkcie xo=0.
23. Zbadać ciągłość funkcji :
]
x
[
x
)
x
(
f
)
d
0
x
0
0
x
x
x
sin
)
x
(
f
)
c
2
−
=
=
≠
=
24. Czy można dobrać parametry a,b
∈
R tak, aby określone niżej funkcje były ciągłe na R:
=
≠
=
≤
≤
−
−
+
>
−
<
+
=
π
>
+
π
≤
+
=
.
0
x
,
b
0
x
,
x
a
ctg
ar
)
x
(
g
1
x
1
,
1
a
bx
2
1
x
lub
1
x
,
ax
x
)
x
(
h
,
2
/
x
,
b
x
sin
2
/
x
,
1
ax
)
x
(
f
2
25.Zbadać,czy w przedziale [1,e] funkcja f(x) = ln x + x2 -1 przyjmuje wartość
π
? Czy
funkcja f(x) przyjmuje w tym przedziale wartość najmniejszą?
).
1
1
(
lim
,
2
3
lim
,
sin
lim
),
(
lim
2
0
2
3
x
x
x
x
tg
x
x
x
x
x
x
x
x
−
−
→
∞
→
∞
→
∞
→
=
−
=
≠
−
≠
−
+
=
=
≠
−
−
+
=
,
1
x
lub
1
x
5
.
0
1
x
,
1
x
,
x
1
1
x
)
x
(
f
)
b
0
x
,
5
.
0
0
x
,
x
x
4
x
4
)
x
(
f
)
a
2
2
2
2
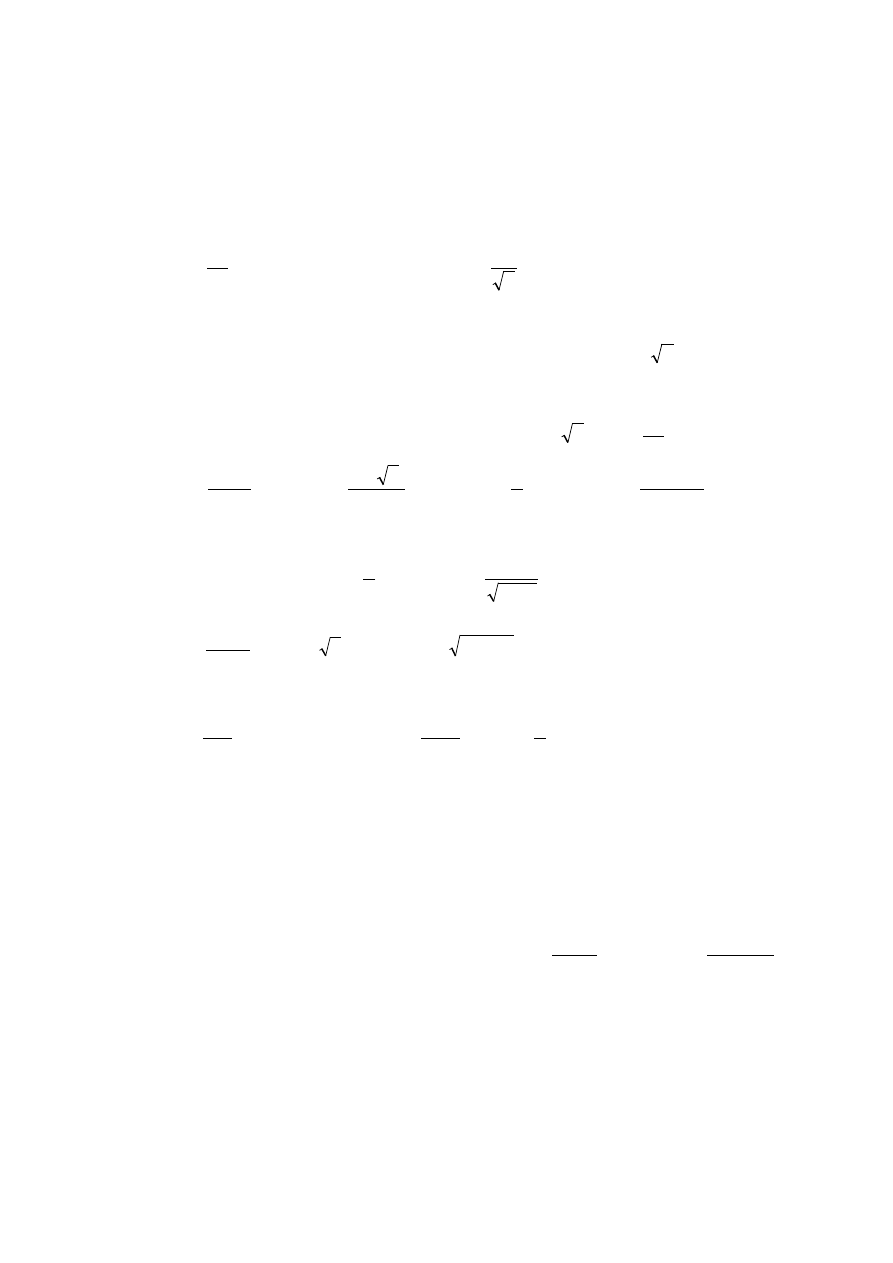
26. Uzasadnić, że równanie
1
2
=
x
x
ma tylko jeden pierwiastek dodatni. Znaleźć go w
przedziale długości 0.25.
LISTA 5
27. Korzystając z definicji obliczyć pochodne podanych funkcji :
.
1
)
(
)
,
2
sin
)
(
)
,
1
)
(
)
2
x
x
p
c
x
x
g
b
x
x
f
a
=
=
=
28*. Korzystając z twierdzenia o pochodnej funkcji odwrotnej znaleźć pochodne funkcji:
.
x
)
x
(
p
)
d
.
x
ctg
ar
)
x
(
h
)
c
,
x
3
sin
arc
)
x
(
g
)
b
,
x
log
)
x
(
f
)
a
5
2
=
=
=
=
29. Korzystając z reguł różniczkowania obliczyć pochodne podanych funkcji:
.
ln
)
(
)
,
1
)
(
)
,
2
1
)
(
)
,
sin
)
(
)
),
2
cos(
)
(
)
,
2
)
1
(
)
(
)
),
3
ln(
)
(
)
3
2
2
2
4
2
2
2
x
x
x
x
k
g
e
x
x
w
f
x
x
x
x
r
e
x
e
x
p
d
x
x
x
x
h
c
x
x
f
b
x
tg
x
f
a
x
x
x
x
−
=
=
+
−
=
=
+
=
+
=
=
−
−
30. Znaleźć pochodną n-tego rzędu funkcji:
.
2
x
1
)
x
(
h
)
c
,
3
x
cos
)
x
(
g
)
b
,
2
)
x
(
f
)
a
x
+
=
=
=
−
31. Napisać równania stycznych do wykresów funkcji we wskazanych punktach;
.
,
ln
)
(
)
,
1
,
3
)
(
)
,
2
,
1
2
)
(
)
0
2
0
3
0
2
e
x
x
x
x
h
c
x
x
x
x
g
b
x
x
x
x
f
a
=
=
=
+
=
=
+
=
32. Na wykresie funkcji f(x) znaleźć punkt , w którym prosta styczna nachylona jest do osi
Ox pod podanym kątem α
33. Punkt materialny porusza się ze zmienną prędkością po osi Ox. Położenie tego punktu w
chwili t jest opisane wzorem x(t) = 3 2t + 2-3t. Obliczyć przyśpieszenie tego punktu w
chwili, w której jego prędkość jest równa 0..
LISTA 6
34.Wyznaczyć przedziały monotoniczności funkcji:
.
x
4
x
1
)
x
(
f
)
d
;
1
x
x
2
)
x
(
f
)
c
;
x
x
cos
)
x
(
f
)
b
;
x
ln
x
2
)
x
(
f
)
a
3
2
2
2
−
=
+
=
−
=
−
=
35*.Wykazać nierówność: arctg x < x - x3/6 dla 0 <x <1.
36.Napisać wielomian Taylora stopnia n w punkcie
0
x
oraz podać postać reszty dla:
.
4
3
,
x
1
x
2
)
x
(
f
)
b
0
,
,
x
x
ln
)
x
(
f
)
a
2
π
=
α
+
−
=
=
α
=
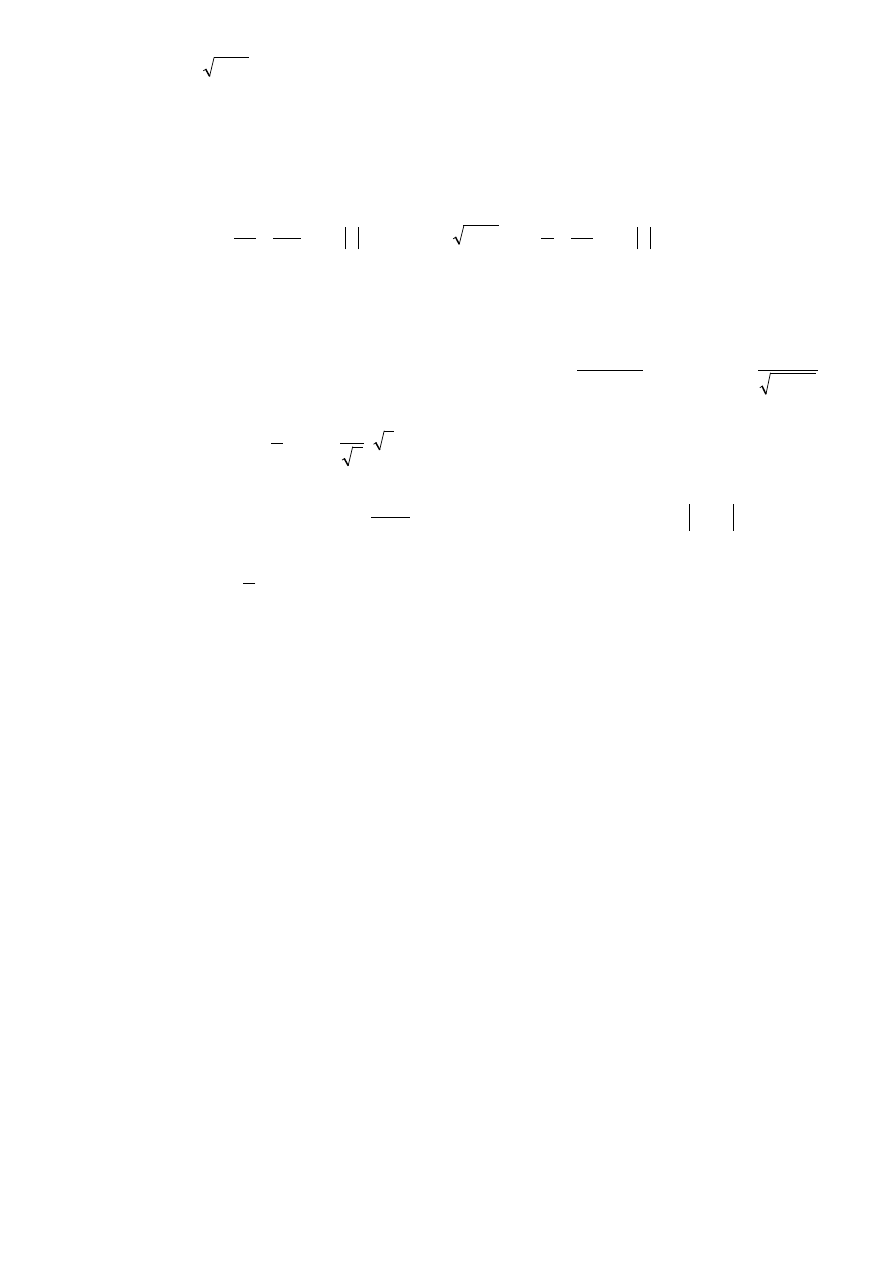
37. Wykorzystując wzór Maclaurina obliczyć:
a) sin0.2 z dokładnością do 0.00001;
b) cos1 z dokładnością do 0.00001;
c) 2
-0.5
z dokładnością do 0.0001.
38.Oszacować dokładności podanych wzorów przybliżonych na podanych przedziałach :
LISTA 7
39. Wyznaczyć ekstrema lokalne oraz zbiór wartości funkcji:
.
9
1
)
(
)
,
4
1
)
(
)
.
,
cos
3
3
cos
)
(
)
;
)
(
)
2
4
3
2
x
x
f
d
x
x
x
f
c
x
x
x
f
b
e
x
x
f
a
x
−
=
+
=
+
=
=
−
40. Wyznaczyć najmniejszą i największą wartość funkcji na wskazanym przedziale
.
2
x
0
,
x
cos
x
sin
)
x
(
f
)
b
,
]
3
,
3
1
[
,
x
ln
2
1
x
ctg
ar
)
x
(
f
)
a
π
≤
≤
+
=
−
=
.
41. Określić przedziały wypukłości i wklęsłości podanych funkcji oraz punkty przegięcia:
.
1
x
2
)
x
(
f
)
d
,
x
x
)
x
(
f
)
c
,
x
x
ln
)
x
(
f
)
b
,
x
sin
)
x
(
f
)
a
5
3
/
5
2
−
−
=
+
=
=
=
42. Zbadać przebieg zmienności podanych funkckji i następnie sporządzić ich wykresy:
a f x
x
x
b f x
x
x
) ( )
,
) ( )
ln(
).
= +
=
+
1
4
2
2
2
43.Danych jest n liczb : a
1
,a
2,
...,a
n
. Znaleźć x , dla którego wyrażenie
∑
=
−
n
i
i
a
x
1
2
)
(
ma
najmniejsza wartość.
LISTA 8
44. Sprawdzić, że funkcje f(x) = 2sin2x, g(x) = - cos2x są funkcjami pierwotnymi tej samej
funkcji.
45. Ciało porusza się po prostej z prędkością :
a) v(t) = t3- 1,
b) v(t) = 2-t
i w chwili t = 0 znajduje się w początku osi. Czy (i w jakiej chwili ) ciało znajdzie się
ponownie w punkcie początkowym? Jaka część osi jest torem ruchu?
46. Obliczyć całki nieoznaczone następujących funkcji:
.
3
n
,
1
x
x
ln
x
)
x
(
f
)
b
3
n
,
3
x
,
1
x
)
x
(
f
)
a
o
2
o
=
=
+
=
=
=
+
=
2
.
0
x
,
8
x
2
x
1
1
x
)
b
1
.
0
x
,
120
x
6
x
x
x
sin
)
a
2
5
3
≤
−
+
≈
+
≤
+
−
≈

x
ln
x
x
ln
1
,
x
x
1
,
)
2
x
(
2
x
4
,
x
1
1
1
)
f
.
)
x
(sin
,
x
tg
,
x
5
sin
x
3
sin
)
e
,
x
5
x
2
x
10
x
,
10
x
3
x
7
,
)
1
x
(
x
3
x
2
,
x
x
x
2
1
x
)
d
4
x
2
x
,
e
1
e
,
x
sin
x
cos
,
)
x
exp(
x
,
4
x
3
1
)
c
,
x
2
cos
e
,
x
sin
x
,
x
ln
x
,
x
1
ctg
ar
,
10
x
)
b
,
x
cos
3
1
x
sin
,
)
x
ln
1
(
x
1
,
x
cos
1
x
sin
,
x
2
x
,
x
tg
)
a
4
3
1
2
3
2
2
2
3
4
2
3
3
2
x
2
x
5
2
3
x
2
2
2
x
2
2
2
+
+
−
+
+
+
+
−
+
−
−
+
+
−
−
+
+
+
+
+
+
+
−
LISTA 9
47. Korzystając z z interpretacji geometrycznej całki oznaczonej obliczyć
(
)
,
[ ]
,
.
2
1
4
1
3
1
4
2
2
2
x
dx
x dx
x dx
+
−
∫
∫
∫
−
−
48.Obliczyć całki oznaczone:
dx
x
9
)
d
.
dx
x
tg
)
c
,
x
1
dx
)
b
,
x
dx
)
x
sin(ln
)
a
1
0
2
4
0
4
/
4
/
e
1
∫
∫
∫
∫
−
+
π
π
−
49 Udowodnić, że:
f x dx
f a
x dx
a
a
( )
(
)
.
0
0
∫
∫
=
−
50. Obliczyć pola obszarów ograniczonych podanymi krzywymi:
a) yx
4
=1, y = 1, y = 16.
b) y = 2x - x
2
,
x + y =0.
c) y = 2
x
, y = 2, x = 0.
51. Obliczyć długości podanych łuków :
a) y
x
x
=
≤ ≤
2
0
11
3
,
c*) y
chx
x
=
≤ ≤
,0
1
.
2
1
,
4
)
2
≤
≤
−
=
x
x
y
b

Wyszukiwarka
Podobne podstrony:
Matematyka 1 zadania z I semestru budownictwa (analiza mat)
Matematyka 1 zadania z I semestru budownictwa (analiza mat)
lab8 analiza mat I
lab8 analiza mat I
Analiza mat I semstr wykłady
Zagadnienia na egzamin [analiza mat. dla leniwych], Matematyka stosowana, Analiza, Analiza matematyc
lab9 analiza mat II
calki+krzywoliniowe, I semstr moje materiały, Matematyka 1 Semsetr, analiza mat zadania
Projekt 2 IE analiza mat(1)
analiza mat-zagadnienia, Fizyka Medyczna UŚ Katowice, Analiza Matematyczna
radzik tadeusz analiza mat 1 internet
Analiza Mat Rachunek rózniczkowy i całkowy funkcji wielu zmiennych
więcej podobnych podstron