Metoda połowienia
Używamy, by policzyć minimum/maksimum funkcji jednej zmiennej (czyli tylko x). Możemy wykorzystać, gdy mamy możliwość policzenia tylko
niektórych punktów.
Pseudokod:

1. Otrzymujemy wzór f(x)=Ax^3+Bx^2+Cx+D lub podobny, oraz przedział <a;b> lub (a;b). Mamy ustalone lub wymyślamy sobie pewne EPS

lub ilość iteracji.

2. L = b-a
3. x

m

= (a+b)/2

4. x

1

= a + 0.25 * L

5. x

2

= b – 0.25 * L

6. f

min

= min{f(x

1

), f(x

2

), f(x

m

)} // jeśli szukamy maksimum to wybieramy max

7. jeśli |x

2

-x

1

|<EPS lub wykonano dostatecznie dużo iteracji to zakończ a wynik to argument x f

min

8. jeśli f

min

=f(x

m

) to a=x

1

, b=x

2

i idź do kroku 2

9. jeśli f

min

=f(x

1

) to b=x

m

i idź do kroku 2

10. jeśli f

min

=f(x

2

) to a=x

m

i idź do kroku 2

Przykład: Znajdź minimum funkcji f(x) = 5x^2 – 12x – 3 w przedziale <0;2>
Iteracja 1
a

1

= 0

b

1

= 2

L

1

= 2

x

m1

= 1, f(1) = 5 – 12 – 3 = -10

x

11

= 0 + 0.25 * 2 = 0.5 f(0.5) = -7.75

x

21

= 2 – 0.25 * 2 = 1.5 f(1.5) = -9.75

Iteracja 2
a

2

= 0.5 // bo w poprzednim kroku fmin = f(xm)

b

2

= 1.5

L

2

= 1

x

m2

= 1 f(1) = -10

x

12

= 0.5 + 0.25 * 1 = 0.75 f(0.75) = -9.1875

x

22

= 1.5 – 0.25 * 1 = 1.25 f(1.25) = -10.1875

Iteracja 3
a

3

= 1

b

3

= 1.5 // w poprzednim kroku fmin = f(x2) wiec b bez zmian

L

3

= 0.5

x

m

= 1.25 f(1.25) = -10.1875

x

13

= 1 + 0.25 * 0.5 = 1.125 f(1.125) = -10.1719

x

23

= 1.5 – 0.25* 0.5 = 1.375 f(1.375) = -10.0469

3-4 iteracje to zazwyczaj dość, można przyjąć, że minimum tej funkcji w tym przedziale to
-10.1875 dla x = 1.25

Metoda złotego podziału
Tak samo, jak przy połowieniu. Używamy do funkcji jednej zmiennej, korzystamy gdy nie wszystkie punkty są dostępne.
Pseudokod:

1. Otrzymujemy wzór f(x)=Ax^3 + Bx^2+Cx+D lub podobny, oraz przedział <a;b> lub (a;b). Mamy ustalone lub wymyślamy sobie pewne EPS

lub ilość iteracji.

2. L = b-a
3. Alfa = b – 0.618 * L
4. Beta = a + 0.618 * L
5. jeśli |beta-alfa|<EPS lub wykonano dostatecznie dużo iteracji to zakończ a wynik to (beta+alfa)/2
6. jeśli f(alfa) < f(beta) to b=betaP, beta=alfaP, alfa = b – 0.618*L, L=b-a, przejdź do kroku nr 5 // w przypadku szukania maksimum

odwracamy znak nierówności, duże P oznacza, że chodzi o wartość tej zmiennej z poprzedniej iteracji, jeśli zmienna nie jest podana to
zostaje jaka była

7. jeśli f(alfa) > f(beta) to a=alfaP, alfa=betaP, beta=a+0.618*L, L=b-a, przejdź do kroku nr 5 // tutaj też odwracamy jeśli szukamy

maksimum

Przykład: Znajdź minimum funkcji f(x) = 5x^2 – 12x – 3 w przedziale <0;2>
Iteracja 1
a = 0
b = 2
L = 2
Alfa = 2 – 0.618 * L = 0.764, f(alfa) = -9.2495
Beta = 1.236, f(beta) = -10.1935
Iteracja 2
a = 0.764
b = 2
L = 1.236
Alfa = 1.236 f(alfa) = -10.1935
Beta = 1.5278 f(beta) = -9.6627
Iteracja 3
a = 0.764
b = 1.5278

L = 0.7638
alfa = 1.0557
beta = 1.236
4 iteracja
a = 1.0557
b = 1.5279
L = 0.4722
Alfa = 1.2361
Beta = 1.3475
3-4 iteracje to zazwyczaj dość, możemy przyjąć, że minimum to 1,2918 (w rzeczywistości 1,2000)

Metoda zmodyfikowanego połowienia
Wykorzystujemy, gdy musimy znaleźć minimum/maksimum funkcji jednej zmiennej, kiedy to minimum znajduje się na samym krańcu
przedziału. Kolejne iteracje są niejako dla picu, żeby tylko zbliżać się do minimum.
Pseudokod:

1. Otrzymujemy punkt a, który wiemy, że jest minimum.
2. Jeśli punkt ten znajduje się na lewym krańcu przedziału to b = prawy kraniec. Jeśli na prawym to b = lewy kraniec.
3. Jeśli a to lewy kraniec, to d = (b-a)/4, b = b - d. Jeśli a to prawy kraniec, to d = (a-b)/4, b = b + d.
4. Powtarzamy 3 krok, aż uznamy, że dokładność jest zadowalająca.

Przykład:
Znaleźć maksimum funkcji x^3 – 2x^2 – 2.
Wiadomo, że maksimum jest w punkcie x = 3, co widać z wykresu. Więc dążymy do tego punktu:

A = 3

B = -1

D = 1

A = 3

B = 0

D = 0,75

A = 3

B = 0,75

D = 0,5625

A = 3

B = 1,3125

D = 0,421875

Kolejne iteracje wyraźnie pokazują, że lewy kraniec b zbiega do punktu a.

Metoda algebraiczna
Wykorzystujemy, gdy musimy znaleźć maksimum lub minimum danej funkcji celu mając podane kilka ograniczeń w postaci nierówności zawarte
w klamrze.
Pseudokod:

1. Otrzymujemy funkcję celu typu F = Ax + By + C oraz ograniczenia w postaci nierówności zawarte w klamrze
2. Przekształcamy ograniczenia tak, aby każdy wyraz wolny (czyli liczba nie mająca x ani y przy sobie) był dodatni. Jeśli trzeba przemnażamy

nierówność przez -1.

3. Zamieniamy nierówności na równania, dodając jednocześnie po jednej zmiennej do każdego równania
4. Uwzględniamy dodatkowe zmienne w funkcji celu, dodając je z mnożnikiem 0
5. Rozwiązujemy kolejno układy równań biorąc kolejno 2 zmienne jako 0. Tworzy się w ten sposób pewna liczba kombinacji, gdyż musimy

sprawdzić wszystkie możliwe warianty 2 zmiennych.

6. Powstałe wyniki sprawdzamy, czy spełniają założenia – wszystkie zmienne muszą być nieujemne. Obliczamy dla powstałych liczb

wartość funkcji celu

7. Wybierają największą (w przypadku szukania maksimum) lub najmniejszą (w przypadku szukania minimum) wartość funkcji celu jako

wynik.

Przykład:
Znajdź maksimum funkcji celu Z = 300x + 200y przy ograniczeniach 2x + 2y <= 10, 3x + 3y <= 24, 2x <= 8.

Wszystkie wyrazy wolne (10, 24, 8) są dodatnie, więc nie trzeba mnożyć niczego przez -1.
Zamieniamy nierówności na równania:
2x + y + a = 10 // a – pierwsza zmienna dodatkowa
3x + 3y + b = 24 // b – druga zmienna dodatkowa
2x + c = 8 // c – trzecia
Nowa funkcja celu: Z = 300x + 200y + 0a + 0b + 0c
Bierzemy kolejne kombinacje 2 zmiennych z 5 i zakładamy, że są one zerami:
x = y = 0
a = 10
b = 24
c = 8
Z = 300*0 + 200*0 + 0*10 + 0*24 + 0*8 = 0 rozwiązanie dopuszczalne

x = a = 0
y = 10
3y + b = 24, b = -6 rozwiązanie niedopuszczalne, b jest ujemne
c = 8

x = b = 0
y + a = 10, a = 2
3y = 24, y = 8
2x + c = 8, c = 8
Z = 300*0 + 200*8 + 0*2 + 0*0 + 0*8 = 1600

x = c = 0
y + a = 10
3y + b = 24
0 + 0 = 8 układ sprzeczny, rozwiązanie niedopuszczalne

y = a = 0
2x = 10, x = 5
3x + b = 24, b = 9
2x + c = 8, c = -2 rozwiązanie niedopuszczalne

y = b = 0 (…) rozwiązanie niedopuszczalne
y = c = 0 (…) Z = 1200
a = b = 0 (…) x = 2, y = 6, a = 0, b = 0, c = 0, Z = 1800
a = c = 0 (…) Z = 1600
b = c = 0 (…) rozwiązanie niedopuszczalne
Odpowiedź: Funkcja osiąga maksimum dla x = 2 i y = 6.

Metoda mnożników Lagrange dla równania
Wykorzystujemy gdy mamy jedno „konkretne” ograniczenie (tzn. inne niż x > 0 x >=0 y > 0 y>= 0) w postaci równania.

Pseudokod:

1. Przerabiamy ograniczenie tak, aby po jednej ze stron mieć tylko 0. Przerzucamy na drugą stronę zmienne x i y.
2. Zapisujemy przerobione ograniczenie i ew. inne (x > 0 i y > 0) w jednej klamerce

3.

Zapisujemy wzór: L = <wzor z zadania> +

λ(

<strona ograniczenia nie będąca zerem>)

4.

Liczymy kolejne pochodne cząstkowe z wyrażenia L po x, po y i po lambda.

5.

Przyrównujemy otrzymane pochodne do zera i traktujemy jak układ równań. Rozwiązujemy go i otrzymujemy x, y, lambda.

6.

Jeśli otrzymujemy kilka wyników to sprawdzamy wartości w otrzymanych punktach i wybieramy najmniejszy/największy.

Przykład:
Znaleźć minimum funkcji f = x^2 + y^2 przy ograniczeniu x+y=1
Przerzucamy zmienne x i y w ograniczeniu: 1 – x – y = 0
Tworzymy funkcje Lagrange: L = x^2 + y^2 +

λ

(1 – x – y)

Liczymy pochodne cząstkowe:
𝜕𝐿
𝜕𝑥

= (𝑥

2

)

′

−

λ(x

′

) = 2x − λ

𝜕𝐿

𝜕𝑦

= (𝑦

2

)

′

−

λ(y

′

) = 2y − λ

𝜕𝐿

𝜕

λ

= 1 − 𝑥 − 𝑦 // przepisujemy to co w nawiasie lambda

Rozwiązujemy powstały układ równań:
2x –

λ = 0

2y - λ = 0

1-x-y = 0
Wynik:
x = y = ½
λ = 1

Metoda mnożników Lagrange dla nierówności
Używamy, gdy mamy tylko jedno konkretne ograniczenie w postaci nierówności.
Pseudokod:

1. Przerzucamy zmienne w ograniczeniu na drugą stronę tak, by mieć 0 po jednej ze stron ograniczenia.
2. Zapisujemy x>=0 i y>=0.
3. Wypisujemy wszystkie założenia: pochodne cząstkowe po x i y <= 0, pochodna cząstkowa po lambda >= 0, pochodne cząstkowe

przemnożone odpowiednio przez x, y i lambda = 0.

4. Zapisujemy funkcję Lagrange: L = (x,y,lambda) = wzór z zadania + lambda(ograniczenie)
5. Liczymy pochodne cząstkowe
6. Zapisujemy pochodne cząstkowe pomnożone odp. Przez x, y i lambda = wynik liczenia pochodnej razy x/y/lambda = 0.
7. Znajdujemy wszystkie możliwe rozwiązania niejako zgadując: cały czas podstawiamy sobie 0 za jedna bądź dwie zmienne i próbujemy

rozwiązać układ. Wypisujemy wszystkie wyniki, które spełniają założenia zadania i założenia pochodnych.

8. Obliczamy wartości w otrzymanych wynikach i wybieramy najmniejszą/największą.

Przykład:
Znajdź minimum funkcji (x-2)^2 + (2y-1) z ograniczeniem x + y <= 5.
x + y <= 5  5 – x – y >= 0
x >= 0
y >= 0
𝜕𝐿
𝜕𝑥

≤ 0

𝜕𝐿
𝜕𝑦

≤ 0

𝜕𝐿

𝜕λ

≥ 0

𝑥

𝜕𝐿
𝜕𝑥

= 0 𝑦

𝜕𝐿
𝜕𝑦

= 0 λ

𝜕𝐿

𝜕λ

= 0

L(x,y,λ) = (x-2)^2 + (2y-1) + λ(5-x-y)

𝜕𝐿

𝜕𝑥

= ((𝑥 − 2)

2

)

′

− λ(x

′

) = (𝑥

2

− 4𝑥 + 4)

′

− λ = 2x − 4 − λ

𝜕𝐿

𝜕𝑦

= (2𝑦 − 1)

′

− λ(y

′

) = 2 − λ

𝜕𝐿

𝜕λ

= 5 − 𝑥 − 𝑦

𝑥

𝜕𝐿

𝜕𝑥

= 𝑥(2x − 4 − λ) = 0

𝑦

𝜕𝐿

𝜕𝑦

= 𝑦(2 − λ) = 0

λ

𝜕𝐿

𝜕λ

= λ(5 − 𝑥 − 𝑦) = 0

Rozwiązania:
x = 0, y = 0,

λ = 0 f(0,0) = 4 – 1 = 3

x = 0, y = 5,

λ = 2 f(0,5) = 4 + 10 – 1 = 13

x = 2, y = 0,

λ = 0 f(2,0) = 0 – 1 = -1

x = 2, y = 3,

λ = 2 f(2,3) = 0 + 6 – 1 = 5

x = 5, y = 0,

λ = 2 f(5,0) = 9 – 1 = 8

Odpowiedz: Minimum tej funkcji w tym przedziale to punkt x = 2, y = 0.

Metoda Simpleks (tylko pierwsza tablica)
Używamy by znaleźć minimum/maksimum funkcji gdy mamy kilka ograniczeń w klamerce.
Pseudokod:

1. Jeśli wyrazy wolne w ograniczeniach są ujemne to przemnażamy to ograniczenie przez -1.
2. Zamieniamy nierówności na równania dodając zmienne pomocnicze.
3. Zapisujemy równania w postaci macierzowej uwzględniając wszystkie zmienne w każdym równaniu.
4. Zapisujemy tablicę simpleksów w odpowiedni sposób, patrz przykład.

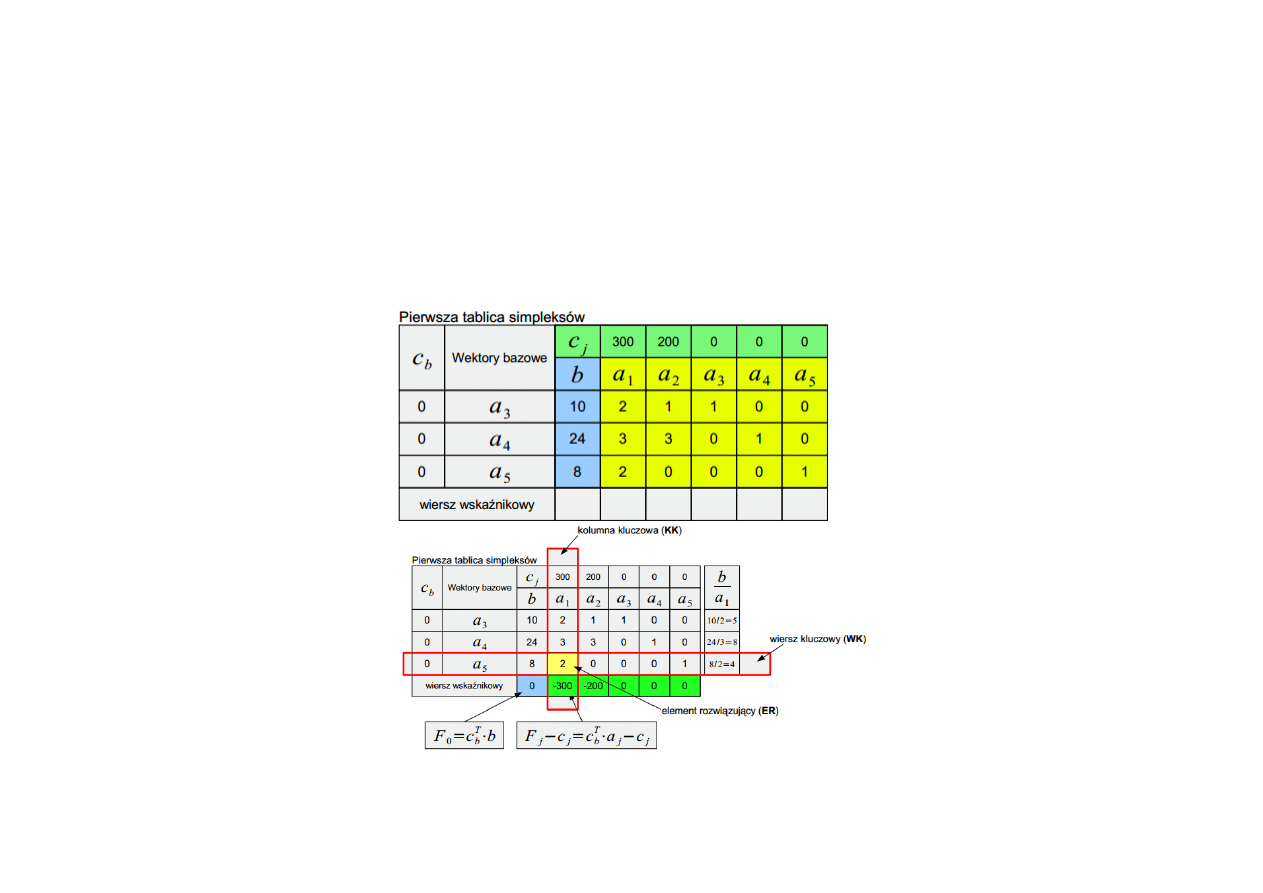
Przykład:
Zmaksymalizuj funkcję F = 300x + 200y przy ograniczeniach 2x + y <= 10, 3x + 3y <= 24, 2x <= 8
Ograniczenia:
2x + y + a = 10
3x + 3y + b = 24
2x + c = 8
Ograniczenia w postaci macierzowej:
Z = 300x + 200y + 0a + 0b + 0c
2x + y + a + 0b + 0c = 10
3x + 3y + 0a + b + 0c = 24
2x + 0y + 0a + 0b + c = 8
a1 a2 a3 a4 a5
2 1 1 0 0 x1 10
A = 3 3 0 1 0 x2 B = 24
2 0 0 0 1 X = x3 8
x4
x5

Zadania egzaminacyjne

Jak rozwiązać?
Można wykorzystać podane na wykładzie zadanie. Wystarczy ładnie przerobić liczby i dobrać inną otoczkę słowną. Najłatwiej wykorzystać
metodę graficzną. Rzeczone zadanie to:

Pewien zakład produkuje dwa typy płytek chodnikowych. Oba typy wymagają zużycia jednakowej ilości surowców (piasek,
woda, żwir, cement). Jeden typ jest barwny i do jego produkcji potrzebna jest farba. Wyprodukowanie 1 tony płytek barwnych
wymaga 2h pracy maszyn, 3h pracy ludzkiej i 2l barwnika. Produkcja tony płyt bezbarwnych wymaga 1h pracy maszyn, 3h pracy ludzkiej.
Zysk: płyty barwne 300 zł/t, płyty bezbarwne 200 zł/t. Dysponujemy 10h pracy urządzeń, 24h pracy ludzkiej i 8l barwnika. Ile
wyprodukować płyt i jakich aby osiągnąć maksymalny zysk.
Do pomocy należy wykorzystać program do metody graficznej z Matlaba.

Rozwiązanie:
Wymyśl coś samodzielnie.

Jak rozwiązać?
Główny problem to dotarcie do okolic, gdzie wartości funkcji są różne od wszechobecnego zera. Nie jest jasne, czy można wykorzystać wiedzę z
rysunku, że punkt minimalny znajduje się w okolicy 0,0 (bądź nim jest). Jeśli tak to można jasno ująć, że przemieszczamy się w okolicę środka
obszaru a następnie korzystamy z jednej z metod optymalizacji dla funkcji dwóch zmiennych. Warto napisać notatkę na początku rozwiązania,
że wiemy o co chodzi tylko nie wiemy jaką wiedzę mamy do dyspozycji (czy np. możemy założyć, że wzór funkcji jest znany czy nie).
Analogicznie słowa minimum, mniejszy itp. Zastępujemy maksimum, większy itp. Jeśli będziemy musieli znaleźć maksimum funkcji.
Rozwiązanie:
Korzystając z wykresu można szacować punkt minimalny na 0,0. W tym celu aby algorytm poszukujący „nie błądził” po obszarach zmiennych
funkcji, gdzie wartości wszędzie wynoszą 0, jest on nakierowywany w stronę punktu 0,0 dopóki wartości są równe 0. Jeśli możemy uznać, że
znamy wzór funkcji lub mamy możliwość obliczenia bądź oszacowania ostatnich argumentów zmiennych, gdzie funkcja ma wartości mniejsze
niż 0 to w algorytmie można by było założyć dążenie do tych zakresów aniżeli konkretnie do punktu 0,0.
Krok 1. Wybierz punkt startowy S i krok k.
Krok 2. Sprawdź wartości funkcji w punktach P(x+krok,y) P(x-krok,y) P(x,y+krok) P(x,y-krok) gdzie P to punkt w którym obecnie jest algorytm a x
i y to jego współrzędne.
Krok 3. Jeśli wszystkie wartości wynoszą 0 to wybierz nowy punkt z podanych 4 w poprzednim kroku tak, aby poruszać się w stronę środka
zakresu wartości (czyli w stronę punktu 0,0) i powtórz krok 2.
Krok 4. Jeśli któraś z wartości jest różna od 0 to wybierz punkt o najmniejszej wartości z podanych. Jeśli wszystkie punkty mają wartości większe
bądź równe niż punkt w którym obecnie jest algorytm to zakończ a punkt ten uznaj za minimum. W przeciwnym wypadku przejdź do punktu 2.

Jak rozwiązać?
W pierwszej kolejności należy nawet byle jak narysować sobie wykres tej funkcji żeby widzieć jak ona wygląda oraz obliczyć wartości w
punktach krańcowych (tutaj -1 i 3) nawet jeśli nie należą one do przedziału. Możliwe jest, że funkcja osiągałaby minimum w którymś z nich, ale
jeśli nie należą do przedziału to znalezienie dokładnego minimum jest niemożliwe, można tylko osiągać coraz bliższą dokładność. Ponadto
wtedy klasyczne metody mogą dać złe wyniki:

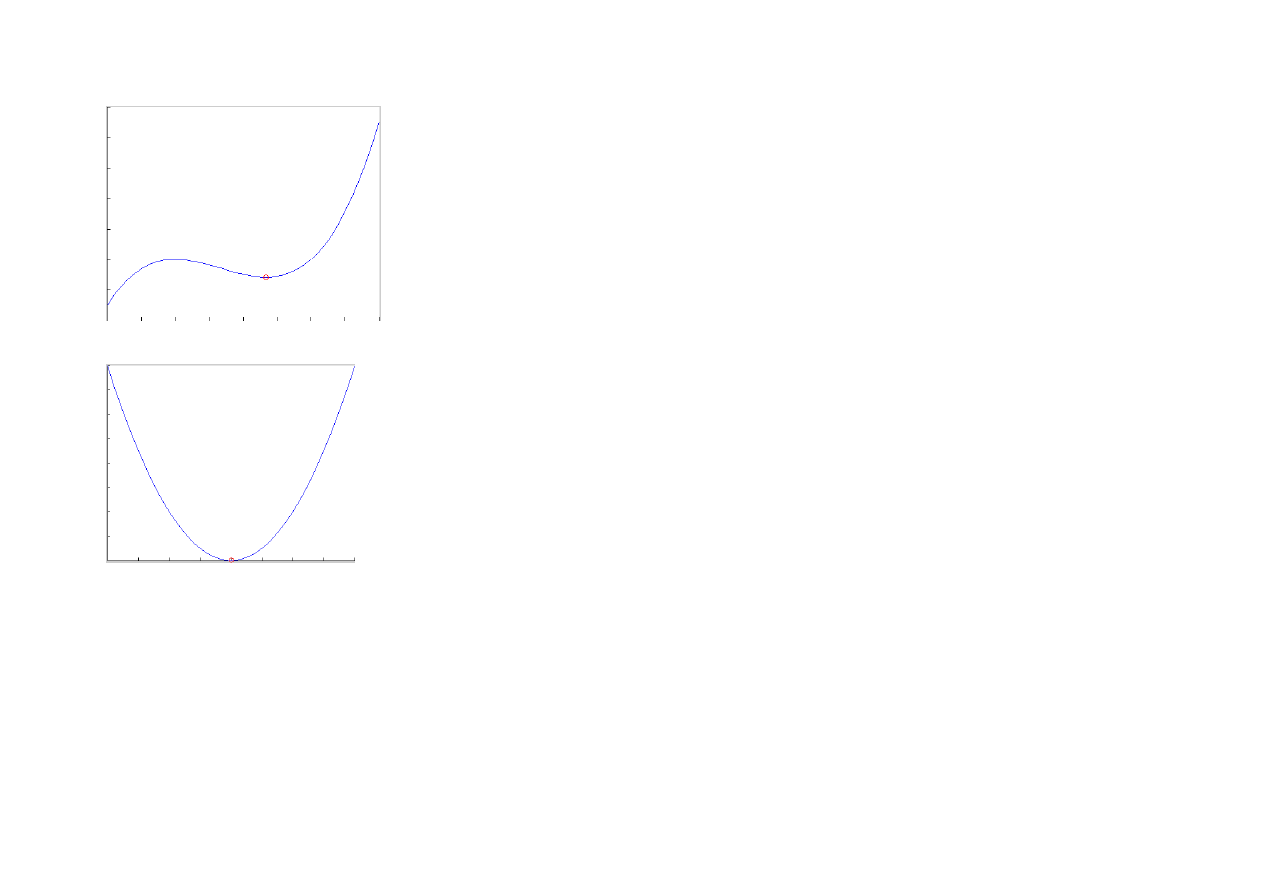
Klasyczna metoda złotego podziału znajduje LOKALNE minimum a nie minimum z całego przedziału.
Metody złotego podziału używamy, jeśli bez cienia wątpliwości minimum znajduje się gdzieś w środku przedziału, np.:

Jeśli minimum może znajdować się na krańcach przedziału (a na zaliczeniu tak zapewne będzie) to korzystamy ze zmodyfikowanej metody
połowienia. Należy też zaznaczyć, że korzystamy z metod bezgradientowych, ponieważ nie mamy możliwości liczenia pochodnej w każdym
punkcie jeśli mamy dostępne tylko niektóre punkty.
Rozwiązanie:
Wykorzystam zmieniony algorytm połowienia, ponieważ minimum funkcji znajduje się w punkcie -1, który nie należy do przedziału. W związku z
tym kolejne iteracje mogą tylko zwracać liczbę zbliżającą się do -1. Nie można użyć metod bezgradientowych, ponieważ nie mamy możliwości
liczenia pochodnej w każdym punkcie.

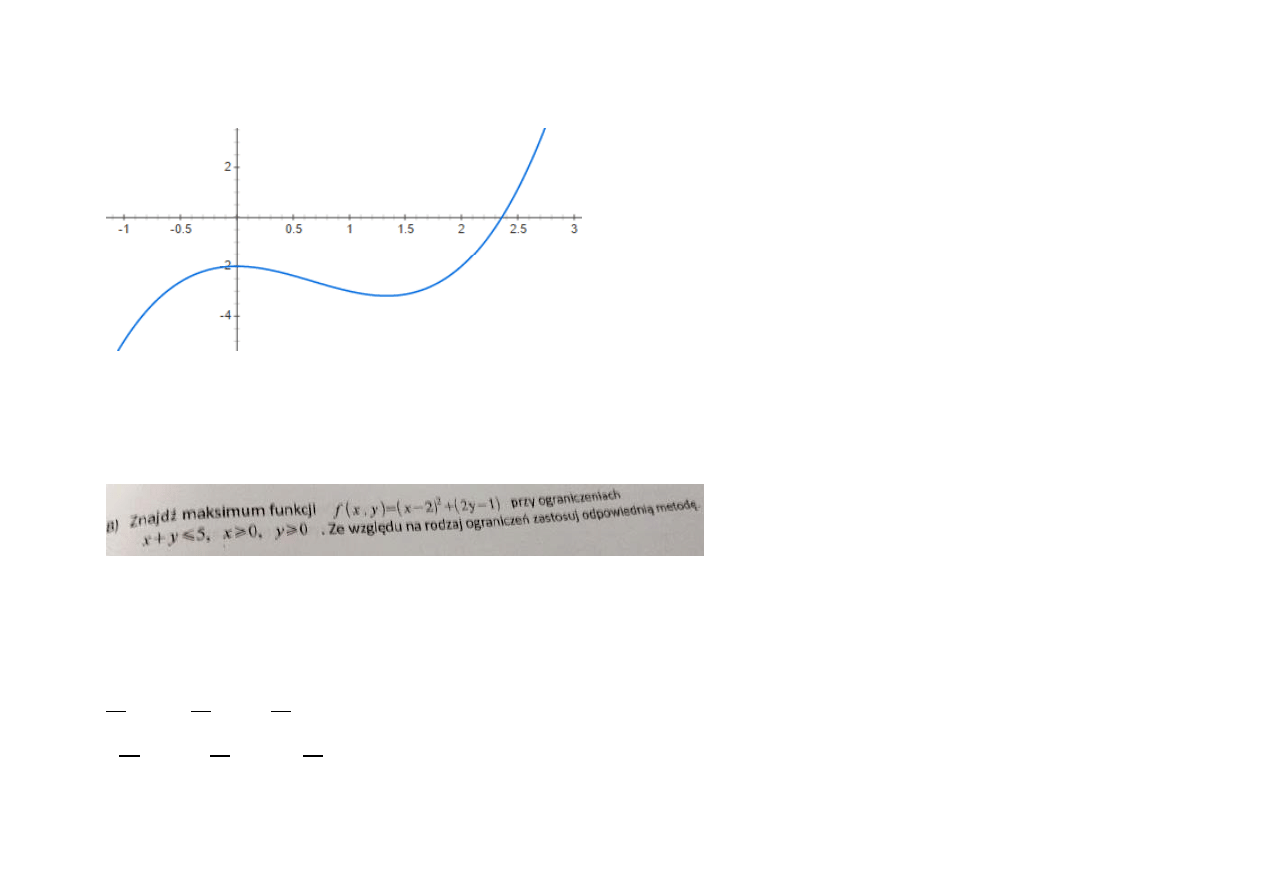
Wykres funkcji:

Wiadomo, że wartość minimalną funkcja osiągnęłaby w punkcie -1. Dążymy do niego poprzez kolejne iteracje:

A = -1

B = 3

D = 1

A = -1

B = 2

D = 0,75

A = -1

B = 1,25

D = 0,5625

A= -1

B = 0,6875

D = 0,421875

Widać wyraźnie, że minimum zbiega do punktu –1.

Jak rozwiązać?
Mamy tylko jedno „konkretne” ograniczenie (x+y <= 5), więc stosujemy metodę mnożników Lagrange dla nierówności.
Rozwiązanie:
x + y <= 5, 5 – x – y > = 0 // (x-2)^2 + (2y-1)
x >= 0
y >= 0
𝜕𝐿
𝜕𝑥

≤ 0

𝜕𝐿
𝜕𝑦

≤ 0

𝜕𝐿

𝜕λ

≥ 0

𝑥

𝜕𝐿
𝜕𝑥

= 0 𝑦

𝜕𝐿
𝜕𝑦

= 0 λ

𝜕𝐿

𝜕λ

= 0

L(x,y,λ) = (x-2)^2 + (2y-1) + λ(5-x-y)

𝜕𝐿

𝜕𝑥

= ((𝑥 − 2)

2

)

′

− λ(x

′

) = (𝑥

2

− 4𝑥 + 4)

′

− λ = 2x − 4 − λ

𝜕𝐿

𝜕𝑦

= (2𝑦 − 1)

′

− λ(y

′

) = 2 − λ

𝜕𝐿

𝜕λ

= 5 − 𝑥 − 𝑦

𝑥

𝜕𝐿

𝜕𝑥

= 𝑥(2x − 4 − λ) = 0

𝑦

𝜕𝐿

𝜕𝑦

= 𝑦(2 − λ) = 0

λ

𝜕𝐿

𝜕λ

= λ(5 − 𝑥 − 𝑦) = 0

Rozwiązania:
x = 0, y = 0,

λ = 0 f(0,0) = 4 – 1 = 3

x = 0, y = 5,

λ = 2 f(0,5) = 4 + 10 – 1 = 13

x = 2, y = 0,

λ = 0 f(2,0) = 0 – 1 = -1

x = 2, y = 3,

λ = 2 f(2,3) = 0 + 6 – 1 = 5

x = 5, y = 0,

λ = 2 f(5,0) = 9 – 1 = 8

Odpowiedz: Maksimum tej funkcji w tym przedziale to punkt x = 0, y = 5.

Jak rozwiązać?
Należy zwrócić uwagę na jeden ujemny wyraz wolny. Mnożymy wyrażenie przez -1, reszta idzie wg schematu.
Rozwiązanie:
2x + y + a = 12

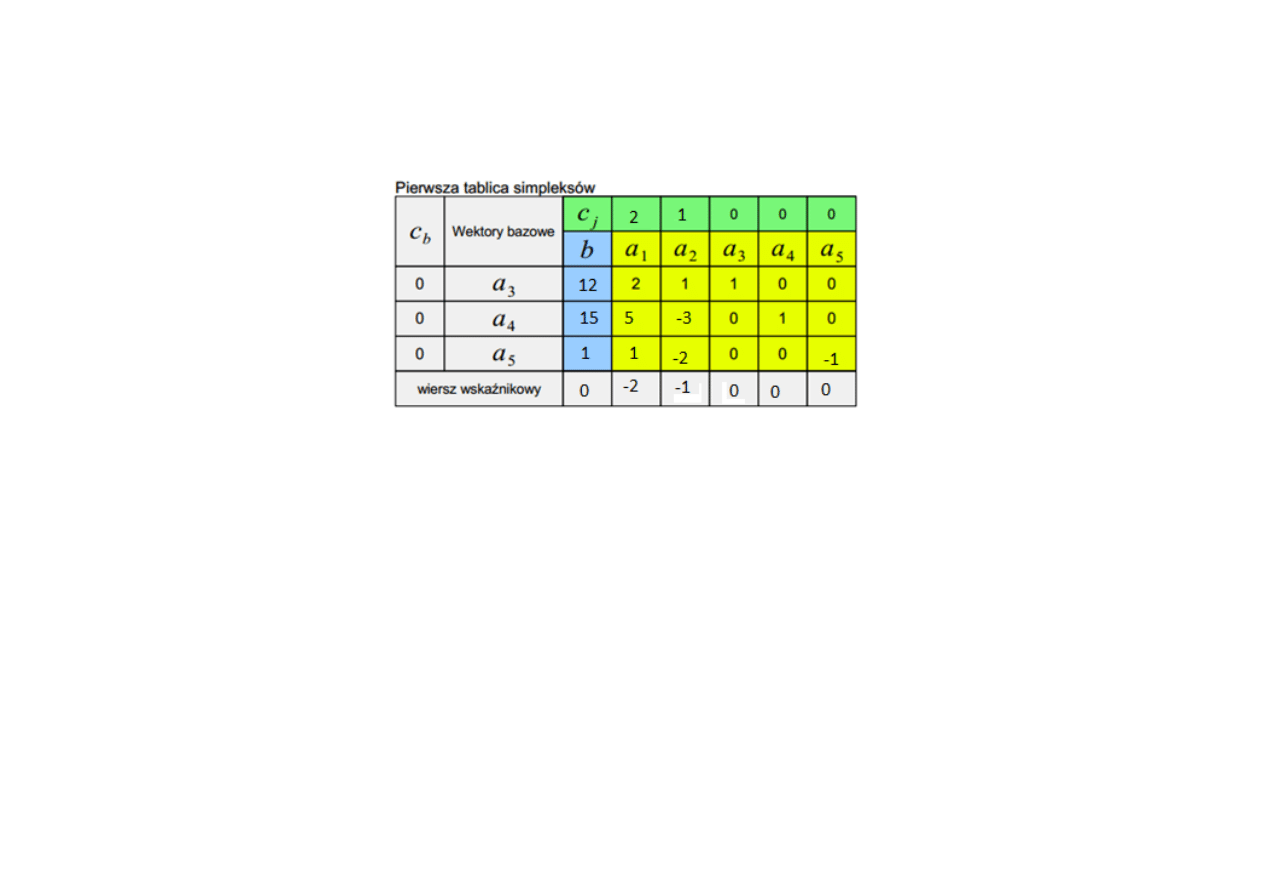
5x – 3x + b = 15
x – 2y – c = 1 // najpierw dodajemy dodatkową zmienną a potem przez -1. Dlatego przy c jest minus.

Z = 2x + y + 0a + 0b + 0c
2x + y + a + 0b + 0c = 12
5x – 3x + 0a + b + 0c = 15
x – 2y + 0a + 0b – c = 1
a1 a2 a3 a4 a5 x1
A = 2 1 1 0 0 x2 12
5 -3 0 1 0 X = x3 B = 15
1 -2 0 0 -1 x4 1
x5