P

o

d

s

ta

w

y

w

y

m

ia

ro

w

a

n

ia

P

o

d

s

ta

w

y

w

y

m

ia

ro

w

a

n

ia

w

s

ta

n

ie

g

ra

n

ic

zn

y

m

n

o

n

o

c

i

w

s

ta

n

ie

g

ra

n

ic

zn

y

m

n

o

n

o

c

i

W

y

m

ia

ro

w

a

n

ie

ko

n

st

ru

kc

ji

p

o

le

g

a

n

a

d

o

b

o

rze

w

y

m

ia

ró

w

i

kszt

a

łt

u

p

rze

kr

o

jó

w

e

le

m

e

n

tó

w

.

P

o

d

st

a

w

d

o

b

o

ru

je

st

p

o

ró

w

n

a

n

ie

:

w

y

tr

zy

m

a

ło

m

a

te

ri

a

łu

-

n

a

p

r

e

n

ie

zr

e

d

u

k

o

w

a

n

e

lu

b

n

o

n

o

p

rze

k

ro

ju

-

s

ił

w

e

w

n

tr

zn

e

W

st

a

n

ie

g

ra

n

iczn

y

m

ko

rzy

st

a

m

y

z

w

ie

lk

o

ci

o

b

licze

n

io

w

y

ch

.

O

b

licze

n

io

w

a

w

y

tr

z

y

m

a

ło

m

a

te

ri

a

łu

g

d

zi

e

:

R

k

-

w

y

tr

z

y

m

a

ło

ch

a

ra

kt

e

ry

st

y

czn

a

,

γ

m

-

w

sp

ó

łcz

y

n

n

ik

b

e

zp

ie

cze

st

w

a

(γ

m

≥

1

.0

)

a

R

≤

R

k

m

k

R

R

γ

=

P

o

d

s

ta

w

y

w

y

m

ia

ro

w

a

n

ia

P

o

d

s

ta

w

y

w

y

m

ia

ro

w

a

n

ia

w

s

ta

n

ie

g

ra

n

ic

zn

y

m

n

o

n

o

c

i

w

s

ta

n

ie

g

ra

n

ic

zn

y

m

n

o

n

o

c

i

W

y

m

ia

ro

w

a

n

ie

ko

n

st

ru

kc

ji

p

o

le

g

a

n

a

d

o

b

o

rze

w

y

m

ia

ró

w

i

kszt

a

łt

u

p

rze

kr

o

jó

w

e

le

m

e

n

tó

w

.

P

o

d

st

a

w

d

o

b

o

ru

je

st

p

o

ró

w

n

a

n

ie

:

w

y

tr

zy

m

a

ło

m

a

te

ri

a

łu

-

n

a

p

r

e

n

ie

zr

e

d

u

k

o

w

a

n

e

lu

b

n

o

n

o

p

rze

k

ro

ju

-

s

ił

w

e

w

n

tr

zn

e

N

a

p

r

e

n

ia

(l

u

b

si

ły

w

e

w

n

tr

zn

e

)

s

w

y

w

o

ła

n

e

ze

w

n

tr

zn

y

m

i

o

b

ci

e

n

ia

m

i

o

b

licze

n

io

w

y

m

i

O

b

ci

e

n

ie

o

b

licze

n

io

w

e

g

d

zi

e

:

F

k

–

o

b

ci

e

n

ie

ch

a

ra

kt

e

ry

st

y

cz

n

e

,

γ

f

-

w

sp

ó

łcz

y

n

n

ik

b

e

zp

ie

cze

st

w

a

(γ

f

≥

1

.0

)

a

F

≥

F

k

k

f

F

F

γ

=

H

ip

o

te

za

n

a

jw

i

k

s

ze

j

e

n

e

rg

ii

H

ip

o

te

za

n

a

jw

i

k

s

ze

j

e

n

e

rg

ii

o

d

k

s

zt

a

łc

e

n

ia

p

o

s

ta

c

io

w

e

g

o

o

d

k

s

zt

a

łc

e

n

ia

p

o

s

ta

c

io

w

e

g

o

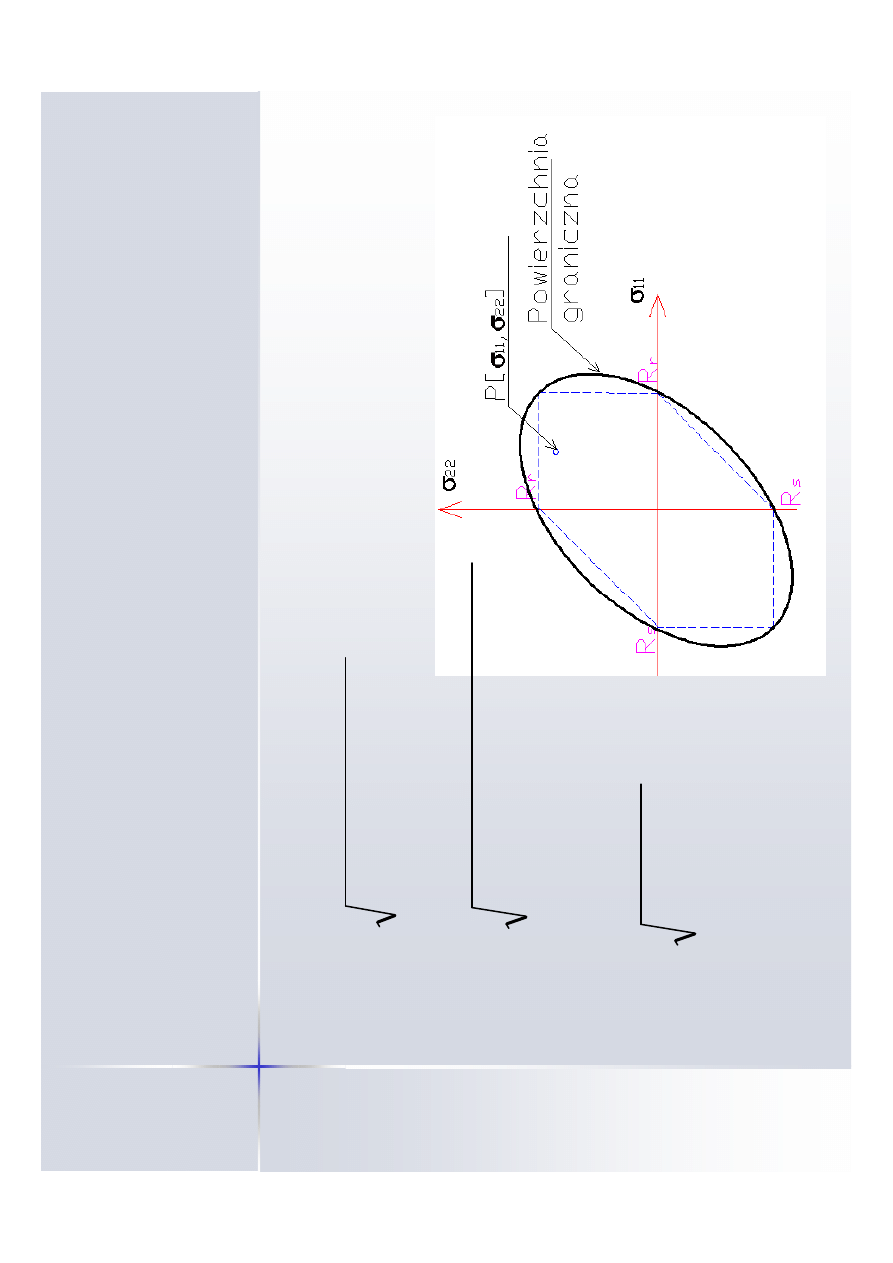
H

ip

o

te

z

a

ta

zo

st

a

ła

o

p

ra

co

w

a

n

a

p

rz

e

z

H

u

b

e

ra

i

M

is

e

s

a

.

W

e

d

łu

g

te

j

h

ip

o

te

z

y

w

y

t

e

n

ia

w

p

rz

yp

a

d

ku

zł

o

o

n

e

g

o

st

a

n

u

n

a

p

r

e

i

p

rz

y

ro

zci

g

a

n

iu

je

d

n

o

o

si

o

w

y

m

b

d

je

d

n

a

ko

w

e

,

je

e

li

o

d

p

o

w

ie

d

n

ie

w

a

rt

o

c

i

je

d

n

o

st

ko

w

e

j

e

n

e

rg

ii

o

d

kszt

a

łce

n

ia

w

ty

ch

st

a

n

a

ch

b

d

so

b

ie

ró

w

n

e

.

(

)

(

)

(

)

2

3

3

1

1

2

2

2

3

3

2

2

2

1

1

2

1

σ

−

σ
+

σ

−

σ
+

σ

−

σ

=

σ

re

d

N

a

p

o

d

st

a

w

ie

te

j

h

ip

o

te

zy

n

a

p

r

e

n

ia

zr

e

d

u

ko

w

a

n

e

w

y

n

o

sz

:

lu

b

(

)

(

)

(

)

(

)

2

2

2

2

2

2

6

2

1

xz

yz

xy

zz

xx

yy

zz

yy

xx

re

d

τ

+
τ

+
τ

+

σ

−

σ
+

σ

−

σ
+

σ

−

σ

=

σ

H

ip

o

te

za

n

a

jw

i

k

s

ze

j

e

n

e

rg

ii

H

ip

o

te

za

n

a

jw

i

k

s

ze

j

e

n

e

rg

ii

o

d

k

s

zt

a

łc

e

n

ia

p

o

s

ta

c

io

w

e

g

o

o

d

k

s

zt

a

łc

e

n

ia

p

o

s

ta

c

io

w

e

g

o

N

a

p

r

e

n

ia

zr

e

d

u

ko

w

a

n

e

w

p

ła

ski

m

st

a

n

ie

n

a

p

r

e

:

lu

b

2

2

1

1

2

2

2

2

1

1

σ
σ

−

σ

+

σ

=

σ

re

d

lu

b

2

2

2

3

xy

yy

xx

yy

xx

re

d

τ
+

σ
σ

−

σ

+

σ

=

σ

W

p

rzy

p

a

d

ku

e

le

m

e

n

tó

w

p

r

to

w

y

c

h

:

2

2

3

xy

xx

re

d

τ
+

σ

=

σ

H

ip

o

te

za

H

ip

o

te

za

H

u

b

e

ra

H

u

b

e

ra

--M

is

e

s

a

M

is

e

s

a

w

s

p

o

in

a

c

h

w

s

p

o

in

a

c

h

--

p

rzy

k

ła

d

p

rzy

k

ła

d

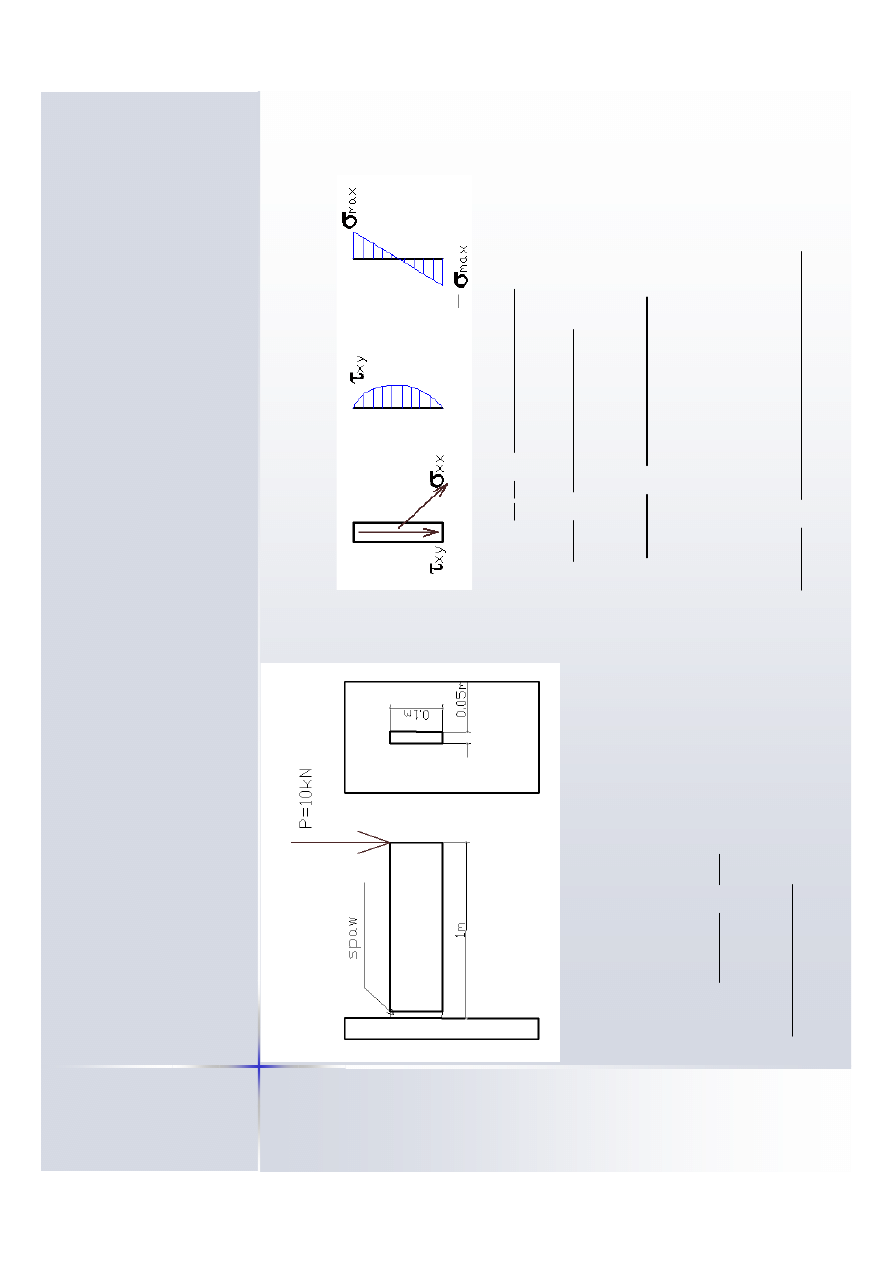
D

w

ie

b

la

ch

y

s

ze

so

b

p

o

ł

czo

n

e

sp

o

in

czo

ło

w

.

W

y

zn

a

czy

n

a

p

r

e

n

ia

zr

e

d

u

ko

w

a

n

e

w

sp

o

in

ie

.

Z

a

ło

o

n

o

,

e

b

la

ch

a

p

io

n

o

w

a

j

e

st

n

ie

sko

cze

n

ie

szt

y

w

n

a

czy

li

b

la

ch

a

p

o

zi

o

m

a

je

st

szt

y

w

n

o

za

m

o

co

w

a

n

a

i

t

w

o

rz

y

w

sp

o

rn

ik

z

si

ła

m

i

w

e

w

n

tr

zn

y

m

i

p

o

ka

za

n

y

m

i

n

a

w

y

kr

e

sa

ch

.

H

ip

o

te

za

H

ip

o

te

za

H

u

b

e

ra

H

u

b

e

ra

--M

is

e

s

a

M

is

e

s

a

w

s

p

o

in

a

c

h

w

s

p

o

in

a

c

h

--

p

rzy

k

ła

d

p

rzy

k

ła

d

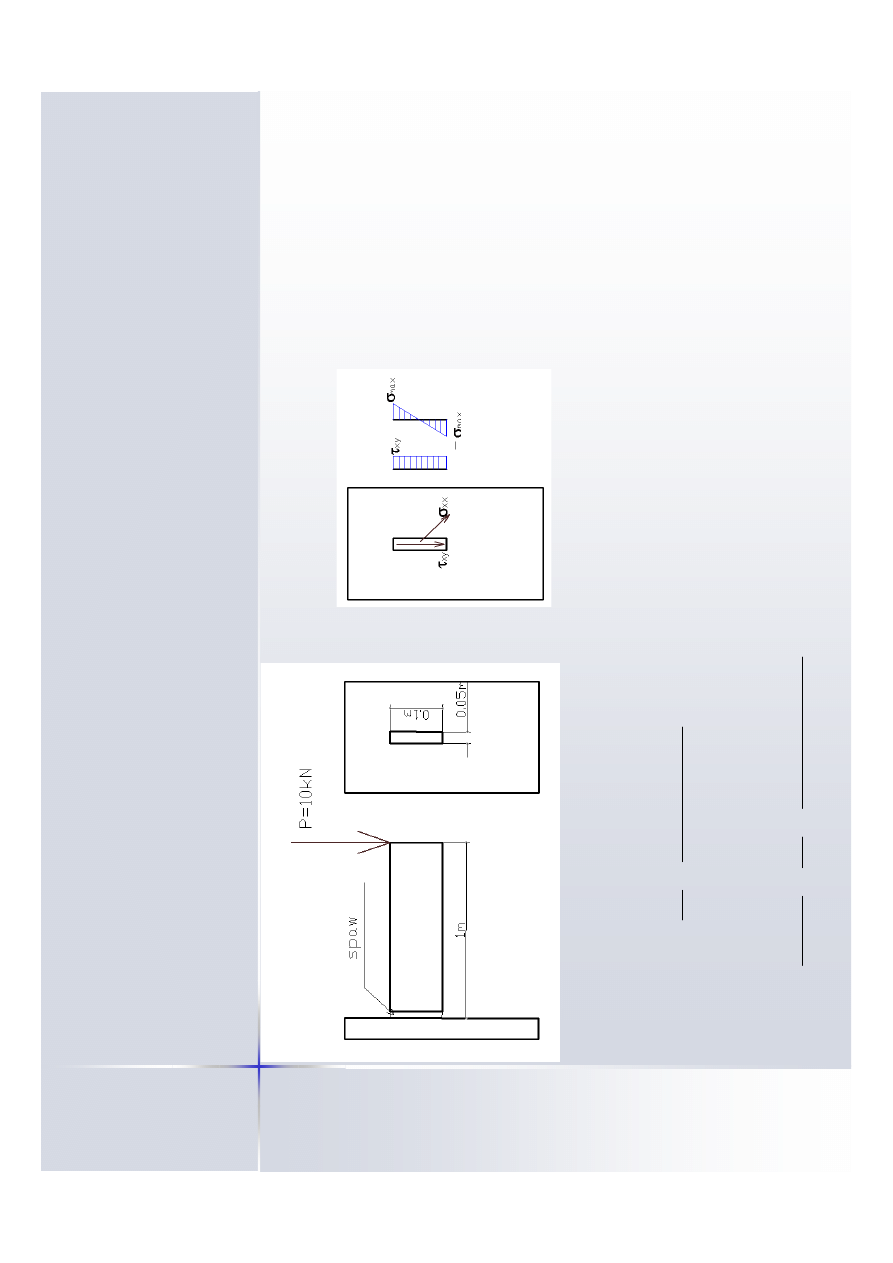
W

y

kr

e

sy

n

a

p

r

e

p

rzy

m

o

co

w

a

n

iu

w

p

r

ci

e

:

kP

a

m

kN

m

W

M

J

M

y

4

8
.

1

2

0

0

0

1

0

3

3
.
8

3

1

3

6

m

a

x

m

a

x

=

⋅

=

=

=

=

σ

−

kN

m

M

1

=

(

)

4

8

3

3

1

0

6

7
.

4

1

6

1

2

1.

0

0

5
.

0

1

2

m

m

m

b

h

J

−

⋅

=

⋅

=

=

3

6

4

8

1

0

3

3
.
8

3

1.

0
5.

0

1

0

6

7
.

4

1

6

5.

0

m

m

m

h

J

W

−

−

⋅

=

⋅

⋅

=

⋅

=

(

)

kP

a

m

m

m

kN

m

Jg

S

T

3

0

0

0

5
.

0

1

0

6

7
.

4

1

6

1

0

5.
6

2

1

0

ˆ

4

8

3

6

m

a

x

=

⋅

⋅

⋅

⋅

=

=

τ

−

−

kN

T

1

=

(

)

(

)

3

6

2

1

0

5.
6

2

8

1.

0

0

5
.

0

4
2

0

ˆ

m

m

m

h

h

b

S

−

⋅

=

⋅

=

=

H

ip

o

te

za

H

ip

o

te

za

H

u

b

e

ra

H

u

b

e

ra

--M

is

e

s

a

M

is

e

s

a

w

s

p

o

in

a

c

h

w

s

p

o

in

a

c

h

--

p

rzy

k

ła

d

p

rzy

k

ła

d

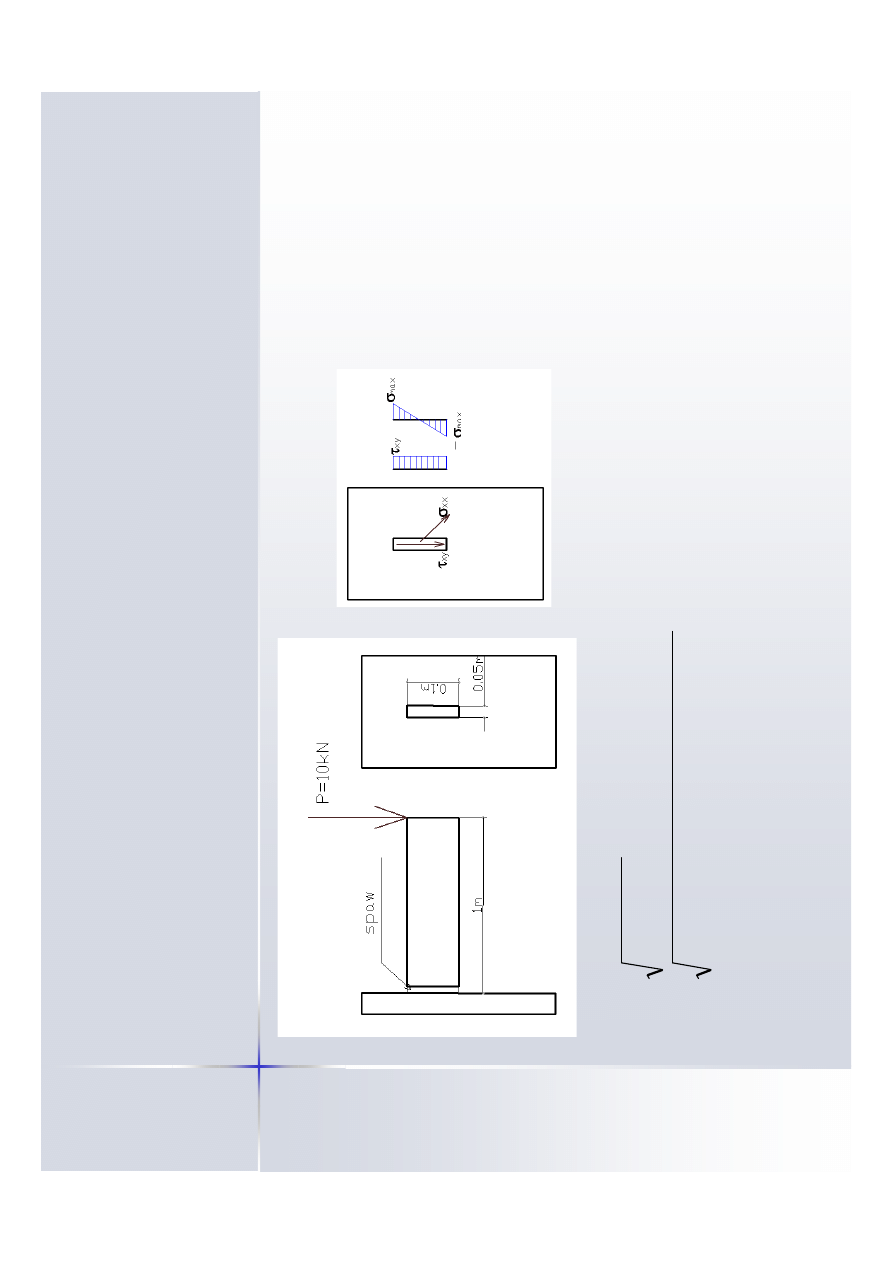
W

y

kr

e

sy

n

a

p

r

e

w

sp

a

w

ie

:

kN

m

M

1

=

4

8

1

0

6

7
.

4

1

6

m

J

−

⋅

=

kN

T

1

=

kP

a

m

kN

m

W

M

J

M

y

4

8
.

1

2

0

0

0

1

0

3

3
.
8

3

1

3

6

m

a

x

m

a

x

=

⋅

=

=

=

σ

−

4

8

1

0

6

7
.

4

1

6

m

J

−

⋅

=

3

6

1

0

3

3
.
8

3

m

W

−

⋅

=

kP

a

m

m

kN

m

b

h

T

xy

2

0

0

0

5
.

0

1.

0

1

m

a

x

=

⋅

=

=

τ

=

τ

S

p

a

w

n

ie

j

e

st

b

e

lk

,

p

o

d

d

a

n

d

zi

a

ła

n

iu

zg

in

a

n

ia

.

Je

st

t

o

kr

ó

tki

f

ra

g

m

e

n

t

n

a

kt

ó

ry

d

zi

a

ła

si

ła

t

n

ca

i

w

t

a

ki

m

p

rzy

p

a

d

ku

n

a

p

r

e

n

ia

st

y

czn

e

s

r

ó

w

n

e

:

N

a

to

m

ia

st

n

a

p

r

e

n

ia

n

o

rm

a

ln

e

r

o

zkł

a

d

a

j

si

t

a

k

sa

m

o

j

a

k

w

b

e

lce

:

H

ip

o

te

za

H

ip

o

te

za

H

u

b

e

ra

H

u

b

e

ra

--M

is

e

s

a

M

is

e

s

a

w

s

p

o

in

a

c

h

w

s

p

o

in

a

c

h

--

p

rzy

k

ła

d

p

rzy

k

ła

d

M

a

ksy

m

a

ln

e

w

a

rt

o

ci

n

a

p

r

e

w

sp

o

in

ie

:

Z

g

o

d

n

ie

z

h

ip

o

te

z

H

u

b

e

ra

-M

ise

sa

:

2

2

3

xy

xx

re

d

τ
+

σ

=

σ

kP

a

xy

2

0

0

m

a

x

=

τ

=

τ

kP

a

xx

4

8
.

1

2

0

0

0

m

a

x

=

σ

=

σ

(

)

(

)

kP

a

kP

a

kP

a

kP

a

kP

a

re

d

1

2

6

0

0

0

2

1

0

0

0

0

6.

0

4

8
.

1

2

0

0

5

2

0

0

3

4

8
.

1

2

0

0

0

2

2

=

⋅

<

=

⋅
+

=

σ

kP

a

kP

a

R

d

o

p

1

2

3

0

0

0

2

0

5

0

0

0

6.

0

=

⋅

=

D

la

st

a

li

S

2

3

5

:

d

o

p

re

d

R

<

σ