1

PARAMETRY SYGNAŁÓW

Wartość maksymalna sygnału

m

X

jest to największa wartość chwilowa jaką sygnał osiąga w

okresie zmienności.
Wartość średnia - średnia arytmetyczna tego sygnału obliczona za jeden okres.

dt

t

x

T

x

T

śr

∫

=

0

)

(

1

Wartość skuteczna

[ ]

dt

t

x

T

x

T

k

s

∫

=

0

2

)

(

1

Współczynnik szczytu

sk

m

s

x

x

k

=

Współczynnik kształtu

śr

sk

k

x

x

k

=

Współczynnik wypełnienia

m

śr

w

x

x

k

=

Częstotliwościowa analiza sygnałów odkształconych

Każdą funkcję okresową

),

(t

f

która spełnia warunki Dirichleta można przedstawić w

postaci szeregu Fouriera, składającego się ze składowej stałej i sumy funkcji
trygonometrycznych o pulsacjach

.

...,

,

3

,

2

,

1

1

1

1

ω

ω

ω

ω

n

Z warunków Dirichleta wynika, że każdy przedział o czasie trwania T można podzielić na
określoną liczbę podprzedziałów, w których funkcja

)

(t

f

jest monotoniczna i ciągła, a w

każdym punkcie nieciągłości istnieją granice: lewostronna

)

(

0

−

t

f

i prawostronna

)

(

0

+

t

f

o

skończonych wartościach.

Przykład funkcji okresowej spełniającej warunki Dirichleta

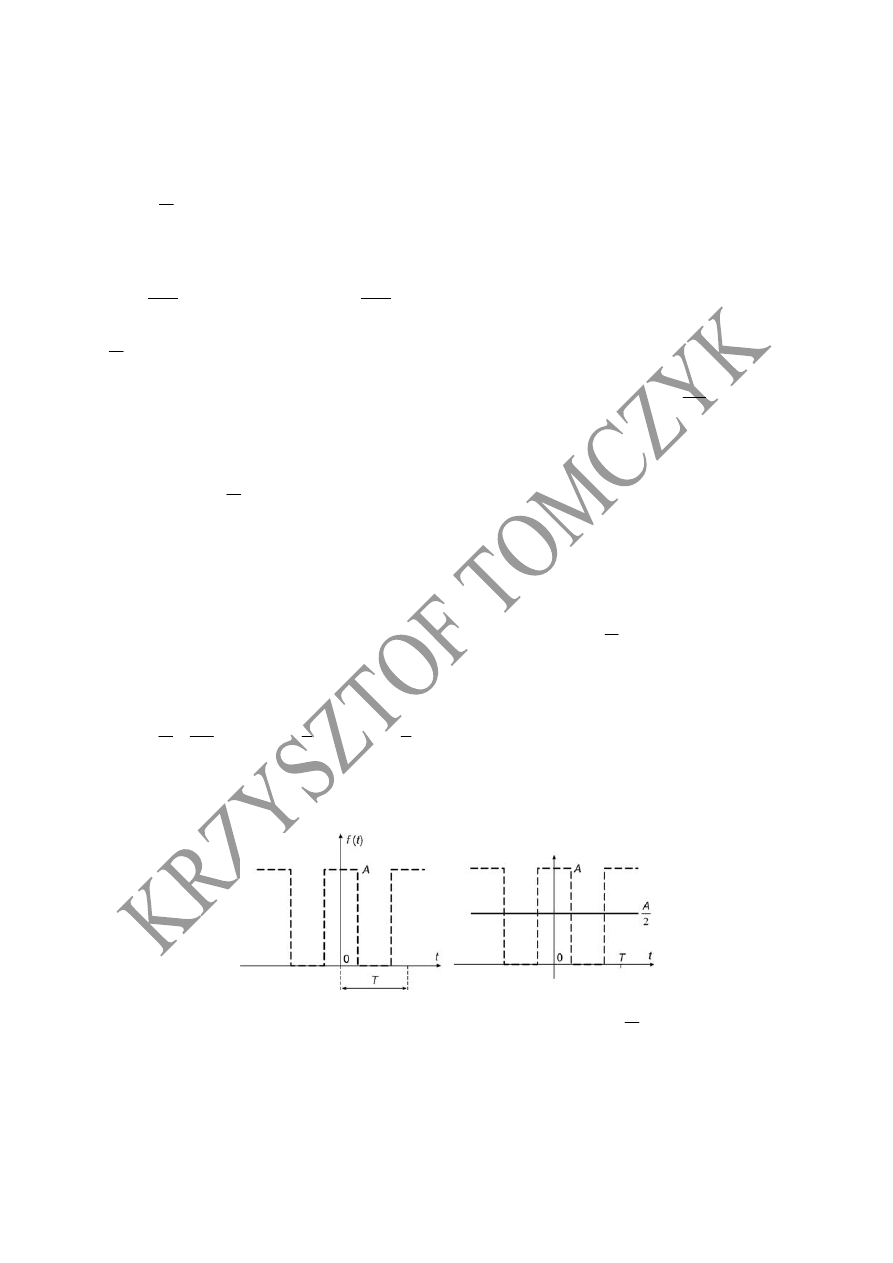
2

Trygonometryczny szereg Fouriera

Szereg Fouriera w postaci trygonometrycznej wyraża się wzorem

[

]

∑

+

+

=

∞

=1

1

1

)

sin(

)

cos(

2

)

(

n

n

n

t

n

b

t

n

a

A

t

f

ω

ω

gdzie:

,

)

cos(

)

(

2

0

1

∫

=

T

n

dt

t

n

t

f

T

M

a

ω

∫

=

T

n

dt

t

n

t

f

T

M

b

0

1

)

sin(

)

(

2

ω

2

A

- składowa stała

n

a i

n

b - amplitudy członów cosinusoidalnych i sinusoidalnych,

T

π

ω

2

1

=

- pulsacja

podstawowa,

1

ω

n

- pulsacje harmoniczne,

n

- liczba naturalna,

T - okres funkcji,

M

-

.

|

)

(

|

max

t

f

Składowa stała

2

A

określona dla

0

=

n

przedstawia wartość średnią funkcji

)

(t

f

za okres

.

T

W zależności od kształtu funkcji okresowej

)

(

t

f

szereg zawiera tylko określone składowe:

1. Jeśli funkcja ta jest parzysta, czyli

),

(

)

(

t

f

t

f

−

=

szereg Fouriera zawiera nieparzyste

cosinusoidy i składową stałą.
2. Jeśli funkcja jest nieparzysta, czyli

),

(

)

(

t

f

t

f

−

=

−

szereg Fouriera zawiera tylko sinusoidy.

3. W przypadku funkcji antysymetrycznej, czyli

),

2

(

)

(

T

t

f

t

f

+

−

=

szereg składa się z

nieparzystych sinusoid i cosinusoid.
Poniższy wzór przedstawia szereg Fouriera dla przykładowej parzystej funkcji

).

(

t

f

⎥⎦

⎤

⎢⎣

⎡

+

+

+

+

=

...

)

5

cos(

5

1

)

3

cos(

3

1

)

cos(

2

2

)

(

1

1

1

t

t

t

A

A

t

f

ω

ω

ω

π

Poniższe rysunki przedstawiają parzystą funkcję

)

(t

f

i jej poszczególne składowe

harmoniczne: 1, 3, 5 oraz składową stałą.

Przykładowa funkcja parzysta

)

(t

f

oraz składowa stała

2

A

3

Funkcja

)

(t

f

oraz pierwsza i trzecia harmoniczna

)

(

1

t

f

i

)

(

3

t

f

Funkcja

)

(t

f

oraz piąta harmoniczna

)

(

5

t

f

i

)

(

2

)

(

1

01

t

f

A

t

f

+

=

Funkcja

)

(t

f

oraz

)

(

)

(

2

)

(

3

1

013

t

f

t

f

A

t

f

+

+

=

i

)

(

)

(

)

(

2

)

(

5

3

1

0135

t

f

t

f

t

f

A

t

f

+

+

+

=

4

KLASYFIKACJA SYGNAŁÓW

Sygnały harmoniczne
Są to sygnały typu

)

sin(

)

(

0

ϕ

ω

+

⋅

=

t

U

t

u

gdzie U jest amplitudą a

ϕ

początkową fazą sygnału.

Widmem sygnału harmonicznego jest jeden prążek, który na osi

ω znajduje się w punkcie

.

0

ω

Sygnały okresowe
Sygnały okresowe powtarzają swoje wartości w jednakowych przedziałach czasu

p

T

, czyli

spełniają warunek

)

(

)

(

p

T

n

t

u

t

u

⋅

±

=

dla

..

.

,

3

,

2

,

1

±

±

±

=

n

Sygnały poliharmoniczne
Są to sygnały składające się z nieskończonej liczby składowych sinusoidalnych o amplitudach

n

U i fazach

n

ϕ

∑

+

⋅

=

∞

=

1

)

sin(

)

(

n

n

n

n

t

U

t

u

ϕ

ω

Widmem sygnału poliharmonicznego jest n prążków o amplitudach

n

U , które na osi

ω

znajdują się w punktach

n

ω

.

Sygnał poliharmoniczny jest sygnałem okresowym jeżeli stosunki wszystkich zawartych w
nim par pulsacji wyrażają się liczbami wymiernymi

wymierna

liczba

m

n

⇒

ω

ω

Sygnały prawie okresowe
Jeżeli nie wszystkie stosunki par pulsacji w sygnale poliharmonicznym wyrażają się liczbami
wymiernymi

a

niewymiern

liczba

m

n

⇒

ω

ω

to sygnał jest sygnałem prawie okresowym.

Nieustalone sygnały przejściowe
Do sygnałów nieustalonych zaliczamy sygnały, które mogą być opisane funkcjami czasu, a
które nie należą do sygnałów okresowych i lub sygnałów prawie okresowych. Przejściowe
sygnały nieustalone w przeciwieństwie do sygnałów okresowych i prawie okresowych nie
mają widma dyskretnego. Mają natomiast widmo ciągłe określane za pomocą transformaty
Fouriera.

∫

⋅

=

∞

∞

−

−

dt

e

t

u

U

t

j

ω

ω

)

(

)

(

przy czym z założenia dla tych sygnałów zachodzi

5

∞

±

→

=

t

dla

t

u

0

)

(

CHARAKTERYSTYKA SYGNAŁÓW

Sygnały charakteryzuje się za pomocą dokonywanych na nich określonych relacji
matematycznych do których najczęściej zaliczamy: wartość średnią, średnią kwadratową,
wariancję, odchylenie standardowe oraz funkcję korelacji własnej nazywanej autokorelacji i
korelacji wzajemnej.

wartość średnia

∫

=

∞

→

−

T

T

u

dt

t

u

T

t

0

)

(

1

lim

)

(

μ

a gdy sygnał jest próbkowany z szerokością próbki

Δ sekund wtedy

Δ

⋅

∑

Δ

Δ

⋅

=

=

−

N

n

u

n

u

N

1

)

(

1

μ

czyli

∑

Δ

=

=

−

N

n

u

n

u

N

1

)

(

1

μ

wartość średnia kwadratowa

∫

=

Ψ

→∞

T

T

u

dt

t

u

T

t

0

2

2

)

(

1

lim

)

(

oraz

∑

Δ

=

Ψ

=

N

n

u

n

u

N

1

2

2

)

(

1

wariancja

∫

−

=

−

∞

→

T

u

T

u

dt

t

u

T

t

0

2

2

]

)

(

[

1

lim

)

(

μ

σ

oraz

2

1

2

]

)

(

[

1

−

=

−

∑

Δ

=

u

N

n

u

n

u

N

μ

σ

odchylenie standardowe jako pierwiastek kwadratowy z wariancji

∫

−

=

−

∞

→

T

u

T

u

dt

t

u

T

0

2

]

)

(

[

1

lim

μ

σ

i

2

1

]

)

(

[

1

−

=

−

∑

Δ

=

u

N

n

u

n

u

N

μ

σ

6

autokorelacja

∫

+

=

∞

→

T

T

uu

dt

t

u

t

u

T

R

0

)

(

)

(

1

lim

)

(

τ

τ

oraz

⎥⎦

⎤

⎢⎣

⎡ ∑

+

Δ

Δ

=

=

∞

→

N

n

N

uu

n

u

n

u

N

R

1

)

(

)

(

1

lim

)

(

τ

τ

Funkcja autokorelacji

)

(

τ

uu

R

charakteryzuje zależność sygnału )

(t

u

poprzez uśrednianie w

przedziale T jego iloczynu chwilach t i

.

τ

+

t

Autokorelacja )

(

τ

uu

R

jest funkcją rzeczywistą i parzystą z maksimum dla

0

=

τ

)

(

)

(

τ

τ

uu

uu

R

R

=

−

Łatwo zauważyć, że dla zerowego przesunięcia

τ autokorelacja

)

0

(

uu

R

jest równa

2

u

Ψ

)

0

(

2

uu

u

R

=

Ψ

natomiast dla

∞

→

T

jej kwadratowy pierwiastek przedstawia wartość średnią

u

μ

)

(

∞

=

uu

u

R

μ

Przykład

)

sin(

)

(

θ

ω

+

=

t

U

t

u

)

cos(

2

]

2

2

cos(

)

[cos(

2

1

2

lim

)

sin(

)

sin(

2

1

lim

)

(

)

(

2

1

lim

)

(

)

(

1

lim

)

(

2

2

2

0

ωτ

θ

ωτ

ω

ωτ

θ

ωτ

ω

θ

ω

τ

τ

τ

U

dt

t

T

U

dt

t

t

U

T

dt

t

u

t

u

T

dt

t

u

t

u

T

R

T

T

T

T

T

T

T

T

T

T

T

uu

=

∫

+

+

−

=

∫

+

+

⋅

+

⋅

∫

+

⋅

=

∫

+

⋅

=

−

∞

→

−

∞

→

−

∞

→

∞

→

korelacja wzajemna

)

(

τ

uy

R

charakteryzuje wzajemność zależność jednego sygnału )

(

t

u

od

wartości drugiego sygnału )

(

t

y

∫

+

=

∞

→

T

T

uy

dt

t

y

t

u

T

R

0

)

(

)

(

1

lim

)

(

τ

τ

Jeżeli

0

)

(

=

τ

uy

R

to mówimy, że sygnały

)

(t

u

i

)

(t

y

są nie są skorelowane.

Korelacja wzajemna

)

(

τ

uy

R

może być zarówno dodatnia jak i ujemna, nie musi mieć

maksimum dla

0

=

τ

i nie musi być funkcją parzystą.

7

Warto zaznaczyć, że dla sygnałów przejściowych funkcje korelacji

)

(

τ

uu

R

i

)

(

τ

uy

R

nie są

dzielone przez T i oblicza się je z następujących wzorów

∫

+

=

T

uu

dt

t

u

t

u

R

0

)

(

)

(

)

(

τ

τ

∫

+

=

T

uy

dt

t

y

t

u

R

0

)

(

)

(

)

(

τ

τ

METODY POMIAROWE

Techniczne metody pomiaru rezystancji
1. Metoda poprawnie mierzonego napięcia - pomiar małych rezystancji

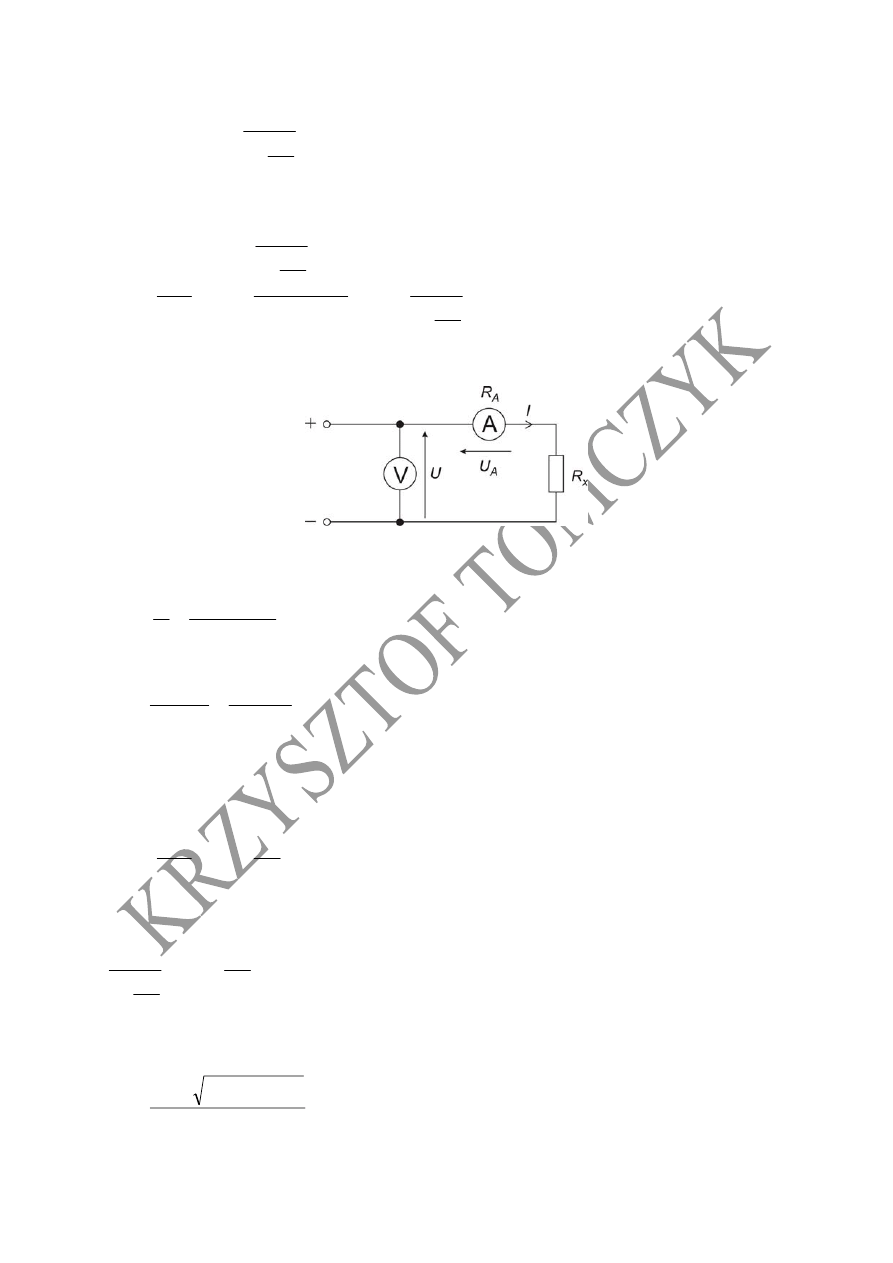
Schemat układu

poprawnie mierzonego

napięcia

Wartość rezystancji mierzonej, wynikająca ze wskazań woltomierza i amperomierza

I

U

R

m

=

odpowiada rezystancji wypadkowej równoległego połączenia rezystancji wewnętrznej
woltomierza

V

R i rezystancji

x

R

x

V

V

V

x

v

x

m

R

R

R

R

R

R

R

R

+

=

+

=

1

W powyższej metodzie występuje błąd spowodowany prądem

V

I pobieranym przez

woltomierz.
Różnica pomiędzy wartością mierzoną

m

R i rzeczywistą

x

R stanowi systematyczny błąd

metody.
Chcąc wyznaczyć wartość

x

R w sposób prawidłowy należy skorygować wartości

wskazywane przez przyrządy

V

V

x

R

U

I

U

I

I

U

R

−

=

−

=

Bezwzględny błąd metody pomiarowej wynosi

8

x

x

V

V

x

m

x

R

R

R

R

R

R

R

−

+

=

−

=

1

Δ

Błąd względny pomiaru

%

100

1

1

%

100

1

%

100

x

V

x

x

x

V

V

x

x

Rx

R

R

R

R

R

R

R

R

R

+

−

=

−

+

=

=

Δ

δ

2. Metoda poprawnie mierzonego prądu - pomiar dużych rezystancji

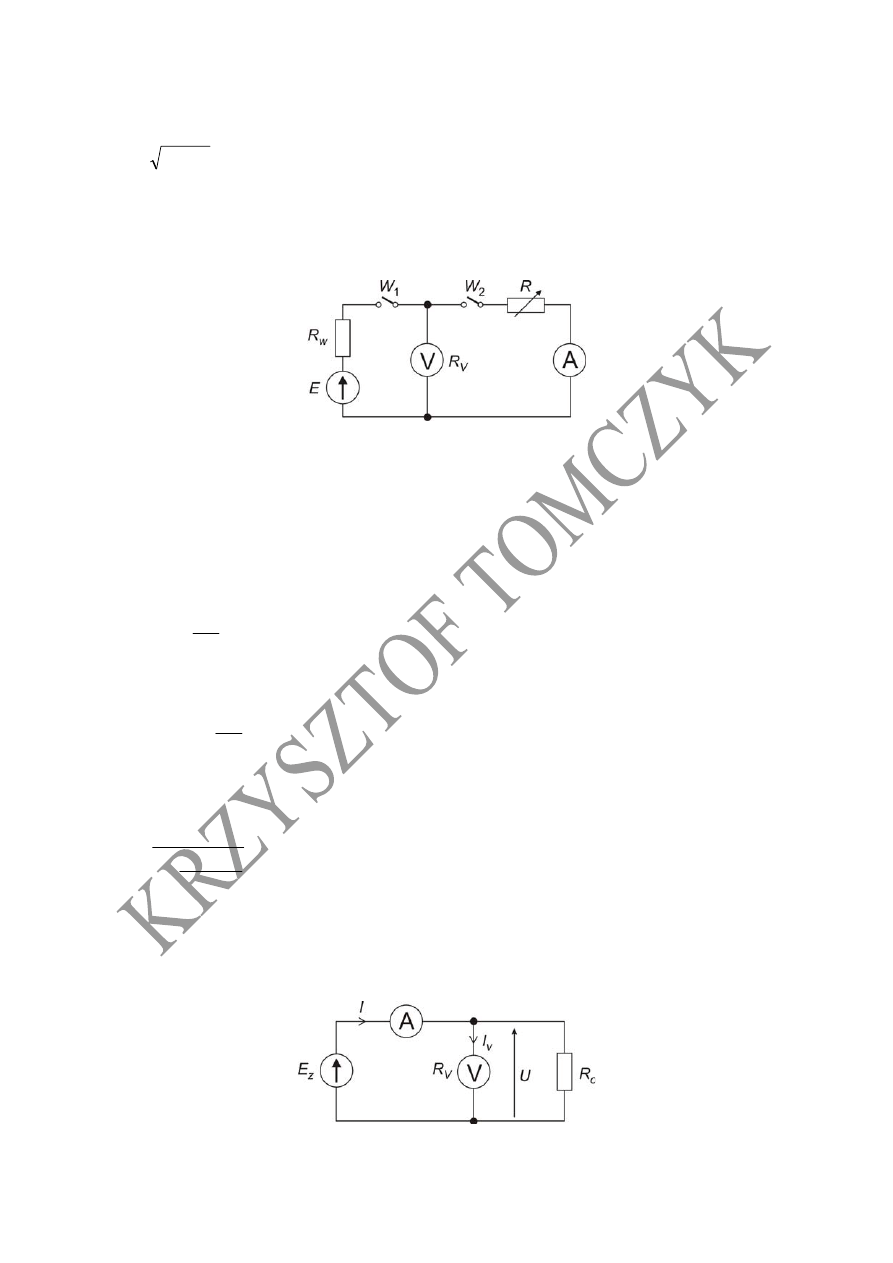
Schemat układu

poprawnie mierzonego prądu

Wartość rezystancji wynikająca ze wskazań przyrządów wynosi

A

x

A

x

m

R

R

I

R

R

I

I

U

R

+

=

+

=

=

)

(

Korygując wskazania przyrządów pomiarowych mamy

I

IR

U

I

U

U

R

A

A

x

−

=

−

=

Błąd bezwzględny metody

A

x

A

x

x

m

x

R

R

R

R

R

R

R

=

−

+

=

−

=

Δ

Błąd względny pomiaru

%

100

%

100

x

A

x

x

Rx

R

R

R

R

=

=

Δ

δ

W szczególnym przypadku błąd metody w obu układach może mieć tę samą wartość
bezwzględną

%

100

1

1

x

V

R

R

+

=

%

100

x

A

R

R

0

2

=

−

−

V

A

x

A

x

R

R

R

R

R

2

4

2

V

A

A

A

x

R

R

R

R

R

+

+

=

9

Dla

V

A

R

R

<<

V

A

x

R

R

R

≈

metody poprawnie mierzonego napięcia i prądu są równoważne.

Pomiar rezystancji wewnętrznej źródła napięcia stałego

Schemat układu do pomiaru rezystancji wewnętrznej źródła napięcia stałego

Rezystancję

w

R wyznacza się poprzez dwukrotny pomiar napięcia na zaciskach źródła:

1

U

- w przypadku, gdy źródło nie jest obciążone ( zamknięty

,

1

W

otwarty

2

W

)

2

U

- w przypadku, gdy źródło obciążone jest rezystancją R ( zamknięty

1

W

i

2

W

)

Rezystancja R powinna być tak dobrana, aby uzyskać wyraźną różnicę pomiędzy

1

U

i

.

2

U

W przypadku pomiaru

1

U

obowiązuje następujące równanie

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

V

w

R

R

U

E

1

1

natomiast na podstawie pomiaru

2

U

i I

w

V

R

R

U

I

U

E

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

+

=

2

2

Rozwiązując powyższy układ równań uzyskuje się wzór określający wartość rezystancji
wewnętrznej źródła

V

w

R

U

U

I

U

U

R

2

1

2

1

−

−

−

=

Pomiar mocy w obwodach stałoprądowych

1. Pomiar mocy odbiornika w układzie poprawnie mierzonego napięcia

Schemat układu do pomiar mocy odbiornika w układzie poprawnie mierzonego

napięcia

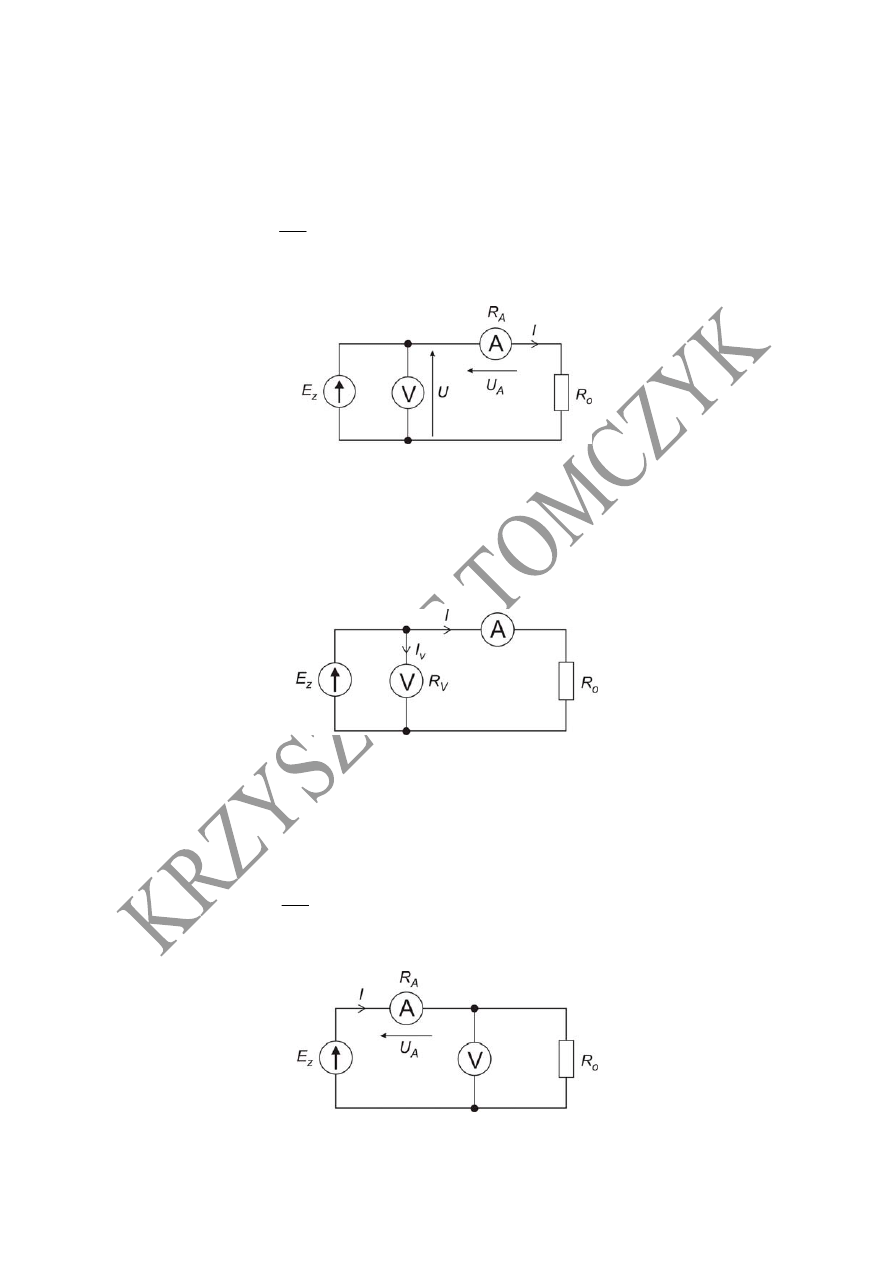
10

Moc wyznaczona na podstawie wskazań przyrządów

I

U

P

m

=

Korygując wskazania przyrządów mamy

(

)

V

m

V

V

o

P

P

R

U

I

U

I

I

U

P

−

=

−

=

−

=

2

2. Pomiar mocy odbiornika w układzie poprawnie mierzonego prądu

Schemat układu do pomiar mocy odbiornika w układzie poprawnie mierzonego

prądu

Po korekcie wskazań przyrządów mamy

(

)

A

m

A

A

o

P

P

R

I

I

U

I

U

U

P

−

=

−

=

−

=

2

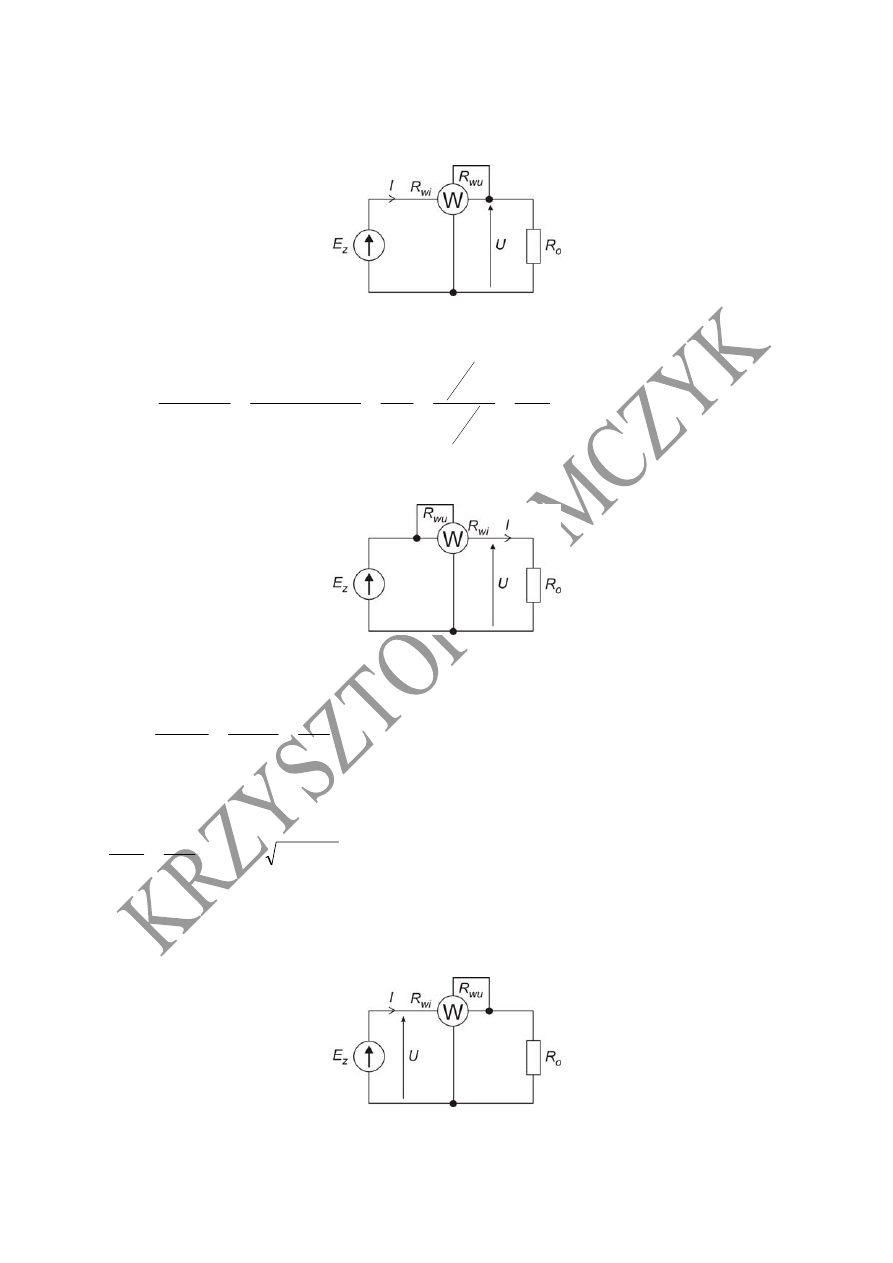
3. Pomiar mocy źródła w układzie poprawnie mierzonego napięcia

Schemat układu do pomiar mocy źródła w układzie poprawnie mierzonego napięcia

Moc wyznaczona na podstawie wskazań przyrządów

I

U

P

m

=

Korygując wskazania przyrządów mamy

(

)

V

m

V

V

z

P

P

R

U

I

U

I

I

U

P

+

=

+

=

+

=

2

4. Pomiar mocy źródła w układzie poprawnie mierzonego prądu

Schemat układu do pomiar mocy źródła w układzie poprawnie mierzonego prądu

11

Po korekcie wskazań przyrządów mamy

(

)

A

m

A

A

z

P

P

R

I

I

U

I

U

U

P

+

=

+

=

+

=

2

Analizując błędy wyznaczenia mocy odbiornika i źródła w układzie poprawnie mierzonego
napięcia mamy:

V

o

m

o

P

P

P

P

=

−

=

Δ

V

o

m

z

P

P

P

P

−

=

−

=

Δ

V

o

V

o

V

o

o

o

R

R

Ro

U

R

U

P

P

P

P

P

=

=

=

Δ

=

2

2

δ

V

o

z

V

z

z

z

R

R

P

P

P

P

P

−

=

−

=

Δ

=

δ

Analogicznie dla układów do pomiaru mocy odbiornika i źródła w układzie poprawnie
mierzonego prądu mamy:

A

o

P

P

=

Δ

A

z

P

P

−

=

Δ

o

A

o

A

o

R

R

R

I

R

I

P

=

=

2

2

δ

o

A

z

R

R

P

−

=

δ

Analogicznie jak w przypadku technicznych pomiarów rezystancji istnieje graniczna wartość
rezystancji odbiornika (źródła) przy której błąd metody jest identyczny dla układu poprawnie
mierzonego napięcia i prądu.
Poniższa tabela przedstawia sposób wyboru układu pomiarowego w zależności od stosunku
rezystancji odbiornika (źródła) do rezystancji przyrządów pomiarowych.

Poprawny pomiar napięcia Poprawny

pomiar

prądu

Realizowany układ

pomiaru mocy

Warunek

V

A

o

R

R

R

>

V

A

o

R

R

R

<

Pomiar mocy odbiornika

V

A

o

R

R

R

=

V

A

z

R

R

R

<

V

A

z

R

R

R

>

Pomiar mocy źródła

V

A

z

R

R

R

=

12

5. Pomiar mocy odbiornika przy użyciu watomierza w układzie poprawnie mierzonego

napięcia

(

)

U

I

I

I

U

P

o

wu

+

=

⋅

=

wu

o

o

wu

R

wu

R

R

R

wu

R

R

wu

wu

R

R

R

U

R

U

P

P

P

P

P

P

P

P

P

=

=

=

−

+

=

−

=

2

2

δ

6. Pomiar mocy odbiornika przy użyciu watomierza w układzie poprawnie mierzonego prądu

(

)

o

A

R

R

I

P

+

=

2

o

wi

o

wi

R

R

wi

R

R

R

I

R

I

P

P

P

=

=

−

=

2

2

δ

Jeśli

wi

wu

δ

δ

=

to

wi

wu

o

o

wi

wu

o

R

R

R

R

R

R

R

=

⇒

=

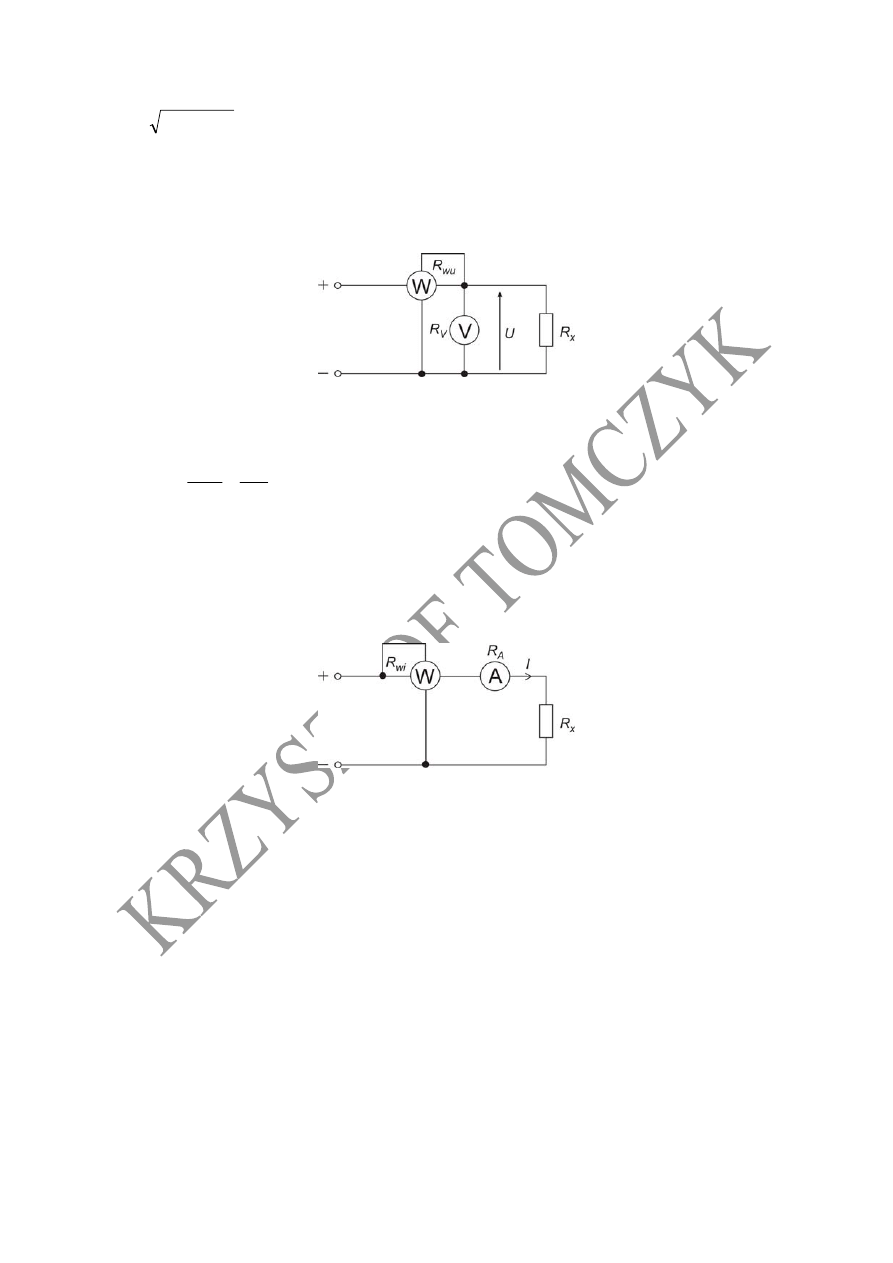
7. Pomiar mocy źródła przy użyciu watomierza w układzie poprawnie mierzonego napięcia

13

wi

R

P

P

P

+

=

wu

o

wu

o

wi

wu

o

wu

o

A

wi

R

wi

R

wi

wu

R

R

R

R

R

R

R

R

R

R

I

R

I

P

P

P

P

P

P

+

⋅

+

−

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

⋅

+

−

=

−

=

−

−

=

1

1

1

2

2

δ

8. Pomiar mocy źródła przy użyciu watomierza w układzie poprawnie mierzonego prądu

wi

R

P

P

P

+

=

)

(

)

(

2

2

2

2

wi

o

wu

wi

o

wu

wu

wi

o

wu

wi

o

wu

wu

o

R

wu

o

R

o

R

wi

R

R

R

R

R

R

U

R

U

R

R

R

R

R

R

U

R

U

P

P

P

P

P

+

+

+

=

+

+

+

=

−

=

−

=

δ

wi

o

wu

wi

o

wu

wi

o

wi

R

R

R

R

R

R

R

R

+

+

−

=

+

+

+

=

1

1

δ

Jeśli

wi

wu

δ

δ

=

to

wi

o

wu

wu

o

wu

o

wi

R

R

R

R

R

R

R

R

+

+

−

=

+

⋅

+

−

1

1

1

1

1

wi

o

wu

wu

wu

wi

R

R

R

R

R

R

R

R

+

=

+

⋅

0

0

1

wi

o

wu

wi

R

R

R

R

R

R

+

=

+

1

1

0

0

wi

wu

wi

wi

R

R

R

R

R

R

R

⋅

+

⋅

=

⋅

+

0

0

2

0

wi

wu

R

R

R

⋅

=

2

0

14

wi

wu

R

R

R

⋅

=

0

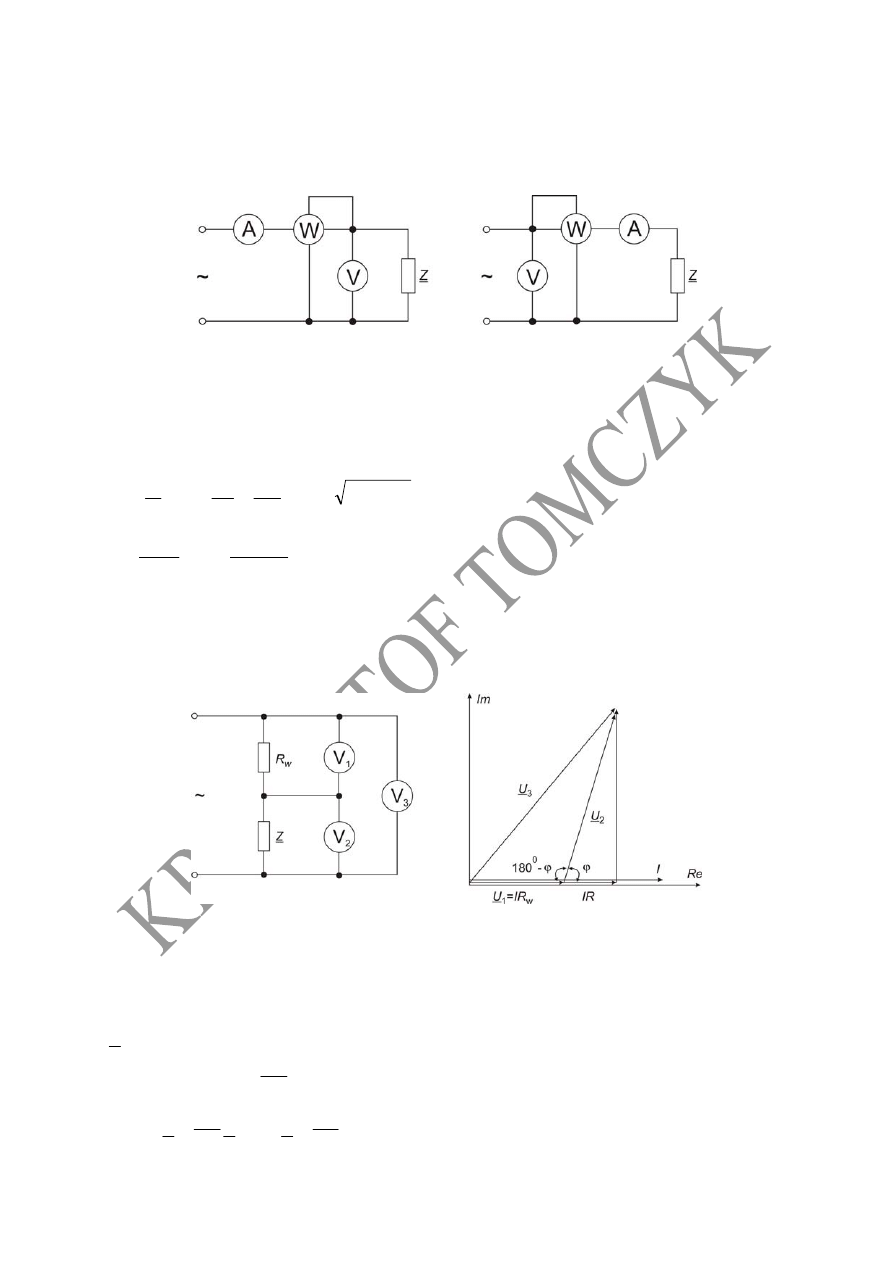
9. Pomiar mocy odbiornika

w układzie poprawnie mierzonego napięcia przy użyciu

watomierza i woltomierza

Schemat układu do pomiaru mocy w układzie poprawnie mierzonego napięcia

Moc wyznaczona na podstawie korekty wskazania watomierza

V

wu

m

x

R

U

R

U

P

P

2

2

−

−

=

m

P - moc wskazywana przez watomierz

10. Pomiar mocy odbiornika w układzie poprawnie mierzonego prądu przy użyciu

watomierza i amperomierza

Schemat układu do pomiaru mocy w układzie poprawnie mierzonego prądu

Moc wyznaczona na podstawie korekty wskazania watomierza

A

wi

m

x

R

I

R

I

P

P

2

2

−

−

=

15

Pomiary impedancji i jej parametrów

1. Pomiar składowych impedancji za pomocą watomierza, woltomierza i amperomierza
a) b)

Schemat układów do pomiaru składowych impedancji za pomocą watomierza, woltomierza

i amperomierza

a) układ poprawnie mierzonego napięcia
b) układ poprawnie mierzonego prądu

Pomijając wpływ rezystancji wewnętrznych przyrządów parametry impedancji można
wyznaczyć w oparciu o wzory:

2

2

2

2

,

,

R

Z

X

P

U

I

P

R

I

U

Z

−

=

=

=

=

X

f

C

f

X

L

π

π

2

1

,

2

=

=

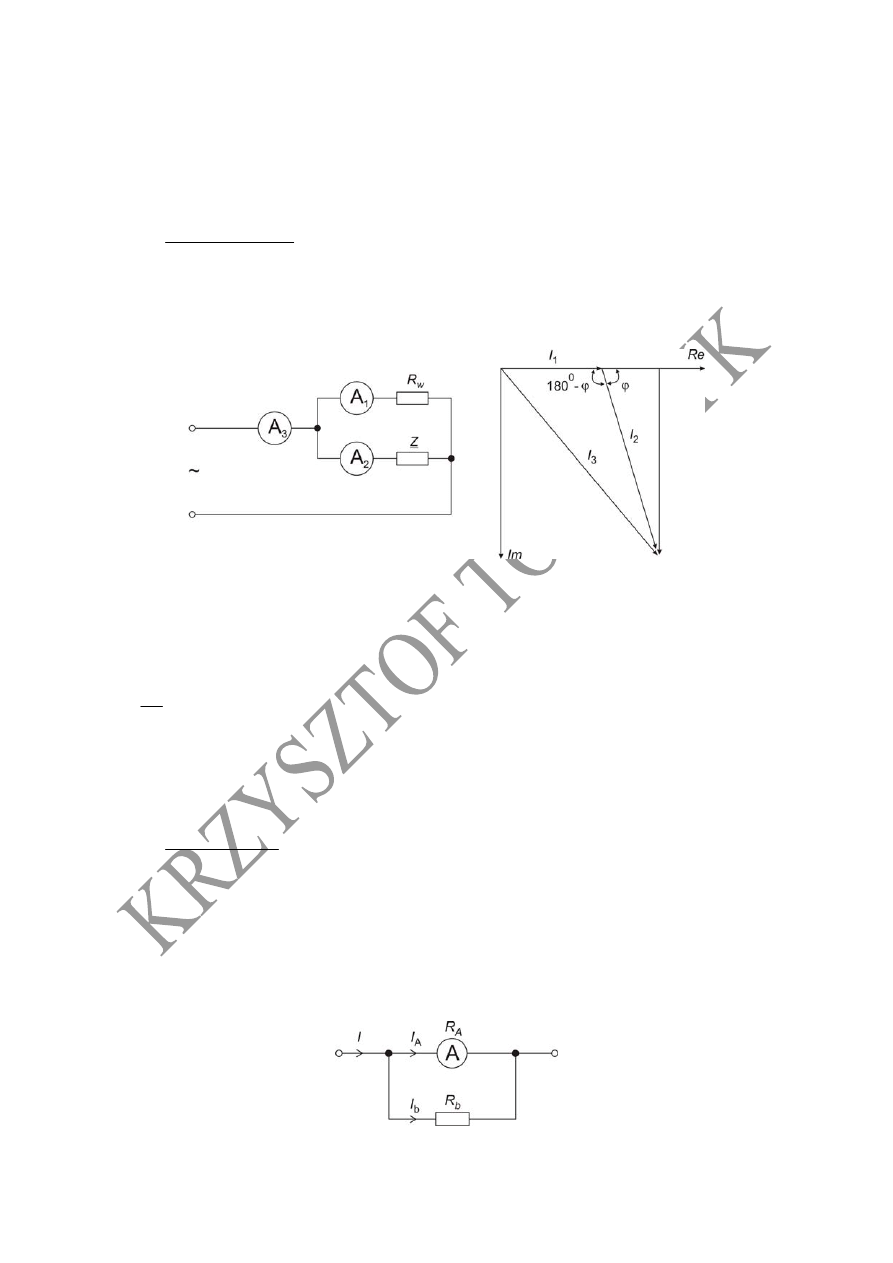
2. Pomiar składowych impedancji metodą trzech woltomierzy
a) b)

Układ do pomiaru składowych impedancji metodą trzech woltomierzy
a) Schemat układu
b) Wykres wskazowy

w

R - rezystancja wzorcowa

jX

R

Z

+

=

w

w

R

U

I

R

I

U

1

1

=

⇒

=

w

w

R

U

U

Z

Z

R

U

Z

I

U

1

2

1

2

=

⇒

=

=

16

)

180

cos(

2

0

2

1

2

2

2

1

2

3

ϕ

−

−

+

=

U

U

U

U

U

ϕ

=

−

−

cos

2

2

1

2

2

2

1

2

3

U

U

U

U

U

2

1

2

2

2

1

2

3

2

cos

U

U

U

U

U

−

−

=

ϕ

3. Pomiar składowych impedancji metodą trzech amperomierzy
a) b)

Układ do pomiaru składowych impedancji metodą trzech amperomierzy

c) Schemat układu
d) Wykres wskazowy

Z

I

R

I

w

2

1

=

w

R

I

I

Z

2

1

=

)

180

cos(

2

0

2

1

2

2

2

1

2

3

ϕ

−

−

+

=

I

I

I

I

I

ϕ

cos

2

2

1

2

2

2

1

2

3

I

I

I

I

I

=

−

−

2

1

2

2

2

1

2

3

2

cos

I

I

I

I

I

−

−

=

ϕ

Rozszerzanie zakresów pomiarowych przyrządów magnetoelektrycznych

1. Rozszerzanie zakresu pomiarowego amperomierzy magnetoelektrycznych

Schemat układu do rozszerzania zakresu pomiarowego amperomierzy magnetoelektrycznych

17

b

R

- rezystancja bocznika

b

b

A

A

R

I

R

I

=

A

b

I

I

I

−

=

(

)

b

A

A

A

R

I

I

R

I

−

=

1

−

=

−

=

A

A

A

A

A

b

I

I

R

I

I

R

I

R

2. Rozszerzanie zakresu pomiarowego woltomierzy magnetoelektrycznych

p

R

- rezystancja posobnika

p

V

U

U

U

+

=

p

V

R

I

U

U

+

=

V

p

U

U

R

I

−

=

V

R

U

I

=

V

p

V

U

U

R

R

U

−

=

V

V

V

V

V

p

R

U

U

U

R

U

U

R

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

−

=

1

)

(

18

KOMPENSATORY NAPIĘCIA STAŁEGO

Pomiar napięcia metodą kompensacyjną realizowany jest poprzez porównanie napięcia
mierzonego

x

E

ze znaną wartością napięcia wzorcowego

w

E

bez poboru prądu z obwodu

kontrolowanego.

Podział metod kompensacyjnych:

1. Kompensacja pojedyncza
2. Kompensacja podwójna

Podział kompensatorów ze względu na dokładność:

1. Laboratoryjne o klasach 0.005, 0,01, 0.02, 0.05
2. Techniczne o klasach dokładności 0,1, 0.2, 0.5 (aktualnie zastąpione woltomierzami

cyfrowymi o dużej dokładności i rezystancji wejściowej)

Podział ze względu na wartości mierzonych napięć:

1. Kompensatory o dużej rezystancji wewnętrznej (wysoko-omowe) do pomiaru napięć

powyżej 100mV (mają prąd pomocniczy w granicach

mA)

1

1

.

0

÷

2. Kompensatory o małej rezystancji wewnętrznej do pomiaru napięć poniżej 100mV

(mają prąd pomocniczy w granicach

mA)

100

10

÷

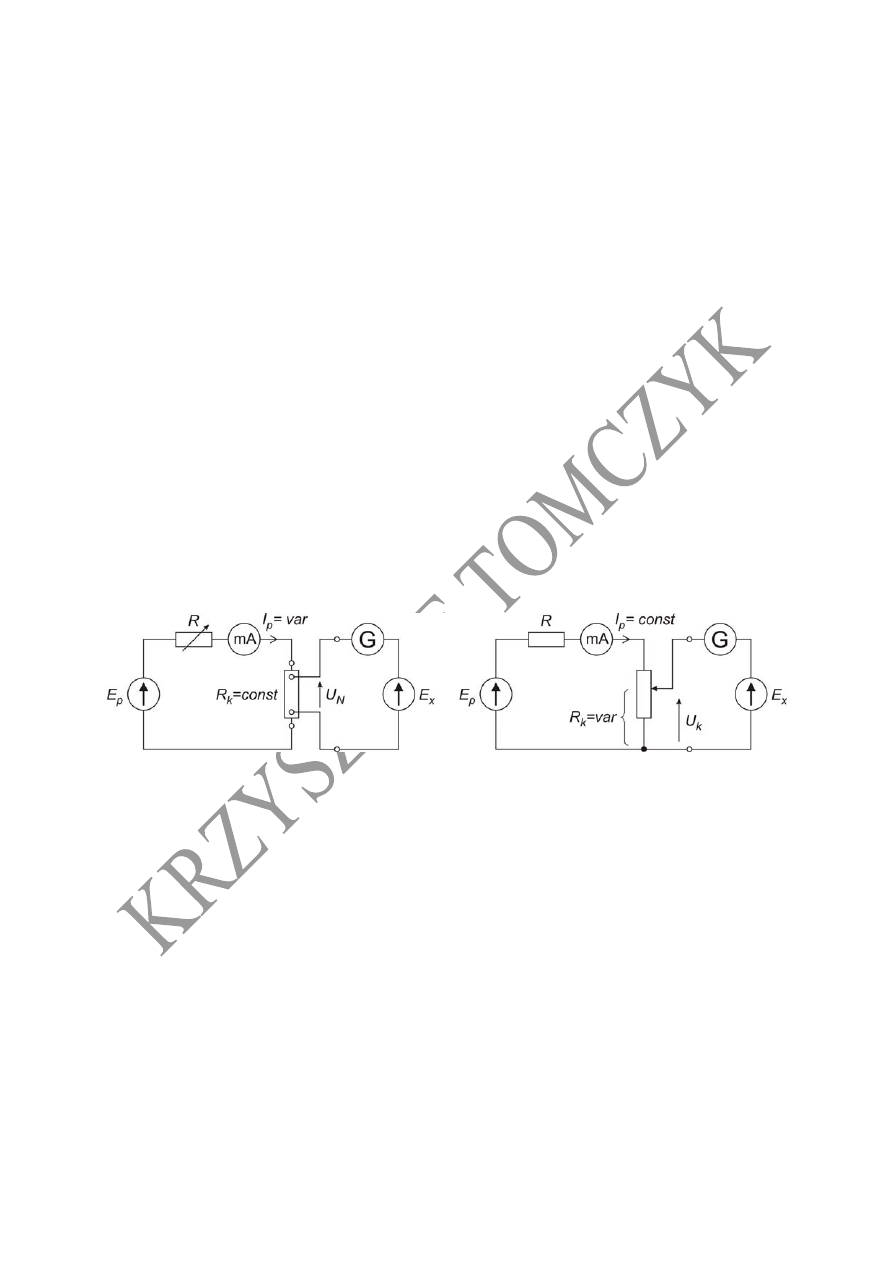
Kompensacja pojedyncza
a) b)

Układy kompensacji pojedynczej

a) o regulowanym prądzie roboczym
b) o stałym prądzie roboczym

W układzie kompensatora o regulowanym prądzie roboczym, wartość prądu roboczego

p

I

regulowana opornikiem

R jest mierzona za pomocą amperomierza. Napięcie mierzone

x

E

porównywane jest ze spadkiem napięcia

N

U

na oporniku wzorcowym

.

N

R

Po uzyskaniu kompensacji (

0

=

G

I

) wartość

x

E

wyznacza się na podstawie wskazania

amperomierza i znanej wartości

N

R

N

p

x

R

I

E

=

W układzie kompensatora o stałym prądzie roboczym, prąd

p

I

o stałej i znanej wartości

wywołuje na oporniku

k

R

(opornik kompensacyjny

)

spadek napięcia, który porównywany

jest z napięciem mierzonym.
Regulując

k

R

doprowadza się układ do stanu kompensacji i wtedy

k

p

x

R

I

E

=

19

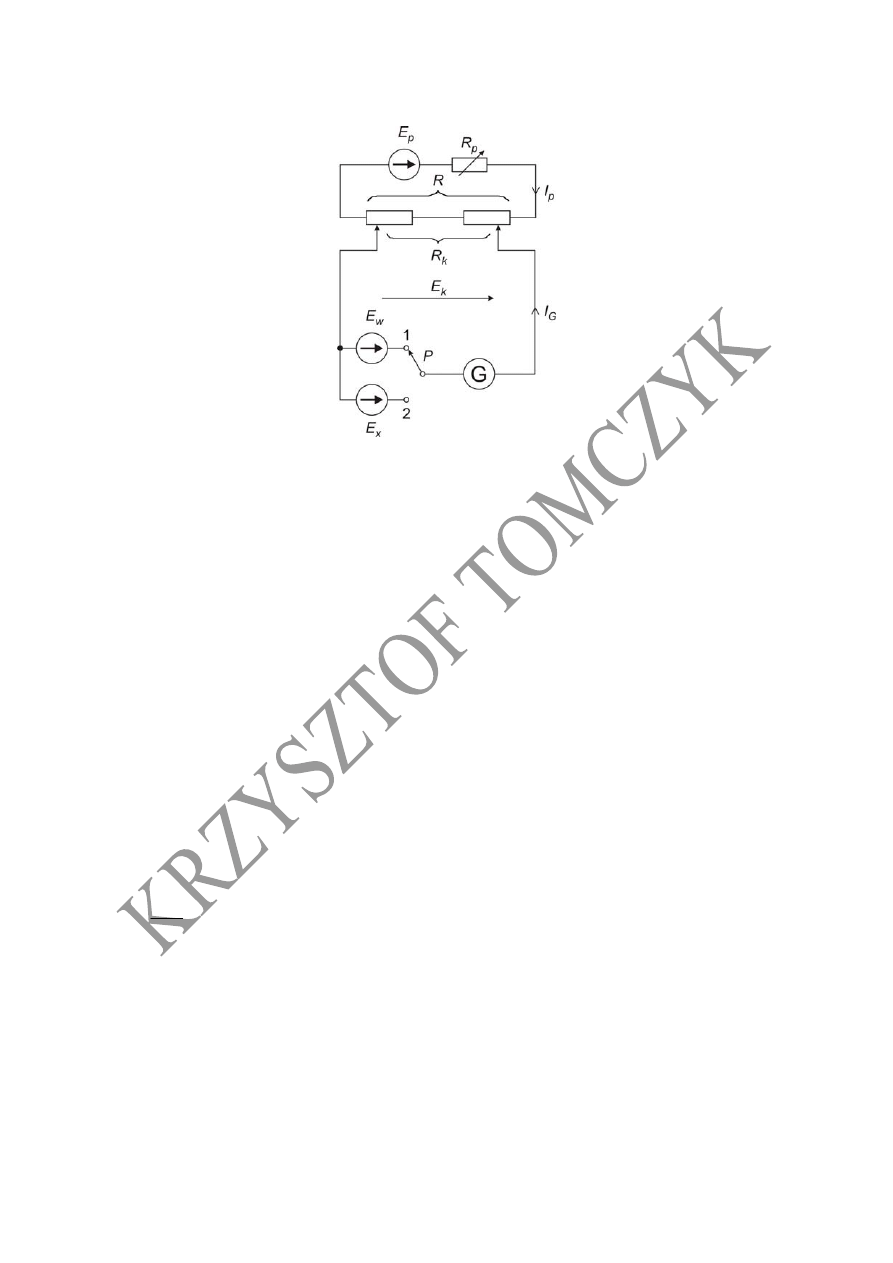
Kompensacja podwójna

Układ kompensacji podwójnej

p

I

- prąd pomocniczy

Zasada kompensacji

Przełączając przełącznik

P w położenie 1 regulujemy

p

R

taki sposób, aby prąd

galwanometru

G

I

był równy zero. Jest to stan kompensacji napięć.

Cały prąd

p

I

płynie przez opornik R, a spadek napięcia

1

k

E

na rezystancji

1

k

R

równy jest

wartości wzorcowej siły elektromotorycznej

w

E

1

k

p

w

R

I

E

=

W analogiczny sposób kompensowane jest napięcie mierzone

,

E

x

poprzez przełączenie

przełącznika

P w położenie 2 i nastawienie na oporniku R takiej rezystancji

2

k

R

dla której

galwanometr będzie w stanie równowagi (

0

=

G

I

).

W stanie kompensacji

2

k

p

x

R

I

E

=

Wstawiając

p

I

ze wzoru na

w

E

do wzoru na

x

E

uzyskuje się

w

k

k

x

E

R

R

E

1

2

=

20

Kompensator Feussnera
W celu zapewnienia dużej dokładności pomiarów kompensacyjnych nie wystarczy precyzyjne
wyznaczenie

.

E

x

Konieczna jest również wysoka dokładność opornika R i duża

rozdzielczość jego regulacji. Takich wymagań nie mogą zapewnić dwie potencjometrycznie
włączone dekady opornika.
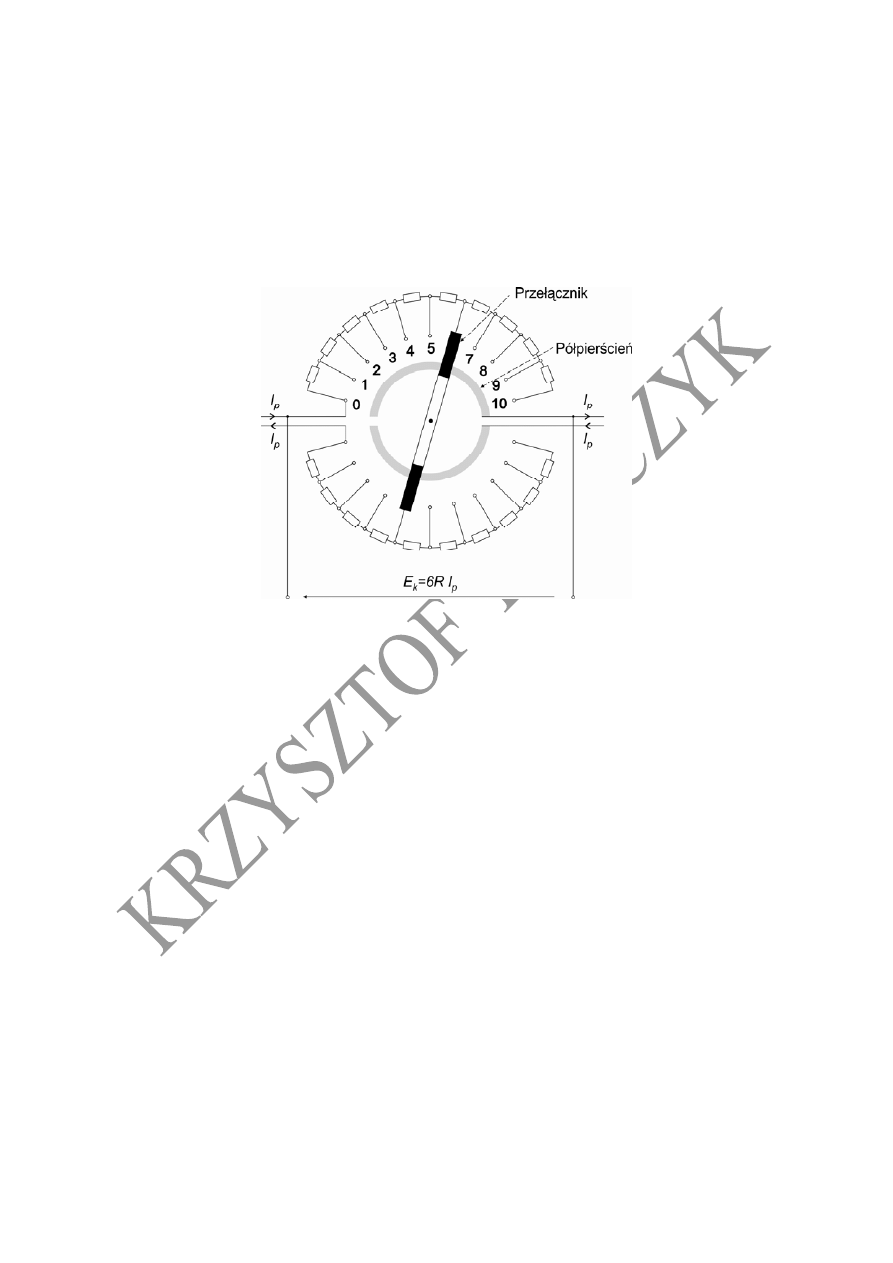
Powyższe wymagania dobrze spełnia dekada Feussnera.

Dekada Feussnera

Prąd pomocniczy

p

I

kompensatora przepływa najpierw przez szereg oporników górnej

gałęzi dekady, a następnie przez górny przełącznik i górną część półpierścienia płynie do
następnych dekad. Wracając trafia do dolnego półpierścienia, a niego przez dolną część
przełącznika płynie przez oporniki dolnej gałęzi dekady.
Konstrukcja dekady Feussnera zapewnia przepływ prądu pomocniczego zawsze przez 10
oporników (przez

n

oporników górnej dekady i przez

n

−

10

oporników dolnej dekady),

niezależnie od ustawienia przełącznika.
Spadek napięcia

k

E

zdejmowanego z górnej gałęzi dekady regulowany jest położeniem

przełącznika.
Pomiędzy dwie zwykłe dekady włączone potencjometrycznie można więc włączyć dowolną
liczbę dekad Feussnera i nastawiać z dowolną rozdzielczością napięcie kompensujące

k

E

przy

p

I

= const.

Poniższy rysunek przedstawia układ kompensatora Feussnera o 3 dekadach Feussnera (III-V)
i dwóch zwykłych dekadach (I, II).
Prąd pomocniczy nastawiany jest za pomocą kilkudekadowego opornika

p

R

w taki sposób,

aby jego wartość była stała i wynosiła

.

μA

100

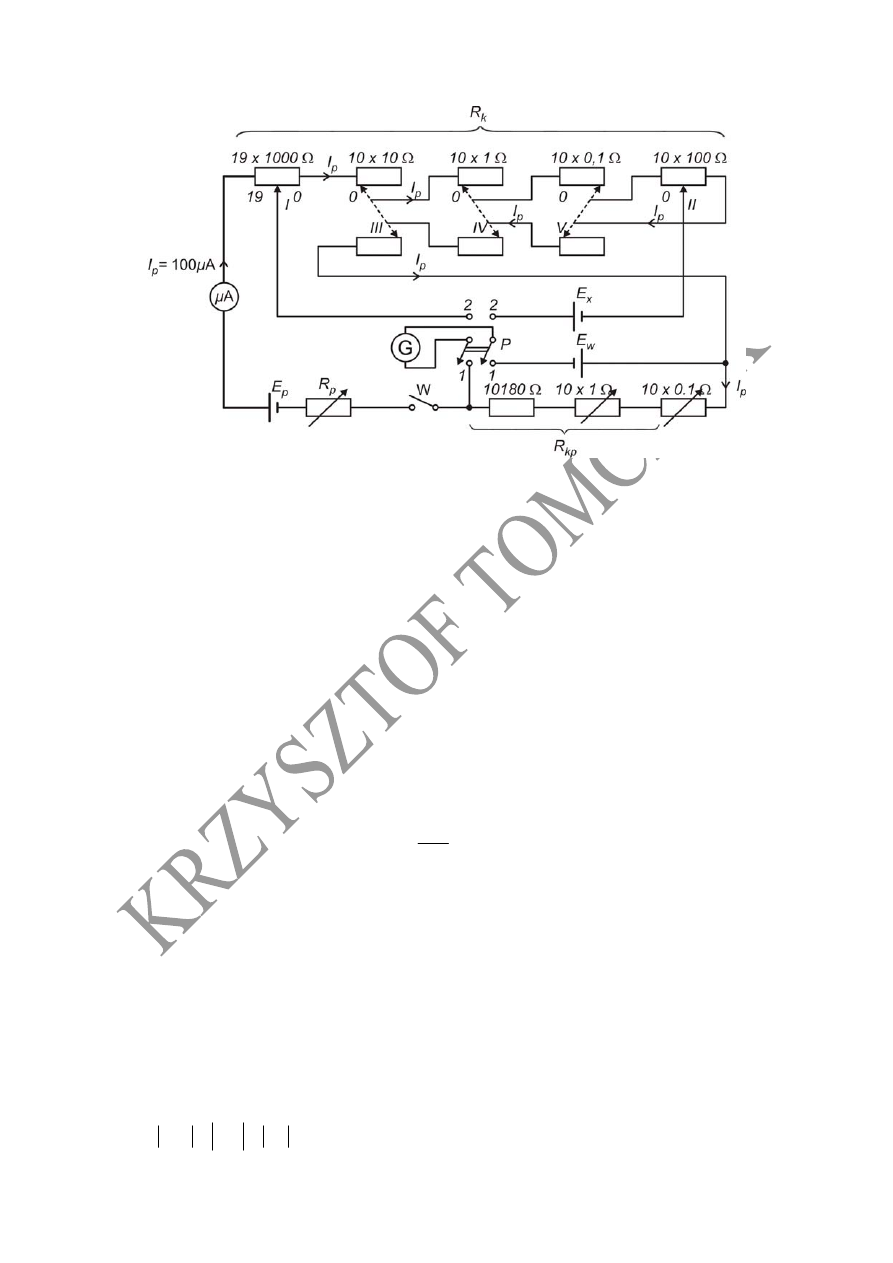
21

Układ kompensatora Feussnera

Zasada kompensacji:

1. Sprawdzić prawidłowość przyłączenia:

x

p

w

E

E

E

,

,

pod względem biegunowości

2. Ze świadectwa legalizacji ogniwa wzorcowego odczytać wartość uwierzytelnioną

SEM i na jej podstawie obliczyć wartość charakterystyczną SEM dla aktualnej
temperatury ogniwa

3. Nastawić

kp

R

na wartość

.

10

4

w

E Dekada

Ω

⋅ 1

.

0

10

służy do uwzględnienia zmiany

w

E

od zmian temperatury

4.
5. Przy otwartym P należy zamknąć W i następnie regulując

p

R

ustawić na μA z

dokładnością wynikającą z jego klasy wartość

p

I

=

.

μA

100

6. Przełączyć P w położenie 1 i regulując

p

R

ustawić

taką dokładną wartość

,

10

4

A

I

p

−

=

dla której wskazanie galwanometru G będzie równe zero,

W takim przypadku zachodzi

kp

w

p

R

E

I

=

7. Przełączyć P w położenie 0
8. Jeżeli znana jest przybliżona wartość

,

x

E

to pokrętłami dekad

k

R

ustawiamy taką

rezystancję

1

k

R

aby iloczyn

1

k

p

R

I

był równy założonej wartości

x

E

9. Stan ten sprawdzamy po przełączeniu P w położenie 2 i doprowadzenie

k

R

do stanu,

dla którego wskazanie galwanometru G będzie równe zero (kontrolujemy stałość
prądu pomocniczego

p

I

przełączając P w położenie 1)

Wtedy

2

k

p

x

R

I

E

=

Po zlogarytmowaniu i zróżniczkowaniu powyższej zależności, otrzymuje się wzór określający
błąd graniczny pomiaru napięcia kompensatorem Feussnera

k

kp

w

x

R

R

E

E

+

+

=

δ

δ

22

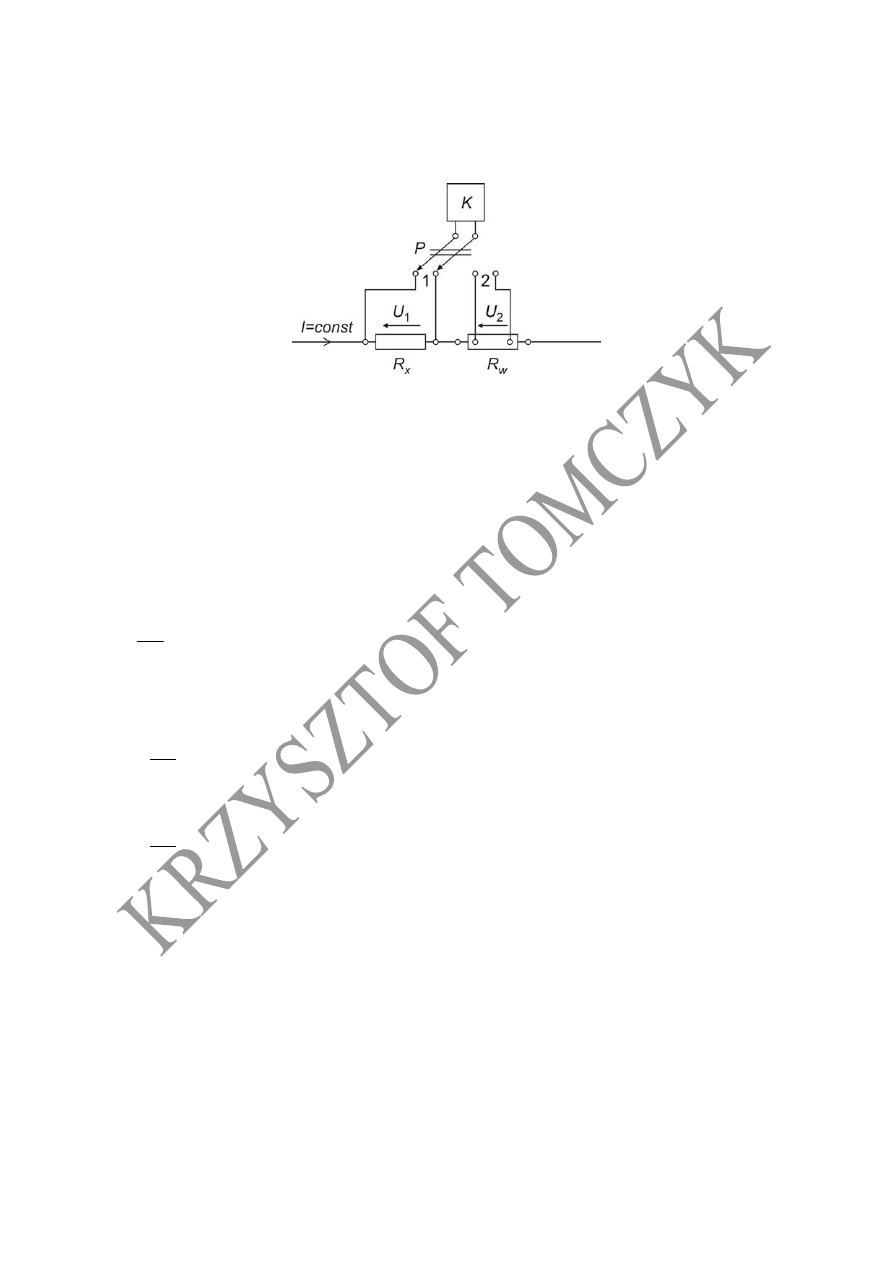
Pomiar rezystancji za pomocą kompensatora

Schemat układu do pomiaru rezystancji za pomocą kompensatora

Rezystancja

x

R

wyznaczana jest poprzez porównanie napięć

1

U

i

,

U

2

wywoływanych tym

samym prądem

.

I

Napięcia te mierzy się dokładnie za pomocą kompensatora.

Jeśli

,

I

const

=

to

Najpierw wyznacza się dokładną wartość prądu mierząc spadek napięcia

1

U

a

w

R

za pomocą

kompensatora.
Wtedy

w

R

U

I

1

=

W drugim pomiarze mierzy się spadek nap.

2

U

na

x

R

powodowany uprzednio

wyznaczonym prądem

I

U

R

x

2

=

więc

w

x

R

U

U

R

1

2

=