POLITECHNIKA BIAŁOSTOCKA

Wydział Budownictwa

i Inżynierii Środowiska

Katedra Ciepłownictwa

Instrukcja do zajęć laboratoryjnych

Temat ćwiczenia

:

POWIERZCHNIA SWOBODNA CIECZY

W

NACZYNIU WIRUJĄCYM WOKÓŁ OSI PIONOWEJ

Ćwiczenie nr

2

Laboratorium z przedmiotu

MECHANIKA PŁYNÓW

Ś13012 L02

Opracował:

Piotr Rynkowski

Białystok,

wrzesień 2012

Kod:

Politechnika Białostocka

Ćwiczenie nr 2

Katedra Ciepłownictwa Powierzchnia swobodna w naczyniu wirującym wokół osi pionowej

2/5

1. Cel ćwiczenia.

Celem ćwiczenia jest zadokumentowanie znanego z wykładów faktu, że powierzchnia

swobodna cieczy w

naczyniu wirującym wokół osi pionowej jest paraboloidą obrotową.

2. Podstawy teoretyczne.

Stan względnego spoczynku zachodzi, gdy ciecz wraz z naczyniem znajduje się w ruchu ze

stałą prędkością kątową, bądź ze stałym przyspieszeniem kątowym. Żaden z elementów nie

przemieszcza się wówczas względem siebie, ani względem naczynia.

Stan względnego spoczynku cieczy opisuje układ równań różniczkowych Eulera:

z

p

Z

y

p

Y

x

p

X

∂

∂

=

ρ

∂

∂

=

ρ

∂

∂

=

ρ

(1)

gdzie:

−

3

kg

m

ρ













-

gęstość płynu,

−

2

X, Y, Z

m

s

 

 

 

-

składowe jednostkowej siły masowej,

−

p = p (x,y,z) [Pa] –

ciśnienie,

−

x,y,z [m] – wymiary liniowe

Mnożąc te równania odpowiednio przez dx, dy i dz oraz dodając stronami otrzymuje się:

(

)

dp

Xdx

Ydy

Zdz

ρ

=

+

+

(2)

Równanie jest podstawowym równaniem równowagi cieczy w stanie względnego spoczynku

i mówi

o związku między ciśnieniem w dowolnym punkcie cieczy, a siłą jaka działa na ciecz w tym

punkcie.

Powierzchnia swobodna cieczy jest powierzchnią jednakowego ciśnienia (powierzchnią

izobaryczną, powierzchnią ekwipotencjalną), na której:

(

)

p

p x, y, z

const ,

czyli dp

0

=

=

=

(3)

W związku z tym równanie przyjmuje postać:

Xdx

Ydy

Zdz

0

+

+

=

(4)

Kształt powierzchni swobodnej poruszającej się w naczyniu cylindrycznym ruchem

jednostajnie obrotowym wokół osi pionowej można opisać teoretycznie równaniem (4). Na dowolny

element płynu działa jednostkowa siła masowa o składowych (rys.1.):

2

2

X

Y

Z

g

x

y

= ϖ
= ϖ

= −

(5)

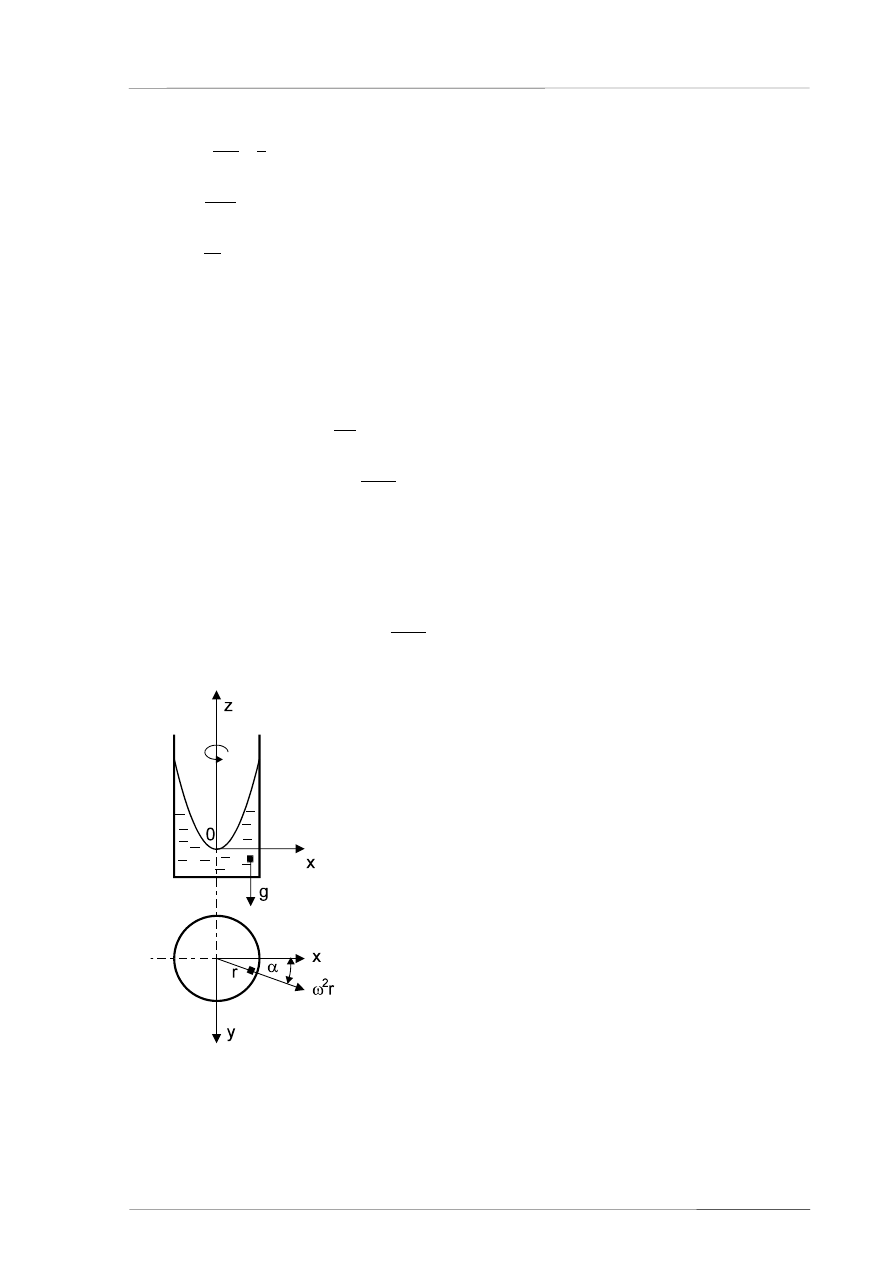
Politechnika Białostocka

Ćwiczenie nr 2

Katedra Ciepłownictwa Powierzchnia swobodna w naczyniu wirującym wokół osi pionowej

3/5

gdzie:

−

n

1

30

s

ϖ =

π

 

 

 

-

prędkość kątowa ruchu naczynia,

−

n

1

min













-

prędkość kątowa,

−

2

g

m

s

 

 

 

- przyspieszenia ziemskie.

Podstawiając wyrażenia (5) do równania (4) otrzymuje się:

(

)

2

2

2

2

2

2

2 2

xdx

ydy

gdz

0

xdx

ydy

gdz

0

i po scakowaniu :

(x

y )

gz

C

2

r

gz

C

2

ϖ

ϖ

ϖ

ϖ

ϖ

+

−

=

+

−

=

+

−

=

−

=

(6)

Stałą całkowania można wyznaczyć z warunków brzegowych:

0

0

r

0, z

z ,

C

gz

=

=

→

= −

(7)

Powierzchni

ę swobodną cieczy w naczyniu wirującym wokół osi pionowej opisuje równanie:

2 2

0

r

z

z

2g

ϖ

=

+

(8)

Rys. 1.

Przyjęcie układu odniesienia

Oś z pokrywa się z osią obrotu i jest zwrócona przeciwnie do

przyspi

eszenia ziemskiego, a początek układu leży na powierzchni

swobodnej (rys.1). Z równania (1) widać, że kształt powierzchni

swobodnej nie zależy od ciężaru właściwego cieczy ani od kształtu

naczynia. Parametrem paraboloidy (1) określającej powierzchnię
swob

odną jest prędkość kątowa.

Parametr ten można wyznaczyć doświadczalnie dwoma

sposobami:

1)

przez bezpośredni pomiar liczby obrotów naczynia,

2)

pośrednio poprzez pomiar współrzędnych r, z dowolnego
punktu powierzchni swobodnej.

Politechnika Białostocka

Ćwiczenie nr 2

Katedra Ciepłownictwa Powierzchnia swobodna w naczyniu wirującym wokół osi pionowej

4/5

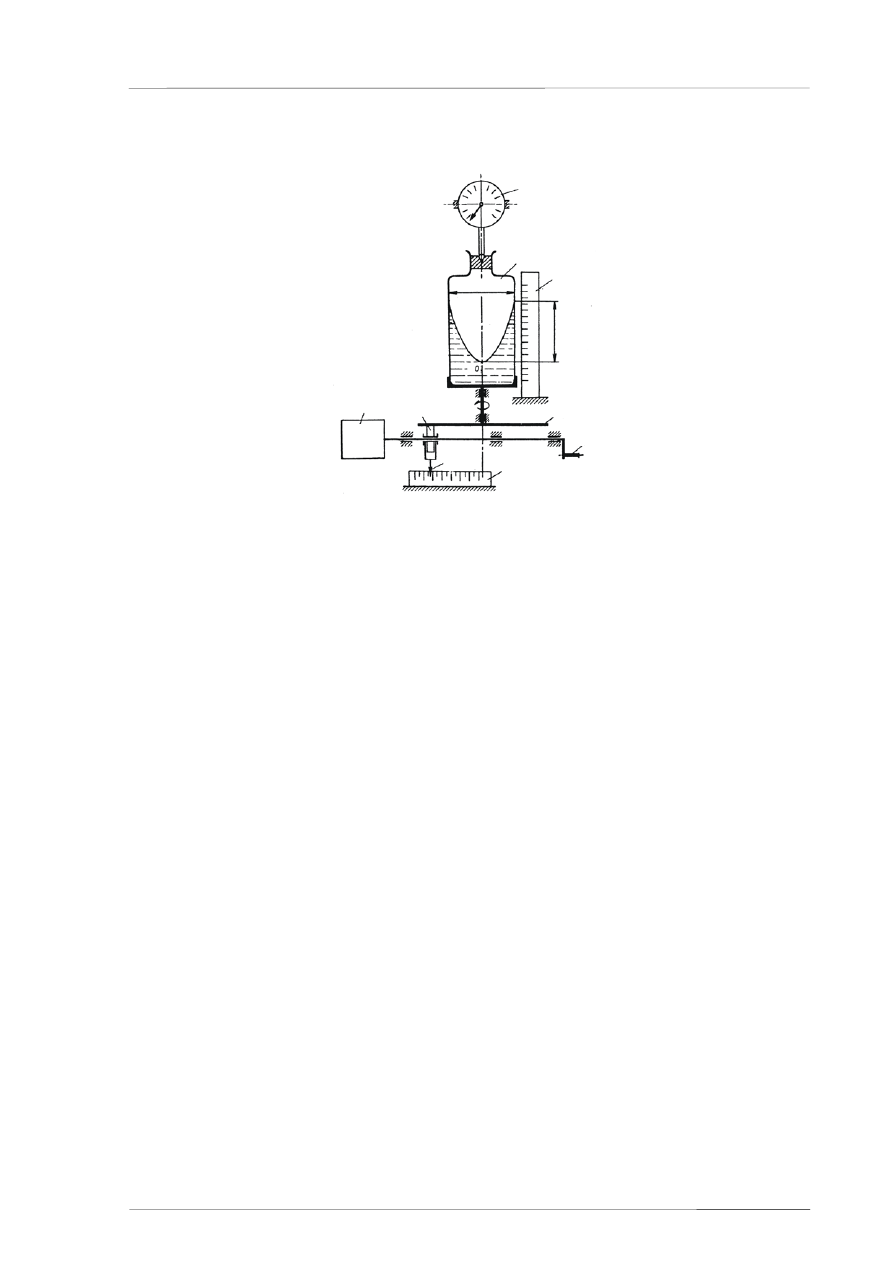
3. Budowa stanowiska.

Schemat stanowiska został pokazany na rysunku nr 2.

A

B

C

Z

Φ

2R

D

G

H

I

F

E

Rys.2. Schemat stanowiska

Poszczególne elementy:
A - obrotomierz (

do pomiaru liczby obrotów wykorzystujemy lampę stroboskopową),

B –

naczynie wirujące wypełnione wodą,

C - skala pionowa,
D - tarcza,
E -

koło napędowe,

F - silnik elektryczny,
G -

korba do przesuwania koła,

H – skala pozioma,
I

-

wskaźnik położenia kółka napędowego E względem skali H.

Naczynie cylindryczne, wypełnione zabarwioną wodą, przezroczyste, o średnicy wewnętrznej

2R = 53,5 mm

wiruje ze stałą liczbą obrotów na minutę wokół swej osi pionowej. Naczynie jest

napędzane za pomocą przekładni ciernej bezstopniowej, sprzęgniętej z silnikiem elektrycznym.

Zmianę obrotów uzyskuje się poprzez przesunięcie koła E. Położenie koła odczytujemy na skali
poziomej H.

Powierzchnia swobodna cieczy przecina powierzchnię naczynia wzdłuż linii będącej

teoretycznie okręgiem. Odległość płaszczyzny tego okręgu od wierzchołka 0 powierzchni swobodnej

została oznaczona literą z na rys. 2 i może być odczytana na skali pionowej C.

4.

Wykonanie ćwiczenia.

a)

Włączyć silnik elektryczny.

b)

Położenia koła napędowego ustawić na początku skali.

c)

Odczytać odległość z na skali pionowej C.

d)

Zmierzyć prędkość wirowania naczynia n

rz

obrotomierzem A.

e)

Zwiększyć prędkość obrotową naczynia i powtórzyć pomiar w sumie sześciokrotnie.

f)

Po zakończeniu pomiarów wykonać sprawozdanie.

Politechnika Białostocka

Ćwiczenie nr 2

Katedra Ciepłownictwa Powierzchnia swobodna w naczyniu wirującym wokół osi pionowej

5/5

5. Wymagania BHP

1.

Do wykonywania ćwiczeń dopuszczeni są studenci, którzy zostali przeszkoleni (na pierwszych

zajęciach) w zakresie szczegółowych przepisów BHP obowiązujących w laboratorium.

2.

W trakcie wykonywania ćwiczeń obowiązuje ścisłe przestrzeganie przepisów porządkowych
i

dokładne wykonywanie poleceń prowadzącego.

3.

Wszystkie czynności związane z uruchamianiem urządzeń elektrycznych należy wykonywać za

zgodą prowadzącego zajęcia.

4.

Zabrania się manipulowania przy urządzeniach i przewodach elektrycznych bez polecenia

prowadzącego.

6. Opracowanie wyników.

Wyniki wpisać w tabeli i uzupełnić obliczenia w dwóch końcowych kolumnach.

Wyniki pomiarów

Wyniki obliczeń

kolejne

położenie

wskaźnika

n

rz

z

n

R

gz

a

=

30

2

π

∆n

n

n

n

rz

a

rz

=

−

⋅ 100%

obr/min

mm

obr/min

%

1

2

3

4

5

6

1.

wyznaczyć równanie przedstawiające wyniki jako równanie regresji ważonej (wagą
każdego pomiaru jest odwrotność kwadratu błędu, zaś

b

=0) —

współczynnik

a

obliczyć

wg równania (10) w instrukcji [5],

2.

obliczyć współczynnik korelacji r — (11) w instrukcji [5] i wartość r

2

.

3. obliczy

ć wariancję empirycznego współczynnika regresji ważonej

2

a

S

— (12) w instrukcji

[5].

7

. Literatura uzupełniająca.

1. W.J. Prosnak, „

Ćwiczenia laboratoryjne z mechaniki płynów” Wydawnictwa Politechniki

Warszawskiej 1975.

2. Walden H. „

Mechanika Płynów”, Wydawnictwa Politechniki Warszawskiej 1978.

3.

Kołodziejczyk L., Mańkowski S., Rubik M., „Pomiary w inżynierii sanitarnej”, Arkady,
Warszawa 1980.

4.

Praca zbiorowa pod redakcją M. Matlaka, A. Szustra, „Ćwiczenia laboratoryjne z mechaniki

płynów”, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa 2002.

5.

Gajewski A.: Instrukcja do zajęć laboratoryjnych: cechowanie rotametru.