
PODSTAWY AUTOMATYKI – ĆWICZENIA
lista zadań nr 1
Transformata Laplace’a
1. Korzystając wprost z definicji znaleźć transformatę Laplace’a funkcji:
a.
3
2
)
(
+
= t
t
y
c.
2
)
(
t
t
y
=
b.
2
)
(
+
−
= t
t
y
d.
1
2
)
(
3
+
=
− t
e
t
y
2. Dana jest odpowiedź na impuls Diraca (funkcja wagi)
)
(
t
g
. Znaleźć transmitancję
operatorową
)
(
s
G
.
a.
(
)
)
(
3
2
)
(
4
3
t
e
e
t
g
t
t
1
−
−
+
−
=
d.
(
)
)
(
3
2
)
(
3
2
2
t
e
te
e
t
t
g
t
t
t
1
−
−
−
+
+
=
b.
(
)
)
(
2
3
)
(
2
3
t
e
e
e
t
g
t
t
t
1
−
−
−
+
+
=
e.
( )
(
)
)
(
2
sin
2
)
(
t
t
e
t
g
t
1
+
=
−
c.
(
)
)
(
3
2
)
(
2
2
t
e
e
t
t
g
t
t
1
−
−
+
=
f.
( )
)
(
sin
)
(
t
t
t
t
g
1
=
3. Dana jest odpowiedź układu na skok jednostkowy
)
(
1
t
y
. Znaleźć transmitancję operatorową
)
(
s
G
.
a.
(
)
)
(
4
2
2
)
(
2
1
t
e
e
t
y
t
t
1
−
−
−
+
=
c.
(
)
(
)
)
(
1
)
(
2
1
t
e
t
e
t
y
t
t
1
−
−
−
+
=
b.
(
)
)
(
2
)
(
2
1
t
te
t
y
t
1
−
=
d.
(
)
)
2
(
2
sin
)
(
1
−
−
=
t
t
t
y
1
4. Dana jest transmitancja operatorowa obiektu
)
(
s
G
. Wyznaczyć odpowiedź układu na
impuls Diraca (funkcję wagi)
)
(
t
g
.
a.
8
6
2
5
)
(
2
+
+
+
=
s
s
s
s
G
d.
(
)
2
2
1
)
(
+
+
=
s
s
s
G
b.
20
9
3
2
)
(
2
+
+
+
=
s
s
s
s
G
e.
(
)
(
)
6
5
3
1
)
(
2
2
+
+
+
+
+
=
s
s
s
s
s
s
G
c.
(
)
1
1
2
)
(
+
+
=
s
s
s
s
G
f.
(
)
3
1
3
2
)
(
+
+
=
s
s
s
G
5. Obiekt opisany jest równaniem różniczkowym. Wyznaczyć transmitancję operatorową
)
(s
G
oraz odpowiedź układu na impuls Diraca (funkcję wagi)
)
(t
g
.
a.
u
u
y
y
y
8
2
10
12
2
+
′
=
+
′
+
′′
b.
u
u
y
y
y
4
8
16
12
2
+
′
=
+
′
+
′′
c.
u
u
y
y
y
6
9
12
15
3
+
′
=
+
′
+
′′
6. Obiekt opisany jest równaniem różniczkowym. Wyznaczyć transmitancję operatorową
)
(s
G
oraz odpowiedź układu na skok jednostkowy
)
(
1
t
y
.
a.
u
u
y
y
y
+
′
=
+
′
+
′′
3
4
b.
u
u
y
y
y
′
+
′′
=
′
+
′′
+
′′′
6
2
6
5
c.
u
u
u
y
y
y
+
′
+
′′
=
+
′
+
′′
4
5
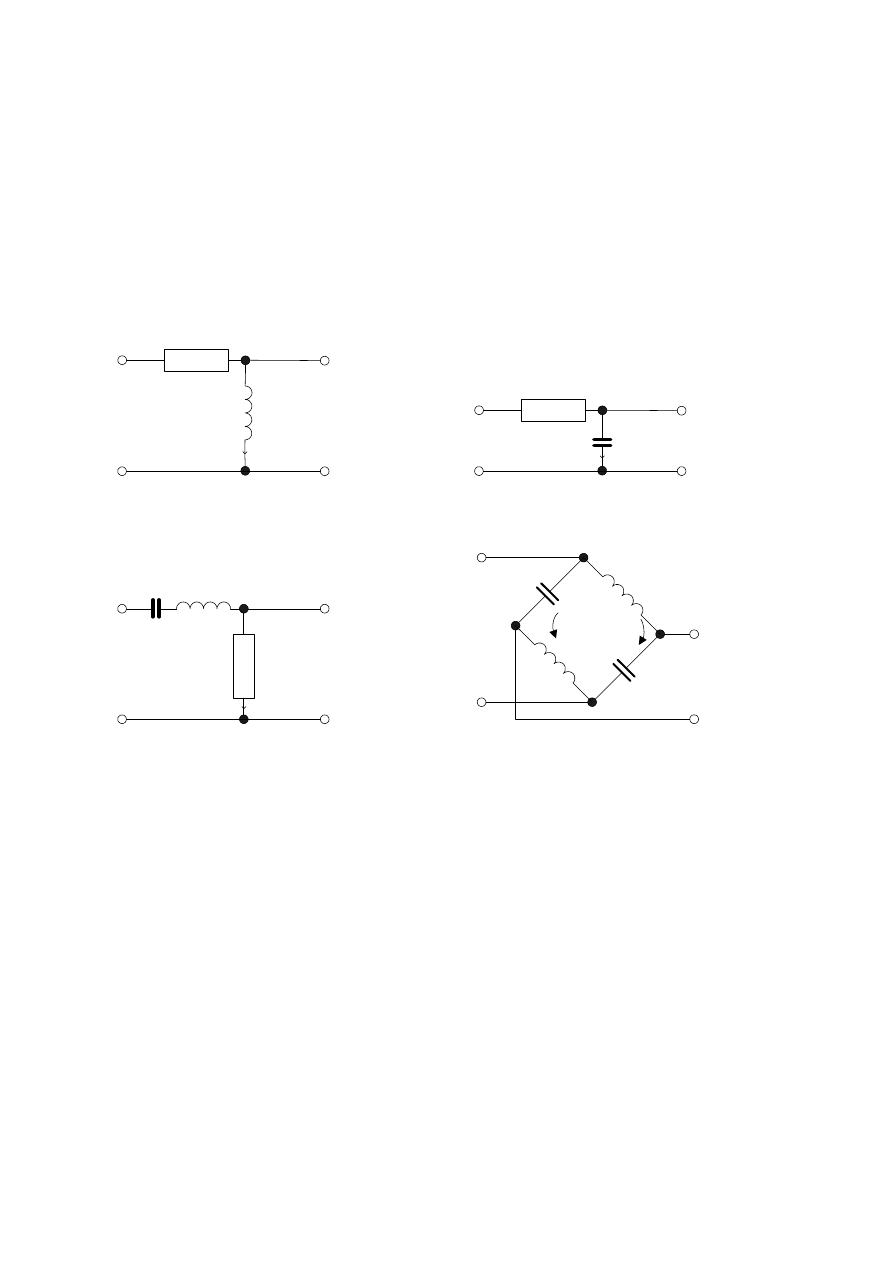
7. Znaleźć transmitancję
)
(s
G
czwórnika elektrycznego:
a.
b.
U
1
U
2
i
L
R
C
U
1
U
2
i
R
c.
d.
U
1
U
2
i
L
R
C
U
1
U
2
i
1
C
L
L
C
i
2

PODSTAWY AUTOMATYKI – ĆWICZENIA
lista zadań nr 2
Charakterystyki czasowe i częstotliwościowe
1. Wykreślić charakterystykę impulsową obiektów opisanych transmitancją operatorową
)
(s
G
:
a.
5
)
(
=
s
G
c.
s
s
G
2
)
(
=
b.
2
1
)
(
+
=
s
s
G
d.
(
)
1
2
5
)
(
+
=
s
s
s
G
2. Wykreślić charakterystykę odpowiedzi na skok jednostkowy obiektów opisanych
transmitancją operatorową identyczną jak w zadaniu I.
3. Wykreślić charakterystykę amplitudowo – fazową (Nyquista) obiektów opisanych
transmitancją operatorową identyczną jak w zadaniu I.
4. Wykreślić logarytmiczną charakterystykę amplitudowo – fazową (na karcie Nicholsa)
obiektów opisanych transmitancją operatorową identyczną jak w zadaniu I.
5. Wykreślić uproszczone logarytmiczne charakterystyki modułu i argumentu (Bodego)
obiektów opisanych transmitancją operatorową
)
(s
G
:
a.
2
1
10
)
(
s
s
s
G
+
=
f.
(
)
10
100
)
(
+
=
s
s
s
G
b.
(
)
2
10
1
)
(
+
=
s
s
G
g.
(
)(
)
1
,
0
1
)
(
+
+
=
s
s
s
s
G
c.
(
)
2
1
1
,
0
1
)
(
+
+
=
s
s
s
G
h.
(
)
(
)(
)
1
100
1
10
01
,
0
)
(
+
+
+
=
s
s
s
s
G
d.
(
)
2
1
)
(
+
=
s
s
s
G
i.
(
)
(
)(
)
1
1
,
0
1
,
0
1
100
10
)
(
+
+
+
=
s
s
s
s
G
e.
(
)(
)
10
1
10
)
(
+
+
=
s
s
s
s
G
j.
(
)
(
)(
)
1
100
1
,
0
1
,
0
1
10
10
)
(
+
+
+
=
s
s
s
s
G
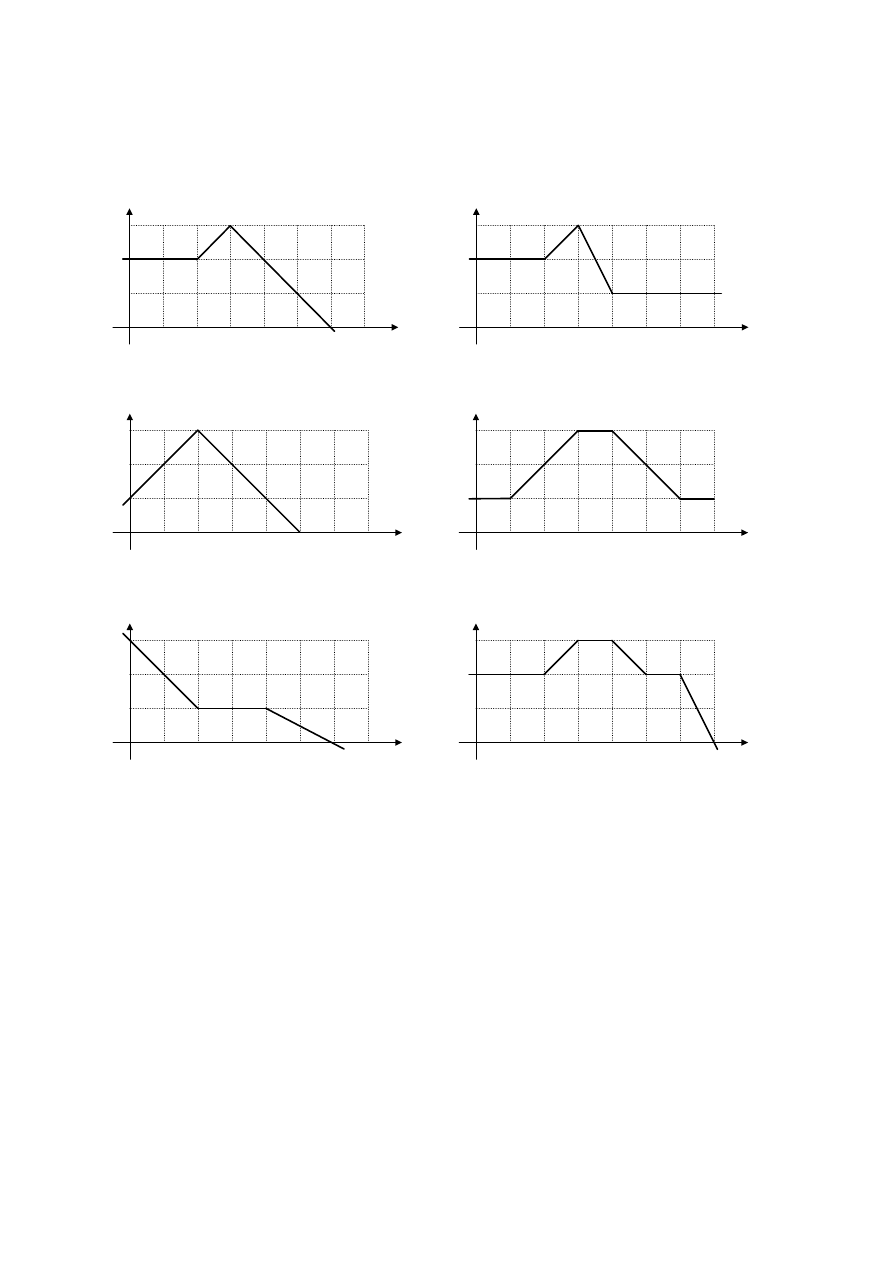
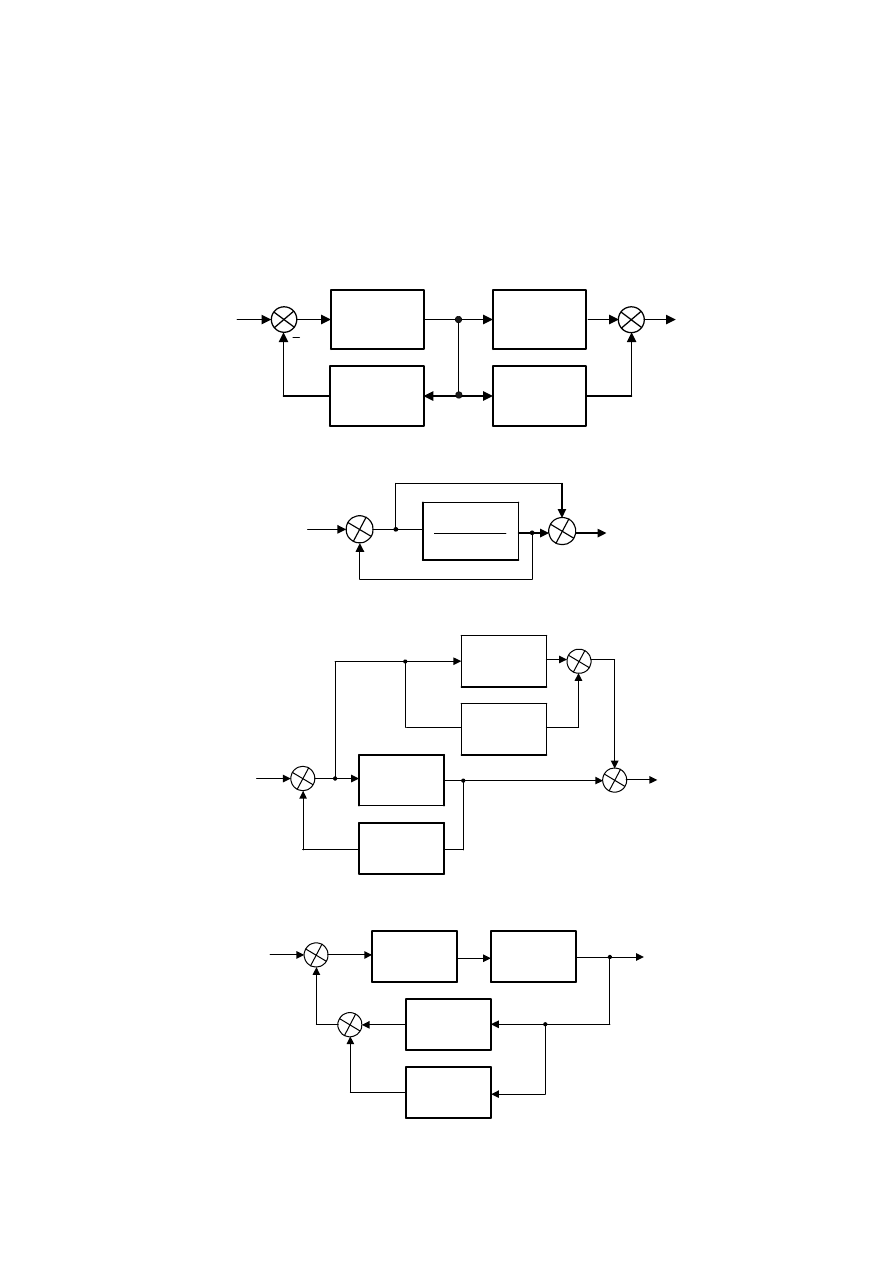
6. Wyznaczyć transmitancję operatorową
)
(s
G
dla układów, których uproszczone
logarytmiczne charakterystyki modułu dane są na rysunkach:
a.
b.
L(
ω
) [dB]
ω
[rad/s]
10
-3
10
-2
10
-1
10
0
10
1
10
2
10
3
20
40
60
L(
ω
) [dB]
ω
[rad/s]
10
-3
10
-2
10
-1
10
0
10
1
10
2
10
3
20
40
60
c.
d.
L(
ω
) [dB]
ω
[rad/s]
20
40
60
10
4
10
-2
10
-1
10
0
10
1
10
2
10
3
...
L(
ω
) [dB]
ω
[rad/s]
10
-3
10
-2
10
-1
10
0
10
1
10
2
10
3
20
40
60
e.
f.
L(
ω
) [dB]
ω
[rad/s]
20
40
60
10
4
10
-2
10
-1
10
0
10
1
10
2
10
3
L(
ω
) [dB]
ω
[rad/s]
10
-3
10
-2
10
-1
10
0
10
1
10
2
10
3
20
40
60
PODSTAWY AUTOMATYKI – ĆWICZENIA
lista zadań nr 3
Algebra schematów blokowych. Uchyby ustalone
1. Wyznaczyć transmitancję zastępczą układów jak na rysunkach:
a.
G
1
G
4
G
3
U(s)
Y(s)
G
2
b.
1
12
2
5
+
+
−
s
s
se
s
–
c.
G
2
–
G
4
G
1
G
3
d.
G
1
–
G
3
G
2
G
4
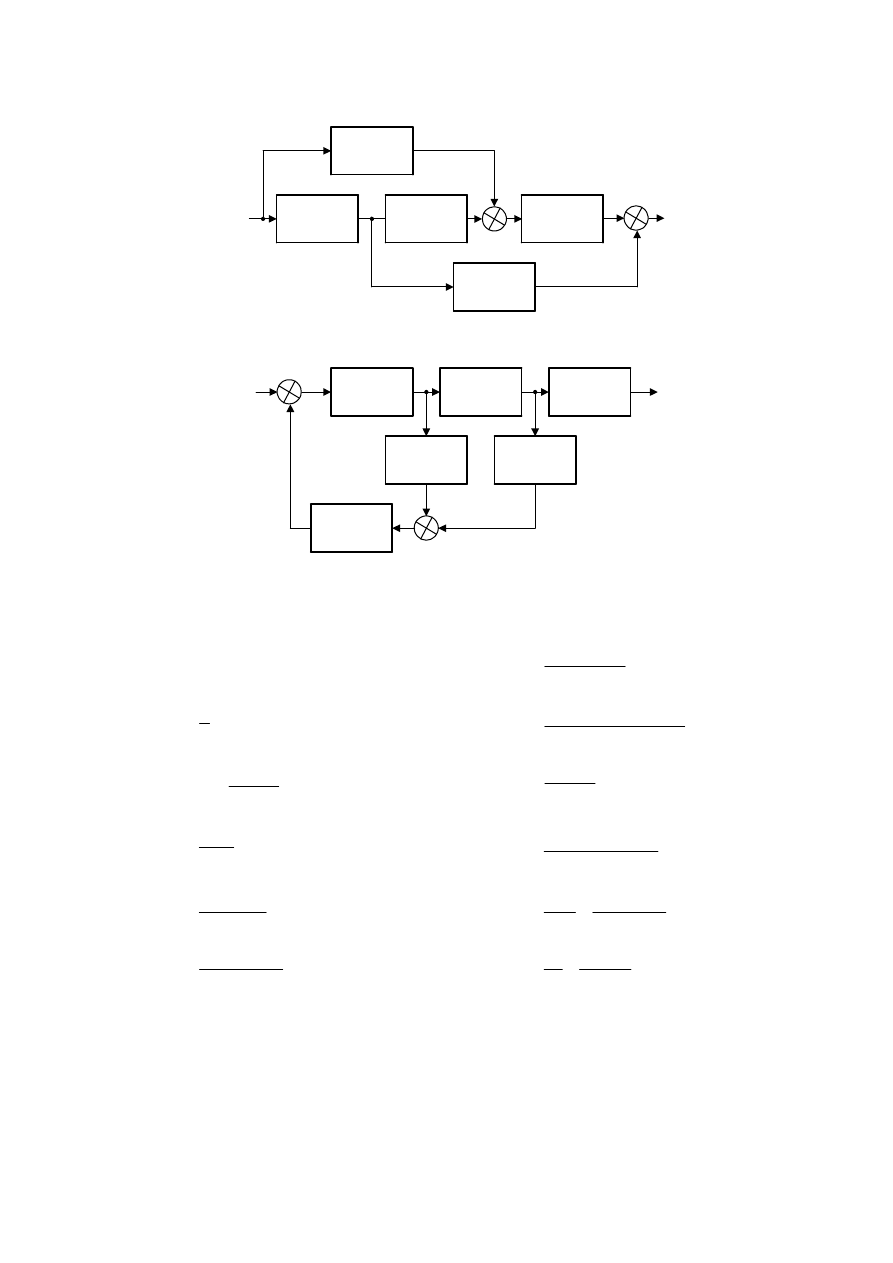
e.
G
1
G
2
G
3
G
5
G
4
f.
–
G
1
G
2
G
3
G
5
G
4
G
6
2. Dana jest transmitancja układu otwartego
)
(
12
s
G
. Obliczyć wartość uchybów położenia,
prędkości i przyspieszenia:
a.
4
)
(
12
=
s
G
g.
2
3
2
12
2
5
,
0
)
(
s
s
s
s
s
G
+
+
+
=
b.
s
s
G
5
)
(
12
=
h.
3
4
2
4
12
2
5
,
0
2
3
4
)
(
s
s
s
s
s
s
G
+
+
+
+
=
c.
2
12
5
)
(
s
s
s
G
+
=
i.
(
)
3
12
1
4
)
(
+
=
s
s
G
d.
5
5
)
(
12
+
=
s
s
G
j.
(
)
(
)(
)
s
s
s
s
s
s
G
+
+
+
=
2
2
2
12
2
1
,
0
)
(
e.
3
2
)
(
2
12
+
+
=
s
s
s
G
k.
1
2
1
1
2
)
(
2
12
+
+
+
+
=
s
s
s
s
G
f.
s
s
s
s
G
3
2
)
(
2
3
12
+
+
=
l.
s
s
s
s
G
2
1
2
)
(
2
2
12
+
+
=
PODSTAWY AUTOMATYKI – ĆWICZENIA
lista zadań nr 4
Stabilność cz.1
1. Korzystając z kryterium Routh’a zbadać stabilność układu o transmitancji podanej poniżej.
Określić liczbę biegunów w prawej i w lewej półpłaszczyźnie.
a.
1
2
3
4
5
1
10
)
(
2
3
4
+
+
+
+
+
=
s
s
s
s
s
s
G
d.
1
2
3
)
(
2
3
+
+
+
=
s
s
s
s
s
G
b.
1
2
3
4
1
)
(
2
3
4
+
+
+
+
=
s
s
s
s
s
G
e.
4
3
2
5
)
(
2
3
+
+
+
=
s
s
s
s
G
c.
6
5
5
5
1
3
)
(
2
3
4
−
−
+
+
+
=
s
s
s
s
s
s
G
f.
1
5
10
)
(
2
3
+
+
+
+
=
s
s
s
s
s
G
2. Dana jest transmitancja
)
(
12
s
G
układu otwartego (ze sztywnym sprzężeniem zwrotnym).
Wykorzystując kryterium Michajłowa zbadać czy układ zamknięty jest stabilny.
a.
1
2
)
(
2
3
12
+
+
+
=
s
s
s
s
G
c.
1
3
2
3
1
)
(
2
3
12
+
+
+
=
s
s
s
s
G
b.
1
3
2
1
)
(
2
3
12
+
+
+
=
s
s
s
s
G
d.
1
)
(
2
12
+
+
=
−
s
s
e
s
G
s
3. Dana jest transmitancja
)
(
12
s
G
układu otwartego. Wykorzystując kryterium Nyquista
zbadać czy układ zamknięty jest stabilny.
a.
(
)
(
)
1
5
,
1
1
4
)
(
2
12
−
+
+
=
s
s
s
s
G
c.
s
s
s
G
−
=
3
12
1
)
(
b.
(
)
(
)
1
1
2
1
)
(
2
12
−
+
+
=
s
s
s
s
G
d.
(
)
6
5
5
)
(
2
12
+
+
=
s
s
s
s
G
4. Dana jest transmitancja
)
(
12
s
G
układu otwartego. Wykorzystując kryterium Nyquista
zbadać dla jakiego k układ zamknięty jest stabilny.
a.
(
)
3
12
4
)
(
+
=
s
k
s
G
c.
(
)(
)(
)
6
4
2
2
)
(
12
+
+
+
=
s
s
s
k
s
G
b.
(
) (
)
3
1
)
(
2
12
+
+
=
s
s
k
s
G
d.
(
)
(
)
1
12
7
35
)
(
2
12
+
+
+
=
s
s
s
k
s
G
PODSTAWY AUTOMATYKI – ĆWICZENIA
lista zadań nr 5
Stabilność cz.2
1. Dana jest transmitancja
)
(
12
s
G
układu otwartego. Wykorzystując kryterium logarytmiczne
zbadać czy układ zamknięty jest stabilny.
a.
(
)
3
12
1
7
)
(
+
=
s
s
G
b.
(
)
(
)
2
4
4
16
)
(
2
12
+
+
+
=
s
s
s
s
G
c.
s
e
s
s
G
5
12
2
3
)
(
−
+
=
2. Dana jest transmitancja
)
(
12
s
G
układu otwartego. Obliczyć zapas fazy i wzmocnienia dla
układu zamkniętego.
a.
(
)
3
12
1
4
)
(
+
=
s
s
G
c.
(
)
(
)
4
16
8
32
)
(
2
12
+
+
+
=
s
s
s
s
G
b.
s
e
s
s
G
2
12
5
,
0
1
)
(
−
+
=
d.
12
10
2
3
)
(
2
12
+
+
=
s
s
s
G
PODSTAWY AUTOMATYKI – ĆWICZENIA
lista zadań nr 6
Zmienne stanu
1. Korzystając z metody bezpośredniej wyznaczyć równania stanu dla obiektu o transmitancji
)
(s
G
przy zerowych warunkach początkowych:
a.
2
3
2
)
(
2
+
−
=
s
s
s
G
c.
6
4
2
1
2
)
(
2
+
+
+
=
s
s
s
s
G
b.
6
2
4
)
(
2
3
+
+
=
s
s
s
G
d.
3
3
1
)
(
2
3
+
+
+
=
s
s
s
s
G
2. Korzystając z metody równoległej wyznaczyć równania stanu dla obiektu o transmitancji
)
(s
G
przy zerowych warunkach początkowych:
a.
6
5
1
)
(
2
+
+
=
s
s
s
G
c.
4
3
5
,
0
3
5
,
0
)
(
2
+
+
+
=
s
s
s
s
G
b.
5
6
1
2
)
(
2
+
+
+
=
s
s
s
s
G
d.
(
)(
)(
)
6
4
2
10
)
(
+
+
+
+
=
s
s
s
s
s
G
3. Korzystając z metody szeregowej wyznaczyć równania stanu dla obiektu o transmitancji
)
(s
G
przy zerowych warunkach początkowych:
a.
(
)
2
2
1
)
(
+
=
s
s
G
c.
(
)
(
)(
)
4
1
4
)
(
+
+
−
=
s
s
s
s
s
G
b.
4
6
2
4
)
(
2
+
+
=
s
s
s
G
d.
(
)
2
2
)
(
2
+
−
=
s
s
s
s
G
4. Dane są równania stanu:
)
(
)
(
)
(
)
(
)
(
)
(
s
U
s
s
Y
s
U
s
s
s
D
CX
B
AX
X
+
=
+
=
Wyznaczyć transmitancję
)
(s
G
.
a.
=
1
1
1
1
A
,
=
1
0
B
,
[
]
0
1
=
C
,
0
=
D
d.
=
4
3
2
1
A
,
=
2
1
B
,
[
]
1
0
=
C
,
0
=
D
b.
=
1
2
2
1
A
,
=
1
1
B
,
[
]
0
1
=
C
,
0
=
D
e.
=
3
3
2
2
A
,
=
4
4
B
,
[ ]
1
1
=
C
,
0
=
D
c.
=
2
1
1
2
A
,
=
0
1
B
,
[
]
0
1
=
C
,
0
=
D
f.
−
−
=
1
3
1
2
A
,
=
2
1
B
,
[
]
2
2
=
C
,
0
=
D

PODSTAWY AUTOMATYKI – ĆWICZENIA
lista zadań nr 7
Transformata Z
1. Korzystając wprost z definicji znaleźć transformatę Z funkcji:
a.
2
)
(
n
n
f
=
d.
)
(
)
(
4
t
e
t
f
t
1
−
=
b.
n
n
f
3
)
(
=
e.
)
(
)
(
t
e
t
f
p
T
t
1
−
=
c.
1
5
)
(
+
= n
n
f
f.
)
(
5
,
0
)
(
2
t
t
t
f
1
=
2. Korzystając z podstawowych własności transformaty, znaleźć transformatę Z funkcji:
a.
(
)
)
(
8
3
)
(
t
t
t
f
1
+
=
d.
)
(
5
,
0
)
(
2
t
t
t
f
1
=
b.
(
)
)
(
5
)
(
t
t
t
f
1
+
−
=
e.
)
(
5
)
(
3
t
e
t
f
t
1
=
c.
)
(
)
(
1
t
t
t
f
1
−
=
f.
(
)
)
(
3
)
(
4
t
e
t
t
f
t
1
−
+
=
3. Obliczyć odpowiedź na impuls Diraca,
)
(n
g
, dla układu impulsowego o transmitancji:
a.
5
6
2
5
,
0
)
(
2
+
+
+
=
z
z
z
z
G
e.
5
,
0
5
,
1
)
(
2
+
+
=
z
z
z
z
G
b.
8
6
2
5
)
(
2
+
+
+
=
z
z
z
z
G
f.
20
9
3
2
)
(
2
+
+
+
=
z
z
z
z
G
c.
10
7
5
,
0
)
(
2
+
+
+
=
z
z
z
z
G
g.
3
4
1
3
)
(
2
+
+
+
=
z
z
z
z
G
d.
15
8
2
4
)
(
2
+
+
+
=
z
z
z
z
G
h.
(
)
2
2
1
)
(
+
+
=
z
z
z
G
4. Obliczyć odpowiedź na skok jednostkowy,
)
(
1
n
y
, dla układu impulsowego o transmitancji:
a.
2
)
(
−
=
z
z
z
G
d.
1
1
2
)
(
−
+
=
z
z
z
G
b.
1
5
,
0
1
)
(
−
=
z
z
G
e.
6
5
)
(
2
+
−
=
z
z
z
z
G
c.
1
1
)
(
+
−
=
z
z
z
G
f.
2
4
)
(
2
−
−
+
=
z
z
z
z
G

5. Dana jest odpowiedź na impuls Diraca
)
(n
g
. Obliczyć transmitancję takiego układu
impulsowego:
a.
n
n
n
g
2
3
3
2
)
(
⋅
+
⋅
=
c.
n
n
n
g
)
2
(
3
)
1
(
2
)
(
1
−
⋅
+
−
⋅
=
−
b.
1
2
5
)
(
+
⋅
=
n
n
g
d.
1
3
)
(
−
=
n
n
n
g
6. Wyznaczyć odpowiednik impulsowy transmitancji układu ciągłego
)
(s
G
dla czasu
próbkowania
s
T
p
1
,
0
=
.
a.
2
3
1
2
)
(
2
+
+
+
=
s
s
s
s
G
d.
4
1
)
(
2
−
=
s
s
G
b.
4
5
2
)
(
2
+
+
−
=
s
s
s
s
G
e.
s
s
s
s
G
2
4
)
(
2
+
+
=
c.
6
5
1
)
(
2
+
+
=
s
s
s
G
f.
1
2
1
)
(
2
+
+
=
s
s
s
G

PODSTAWY AUTOMATYKI – ĆWICZENIA
lista zadań nr 8
Równania różnicowe
1. Znaleźć równanie różnicowe wiążące sygnały wejściowy i wyjściowy dla układu
impulsowego o transmitancji
)
(z
G
, zakładając zerowe warunki początkowe. Obliczyć
wartość próbki sygnału wyjściowego
)
3
(
y
, dla sygnału wejściowego
)
(
)
(
t
t
u
1
=
.
a.
5
6
1
)
(
2
+
−
+
=
z
z
z
z
G
c.
10
2
)
(
+
=
z
z
G
b.
6
5
1
)
(
2
+
+
=
z
z
z
G
d.
2
1
)
(
2
−
=
z
z
G
2. Rozwiązać równanie różnicowe dla podanych warunków początkowych.
a.
0
)
1
(
4
)
(
=
−
−
n
y
n
y
,
1
)
1
(
=
−
y
b.
0
)
2
(
9
)
(
=
−
−
n
y
n
y
,
1
)
1
(
=
−
y
,
1
)
2
(
=
−
y
c.
0
)
2
(
2
)
1
(
3
)
(
=
−
+
−
−
n
y
n
y
n
y
,
2
)
1
(
=
−
y
,
1
)
2
(
=
−
y
d.
0
)
2
(
2
)
1
(
3
)
(
=
−
+
−
−
n
y
n
y
n
y
,
3
)
1
(
=
−
y
,
2
)
2
(
=
−
y
e.
0
)
2
(
2
)
1
(
)
(
=
−
−
−
+
n
y
n
y
n
y
,
3
)
1
(
=
−
y
,
6
)
2
(
=
−
y
3. Rozwiązać układ równań różnicowych dla podanych warunków początkowych.
a.
−
−
=
+
+
)
(
)
(
1
2
3
4
)
1
(
)
1
(
2
1
2
1
n
x
n
x
n
x
n
x
,
2
)
0
(
1
=
x
,
1
)
0
(
2
=
x
b.
−
−
=
+
+
)
(
)
(
1
3
4
6
)
1
(
)
1
(
2
1
2
1
n
x
n
x
n
x
n
x
,
1
)
0
(
1
=
x
,
2
)
0
(
2
=
x
c.
−
−
=
+
+
)
(
)
(
2
3
3
4
)
1
(
)
1
(
2
1
2
1
n
x
n
x
n
x
n
x
,
3
)
0
(
1
=
x
,
1
)
0
(
2
=
x
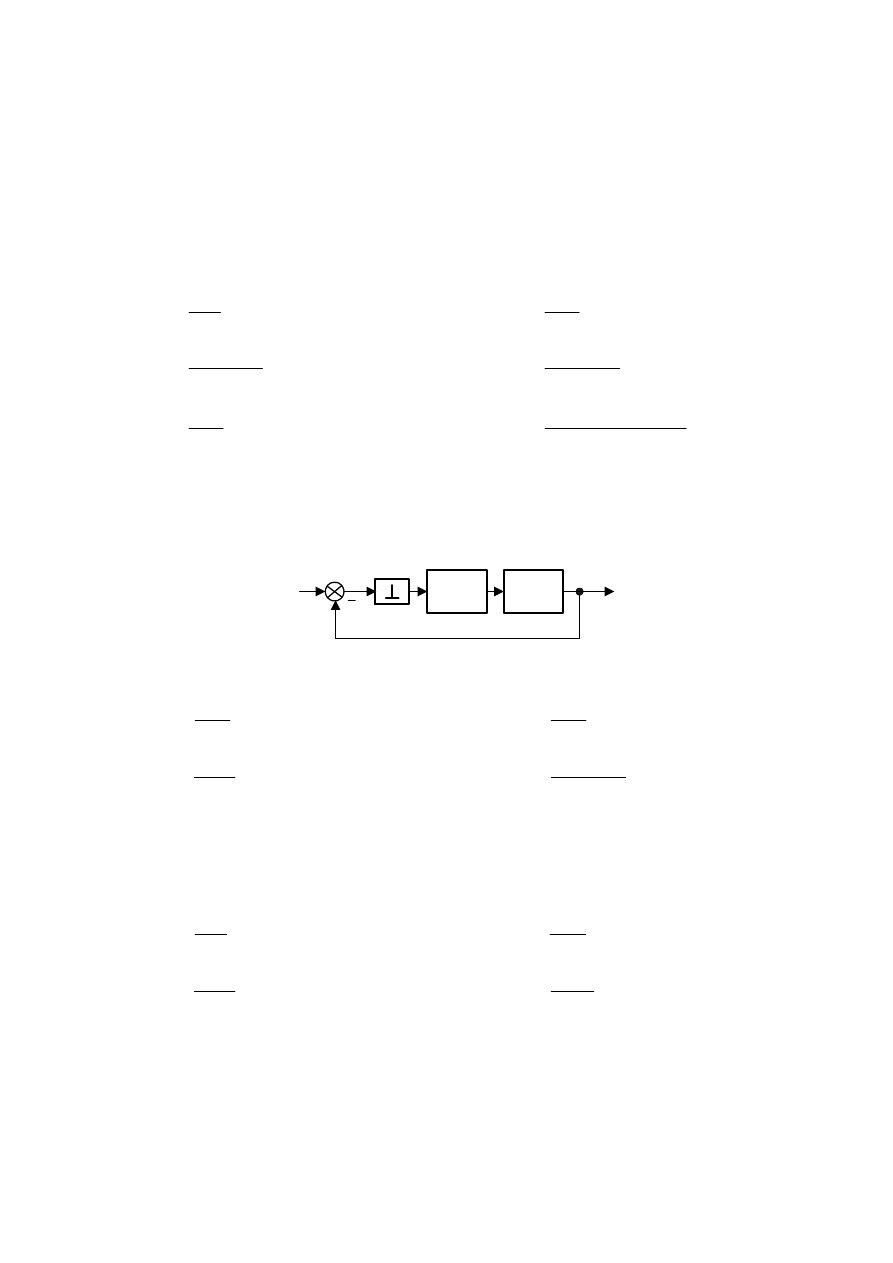
PODSTAWY AUTOMATYKI – ĆWICZENIA
lista zadań nr 9
Ekstrapolatory
1. Obliczyć transmitancję
)
(z
G
obiektu o transmitancji
)
(s
G
przy zastosowaniu ekstrapolatora
zerowego rzędu.
a.
1
1
)
(
+
=
s
s
G
,
s
T
p
1
=
d.
5
2
)
(
+
=
s
s
G
,
s
T
p
10
=
b.
)
5
,
0
ln(
2
)
(
+
=
s
s
G
,
s
T
p
1
=
e.
2
3
1
)
(
2
+
−
=
s
s
s
G
,
s
T
p
1
=
c.
5
2
)
(
+
=
s
s
G
,
s
T
p
1
,
0
=
f.
(
)(
)
)
2
ln(
)
4
ln(
1
)
(
−
−
+
=
s
s
s
s
G
,
s
T
p
1
=
2. W układzie jak na rys. 9.1 zastosowano ekstrapolator zerowego rzędu. Obliczyć wartości
pierwszych
n
próbek sygnałów odpowiedzi
)
(n
y
i błędu
)
(n
e
przy pobudzeniu skokiem
jednostkowym (
s
T
p
1
=
).
G
E
(
s)
G
0
(
s)
T
p
Rys. 9.1. Układ regulacji z ekstrapolatorem.
a.
2
1
)
(
0
+
=
s
s
G
,
7
=
n
c.
4
5
,
0
)
(
0
+
=
s
s
G
,
4
=
n
b.
1
3
3
)
(
0
+
=
s
s
G
,
5
=
n
d.
8
6
1
)
(
2
0
+
+
=
s
s
s
G
,
4
=
n
3. W układzie jak na rys. 9.1 zastosowano ekstrapolator zerowego rzędu. Obliczyć wartości
pierwszych pięciu próbek sygnałów odpowiedzi
)
(n
y
i przy pobudzeniu skokiem prędkości
(
s
T
p
1
=
).
a.
1
1
)
(
0
+
=
s
s
G
c.
2
1
)
(
0
−
=
s
s
G
b.
1
3
1
)
(
0
+
=
s
s
G
d.
3
2
5
,
0
)
(
0
−
=
s
s
G
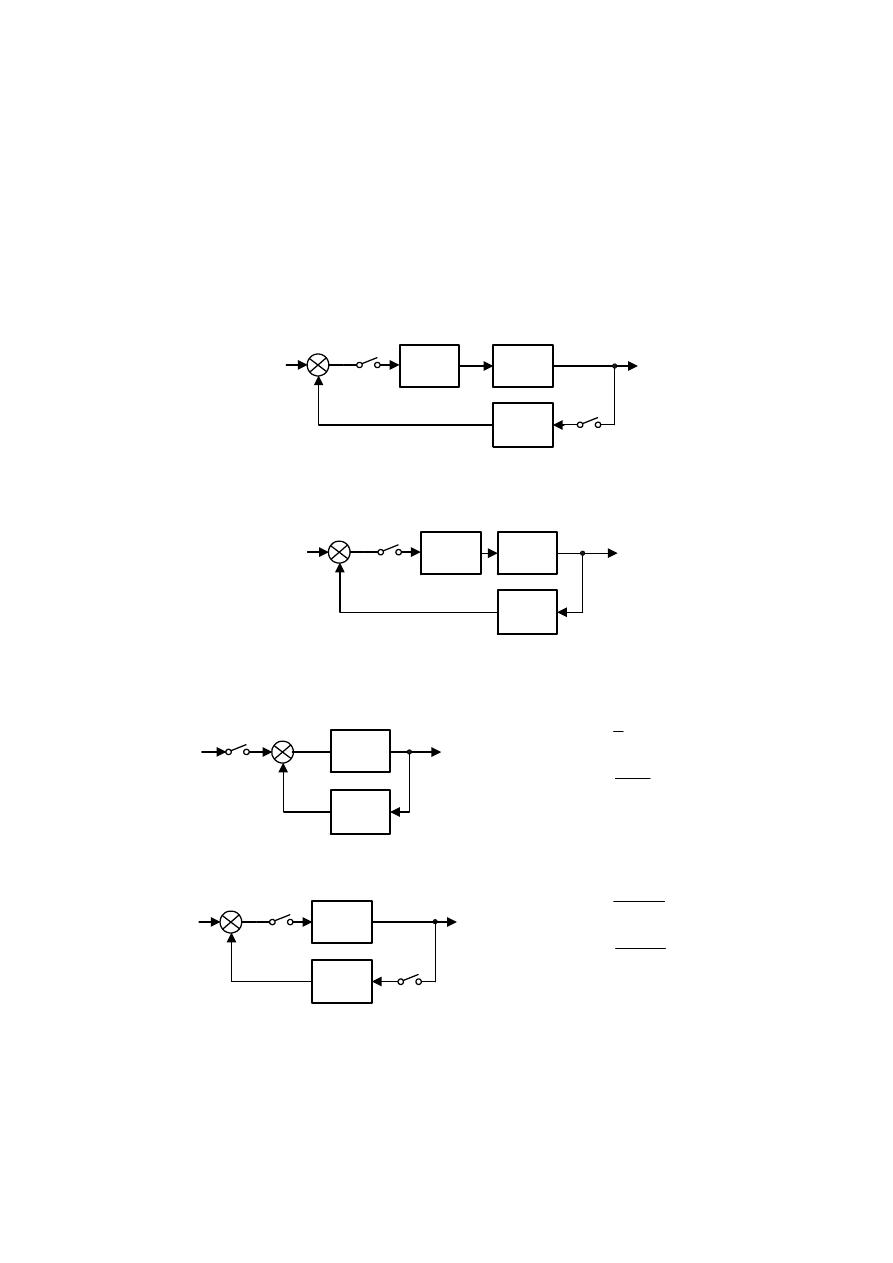
PODSTAWY AUTOMATYKI – ĆWICZENIA
lista zadań nr 10
Algebra schematów blokowych
Uchyby ustalone
1. Wyprowadzić wzór na dyskretną transmitancję zastępczą układów jak na rysunkach:
a.
Y(s)
U(s)
E(s)
−
T
p
G
1
(s)
G
2
(s)
G
3
(s)
T
p
b.
Y(s)
U(s)
E(s)
−
T
p
G
1
(s)
G
2
(s)
G
3
(s)
2. Wyznaczyć transmitancję zastępczą układów jak na rysunkach:
a.
G
2
(s)
Y(s)
U(s)
E(s)
−
T
p
G
1
(s)
s
s
G
1
)
(
1
=
2
1
)
(
2
+
=
s
s
G
1
=
p
T
b.
Y(s)
U(s)
E(s)
−
T
p
G
1
(s)
G
2
(s)
T
p
2
ln
1
)
(
1
−
=
s
s
G
3
ln
2
)
(
2
−
=
s
s
G
1
=
p
T
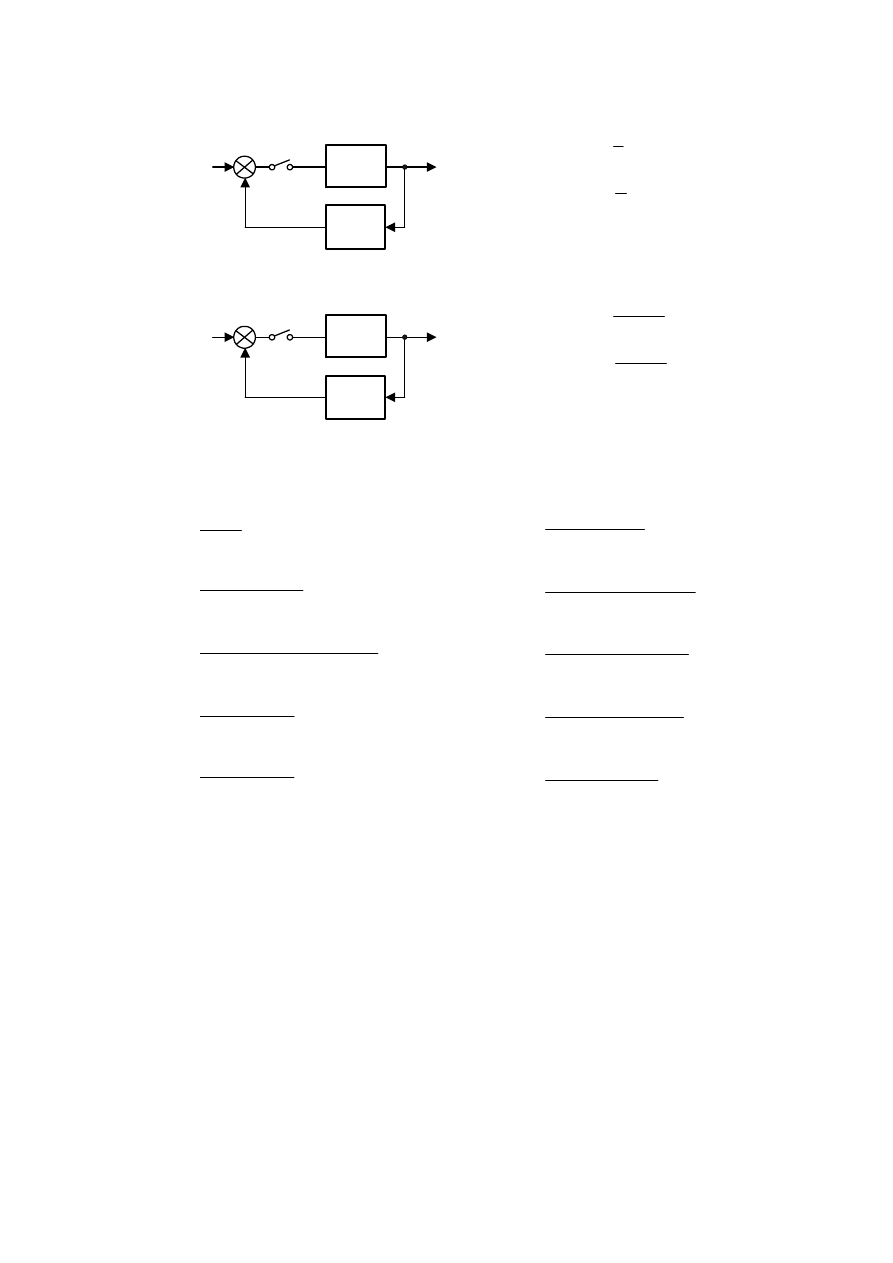
c.
G
2
(s)
Y(s)
U(s)
E(s)
−
T
p
G
1
(s)
s
s
G
1
)
(
1
=
s
s
G
2
)
(
2
=
1
=
p
T
d.
G
2
(s)
Y(s)
U(s)
E(s)
−
T
p
G
1
(s)
2
ln
1
)
(
1
−
=
s
s
G
2
ln
2
)
(
2
−
=
s
s
G
1
=
p
T
3. Dana jest transmitancja układu otwartego
)
(
12
z
G
. Obliczyć wartość uchybów położenia,
prędkości i przyspieszenia (
s
T
p
1
=
):
a.
1
2
2
)
(
12
−
=
z
z
G
f.
5
,
0
5
,
1
25
,
0
5
,
0
)
(
2
12
+
−
−
=
z
z
z
z
G
b.
9
,
0
7
,
0
1
)
(
2
12
−
−
=
z
z
z
G
g.
1
,
0
8
,
0
9
,
1
12
,
0
96
,
0
2
)
(
2
3
2
12
+
+
−
−
−
=
z
z
z
z
z
z
G
c.
125
,
5
75
,
0
5
,
1
5
)
(
2
3
12
−
+
−
=
z
z
z
z
G
h.
5
,
0
2
5
,
2
625
,
0
25
,
1
)
(
2
3
2
12
−
+
−
+
−
=
z
z
z
z
z
z
G
d.
1
,
1
1
,
0
1
2
,
0
)
(
2
12
−
+
+
=
z
z
z
z
G
i.
5
,
0
5
,
1
625
,
0
75
,
0
3
)
(
2
3
2
12
+
−
−
+
=
z
z
z
z
z
G
e.
1
,
1
1
,
0
1
4
,
0
)
(
2
12
−
+
+
−
=
z
z
z
z
G
j.
1
3
3
1
9
,
2
3
,
2
)
(
2
3
2
12
−
+
−
+
−
=
z
z
z
z
z
z
G
PODSTAWY AUTOMATYKI – ĆWICZENIA
lista zadań nr 11
Stabilność
1. Dana jest transmitancja
)
(
12
z
G
układu otwartego. Zbadać stabilność układu zamkniętego,
wykorzystując podstawowy warunek stabilności układów dyskretnych.
a.
6
,
1
3
,
1
2
)
(
2
−
−
=
z
z
z
G
c.
38
,
0
8
,
1
2
)
(
2
−
−
=
z
z
z
G
b.
92
,
1
4
,
0
2
)
(
2
−
−
=
z
z
z
G
d.
96
,
0
3
2
)
(
2
−
−
+
=
z
z
z
z
G
2. Korzystając z kryterium Jury’ego zbadać stabilność układu o transmitancji:
a.
1
2
3
4
5
3
)
(
2
3
4
+
+
+
+
+
=
z
z
z
z
z
z
G
e.
2
2
2
2
4
1
5
2
)
(
2
3
4
2
+
+
+
+
+
+
=
z
z
z
z
z
z
z
G
b.
1
2
4
2
1
)
(
2
3
4
2
+
+
+
+
+
+
=
z
z
z
z
z
z
z
G
f.
4
3
2
5
5
)
(
2
3
4
+
+
+
+
=
z
z
z
z
z
G
c.
2
2
4
3
1
3
)
(
2
3
4
3
+
−
+
−
+
=
z
z
z
z
z
z
G
g.
1
2
2
3
3
4
)
(
2
3
4
+
−
+
−
+
=
z
z
z
z
z
z
G
d.
2
3
2
3
3
1
2
)
(
2
3
4
2
3
+
+
+
+
+
+
=
z
z
z
z
z
z
z
G
h.
1
2
1
2
)
(
2
3
4
+
−
+
−
+
=
z
z
z
z
z
z
G
3. Dana jest transmitancja
)
(
12
z
G
układu otwartego. Wykorzystując kryterium Nyquista
zbadać czy układ zamknięty jest stabilny
(
)
s
T
p
1
=
.
a.
5
,
1
1
)
(
12
−
=
z
z
G
c.
2
,
2
1
)
(
12
−
=
z
z
G
b.
8
,
1
2
)
(
12
−
=
z
z
G
d.
2
,
1
8
,
0
)
(
12
−
=
z
z
G
4. Dana jest transmitancja
)
(
12
z
G
układu otwartego. Wykorzystując kryterium Nyquista
zbadać dla jakiego k układ zamknięty jest niestabilny
(
)
s
T
p
1
=
.
a.
5
,
0
)
(
12
+
=
z
k
z
G
d.
4
,
0
3
2
)
(
12
+
=
z
k
z
G
b.
2
,
0
2
)
(
12
+
=
z
k
z
G
e.
8
,
1
2
)
(
12
−
=
z
k
z
G
c.
8
,
0
)
(
12
+
=
z
k
z
G
f.
6
,
9
12
1
,
0
)
(
12
+
=
z
k
z
G

Wyszukiwarka
Podobne podstrony:
PA lista zadań AiR KRK odp student 1
Fizyka lista zadan 1 id 176924 Nieznany
Lista zadań 5 6
Lista zadan 9
4 lista zadan
IV lista zadan z Fizyki Transport, 1 Studia PWR (Transport 1 Rok 1 Semestr), Fizyka PWR dr.Henryk Ka
Funkcje zespolone lista zadań
lista zadan geometria
Lista zadan 6
UP Wrocław lista zadan, Technologia Informacyjna semestr 1 oraz Informatyka i komputerowe wspomagan
LISTA ZADAN 4
1. LISTA ZADAŃ STATYSTYKA WSB, statystyka
Cw 3 wykresy symboliczne i wektorowe lista zadan
Lista zadań 2
lista zadan makro
Lista zadan nr 1 z matematyki dyskretnej
liczby zespolone lista zadań
Fizyka I Lista zadań numer 2
więcej podobnych podstron