Arkusz 03: Siły przekrojowe. Arkusz przeznaczony do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn” na II roku dziennych studiów
Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 2014/2015.

Notatki do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn”

Notatki do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn”

Arkusz 03: Siły przekrojowe

Arkusz 03: Siły przekrojowe

Poniższe notatki zawierają podstawowe wskazówki, co do tego, co należy umieć na zajęcia. Podane informacje są
skrótowe i wymagają poszerzenia ich o wiedzę, którą można znaleźć w literaturze. Są jednak przewodnikiem po
podstawowych zagadnieniach i ich aspektach, których znajomość będzie wymagana na zajęciach. Plik ten może
stanowić bazę dla notatek własnych robionych podczas zajęć.

Symbol ten wskazuje, że podane są wymagania do zajęć

Symbol ten oznacza przykład liczbowy, zadanie (rozwiązane, bądź do rozwiązania)

Symbol ten wskazuje źródła i literaturę, z których należy skorzystać lub potrzebę skorzystania z nich

Symbol ten oznacza zadanie domowe lub zadanie, które ugruntowuje wiedzę z danego paragrafu

Zadanie 1
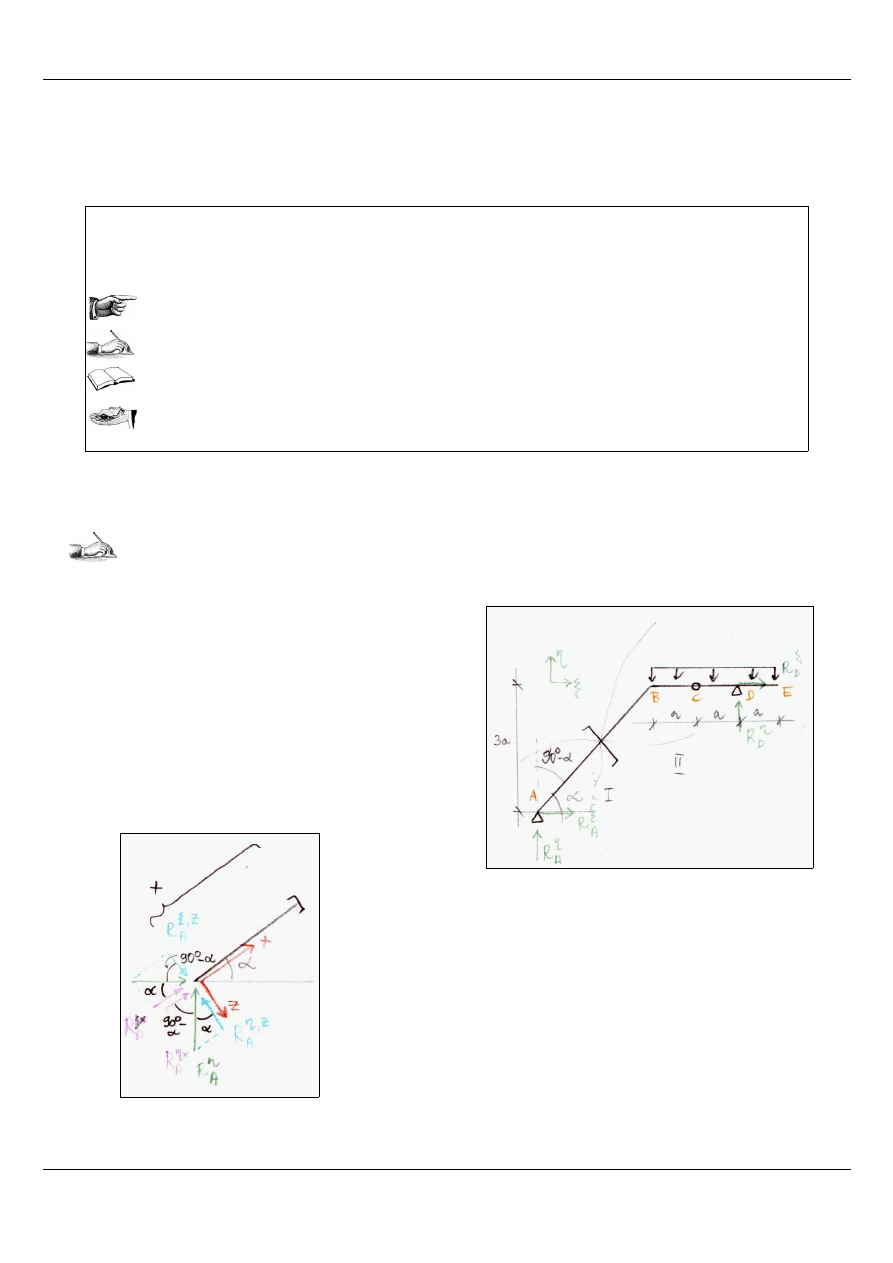
Dla zadanej konstrukcji (Rysunek 1) określić siły przekrojowe. Jako ćwiczenie dodatkowe polecam przyjąć
sobie konkretne wymiary a i obciążenie q i obliczyć, jakie wielkości sił otrzymamy wówczas.

(1) Sprawdzenie statycznej wyznaczalności.

Konstrukcja jest statycznie i kinematycznie wyznaczalna.

(2) Wyznaczenie reakcji

Korzystamy z trzech podstawowych równań równowagi i
jednego dodatkowego równania, które mówi, że suma
momentów względem punktu przegubu dla jego prawej lub
lewej strony jest równa 0.
Zakładamy, że obliczyliśmy i już znamy wartości reakcji:

R

A

ξ

, R

A

η

, R

D

ξ

, R

D

η

.

(3) Siły przekrojowe

Ponieważ obliczenie sił w ryglu jest analogiczne, jak dla zwykłych
belek, pozostawię to do samodzielnej analizy Rozwiązujących.
Poniżej przedstawię natomiast sposób obliczenia sił w pręcie
ukośnym. Każdą z sił rozkładamy na jej składowe równoległe do
osi x i z lokalnego układu współrzędnych. Na rysunkach są one
odpowiednio zaznaczone: do x – jako fioletowe, do y – jako
niebieskie (Rysunek 2, Rysunek 3).

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

1

Rysunek 1: Konstrukcja dla zadania.

Rysunek 2: Analiza części I

Arkusz 03: Siły przekrojowe. Arkusz przeznaczony do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn” na II roku dziennych studiów
Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 2014/2015.

Przedział AB:

x

∈ (0 , ∣ ̄

AB

∣), ∣ ̄

AB

∣=

3a

cos

(90

o

α)

= 3a

sin

α

Rozważmy najpierw wszystkie siły przekrojowe jako wynik redukcji układu sił zewnętrznych przyłożonych do części I:

F

x

( x) =

I

[ R

A

ξ , x

+ R

A

η, x

]=

I

[ R

A

ξ

⋅cos α + R

A

η

⋅cos(90

o

α)]

F

z

(x) =

I

[R

A

ξ , z

R

A

η , z

]=

I

[ R

A

ξ

⋅cos(90

o

α)

R

A

η

⋅cosα ]=

I

[R

A

ξ

⋅sin α + R

A

η

⋅sin(90

o

α)]

M

y

( x) =

I

[R

A

ξ , z

⋅x

R

A

η , z

⋅x]=

I

[ R

A

ξ

⋅cos(90

o

α)⋅x

R

A

η

⋅cosα⋅x]

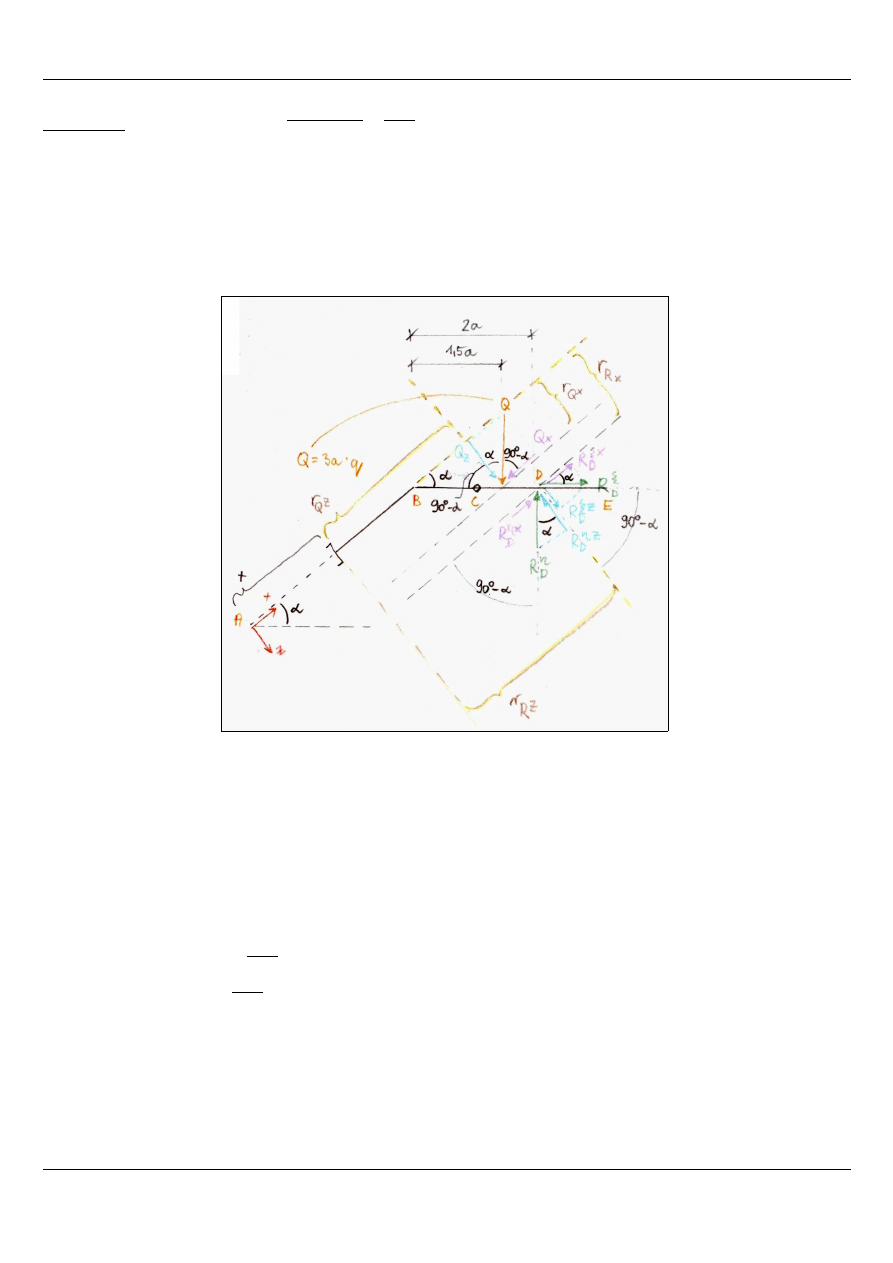
Teraz spójrzmy jak rozkładają się składowe dla części II:

F

x

(x) =

II

[ Q

x

+ R

D

ξ , x

+ R

D

η , x

] =

II

[ Q⋅cos(90

o

α) + R

D

ξ

⋅cos α + R

D

η

⋅cos(90

o

α)]

F

z

(x) =

II

[Q

z

+ R

D

ξ , z

R

D

η , z

]=

II

[Q⋅cosα + R

D

ξ

⋅cos(90

o

α)

R

D

η

⋅cosα ]

=

II

[ Q⋅sin(90

o

α ) + R

D

ξ

⋅sin α + R

D

η

⋅sin(90

o

α )]

Zanim obliczone zostaną momenty M

y

(x) potrzeba zanalizować, które składowe sił będą brały udział w jego generowaniu

oraz zaznaczyć ramiona ich działania Będą działały wszystkie, zarówno x-owe, jak i z-owe składowe na następujących
ramionach:

r

Q x

= 1,5 a⋅cos(90

o

α)

r

R x

= 2a⋅cos(90

o

α)

r

Q z

=∣ ̄

AB

∣ + 1,5a⋅cosα

x

=

3a
sin

α

+ 1,5 a⋅cos α

x

r

R z

=∣ ̄

AB

∣ + 2a⋅cos α

x

=

3a
sin

α

+ 1,5a⋅cosα

x

A zatem moment będzie wynosił:

M

y

(x) =

II

[ Q

x

⋅r

Q x

+ R

D

ξ , x

⋅r

R x

+ R

D

η , x

⋅r

R x

Q

z

⋅r

Q z

R

D

ξ , z

⋅r

R z

+ R

D

η , z

⋅r

R z

]

=

II

[ Q⋅cos(90

o

α )⋅r

Q x

+ R

D

ξ

⋅cosα⋅r

R x

+ R

D

η

⋅cos(90

o

α)⋅r

R x

Q

⋅cos α⋅r

Q z

R

D

ξ

⋅cos(90

o

α )⋅r

R z

+R

D

η

⋅cosα⋅r

R z

]

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

2

Rysunek 3: Analiza części II