1

Strop monolityczny płytowo-żebrowy

Zaprojektować monolityczny strop płytowo-żebrowy (między piętrowy) w pomiesz-
czeniu składu podręcznego – środowisko klasy XC1. Do wykonania stropu przewi-
dziano beton
klasy B25 ( f

cd

=13,3 MPa, f

ck

=20 MPa, f

ctd

=1,0MPa).

Do zbrojenia płyt – stal klasy A-I (f

yk

=240 MPa, f

yd

=210 MPa).

Do zbrojenia żeber i podciągów – stal klasy A-III (f

yk

=410 MPa, f

yd

=350 MPa).

Obciążenie zmienne stropu wynosi 3,50 kN/m

2

.

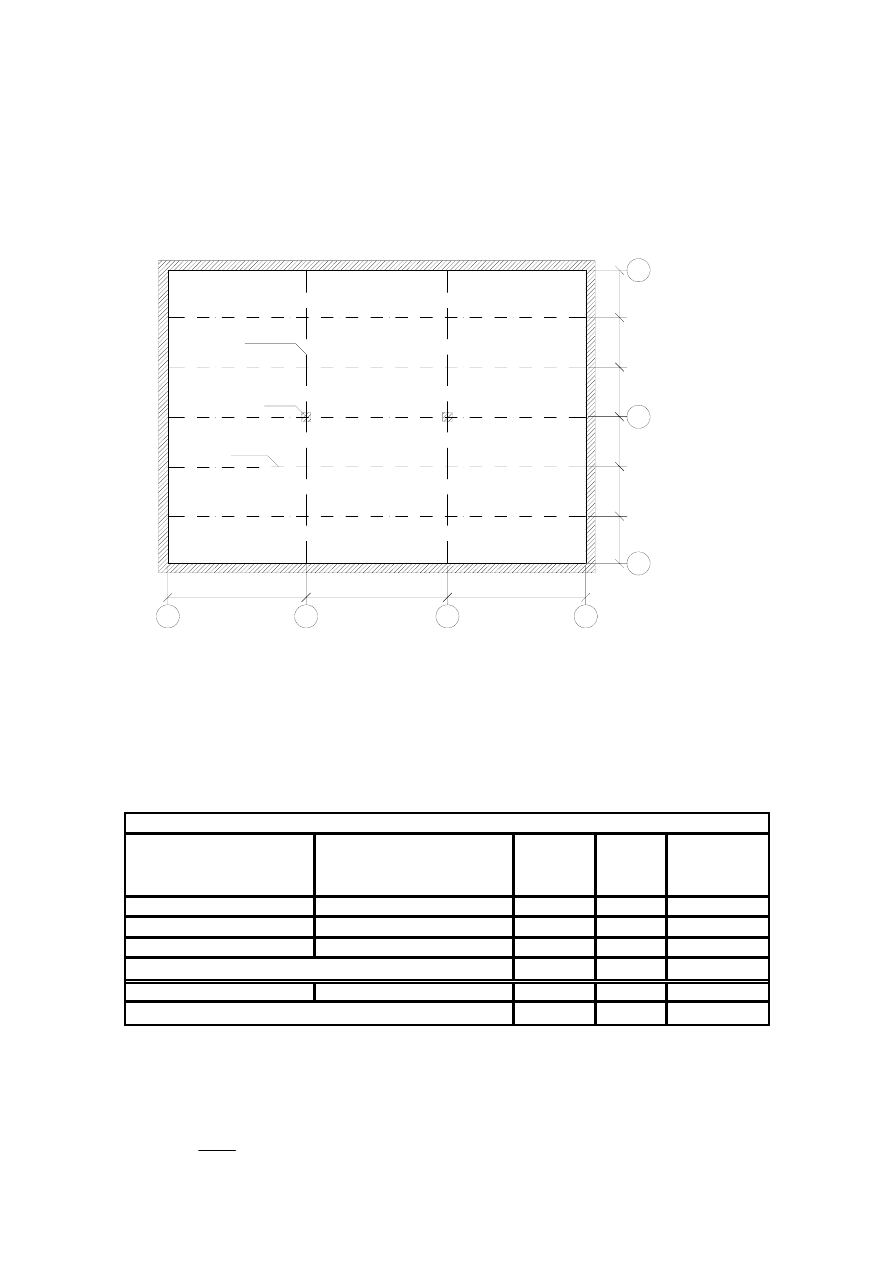
Żebro

Podciąg

Słup

C

B

4

3

2

A

1

19

0

200

200

20

0

20

0

190

558

570

558

1. Obliczanie zbrojenia na moment zginający – stan graniczny nośności.

1.1. Płyta.

Płytę należy obliczać, jak opartą na żebrach belkę ciągłą wieloprzęsłową o szeroko-

ści b=1m, metodą plastycznego wyrównania momentów. Grubość płyty przyjęto h

f

=60mm

1.1.1. Zebranie obciążeń.

0,315

1,2

0,378

0,420

1,3

0,546

1,500

1,1

1,650

2,235

2,574

3,500

1,3

4,550

5,735

7,124

Stałe + zmienne g+q=p

Terakota

0,015*21

Głaź cementowa

0,02*21

RAZEM g=

0,06*25

Ciężar własny płyty

Zmienne q=

3,500

Nazwa obciążenia stropu

Nazwa materiału

Wyrażenie matematyczne

obc.char.

kN/m

2

wsp.obc

g

f

obc.obl. kN/m

2

1.1.2. Rozpiętość obliczeniowa przęseł.

Rozpiętość efektywna przęseł skrajnych.

1,80m

2

0,20

1,90

l

eff

=

−

=

2

Rozpiętość efektywna przęseł środkowych.

1,80m

0,20

2,00

l

eff

=

−

=

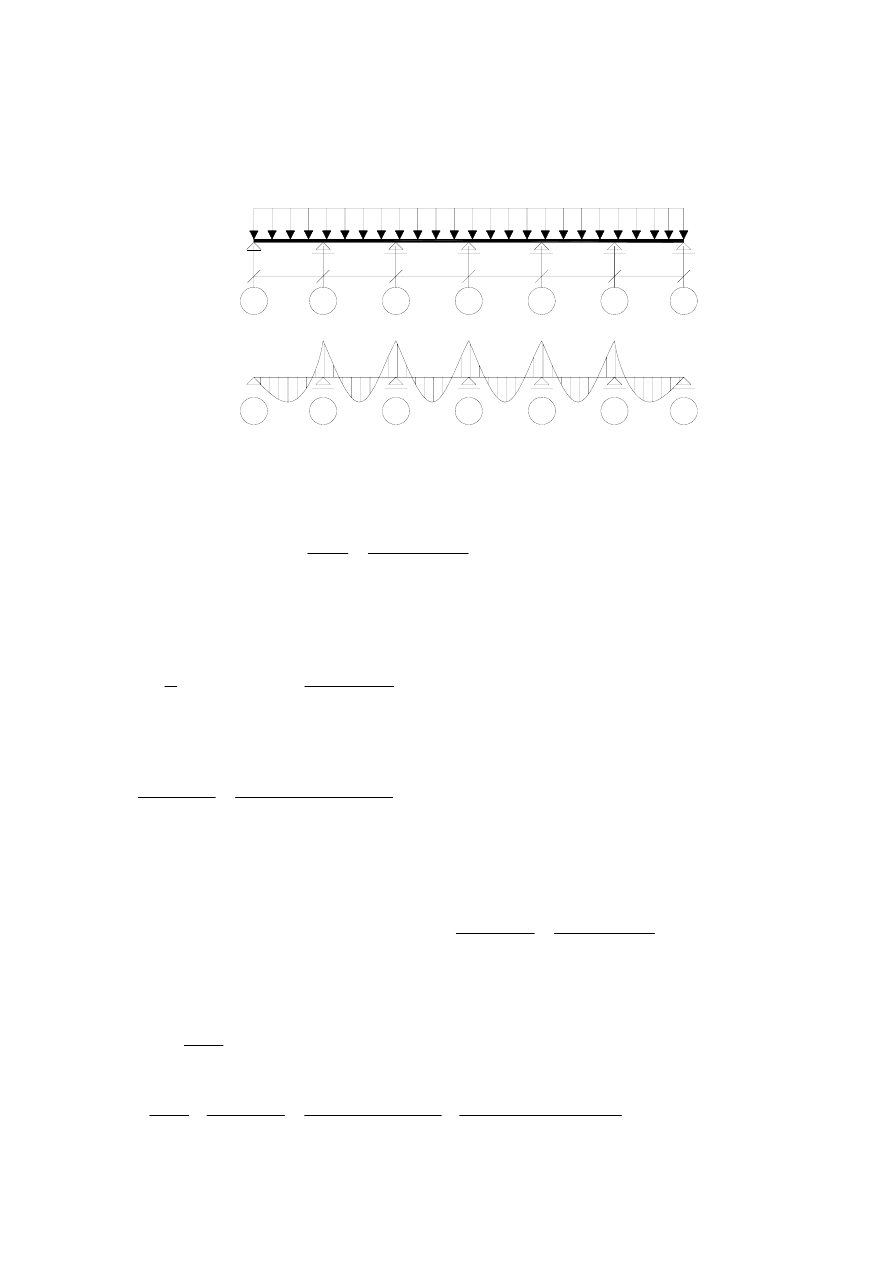
Schemat statyczny to belka o sześciu przęsłach, których rozpiętość l

eff

=1,80m i sze-

rokości b=1,00 m

C

f

e

B

d

c

A

leff=1800 leff=1800 leff=1800 leff=1800 leff=1800 leff=1800

A

c

d

B

e

f

C

1.1.3. Momenty zginające.

Momenty w przęsłach skrajnych Ac i fC oraz nad podporami c i f.

2,10kNm

11

1,80

7,124

11

l

p

M

M

M

M

2

2
eff

c

f

fC

Ac

⇒

⋅

=

⋅

=

−

=

−

=

=

Zasięg momentów ujemnych w przęśle Ac i fC od zastępczego obciążenia oblicze-
niowego

2

2

2

3,71kN/m

4

4,55kN/m

kN/m

,

2

4

q

g

p`

=

+

=

+

=

574

oblicza się wg wzoru:

(

)

0,43m

3,71kN/m

8

1,80m

7,124kN/m

p`

8

l

q

g

x

2

2

eff

=

⋅

⋅

=

⋅

⋅

+

=

Momenty w przęsłach środkowych CD, dB, Be i ef
oraz nad podporami środkowymi d, B, e

1,44kNm

16

1,80

7,124

16

l

q)

(g

M

M

M

M

M

M

M

2

2
eff

e

B

d

ef

Be

dB

cd

⇒

⋅

=

⋅

+

=

−

=

−

=

−

=

=

=

=

Momenty ujemne w przęśle cd i ef oraz ich zasięg oblicza się za pomocą równania:

( )

0

M

x

R

2

x

p`

x

M

c

c

2

α

=

+

⋅

+

⋅

−

=

3,71kN

1,8

1,44kNm

2,10kNm

2

1,8m

3,71kN/m

l

M

M

2

l

p`

R

2

eff

d

c

eff

c

=

−

+

⋅

=

+

−

+

⋅

=

3

Podstawiając do wzoru:

0

2,10)

(

1,86)

(

4

3,71

∆

0

2,10

x

3,71

x

1,86

2

2

<

−

⋅

−

⋅

−

=

=

−

⋅

+

⋅

−

Ponieważ

∆<0 więc na całej długości przęseł momenty mają wartość ujemną.

W połowie rozpiętości tych przęseł (x=0,9m) moment ma wartość:

0,26kNm

M

2,10

0,9m

3,71kN

2

(0,9m)

3,71kN/m

M

x

2

2

x

−

=

−

⋅

+

⋅

−

=

Ponieważ bezwzględna wartość tego momentu zwiększa się w kierunku podpór na-
leży obliczając zbrojenie przęsłowe przyjąć wartość zastępczą momentu:

0,677kNm

M

0,26kNm

2

1,44kNm

2,10kNm

3

1

M

2

M

M

3

1

M

cdzast

x

d

c

cdzast

−

=

⎟

⎠

⎞

⎜

⎝

⎛

−

−

−

⋅

=

⎟

⎠

⎞

⎜

⎝

⎛

+

+

⋅

=

1.1.4. Wymiarowanie zbrojenia.

Wymiarowanie zbrojenia przęseł skrajnych Ac i fC oraz podpór przyskrajnych c i f.
Przyjęto wstępnie pręty zbrojeniowe

φ8 i otulinę c= 15 mm z odchyłką ∆c= 5 mm.

Wysokość użyteczna przekroju:

0,036m

d

0,005

-

0,008

0,5

0,015

0,060

d

∆c

0,5

-

c

-

h

d

=

⋅

−

−

=

−

⋅

=

ϕ

Współczynnik nośności

µ

sc

(

)

0,122

µ

1,33kN/cm

3,6cm

100cm

210kNcm

µ

f

d

b

M

µ

sc

2

2

sc

cd

2

sc

=

⋅

⋅

=

⋅

⋅

=

Na podstawie

µ

sc

należy obliczyć

ξ

0,131

0,122

2

1

1

ξ

µ

2

1

1

ξ

sc

=

⋅

−

−

=

⋅

−

−

=

Z wartości

ξ wyznacza się ζ

0,935

0,131

0,5

1

ζ

0,5ξ

1

ζ

=

⋅

−

=

−

=

4

Pole przekroju zbrojenia:

2

s1

2

s1

yd

s1

2,97cm

A

21kN/cm

3,6cm

0,935

210kNcm

A

f

d

ζ

M

A

=

⋅

⋅

=

⋅

⋅

=

Minimalne pole przekroju zbrojenia:

2

s1

2

min

s1,

min

s1,

min

s1,

2

s1

2

min

s1,

min

s1,

yk

ctm

min

s1,

2,97cm

A

0,468cm

A

3,6cm

100cm

0,0013

A

d

b

0,0013

A

oraz

2,97cm

A

0,86cm

A

3,6cm

100cm

240MPa

2,2MPa

0,26

A

d

b

f

f

0,26

A

=

≤

=

⋅

⋅

=

⋅

⋅

=

=

≤

=

⋅

⋅

⋅

=

⋅

⋅

⋅

=

Z tablicy 5-31 należy przyjąć rozstaw prętów zbrojenia.
Przyjęto

φ 8 co 160 mm A

s1

=3,14 cm

2

W miejscu połączenia płyty z żebrem i wieńcem należy zastosować dodatkowe zbro-
jenie górne również przyjęto

φ 8 co 160 mm. Długość tych prętów jest uzależniona od

zasięgu momentów ujemnych i długości zakotwienia prętów.

Wymiarowanie zbrojenia przęseł środkowych cd, dB, Be, i ef oraz podpór przyskraj-
nych d, B i e.

Współczynnik nośności

µ

sc

(

)

0,084

µ

1,33kN/cm

3,6cm

100cm

144kNcm

µ

f

d

b

M

µ

sc

2

2

sc

cd

2

sc

=

⋅

⋅

=

⋅

⋅

=

Na podstawie

µ

sc

należy obliczyć

ξ

0,088

0,084

2

1

1

ξ

µ

2

1

1

ξ

sc

=

⋅

−

−

=

⋅

−

−

=

Z wartości

ξ wyznacza się ζ

0,956

0,088

0,5

1

ζ

0,5ξ

1

ζ

=

⋅

−

=

−

=

5

Pole przekroju zbrojenia:

2

s1

2

s1

yd

s1

1,99cm

A

21kN/cm

3,6cm

0,956

144kNcm

A

f

d

ζ

M

A

=

⋅

⋅

=

⋅

⋅

=

Minimalne pole przekroju zbrojenia:

2

s1

2

min

s1,

min

s1,

min

s1,

2

s1

2

min

s1,

min

s1,

yk

ctm

min

s1,

1,99cm

A

0,468cm

A

3,6cm

100cm

0,0013

A

d

b

0,0013

A

oraz

1,99cm

A

0,86cm

A

3,6cm

100cm

240MPa

2,2MPa

0,26

A

d

b

f

f

0,26

A

=

≤

=

⋅

⋅

=

⋅

⋅

=

=

≤

=

⋅

⋅

⋅

=

⋅

⋅

⋅

=

Z tablicy 5-31 należy przyjąć rozstaw prętów zbrojenia.
Przyjęto

φ 8 co 160 mm A

s1

=3,14 cm

2

. W miejscu połączenia płyty z żebrem i wień-

cem należy zastosować dodatkowe zbrojenie górne również przyjęto

φ 8 co 160 mm.

Przęsła cd i ef muszą być zazbrojone na momenty ujemne

0,677kNm

M

cdzast

−

=

Współczynnik nośności

µ

sc

(

)

0,039

µ

1,33kN/cm

3,6cm

100cm

67,7kNcm

µ

f

d

b

M

µ

sc

2

2

sc

cd

2

sc

=

⋅

⋅

=

⋅

⋅

=

Na podstawie

µ

sc

należy obliczyć

ξ

0,040

0,039

2

1

1

ξ

µ

2

1

1

ξ

sc

=

⋅

−

−

=

⋅

−

−

=

Z wartości

ξ wyznacza się ζ

0,980

0,040

0,5

1

ζ

0,5ξ

1

ζ

=

⋅

−

=

−

=

6

Pole przekroju zbrojenia:

2

s1

2

s1

yd

s1

0,91cm

A

21kN/cm

3,6cm

0,980

67,7kNcm

A

f

d

ζ

M

A

=

⋅

⋅

=

⋅

⋅

=

Minimalne pole przekroju zbrojenia:

2

s1

2

min

s1,

min

s1,

min

s1,

2

s1

2

min

s1,

min

s1,

yk

ctm

min

s1,

0,91cm

A

0,468cm

A

3,6cm

100cm

0,0013

A

d

b

0,0013

A

oraz

0,91cm

A

0,86cm

A

3,6cm

100cm

240MPa

2,2MPa

0,26

A

d

b

f

f

0,26

A

=

≤

=

⋅

⋅

=

⋅

⋅

=

=

≤

=

⋅

⋅

⋅

=

⋅

⋅

⋅

=

Z tablicy 5-31 należy przyjąć rozstaw prętów zbrojenia.
Przyjęto

φ 8 co 160 mm A

s1

=3,14 cm

2

.

1.2. Żebro.

Na żebro działa obciążenie z pasma szerokości równej osiowemu rozstawowi żeber

a=2,00m. Wysokość żebra przyjęto z warunku

38cm

15

570

15

l

h

eff

=

⇒

=

szerokość

ostateczną wysokość przyjęto h= 400mm, a szerokość

20cm

2

40

2

h

b

=

⇒

=

1.2.1. Zebranie obciążeń.

4,470

5,148

1,700

1,1

1,870

6,170

7,018

7,000

1,3

9,100

13,170

16,118

Nazwa obciążenia żebra

Nazwa materiału

Wyrażenie matematyczne

obc.char.

kN/m

2

wsp.obc

g

f

obc.obl. kN/m

2

Stałe + zmienne g+q=p

Obciążenia od płyty

2,235*2,0

Ciężar żebra

0,20*(0,40-0,06)*25

RAZEM g=

Zmienne q=

3,5*2,0

1.2.2. Rozpiętość obliczeniowa przęseł.

Rozpiętość efektywna przęseł skrajnych.

5,50m

l

eff

=

7

Schemat statyczny i wykres momentów zginających.

leff=5500

leff=5500

leff=5500

4

3

2

1

1

2

3

4

1.2.3. Siły przekrojowe.

Momenty zginające:

85,493kNm

M

8

6,50m

16,188kN/m

M

8

l

p

M

α

α

2

α

=

⋅

=

⋅

=

Siły tnące:

52,611kN

V

V

2

6,50m

16,188kN/m

V

V

2

l

p

V

V

Sd

α

Sd

α

Sd

α

=

=

⋅

=

=

⋅

=

=

1.2.4. Wymiarowanie zbrojenia.

Przyjęto wstępnie pręty zbrojeniowe głównego

φ20, strzemion φ

1

10 oraz otulinę

c=15mm z odchyłką

∆c= 5 mm.

Wysokość użyteczna przekroju:

0,36m

d

0,02

0,5

0,01

0,005

0,015

0,4

d

φ

0,5

φ

∆c

c

h

d

1

=

⋅

−

−

−

−

=

⋅

−

−

−

−

=

Określenie szerokości b

eff

płyty współpracującej z żebrem:

0,92m

0,06

6

2

0,20

b

h

6

2

b

b

2

b

b

2,0m

1,5m

5

6,50m

0,20m

b

b

5

l

b

b

eff

f

w

eff1

w

eff

eff

eff

w

eff

=

⋅

⋅

+

=

⋅

⋅

+

=

⋅

+

=

≤

=

+

=

≤

+

=

8

Należy przyjąć wartość mniejszą, czyli b

eff

=0,92m

Obliczenie momentu zginającego przenoszonego przez przekrój.

242,273kNm

cm

24227,28kN

M

2

6cm

36cm

1,33kN/cm

6cm

92cm

M

2

h

d

f

h

b

M

f

2

f

f

cd

f

eff

f

⇒

=

⎟

⎠

⎞

⎜

⎝

⎛

−

⋅

⋅

⋅

=

⎟

⎠

⎞

⎜

⎝

⎛ −

⋅

⋅

⋅

=

Ponieważ M

f

=272,273kNm

> M=85,493kNm to oś obojętna jest usytuowana w płycie

a przekrój należy wymiarować jako pozornie teowy o wymiarach b

eff

x d,

czyli 0,92m x 0,36m. Stal klasy A-III f =410MPa, f =350MPa

yk

yd

Współczynnik nośności

µ

sc

(

)

0,054

µ

1,33kN/cm

36cm

92cm

8549,3kNcm

µ

f

d

b

M

µ

sc

2

2

sc

cd

2

eff

sc

=

⋅

⋅

=

⋅

⋅

=

Na podstawie

µ

sc

należy obliczyć

ξ

0,056

0,054

2

1

1

ξ

µ

2

1

1

ξ

sc

=

⋅

−

−

=

⋅

−

−

=

Z wartości

ξ wyznacza się ζ

0,972

0,056

0,5

1

ζ

0,5ξ

1

ζ

=

⋅

−

=

−

=

Pole przekroju zbrojenia:

2

s1

2

s1

yd

s1

6,98cm

A

35kN/cm

36cm

0,972

8549,3kNcm

A

f

d

ζ

M

A

=

⋅

⋅

=

⋅

⋅

=

9

Minimalne pole przekroju zbrojenia:

2

s1

2

min

s1,

min

s1,

min

s1,

2

s1

2

min

s1,

min

s1,

yk

ctm

min

s1,

6,98cm

A

4,31cm

A

36cm

92cm

0,0013

A

d

b

0,0013

A

oraz

6,98cm

A

5,41cm

A

36cm

92cm

350MPa

2,2MPa

0,26

A

d

b

f

f

0,26

A

=

≤

=

⋅

⋅

=

⋅

⋅

=

=

≤

=

⋅

⋅

⋅

=

⋅

⋅

⋅

=

Z tablicy 5-31 należy przyjąć rozstaw prętów zbrojenia.
Przyjęto 5

φ 14 co A

s1

=7,70 cm

2

2. Obliczenia zbrojenia na siłę poprzeczną.

2.1. Żebro.

Maksymalna wartość siły poprzecznej przy podporach V =V = 52,611kN.

1

2

Przyjęto strzemiona dwuramienne

φ6

2.2. Wymiarowanie zbrojenia.

Graniczna siła poprzeczna ze względu na ukośne rozciąganie w przekroju bez po-

przecznego zbrojenia na ścinanie.

(

)

(

)

1,0

1,24

0,36

-

1,6

d

-

1,6

k

d

b

0,15σ

ρ

40

1,2

f

k

0,35

V

w

cp

l

ctd

Rd1

≥

=

⇒

=

⋅

⋅

+

⋅

+

⋅

⋅

⋅

=

Obliczeniowa wytrzymałość betonu na rozciąganie.

1,0MPa

f

ctd

=

Założono doprowadzenie do podpory wszystkich prętów z przęsła, czyli 4

φ 14.

Stopień zbrojenia.

0,009

ρ

36cm

20cm

6,16cm

ρ

d

b

A

ρ

l

2

l

w

sL

l

=

⋅

=

⋅

=

Wartość granicznej siły poprzecznej.

(

)

(

)

48,767kN

V

52,611kN

V

V

36cm

20cm

0

0,15

0,009

40

1,2

0,1kN/cm

1,24

0,35

V

Rd1

Sd

1

2

Rd1

=

≥

=

=

⋅

⋅

⋅

+

⋅

+

⋅

⋅

⋅

=

10

Ponieważ warunek

nie jest spełniony występuje tu odcinek drugiego ro-

dzaju.

Rd1

Sd

V

V

≤

Nośność obliczeniowa na ścinanie ze względu na ściskanie betonu.

52,611kN

V

V

179,263kN

V

2

1

2

32,4cm

20cm

cm

kN

1,33

0,52

V

0,52

250

20MPa

0,6

250

f

0,6

ν

32,4cm

36cm

0,9

d

0,9

z

Θ

ctg

1

ctgΘ

z

b

f

ν

V

Sd

1

Rd2

2

2

Rd2

ck

2

w

cd

Rd2

=

=

≥

=

+

⋅

⋅

⋅

⋅

=

=

−

⇒

−

=

=

⋅

⇒

⋅

=

+

⋅

⋅

⋅

⋅

=

Długość odcinak ścinania (odcinek 2 rodzaju)

1,08m

6,5m

6

1

l

6

1

0,238m

c

16,118kN/m

48,767kN

52,611kN

c

p

V

V

c

eff

s

s

Rd1

Sd

s

=

⋅

⇒

≤

=

−

=

−

=

Ponieważ obliczony odcinek ścinania c

s

jest mniejszy od wartości minimalnej, przyję-

to zagęszczony rozstaw strzemion na odcinku 1,10m

Siła poprzeczna, jaką mają przenieść strzemiona

46,809kN

V`

V

0,36m

16,118kN/m

52,611kN

V`

V

d

p

V

V`

V

Sd

Rd3

Sd

Rd3

1

Sd

Rd3

=

=

⋅

−

=

=

⋅

−

=

=

Wymagany rozstaw strzemion s

1

(

)

14,73cm

s

2

36cm

0,9

46,809kN

19kN/cm

0,56cm

s

ctgθ

z

V

f

A

s

1

2

2

1

Rd3

ywd1

sw1

1

=

⋅

⋅

⋅

⋅

=

⋅

⋅

⋅

=

Rozmieszczenie strzemion.
Maksymalny dopuszczalny odstęp strzemion s

max

40cm

27cm

s

27cm

36cm

0,75

s

40cm

d

0,75

s

max

max

max

≤

=

⇒

⋅

=

≤

⋅

=

11

Maksymalny rozstaw strzemion s

max

ze względu na wymagany minimalny stopień

zbrojenia na ścinanie.

17,18cm

s

20cm

0,00163

0,56cm

s

b

ρ

A

s

0,00163

220MPa

20MPa

0,08

ρ

f

f

0,08

ρ

max

2

max

w

w1min

sw1

max

w1min

yk

ck

w1min

=

⋅

=

⋅

=

⇒

⋅

=

⋅

=

W strefie przypodporowej na odcinku c

s

=110cm przyjęto zagęszczony rozstaw

strzemion s=14cm

3. Stan graniczny użytkowalności – obliczenie ugięć.

06

18

cm

36

cm

650

d

l

eff

,

=

=

Stopień zbrojenia

ρ

l

0,856%

ρ

100

36cm

20cm

6,16cm

ρ

100

d

b

A

ρ

l

2

l

s1

l

=

⋅

⋅

=

⋅

⋅

=

Ponieważ spełniony jest warunek

06

18

d

l

22

d

l

eff

eff

,

max

=

≥

=

⎟

⎠

⎞

⎜

⎝

⎛

nie jest konieczne szczegółowe obliczanie ugięcia żebra.

Sprawdzenie szerokości rozwarcia rys ukośnych.

ck

s

w

2

k

f

E

ρ

λ

τ

4

w

⋅

⋅

⋅

⋅

=

Stopień zbrojenia strzemionami.

002

,

0

20cm

14cm

0,56cm

ρ

b

s

A

ρ

2

w

w

1

sw1

w

⇒

⋅

=

⋅

=

12

Współczynnik

λ

00mm

0

1

λ

6mm

1,0

0,002

3

1

λ

φ

η

ρ

3

1

λ

1

1

w

=

⇒

⋅

⋅

=

⋅

⋅

=

Szerokość rozwarcia rys ukośnych wynosi

2

w

Sd

0,073kN/cm

τ

36cm

20cm

52,611kN

τ

d

b

V

τ

=

⋅

=

⋅

=

(

)

0,3mm

w

0,266mm

0,0266cm

w

2kN/cm

20000kN/cm

0,002

100cm

0,073kN/cm

4

w

lim

k

2

2

2

2

k

=

≤

=

=

⋅

⋅

⋅

⋅

=

Szerokość rys jest mniejsza od szerokości granicznej.