Akademia Górniczo-Hutnicza
Katedra Robotyki i Mechatroniki
Identyfikacja i analiza sygnałów
Laboratorium 6
Elementy algebry liniowej
Akademia Górniczo-Hutnicza
Katedra Robotyki i Mechatroniki
Identyfikacja i analiza sygnałów
Laboratorium 6
Elementy algebry liniowej
Algorytmy algebry liniowej stosowane w identyfikacji układów
dynamicznych
Jedna z definicji identyfikacji układów dynamicznych jaką można znaleźć w literaturze brzmi
następująco:
Przez identyfikację rozumiemy złożony proces badawczy, w którym na podstawie
analizy danych a priori i a posteriori o badanym, istniejącym lub projektowanym
obiekcie, dokonuje się syntezy modelu dobrze (w sensie przyjętego kryterium)
opisującego obiekt oraz na tyle uproszczonego, żeby jego analiza była możliwa do
przeprowadzenia i dostarczała nowych informacji o obiekcie. (Giergiel J., Uhl T.,
Identyfikacja układów mechanicznych, PWN Warszawa 1990).
Ponieważ identyfikację można w skrócie określić jako szukanie nieznanej struktury i
parametrów modeli układów na podstawie wstępnej wiedzy o ich budowie i działaniu oraz na
podstawie pomiarów dokonywanych na tych układach, w praktyce proces ten można
sprowadzić do rozwiązania układu równań z wieloma niewiadomymi. Układy równań są
często niedookreślone (mniej równań niż niewiadomych) lub nadokreślone (więcej równań
niż niewiadomych) i często są one niemożliwe do rozwiązania przy użyciu klasycznych
przekształceń algebraicznych. Dlatego w identyfikacji układów mechanicznych często
stosowane są zaawansowane narzędzia matematyczne. Do podstawowych algorytmów
algebry liniowej stosowanych w identyfikacji układów dynamicznych należą rozkłady
macierzowe:
- rozkład macierzy względem wartości własnych (tzw. zagadnienie własne),
- rozkład macierzy względem wartości szczególnych,
- rozkład macierzy LU,
Ponieważ dla układów rzeczywistych wymiarowość problemu jest zwykle duża, algorytmy te
realizowane są numerycznie.
Rozkład macierzy względem wartości własnych
Podstawowym narzędziem algebry liniowej stosowanym w identyfikacji jest rozkład
macierzy na wartości własne, zwany też zagadnieniem własnym (z ang. eigenvalue problem).
Jest on stosowany w celu rozwiązywania układów równań jednorodnych, a więc takich w
których prawa strona wszystkich równań wynosi 0. Z tego typu układami równań mamy
często do czynienia w zagadnieniach mechaniki konstrukcji np. w przypadku analizy drgań
swobodnych układu. Wówczas rzeczony układ równań ma rozwiązanie trywialne (zerowe). W
celu wyznaczenia nietrywialnych rozwiązań tego typu równań stosowane jest właśnie
zagadnienie własne.
Zagadnienie własne jest to problem znalezienia wektora
φ
(tzw. wektora własnego) i liczby λ
(tzw. wartości własnej) właściwych danej macierzy A, takich że spełniona jest równość:
φ
λ
φ
⋅
=
⋅
A
(1)
gdzie: A jest macierzą n x n zawierającą współczynniki układu
Nie zawsze układ równań, którego chcemy znaleźć rozwiązanie, przyjmuje tak prostą postać.
Nierzadko mamy do czynienia z tzw. uogólnionym zagadnieniem własnym.
φ
λ
φ
⋅
⋅
=
⋅
B
A
(2)
gdzie: B jest macierzą n x n
Jeśli macierz B jest nieosobliwa to problem uogólniony można przekształcić do postaci:
φ
λ
φ
⋅
=
⋅
−
A
B
1
(3)
czyli do problemu własnego w podstawowej wersji. Konwersja problemu uogólnionego do
standardowego problemu wiąże się z koniecznością znalezienia macierzy B
-1
czyli
wykonaniem dodatkowych obliczeń.
Wynikiem rozwiązania zagadnienia własnego są dwie macierze: pierwsza z nich, macierz
wartości własnych
Λ
zawiera na głównej przekątnej wartości własne, druga
Φ
zawiera
wektory.
W układach dynamicznych zagadnienie własne stosowane jest przede wszystkim w analizie
modalnej, czyli w analizie drgań własnych układu. Wówczas interpretacja wartości własnych
i wektorów własnych jest następująca:
- i-ta wartość własna określa biegun układu:
ω
δ
λ
j
+
=
(4)
gdzie:
δ
współczynnik tłumienia odniesiony do częstości drgań własnych nietłumionych
ω
częstość drgań własnych tłumionych
Posiadając te dwie informacje możemy wyznaczyć częstość drgań własnych nietłumionych:
2
2
ω
δ
+
=
Ω
(5)
- i-ty wektor własny zawiera skalowane amplitudy przemieszczeń lub prędkości drgań
związane z i-tą częstością drgań własnych.
PRZYKŁAD
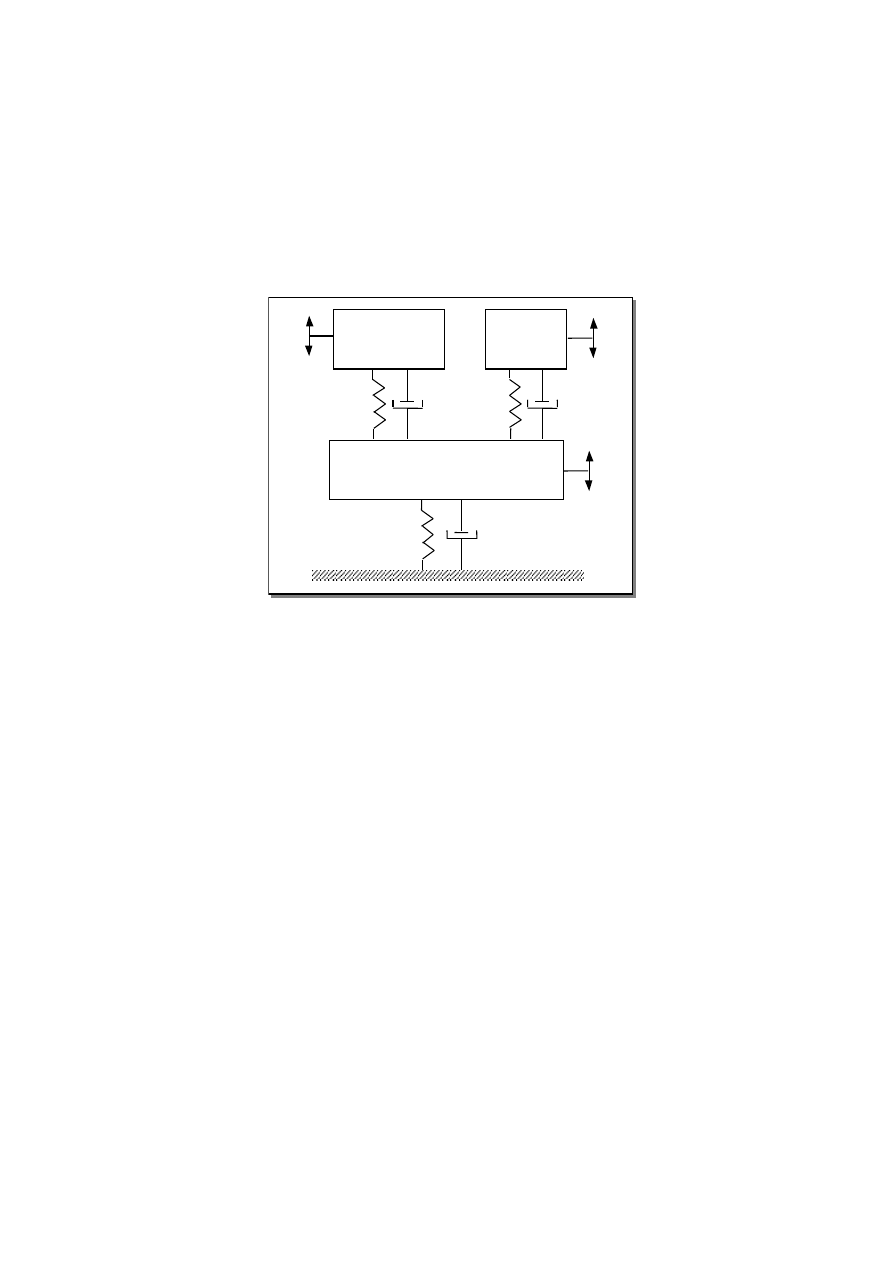
Rozważmy układ dynamiczny jak na rysunku:
Rys. 1. Struktura symulowanego modelu
Należy znaleźć parametry modalne układu (częstości drgań własnych, współczynniki
tłumienia i wektory modalne) dla następujących danych:
Masy:
M1=5 [kg]
M2=2 [kg]
M3=1 [kg]
Współczynniki tłumienia:
C1 = 10 [N s/m]
C2 = 5 [N s/m]
C3 = 6 [N s/m]
Współczynniki sztywności:
K1 = 60000 [N/m]
K2 = 12000 [N/m]
K3 = 10000 [N/m]
W pierwszym kroku należy wyznaczyć równania ruchu układu i zapisać je w formie
macierzowej:
[ ]
[ ]
[ ]
F
x
K
x
C
x
M
=
⋅
+
⋅
+
⋅
˙
˙˙
(6)
Następnie należy poddać równanie (6) transformacji Laplace’a:
[ ]
[ ] [ ]
(
)
( )
[
]
( )
[
]
s
F
s
X
K
C
s
M
s
=
⋅
+
⋅
+
⋅
2
(7)
K1
K3
K2
C2
C3
C1
M2
M3
M1
x3
x2
x1
Jeżeli założymy, że wektor F jest zerowy (drgania swobodne układu) to mamy do czynienia z
typowym jednorodnym układem równań. Aby znaleźć jego rozwiązania nietrywialnie musimy
wykonać następujące przekształcenia:
[ ]
[ ]
(
)
[ ] [ ]
(
)
[ ]
[ ] [ ]
(
)
0
0
0
=
+
⋅
⇒
=
⋅
+
⋅
=
⋅
−
⋅
B
A
s
Y
B
A
s
M
s
M
s
(8)
Gdzie:
[ ] [ ] [ ]
[ ] [ ]
=
C
M
M
A
0
,
[ ]
[ ] [ ]
[ ] [ ]
−
=
K
M
B
0
0
,
[ ]
[ ]
[ ]
⋅
=
X
X
s
Y
Aby rozwiązać równanie (8) musimy zastosować uogólnione zagadnienie własne w postaci
danej wzorem (2). Aby przyspieszyć nasze obliczenia cała analiza zostanie przeprowadzona
przy pomocy oprogramowania Matlab. Do rozwiązania zagadnienia własnego w pakiecie
Matlab służy polecenie eig.
Poniżej zamieszczono fragment programu dotyczący rozwiązania zagadnienia własnego dla
rozważanego przykładu
% Liczba stopni swobody
n=3;
% Masy w układzie
m1=5;
m2=2;
m3=1;
% Współczynniki tłumienia
al1 = 10;
al2 = 5;
al3 = 6;
% Współczynniki sztywności
k1 = 60000;
k2 = 12000;
k3 = 10000;
% Macierze współczynników
% Mas
M = [m1, 0, 0;
0, m2, 0;
0, 0, m3];
% Ws. tłumienia
C = [al1+al2+al3, -al2, -al3;
-al2, al2, 0;
-al3, 0, al3];
% Ws. sztywności
K = [k1+k2+k3, -k2, -k3;
-k2, k2, 0;
-k3, 0, k3];
% Budowanie macierzy do równań stanu w oparciu o wzor (8)
ZER = zeros(size(M));
A = [ZER,M;M,C];
B = [-M,ZER;ZER,K];
% Rozwiązanie uogólnionego zagadnienia wlasnego
[PHI,LAMBDA]=eig(-B,A);
% Czestotliwosci drgan wlasnych tlumionych [Hz]
WD=imag(diag(LAMBDA))/2/pi;
% Czestotliwosci drgan wlasnych [Hz]
WW=sqrt(imag(diag(LAMBDA)).^2+real(diag(LAMBDA)).^2)/2/pi;
% Tlumienie modalne
KSI=-real(diag(LAMBDA))./sqrt(imag(diag(LAMBDA)).^2+real(diag(LAMBDA)).^2);
Powyższy algorytm pozwolił na wyznaczenie częstości drgań własnych układu tłumionych i
nietłumionych oraz związanych z nimi współczynników tłumienia modalnego i postaci drgań
własnych. W oparciu o powyższe dane możliwa jest synteza charakterystyk
częstotliwościowych układu w postaci widmowych funkcji przejścia. Synteza ta przebiega
zgodnie z następującym wzorem:
( )
∑
=
−
+
−
=
N
k
k
ijk
k
ijk
ij
j
r
j
r
H
1
*
*
λ
ω
λ
ω
ω
(9)
gdzie: H
ij
(
ω
) – widmowa funkcja przejścia pomiędzy odpowiedzią mierzoną w
punkcie i a wymuszeniem w punkcie j,
N – liczba postaci drgań własnych, które mają udział w dynamicznej
odpowiedzi konstrukcji w rozważanym zakresie częstotliwości
r
ijk
– reszta modalna dla k-tej postaci drgań własnych,
jk
ik
k
ijk
a
r
φ
φ
=
λ
k
– wartość bieguna dla k-tej postaci drgań własnych
* - oznacza liczbę sprzężoną
Poniżej zamieszczono fragment programu, który pozwala na syntezę widmowych funkcji
przejścia układu.
% Estymacja współczynników skalujących
AAA=PHI'*A*PHI;
for
a=1:n
AN(:,2*a-1)=AAA(:,2*a);
AN(:,2*a)=AAA(:,2*a-1);
end
;
QQ=inv(AN);
Q=diag(QQ);
% Synteza WFP zgodnie ze wzorem (9)
for
c=1:3
jj=[1:3];
f=[0:0.25:40];
for
b=1:length(f)
for
a=1:n
htemp=0;
for
r=1:2*n
htemp=htemp+((Q(r)*PHI(n+a,r)* PHI(n+jj(c),r))/
(i*f(b)*2*pi- LAMBDA(r,r)));
end
;
H{a,c}(b)=htemp*(-1)*(f(b)*2*pi)^2;
end
;
end
;
end
;
plot(f,abs(H{1,3}))
Częstotliwości drgań własnych układu symulacyjnego wynoszą więc odpowiednio:
10.4590 Hz
14.6984 Hz
22.2519 Hz
Współczynniki tłumienia modalnego wynoszą:
0.0105
0.0233
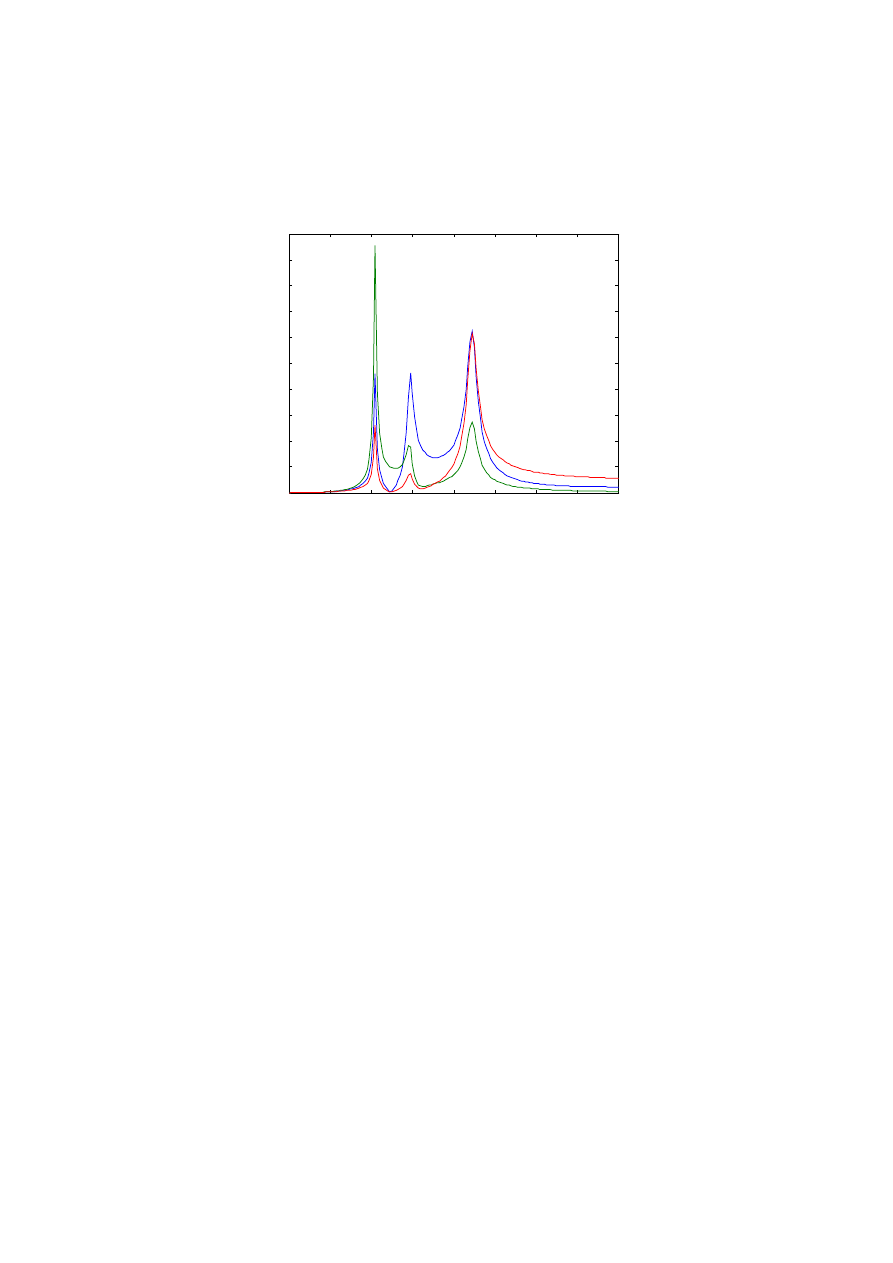
0.0251
Synteza widmowych funkcji przejścia pozwoliła na wyświetlenie następujących
charakterystyk:
0
5
1 0
1 5
2 0
2 5
3 0
3 5
4 0
0
0 . 5
1
1 . 5
2
2 . 5
3
3 . 5
4
4 . 5
5
[ H z ]
M
a
g
n
it
u
d
e
F R F s o f t h e 3 D O F s y s t e m
Rys. 2. Widmowe funcie przejścia symulowanego modelu
Rozkład macierzy względem wartości szczególnych
Kolejnym ważnym narzędziem algebry liniowej powszechnie wykorzystywanym w
identyfikacji jest rozkład macierzy na wartości szczególne (z ang. singular value
decompositions - SVD). Pozwala on na określenie głównych kierunków dynamiki układu i
jest często wykorzystywany w statystyce, analizie sygnałów, analizie obrazów i identyfikacji.
Jego podstawowe zastosowania w identyfikacji to analiza układów źle postawionych, których
macierze współczynników są źle uwarunkowane. Inne zastosowania to rozwiązywanie
układów równań algebraicznych, gdzie liczba zmiennych jest różna od liczby równań.
Zastosowanie to jest realizowane poprzez pseudoinwersję niekwadratowej macierzy
współczynników. Innym ważnym zastosowaniem rozkładu na wartości szczególne jest
aproksymacja macierzy.
Rozkład macierzy [A]
∈
R
mxn
(m
≥
n) na wartości szczególne można opisać następującym
wzorem:
[ ] [ ][ ][ ]
{ } { }
T
i
n
i
i
i
T
v
u
V
U
A
∑
=
=
Σ
=
1
σ
(10)
gdzie: [U], [V]: orthonormal macierze wartości szczególnych: [U]
T
[U] = [V]
T
[V] = [I]
n
,
[ ]
=
Σ
n
σ
σ
0
0
0
0
0
0
1
⋱
: macierz diagonalna taka, że:
σ
1
≥
…
≥
σ
n
≥
0,
σ
i
: wartość szczególna macierzy [A];
{v
i
}, {u
i
}: prawy i lewy wektory szczególne macierzy [A].
Dodatkowo istnieje kilka specjalnych wariantów opisywanego rozkładu:
•
Zredukowany rozkład na wartości szczególne – ponieważ wartości szczególne są usze-
regowane malejąco i podstawowa informacja o układzie zawarta jest w pierwszych
wartościach i wektorach szczególnych, aby przyspieszyć obliczenia wylicza się tylko
n pierwszych wartości szczególnych,
•
Kompaktowy rozkład na wartości szczególne – z tych samych powodów co powyżej
liczy się tylko niezerowe wartości szczególne i związane z nimi wektory,
•
Odcięty rozkład na wartości szczególne – podobnie jak poprzednio aby przyspieszyć
obliczenia liczy się tylko wartości szczególne większe od zadanej wartości progowej.
Pomimo, że rozkład na wartości szczególne jest operacją bardziej ogólną to znaczy może być
zastosowany do dowolnej macierzy o wymiarach m × n, podczas gdy zagadnienie własne
może być rozwiązane jedynie dla pewnej klasy macierzy kwadratowych, to istnieje pomiędzy
nimi ścisły związek. W przypadku szczególnym, gdy [A] jest macierzą hermitowską dodatnio
określoną tzn. wszystkie jej wartości własne są rzeczywiste i dodatnie, wtedy wartości własne
są równe wartościom szczególnym, a wektory własne - wektorom szczególnym. W przypadku
ogólnym zależność pomiędzy oboma rozkładami może być zapisana jako:
[ ] [ ] [ ][ ] [ ] [ ][ ][ ] [ ] [ ] [ ]
(
)
[ ]
T
T
T
T
T
T
V
V
V
U
U
V
A
A
Σ
Σ
=
Σ
Σ
=
(11)
[ ][ ] [ ][ ][ ] [ ][ ] [ ] [ ] [ ][ ]
(
)
[ ]
T
T
T
T
T
T
U
U
U
V
V
U
A
A
Σ
Σ
=
Σ
Σ
=
(12)
Prawe strony tych równań opisują rozkład na wartości własne ich lewych stron w funkcji
macierzy rozkładu na wartości szczególne.
Jak już wspomniano jednym z zastosowań rozkładu na wartości szczególne jest
rozwiązywanie układów równań niedookreślonych lub nadokreślonych. Z taką sytuacją mamy
do czynienia np. przy identyfikacji sił wymuszających, gdzie liczba odpowiedzi układu
używanych do wyznaczania obciążenia jest większa od liczby identyfikowanych sił.
Nierówność taka stosowana jest w celu poprawy uwarunkowania metody i minimalizacji
błędów identyfikacji.
PRZYKŁAD
Rozważmy układ dynamiczny jak na rysunku 1. Załóżmy, że układ jest wymuszony w masie
m
1
siłą f o charakterze losowym. Z pewnych przyczyn siła ta nie może być mierzona, więc
należy ją zidentyfikować na podstawie znanego modelu układu H i odpowiedzi tego układu x
na identyfikowane wymuszenie. Model układu dany jest w postaci syntezowanych
widmowych funkcji przejścia z poprzedniego przykładu. Układ opisany jest więc
następującym równaniem:
f
H
x
⋅
=
(13)
Tego typu zagadnienie zwane jest zadaniem prostym. Zadanie identyfikacji siły f to zadanie
odwrotne identyfikacji i dane jest wzorem:
x
H
f
⋅
=
−
1
(14)
Do identyfikacji użyto trzech odpowiedzi układu mierzonych na masach 1, 2 i 3, a
identyfikowana siła jest tylko jedna, więc rozmiar macierzy H wynosi {3 x 1}. Nie da się
zatem dokonać inwersji macierzy H taka operacja możliwa jest tylko dla macierzy
kwadratowych. Należy więc dokonać pseudoinwersji macierzy H w oparciu o rozkład na
wartości szczególne:
T
V
U
H
⋅
Σ
⋅
=
(15)
gdzie:
Σ
= diag(
σ
1
,..,
σ
r
, 0,..., 0) o rozmiarze n x m,
0
...
1
>
≥
≥
r
σ
σ
,
r – rząd macierzy H,
U, V – macierze ortogonalne o wymiarach odpowiednio n x n i m x m.
Podstawiając równanie (15) do (14) otrzymuje się układ równoważny:
β
ξ =
⋅
Σ
(16)
gdzie:
f
V
T
⋅
=
ξ
(17)
x
U
T
⋅
=
β
(18)
Macierzowe równanie (16) możemy zapisać w postaci układu równań:
=
=
=
⋅
=
⋅
+
n
r
r
r
r
β
β
β
ξ
σ
β
ξ
σ
0
0
1
1
1
1
⋮
⋮
(19)
Zakładając, że równanie (14) jest niesprzeczne [8], [9] z układu równań (19) możemy
jednoznacznie wyliczyć r pierwszych składowych wektora
ξ.
Rozwiązanie równania (14)
powstaje więc z rozwiązania układu (19) ze względu na
ξ
w wyniku przekształcenia:
ξ⋅
=
V
f
(20)
Aby przyspieszyć nasze obliczenia cała analiza zostanie przeprowadzona przy pomocy
oprogramowania Matlab. Do rozwiązania zagadnienia własnego w pakiecie Matlab służy
polecenie svd.
Poniżej zamieszczono fragment programu dotyczący rozwiązania zagadnienia własnego dla
rozważanego przykładu.
% definicja sygnału wymuszenia
% definicja wektora czasu
t=[0:1/80:10];
% definicja wektora siły o charakterze losowym
f_zadane_1=10*rand(size(t));
% rozdzielczosc czestotliwosciowa
nn=round(80/0.25);
% transformata Fouriera
f_zadane_1_freq=(fft(f_zadane_1,nn)*2)/nn;
dl=length(f_zadane_1_freq);
f_zadane_freq{1}=f_zadane_1_freq(1:ceil(dl/2)+1);
f_zadane_freq{1}(1:5)=0;
% wyliczenie odpowiedzi na wymuszenie w masie nr 1
frfs=H(:,1);
for
a=1:length(f)
tfrfs=[];
tforces=[];
for
b=1:length(f_zadane_freq)
tforces(b)=f_zadane_freq{b}(a);
end
;
for
c=1:size(frfs,2)
for
b=1:size(frfs,1)
tfrfs(b,c)=frfs{b,c}(a);
end
;
end
;
tresps=tfrfs*tforces';
for
b=1:size(frfs,1)
resp{b}(a)=tresps(b);
end
;
end
;
% wyliczenie wektora siły wymuszającej f
for
a=1:length(resp{1})
% tworzenie tymczasowego wektora widm odpowiedzi i WFP dla kolejnych
% czestotliwosci
tresps=[];
for
b=1:length(resp)
tresps(b)=resp{b}(a);
end
;
for
c=1:size(frfs,2)
for
b=1:size(frfs,1)
tfrfs(b,c)=frfs{b,c}(a);
end
;
end
;
tresps=tresps.';
% rozwiazanie rownania f=(H^-1)*p metoda rozkladu na wartosci szczegol-
ne
[u,sig,v]=svd(tfrfs);
r=rank(tfrfs);
beta=u'*tresps;
for
b=1:r
en(b)=beta(b)/sig(b,b);
end
;
for
b=r+1:size(v,1)
e2(b)=0;
end
;
if
r>0
esizen=size(en,2);
esize2=size(e2,2);
en=[en,zeros(1,size(v,1)-esizen)];
e2=[zeros(1,size(v,1)-esize2),e2];
x1=v*en';
x2=v*e2';
ftemp=x1+x2;
else
esize2=size(e2,2);
e2=[zeros(1,size(v,1)-esize2),e2];
x2=v*e2';
ftemp=x2;
end
;
for
b=1:length(ftemp)
Identforce{b}(a)=ftemp(b);
end
;
end
;
Wykonanie powyższego skryptu powoduje wyliczenie następujących przebiegów.
0
5
1 0
1 5
2 0
2 5
3 0
3 5
4 0
0
0 . 2
0 . 4
0 . 6
0 . 8
1
1 . 2
1 . 4
[ H z ]
M
a
g
n
it
u
d
e
R e s p o n s e s p e c t r a o f t h e 3 D O F s y s t e m
0
5
1 0
1 5
2 0
2 5
3 0
3 5
4 0
0
0 . 1
0 . 2
0 . 3
0 . 4
0 . 5
0 . 6
0 . 7
[ H z ]
M
a
g
n
it
u
d
e
C o m p a r i s o n o f a p p l i e d a n d i d e n t i f i e d f o r c e s p e c t r u m
Rys. 3. Widma odpowiedzi i wymuszenie dla symulowanego układu
Rozkład macierzy typu LU
Metoda LU jest metodą rozwiązywania
x
A
y
⋅
=
(21)
Pozwala także na szybkie wyliczenie
współczynników zapisywana jest jako iloczyn dwóch
: dolnej (ang. lo-
wer - L) i górnej (ang. upper - U), tj. z elementami zerowymi - odpowiednio - powyżej i poni-
żej
U
L
A
⋅
=
(22)
=
=
nn
n
n
nn
n
n
u
u
u
u
u
u
U
l
l
l
l
l
l
L
⋯
⋮
⋱
⋮
⋮
⋯
⋯
⋯
⋮
⋱
⋮
⋮
⋯
⋯
0
0
0
,
0
0
0
2
22
1
12
11
2
1
22
21
11
(23)
Układ równań przyjmuje wówczas postać:
x
U
L
y
⋅
⋅
=
(24)
a jego rozwiązanie sprowadza się do rozwiązania dwóch układów równań z macierzami trój-
kątnymi, które z kolei rozwiązuje się bardzo prosto:
z
x
U
z
L
y
=
⋅
⋅
=
(25)
Wyznacznik macierzy A tej postaci można obliczyć korzystając z
)
det(
)
det(
)
det(
U
L
U
L
⋅
=
⋅
(26)
oraz z faktu, że wyznacznik macierzy trójkątnej jest iloczynem elementów na przekątnej. Po-
nadto przeważnie przy rozkładzie LU na przekątnej jednej z macierzy znajdują się jedynki –
wtedy wyznacznik macierzy A jest równy wyznacznikowi albo macierzy L albo U.
Zalety metody:
•
bardzo oszczędna gospodarka pamięcią
•
wymaga najmniejszej liczby operacji w porównaniu z innymi metodami dokładnymi
(nie biorąc pod uwagę procedur specjalnych).
W Matlabie do rozkładu LU macierzy A wykorzystywane jest polecenie lu.
Zadania do samodzielnego wykonania
1. Dla układu jak na rysunku dobierz tak parametry macierzy M, C i K aby pierwsza czę-
stość drgań własnych znajdowała się nieco poniżej 5 Hz, a druga powyżej 50 Hz.
2. Dla dobranych w poprzednim zadaniu parametrów dokonaj syntezy widmowych
funkcji przejścia w oparciu o wzór (9) oraz o wzór
ω
j
s
K
C
s
M
s
s
H
=
+
⋅
+
⋅
=
2
1
)
(
.
Porównaj wyniki.
3. Dla układu z zadania 1 przeprowadź analizę modalną zastępując rozkład na wartości
własne rozkładem na wartości szczególne. Skomentuj otrzymane wyniki.
4. Rozwiąż układ równań (21), gdzie A będzie macierzą losowych współczynników o
wymiarach 1000 x 1000, a wektor y to wektor losowych wyrazów wolnych o
rozmiarze 1000 x 1. Zastosuj metodę klasyczną i metodę LU. Porównaj czasy obliczeń
(tic, toc)