
Sygnały i Systemy
Sygnały i Systemy
Wykład 3
Systemy dyskretne – transmitancja Z
Grzegorz Masłowski
Politechnika Rzeszowska
Zakład Podstaw Elektrotechniki i Informatyki
E-mail:
maslowski@prz.edu.pl
http://maslowski.sd.prz.edu.pl/
SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
System liniowy niezmienny w czasie (LTI)
System liniowy niezmienny w czasie (LTI)
x1
x3
y
układ
liniowy
System liniowy
LTI
W układach liniowych obowiązuje zasada superpozycji, zgodnie z którą
sygnał na wyjściu można wyznaczyć jako sumę sygnałów wyjściowych
pochodzących od wszystkich sygnałów wejściowych
Zasada superpozycji nie obowiązuje w układach nieliniowych, w których nie
można sygnału wyjściowego rozdzielić na składniki pochodzące od różnych
sygnałów wejściowych.
y y
y
y
x
y
= 1+ 2+ 3
c =c
SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Opis matematyczny układów dyskretnych
Opis matematyczny układów dyskretnych
System
dyskretny
y
[n]
x
[n]
System dyskretny przetwarza wejściowy ciąg próbek w wyjściowy
ciąg próbek, który zależy nie tylko od sygnału wejściowego, ale
również od własności układu dyskretnego.
System dyskretny opisują tzw. równania rekurencyjne, które uzyskuje
się z równań różnicowych, a te z kolei wyprowadza się na podstawie
równań różniczkowych zastępując pochodne ilorazami różnicowymi.
dyskretny

SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Przykład 1: dyskretny model kondensatora
Przykład 1: dyskretny model kondensatora
Wyprowadzone zostanie równanie rekurencyjne opisujące zależność
pomiędzy dyskretnym sygnałem napięcia panującym na
kondensatorze (sygnał wejściowy) a dyskretnym sygnałem prądu
płynącego przez ten kondensator (sygnał wyjściowy)
du( )
( )
d
t
i t
C
t
=
( )
(
)
( )
u t
u t
t
i t
C
t
−
− ∆
=
∆
Model ciągły wykorzystujący operację
różniczkowania (system liniowy I rzędu)
Równanie różnicowe otrzymuje się, gdy
pochodną zastąpi się poprzez iloraz różnicowy
SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Przykład 1: dyskretny model kondensatora
Przykład 1: dyskretny model kondensatora
(
)
((
1) )
(
)
u nT
u n
T
i nT
C
T
−
−
=
T
t
=
=
∆
const
Jeśli w ilorazie różnicowym przedział czasu ∆t
jest równy okresowi próbkowania T sygnału
analogowego to równanie różnicowe opisuje
zależność pomiędzy pomiędzy ciągiem próbek
wejściowych i wyjściowych.
T
[ ]
[
1]
[ ]
u n
u n
i n
C
T
−
−
=
Często pomija się symbol T w argumencie
funkcji i wykorzystuje się wcześniej
wspominaną notację funkcyjną (z nawiasami
kwadratowymi)
Równanie rekurencyjne dla
dyskretnego modelu kondensatora
SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
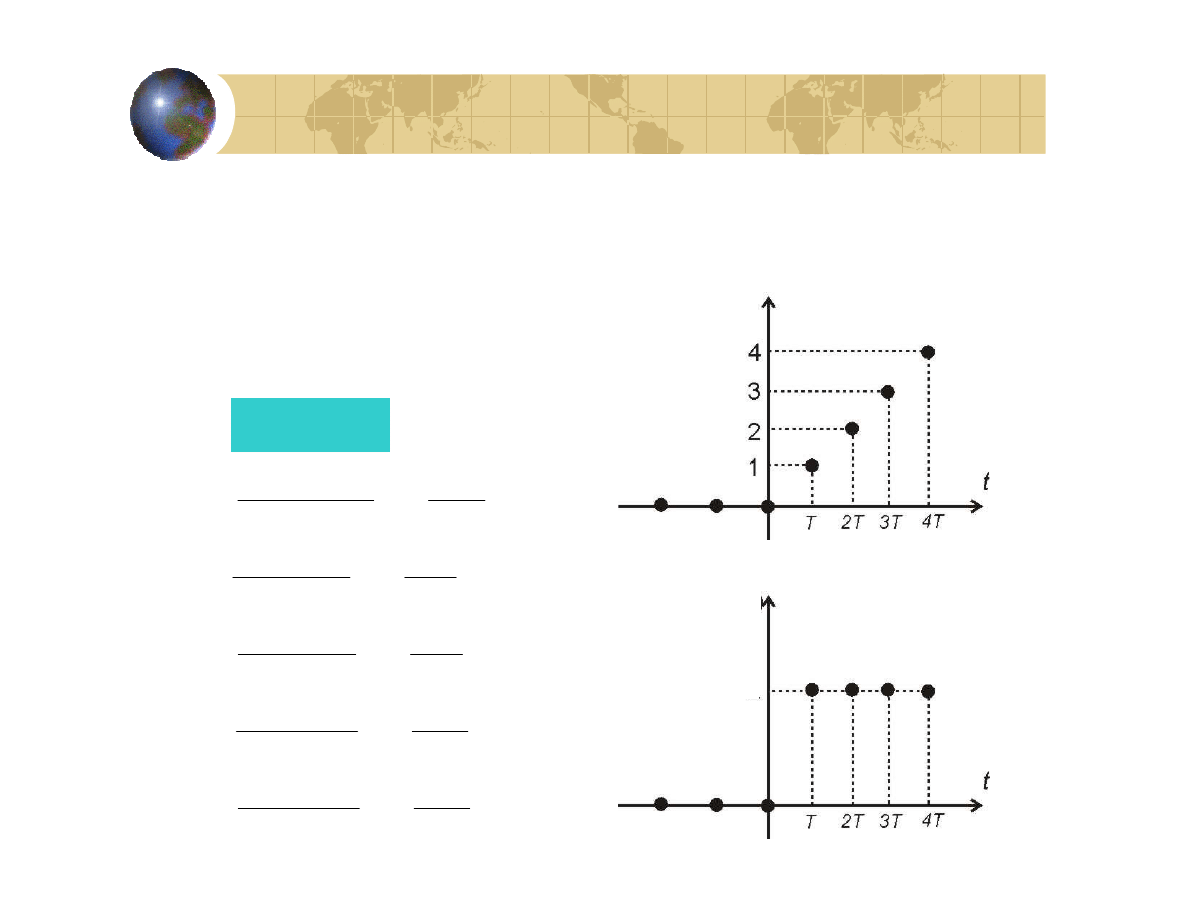
Przykład 1: dyskretny model kondensatora
Przykład 1: dyskretny model kondensatora
[0]
0; [1] 1; [2]
2;
[3]
3; [4]
4
u
u
u
u
u
=
=
=
=
=
Dla
T
=1s
u(nT)
[0]
[ 1]
0 0
[0]
0
1
[1]
[0]
1 0
[1]
1
[2]
[1]
2 1
[2]
1
[3]
[2]
3 2
[3]
1
[4]
[3]
4 3
[4]
1
u
u
i
C
C
T
u
u
i
C
C
C
T
u
u
i
C
C
C
T
u
u
i
C
C
C
T
u
u
i
C
C
C
T
−
−
−
=
=
=
−
−
=
=
=
−
−
=
=
=
−
−
=
=
=
−
−
=
=
=
C
i(nT)

SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Równanie rekurencyjne opisujące liniowy
Równanie rekurencyjne opisujące liniowy
system dyskretny m
system dyskretny m--tego rzędu
tego rzędu
1
0
1
[ ]
[
1]
[
]
[ ]
[
1]
[
],
0
m
m
y n
a y n
a y n m
b x n
b x n
b x n m
n
+
−
+
+
−
=
+
−
+
+
−
≥
K
K
[ 1], [ 2],
[
]
y
y
y m
−
−
−
K
[ 1], [ 2],
[
]
0
x
x
x
m
−
−
−
=
K
sygnał wejściowy przyłożony w
chwili t=0 (n=0)
warunki początkowe dla n=0
Rozwi
ą
zanie ogólne równania zale
ż
y od m parametrów,
które stanowi
ą
warunki pocz
ą
tkowe.

SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Odpowiedź wymuszona i swobodna systemu
Odpowiedź wymuszona i swobodna systemu
Odpowiedzią wymuszoną nazywamy rozwiązanie równania
rekurencyjnego dla warunków początkowych zerowych (odpowiedź
ta zależy tylko od wymuszenia i nie zależy od stanu początkowego
systemu)
1
[ ]
[
1]
[
]
0
m
y n
a y n
a y n m
+
−
+
+
−
=
K
Odpowiedzią swobodna nazywamy rozwiązanie równania
jednorodnego
Odpowiedź swobodna zależy od stanu początkowego systemu
(warunków początkowych) i nie zależy od wymuszenia

SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
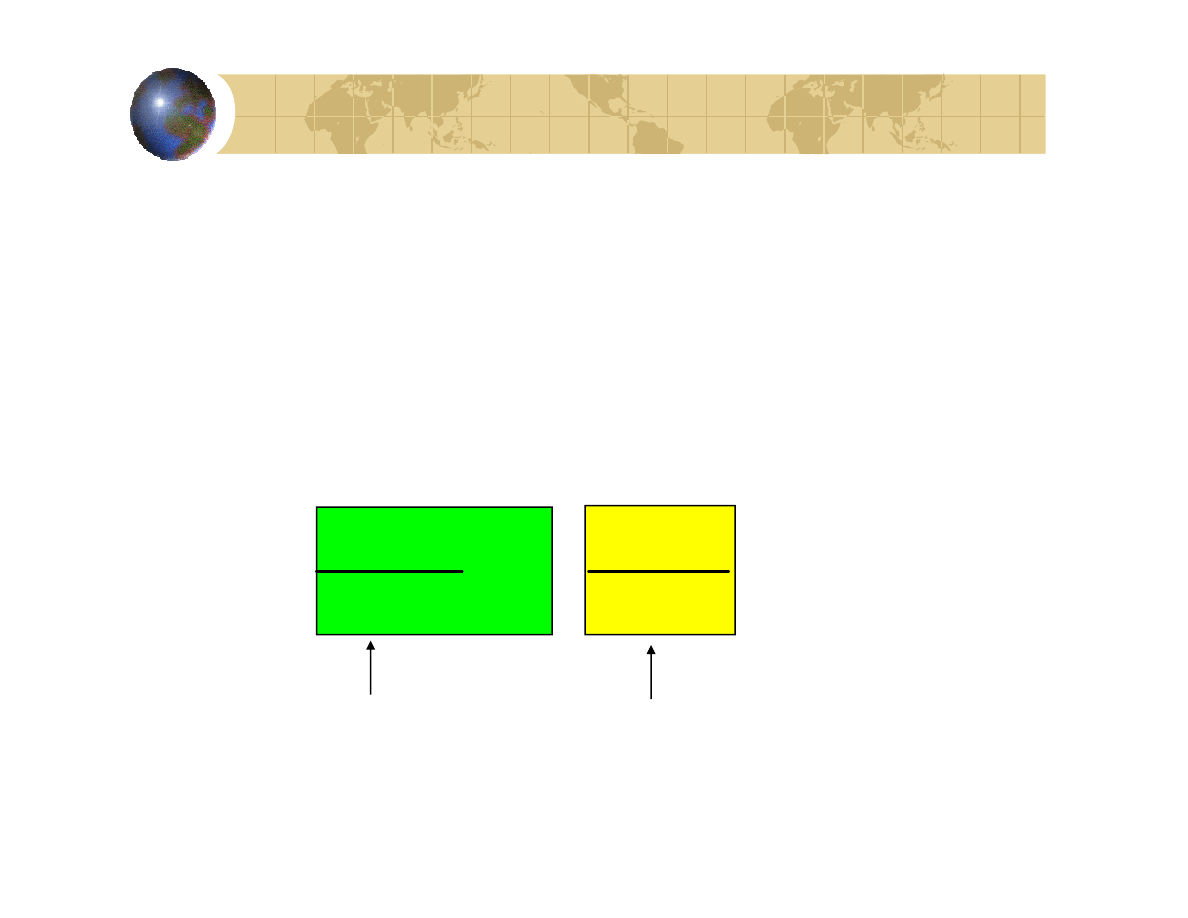
Wykorzystanie przekształcenia Z do wyznaczania
Wykorzystanie przekształcenia Z do wyznaczania
odpowiedzi systemu na zadane wymuszenie
odpowiedzi systemu na zadane wymuszenie
1) Wyznaczyć transformatę Z równania
rekurencyjnego
2) Rozwiązać uzyskane równanie
algebraiczne względem Y(z)
3) Wyznaczyć transformatę odwrotną
funkcji zespolonej Y(z)
SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
System liniowy pierwszego rzędu
System liniowy pierwszego rzędu
1
0
1
[ ]
[
1]
[ ]
[
1],
0
y n
a y n
b x n
b x n
n
+
−
=
+
−
≥
{
}
1
1
1
0
1
( )
( )
[ 1]
( )
( )
Y z
a z Y z
y
b X z
b z X z
−
−
+
+
−
=
+
{
}
1
0
1
( )
( )
[ 1]
( )
( )
Y z
a z Y z
y
b X z
b z X z
+
+
−
=
+
1
0
1
1
1
1
1
1
[ 1]
( )
( )
( )
( )
1
1
w
s
b
b z
a y
Y z
X z
Y z
Y z
a z
a z
−
−
−
+
−
−
=
+
=
+
+
+
Transformata
odpowiedzi
wymuszonej
Transformata
odpowiedzi
swobodnej

SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Odpowiedź swobodna
Odpowiedź swobodna
1
1
1
1
1
[ 1]
( )
[ 1]
(
)
1
s
a y
z
Y z
a y
z
a
a z
−
−
−
=
= −
−
− −
+
1
[ ]
[ 1](
)
[ 1](
)
n
n
y n
a y
a
y
a
+
= −
−
−
=
−
−
1
1
1
1
[ ]
[ 1](
)
[ 1](
)
n
n
s
y n
a y
a
y
a
+
= −
−
−
=
−
−
1
1
[ ]
[ 1](
)
n
s
y n
y
a
+
=
−
−
gdzie
1
1
z
a
= −
jest biegunem transmitancji systemu pierwszego rzędu
(patrz kolejne slajdy)
odpowiedź swobodna
SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Koncepcja transmitancji systemów dyskretnych
Koncepcja transmitancji systemów dyskretnych
System
dyskretny
y
[
n
]
x
[
n
]

SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Transmitancja systemu dyskretnego pierwszego rzędu
Transmitancja systemu dyskretnego pierwszego rzędu
Transmitancją systemu dyskretnego nazywa się stosunek transformat
sygnału wyjściowego do wejściowego przy warunkach poczatkowych
zerowych
1
0
1
1
( )
( )
( )
w
b
b z
Y z
X z
Y z
−
−
+
=
=
1
1
( )
( )
( )
1
w
Y z
X z
Y z
a z
−
=
=
+
1
0
1
1
1
( )
( )
( )
1
w
b
b z
Y z
H z
X z
a z
−
−
+
=
=
+
Transmitancją systemu nie zależy od sygnału wejściowego i
wyjściowego lecz wyłącznie od rodzaju tego systemu określonego
poprzez współczynniki b
0
, b
1
i a
1
.

SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Przykład 2:
Przykład 2:
Wyznaczyć transmitancję Z modelu dyskretnego kondensatora:
[ ]
[
1]
[ ]
u n
u n
i n
C
T
−
−
=
Równanie rekurencyjne dla
dyskretnego modelu kondensatora
Dokonując przekształcenia Z lewej i prawej strony równania otrzymuje się:
1
( ) ( ( )
[ 1])
( )
U z
U z z
u
I z
C
T
−
−
+
−
=
Zakładając zerowy warunek początkowy u[-1]=0:
1
( )
( )(1
)
C
I z
U z
z
T
−
=
−
1
( )
1
( )
(1
)
( )
I z
C
C z
H z
z
U z
T
T
z
−
−
=
=
−
=
SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Przykład 3:
Przykład 3:
Wyznaczyć odpowiedź i transmitancję systemu pierwszego rzędu
opisanego równaniem rekurencyjnym:
[ ] 3 [
1]
2 [ ],
0
[ 1]
5
y n
y n
u n
n
y
−
−
=
≥
−
=
Dokonując przekształcenia Z lewej i prawej strony równania otrzymuje się:
{
}
1
( ) 3
( )
[ 1]
2
1
z
Y z
z Y z
y
z
−
−
+
−
=
−
(
)
1
( ) 1 3
15
2
1
z
Y z
z
z
−
−
−
=
−
(
)(
)
2
2
15
( )
1
3
3
z
z
Y z
z
z
z
=
+
−
−
−
transformata
odpowiedzi
wymuszonej
transformata
odpowiedzi
swobodnej

SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Przykład 3:
Przykład 3:
(
)(
)
1
2
( )
2
1
3
1
3
w
Y z
c
c
z
z
z
z
z
z
=
=
+
−
−
−
−
(
)
2
1
1
z
c
z
=
−
= −
(
)(
)
(
)
1
1
2
1
1
1
3
z
z
c
z
z
z
=
=
−
= −
−
−
(
)(
)
(
)
2
3
2
6
3
3
1
3
2
z
z
c
z
z
z
=
=
−
=
=
−
−
(
)(
)
( )
2
1
3
1
3
1
3
w
Y z
z
z
z
z
z
z
=
= −
+
−
−
−
−

SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Przykład 3:
Przykład 3:
3
( )
1
3
w
z
z
Y z
z
z
= −
+
−
−
15
( )
3
s
z
Y z
z
=
−
( )
( )
( )
w
s
Y z
Y z
Y z
=
+
[ ]
[ ]
[ ]
w
s
y n
y n
y n
=
+
[ ]
[ ] 3 3
15 3
18 3
[ ]
0
n
n
n
y n
u n
u n
n
= −
+ ⋅
+
⋅
=
⋅
−
≥
(
)
[ ]
18 3
1
[ ]
n
y n
u n
=
⋅
−
[ ] 18 3
[ ]
[ ]
n
y n
u n
u n
=
⋅
−
lub bez warunku
0
n ≥

SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Przykład 3:
Przykład 3:
1
0
1
1
1
( )
( )
( )
1
w
b
b z
Y z
H z
X z
a z
−
−
+
=
=
+
(
)(
)
2
2
( )
1
3
w
z
Y z
z
z
=
−
−
( )
2
1
z
X z
z
=
−
(
)(
)
( )
1
3
w
Y z
z
z
=
−
−
( )
2
1
X z
z
=
−
(
)(
)
2
2
1
( )
1
3
2
z
z
H z
z
z
z
−
=
−
−
(
)
( )
3
z
H z
z
=
−
Pojedynczy biegun
transmitancji
1
3
z =

SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
System liniowy drugiego rzędu
System liniowy drugiego rzędu
1
2
0
1
2
[ ]
[
1]
[
2]
[ ]
[
1]
[
2],
0
y n
a y n
a y n
b x n
b x n
b x n
n
+
−
+
−
=
+
−
+
−
≥
Po dokonaniu transformaty Z obydwu stron i uporządkowaniu
wyrazów otrzymuje się ogólną postać
( )
( )
( )
( )
( )
( )
( )
( )
w
s
w
s
L z
L z
Y z
X z
Y z
Y z
M z
M z
=
+
=
+
gdzie
1
2
1
2
( )
1
M z
a z
a z
−
−
= +
+
1
2
0
1
2
( )
w
L z
b
b z
b z
−
−
=
+
+
( )
s
L z
zależy od warunków początkowych
wyrazów otrzymuje się ogólną postać

SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Transmitancja systemu liniowy drugiego rzędu
Transmitancja systemu liniowy drugiego rzędu
1
2
0
1
2
1
2
1
2
( )
1
b
b z
b z
H z
a z
a z
−
−
−
−
+
+
=
+
+
( )
( )
( )
( )
( )
w
w
Y z
L z
H z
X z
M z
=
=
( )
( ) ( )
w
Y z
H z X z
=
Transformata odwrotna transmitancji H(z) jest równa odpowiedzi
impulsowej systemu (odpowiedzi na deltę Kroneckera)
1
2
1
2
1 a z
a z
−
−
+
+
{
}
{
}
1
1
1
( )
( )
[ ]
( )
m
n
k k
k
Z
H z
Z
Y z
h n
c z
z
−
−
=
=
=
=
∑
δ
gdzie z
k
są biegunami transmitancji H(z)
{
}
( )
[ ]
1
X z
Z
n
=
=
δ
gdy
( )
( )
Y z
H z
=
δ

SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Stabilność systemów liniowych
Stabilność systemów liniowych
1
[ ]
( )
m
n
k k
k
h n
c z
z
=
=
∑
System jest stabilny gdy odpowiedź impulsowa h[n] określona
szeregiem
1
k =
dąży do zera, gdy n dąży do nieskończoności (czyli gdy czas
obserwacji dąży do nieskończoności).
Zatem wszystkie bieguny transmitancji powinny leżeć na
płaszczyźnie zespolonej wewnątrz okręgu o promieniu 1.
1
k
z <

SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Schematy blokowe systemów dyskretnych
Schematy blokowe systemów dyskretnych
Często związki pomiędzy dyskretnymi sygnałami wejściowymi i
wyjściowymi opisuje się graficznie za pomocą dyskretnych
schematów z podstawowymi działaniami
SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
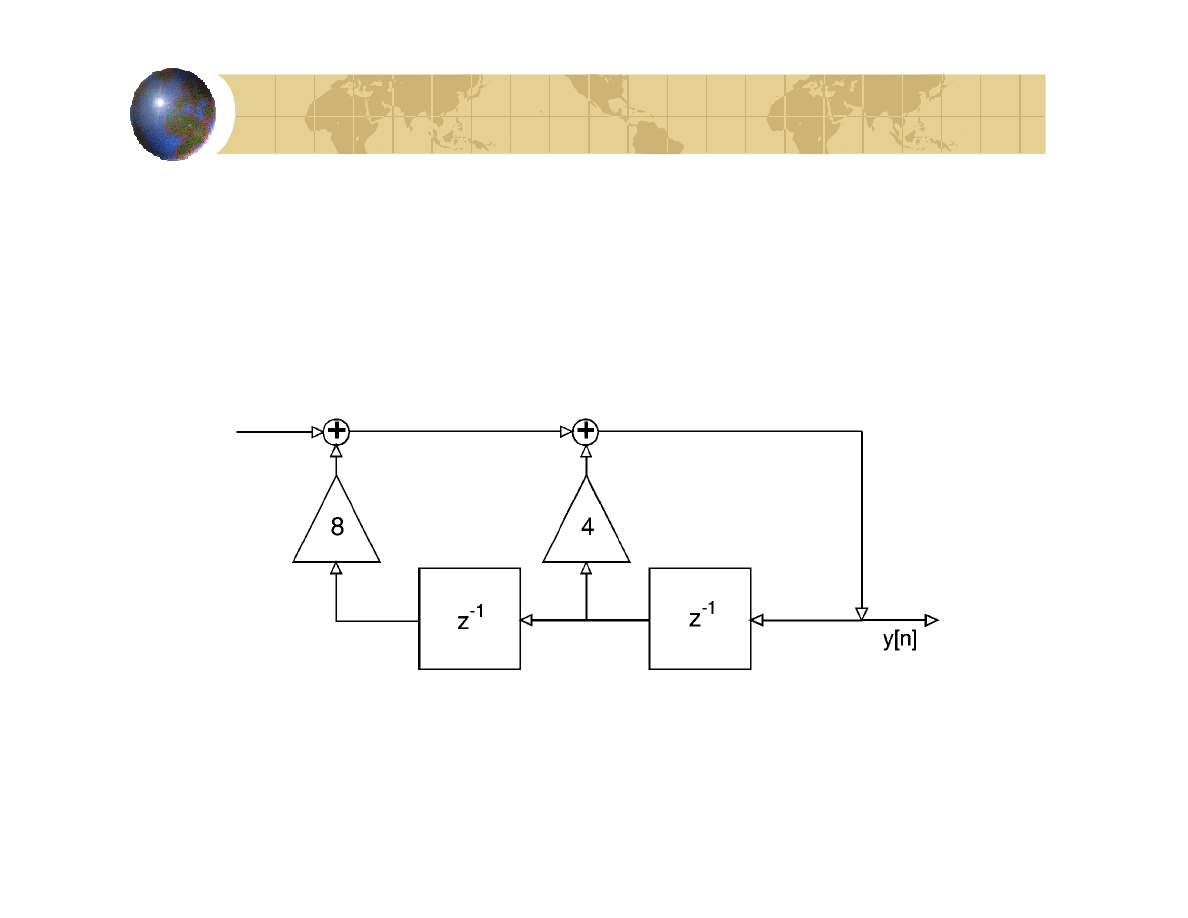
Przykład 4:
Przykład 4:
Wyznaczyć: a) równanie rekurencyjne opisujące system dyskretny
drugiego rzędu, b) transmitancję tego systemu c) oraz odpowiedź
impulsową wykorzystując do tych celów schemat blokowy:
]
[
]
[
n
n
x
δ
=
Zakładamy dodatkowo zerowe warunki początkowe:
0
]
2
[
]
1
[
=
−
=
−
y
y

SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Rozwiązanie:
Rozwiązanie:
a) Równanie rekurencyjne
]
2
[
8
]
1
[
4
]
[
]
[
−
+
−
+
=
n
y
n
y
n
x
n
y
b) Transmitancja układu dyskretnego
b) Transmitancja układu dyskretnego
1
2
( )
( )
4 ( )
8 ( )
Y z
X z
Y z z
Y z z
−
−
=
+
+
{
}
1
2
( ) 1 4
8
( )
Y z
z
z
X z
−
−
−
−
=
2
1
2
2
( )
1
( )
( )
1 4
8
4
8
Y z
z
H z
X z
z
z
z
z
−
−
=
=
=
−
−
−
−
( )
( )
w
Y z
Y z
=

SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Rozwiązanie:
Rozwiązanie:
( )
( ) ( )
( )
Y z
H z X z
H z
=
=
{
}
( )
[ ]
1
X z
Z
n
δ
=
=
gdyż
2
z
c) Odpowiedź impulsowa w postaci operatorowej
Aby przedstawić sygnał wyjściowy jako dyskretny ciąg próbek należy
dokonać transformaty odwrotnej Z dla sygnału Y(z).
W tym celu powyższą funkcję zapisujemy w postaci:
2
2
( )
4
8
z
Y z
z
z
=
−
−
2
( )
4
8
Y z
z
z
z
z
=
−
−

SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Rozwiązanie:
Rozwiązanie:
Nast
ę
pnie znajdujemy pierwiastki mianownika,
czyli
bieguny transformaty !!!
( )
Y z
z
=
2
1
2
(
5, 45)(
1, 45)
4
8
0 to
16
32
6,9
4
6,9
4
6,9
5, 45
1, 45
2
2
z
z
z
z
z
z
z
∆
=
−
+
−
− =
=
+
=
+
−
=
=
=
= −

SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Rozwiązanie:
Rozwiązanie:
Wyrażenie po prawej stronie równania przedstawiamy w postaci:
1
2
( )
(
5, 45)(
1, 45)
(
5, 45)
(
1, 45)
c
c
Y z
z
z
z
z
z
z
=
=
+
−
+
−
+
Inny sposób wyznaczania współczynników
1
2
(
1, 45)
(
5, 45)
( )
(
5, 45)(
1, 45)
(
5, 45)(
1, 45)
c z
c z
Y z
z
z
z
z
z
z
+
+
−
=
=
−
+
−
+
Inny sposób wyznaczania współczynników
1
2
1
2
1
2
1
2
1
2
(
1, 45)
(
5, 45)
1, 45
5, 45
1
1, 45
5, 45
0
z
c z
c z
c z
c z
c
c
c
c
c
c
=
+
+
−
=
+
+
−
+
=
−
=
1
2
0.79
0.21
c
c
=
=

SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Rozwiązanie:
Rozwiązanie:
W ostatnim etapie odwracania transformaty Z sygnału wyjściowego
dokonujemy przekształcenia:
( )
0.79
0.21
(
5, 45)
(
1, 45)
z
z
Y z
z
z
=
+
−
+
(
5, 45)
(
1, 45)
z
z
−
+
A następnie zapisujemy transformatę odwrotną lewej i prawej strony
równania operatorowego:
{
}
[ ]
0.79 5, 45
0.21 ( 1, 45)
[ ]
n
n
y n
u n
=
⋅
+
⋅ −
Równanie to opisuje już sygnał wyjściowy w dyskretnych chwilach
czasowych.

SYGNAŁY I SYSTEMY
SYGNAŁY I SYSTEMY -- dr inż. Grzegorz Masłowski
dr inż. Grzegorz Masłowski
Politechnika Rzeszowska
Politechnika Rzeszowska
Zadanie:
Zadanie:
2. Czy rozpatrywany system jest stabilny, a jeśli nie to dlaczego?
1. Narysować przebieg czasowy sygnału wyjściowy, wiedząc że okres
próbkowania T=1ms dla pierwszych 10 próbek (n=0, 1, 2, ...,10)
3. Zaproponować takie zmiany w schemacie blokowym, aby system
był stabilny.
Wyszukiwarka
Podobne podstrony:
cz03 Systemy dyskretne
3 Cwiczenia zadania3 systemy dyskretne id 606490 (2)
1 kolokwium, zadania2 systemy dyskretne
zadania3 systemy dyskretne
Komputerowy system do?dań?ektywności metaheurystyki ''System Mrówek'' w zakresie optymalizacji dyskr
Systemy reprezentantów, matematyka dyskretna
Zastosowanie symulacji dyskretnej w obsłudze systemów kolejkowych
B8 Algorytmy optymalizacji w dyskretnych systemach produkcyjnych
System nawigacji satelitarnej GPS cz03
System finansowy w Polsce 2
Systemy operacyjne
Systemy Baz Danych (cz 1 2)
Współczesne systemy polityczne X
System Warset na GPW w Warszawie
003 zmienne systemowe
elektryczna implementacja systemu binarnego
więcej podobnych podstron