Cyfrowe przetwarzanie sygnałów

Transformata Fouriera

z dyskretnym czasem (04)

Sławomir Kulesza

Wykład fakultatywny dla studentów

III r. spec. Informatyka ogólna

Rok akademicki 2012/2013

Transformata Fouriera

z dyskretnym czasem

●

Transformata Fouriera z dyskretnym czasem
(DTFT – Discrete-Time Fourier Transform) –
reprezentacja sygnału z dyskretnym czasem
postaci:

x [n] →

DTFT

X

(

e

j ω

)

=

∑

n=−∞

∞

x [n]e

−

j ω n

●

DTFT impulsu jednostkowego:

δ[

n] →

DTFT

X

(

e

j ω

)

=

∑

n=−∞

∞

δ[

n]e

−

j ω n

=

1

Odwrotna transformata Fouriera

z dyskretnym czasem

●

Odwrotna transformata Fouriera z dyskretnym
czasem (iDTFT – inverse Discrete-Time
Fourier Transform):

X

(

e

j ω

)

→

iDTFT

x [n]=

1

2 π

∫

−π

π

X

(

e

j ω

)

e

j ω n

d ω

●

Wzajemna równoważność transformat:

x [n]⇔

F

X

(

e

j ω

)

Własności DTFT

●

Okresowość:

●

Powyższa relacja opisuje zjawisko aliasingu w
dziedzinie częstości.

X

(

e

j (ω+2 π k )

)

=

X

(

e

j ω

)

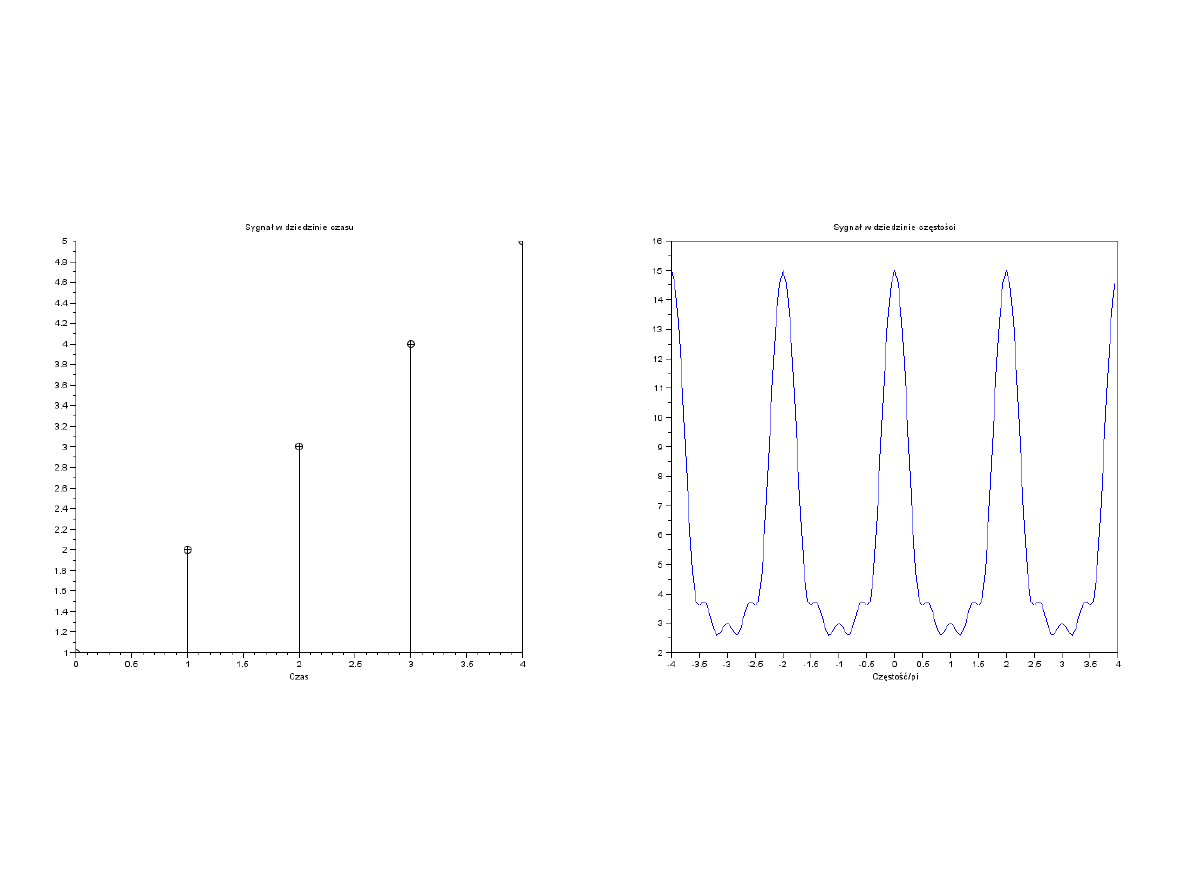
Aliasing w dziedzinie częstości

Widmo fourierowskie

●

DTFT w postaci wykładniczej:

X

(

e

j ω

)

=

∣

X

(

e

j ω

)

∣

e

j θ(ω)

Widmo amplitudowe

Widmo fazowe

Własności DTFT

●

DTFT sygnału zawiniętego:

●

DTFT sygnału sprzężonego:

F {x [−n]}= X

(

e

−

j ω

)

F {x ' [−n]}= X '

(

e

j ω

)

Symetria DTFT

Zbieżność DTFT

●

Transformata DTFT jest zbieżna (istnieje), gdy
sygnał x[n] jest bezwzględnie sumowalny:

∑

n=−∞

∞

∣

x [n]∣<∞

∣

X

(

e

j ω

)

∣

=

∣

∑

n=−∞

∞

x [n]e

−

j ω n

∣

≤

...

...≤

∑

n=−∞

∞

∣

x [n]∣

∣

e

−

j ω n

∣

≤

∑

n=−∞

∞

∣

x [n]∣<∞

Własności DTFT

Odpowiedź częstotliwościowa

układów LTI z dyskretnym czasem

●

Wiele sygnałów można przedstawić jako
superpozycję sygnałów sinusoidalnych z
nieciągłym czasem. Odpowiedź dowolnego
układu LTI można zatem określić znając jego
odpowiedź na pojedynczy sygnał sinusoidalny.

●

Sygnał sinusoidalny można uogólnić jako
zespolony sygnał wykładniczy, stąd
zainteresowanie odpowiedzią układów LTI na
pobudzenie wykładnicze.

Funkcje własne układu LTI

●

Ważną cechą układów LTI jest istnienie
funkcji własnych (eigenfunctions).
Odpowiedź układu na pobudzenie funkcją
własną jest tożsama przemnożeniu tejże
funkcji przez pewną stałą (w ogólności:
zespoloną):

y [n]= ̃C⋅x [n]

Funkcje własne układów LTI

●

Niech pobudzenie układu jest zespolonym
sygnałem wykładniczym postaci:

●

Odpowiedź układu jest splotem pobudzenia i
odpowiedzi impulsowej:

x [n]=e

j ω n

, n∈ℤ

y [n]=

∑

k=−∞

∞

h[ k ] x [n−k ]=

∑

k=−∞

∞

h[ k ]e

j ω(n−k)

y [n]=

(

∑

k=−∞

∞

h[k ]e

−

j ω k

)

e

j ω n

Funkcje własne układów LTI

●

Ostatecznie:

●

Wykładniczy sygnał zespolony jest więc
funkcją własną układu LTI.

y [n]=H

(

e

j ω

)

e

j ω n

Odpowiedź częstotliwościowa

układu LTI

●

Odpowiedzią częstotliwościową (

frequency

response

) układu LTI jest wielkość:

●

Odpowiedź częstotliwościowa układu LTI jest
tożsama transformacie jego odpowiedzi
impulsowej i opisuje układ w domenie
częstotliwości.

H

(

e

j ω

)

=

∑

k=−∞

∞

h[k ]e

−

j ω k

Odpowiedź częstotliwościowa

●

Odpowiedź częstotliwościowa jest w ogólności
zespoloną funkcją częstości ω, zatem:

●

Lub w postaci wykładniczej:

H

(

e

j ω

)

=

H

ℜ

(

e

j ω

)

+

j H

ℑ

(

e

j ω

)

H

(

e

j ω

)

=

∣

H

(

e

j ω

)

∣

e

j θ(ω)

Odpowiedź amplitudowa i fazowa

●

Odpowiedź amplitudowa (magnitude
response) układu LTI to moduł odpowiedzi
częstotliwościowej:

●

Odpowiedź fazowa (phase response) to kąt
fazowy odpowiedzi częstotliwościowej:

∣

H

(

e

j ω

)

∣

=

√

H

ℜ

2

(

e

j ω

)+

H

ℑ

2

(

e

j ω

)

θ(ω)=

atan

(

H

ℑ

(

e

j ω

)

H

ℜ

(

e

j ω

)

)

Wzmocnienie układu

●

Do celów projektowych często łatwiej
posługiwać się odpowiedzią amplitudową
układu wyrażoną w [dB]:

●

Funkcja G opisuje wzmocnienie układu (gain
function).

●

Funkcja: A = -G opisuje tłumienie układu
(attenuation function)

G

(

ω

)

=

20 log

10

∣

H (e

j ω

)

∣

Opis układów LTI w dziedzinie

częstości

●

Niech dane są sygnały z nieciągłym czasem:
x[n] (pobudzenie) oraz y[n] (odpowiedź układu
LTI), oraz ich transformaty dtft.

●

Ponieważ odpowiedź układu w dziedzinie
czasu jest splotem:

y [n]= x [n]⊗h[n]

●

Odpowiedź układu w dziedzinie częstości jest
iloczynem transformat dtft

:

Y

(

e

j ω

)

=

F

(

y [n]

)

=

X

(

e

j ω

)

⋅

H

(

e

j ω

)

Opis układów LTI w dziedzinie

częstości

●

Wynika stąd, że:

●

Odpowiedź częstotliwościowa wynosi więc:

Y

(

e

j ω

)

=

X

(

e

j ω

)

⋅

H

(

e

j ω

)

H

(

e

j ω

)

=

Y

(

e

j ω

)

X

(

e

j ω

)

Odpowiedź częstotliwościowa

układu FIR

●

Odpowiedź układów FIR w dziedzinie czasu
ma postać:

●

Odpowiedź częstotliwościowa ma wówczas
postać:

y [n]=

∑

k=N

1

N

2

h[k ] x [n−k ]

H

(

e

j ω

)

=

∑

k=N

1

N

2

h[ k ]e

−

j ω k

Odpowiedź częstotliwościowa

układu IIR

●

Odpowiedź układów IIR w dziedzinie czasu
ma postać:

●

W dziedzinie częstości otrzymujemy wówczas:

∑

k=0

N

a

k

y [n−k ]=

∑

k=0

M

b

k

x [n−k ]

∑

k=0

N

a

k

e

−

j ω k

Y (e

j ω

)=

∑

k=0

M

b

k

e

−

j ω k

X (e

j ω

)

Odpowiedź częstotliwościowa

układu IIR

●

Ostatecznie odpowiedź układów IIR w
dziedzinie częstości jest funkcją wymierną:

H (e

j ω

)=

Y (e

j ω

)

X (e

j ω

)

=

∑

k=0

M

b

k

e

−

j ω k

∑

k=0

N

a

k

e

−

j ω k

Odpowiedź przejściowa układów LTI

●

Odpowiedź układu LTI opisywanego LCCDE
składa się z dwóch części: rozwiązania
jednorodnego y

c

[n] oraz szczególnego y

p

[n].

●

Odpowiedź jednorodna jest wielomianem
postaci:

gdzie: λ

k

są pierwiastkami wielomianu

charakterystycznego

y

c

[

n]=

∑

k=1

N

α

k

λ

k

n

Odpowiedź przejściowa układu LTI

●

Aby układ był stabilny, wszystkie pierwiastki
wielomianu charakterystycznego muszą
spełniać warunek:

Sprawia on, że y

c

[n] zanika z czasem do zera.

●

Rozwiązanie jednorodne jest także nazywane
odpowiedzią przejściową (transient
response) układu LTI.

∣

λ

k

∣

<

1, k =1, 2, ... N

Odpowiedź przejściowa a

stacjonarna układów LTI

●

Odpowiedź układu LTI na pobudzenie sygnałem
przyczynowym (n > n

0

) w postaci sygnału

sinusoidalnego z czasem dyskretnym o stałej
amplitudzie będzie składać się z dwóch części:

●

Odpowiedzi stacjonarnej (steady-state
response), będącej sygnałem sinusoidalnym o
stałej amplitudzie i tej samej częstości, co
pobudzenie

●

Odpowiedzi przejściowej (transient response),
będącej sygnałem zanikającym do zera po
czasie n

1

> n

0

.

Odpowiedź stacjonarna

●

Niech układ LTI jest pobudzany sygnałem
obustronnym:

●

Wówczas odpowiedź układu ma postać:

x [n]= A cos(ω

0

n)

y [n]= A

∣

H (e

j ω

0

)

∣

cos(ω

0

n+θ(ω

0

))

y [n]= A

∣

H (e

j 0

)

∣

●

Stąd, odpowiedź stacjonarna ma postać:

Odpowiedź stacjonarna

●

Niech układ jest pobudzany sygnałem
przyczynowym, wykładniczym postaci:

●

Odpowiedź stacjonarna ma wówczas postać:

●

Odpowiedź przejściowa ma z kolei postać:

x [n]=e

j ω n

μ [

n]

y

st

[

n]=H (e

j ω

)

e

j ω n

y

tr

[

n]=−

(

∑

k =n+1

∞

h[k ]e

−

j ω k

)

e

j ω n

Filtrowanie sygnałów

●

Podstawowym zadaniem układów LTI jest
filtrowanie sygnałów, czyli selektywne
przenoszenie różnych składowych
częstotliwościowych sygnału pobudzającego.

●

Idea filtracji zasadza się na doborze
współczynników odpowiedzi amplitudowej,
odpowiadających składowym sinusoidalnym
występującym w sygnale wejściowym.

Idealny filtr LTI

●

Rozważmy idealny filtr LTI z dyskretnym
czasem opisywany odpowiedzią amplitudową
postaci:

●

Niech pobudzenie ma postać:

∣

H (e

j ω

)

∣

=

{

1⇔0≤∣ω∣≤ω

c

0⇔ω

c

≤∣ω∣≤π

x [n]= A cos(ω

1

n)+ B cos(ω

2

n)

Idealny filtr LTI

●

Z uwagi na liniowość, odpowiedź układu ma
postać:

●

Korzystając ze znajomości odpowiedzi
amplitudowej, dostajemy ostatecznie:

Układ zachowuje się jak filtr dolnoprzepustowy

y [n]= A

∣

H (e

j ω

1

)

∣

cos(ω

1

n+θ(ω

1

))+

...

B

∣

H (e

j ω

2

)

∣

cos(ω

2

n+θ(ω

2

))

y [n]≈ A

∣

H (e

j ω

1

)

∣

cos(ω

1

n+θ(ω

1

))

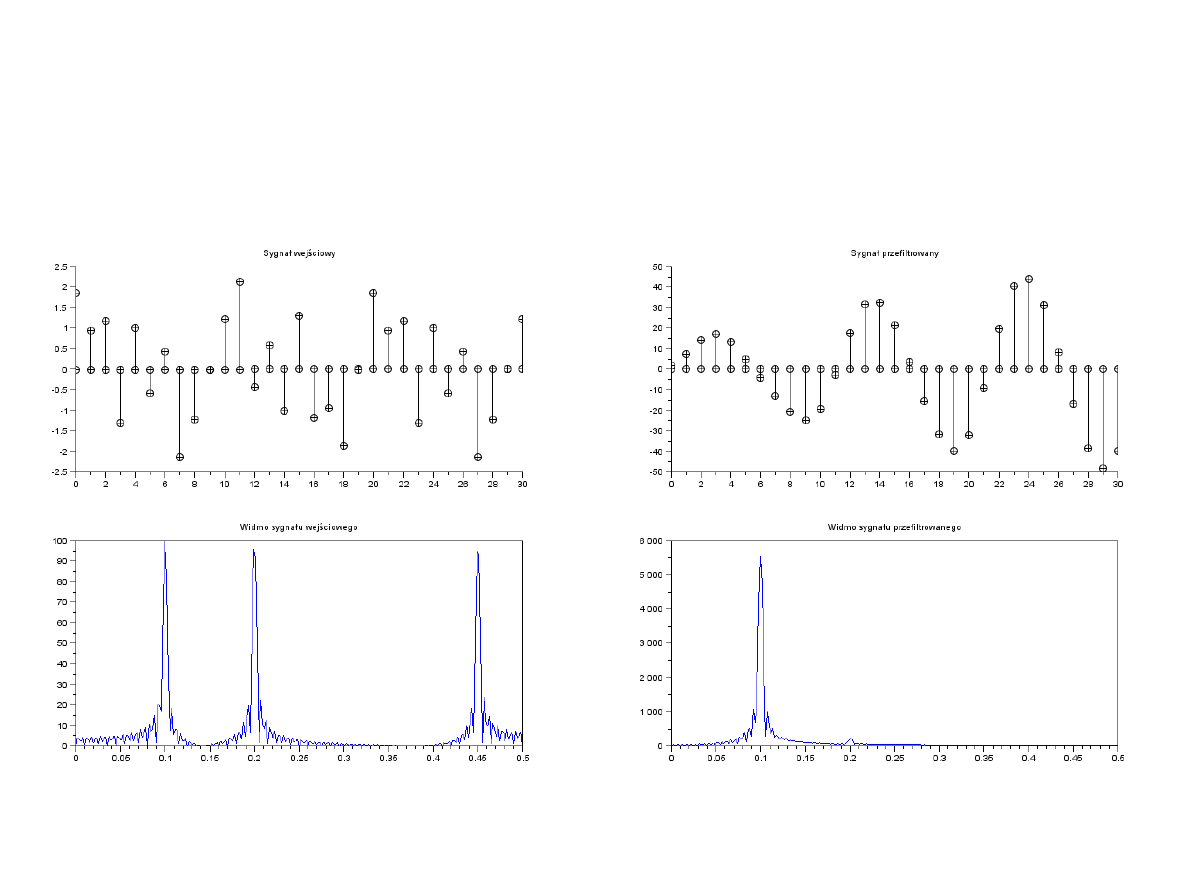
Filtrowanie sygnałów

Projekt prostego filtra FIR (HP)

●

Załóżmy, że dany jest sygnał sinusoidalny
postaci:

●

Szukamy współczynników odpowiedzi
impulsowej symetrycznego, 3-punktowego
filtra FIR o charakterystyce
dolnoprzepustowej:

x [n]=cos(0.1 n)+cos(0.4 n)

h[n]=[α

↑ 1

,α

2,

α

1

]

Projekt prostego filtra FIR (HP)

●

Należy wybrać takie współczynniki odpowiedzi
impulsowej h[n], aby odpowiedź układu na
zadane pobudzenie zawierała wyłącznie
składową o częstości ω

2

=0.4

●

Odpowiedź częstotliwościową można wyrazić
jako:

●

Odpowiedź amplitudowa ma postać:

H (e

j ω

)=

(

2 α

1

cos(ω)+α

2

)

e

−

j ω

∣

H (e

j ω

)

∣

=

2 α

1

cos(ω)+α

2

Projekt prostego filtra FIR (HP)

●

Znając współczynniki odpowiedzi
amplitudowej:

●

Rozwiązujemy układ równań:

●

Którego rozwiązaniem jest:

∣

H (e

j ω

)

∣

=

{

0⇔ω=0.1

1⇔ω=0.4

{

2α

1

cos(0.1)+α

2

=

0

2 α

1

cos(0.4)+α

2

=

1

α

1

≈−

6.762 , α

2

≈

13.456

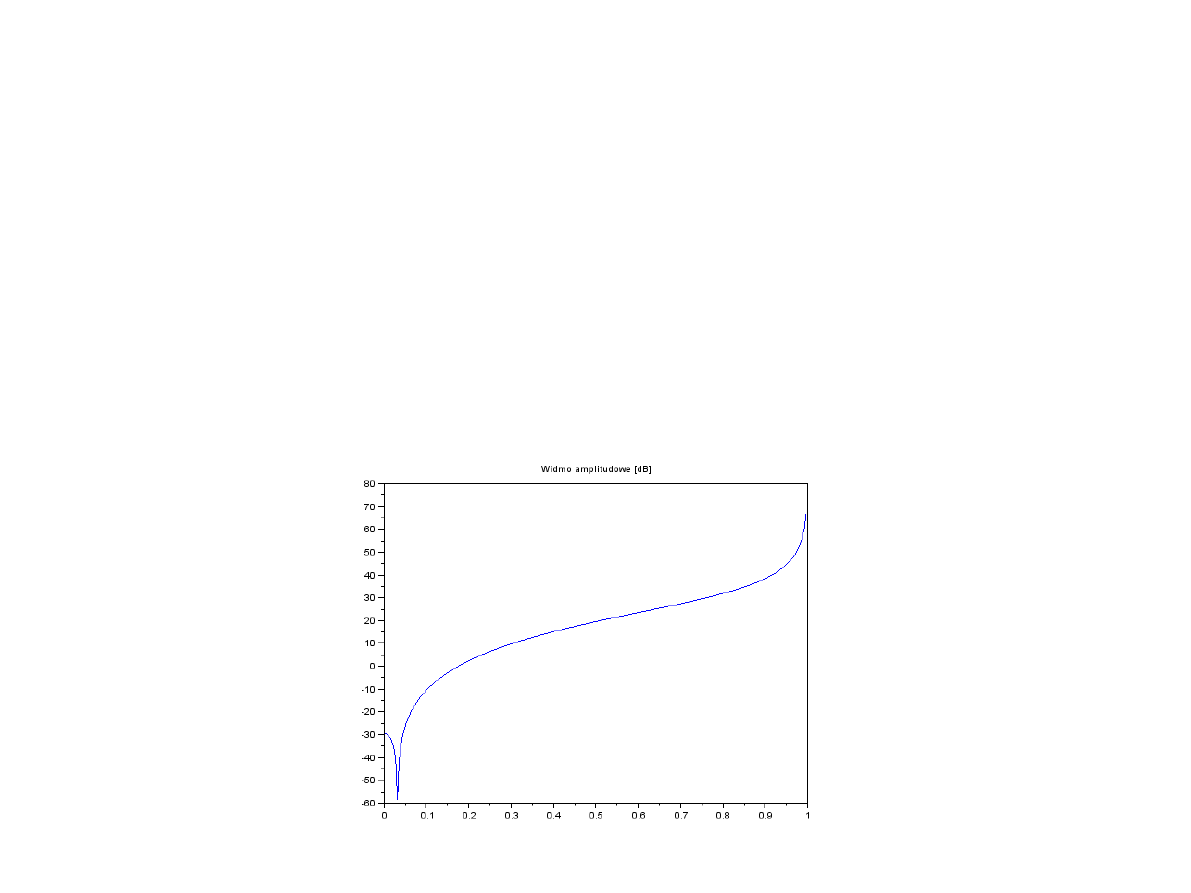
Projekt prostego filtra FIR (HP)

●

Ostatecznie, odpowiedź impulsowa ma
postać:

h[n]=[−6.762

↑

,13.456 ,−6.762]

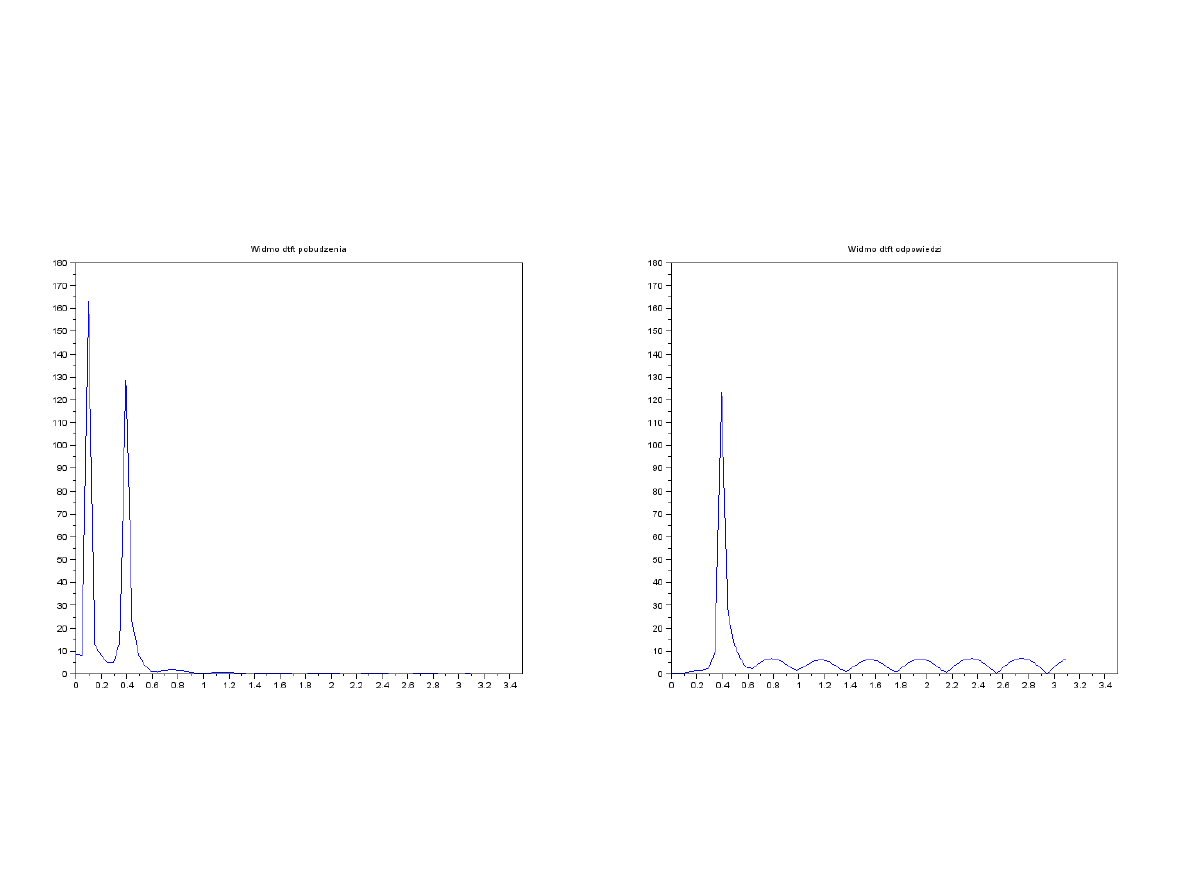
Filtracja HP sygnału

Projekt prostego filtra FIR (LP)

●

Postępując analogicznie zaprojektujmy 3-
punktowy, symetryczny filtr FIR
dolnoprzepustowy LP.

●

Odpowiednie współczynniki odpowiedzi
impulsowej wynoszą:

α

1

≈

6.762 , α

2

≈−

12.456

h[n]=[6.762

↑

,−12.456 , 6.762]

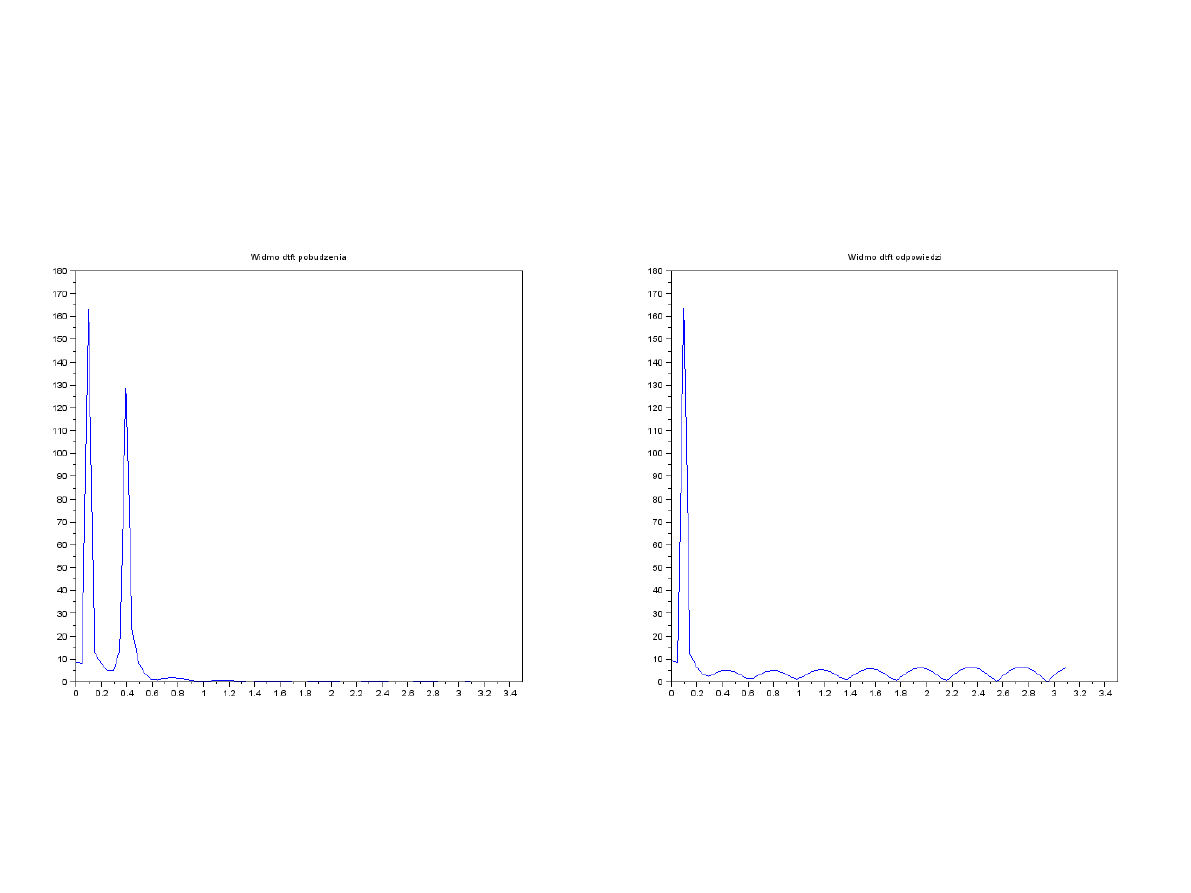
Filtracja LP sygnału