13. WSTĘP DO TEORII PLASTYCZNOŚCI

1

13.



13. WSTĘP DO TEORII PLASTYCZNOŚCI

13.1. TEORIA PLASTYCZNOŚCI

Teoria plastyczności zajmuje się analizą stanów naprężeń ciał, w których w wyniku działania

obciążeń powstają trwałe odkształcenia - DEFORMACJE.

CECHA PLASTYCZNOŚCI – trwałe deformacje po usunięciu przyczyn. Przykładem może być

rozciąganie próbki w jednoosiowym stanie naprężeń.

13.2. MODELE CIAŁA SPRĘŻYSTO PLASTYCZNEGO

CIAŁO SPRĘŻYSTO – PLASTYCZNE to ciało, dla którego zależność odkształceń od naprężeń jest

zgodna z jednym z poniższych wykresów.

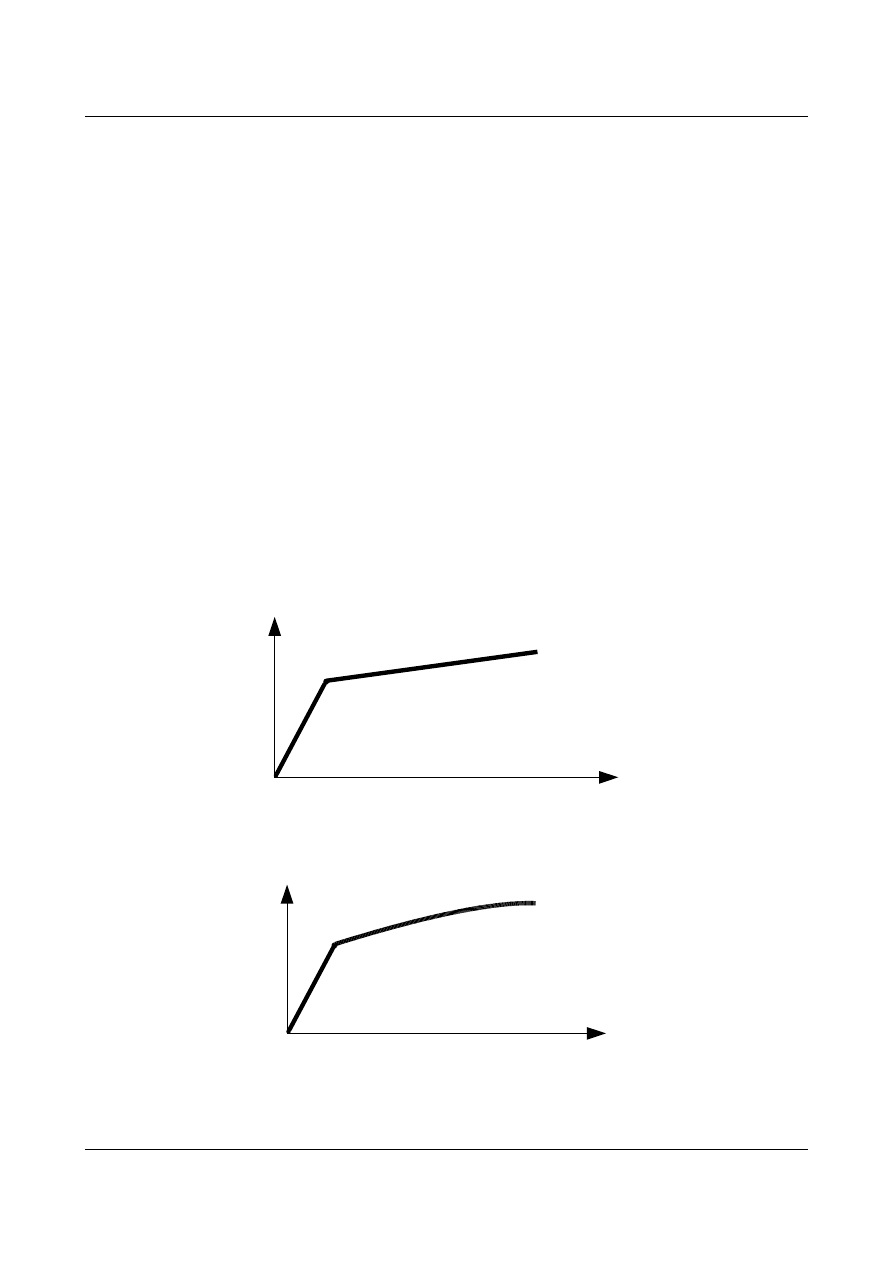
a) model ciała sprężysto - plastycznego ze wzmocnieniem liniowym (Rys. 13.1.)

i nieliniowym (Rys. 13.2.)

Rys. 13.1. Model ciała sprężysto - plastycznego ze wzmocnieniem liniowym

Rys. 13.2. Model ciała sprężysto - plastycznego ze wzmocnieniem liniowym

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

E





E

13. WSTĘP DO TEORII PLASTYCZNOŚCI

2

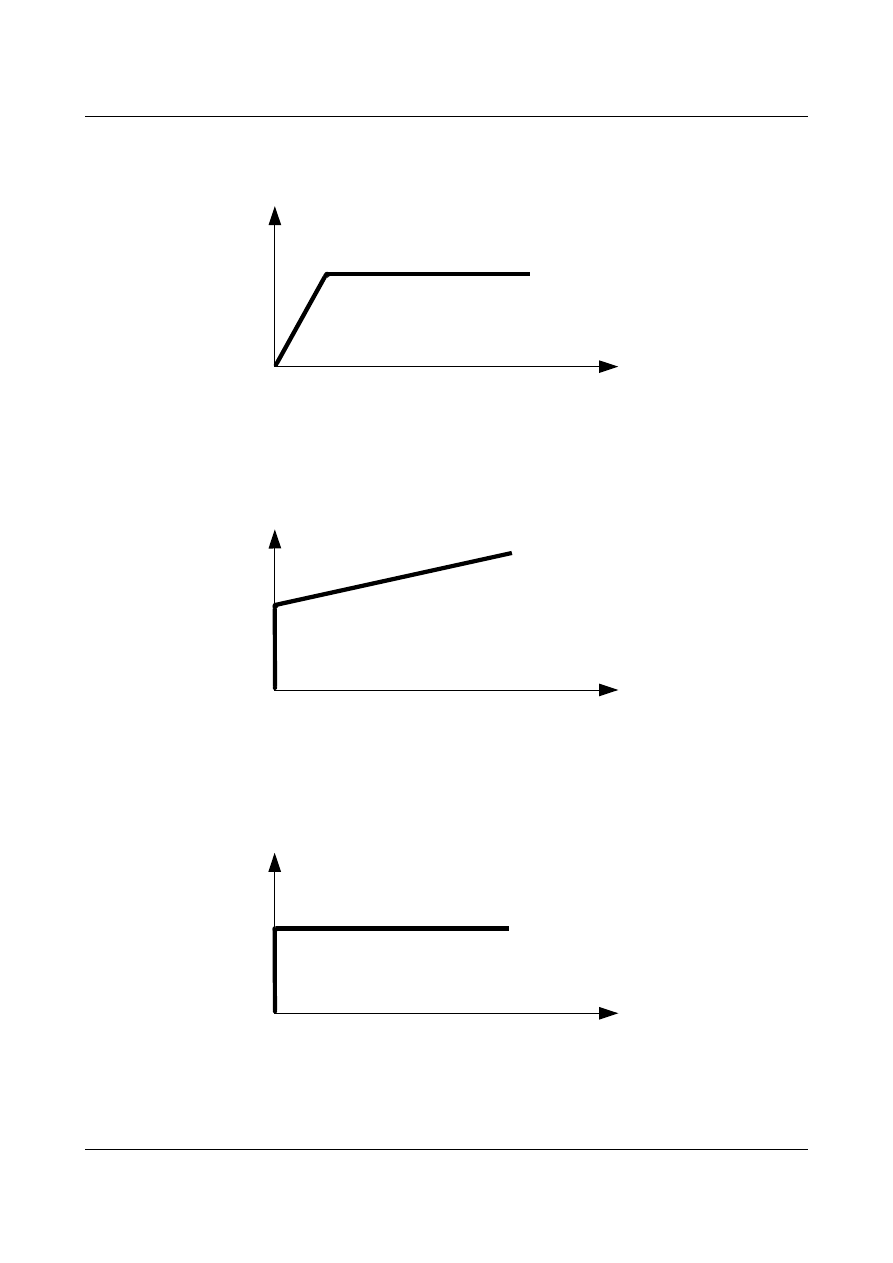
b) model ciała sprężysto – idealnie – plastycznego (Rys. 13.3.)

Rys. 13.3. Model ciała sprężysto – idealnie – plastycznego

c) model ciała sztywno - plastycznego ze wzmocnieniem (Rys. 13.4.)

Rys. 13.4. Model ciała sztywno - plastycznego ze wzmocnieniem

d) model ciała sztywno – idealnie – plastycznego (Rys. 13.5.)

Rys. 13.5. Model ciała sztywno – idealnie – plastycznego

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater



E

E



E



13. WSTĘP DO TEORII PLASTYCZNOŚCI

3

13.3. HIPOTEZY WYTRZYMAŁOŚCIOWE

13.3.1. HIPOTEZA HMH (HUBERA – MISESA – HENCKY'EGO)

Huber

–

zaobserwował, że nie jest możliwe przejście w stan plastyczny ciał z odkształceniami
objętościowymi.

–

musi nastąpić zmiana postaciowa a nie objętościowa, co świadczy o tym, że decyduje
energia typu postaciowego

“Materiał przechodzi w stan plastyczny wtedy gdy energia odkształcenia postaciowego osiąga

wartość krytyczną właściwą danemu materiałowi lecz niezależną od rodzaju stanu naprężeń”

=

1

6 ⋅G

⋅

0

(13.1)

s

o -

intensywność dewiatora naprężeń

G – moduł Kirchoff'a

s

i

=



3
2

⋅



s

jk

⋅s

jk

s

i

=

0

(13.2)

s

jk

– elementy dewiatora naprężeń

Wzór na naprężenia zredukowane w punkcie:



0

=

1



2

⋅





11

−

22



2



22

−

33



2



33

−

11



2

6 

12

2



23

2



31

2



(13.3)

Naprężenia w punkcie w głównym stanie naprężeń:



0

=

1



2

⋅





I

−

II



2



II

−

III



2



III

−

I



2

(13.4)

Naprężenia w punkcie w jednoosiowym stanie naprężeń:



0

=

1



2

⋅



2



I

2

=

I

(13.5)

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

13. WSTĘP DO TEORII PLASTYCZNOŚCI

4

Wartość tensora, dla którego energia sprężysta osiągnie taką wartość, dla której ciało przejdzie w

stan plastyczny można przedstawić wykorzystując stan naprężenia.

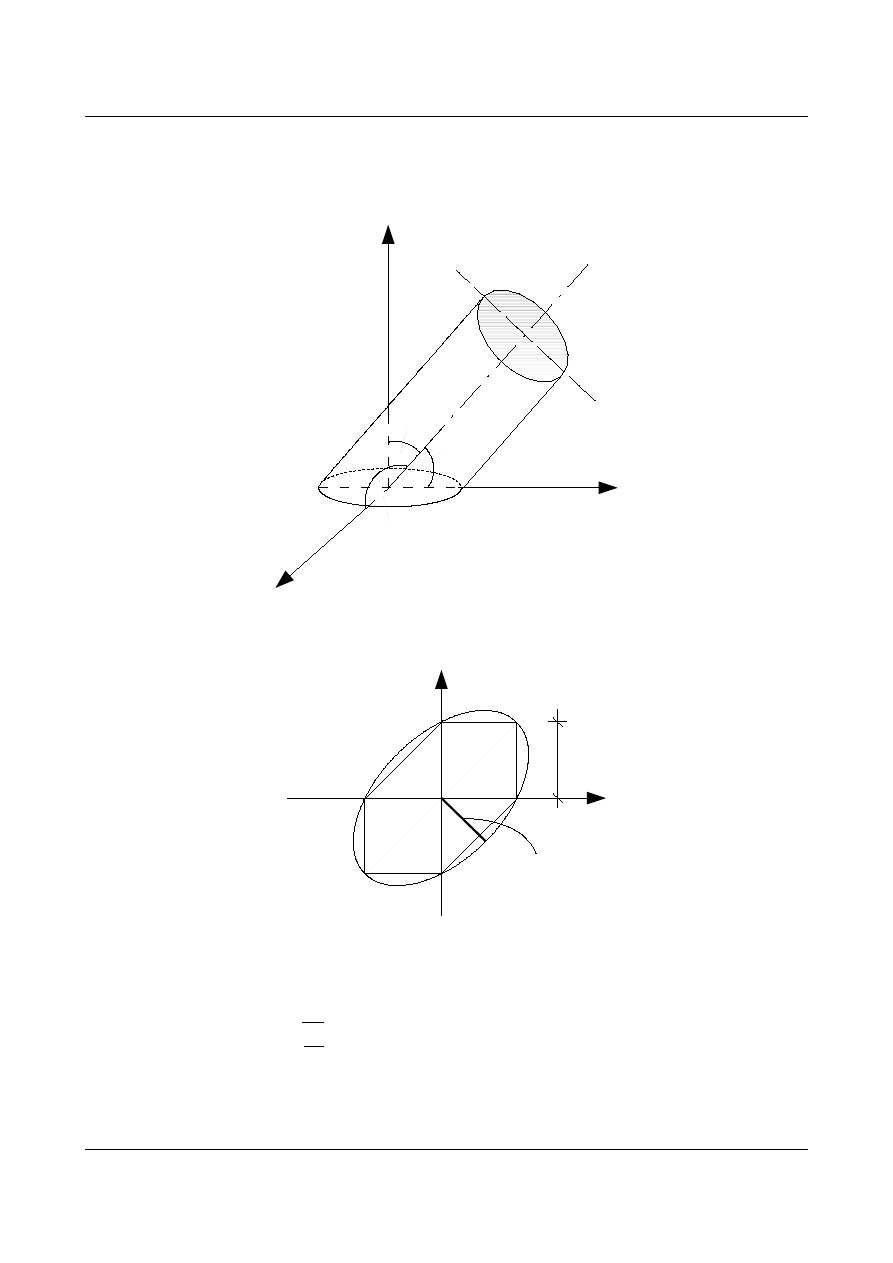
Rys. 13.6. Walec

Rys. 13.7. Płaski stan naprężeń

Naprężenie w głównym stanie naprężeń, gdzie występują tylko trzy zmienne można przedstawić w

trójosiowej przestrzeni naprężeń głównych. Obrazem geometrycznym tego równania jest walec kołowy

(Rys. 13.6.) o promieniu

r

=



2

3

⋅

0

. Oś walca tworzy ten sam kąt z każdą osią układu współrzędnych



I

,



II

,



III

. Jest to tzw. oś aksjatorów.

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater



I



III



II







max

s

2

s

1

13. WSTĘP DO TEORII PLASTYCZNOŚCI

5

3 cos

2

=1

arccos





3

3

=54,74

A

(13.6)

Walec jest geometrycznym obrazem naprężeń:

–

współrzędne punktów wypełniających wnętrze walca odpowiadają sprężystym stanom
naprężenia.

–

Uplastycznienie zachodzi dla każdego stanu naprężenia odpowiadającego punktom
leżącym na pobocznice walca.

13.3.2. HIPOTEZA TRESKI

Podstawą do sformułowania tego warunku była obserwacja linii Lüdersa, które powstają w

początkowej fazie uplastyczniania próbki rozciąganej. Ponieważ kąt nachylenia tych linii do osi próbki jest
bliski 45

°

i odpowiada płaszczyznom maksymalnych naprężeń stycznych co oznacza, że:

–

tam musi nastąpić zerwanie więzi w wyniku działania sił stycznych

–

tam będzie poślizg kryształów

„Materiał przechodzi w danym punkcie w stan plastyczny wówczas, gdy maksymalne naprężenie

styczne osiągnie pewną graniczną wartość, charakterystyczną dla tego materiału”



ekst

=

{



1

=

∣

2

−

3

∣

2



2

=

∣

1

−

3

∣

2



3

=

∣

1

−

2

∣

2

(13.7)

Podobnie jak w przypadku teorii HMH także i tutaj można skorzystać z jednoosiowego stanu

naprężenia:



2

=

3

=0



1

≠0



ekst

=



0

2

(13.8)

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

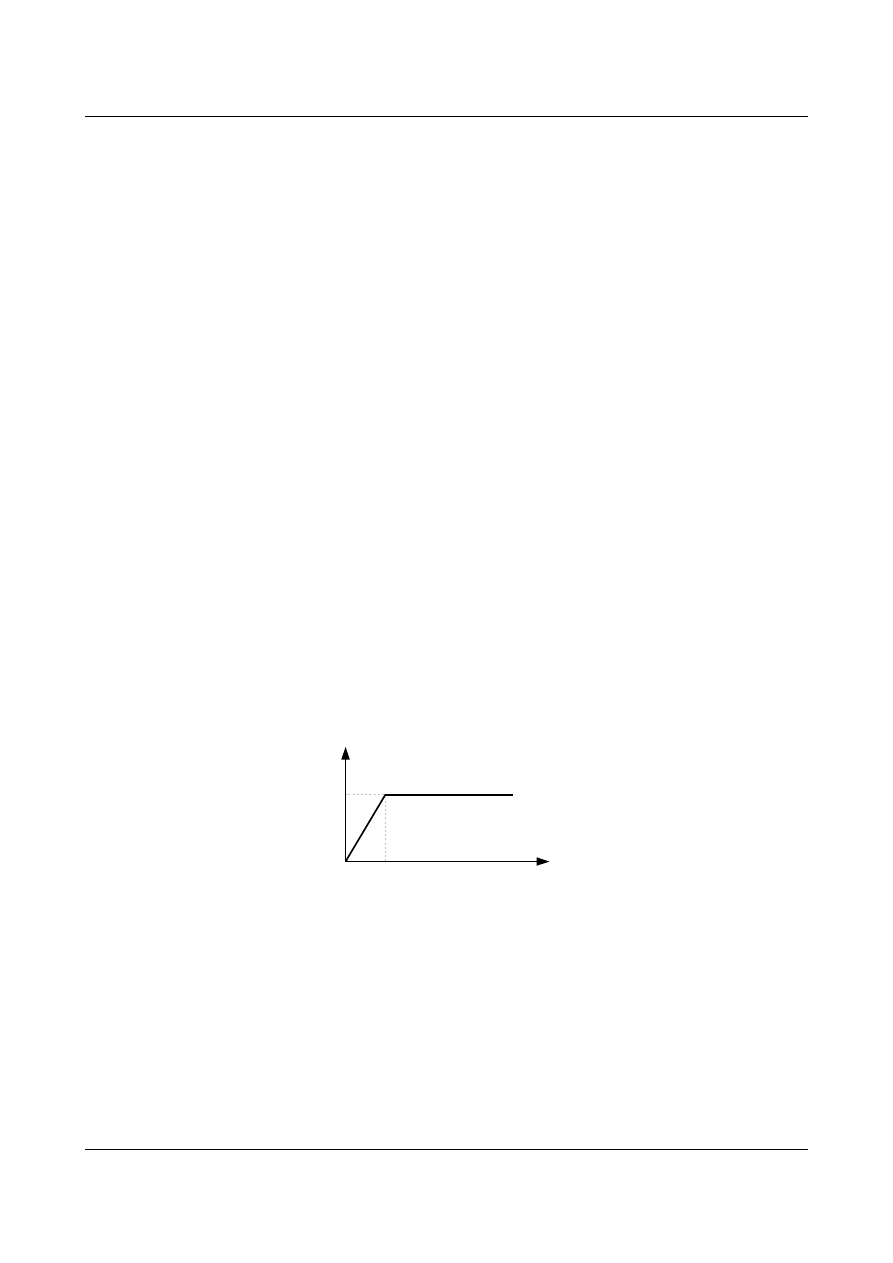
13. WSTĘP DO TEORII PLASTYCZNOŚCI

6

W przypadku teorii Treski geometrycznym obrazem będzie graniastosłup foremny 0 podstawie

sześciokąta, który jest wpisany w walec Hubera. Opisują go zależności:

∣

2

−

3

∣∧

0

∣

1

−

3

∣∧

0

∣

1

−

2

∣∧

0

(13.9)

Graniastosłup jest geometrycznym obrazem naprężeń:

–

współrzędne punktów wypełniających wnętrze graniastosłupa odpowiadają sprężystym
stanom naprężenia

–

uplastycznienie zachodzi dla każdego stanu naprężenia odpowiadającego punktom
leżącym na pobocznicy graniastosłupa

13.4. SPRĘŻYSTO PLASTYCZNE ZGINANIE BELKI

Założenia:

–

belka jest swobodnie podparta

–

rozpatrujemy przypadek czystego zginania

–

model ciała: sprężysto – idealnie – plastyczny (Rys. 13.8.)

–

Przekrój belki: dowolny przekrój pryzmatyczny (Rys. 13.9.)

Rys. 13.8. Model ciała sprężysto idealnie plastyczny

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater







0



0

13. WSTĘP DO TEORII PLASTYCZNOŚCI

7

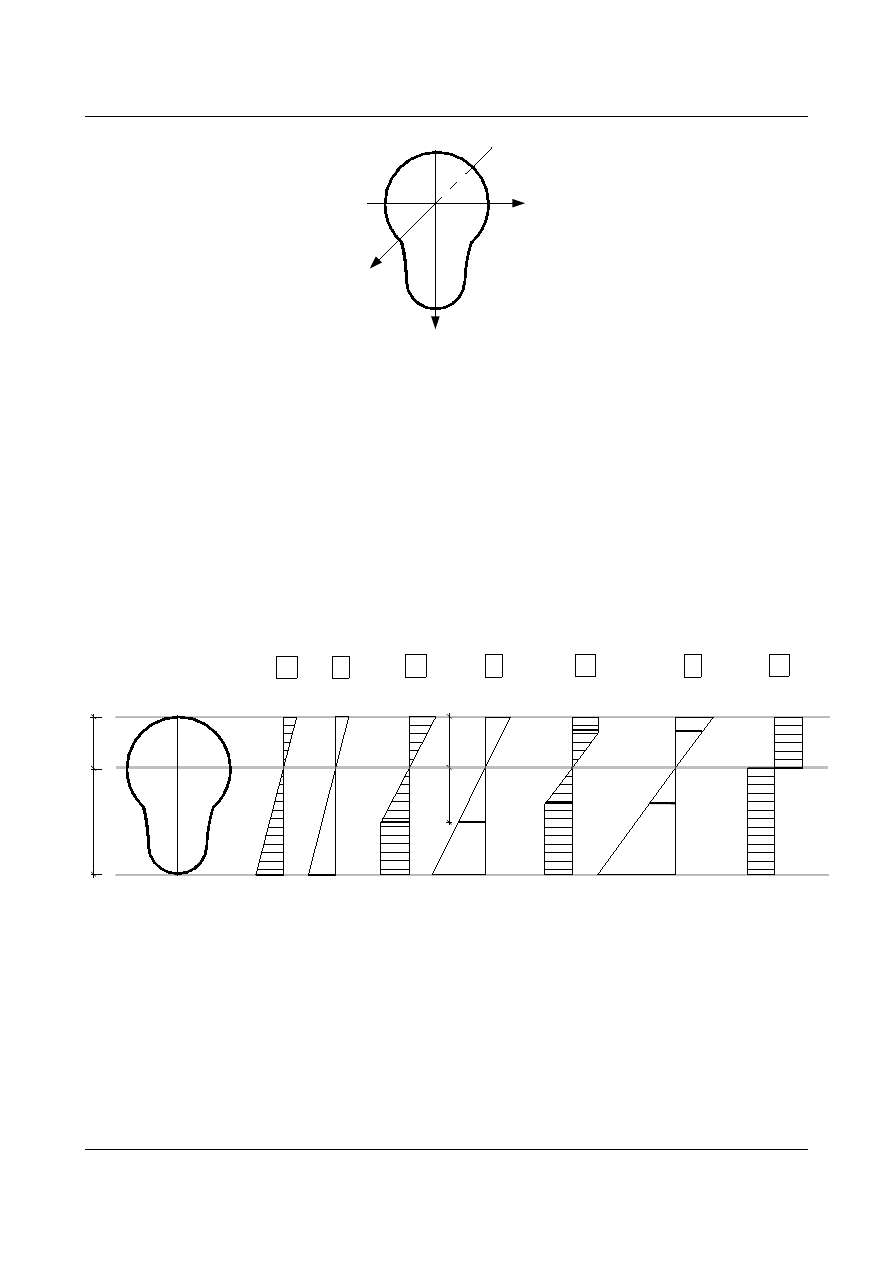
Rys. 13.9. Przekrój pryzmatyczny

Warunki równowagi

1) Siła normalna

N

=

∫

A



x

dA

=0

(13.10)

2) Moment zginający

M

=constans

M

=

∫

A



x

⋅y dA

(13.11)

Rys. 13.10. Rozkład naprężeń i odkształceń

Stan A (patrz Rys. 13.10.)

Naprężenia w dowolnym punkcie:

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

h

g

h

d

A

g















A

d



0



0



0



0



0



0



0

h

g

h

g



0



0



0



0



0

Stan A

Stan B

Stan C

Stan D

x

z

y

13. WSTĘP DO TEORII PLASTYCZNOŚCI

8



x

=

M

I

x

⋅y

(13.12)

Naprężenia w skrajnym włóknie dolnym:



o

=

M

I

x

⋅h

d

(13.13)

Odkształcenia

=⋅



0

E

(13.14)

Stan B (patrz Rys. 13.10.)

Naprężenia w strefie sprężystej:



x

=E⋅=E⋅

1



⋅y

(13.15)

Z 1) warunku równowagi:

∫

−h

g

h

g



x

dA



∫

h

g

h

d



0

dA

=0

(13.16)

Po podstawieniu

s

x

, dA i wyciągnięciu przed całkę wielkości stałych otrzymamy:

E

⋅

1



∫

−h

g

h

g

y

⋅b ydy

0

⋅

∫

h

g

h

d

b

 ydy=0

(13.17)

E



S

s



0

⋅A

p

=0

(13.18)

Gdzie:

S

s

– moment statyczny części przekroju w zakresie naprężeń sprężystych

A

p

– pole części przekroju w zakresie naprężeń plastycznych

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

13. WSTĘP DO TEORII PLASTYCZNOŚCI

9

Z 2) warunku równowagi:

∫

−h

g

h

g



x

⋅y dA

∫

h

g

h

d



0

⋅ydA=M

(13.19)

Po podstawieniu

s

x

, dA i wyciągnięciu przed całkę wielkości stałych otrzymamy:

E

⋅

1



∫

−h

g

h

g

y

2

⋅b ydy

0

⋅

∫

h

g

h

d

y

⋅b ydy=M

(13.20)

E



I

s



0

⋅S

p

=M

(13.21)

Gdzie:

I

s

– moment bezwładności części przekroju w zakresie naprężeń sprężystych

S

p

– moment statyczny części przekroju w zakresie naprężeń plastycznych

Stan C (patrz Rys. 13.10.)

Stan ten jest podobny do stanu B, zwiększa się tylko zakres strefy plastycznej.

Analizując warunki równowagi otrzymamy takie same zależności:

E



S

s



0

⋅A

p

=0

(13.22)

E



I

s



0

⋅S

p

=M

(#.23)

Stan D (patrz Rys. 13.10.)

Z 1) warunku równowagi:

∫

h

g

h

d



0

dA

=0

(13.24)

Po podstawieniu dA i wyciągnięciu przed całkę wielkości stałych otrzymamy:

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

13. WSTĘP DO TEORII PLASTYCZNOŚCI

10



0

⋅

∫

h

g

h

d

b

 ydy=0

(13.25)



0

⋅A

p

=0

(13.26)

Z 2) warunku równowagi:

∫

h

g

h

d



0

⋅ydA=M

(13.27)

Po podstawieniu dA i wyciągnięciu przed całkę wielkości stałych otrzymamy:



0

⋅

∫

h

g

h

d

y

⋅b ydy=M

(13.28)



0

⋅S

p

=M

(13.29)

Środek ciężkości dzieli przekrój na dwie części o takiej samej wartości momentu statycznego. Pola

powierzchni tych dwóch części nie muszą być takie same (A

g

≠ A

d

)

, zatem warunek 1)



0

⋅A

p

=0

nie

będzie spełniony.

Nastąpi przesunięcie osi ciężkości przekroju.
S

p

z drugiego warunku musi być policzone względem nowego położenia osi.

Wiemy, że



0

=

M
S

p

(13.30)

Oraz, że



max

=

M
W

(13.31)

Dla przekroju idealnie plastycznego (Rys. 13.10. - stan D)



0

=W

pl

(13.32)

Gdzie: W

pl

– wskaźnik oporu plastycznego

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

13. WSTĘP DO TEORII PLASTYCZNOŚCI

11

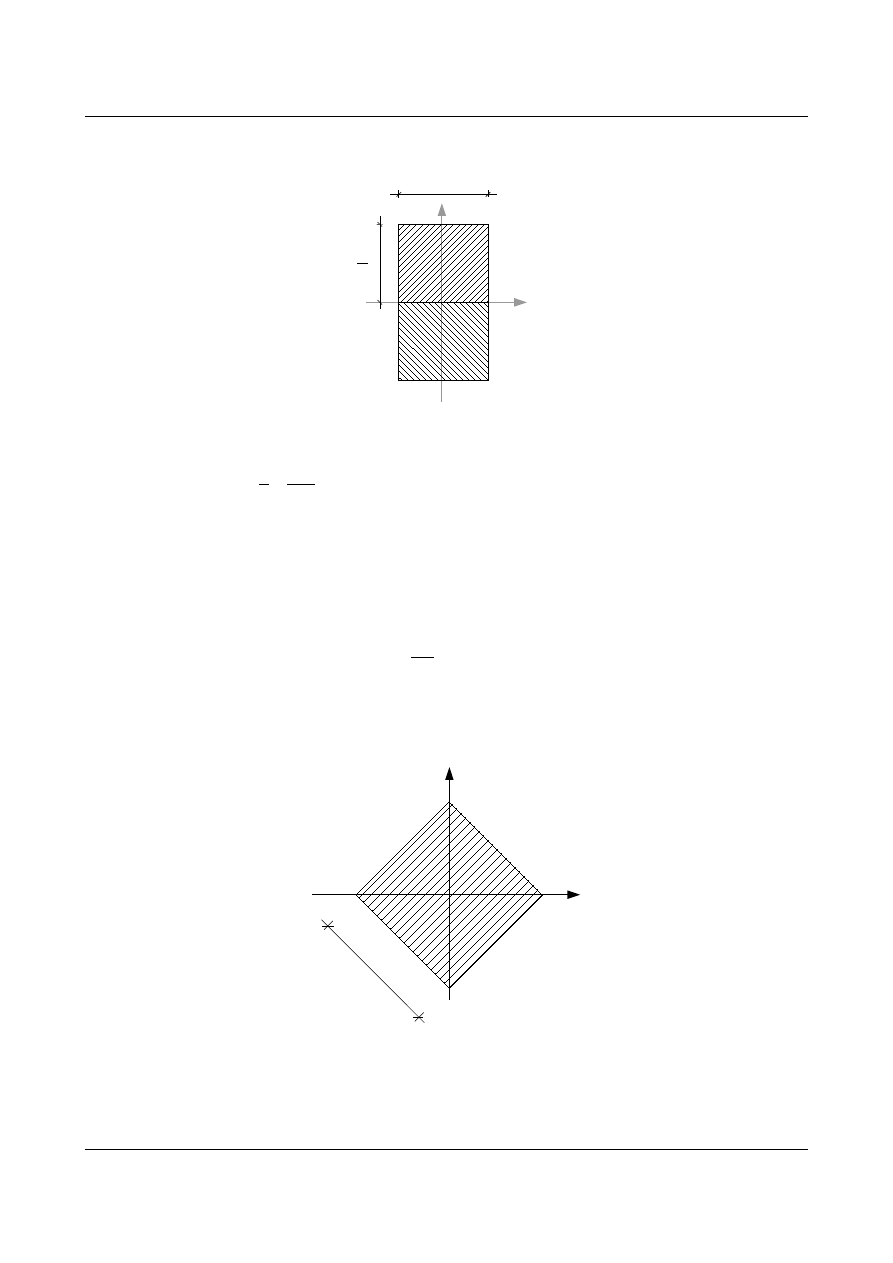
Dla przekroju prostokątnego:

Rys. 13.11. Przekrój prostokątny

W

pl

=2 ⋅[b⋅h⋅0,5⋅

h
4

]=

b

⋅h

2

4

Dla prętów o innych przekrojach geometrycznych W

pl

wynosi:

–

dla przekroju kołowego:

W

pl

=

4 r

3

3

(13.33)

–

dla przekroju w kształcie rombu:

Rys. 13.12. Przekrój w kształcie rombu

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

a

b

h
2

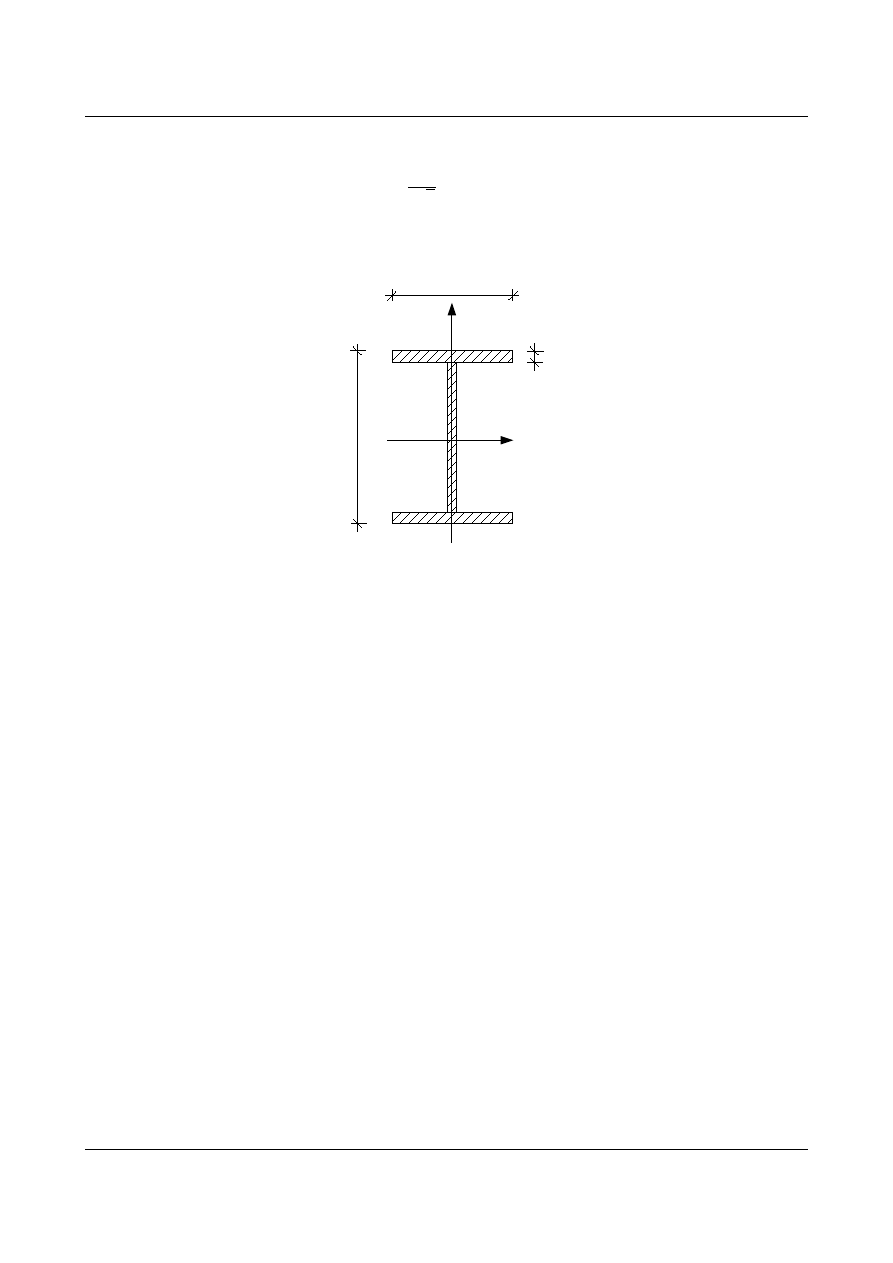
13. WSTĘP DO TEORII PLASTYCZNOŚCI

12

W

pl

=

a

3

3



2

(13.34)

–

dla przekroju teowego:

Rys. 13.13. Przekrój teowy

Pomijamy środnik, co daje nam w rezultacie

W

pl

=t⋅b⋅h

(13.35)

Aściukiewicz P., Baron P., Gawron U., Krzysztoń A., Ratajczak D., Wojciechowski M.

AlmaMater

b

t

h