______________________________________________________________________________________________
Laboratorium Metody Numeryczne w Wymianie Ciepła, Wydział Mechaniczny Energetyki i Lotnictwa, PW
Mirosław Seredyński,
msered@itc.pw.edu.pl
Piotr Łapka,
plapka@itc.pw.edu.pl
Przykład 1: Krzepni
ę
cie w kostce
.
(czyste przewodzenie – brak konwekcji, model liniowy g
s
(T))
Model fizyczny
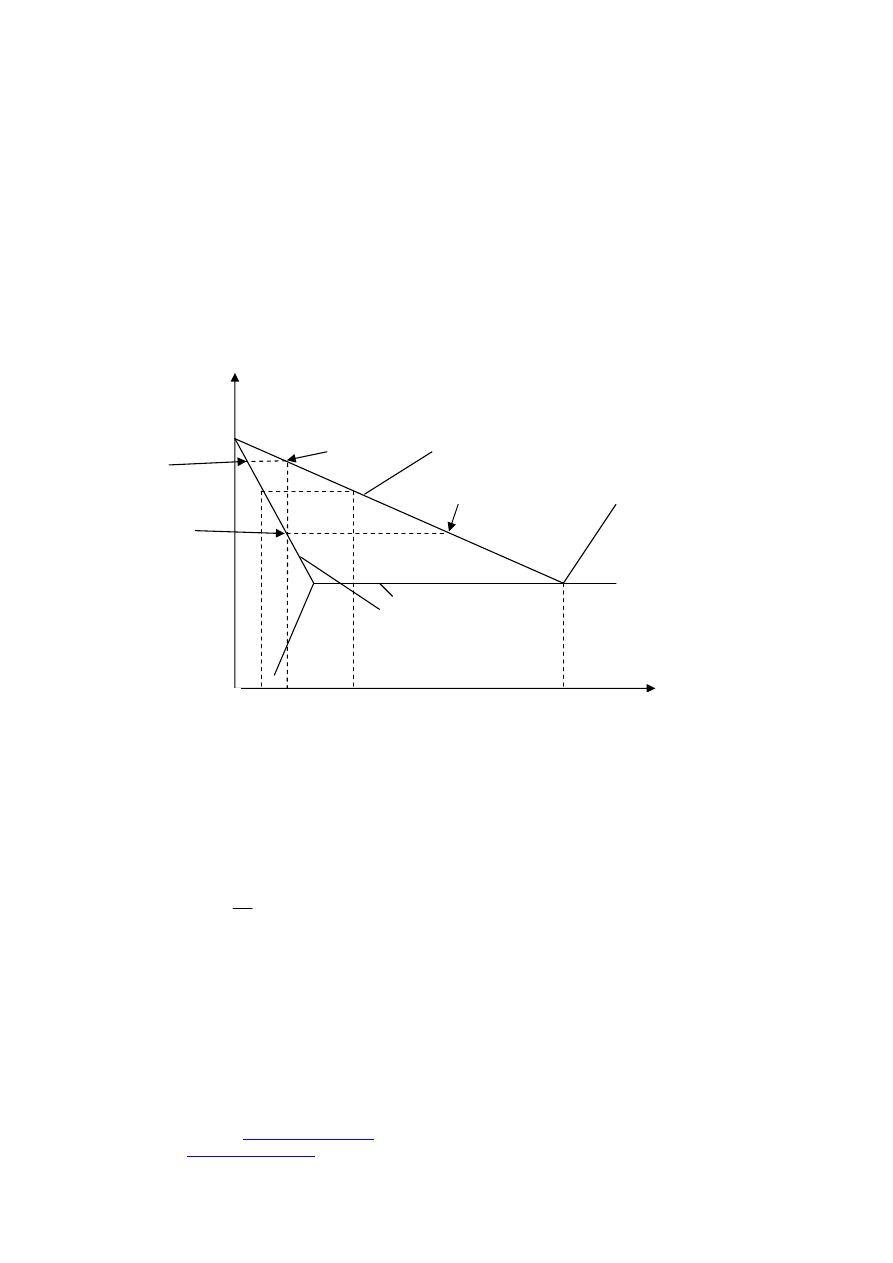
Na rysunku 1 przedstawiony jest fragment wykresu równowagi fazowej dla stopu podwójnego z
eutektyką (pkt. E) w układzie współrzędnych temperatura – stężenie.
Rysunek 1
Wykres równowagi fazowej dla stopu podwójnego z eutektyką. Początkowe stężenie stopu
wynosi C
0
, stężenie odpowiadające eutektyce C
E
, stężenia w fazie stałej i ciekłej odpowiednio C
s
i C
l
.
Faza ciekła jest ograniczona od dołu linią liquidusu, faza stała jest ograniczona od góry linią
solidusu. Na wykresie zostały przedstawione w postaci zlinearyzowanej. W tym przypadku
można przedstawić je w postaci funkcji:
C
k
m
T
T
C
m
T
T
p
l
m
Sol
l
m
Liq
+
=
+
=
gdzie T
m
to temperatura krzepnięcia czystej substancji A, m
l
– współczynnik nachylenia linii
liquidusu, k
p
– współczynnik rozdziału faz, C – stężenie składnika B w fazie ciekłej.
Współczynniki m
l
i k
p
są zdefiniowane następująco:
faza stała
T
0
E
C
S
T
m
C
E
T
E
T
C
T
C
L
C
0
linia
liquidusu
linia
solidusu
100% A
100% B
ciecz
L
1
L
2
S
1
S
2
______________________________________________________________________________________________
Laboratorium Metody Numeryczne w Wymianie Ciepła, Wydział Mechaniczny Energetyki i Lotnictwa, PW
Mirosław Seredyński,
msered@itc.pw.edu.pl
Piotr Łapka,
plapka@itc.pw.edu.pl
s
l
p
E
E
m
l
C
C
k
C
T
T
m
=
−
−
=
Ponieważ występują różne rozpuszczalności składnika B w fazach stałej i ciekłej, na granicy faz
ma miejsce segregacja składnika. Stężenie w fazie ciekłej zmienia się wzdłuż linii L
1
do L
2
,
stężenie w fazie stałej zmienia się wzdłuż linii S
1
do S
2
.
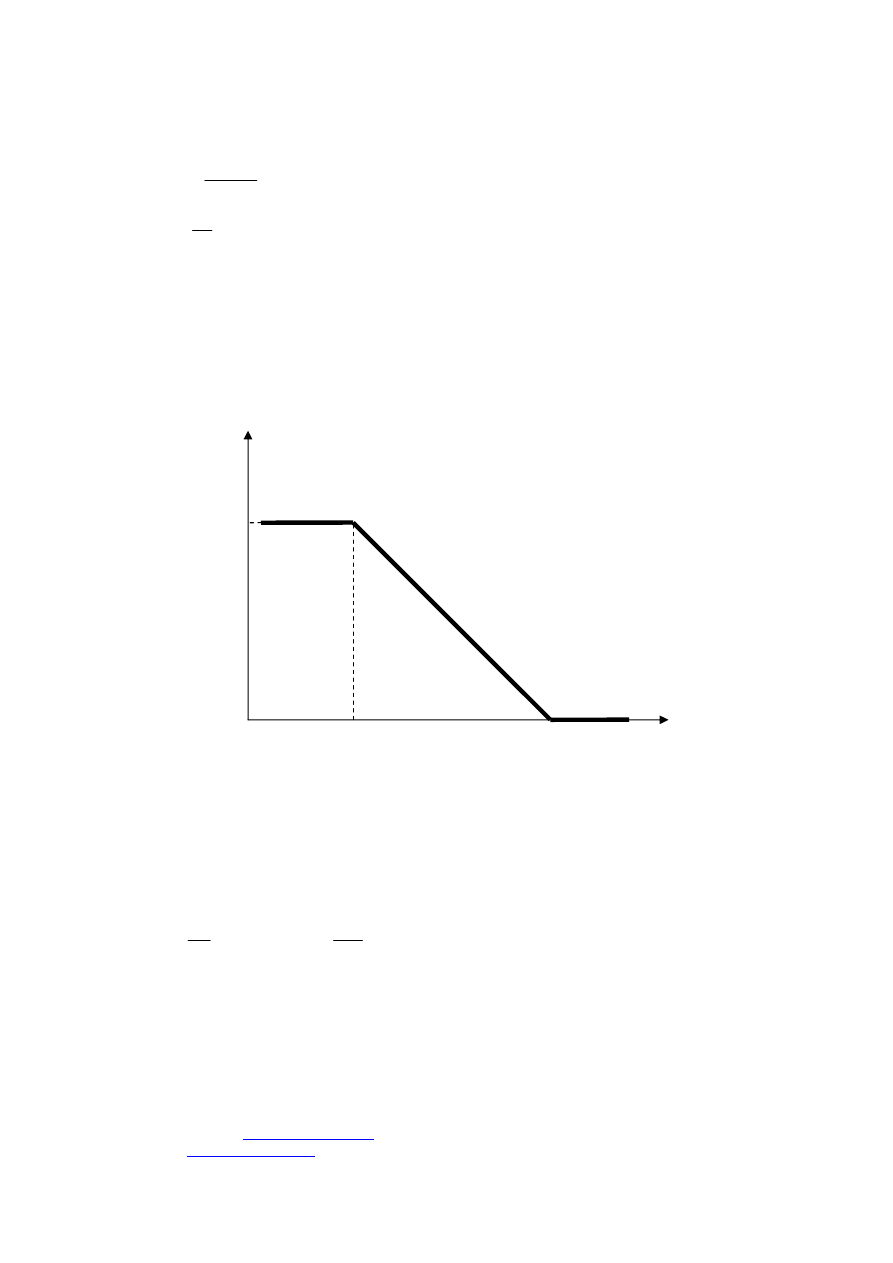
W programie FLUENT istnieje tylko jeden wbudowany model krzepnięcia stopu binarnego,
oparty na założeniu, że udział fazy ciekłej jest funkcją liniową w zakresie pomiędzy temperaturą
solidusu i liquidusu (rys. 2).
Rysunek 2
Zależość udziału fazy stałej od temperatury w modelu krzepnięcia dostępnym w programie
FLUENT.
Model matematyczny
Równanie przewodzenia ciepła, w warunkach braku konwekcji ma postać
(
)
t
g
L
T
k
t
T
c
S
w
∂
∂
+
∇
⋅
∇
=
∂
∂
ρ
ρ
gdzie c
w
– ciepło właściwe, ρ – gęstość, k – współczynnik przewodzenia ciepła, L – ciepło
topnienia, g
S
– udział fazy stałej.
W równaniu tym pojawia się człon źródłowy (drugi po prawej stronie) związany w wydzielaniem
ciepła podczas procesu krzepnięcia. Równanie to uzupełnione jest o zależność łączącą udział fazy
stałej i temperaturę (rys. 2)
g
S
T
T
Liq
(C
0
)
T
Sol
(C
0
)
1
0

______________________________________________________________________________________________
Laboratorium Metody Numeryczne w Wymianie Ciepła, Wydział Mechaniczny Energetyki i Lotnictwa, PW
Mirosław Seredyński,
msered@itc.pw.edu.pl
Piotr Łapka,
plapka@itc.pw.edu.pl
( )
( )
( )
( )
( )
( )
( )
<
<
<
−
−
<
=
T
C
T
dla
C
T
T
C
T
dla
C
T
C
T
T
C
T
C
T
T
dla
g
Liq
Liq
Sol
Sol
Liq
Liq
Sol
S
0
0
0
0
0
0
0
0
1
Warunki brzegowe na ściankach:
•
ś
cianka lewa – α = 1000 W/(m
2
K), T
f
= 300 K
•
ś
cianka dolna – α = 1000 W/(m
2
K), T
f
= 300 K
•
ś
cianka prawa – adiabatyczna
•
ś
cianka górna – adiabatyczna.
Temperatura początkowa wynosi 950 K.
______________________________________________________________________________________________
Laboratorium Metody Numeryczne w Wymianie Ciepła, Wydział Mechaniczny Energetyki i Lotnictwa, PW
Mirosław Seredyński,
msered@itc.pw.edu.pl
Piotr Łapka,
plapka@itc.pw.edu.pl
Obliczenia w programie FLUENT.
1.
Otwarcie programu FLUENT– przez kliknięcie odpowiedniej ikonki na pulpicie.
Uruchomienie programu w wersji 2D, obliczenia prowadzone są w podwójnej precyzji
(wybór wersji 2ddp).
2.
Wczytanie siatki z programu GAMBIT (*.msh)
File → Read → Case
3.
Sprawdzenie siatki
Grid → Check
Wyświetlany jest m. in. minimalna objętość i pole najmniejszej ścianki (muszą być dodatnie)
oraz zakres współrzędnych, jaki zajmuje siatka. Warto w tym miejscu sprawdzić jednostki, w
których wykonana jest siatka i w razie potrzeby przeskalować obszar lub wprowadzać
przeskalowane wartości parametrów fizycznych.
4.
Podstawowe ustawienia solvera
Define → Models → Solver (segregated, 2D, unsteady) → OK
Define → Models → Energy (Energy equation: OK) → OK (dołączenie równania energii)
Define → Models → Solidification & melting (Solidification/melting: OK; mushy zone
constant: 100000) → OK (model liniowy g
s
(T))
Pojawia się informacja, że trzeba zdefiniować nowe parametry fizyczne.
Wartość stałej w polu „mushy zone” na znaczenie tylko w przypadku konwekcji.
5.
Właściwości materiałowe
Define → Materials
Dopisać nowy materiał:
•
name: al_cu (wpisać z klawiatury)
•
change/create
•
overwrite air?: no (nie zapisywać w miejsce powietrza)
•
z menu rozwijalnego Fluid materials wybrać al_cu
•
density: 2450 [kg/m
3
]
•
cp – będzie wyrażona w funkcji temperatury jako funkcja kawałkami liniowa.
Należy więc określić wartości ciepła właściwego dla pewnego zbioru temperatur.
T [K]
Cp [J/(kg K)]
300
766
873
766
923
1175
960
1175
Dokonuje się tego wybierając z listy rozwijalnej opcję „piecewise-linear”. Ciepło
______________________________________________________________________________________________
Laboratorium Metody Numeryczne w Wymianie Ciepła, Wydział Mechaniczny Energetyki i Lotnictwa, PW
Mirosław Seredyński,
msered@itc.pw.edu.pl
Piotr Łapka,
plapka@itc.pw.edu.pl
właściwe wyrażone jest w funkcji temperatury (domyślnie) w 4 punktach
charakterystycznych, należy wybrać cyfrę 4 po prawej stronie, następnie wpisać
wartości temepratur i Cp dla tych punktów
•
thermal conductivity - będzie wyrażona w funkcji temperatury jako funkcja
kawałkami liniowa
T [K]
k [J/(kg K)]
300
153
873
153
923
77
960
77
Wartości te wprowadza się podobnie jak wyżej Cp.
•
viscosity: (nie ma znaczenia w przypadku braku konwekcji)
•
melting heat: 3,778E5 [J/ kg]
•
solidus temperature: 873 [K]
•
liquidus temperature: 923 [K]
•
change/create
•
close
Założenia dot. materiału:
•
zależność udziału fazy stałej od temperatury jest w granicach zakresu topnienia
funkcją liniową.
•
Parametry fizyczne są stałe w obrębie faz oraz zależą liniowo od udziału fazy
6.
Warunki brzegowe
Define → Boundary conditions → sc_dolna (nazwa zdefiniowana przez użytkownika) →
set
•
convection (warunek brzegowy III rodzaju)
•
heat transfer coefficient: 1000 [W/m
2
K]
•
Free stream temperature: 300 [K]
Tak samo dla ścianki po lewej stronie.
Dla ścianek po prawej stronie i na górze ustalić symetrię (np. Define → Boundary
conditions → sc_prawa (nazwa zdefiniowana przez użytkownika) → symmetry →
OK). Można też nie modyfikować ustawień dla tych ścianek, w programie domyślnie
przyjęte jest, że gęstość strumienia ciepła jest równa zero.
7.
Przypisanie substancji do wnętrza obszaru.
Define → Boundary conditions → wnetrze (nazwa zdefiniowana przez użytkownika) →
set
•
material name: al_cu
•
source terms: no
•
fixed values: no
•
porous zone: no

______________________________________________________________________________________________
Laboratorium Metody Numeryczne w Wymianie Ciepła, Wydział Mechaniczny Energetyki i Lotnictwa, PW
Mirosław Seredyński,
msered@itc.pw.edu.pl
Piotr Łapka,
plapka@itc.pw.edu.pl
•
OK
8.
Wybór i ustawienia solvera
Solve → Controls → Solution
•
equations: energy (wyłączyć równania przepływu)
•
OK
9.
Inicjalizacja
Solve → Initialize → Initialize
•
temperature: 950 K (temperatura początkowa)
•
Init
10.
Wizualizacja zbieżności
Solve → Monitors → Residual
•
options → plot: OK
•
OK
11.
Zapisanie historii udziału fazy ciekłej w obszarze do pliku
Solve → Monitors → Volume...
•
Volume monitors: 1
•
name: udzial_gl (plot: no, print: no, write: yes, every: time step)
define →
•
Field variable: solidification/melting
•
(w oknie poniżej): liquid fraction
•
Cell zones: wnetrze (nazwa wnetrza wprowadzona przez użytkownika)
•
Report type: Volume-Average
•
file name: udzial_gl.out
•
OK
•
OK
12.
Całkowanie po czasie.
•
time step size: 1 [s]
•
number of time steps: 50
•
time stepping method: fixed
•
max iterations per time step: 100
•
iterate
13.
Zapisanie wyników do pliku.
File → Write → Case&Data
14.
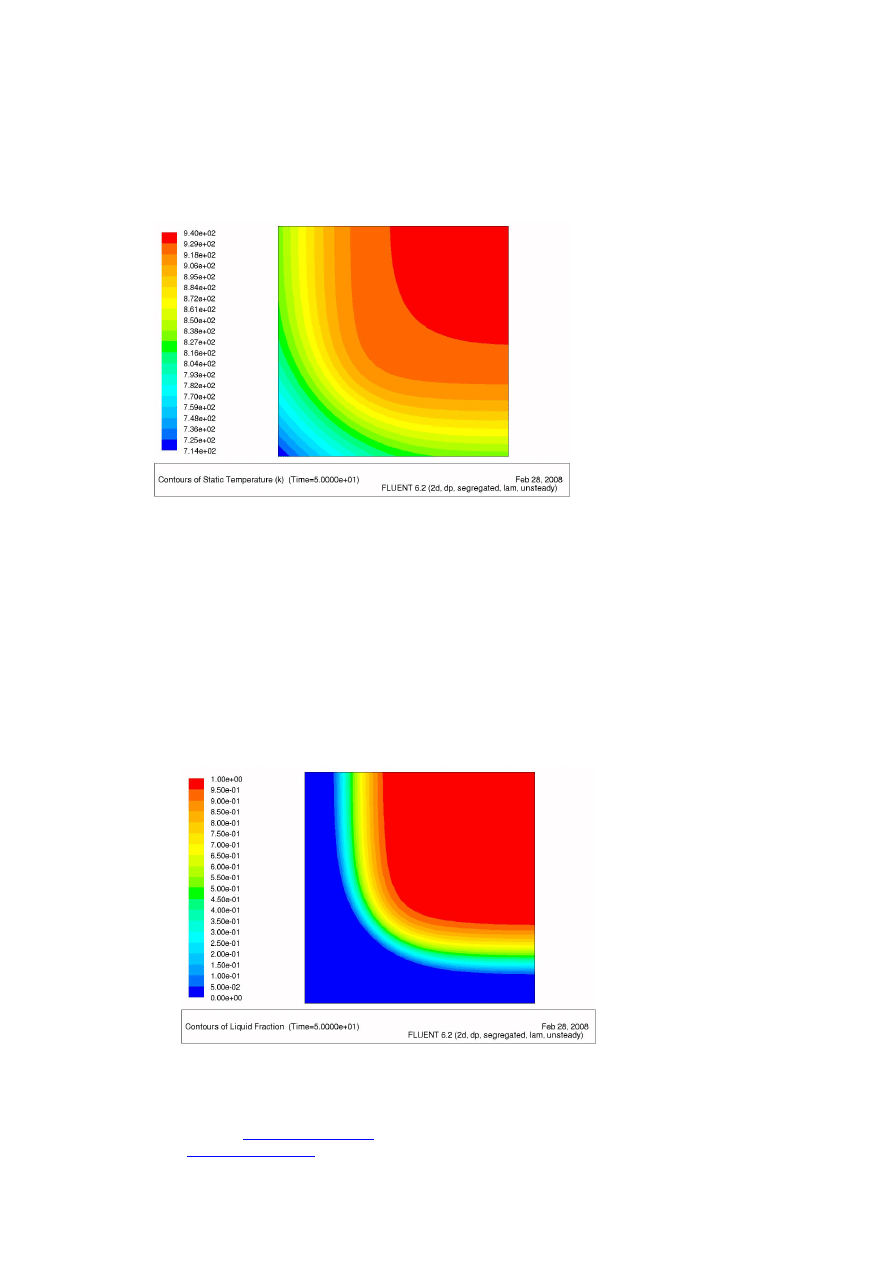
Graficzne przedstawienie wyników.
Wykres temperatury
Display → Contours
•
options → filled: OK
______________________________________________________________________________________________
Laboratorium Metody Numeryczne w Wymianie Ciepła, Wydział Mechaniczny Energetyki i Lotnictwa, PW
Mirosław Seredyński,
msered@itc.pw.edu.pl
Piotr Łapka,
plapka@itc.pw.edu.pl
•
contours of: temperature
•
display
Zapisywanie do pliku.
File → Hardcopy
•
Format: ....
•
save
Wykres udziału fazy ciekłej
Display → Contours
•
options → filled: OK
•
contours of: solidification/melting
•
fiquid fraction
•
display

______________________________________________________________________________________________
Laboratorium Metody Numeryczne w Wymianie Ciepła, Wydział Mechaniczny Energetyki i Lotnictwa, PW
Mirosław Seredyński,
msered@itc.pw.edu.pl
Piotr Łapka,
plapka@itc.pw.edu.pl
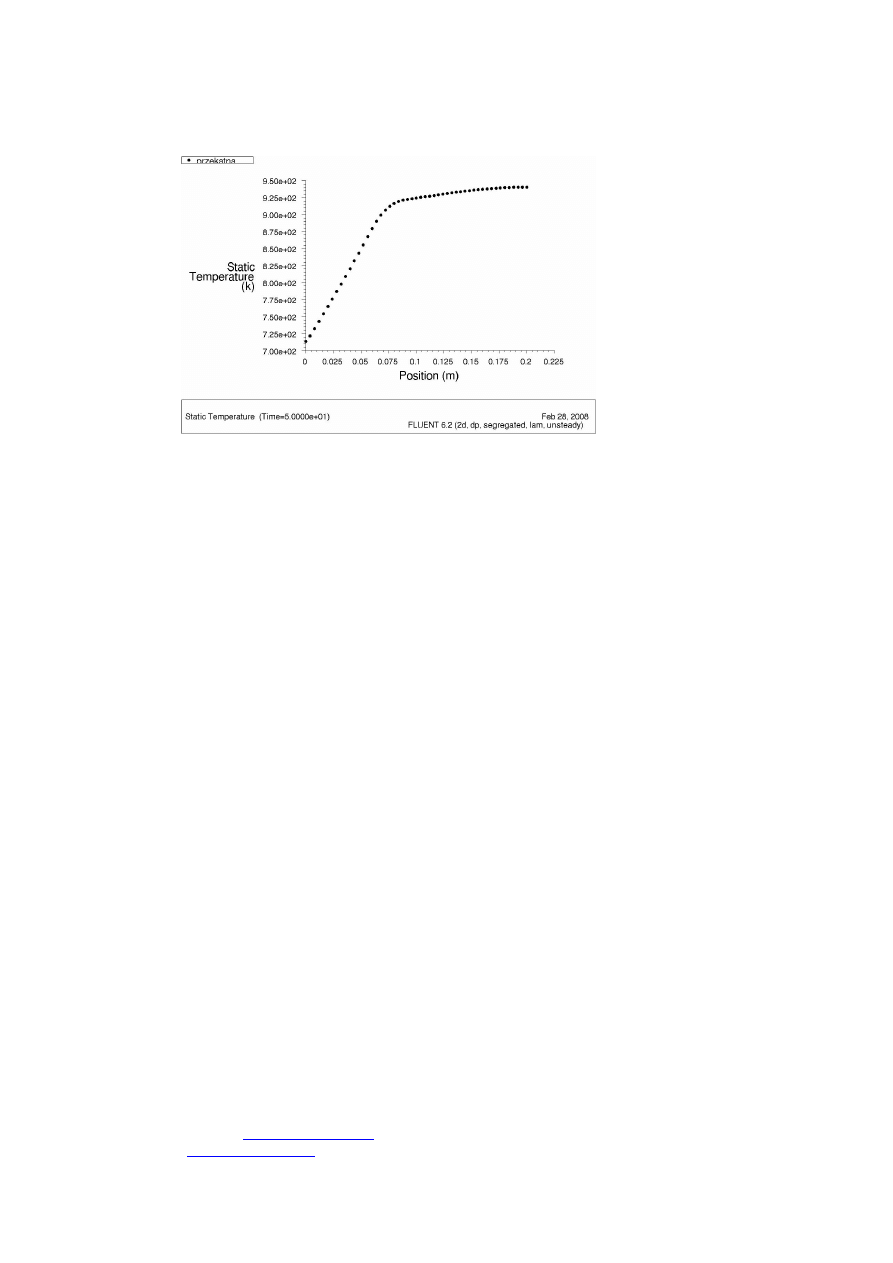
Profil temperatury wzdłuż przekątnej obszaru.
Przekątna:
Surface → Line/Rake
•
Type: Line
•
x0: 0
•
y0: 0
•
x1: 0.1
•
y1: 0.1
•
New Surface Name: przekatna
Plot → XY Plot ...
•
Plot Direction (x: 1, y: 1)
•
Y axis function: Temperature
•
(okno poniżej): Static Temeprature
•
X axis function: Curve Length
•
Surfaces: przekatna (nazwa przekątnej wprowadzona przez użytkownika)
zmiana ustawień linii wykresu.....
→
curves...
•
Line style: pattern: (z listy rozwijalnej – ciągła)
•
Line style: weight: 3
•
Apply
•
Close
•
Plot
zmiana ustawień opisu osi....
→
Axes...
•
Axis: Y
•
Number format: float
•
Precision: 0
•
Apply
•
Close
ponownie tworzę wykres....
•
Plot (efekt poniżej)
______________________________________________________________________________________________
Laboratorium Metody Numeryczne w Wymianie Ciepła, Wydział Mechaniczny Energetyki i Lotnictwa, PW
Mirosław Seredyński,
msered@itc.pw.edu.pl
Piotr Łapka,
plapka@itc.pw.edu.pl
Wyszukiwarka
Podobne podstrony:
CW1b ARK
CW1b ARKv2014
CW1b INST
CW1b INSTv2014
CW1b INSTv2014
Cw1b ?danie zabrudzeniowe na izolatorach linii wysokiego i średniego napięcia
CW1b ARK
word cw1b, wszop ZZIP, II semestr, Technologia informacyjna
CW1b INST
CW1b ARK
cw1b
cw1b
cw1b
więcej podobnych podstron