wer. 2014 MT

1

LABORATORIUM MECHANIKI EKSPERYMENTALNEJ

Instrukcja do ćwiczenia

1b

Wyznaczanie momentów bezwładności elementów

maszyn metodą wahadła fizycznego

Cel

ć

wiczenia

Celem

ć

wiczenia jest zapoznanie z eksperymentalnymi i analitycznymi metodami wy-

znaczania masowych momentów bezwładno

ś

ci cz

ęś

ci maszyn. W ramach realizowa-

nego

ć

wiczenia stosuje si

ę

metod

ę

wahadła fizycznego.

.

Literatura

1. J.Leyko, Mechanika Ogólna, tom II, rozdz. VII.
2. K.Zarankiewicz, Mechanika Teoretyczna, tom III, rozdz. X.

Zagadnienia kontrolne

1. Definicje masowych momentów bezwładno

ś

ci bryły sztywnej i układu punktów ma-

terialnych:

a) wzgl

ę

dem płaszczyzny,

b) wzgl

ę

dem osi,

c) wzgl

ę

dem punktu.

2. Zale

ż

no

ś

ci pomi

ę

dzy momentami bezwładno

ś

ci w prostok

ą

tnym układzie współrz

ę

d-

nych (np. momentem biegunowym a momentami wzgl

ę

dem trzech prostopadłych osi).

3. Moment dewiacyjny dla układu punktów materialnych i bryły sztywnej
4. Twierdzenie Steinera dla osi równoległych i umiej

ę

tno

ść

jego stosowania przy wy-

znaczaniu momentu bezwładno

ś

ci

5. Masowe momenty bezwładno

ś

ci wzgl

ę

dem osi: walca, pr

ę

ta, prostopadło

ś

cianu,

płyty prostok

ą

tnej, tarczy kołowej, pier

ś

cienia – wzory i umiej

ę

tno

ść

stosowania

6. Promie

ń

bezwładno

ś

ci i masa zredukowana dla momentów bezwładno

ś

ci

7. Główne i główne centralne osie bezwładno

ś

ci

8. Równanie ruchu obrotowego bryły sztywnej
9. Okres waha

ń

wahadła fizycznego i jego pomiar

10. Wielko

ś

ci, od których zale

ż

y okres waha

ń

i cz

ę

sto

ść

kołowa ruchu wahadła fizycz-

nego
11. Opis matematyczny ruchu wahadła fizycznego (dokładny i przybli

ż

ony) i warunek

przej

ś

cia do przybli

ż

onego równania ruchu

12. Zale

ż

no

ść

pomi

ę

dzy cz

ę

sto

ś

ci

ą

kołow

ą

a okresem

13. Analityczne wyznaczenie momentów bezwładno

ś

ci ciała zło

ż

onego z prostych

elementów
14. Zasadniczy przebieg

ć

wiczenia

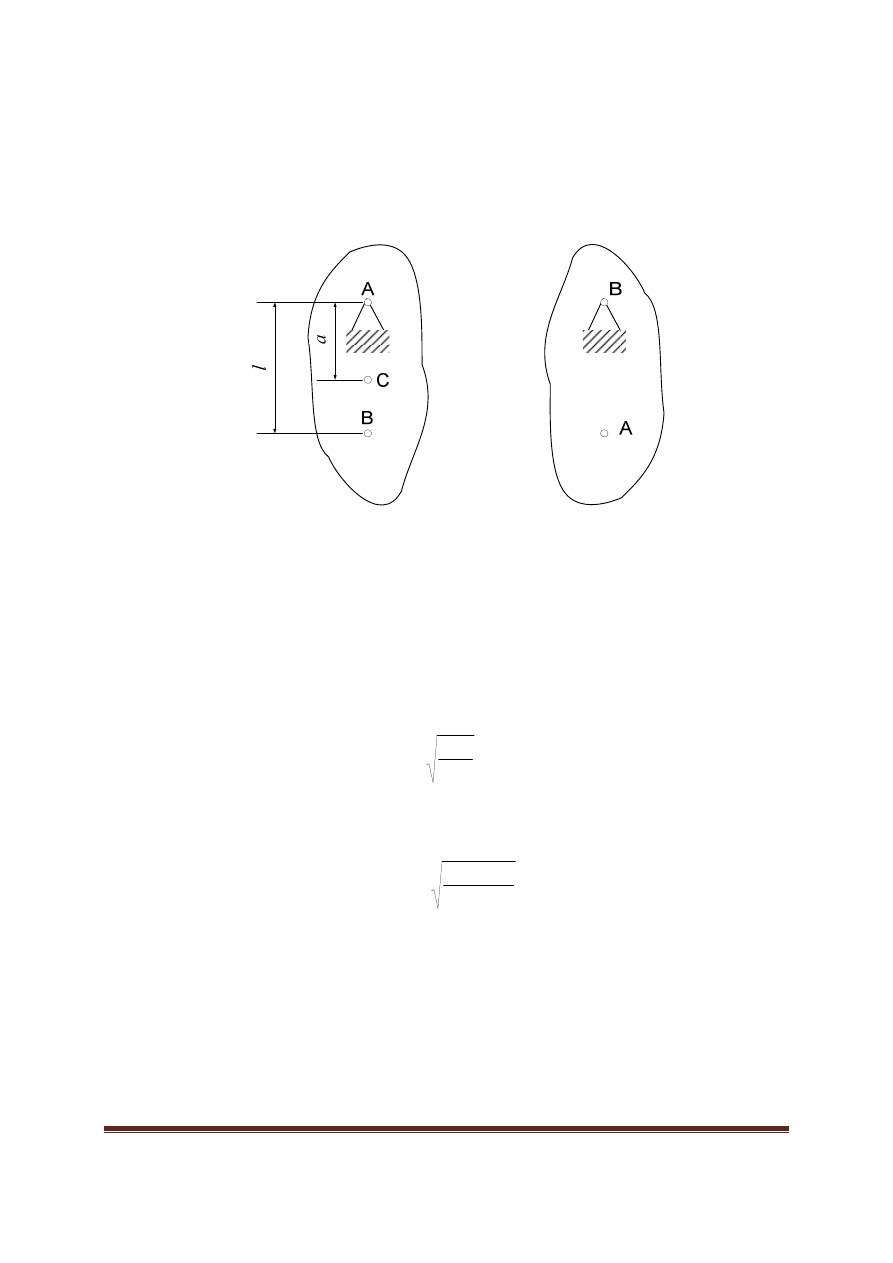
wer. 2014 MT

2

Uwaga! Instrukcja dotyczy podstaw samego

ć

wiczenia. Aby opanowa

ć

materiał

dotycz

ą

cy powy

ż

szych zagadnie

ń

nale

ż

y si

ę

gn

ąć

do podanej literatury.

1. Podstawy teoretyczne dotycz

ą

ce przeprowadzenia eksperymentu

Wahadłem fizycznym nazywamy dowolne ciało sztywne mog

ą

ce si

ę

obraca

ć

wo-

kół osi poziomej, które wykonuje drgania pod wpływem siły grawitacji (rysunek 1).

Rys. 1. Przekrój wahadła fizycznego i punkty zawieszenia A i B

Na rysunku 1 przedstawiono przekrój takiego ciała w płaszczy

ź

nie prostopadłej do

osi obrotu i przechodz

ą

cej przez

ś

rodek masy ciała. Wybrany punkt, w którym o

ś

ob-

rotu przebija wspomnian

ą

płaszczyzn

ę

, mo

ż

emy nazwa

ć

punktem zawieszenia wa-

hadła (na rysunku punkt A lub B w zale

ż

no

ś

ci od sposobu zawieszenia wahadła).

Mamy wyznaczy

ć

moment bezwładno

ś

ci wahadła wzgl

ę

dem osi przechodz

ą

cej

przez

ś

rodek masy C i równoległej do osi obrotu przechodz

ą

cej przez punkt A.

Okres drga

ń

wahadła fizycznego wynosi odpowiednio:

- gdy o

ś

obrotu przechodzi przez punkt A:

mag

J

T

A

A

π

2

=

,

(1a)

- gdy o

ś

obrotu przechodzi przez punkt B:

g

a

l

m

J

T

B

B

)

(

2

−

=

π

,

(1b)

gdzie: J

A

–moment bezwładno

ś

ci wahadła wzgl

ę

dem osi przechodz

ą

cej przez

punkt A,
J

B

–moment bezwładno

ś

ci wahadła wzgl

ę

dem osi przechodz

ą

cej przez punkt B,

a

– odległo

ść

punktu A od

ś

rodka masy C,

l

– odległo

ść

pomi

ę

dzy punktami A i B z rysunku 1 (mi

ę

dzy osiami obrotu),

m – masa wahadła.

St

ą

d, momenty bezwładno

ś

ci wzgl

ę

dem osi przechodz

ą

cych odpowiednio

przez punkty A i B wynosz

ą

:

wer. 2014 MT

3

2

2

4

π

A

A

mgaT

J

=

]

[

2

m

kg

⋅

(2a)

(

)

2

2

4

π

B

B

T

a

l

mg

J

−

=

]

[

2

m

kg

⋅

(2b)

Korzystaj

ą

c z twierdzenia Steinera i z zale

ż

no

ś

ci (2a i 2b) mo

ż

na okre

ś

li

ć

mo-

ment bezwładno

ś

ci badanego elementu wzgl

ę

dem osi przechodz

ą

cej przez

ś

rodek

masy oraz odległo

ść

punktu zawieszenia A od

ś

rodka masy:

m

a

agT

J

A

c













−

=

2

2

2

4

π

]

[

2

m

kg

⋅

(3)

]

[m

(4)

2. Oszacowanie niepewno

ś

ci pomiarowej

Załó

ż

my dalej,

ż

e niepewno

ś

ci poszczególnych pomiarów s

ą

niezale

ż

ne i losowe.

Aby upro

ś

ci

ć

obliczenia przyjmijmy,

ż

e niepewno

ść

oszacowania g (przyspieszenia

ziemskiego) jest pomijalnie mała (bliska zeru) w porównaniu do innych niepewno

ś

ci.

Dla uproszczenia przyjmijmy,

ż

e pomiar

a

obarczony jest niepewno

ś

ci

ą

:

(5)

Ogólna zale

ż

no

ść

okre

ś

laj

ą

ca jak przenosz

ą

si

ę

bł

ę

dy wielko

ś

ci mierzonych na

wyznaczan

ą

po

ś

rednio wielko

ść

, przy zało

ż

eniu niezale

ż

no

ś

ci bł

ę

dów wielko

ś

ci mie-

rzonych, przedstawia si

ę

nast

ę

puj

ą

co

1

:

2

2

...













∆

∂

∂

+

+













∆

∂

∂

=

∆

z

z

y

x

x

y

y

(6)

gdzie y(x,..z) jest wielko

ś

ci

ą

wyznaczan

ą

metod

ą

po

ś

redni

ą

na podstawie pomiaru

warto

ś

ci x,...z.

Ostatecznie mo

ż

na zapisa

ć

,

ż

e niepewno

ść

oszacowania momentu bezładno

ś

ci

elementu wzgl

ę

dem osi przechodz

ą

cej przez

ś

rodek ci

ęż

ko

ś

ci wynosi:

2

2

2

2

2

2

2

2

2

4

4

2

4















∆















−

+













∆

+















∆















−

=

∆

m

a

agT

T

agmT

a

m

a

gT

J

A

A

A

A

c

π

π

π

]

[

2

m

kg

⋅

(7)

1

Aby poszerzyć wiedze z tego zakresu sięgnij po książkę: John R. Taylor; Wstęp do analizy błędu pomiarowego;

PWN Warszawa 1999 i późniejsze wydania (rozdział 3).

(

)

l

T

T

g

l

glT

a

B

A

B

2

2

2

2

2

2

8

4

π

π

−

+

−

=

l

a

∆

≈

∆

wer. 2014 MT

4

Podobnie niepewno

ść

towarzysz

ą

c

ą

pomiarowi metod

ą

po

ś

redni

ą

momentu bez-

władno

ś

ci elementu wzgl

ę

dem osi przechodz

ą

cej przez punkt A i punkt B mo

ż

na

oszacowa

ć

jako:

2

2

2

2

2

2

2

2

4

4

2

4















∆

+













∆

+















∆

=

∆

a

mgT

T

mgaT

m

gaT

J

A

A

A

A

A

π

π

π

]

[

2

m

kg

⋅

(8)

2

2

2

2

2

2

2

2

2

2

2

4

4

4

)

(

2

4

)

(















∆

+















∆

+













∆

−

+















∆

−

=

∆

l

mgT

a

mgT

T

T

a

l

mg

m

T

a

l

g

J

B

B

B

B

B

B

π

π

π

π

]

[

2

m

kg

⋅

gdzie:

l

T

T

B

A

∆

∆

∆

,

,

s

ą

niepewno

ś

ciami pomiarowymi wielko

ś

ci mierzonych bezpo-

ś

rednio: okresów waha

ń

wahadła podwieszonego na osiach przechodz

ą

cych przez

punkty A i B oraz odległo

ś

ci pomi

ę

dzy A i B.

3. Przebieg

ć

wiczenia

Opis kolejnych kroków, które nale

ż

y wykona

ć

znajduje si

ę

w arkuszu sprawozdania.

Poni

ż

ej zwrócono uwag

ę

na pewne istotne zagadnienia.

1.

Ć

wiczenie mo

ż

na wykona

ć

w ró

ż

nych wariantach dokr

ę

caj

ą

c do zasadniczej

cz

ęś

ci wahadła dodatkowe walce (wariant

ć

wiczenia zadaje prowadz

ą

cy).

Poni

ż

ej przedstawiono tabel

ę

dotycz

ą

c

ą

mo

ż

liwych wariantów

ć

wiczenia. Dla

ułatwienia weryfikacji wyników przestrzegaj

ś

ci

ś

le tego co podano w tabeli

i zamieszczono na szkicu obok.

2. Narysuj badane wahadło fizyczne zgodnie z zasadami rysunku technicznego

i zwymiaruj je. Zrób to tak, aby móc pó

ź

niej na podstawie rysunku obliczy

ć

analitycznie moment bezwładno

ś

ci badanego wahadła.

3. Okre

ś

l mas

ę

całego wahadła (razem z dodatkowymi elementami je

ś

li wyst

ę

pu-

j

ą

) i w pó

ź

niejszych obliczeniach przyjmij jednorodno

ść

materiału wszystkich

elementów wahadła fizycznego. G

ę

sto

ść

materiału, z którego wykonane jest

wahadło nale

ż

y okre

ś

li

ć

na podstawie obj

ę

to

ś

ci bryły wahadła i zmierzonej

Wariant

Dodatkowy ele-

ment I

Dodatkowy ele-

ment II

1

bez

bez

2

o większej masie

bez

3

o mniejszej masie

bez

4

o większej masie

o mniejszej masie

5

oba elementy połą-

czone ze sobą

bez

Podwieszenie A

Podwieszenie B

Dodatkowy

element I

Dodatkowy

element II

wer. 2014 MT

5

masy. Mo

ż

esz sprawdzi

ć

swój wynik odnosz

ą

c si

ę

do przybli

ż

onej warto

ś

ci

tablicowej g

ę

sto

ś

ci mosi

ą

dzu.

4. Okre

ś

l odległo

ść

pomi

ę

dzy osiami podwiesze

ń

(czy te

ż

punktami A i B z ry-

sunku 1) z dokładno

ś

ci

ą

do ±0,5 mm.

5. Przy do

ś

wiadczalnym wyznaczaniu momentu bezwładno

ś

ci nale

ż

y zmierzy

ć

czas 10 wahni

ęć

(10 okresów ruchu) elementu.

6. Ka

ż

dy pomiar nale

ż

y powtórzy

ć

20 razy dla dwóch ró

ż

nych podwiesze

ń

ele-

mentu A i B.

7. Przy wyznaczaniu analitycznym momentów bezwładno

ś

ci wykorzystaj wcze-

ś

niej obliczon

ą

g

ę

sto

ść

oraz przyjmij,

ż

e pr

ę

t ł

ą

cz

ą

cy dwie tuleje wahadła ma

przekrój kołowy. Przyjmij

ś

rednic

ę

zast

ę

pcz

ą

przy takim uproszczeniu. We

wnioskach wyja

ś

nij dlaczego przyj

ą

łe

ś

tak

ą

a nie inna warto

ść

.

8. Obliczenia przeprowad

ź

w sposób weryfikowalny tzn. wyja

ś

nij poszczególne

kroki (nazwij konkretnie to co w danym momencie obliczasz), przedstaw wzór,
podstawienie i wynik.

9. We wnioskach, oprócz wspomnianych wy

ż

ej zagadnie

ń

, nale

ż

y ustosunkowa

ć

si

ę

do otrzymanych wyników, a w szczególno

ś

ci do przyczyn ewentualnie wy-

st

ę

puj

ą

cych ró

ż

nic pomi

ę

dzy warto

ś

ciami uzyskanymi z oblicze

ń

analitycz-

nych oraz z eksperymentu, uwzgl

ę

dniaj

ą

c przy tym oszacowanie niepewno

ś

ci

pomiarowej. Dodatkowo mo

ż

esz wykona

ć

symulacje i odpowiedzie

ć

na pyta-

nie: czy np. wybór innej charakterystycznej

ś

rednicy przekroju kołowego zmie-

ni istotnie wynik? We wnioskach zamie

ś

ci

ć

swoje spostrze

ż

enia. Zastanów

si

ę

tak

ż

e nad najbardziej istotnymi

ź

ródłami niepewno

ś

ci pomiarowej w przyj

ę

-

tej metodzie.