
Tadeusz Tatara
1
ANALIZA WYTĘŻENIA ŚCIAN NOŚNYCH W NISKICH BUDYNKACH
MUROWYCH W WARUNKACH WSTRZĄSÓW GÓRNICZYCH
1. Wiadomości ogólne
Problematyka działania drgań powierzchniowych wzbudzanych podziemnymi wstrząsami
generowanymi eksploatacją górniczą w obszarach Górnośląskiego Zagłębia Weglowego (GZW) i
Lubińsko – Głogowskiego Okręgu Miedziowego (LGOM) na zabudowę powierzchniową, stała
się ważnym problemem społecznym i gospodarczym. Waga tematu wzrosła w ostatnich kilku
latach, w związku ze zwiększeniem się sejsmiczności terenu LGOM oraz poczucia zagrożenia
mieszkańców.
Na terenach GZW i LGOM mieszkalna zabudowa mieszkalna jest zróżnicowana. Zabudowę tę
stanowią: a) jednorodzinne niskie budynki murowe (od 1 – 3 kondygnacji), b) wielorodzinne
budynki o średniej wysokości (5- kondygnacyjne), c) wielorodzinne budynki wysokie o 11 i 12
kondygnacjach.
Budynki wielorodzinne w zdecydowanej większości wzniesione są metodami
uprzemysłowionymi (wielka płyta, wielki blok). Te klasy budynków były przedmiotem
wcześniejszych badań i analiz (por. m.in. [
7, 17
]). Ostatnio wydana praca wykonana w ITB
dotyczy analizy wielkopłytowych budynków 5 kondygnacyjnych poddanych wpływom wstrząsów
górniczych [
4
]. Z kolei problematyka wzmacniania budynków, z obszaru LGOM, wykonanych w
systemie Wrocławskiej Wielkiej Płyty (WWP) jest przedmiotem pracy [
26
].
Na terenach objętych wpływami eksploatacji górniczych niskie budynki murowe w dużym
procencie występują w obszarach wiejskich i małych miast. Na terenie GZW i LGOM duża część
tych budynków jest w znacznym stopniu już zamortyzowana. Występują również budynki
całkiem nowe lub wzniesione w ostatnim dwudziesto- i trzydziestoleciu. W związku z
powyższym różny jest stan techniczny tych obiektów. Stan techniczny części z tych budynków
jest zły z powodu braku konserwacji i bieżących remontów.
1
Dr hab. inż. – Politechnika Krakowska, Instytut Mechaniki Budowli, ul. Warszawska 24, 31 - 155 Kraków.

O skali zjawiska działania wstrzasów górniczych na tradycyjną zabudowę świadczą dane z
lat
80. ubiegłego stulecia, zaczerpnięte z [
16
]. Spośród 10500 budynków w Bytomiu około 80%
stanowi stara, tradycyjna zabudowa miejska z początku XX wieku. Różnym uszkodzeniom
wymagającym remontów podlegało 2200 budynków, czyli ok. 20%. Przykładowo w 1982 r., trzy
silne wstrząsy (07.12.1982 o En = 1
2
10
9
J, 02.12.1982 o En = 7
2
10
8
J i 06.04.1982 o En = 1
2
10
9
J)
w tym rejonie uszkodziły odpowiednio 453,165 i 588 budynków.
Stare budynki murowe stanowią również duży procent zabudowy mieszkalnej na terenach
objętych wpływami trzęsień ziemi. Analiza wyników przeglądów stanu technicznego budynków
po trzęsieniach ziemi dowodzi, że w budynkach murowych uszkodzenia mogą być spowodowane
między innymi brakiem odpowiednich wzmocnień w poziomach stropów i dachu, oraz
zastosowaniem nieodpowiednich (do obciążeń) kotew stalowych wiążących budynek [
2
].
Precyzyjne określenie przyczyn uszkodzeń w budynkach z terenów górniczych, wymaga
zawsze pogłębionej analizy. Wiele z tych uszkodzeń ma znamiona takie jak uszkodzenia
wywołane działalnością górniczą, a nie są nią spowodowane. Z prawie 25-letnich badań
uszkodzeń różnych typów budynków w obszarze GZW wynika, że 56% uszkodzeń obiektów było
spowodowanych zarówno wpływem eksploatacji górniczej, jak i zużyciem technicznym, brakiem
odpowiedniej konserwacji i zabezpieczeniem przed działaniem wody i wilgoci oraz błędami
wykonawczymi [
12
]. Istotnym zagadnieniem z punktu widzenia użytkownika obiektów
budowlanych na obszarach wpływów górniczych jest także ocena właściwości użytkowych
projektowanych i istniejących budynków [
13
].
W pracy przedstawiono analizę teoretyczną zachowania się typowego niskiego budynku
murowego poddanego wpływom dynamicznym pochodzenia górniczego. Analiza teoretyczna
wymaga budowy modelu obliczeniowego, za pomocą którego można dokonać oceny wytężenia
poszczególnych elementów konstrukcyjnych budynku. W analizach wykorzystano przebiegi
najintensywniejszych drgań powierzchniowych zarejestrowanych w stacjach sejsmicznych w
LGOM. Wartości maksymalnych naprężeń obliczano za pomocą metody THA (time history
analysis), a także metodą spektrum odpowiedzi (RSA) wykorzystując unormowane, wzorcowe
spektrum odpowiedzi.
2. Przyjęty model obliczeniowy niskich budynków murowych
Do analizy wybrano niski budynek jednorodzinny (typowy w polskich warunkach), murowy,
otynkowany, dwukondygnacyjny, w całości podpiwniczony, o poprzeczno – podłużnym układzie
ścian nośnych. Budynek wzniesiony został na początku lat 70. ubiegłego stulecia. Budynek
można uznać za reprezentatywny dla tej klasy obiektów z uwagi na konstrukcję, wymiary,
materiały, z których został wykonany oraz sposób posadowienia. Wymiary rzutu poziomego
budynku, jego wysokość od poziomu terenu i głębokość posadowienia fundamentów wynoszą
odpowiednio 9.50 x 10.00, 8.15 i 1.1m. Ławy fundamentowe są betonowe, a ściany piwnic
wykonano z bloków żużlobetonowych i z cegły. Mury zewnętrzne kondygnacji parteru i I piętra
są warstwowe z bloków PGS i z cegły, a wewnętrzne z pustaków PGS oraz z cegieł. Stropy nad
piwnicami i parterem są płytowe, żelbetowe. Stropodach wykonany jest z płyty żelbetowej i
ocieplony żużlem. Podłoże gruntowe stanowi pospółka żwirowo - piaskowa. Rzut piętra budynku
pokazano na
rys. 1
.
Elementy nośne (ściany, stropy) modelowano elementami skończonymi typu "plate/shell"
(element powłokowy, czterowęzłowy o pięciu stopniach swobody w każdym węźle). Rozważono
model budynku przyjmując monolityczne połączenia żelbetowych stropów i ścian nośnych oraz

ciężkie ocieplenie stropodachu w postaci żużlu paleniskowego (takie ocieplenie jest
charakterystyczne dla starszych budynków jednorodzinnych). Ściany nośne zbudowane zostały z
2400 elementów. W modelu uwzględniono
odmienne własności materiałów składowych
murów, obciążenia wynikające z ciężaru tynku,
ocieplenia stropodachu oraz 40% obciążenia
użytkowego zgodnie z normą [
21
]. Elementy
murowe przyjęto jako jednorodne, traktując takie
założenie jako wystarczająco dokładne z punktu
widzenia dokładności obliczeń inżynierskich [
6,
15
]. Wartości współczynników charaktery-
zujących właściwości fizyczne materiałów
przyjeto zgodnie z normami [
20, 21, 23, 24
] i
zestawionymi w monografii [
28
]. W modelu
uwzględniono istotne z punktu widzenia szty-
wności układu elementy, m.in. biegi schodów, otwory, nadproża. Wpływ podłoża gruntowego
uwzględniono poprzez sprężyste zamocowanie modelu w podłożu, za pomocą elementów w
postaci sprężyn przyłożonych, w trzech kierunkach (x, y, z), w poziomie spodu fundamentu
(wykorzystano 291 elementów brzegowych modelujących podłoże gruntowe). Charakterystyki
sprężyn odpowiadały własnościom podłoża gruntowego; ich wartości zaczerpnięto z pracy [
28
].
Analizę dynamiczną przeprowadzono w zakresie sprężystym przy użyciu programu elementów
skończonych ALGOR [
1
] i objęła ona: a) dobór teoretycznego modelu budynku, b) wyznaczenie
cech dynamicznych budynku na podstawie jego badań w skali naturalnej i teoretycznego modelu,
c) obliczenie teoretycznej odpowiedzi modelu budynku w dziedzinie czasu na reprezentatywne,
rzeczywiste, pomierzone wymuszenia kinematyczne, d) obliczenie odpowiedzi modelu budynku z
wykorzystaniem unormowanego, wzorcowego spektrum odpowiedzi, e) oszacowanie naprężeń w
wybranych elementach konstrukcyjnych budynku na podstawie obliczeń.
Kryterium przydatności modelu budynku stanowią: a) obliczone częstotliwości drgań
własnych (odrębnie w kierunku poprzecznym (x) i podłużnym (y)) porównywalne z
pomierzonymi częstotliwościami, b) obliczone teoretyczne odpowiedzi dynamiczne modelu
budynku na pomierzone wymuszenia porównywalne z pomierzonymi w budynku w skali
naturalnej.
3. Odpowiedź dynamiczna układu o skończonej liczbie stopni swobody
na wymuszenia kinematyczne
Wykorzystując ogólne równanie ruchu, drgania dyskretnego układu o n stopniach swobody,
podlegającego kinematycznym wymuszeniom przez podłoże zapisuje się jako [
9
]:
)}
(
{
)
(
)
(
]
[
)
(
t
a
B
t
U
K
t
U
C
t
U
B
(
1
)
w którym: [B], [K], [C] - odpowiednio macierz bezwładności, sztywności i tłumienia układu,
)
(
,
)
(
,
)
(
t
U
t
U
t
U
- wektory odpowiednio przyspieszeń, prędkości i przemieszczeń,
)
(t
a
- wektor wymuszeń (przyspieszeń).
Wekor wymuszeń
)
(t
a
ma postać:
cm
Rys. 1. Rzut piętra budynku

)
(
)
(
)
(
)
(
2
1
t
a
t
a
t
a
t
a
n
(
2
)
a każdy i-ty element a
i
(t) wektora przyspieszenia {a(t)} zależny jest od kierunku i-tego stopnia
swobody. Ruch podłoża w miejscu lokalizacji konstrukcji w dowolnej chwili czasu t, opisuje
sześć składowych przyspieszenia drgań powierzchniowych wg relacji (
3
):
)
(
)
(
)
(
)
(
)
(
)
(
)}
(
{
t
a
t
a
t
a
t
a
t
a
t
a
t
a
z
g
y
g
x
g
gz
gy
gx
g
(
3
)
w której:
a
gx
(t), a
gy
(t), a
gz
(t) - wartości przyspieszeń składowych translacyjnych drgań w kierunkach
poziomych x, y i w kierunku pionowym z, a
gθx
(t), a
gθy
(t), a
gθz
(t) - wartości przyspieszeń
składowych obrotowych drgań wokół osi x, y i z.
Wektor przyspieszenia {a(t)} w równaniu ruchu (
1
) wyraża się poprzez sześć składowych
przyspieszenia a
gx
(t), a
gy
(t), a
gz
(t), a
gθx
(t), a
gθy
(t) i a
gθz
(t), traktowanych jako wymuszenie
kinematyczne układu, wg relacji (
4
) [
11
]:
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
6
5
1
6
,
1
22
21
16
12
11
2
1
t
a
t
a
t
a
t
a
t
a
t
a
I
I
I
I
I
I
I
I
I
t
a
I
t
a
t
a
t
a
t
a
t
a
t
a
I
t
a
t
a
t
a
t
a
z
g
y
g
x
g
gz
gy
gx
n
n
n
n
g
z
g
y
g
x
g
gz
gy
gx
n
(
4
)
w której macierz
I
ma wymiar n x 6 i składa się z wartości 0 lub 1. Wykorzystując zależność
(
4
), równanie ruchu (
1
) przyjmie ostatecznie postać:
)}
(
{
)
(
)
(
]
[
)
(
t
a
I
B
t
U
K
t
U
C
t
U
B
g
(
5
)
Gdy wymuszenie kinematyczne układu jest w postaci pomierzonych przebiegów dwóch
poziomych i pionowej składowej przyspieszenia drgań powierzchniowych, macierz
I
redukuje
się do macierzy o wymiarze n x 3. W przypadku analizowania drgań płaskiego układu poddanego
poziomemu wymuszeniu kinematycznemu, macierz
I
przyjmuje postać tzw. wektora wpływu
{r} o n elementach równych 1 [
3
]. W dalszych analizach przyjęto, że macierz tłumienia [C]
układu jest proporcjonalna do macierzy bezwładności [B] i sztywności [K] [
3, 14
], co odpowiada

założeniu hipotezy sztywnościowo – bezwładnościowego tłumienia. Pomijając w równaniu (
5
)
efekt tłumienia i przyjmując {a
g
(t)} ≡ {0} otrzyma się równanie
drgań własnych układu o
skończonej liczbie stopni swobody. Tłumienie drgań budynku określano poprzez ułamek
tłumienia krytycznego ξ, wyznaczając logarytmiczny dekrement tłumienia δ [
16
].
Do obliczenia odpowiedzi dynamicznej układu o n stopniach swobody wykorzystuje się także
metodę spektrum odpowiedzi (RSA), która wykazuje wiele podobieństwa z metodą analizy
modalnej. W metodzie spektrum odpowiedzi wymagana jest znajomość macierzy modalnej [Φ]
układu, utworzonej z wektorów postaci drgań własnych {φ}
i
, odpowiadających częstotliwościom
drgań własnych ω
i
W metodzie analizy modalnej rozwiązania układu równań (
5
) poszukujemy
wykorzystując transformację:
q
u
(
6
)
gdzie:
[Φ] - macierz modalna układu,
{q} - wektor współrzędnych normalnych.
Wykorzystanie zależności (
6
) w równaniu (
5
) daje:
)}
(
{
t
a
I
B
q
K
q
C
q
B
g
T
T
T
T
(
7
)
Przyjmując model sztywnościowo – bezwładnościowego tłumienia i uwzględniając warunki
ortogonalności otrzymujemy i-te równanie "modalne":
i
i
i
i
i
i
i
p
q
q
q
2
2
i = 1,2...n
(
8
)
W przypadku gdy wymuszenie kinematyczne układu jest w postaci pomierzonych przebiegów
dwóch poziomych i pionowej składowej przyspieszenia drgań powierzchniowych wówczas prawa
strona równania (
8
) przyjmie postać [
11
]:
)
(
)
(
)
(
)}
(
{
)}
(
{
}
{
]
[
}
{
]
[
]
[
}
{
3
2
1
t
a
t
a
t
a
t
a
t
a
B
I
B
p
z
i
y
i
x
i
g
i
g
i
T
i
T
i
i
(
9
)
gdzie: Γ
i
- macierz współczynników udziału i–tej postaci drgań własnych.
Równanie modalne (
8
) opisuje drgania wymuszone układu o jednym stopniu swobody
(oscylatora) o częstotliwości ω
i
, przy zadanym ułamku tłumienia krytycznego ξ
i
. W metodzie
spektrum odpowiedzi przyjmuje się, że rozwiązanie i-tego równania „modalnego” jest znane i
jest maksymalną wartością bezwzględną przyspieszenia oscylatora, a więc jest to wartość
przyspieszeniowego spektrum odpowiedzi S
a
[
11
].
Wykorzystując wzorcowe, unormowane spektra odpowiedzi dla rejonów górniczych GZW i
LGOM, opisane zależnościami podanymi m.in. w pracy [
28
], maksymalne bezwzględne
przyspieszenie układu odpowiadające i-tej częstotliwości drgań własnych oblicza się z zależności
[
11
]:
}
)
,
(
{
}
{
)}
(
{
max
max
p
i
i
i
i
i
a
f
t
y
i = 1,2...n
(
10
)
w której:
max
max
max
max
)
,
(
)
,
(
)
,
(
}
)
,
(
{
pz
i
i
z
py
i
i
y
px
i
i
x
p
i
i
a
f
a
f
a
f
a
f
i = 1,2...n
(
11
)

gdzie: β
x
(f
i
,ξ
i
), β
y
(f
i
,ξ
i
), β
z
(f
i
,ξ
i
) – wartość unormowanego, wzorcowego spektrum odpowiedzi
odpowiadająca i-tej częstotliwości drgań własnych i ułamkowi tłumienia krytycznego
odpowiednio w kierunku x, y i z,
a
pxmax
, a
pymax
, a
pzmax
– maksymalne wartości prognozowanych lub pomierzonych
przyspieszeń składowych drgań powierzchniowych odpowiednio w kierunku x, y i z.
4. Weryfikacja doświadczalna przyjętego modelu budynku murowego
Cechy dynamiczne budynku wyznaczono na podstawie wyników wcześniejszych pomiarów
jego drgań swobodnych [8] oraz analitycznie wykorzystując jego przestrzenne modele MES [
28
].
Przeprowadzoną weryfikację i jej wyniki przedstawiono szczegółowo w monografii [
28
]. Wyniki
analiz pozwoliły określić podstawowe częstotliwości drgań własnych i odpowiedzi dynamiczne
(na rozpatrywane wymuszenia) budynku i jego modelu. Przykładowo w
tabeli 1
zestawiono
obliczone częstotliwości drgań własnych przyjętego modelu i pomierzone częstotliwości budyn-
ku. Z porównania podstawowych
częstotliwości drgań postępowych
pomierzonych i obliczonych wynika
ich dobra zgodność. Ułamek tłumienia
krytycznego ξ obliczono wykorzy-
stując pomierzone przebiegi drgań
swobodnych budynku w poziomie dachu [
8, 28
]. Do dalszych obliczeń dynamicznych przyjęto
wartość ułamka tłumienia krytycznego
= 5%; wartość ta zwykle jest przyjmowana w budynkach
murowych. Taka wartość
jest także zgodna z zaleceniami projektu Eurokodu 8 [
10
].
5. Przyjęte wymuszenia kinematyczne pochodzenia górniczego
Dokonując wyboru przebiegów drgań od wstrząsów pochodzenia górniczego przyjmowanych
w obliczeniach za wymuszenia kinematyczne, można kierować się kilkoma kryteriami.
Pierwszym z nich jest intensywność przebiegu drgań, którą można określić poprzez maksymalne
przyspieszenie złożonych drgań a
max
. Dalszymi kryteriami mogą być odległość epicentralna r
e
,
droga propagacji fal od źródła do miejsca odbioru, energia wstrząsu En oraz czas trwania
najintensywniejszej fazy drgań. Wykorzystano pełne przebiegi składowych poziomych
powierzchniowych drgań zarejestrowanych w stacjach sejsmicznych na terenie LGOM.
Przykładowe przebiegi składowych poziomych
przyspieszeń drgań powierzchniowych od wstrząsów
górniczych z terenu LGOM (wraz z wynikami ich
analiz amplitudowo – częstotliwościowych), przyjęte
w analizach wpływu tych drgań na konstrukcję
budynku podano w pracy [
28
]. Przebiegi te
przypisano do jednej z 5-ciu zaproponowanych klas
obciążenia, w zależności od wartości a
max
– por.
tabela 2
.
W ostatnim okresie czasu na terenie LGOM miał
miejsce wstrząs o bardzo dużej intensywności.
Wstrząs ten był już przedmiotem analiz w pracach [
5, 29
]. Przykładowo na
rys. 2a, b
pokazano
przebiegi składowych poziomych (x, y) drgań wywołanych tym wstrząsem. Na podstawie
Tabela 2 Podział przebiegów składowych
poziomych przyspieszeń drgań z terenu
LGOM
Klasa
obciążenia
Przedział wartości
a
max
(cm/s
2
)
I
< 10, 30)
II
< 30, 45)
III
< 45, 65)
IV
< 65, 85)
V
> 85
Tabela 1. Obliczone i pomierzone częstotliwości [Hz]
drgań własnych budynku
Częstotliwości
f
1x
f
1y
f
1tors.
f
2x
f
2y
obliczone
6.90
6.38
10.42 18.24 17.82
pomierzone
6.4
6.3
-
-
-
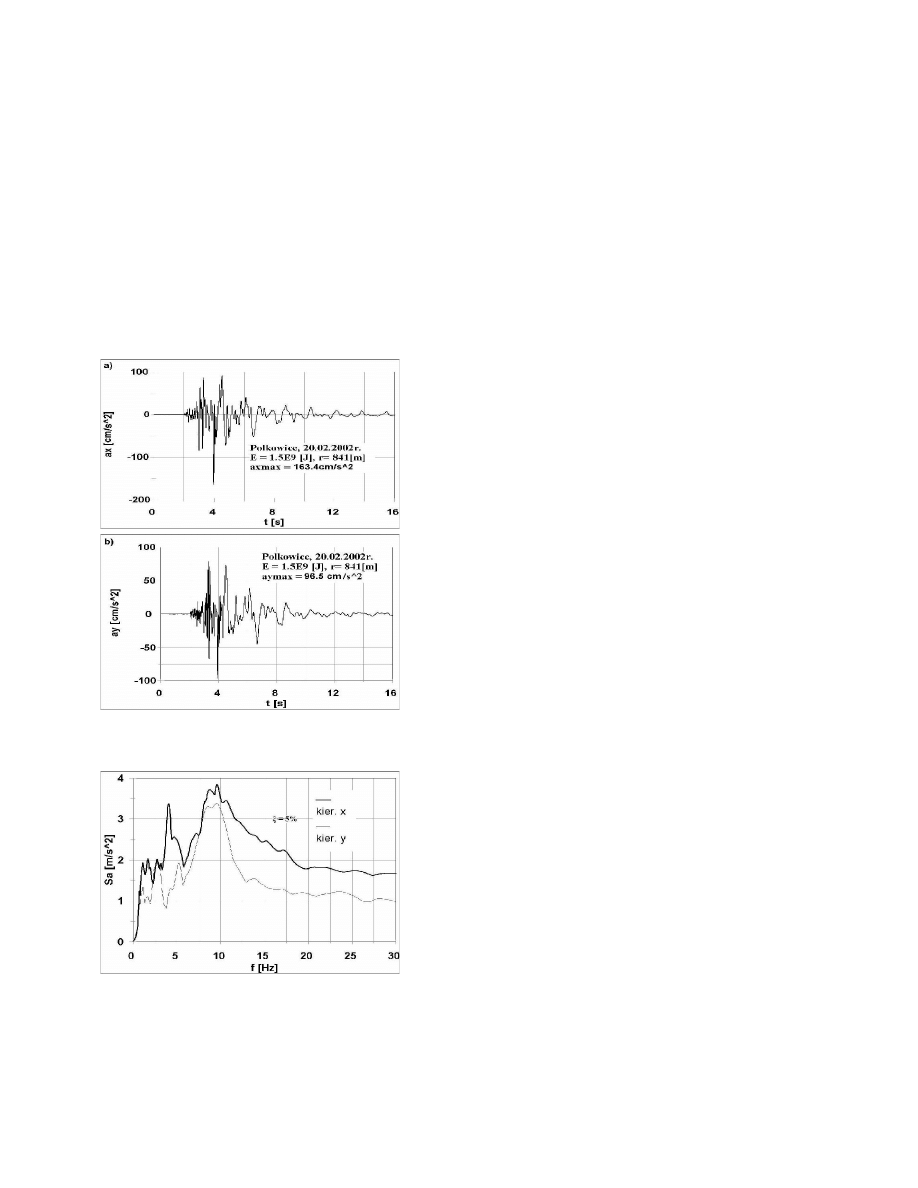
wykresu przyspieszeniowego spektrum odpowiedzi przebiegu drgań z
rys. 2a, b
w składowych
(x) i (y) wyróżnić można niższe dominujące częstotliwości wynoszące odpowiednio ok. 3.9 i
3.3Hz oraz pasmo wyższych dominujących częstotliwości 8.4 – 9.6 Hz –
por. rys. 3.
Krok
dyskretyzacji (
t) przebiegów drgań z
rys. 2a, b
wynosi 0.002s i ta wartość została przyjęta w
dalszych obliczeniach.
6. Obliczone odpowiedzi dynamiczne modelu budynku na przyjęte wymuszenia
kinematyczne pochodzenia górniczego
Metody wykorzystywane do określania dodatkowych obciążeń dynamicznych na budynki
poddane działaniom wstrząsów górniczych są podobne jak na terenach objętych wpływami trzę-
sień ziemi. Współczesne normy sejsmiczne wielu
krajów podają wzory na obliczanie sił sejsmicznych
działających na budowle na skutek ruchów podłoża
gruntowego wywołanych trzęsieniami ziemi z
wykorzystaniem znormalizowanego spektrum
odpowiedzi.
Obliczenia dynamiczne wykonano w dziedzinie
czasu. Wykorzystano opisane w
p. 4
wymuszenia i
przyjęto podane w
p. 2
założenia i model budynku.
Celem obliczeń było również m.in. określenie stanu
wytężenia ścian budynku poprzez wyznaczenie w
nich naprężeń; określano miejsca i wartości
maksymalnych rozciągających naprężeń głównych.
W każdym kroku czasowym (
t) wyznaczano mapy
naprężeń głównych. Porównano poziomy
odpowiedzi dynamicznej modeli w przypadku
jedno-, dwu- i trzykierunkowego działania
przyjętego wymuszenia kinematycznego. W
obliczeniach wykorzystano metodę Newmark’a,
bezpośredniego całkowania równań ruchu [
19
].
Obliczenia
dynamiczne
przeprowadzono
zakładając: a) działanie tylko jednej składowej
wymuszenia, co jest zgodne z zaleceniami projektu
Eurokodu 8 [
10
], b) równoczesne działanie dwóch
składowych poziomych wymuszenia (x), (y), c)
równoczesne działanie trzech składowych
wymuszenia (x), (y) i (z).
Szczegółowe wyniki obliczeń dynamicznych od
przyjętych wymuszeń kinematycznych zaliczonych
do poszczególnych klas obciążeń podano w
monografii [
28
]. W prezentowanej pracy skupiono
się na analizach wyników obliczeń modelu budynku
poddanego wymuszeniom od wstrząsu, którego
przebiegi składowych poziomych (x), (y)
Rys. 2. Przykładowe przebiegi składowych
poziomych x (a) i y(b) najintensywniejszych
drgań z obszaru LGOM
Rys. 3. Przyspieszeniowe spektra odpowiedzi
wykonane na podstawie przebiegów drgań z rys.
2a, b
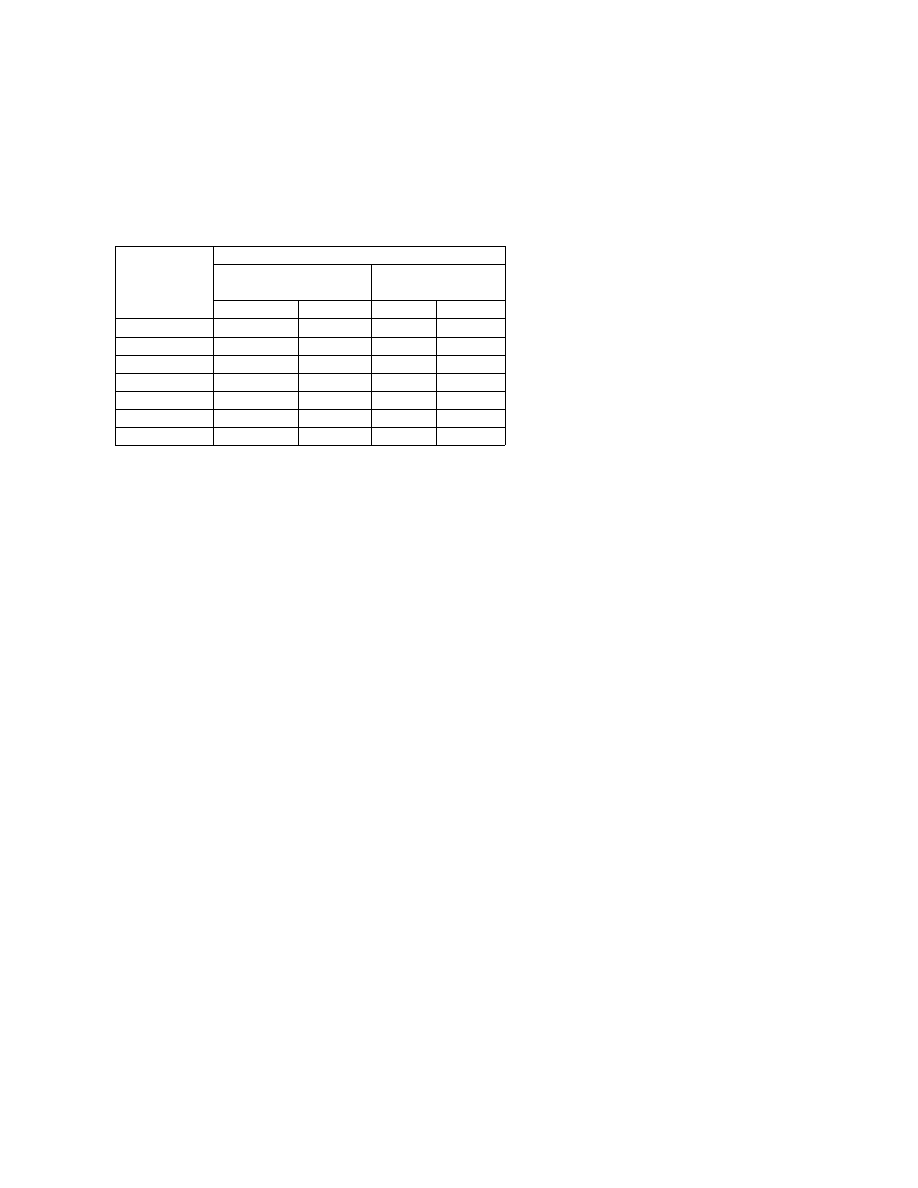
drgań pokazano na
rys. 2a, b
. W
tabeli 3
zestawiono wartości maksymalnych naprężeń
rozciągających w poszczególnych ścianach oraz czas, w którym te naprężenia wystąpiły, od
wymuszenia jedno- i dwukierunkowego z
rys. 2a, b
.
Z analiz przeprowadzonych w
monografii [
28
] wynika, że w praktyce
można pominąć wpływ składowej
pionowej (z) wymuszenia na
odpowiedź dynamiczną modelu
budynku. W przypadku analizowa-
nego tu wymuszenia dwukierunko-
wego, maksymalne wartości naprężeń
głównych w poszczególnych ścianach,
pojawiają się w tym samym czasie co
w przypadku wymuszenia jedno-
kierunkowego. W analizowanych
przypadkach wymuszeń dwukierunko-
wych w monografii [
28
], maksymalne
wartości naprężeń głównych w poszczególnych ścianach pojawiają się w tym samym lub
późniejszym czasie niż w przypadku wymuszenia jednokierunkowego. Z porównania wartości
maksymalnych naprężeń głównych wynika, że ich największe wartości pojawiają się, we
wszystkich rozważanych tu przypadkach obciążeń w jednej z zewnętrznych ścian budynku
oznaczonej jako XZ3 –
por. rys. 1
. Ta część budynku w obrębie ściany XZ3 jest najsztywniejsza i
to wyjaśnia otrzymane wyniki. Podobne rezultaty otrzymano od obciążeń analizowanych w pracy
[
28
].
Z porównania obliczonych maksymalnych wartości naprężeń w poszczególnych ścianach
budynku, uwzględniając wymuszenia jedno- i dwukierunkowe z obszaru LGOM wynika, że nie
można w sposób jednoznaczny przyjąć założenia do celów praktycznych o wystarczająco
dokładnym uwzględnianiu tylko jednej składowej drgań. Można założyć, że lokalne warunki
gruntowe wpływają na charakterystykę częstotliwościową dochodzącego do obiektu wymuszenia,
skutkując różną „zawartością” dominujących częstotliwości w składowych (x) i (y) przebiegów
drgań. Powoduje to różne reakcje modelu na przyjmowane do obliczeń wymuszenia. Dotyczy to
zwłaszcza wymuszeń ze strefy epicentralnej oraz pomierzonych w dalszej odległości
epicentralnej [
28
]. W przypadku wymuszeń o największej intensywności i prawie identycznej
charakterystyce częstotliwościowej obu składowych drgań (por.
rys. 3
), uwzględnienie tylko
jednej składowej drgań jest w pełni uzasadnione - por.
tabela 3
oraz [
28
]. Gdy w przebiegach
drgań przyjmowanych jako wymuszenia kinematyczne, dominują częstotliwości bliskie
częstotliwościom drgań własnych budynków, wówczas obliczone wartości maksymalnych
głównych naprężeń rozciągających mogą być nawet kilkakrotnie większe, w porównaniu z
wartościami obliczonymi od działania wymuszeń, nawet o znacznie większej intensywności, ale
o innych charakterystykach częstotliwościowych [
28
].
Z porównania zestawień największych z maksymalnych wartości, rozciągających naprężeń
głównych, w przypadku wykorzystania reprezentatywnych wymuszeń z terenu LGOM
przedstawionych w [
28
] oraz pokazanych w prezentowanej pracy wynika, że przy wartościach
a
max
> 100cm/s
2
graniczne naprężenia rozciągające w nadprożach i w elementach murowych są
przekroczone – por.
tabela 3
. Struktura częstotliwościowa przebiegu drgań ma decydujący wpływ
na poziom odpowiedzi budynku; gdy dominujace czestotliwości przebiegów drgań są bliskie
Tabela 3. Wartości maksymalnych, rozciągających
naprężeń głównych
[kPa] w ścianach budynku oraz
czas t [s] ich pojawienia się
Nr
i oznaczenie
ściany
Wymuszenie z rys. 2a,b
Jednokierunkowe
(kier. x)
Dwukierunkowe
(kier. x, y)
σ
t
σ
t
1 - (XZ 1)
286.9
2.022
286.9
2.022
2 - (XZ 2)
633.4
2.570
633.7
2,570
3 - (XZ 3)
1443.7
2.018
1444.5
2.018
4 - (YZ 4)
215.8
2.022
215.8
2.022
5 - (YZ 5)
550.9
2.572
551.4
2.572
6 - (YZ 6)
467.4
2.014
467.6
2.014
7 - (YZ 7)
219.1
2.578
219.3
2.578
czestotliwościom drgań własnych budynku wówczas dochodzi do rezonansu i graniczne
naprężenia w elementach nośnych obiektu mogą zostać przekroczone.
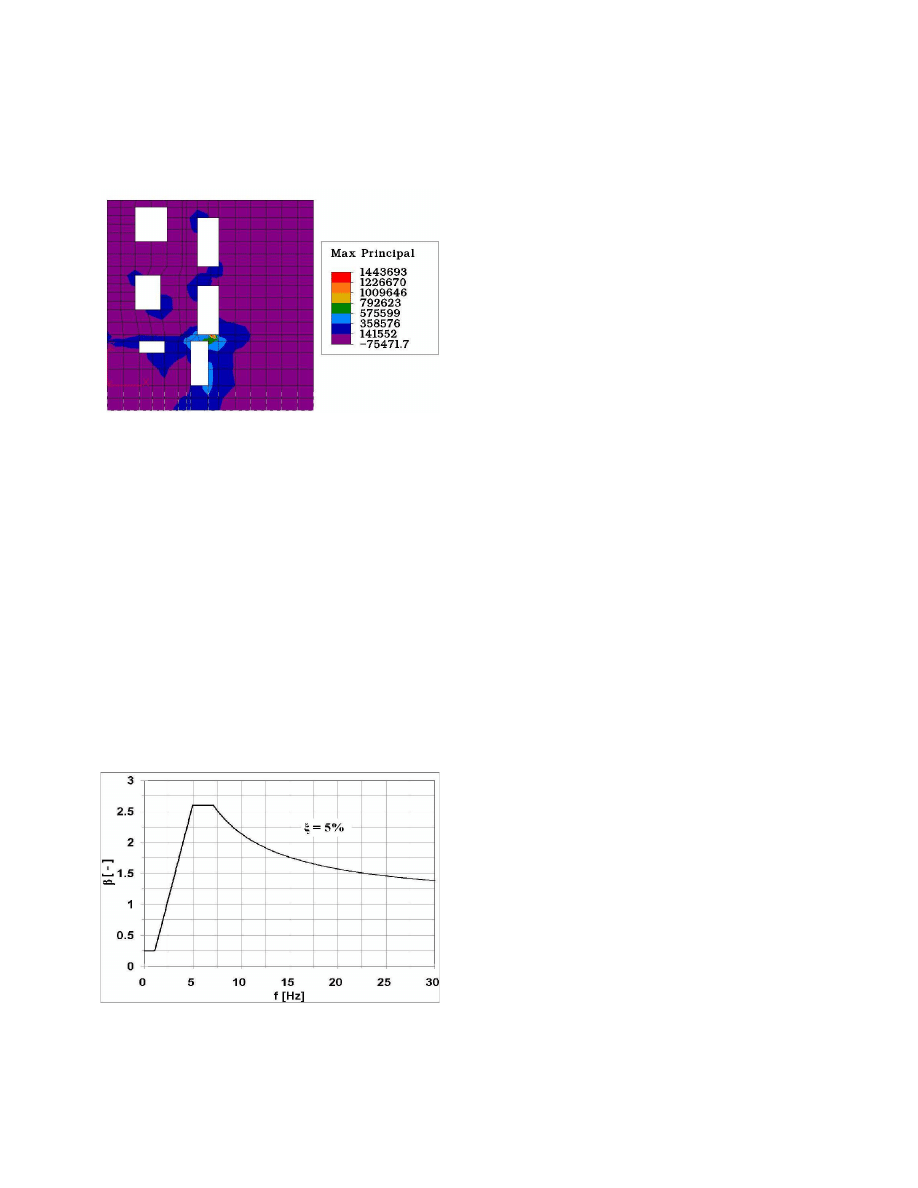
Na
rys. 4
pokazano przykładową mapę naprężeń głównych w jednej ze ścian zewnetrznych
(XZ3) od wymuszenia z
rys. 2a
(przypadek
jednokierunkowego wymuszenia) - wartości
naprężeń podano w [Pa]. W ścianie tej, w
przypadku działania zarówno wymuszenia
jednokierunkowego jak i dwukierunkowego,
maksymalne naprężenia występują w
poziomie żelbetowego stropu nad piwnicą i
mają praktycznie takie same wartości – por.
tabela 3.
Z analizy map maksymalnych naprężeń
głównych w poszczególnych ścianach
wynika, że ich koncentracja występuje przede
wszystkim w poziomie piwnicy i parteru w
nadprożach nad otworami okiennymi lub
drzwiowymi oraz w poziomie stropu nad
piwnicą. Od najintensywniejszych wymuszeń z terenu LGOM maleją naprężenia w ścianach
powyżej poziomu stropu piwnic; ich największe wartości występują w poziomie nadproży
okiennych i drzwiowych, wokół naroży otworów okiennych i drzwiowych oraz nieco poniżej
poziomu stropodachu [
28
].
7. Odpowiedź dynamiczna modelu budynku obliczona z wykorzystaniem wzorcowego,
unormowanego spektrum odpowiedzi
Analiza wyników obliczeń dynamicznych w czasie (THA) przedstawiona w monografii [
28
]
pokazała, że składowa pionowa drgań powierzchniowych wzbudzanych wstrząsami górniczymi
nie ma istotnego wpływu na stan zachowania się modelu budynku. W związku z tym
wykorzystując wzorcowe, unormowane spektrum odpowiedzi – por.
rys. 5
i zależność (
11
),
obliczenia przeprowadzono z pominięciem składowej pionowej tego spektrum β
z
(f
i
,ξ
i
).
Obliczenia wykonano wykorzystując
odpowiedni moduł programu ALGOR [
1
] i
działanie tylko jednej
β
x
(f
i
,ξ
i
)
oraz
równoczesne działanie dwóch składowych
poziomych spektrum
β
x
(f
i
,ξ
i
), β
y
(f
i
,ξ
i
).
Wartości maksymalnych przyspieszeń
składowych poziomych drgań a
pxmax
, a
pymax
,
były równe maksymalnym wartościom
przyspieszeń składowych poziomych drgań
przyjmowanych w obliczeniach odpowiedzi
modelu budynku w dziedzinie czasu.
Pozwoliło to na porównanie obliczanych
wartości naprężeń przy użyciu analizy dyna-
micznej w dziedzinie czasu (THA) i metody spektrum odpowiedzi (RSA).
Rys. 4 Rozkład maksymalnych głównych naprężeń w
ścianie (XZ3) od jednokierunkowego działania
wymuszenia z rys. 2a
Rys. 5 Wzorcowe spektrum dla obszaru LGOM
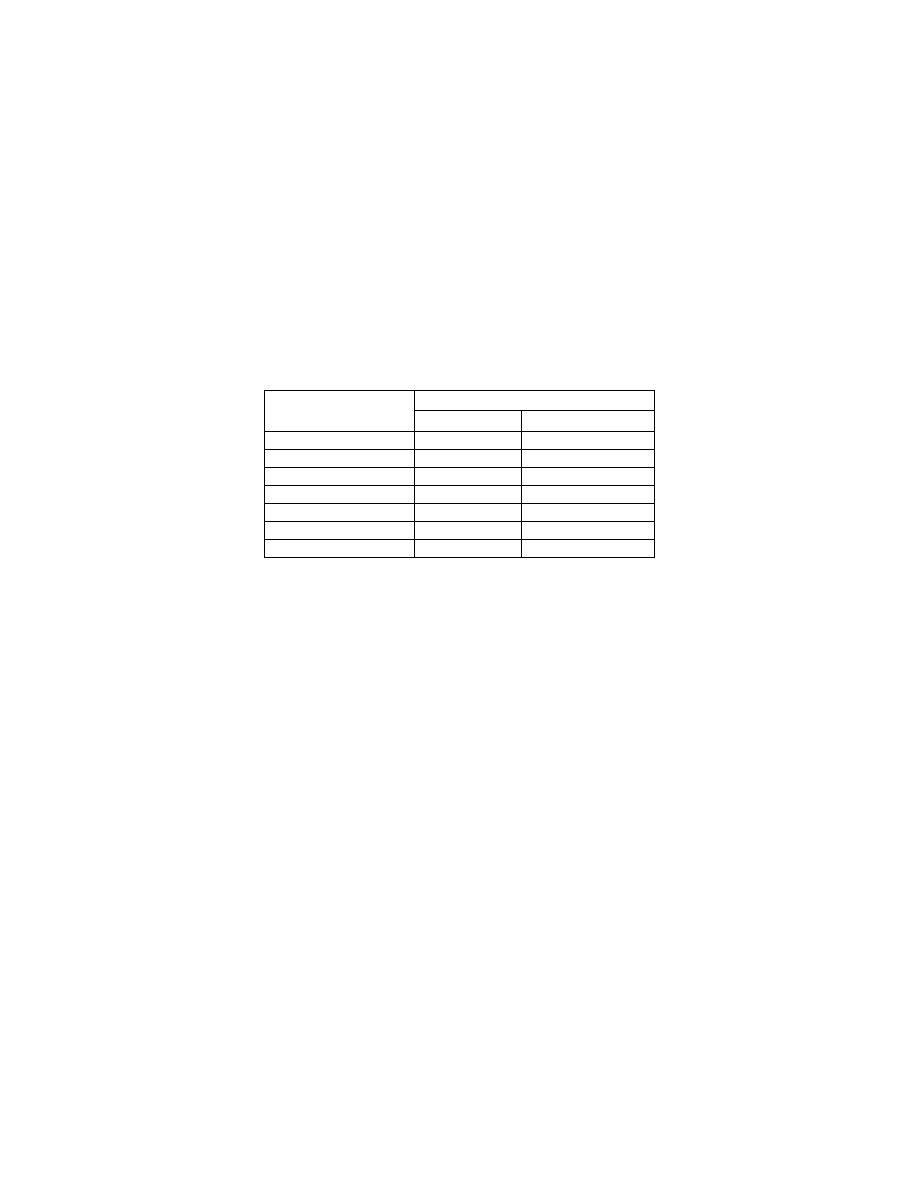
Sumaryczne wartości przemieszczeń, prędkości, przyspieszeń, sił i naprężeń obliczone metodą
spektrum odpowiedzi, wyznacza się na podstawie jednej z metod [
11, 18, 25, 27
]: a) ABS (the
maximum absolute response), b) SRSS (square root of the sum of the squares), c) CQC (complete
quadratic combination), d) NRC (Nuclear Regulatory Comission), e) SNiP. W analizowanym
modelu budynku, częstotliwości drgań własnych są sprzężone [
28
]. Do obliczenia sumarycznych
wartości odpowiedzi modelu metodą spektrum odpowiedzi wykorzystano metodę NRC.
W
tabeli 4
przykładowo podano obliczone metodą spektrum odpowiedzi maksymalne wartości
głównych naprężeń rozciągających w ścianach modelu budynku przy uwzględnieniu
maksymalnych wartości przyspieszeń składowych poziomych drgań z
rys. 2a, b.
Wykorzystano
zależności opisujące wzorcowe spektrum odpowiedzi w obszarze LGOM [
28
]. W obliczeniach
przyjęto wartość ułamka tłumienia krytycznego ξ = 5%. Z analizy i porównania wartości
naprężeń obliczonych metodą ścisłą (MES) i metodą spektrum odpowiedzi wynika, że metoda
spektrum odpowiedzi daje zawyżone wartości względem otrzymanych metodą ścisłą (por.
tabela
3
i
tabela 4
oraz [
28
]). Wartości obliczone za pomocą metody spektrum odpowiedzi należy
traktować jako przybliżone i stanowiące ograniczenie odpowiedzi układu od góry.
8. Wnioski i uwagi końcowe
Zaproponowany i zweryfikowany doświadczalnie model budynku może być wykorzystany i
przydatny do obliczania dynamicznej odpowiedzi niskich budynków murowych
podlegających drganiom powierzchniowym.
Wyznaczone teoretycznie charakterystyki dynamiczne są porównywalne z uzyskanymi z
pomiarów na obiekcie rzeczywistym.
Obliczone dynamiczne naprężenia rozciągające w ścianach nośnych od wymuszeń
drganiami wywołanymi wstrząsami górniczymi o maksymalnych przyspieszeniach
składowych poziomych drgań powierzchniowych o a
max
≤ 40cm/s
2
, nie przekraczają wartości
granicznych w murowych ścianach nośnych [
28
]. W przypadku wymuszeń o większej
intensywności, wartości maksymalnych głównych naprężeń rozciągających są większe i ich
koncentracja występuje w poziomie żelbetowego stropu nad piwnicą. Koncentracja
maksymalnych, głównych naprężeń rozciągających występuje przede wszystkim w poziomie
piwnicy, parteru przy otworach drzwiowych i okiennych oraz w poziomie stropu nad
piwnicą. Maksymalne naprężenia rozciągające, głównie zlokalizowane są w obszarach
Tabela 4. Wartości maksymalnych, rozciągających
naprężeń głównych
[kPa] w ścianach budynku
obliczonych z wykorzystaniem wzorcowego spektrum
odpowiedzi
Nr
i oznaczenie ściany
Uwzględnienie a
max
z rys. 2a,b
kier. x
kier. x, y
1 - (XZ 1)
608.2
720.9
2 - (XZ 2)
1516.7
1779.8
3 - (XZ 3)
3342.03
3883.02
4 - (YZ 4)
454.7
547.05
5 - (YZ 5)
1191.02
1407.5
6 - (YZ 6)
1479.98
1738.6
7 - (YZ 7)
724.51
850.6

nadproży otworów okiennych lub drzwiowych lub też w poziomie posadzki piwnicy przy
otworach drzwiowych.
Z analiz map naprężeń wynika, szczególnie przy wymuszeniach o znacznej intensywności
(a
max
> 80cm/s
2
), że naprężenia rozciągające przekraczające wartości graniczne mogą
pojawić się w murowych ścianach.
Wbrew intuicyjnemu przypuszczeniu budynki uszkodzone, a nawet będące w bardzo złym
stanie technicznym nie ulegają dostrzegalnej szybkiej destrukcji, nawet przy wysokim
poziomie drgań. W wielu rejonach LGOM są budynki w bardzo złym stanie technicznym,
podlegające przez kilka lat drganiom od wstrząsów górniczych i nie dostrzega się w nich
wyraźnego postępu degradacji, co można stwierdzić porównując inwentaryzacje uszkodzeń
przeprowadzone w latach uprzednich ze stanem obecnym. Obecne intensywniejsze
uszkodzenia budynków w rejonie LGOM są w głównej mierze procesem naturalnego ich
zużycia i stan taki byłby prawie taki sam, gdyby nie było eksploatacji górniczej. Jeżeli
budynki wiele lat temu były uszkodzone, to nie można zakładać, że proces dalszej
degradacji został zahamowany, że ustały przyczyny, które spowodowały uszkodzenia i że
aktualnie zwiększone uszkodzenia to wynik tylko intensyfikacji starych uszkodzeń na
skutek wstrząsów górniczych. Można więc, jedynie przypuszczać, że wstrząsy górnicze
mogły w pewnym, trudnym do określenia stopniu, przyczynić się do intensyfikacji
uszkodzeń pochodzenia poza górniczego.
Piśmiennictwo
1. Algor code. 1998. Docutech. Pittsburgh PA: Algor Inc.
2.
Bruneau M., State of art report on seismic performance of unreinforced masonry buildings, J.
Struct. Engng., Vol. 120, No 1, 1994, 230 – 251.
3. Chmielewski T., Zembaty Z., Podstawy dynamiki budowli, „Arkady”, Warszawa 1998.
4. Cholewicki A., Budynki wielkopłytowe podlegające wstrząsom górniczym, ITB, Z.3, Seria:
Instrukcje, wytyczne, poradniki, Warszawa 2002.
5.
Cholewicki A., Chyży T., Szulc J., Wnioski z analizy i oceny skutków w budynku wysokim w
Polkowicach po wstrząsie górniczym w dniu 20.02.2002., X Symp. Wpływy sejsmiczne i
parasejsmiczne na budowle, Kraków 2003, str. 79 – 88.
6. Ciesielski R., Wpływ obciążeń dynamicznych na konstrukcje murowe, XIII Ogólnopolska
konferencja “Warsztat pracy projektanta konstrukcji”, Ustroń, 1999, 63 – 96.
7.
Ciesielski R., Kuźniar K., Maciąg E., Tatara T., Damping of vibration in precast buildings with
bearing concrete walls, Archives of Civil Engineering, Vol. XLI, issue 3, 1995, 329-341.
8. Ciesielski R, Maciąg E., Tatara T., Evaluation of dynamic properties of masonry buildings on
the basis of traffic induced vibrations, Proc. Conf. "Traffic Effects on Structures and
Environment", Strbskie Pleso (Czechoslovakia), 1987, 445-451.
9. Clough R.W., Penzien J., Dynamics of structures, Mc Graw – Hill Book, New York, 1975.
10. Eurocode 8: Earthquake resistant design of structures – second draft 1993 CEN/TC
250/SC8/N85.
11. Hart G.C., Wong K., Structural dynamics for structural engineers, John Wiley&Sons Inc.,
New York, 2000.
12. Kawulok M. i in., O uszkodzeniach budynków w obszarach ujawniania się wpływów
eksploatacji górniczej, Konferencja “Ochrona powierzchni i obiektów budowlanych przed
szkodami górniczymi”, Katowice, 1995, 339 – 342.

13. Kawulok M., Ocena właściwości użytkowych budynków z uwagi na oddziaływania górnicze,
ITB, Seria: Roprawy, Warszawa 2000.
14. Langer J., Dynamika ustrojów prętowych, Mechanika budowli z elementami ujecia
komputerowego, Arkady, Warszawa, 1984.
15.
Lipski Z., Wawrzynek A., Kubica J., Analiza stanu wytężenia wywołanego wstrząsami
górniczymi w budynkach jednorodzinnych w świetle PN-99/B-03002, XLVI Konferencja
Naukowa KILiW PAN i KN PZITB, Krynica 2000, 99-106.
16. Ledwoń J.A.; Aktualne zagadnienia ochrony miasta Bytomia przed szkodami górniczymi,
XXXI Konf. Nauk. KILiW PAN i KN PZITB, 1985, 129-136.
17. Maciąg E., Kuźniar K., Tatara T., Zastosowanie analizy modalnej do oceny drgań
prefabrykowanych budynków podlegających wymuszeniom kinematycznym, Archiwum
Inżynierii Lądowej, Vol. 32, No 1, 1986, 129-139.
18. Naeim F. (ed.), The seismic design handbook, Boston, Kluwer 2001.
19. Newmark N.M., Rosenblueth E., Fundamentals of earthquake engineering, Prentice Hall Inc.,
Englewood Cliffs, New York, 1981.
20.
PN-84/B-03264, Konstrukcje betonowe, żelbetowe i sprężone. Obliczenia statyczne i
projektowanie.
21. PN-B-03264:1999, Konstrukcje betonowe, żelbetowe i sprężone. Obliczenia statyczne i
projektowanie.
22. PN-85/B-02170, Ocena szkodliwości drgań przekazywanych przez podłoże na budynki.
23.
PN-87/B-03002, Konstrukcje murowe. Obliczenia statyczne i projektowanie.
24. PN-B-03002:1999, Konstrukcje murowe niezbrojone. Projektowanie i obliczanie.
25. Poljakow S.W., Sejsmostojkije konstrukcii zdanij, Izd. Wysszaja Szkoła, Moskwa 1969.
26. Sieczkowski J., Dmochowski G., Bielawski Cz., Wzmacnianie budynków systemu WWP w
Głogowie, Inż. I Bud., Nr 11/97, str. 563 – 568.
27. Spyrakos C.C., Finite element modeling in engineering practice, Pittsburgh, PA, 1996.
28. Tatara T., Działanie drgań powierzchniowych wywołanych wstrząsami górniczymi na niską
tradycyjną zabudowę mieszkalną, Zeszyty Naukowe Politechniki Krakowskiej, Inżynieria
Lądowa nr 74, Kraków 2002.
29. Zembaty Z., Rockburst induced ground motion – a comparative study, Soil Dynamics and
Earthquake Engineering, 24, (2004), 11-23.
Wyszukiwarka
Podobne podstrony:
analiza notatki 3 id 559208 Nieznany (2)
Lab5 Analiza sygnalu mowy Lab5 Nieznany
analiza ilosciowa 6 id 60541 Nieznany (2)
dodatkowe1 analiza 11 12 2 sem Nieznany
4 Analiza progu rentownosci id Nieznany (2)
Analiza finansowa wskazniki cd Nieznany (2)
dodatkowe8 analiza 2011 12 id 1 Nieznany
analiza zwiazkow organiczna id Nieznany (2)
Analiza struktury id 61534 Nieznany (2)
analiza ilosciowa 2 id 60539 Nieznany
analiza sk adu aminokwasowego g Nieznany (2)
B14 analiza plu przedzialy id 7 Nieznany
Cw Analiza finansowa bankow id Nieznany
analiza lancucha wartosci (7 st Nieznany
Analiza czynnikowa id 59935 Nieznany (2)
Darfur analiza kryzysu id 13186 Nieznany
Analiza Finansowa 3 id 60193 Nieznany (2)
więcej podobnych podstron