Planowanie  sieci  transportowych  

4.  Modelowanie  w  planowaniu  

transportu  

dr  inż.  Lech  Michalski  

Politechnika  Gdańska,  Wydział  Inżynierii  Lądowej  i  Środowiska,  Katedra  Inżynierii  Drogowej  

1

Plan  wykładu  

• 

Rola  modeli  

• 

Pożadane  cechy  modeli  i  ich  klasy  

• 

Rodzaje  modeli  w  modelowaniu  podróży  

• 

Modele  obszaru  (przestrzeni)  

• 

Modele  sieci  

• 

Modele  ruchu  

1.  Rola  modeli  w  procesie  planowania  

• 

Matematyczne  modelowanie  ruchu  (podróży)  

służy  

• 

Opisaniu  zachowań  transportowych  obecnych  

i  przyszłych  

• 

Oszacowaniu  potrzeb  przewozowych  

• 

Określenie  niezbędnych  działań  

organizacyjnych  i  inwestycyjnych  

• 

Ocena  skutków  proponowanych  rozwiązań  

2.  Pożądane  cechy  modeli  

• 

Dopasowanie  i  precyzja  

• 

Oszczedność  danych  i  żródeł  obliczeniowych  

• 

Zdolność  do  reprezentowania  procesów  i  
oddziaływań  

• 

Własciwe  rozmieszczenie  geograficzne  

Remenber:  „All  models  are  wrong,  however,  some  are  useful”  (Wszystkie  

modele  są  złe,  kilka  jest  użytecznych)  

Joseph  Sussman  

Klasy  modeli  możliwych  w  analizach  

transportowych  

• 

Prosta  formuła  y=f(x)  (np.  wypadki  jako  funkcja  pracy  

przewozowej)  

• 

modele  szeregów  czasowych  (np.  zmiany  wskaźnika  

motoryzacji)  

• 

Uśrednianie  i  wygładzanie  (np  średnie  prognozy)  

• 

Analiza  regresji  (np.  w  dokładniejszym  prognozowaniu)  

• 

Modele  estymacji  macierzowej  (np.  macierz  żródło  –  cel)  

• 

Modele  elastyczności  (np.  reprezentujące  wpływ  na  

transport  publiczny  cen  paliw  lub  częstotliwości  jazdy)  

• 

Modelowanie  wyboru  pomiędzy  alternatywami  

• 

Modele  symulacyjne  

Klasyfikacja  modeli  ruchu  (1)  

• 

Statyczne  

• 

Modele  średnich  sytuacji  

• 

Dynamiczne  

• 

Modele  sytuacji  zmiennych  w  czasie  

• 

Dyskretne  

• 

Niezależne  zmienne  wyrażone  w  liczbach  całkowitych  

• 

Stochastyczne  lub  deterministyczne  

• 

Modele  zakładają  zmienność  np.  czasu  reakcji,  każda  

symulacja  może  dać  inne  rezultaty  

• 

Kroków  czasowych  lub  zdarzeniowe  

• 

Co  1  s  lub  co  zdarzenie  

6

Klasyfikacja  modeli  ruchu  (2)  

• 

Bazujace  na  swoich  własnościach  

• 

Interpretacja  fizyczna  

• 

Dyskretne  a  ciagłe  

• 

Deterministyczne  a  stochastyczne  

• 

Bazujace  na  dynamicznym  potoku  

• 

Makroskopowe  

• 

Mezoskopowe  

• 

Mikroskopowe  

• 

Nanoskopowe  

7

Podejście  mikroskopowe  

• 

Mapy  pojedynczych  pojazdów  

• 

Reprezentują  

• 

Zintegrowaną  sieć  

• 

Szeroki  zakres  urządzeń  sterowania  

• 

Różne  klasy  pojazdów  

• 

Modelują  ruch  pojedynczych  pojazdów  

• 

Car  following  

• 

Zmiany  pasa  

• 

Sploty  i  rozploty  

• 

Autobusy  

• 

Uwzględniają  zachowania  

• 

Przed  podróżą  

• 

W  trakcie  podróży  

• 

Agresywność  i  podporządkowanie  się  

8

Podejście  makroskopowe  

• 

Dyskretyzacja  w  czasie  i  przestrzeni  

• 

Rozległe  sieci,  ograniczone  szczegóły  

• 

Brak  identyfikacji  pojedynczych  pojazdów  w  

potoku  

• 

Charakteryzacja  poprzez  wartości  

makroskopowe  jak  prędkość,  gęstość,  

natężenie  

• 

Potok  traktowany  jako  ciągły  płynny  potok  w  

dynamice  płynów  

9

Podejście  mezoskopowe  

• 

Pojedyńcze  pojazdy,  zagregowane  zachowania  

na  połączeniach  w  sieci  

• 

Typy  

• 

prędkość  =  f(gęstości)  

• 

automaty  komórkowe  (automata  theory)  

• 

Ogólne  zasady  

• 

zdefiniować  zasady  dla  wszystkich  uczestników  ruchu  

• 

zdefiniować  punkt  początkowy  

10

3.  Rodzaje  modeli  w  procesie  

modelowania  ruchu  

• 

Model  obszaru  

• 

Model  sieci  transportowej    

• 

Model  ruchu  

4.  Model  obszaru  

• 

Zasady  ustalania  granic  obszaru  i  podziału  na  rejony  

• 

Zapis  struktury  modelu  obsaru  

» 

Q=(Z,  E)  

 

 zbiór  elementów  obszaru  

» 

Z=(1,2…..i…..m)    zbiór  rejonów  w  obszarze  

» 

E=(m+1,  .j….n)    zbiór  wlotów  do  obszaru  

» 

i=1,2,…m    

 numery  rejonów  

» 

J=m+1,….n    

 

 numery  wlotów  

• 

Charakterystyka  obszaru  –  wartości  mające  wpływ  na  

wielkość  i  kierunek  generowanego  ruchu  np.  LM,  

LMP,    

5.  Model  sieci  

• 

Elementy  mające  wpływ  na  rozkład  ruchu  

• 

Struktura  sieci  (graf)  

» 

G  {  W,  L  }  

» 

W={  1,2….i….m  }  

» 

i=1,2,...m  

» 

L={l=<i,j>;  i,  j  ЄW  }  

• 

Sieć  jest  spójna  jeśli  pomiędzy  każdą  parą  

węzłów  istnieje  co  najmniej    jedna  droga  

Podstawowe  strukturalne  własności  

grafu  

• 

Symetria  i  asymetria  

• 

Dopasowanie  lub  niedopasowanie  

• 

Kompleksowość  

• 

Łączność/spójność  

• 

Uzupełnianie  

• 

Korzenie,  drzewa,  przesmyk  

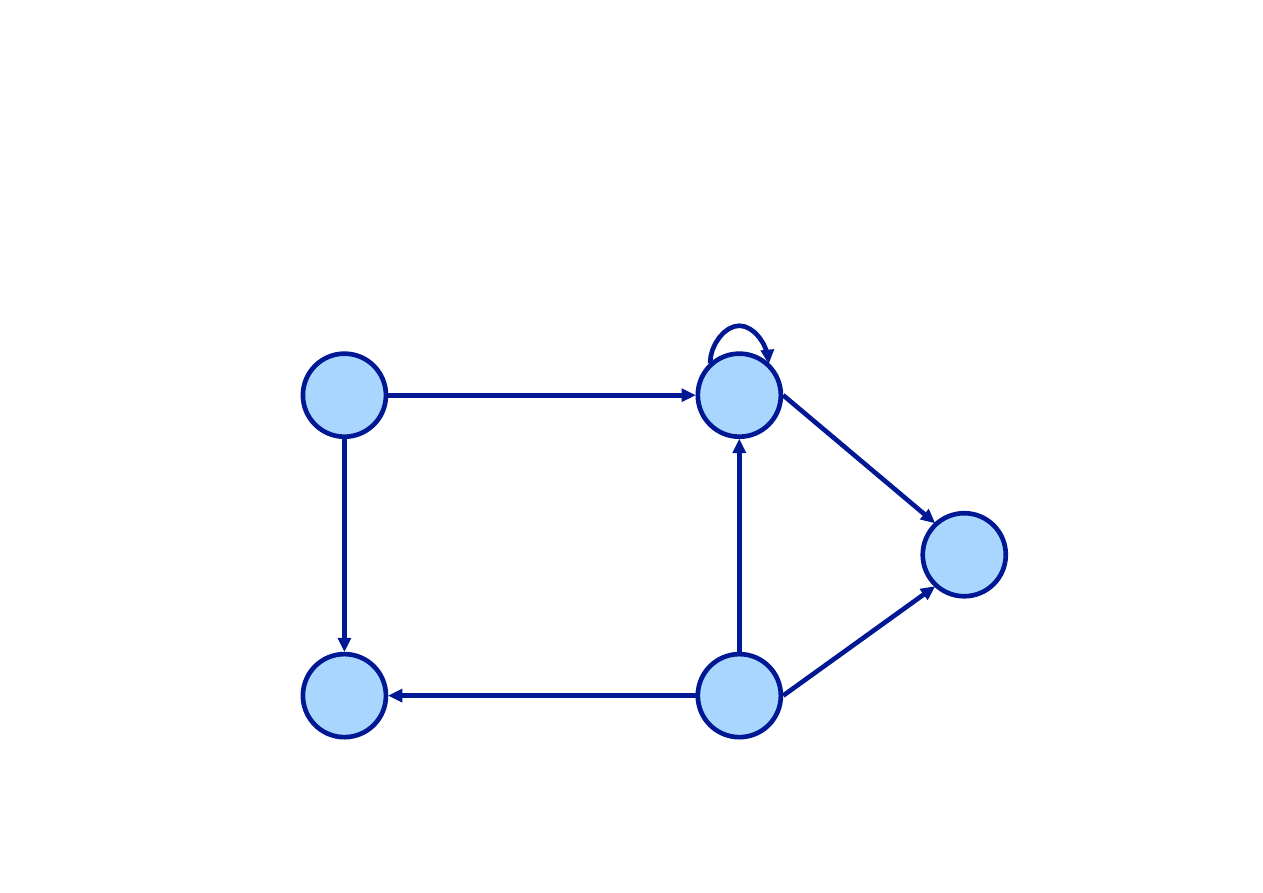
Podstawowy  graf  przedstawiający  

sieć  transportową  

1

2

3

4

5

wierzchołek (

węzeł

)

krawędź (

połączenie

)

klamra

Copyright © 1998-2010, Dr. Jean-Paul Rodrigue, Dept. of Global Studies & Geography, Hofstra University.

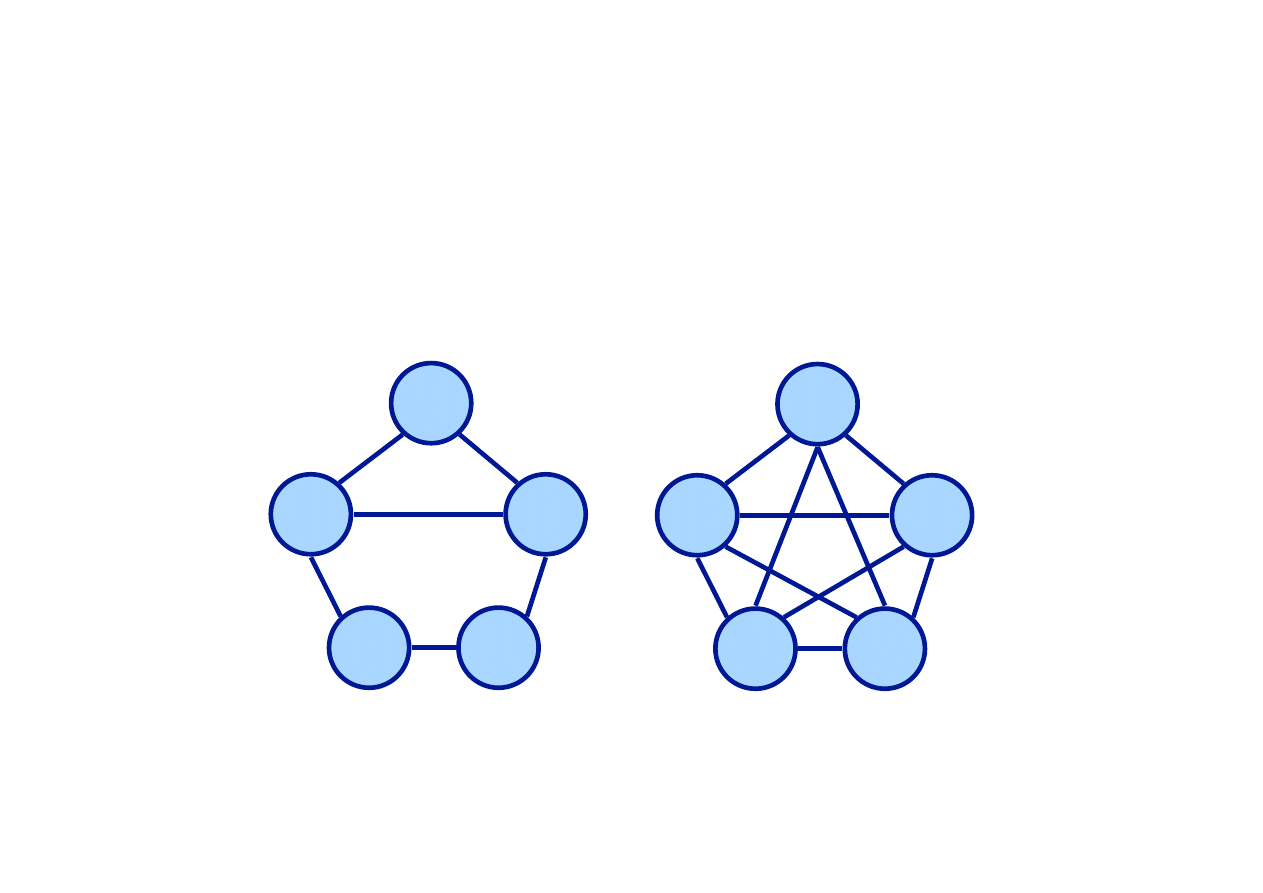
Graf  płaski  i  niepłaski  

Płaski

niepłaski

A

B

Copyright © 1998-2010, Dr. Jean-Paul Rodrigue, Dept. of Global Studies & Geography, Hofstra University.

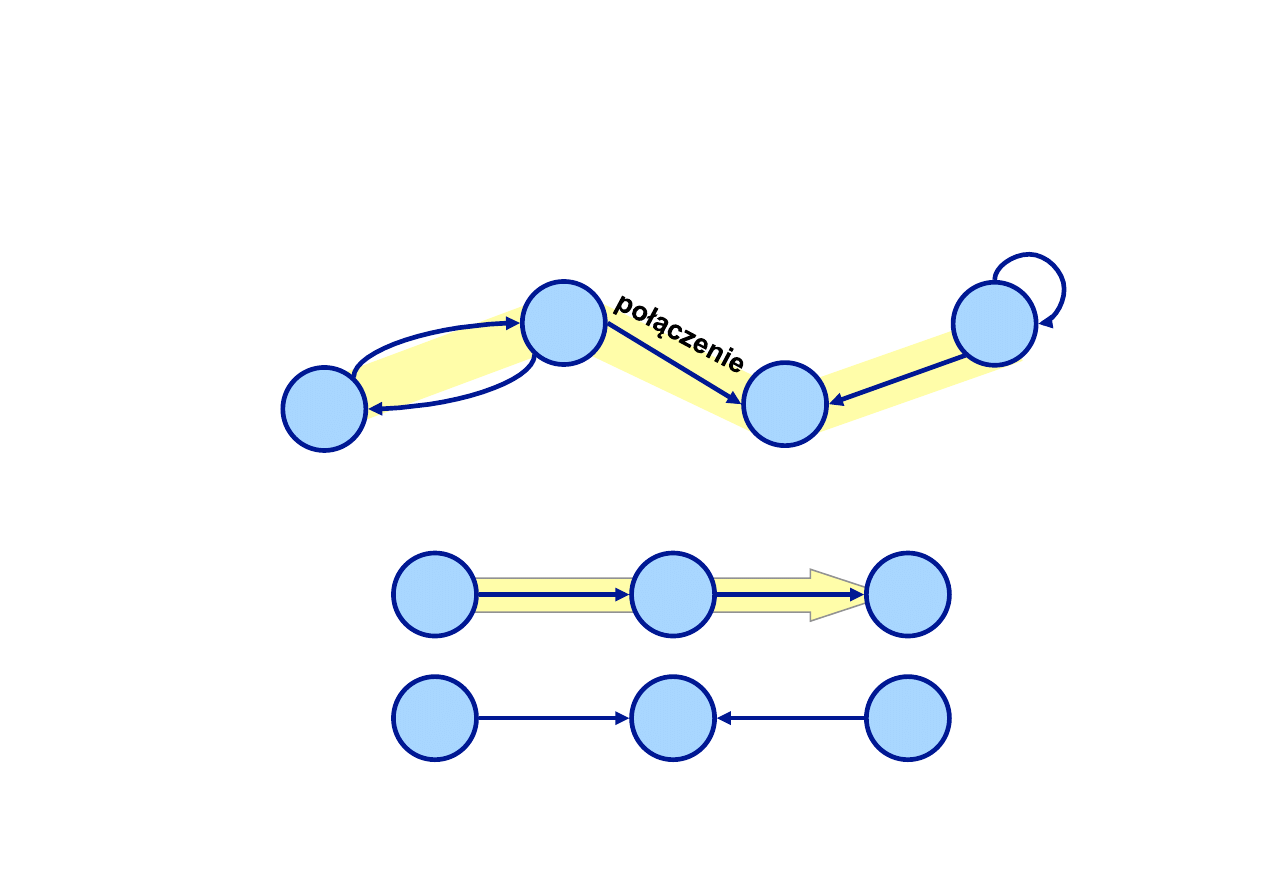
Połączenie  i  ścieżka  

1

2

3

4

łącze

1

2

3

B

1

2

3

C

ścieżka (1 to 3)

A

Copyright © 1998-2010, Dr. Jean-Paul Rodrigue, Dept. of Global Studies & Geography, Hofstra University.

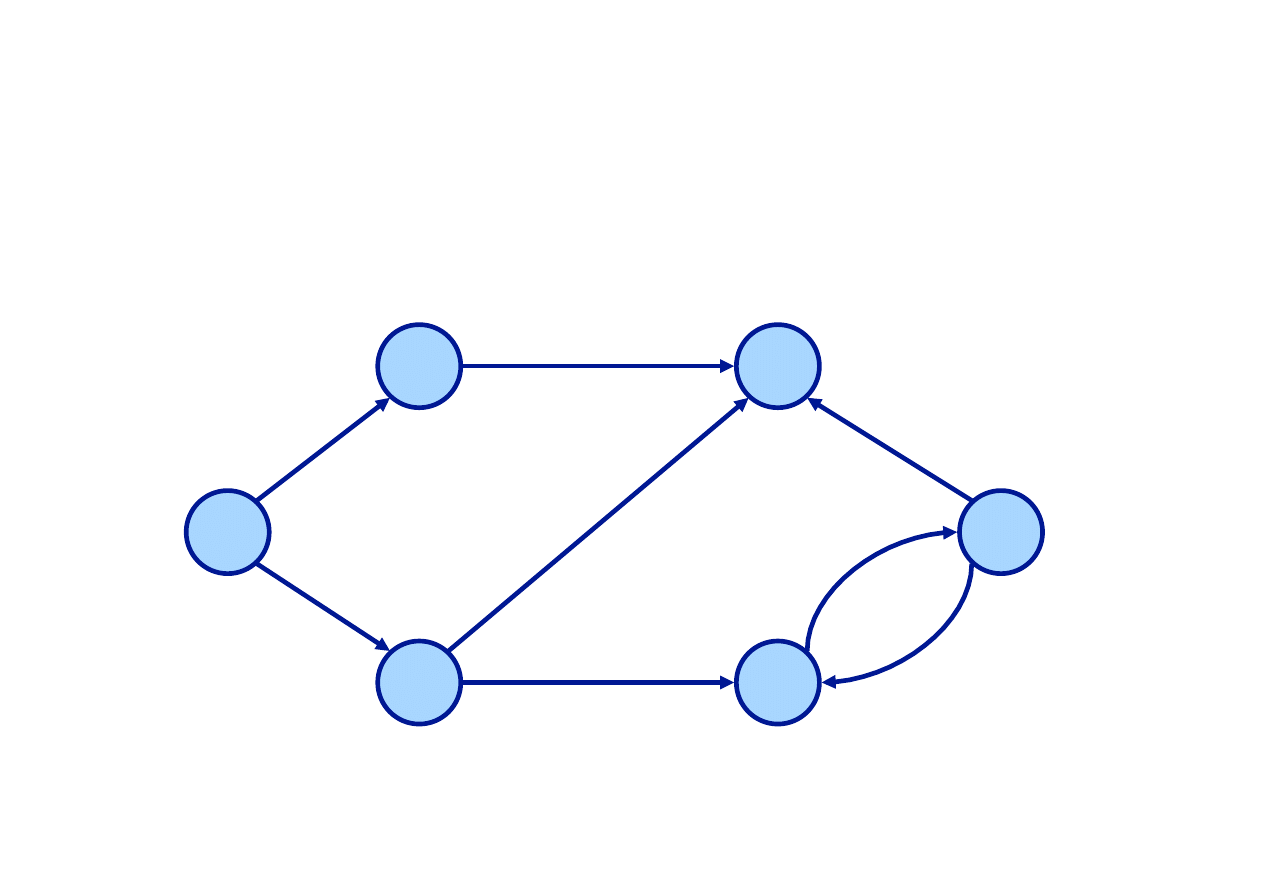
Długość  łącza,  połączenia  lub  ścieżki  

1

2

3

4

5

6

2 km

5 km

6 km

7 km

4 km

2 km

2 km

3 km

Copyright © 1998-2010, Dr. Jean-Paul Rodrigue, Dept. of Global Studies & Geography, Hofstra University.

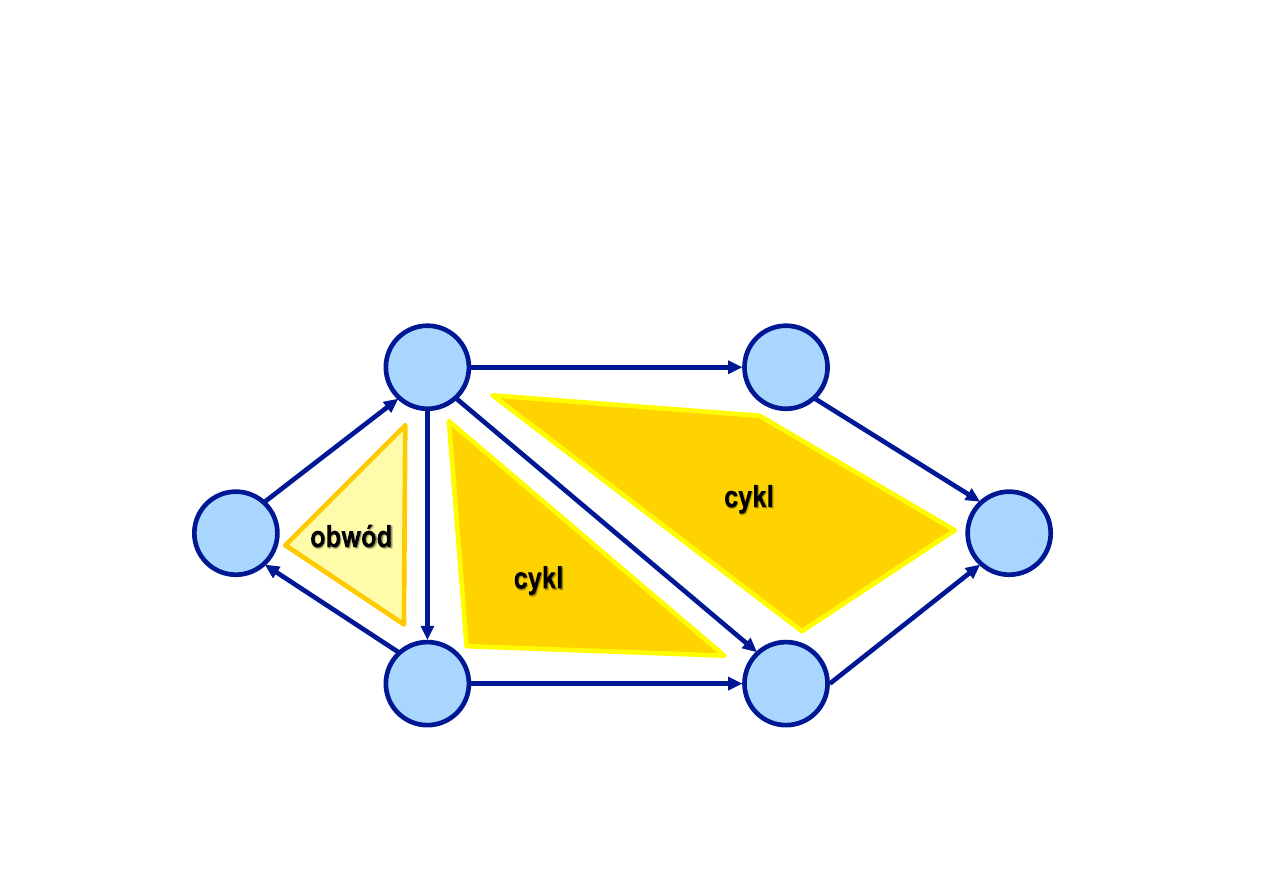
Cykl  i  obwód    

1

2

3

4

5

6

Copyright © 1998-2010, Dr. Jean-Paul Rodrigue, Dept. of Global Studies & Geography, Hofstra University.

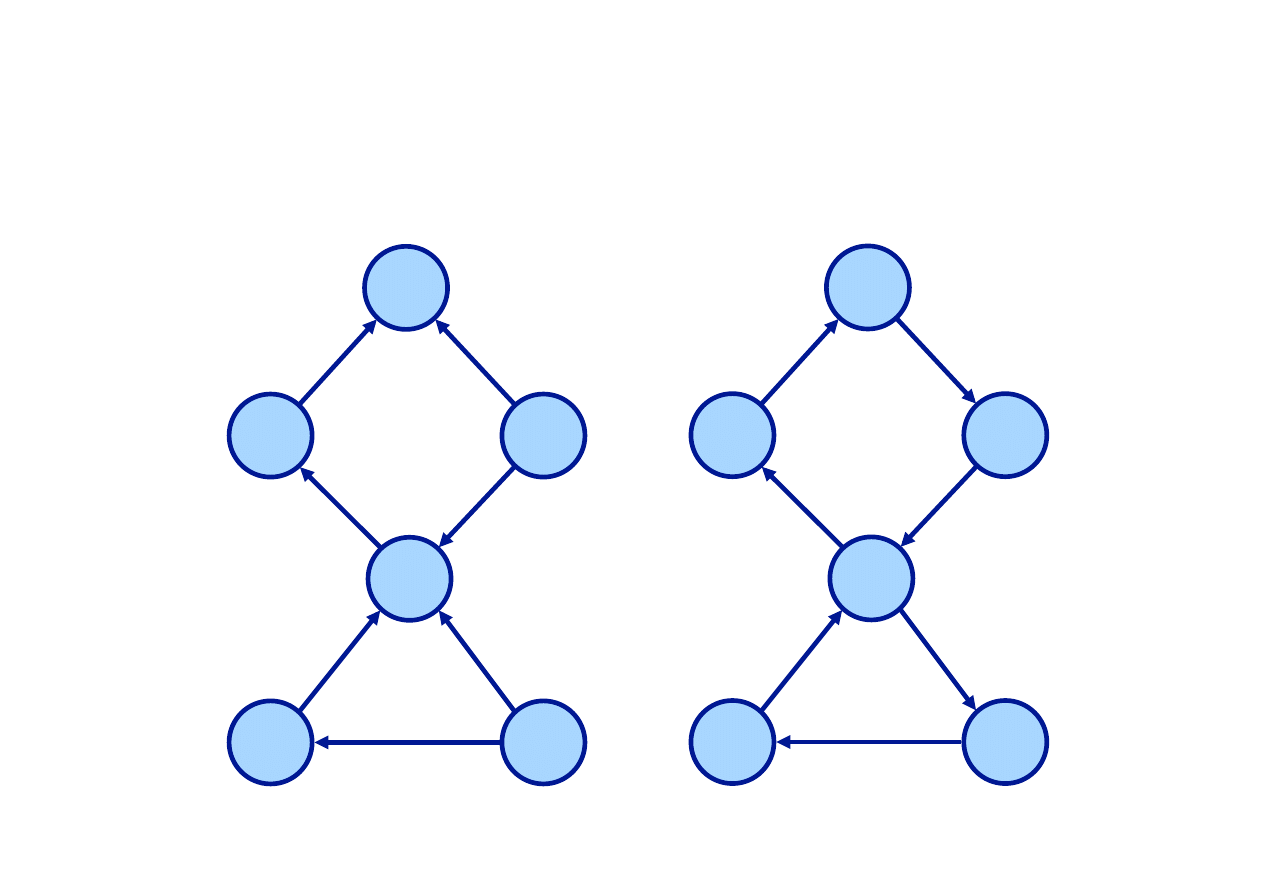
Łączność  w  grafie  

1

2

3

4

5

6

A

1

2

3

4

5

6

B

Copyright © 1998-2010, Dr. Jean-Paul Rodrigue, Dept. of Global Studies & Geography, Hofstra University.

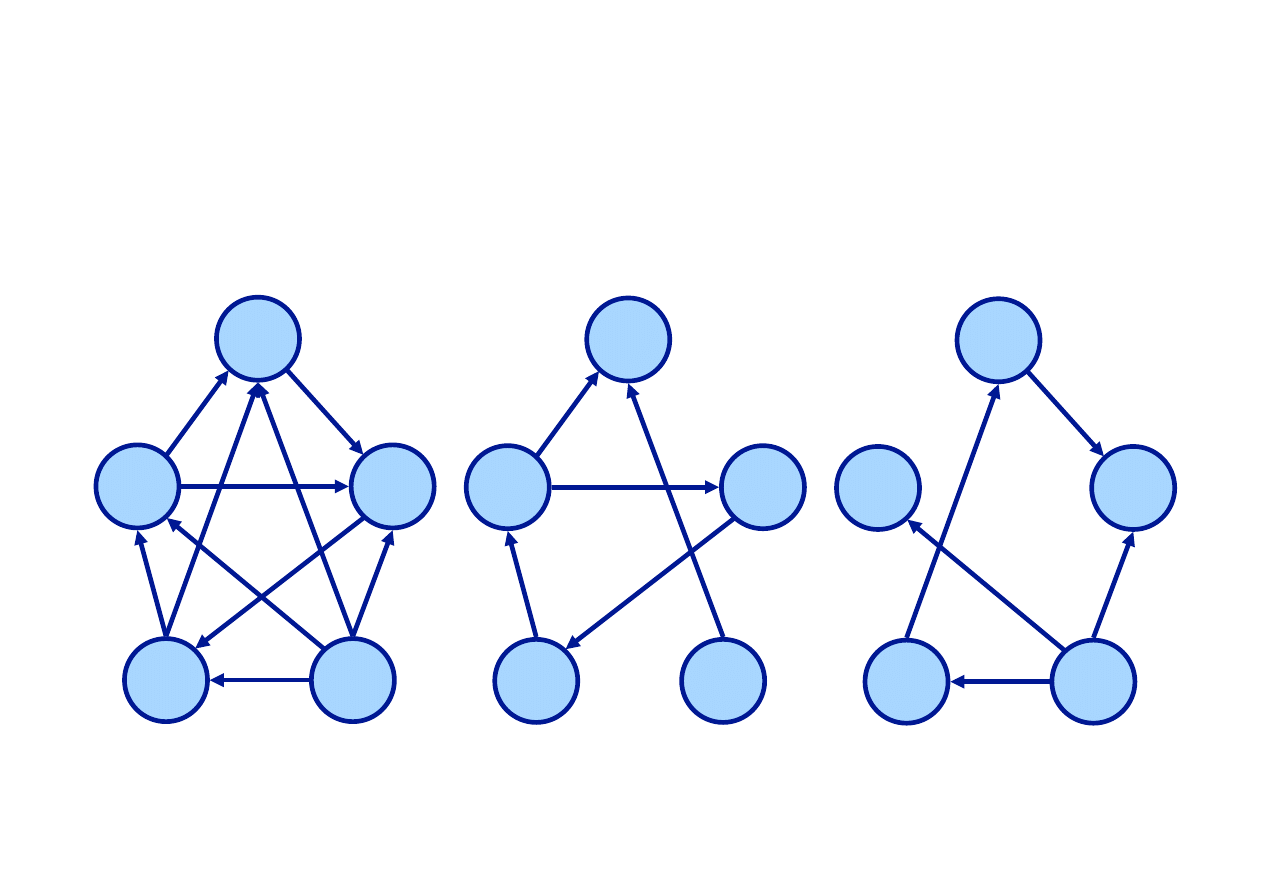
Grafy  komplementarne  

1

2

3

4

5

1

2

3

4

5

1

2

3

4

5

G=X+Y

X

Y

Copyright © 1998-2010, Dr. Jean-Paul Rodrigue, Dept. of Global Studies & Geography, Hofstra University.

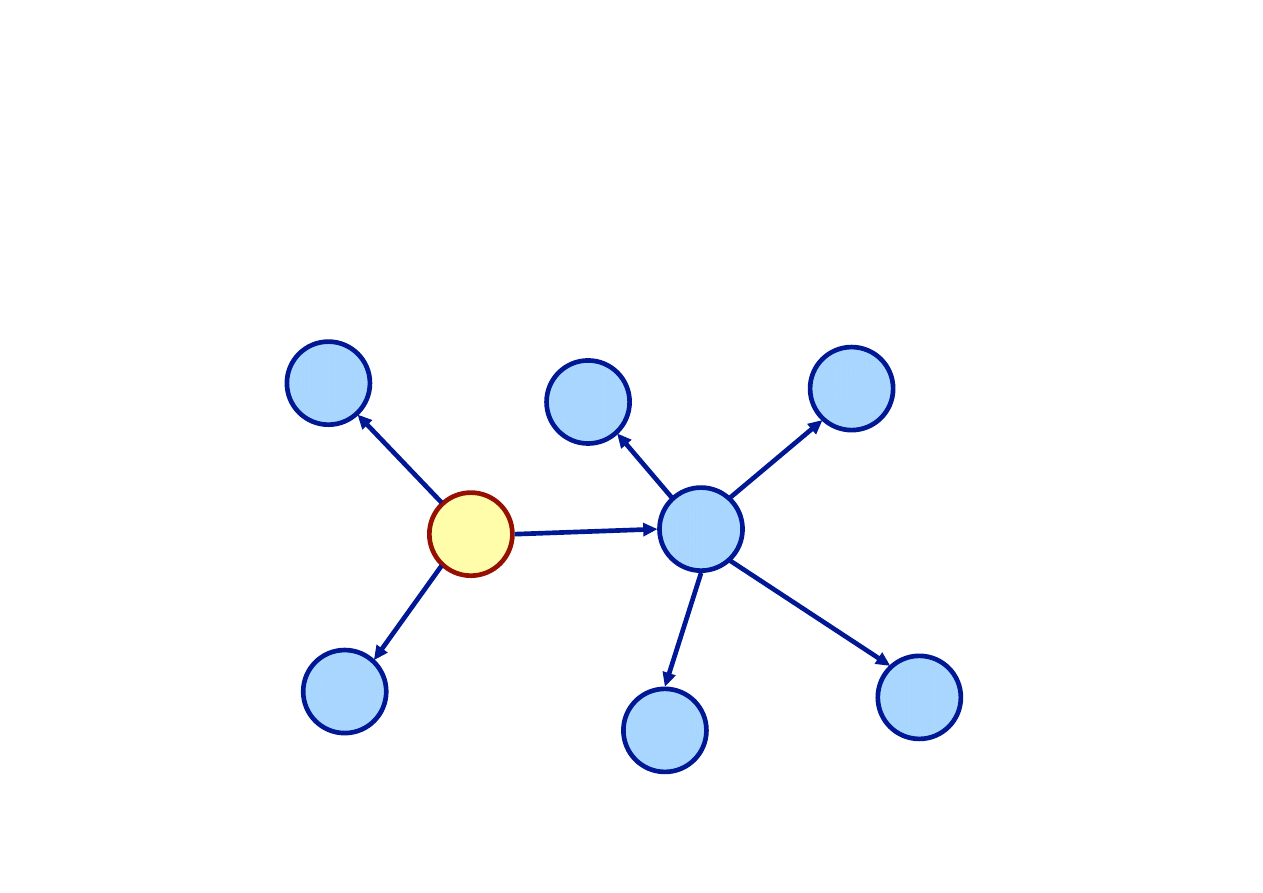
Graf  rozgałęźny    

1

2

3

4

5

6

8

7

korzeń

Copyright © 1998-2010, Dr. Jean-Paul Rodrigue, Dept. of Global Studies & Geography, Hofstra University.

6.  Modelowanie  oddziaływań  

pomiędzy  transportem  a  

zagospodarowaniem  przestrzennym    

• 

Modelowanie  statyczne.  Określenie  stanu  systemu  w  danej  

chwili  poprzez  klasyfikacje  i  działania  arytmetyczne  na  

reprezentatywnych  zmiennych  

• 

Modelowanie  systemowe.  Określenie  zachowania  systemu  

przy  danych  zależnościach  pomiędzy  zmiennymi.  Przykładowo  

model  grawitacyjny  

• 

Modelowanie  oddziaływań  między  systemami.  Próba  

integracji  kilku  modeli  do  formy  meta-­‐systemu  (system  

kompleksowy  i  rozległy)  

• 

Modelowanie  w  środowisku  podejmowania  decyzji.  Dotyczy  

nie  tylko  samych  zależności  „transport  a  zagospodarowanie”,  

ale  także  zastosowanie  wyników  przy  formułowaniu  strategii  i  

rekomendacji.    

Model  transport/zagospodarowanie  

przestrzenne    

jako  procedura  sekwencyjna  

• 

Generacja  podróży.  Określenie  stopnia  w  jakim  dana  jednostka  

przestrzenna  jest  źródłem  i  celem  ruchu.  

• 

Rozkład  podróży.  Model,  który  określa  przemieszczanie  pomiędzy  

źródłem  i  celem,  mogący  uwzględnić  przeszkody  takie  jak  

odległość.  

• 

Podział  modalny.  Przemieszczenia  pomiędzy  źródłem  i  celem  są  

rozdzielone  pomiędzy  środki  transportu,  zależnie  od  dostępności  

środka,  kosztów  i  preferencji.    

• 

Obciążenie  ruchem.  Wszystkie  podróże    z  podziałem  na  źródłowe,  

docelowe  oraz  srodki  transportu  obciążają  sieć  transportową.    

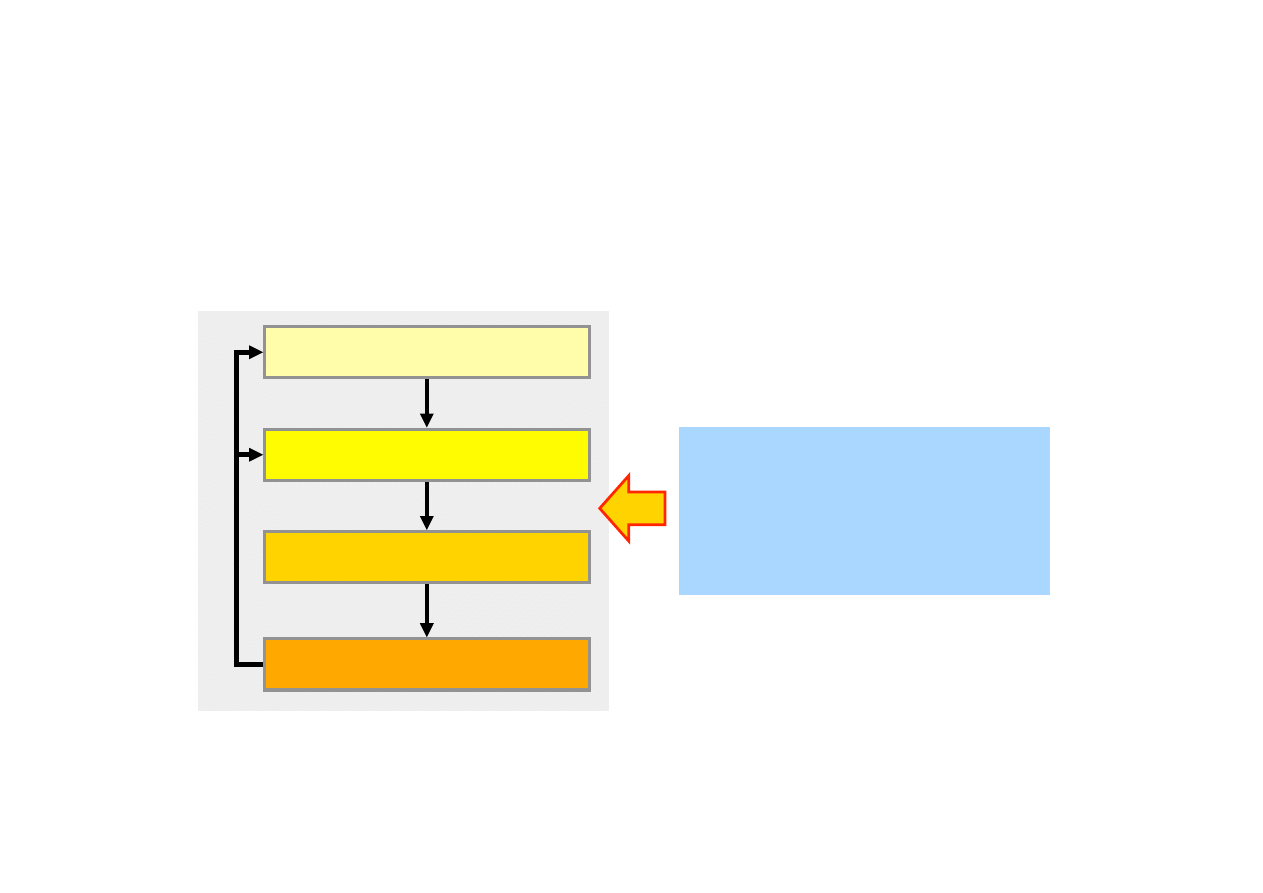
Model  4  poziomowy    

Generacja podróży

Rozkład podróży

Podział przwozów

Obciążenie ruchem

•  dane o zagospodarowaniu
•  czynniki generacji podróży
•  czynniki oporu przestrzeni
•  czynniki kalibracji
•  sieć transportowa

Fe

edba

ck

Copyright © 1998-2010, Dr. Jean-Paul Rodrigue, Dept. of Global Studies & Geography, Hofstra University.

Wymagane  dane  do  modelu  

• 

Zagospodarowanie  przestrzenne  

• 

Czynniki  generacji  podróży  

• 

Czynniki  oporu  przestrzeni  

• 

Czynniki  kalibracji  

• 

Sieć  transportowa  

Modele  generacji  podróży  

• 

Zwykle  na  poziomie  rejonu  (zony)  

• 

Najczęściej  klasyfikacja  krzyżowa  (cross-­‐

classificaron,  category  analysis)  i  analiza  regresji  

wielokrotnej;    

• 

Klasyfikacja  umożliwia  identyfikację  specyficznych  

grup  socjoekonomicznych  w  populacji  mającej  

podobne  charakterystyki  generacji  podróży  

• 

Analiza  regresji  określa  liczbę  podróży  

wytwarzanych  przez  rejon  jako  funkcja  wielu  

zmiennych  niezależnych  

Modele  przestrzennego  rozkładu  

podróży  

• 

Najczęściej  używaną  techniką  jest  model  

grawitacyjny  

• 

Jest  wiele  form  modelu  grawitacyjnego  i  wiele  

technik  kalibracji  tego  modelu.  Klasyfikacja  

krzyżowa  lub  regresja  wielokrotna  może  być  

także  uzywana  do  obliczania  liczby  podróży  

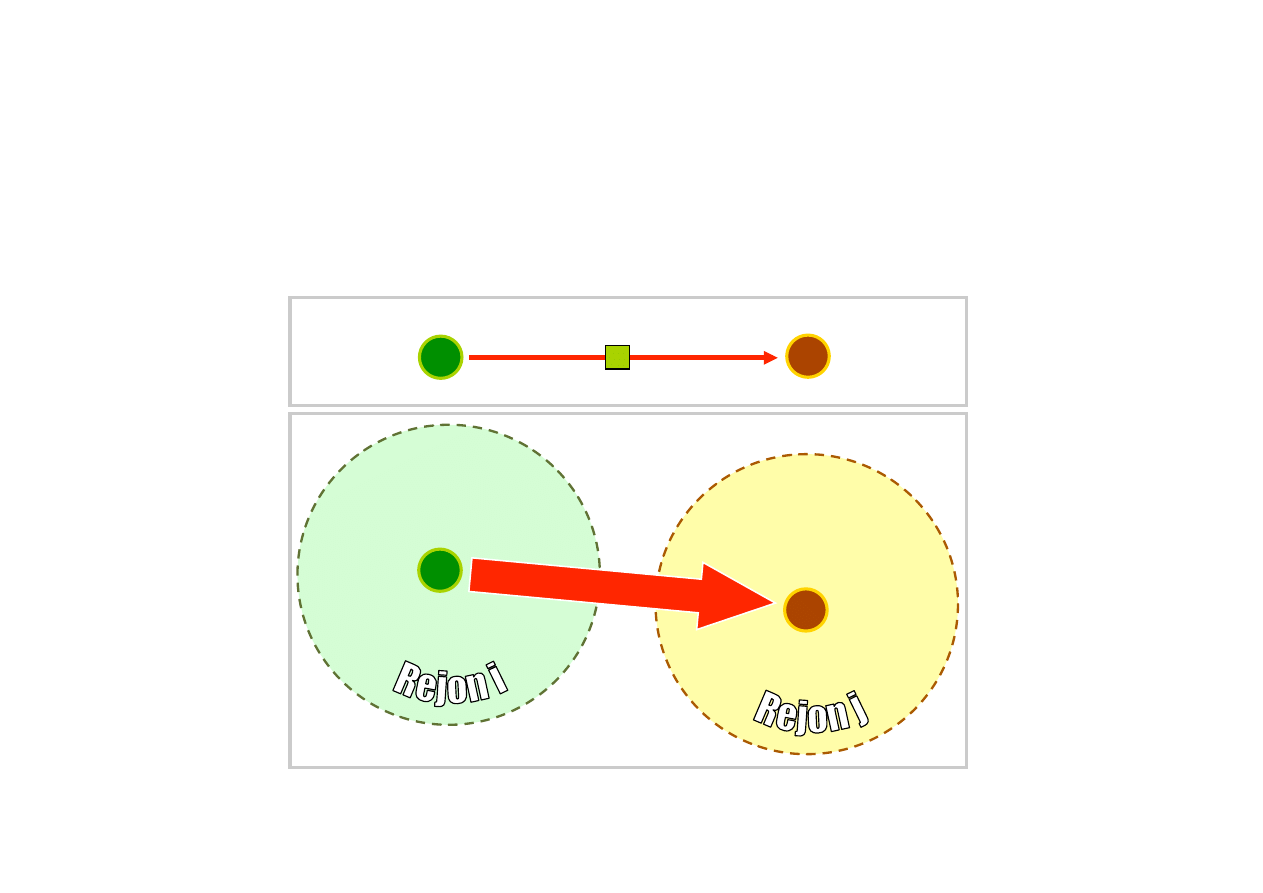
Przedstawienie  przemieszczenia  jako  

interakcja  przestrzenna  

i

Tij = 50

j

Centroid

Centroid

i

j

Wektor

Przemieszczenie

Interakcja przestrzenna

Copyright © 1998-2010, Dr. Jean-Paul Rodrigue, Dept. of Global Studies & Geography, Hofstra University.

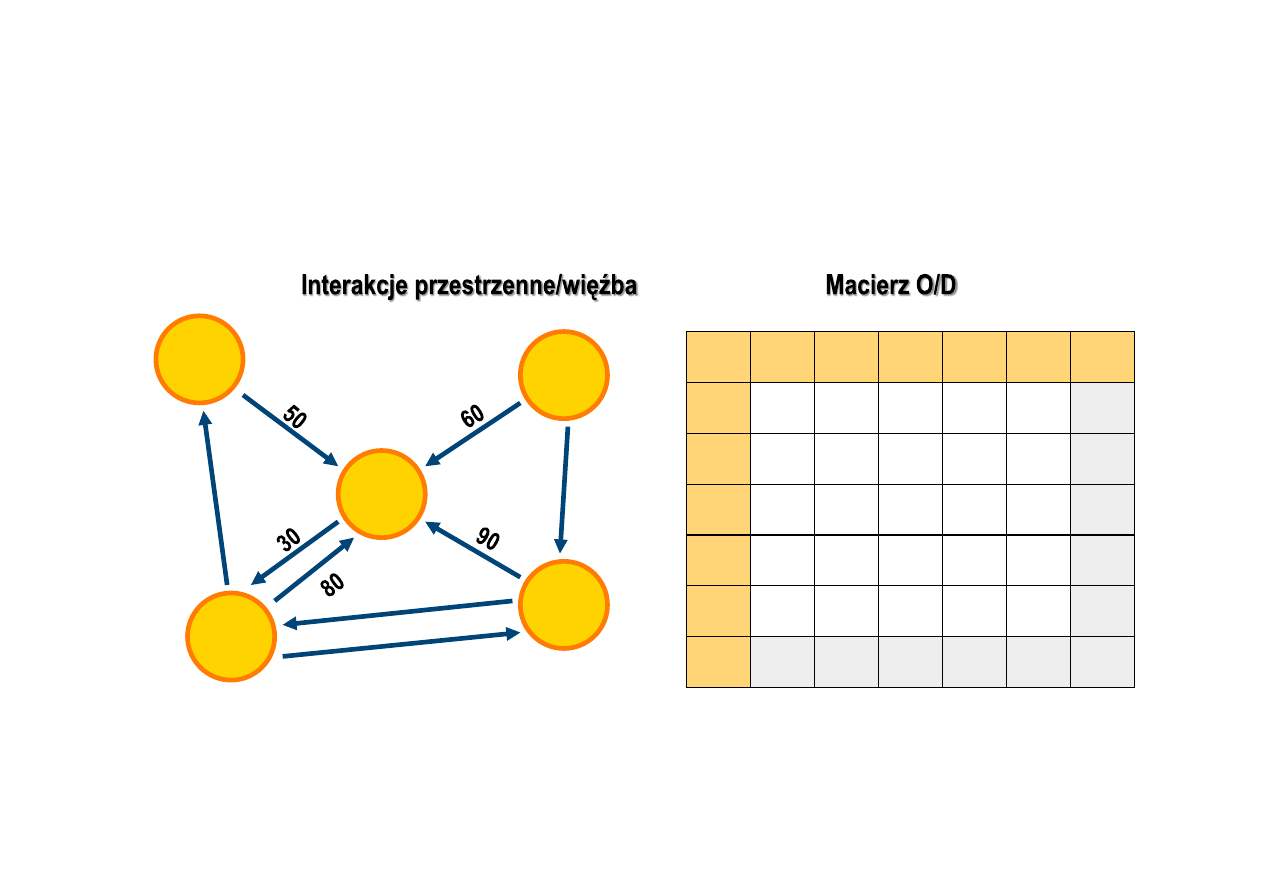
Konstruowanie  macierzy    O/D  

A

B

C

D

E

Ti

A

0

0

50

0

0

50

B

0

0

60

0

30

90

C

0

0

0

30

0

30

D

20

0

80

0

20

120

E

0

0

90

10

0

100

Tj

20

0

280

40

50

390

A

C

B

E

D

20

20

10

30

Copyright © 1998-2010, Dr. Jean-Paul Rodrigue, Dept. of Global Studies & Geography, Hofstra University.

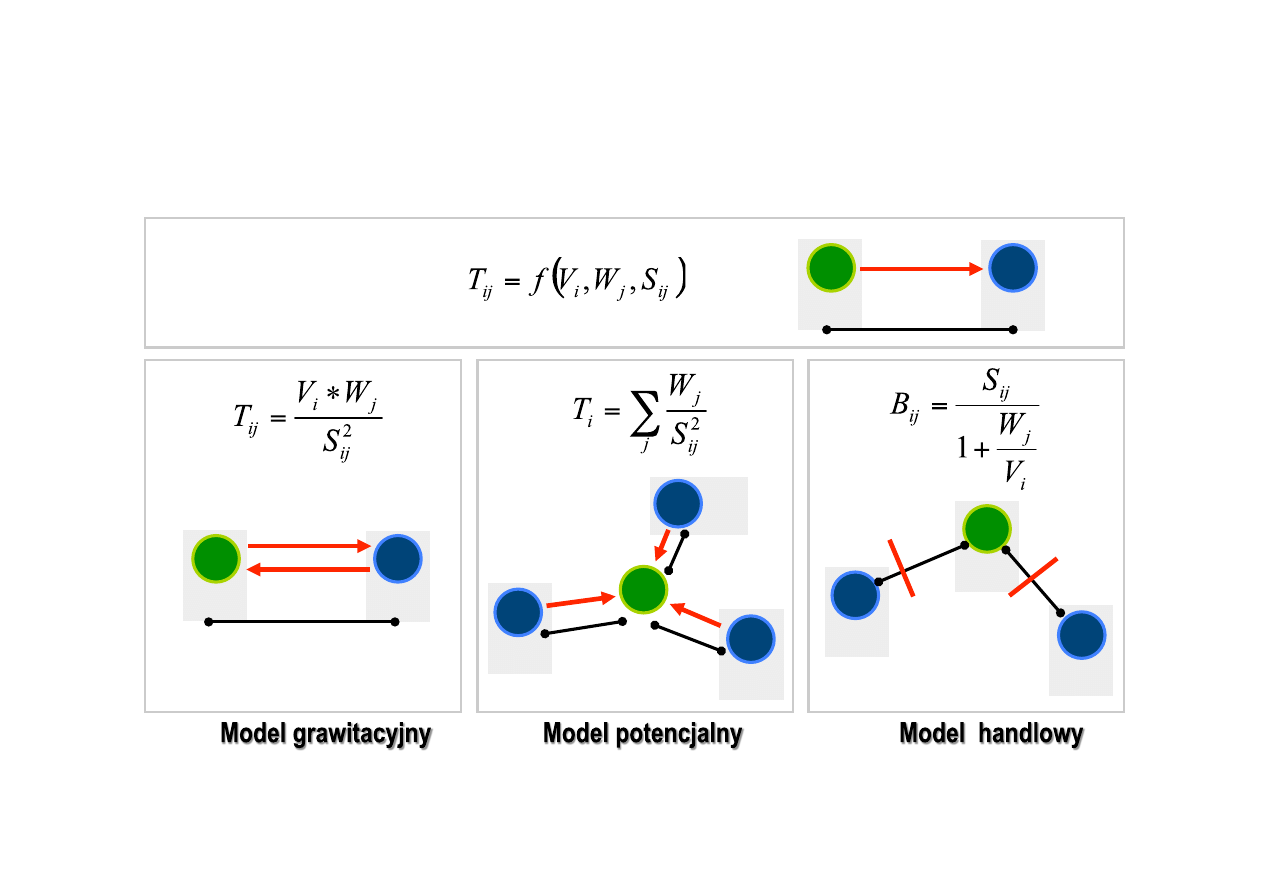
Trzy  podstawowe  modele  interakcji  

i

j

Formuła ogólna:

V

W

T

ij

S

ij

i

j

35

20

S

ij

= 8

T

ij

= 10.9

T

ji

= 10.9

i

j

k

l

20

15

35

3

5

6

1.0

0.6

2.2

T

i

= 3.8

i

j

k

15

40

35

7

6

B

ij

= 4.9

B

ik

= 2.8

Copyright © 1998-2010, Dr. Jean-Paul Rodrigue, Dept. of Global Studies & Geography, Hofstra
University.

Model  wyboru  środka  transportu  

• 

Udział  w  podróżach  kierowców,  pasażerów  

rowerzystów,  pieszych  itp.  

• 

Modelowanie  logitowe  uwzględniające  

preferencje  użytkowników  jako  

prawdopodobieństwo  użycia  środka  

transportu  na  każdym  połączeniu  źródło  –  cel  

Obciążenie    ruchem  

• 

Szacowane  przestrzenne  wzorce  przemieszczeń  

różnymi  środkami  transportu,  podróże  są  

przypisywane  różnym  połączeniom  

transportowym  

• 

Są  wykonywane  głównie  z  zastosowaniem  

operacyjnych  metod  badawczych  

umożliwiających  minimalizację  kosztów  lub  czasu  

podróży  lub  czasu  w  sieci  transportowej  

• 

Modele  “ograniczonej  przepustowości”  i  

“wszystko  albo  nic”  lub    “wielu  ścieżek”