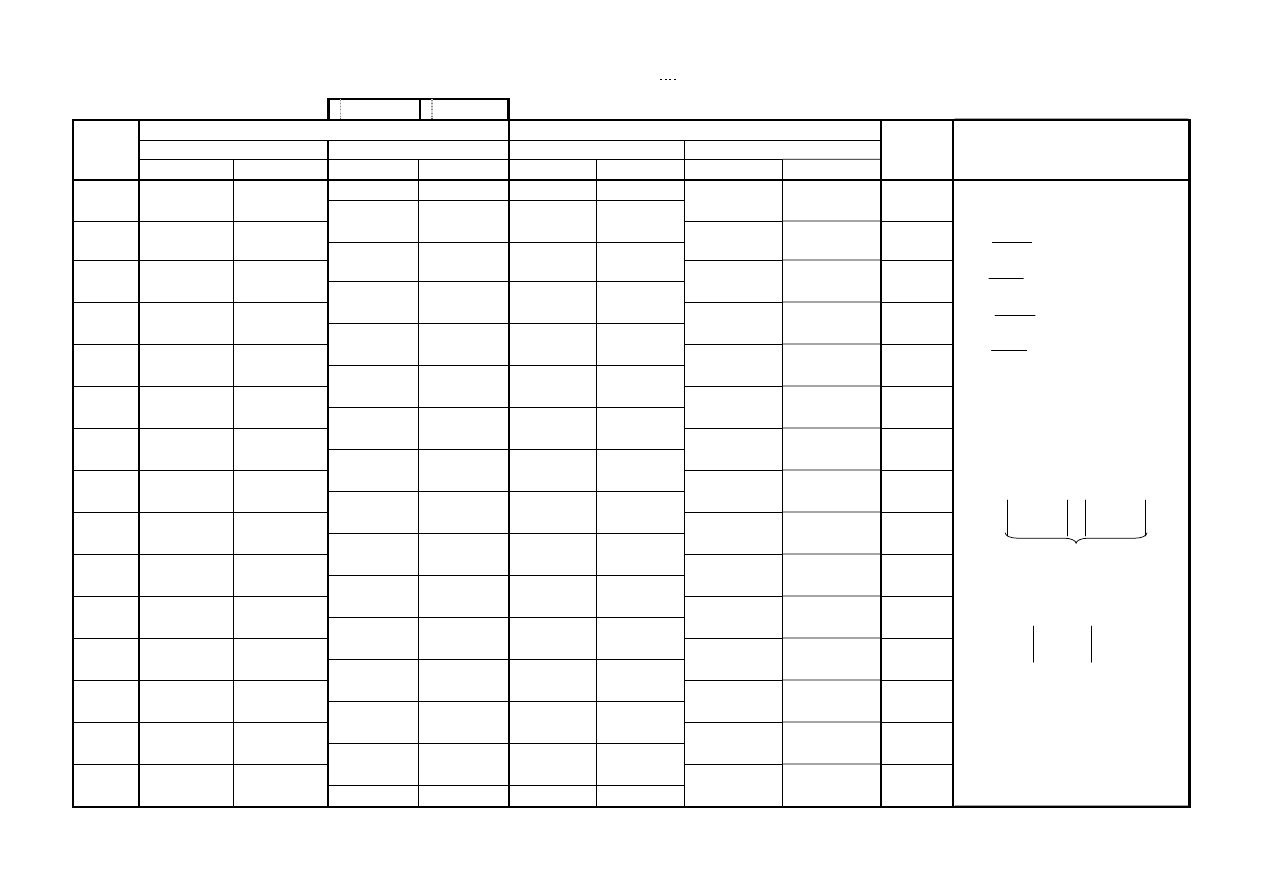
Przeliczanie współrzędnych z jednego układu prostokątnego na drugi

Transformacja współrzędnych dla 3 punktów dostosowania

u =

v =

Oznaczenie

lub nr

punktu

Układ pierwotny

Układ wtórny

Oznaczenie

lub nr punk-

tu

Wzory, obliczenia pomocnicze,

uwagi, szkice

Współrzędne Przyrosty

Przyrosty

Współrzędne

X

P

Y

P

Δx

P

Δy

P

Δx

W

Δy

W

X

W

Y

W

Obliczenie współrzędnych bieguna przekształ-
cenia B w obu układach:
( n – liczba punktów dostosowania)

X

X

n

Y

Y

n

B

P

dost

P

B

P

dost

P

= ∑

= ∑

=

=

X

X

n

Y

Y

n

B

W

dost

W

B

W

dost

W

= ∑

= ∑

=

=

Obliczenie w obu układach przyrostów po-
między poszczególnymi punktami dostosowa-
nia a biegunem (zamieścić w osobnej tabeli):

Δ

Δ

Δ

Δ

x

X

X

y

Y

Y

x

X

X

y

Y

Y

i

P

i

P

B

P

i

P

i

P

B

P

i

W

i

W

B

W

i

W

i

W

B

W

=

−

=

−

=

−

=

−

;

;

Obliczenie współczynników transformacji: u,

v.

( , )

.....

[ ],[ ]

u v

x

y

x

y

x

y

x

y

P

P

W

W

n

P

n

P

n

W

n

W

= Δ

Δ

Δ

Δ

Δ

Δ

Δ

Δ

1

1

1

1

1 2

n tabel

Obliczenie przyrostów w układzie wtórnym

pomiędzy kolejnymi punktami, na podstawie
analogicznych przyrostów w układzie pier-
wotnym:

(

,

)

,

Δ

Δ

Δ

Δ

x

y

x

y

u

v

W

W

P

P

=

1 2

...............................

...............................

...............................

...............................

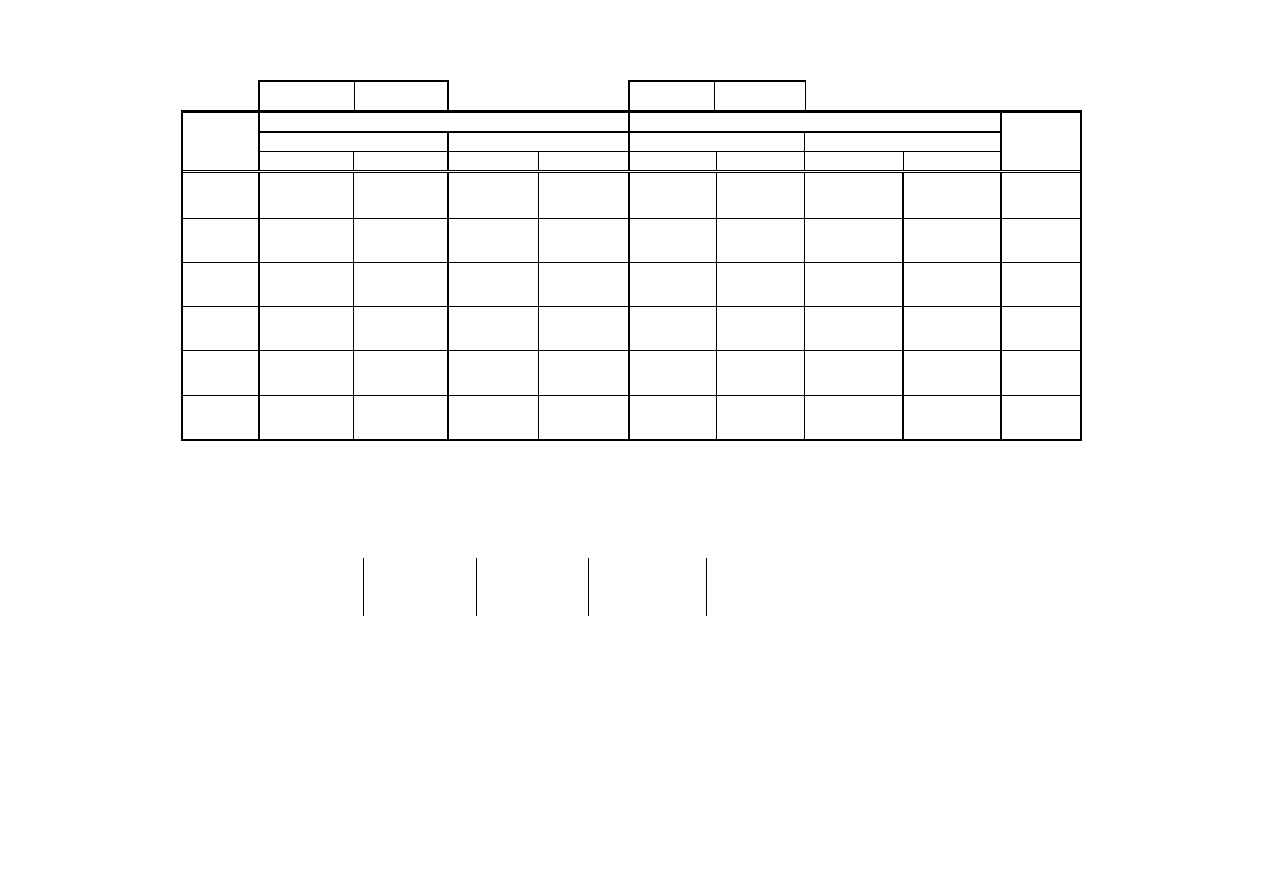
Obliczenie w obu układach przyrostów pomiędzy poszczególnymi punktami dostosowania a biegunem:

X

B

P

= Y

B

P

=

X

B

W

=

Y

B

W

=

Oznaczenie

punktu

dostosowania

Układ pierwotny

Układ wtórny

Oznaczenie

punktu

dostosowania

Współrzędne Przyrosty Współrzędne Przyrosty

X

P

Y

P

Δx

P

Δy

P

X

W

Y

W

Δx

W

Δy

W

Zestawienie formy rachunkowej do obliczenia współczynników transformacji:

( , )

.......... ..........
.......... ..........

.......... ..........
.......... ..........

.......... ...........
.......... ...........

(.................

[ ],[ ]

u v

=

=

1 2

.,................)