O

grzewajmy niewielki kawa∏ek
metalu, a˝ zacznie odparowy-
waç. Gazowy metal wpuÊçmy

przez wàskà dysz´ do komory pró˝nio-
wej. Co si´ stanie? Struga czàstek kon-
densuje si´ w maleƒkie skupiska – kla-
stery – czasem ledwie kilkuelementowe,
kiedy indziej zawierajàce nawet dzie-
siàtki tysi´cy atomów. Metaliczne kla-
stery znacznie mniejsze od kropel wody
lub ziaren piasku to nowa fascynujàca
forma organizacji materii.

Wi´kszoÊç tego rodzaju ekspery-

mentów dotyczy bardzo drobnych
obiektów, w zasadzie jednak klastery
mogà byç ca∏kiem du˝e – zajmujà miej-
sce gdzieÊ pomi´dzy izolowanymi ato-
mami i czàsteczkami a makroskopowy-
mi zlepkami cia∏ sta∏ych lub cieczy.
W pewnym sensie ∏àczà wi´c mikro-
i makrokosmos, a dla teoretyka sà êró-
d∏em intrygujàcych problemów fizycz-
nych: dlaczego niektóre klastery sà
trwalsze od innych? ile potrzeba ato-

mów, aby ma∏y zlepek zaczà∏ przypo-
minaç makroskopowà grudk´? I wresz-
cie jak zmienia si´ struktura podczas do-
dawania kolejnych atomów?

Zjawiskami zwiàzanymi z klaste-

rami interesujà si´ nie tylko fizycy teo-
retycy. Chemicy przemys∏owi na przy-
k∏ad wiedzà z praktyki, ˝e obiekty te
mogà byç wyjàtkowo dobrymi kata-
lizatorami. Jednak aby efektywnie
badaç ich w∏aÊciwoÊci, nale-
˝y dok∏adnie zrozumieç pod-

Klastery metali

i liczby magiczne

Badania okruchów materii pomagajà wyjaÊniç,

dlaczego w∏aÊciwoÊci ma∏ych zlepków atomów tak bardzo ró˝nià si´

od makroskopowych próbek cia∏ sta∏ych

Matthias Brack

SLIM FILMS

Â

WIAT

N

AUKI

Luty 1998 35

stawowe zasady, w
myÊl których powsta-
jà. Minione dziesi´cio-
lecie znacznie zbli˝y∏o nas
do tego celu.

Magia trwa∏oÊci

Podstawowà osobliwoÊcià, którà na-

ukowcy muszà wyt∏umaczyç, jest zja-
wisko szczególnie uprzywilejowanego
pojawiania si´ klasterów okreÊlonych
rozmiarów. Chemicy zetkn´li si´ ju˝
z tym problemem przed mniej wi´cej
130 laty podczas formu∏owania uk∏adu
okresowego pierwiastków. Otó˝ stwier-
dzili, ˝e niektóre pierwiastki wyró˝nia-
jà si´ trwa∏oÊcià, a ich atomy charak-
teryzujà si´ pewnymi szczególnymi
liczbami elektronów. Gazowe pierwiast-
ki o 2, 10, 18, 36 i 54 elektronach na-
zwali „szlachetnymi”, poniewa˝ b´dàc
chemicznie oboj´tne, nie oddzia∏ywa∏y
z innymi, „pospolitymi”.

W naszym stuleciu fizycy odkryli wy-

jàtkowà trwa∏oÊç jàder atomowych za-
wierajàcych 2, 8, 20, 28, 50, 82 i 126 pro-
tonów lub neutronów. Liczby te nazwali
wi´c magicznymi. „Magicznie stabil-
ne” jest na przyk∏ad jàdro o∏owiu ze

swymi 82 protona-

mi (jeden z izo-

topów o∏owiu,

zawierajàcy 126

neutronów, nazy-

wany jest podwój-

nie magicznym) .

Okaza∏o si´, ˝e klastery

atomowe równie˝ mogà byç

„magiczne”. W roku 1984 grupa

naukowców z University of Cali-
fornia w Berkeley zajmowa∏a si´
klasterami tworzonymi przez gorà-
ce atomy sodu. Zauwa˝ono wów-

czas szczególnie cz´ste wyst´po-
wanie zlepków o 8, 20, 40 lub 58
atomach. Twory te musia∏y wi´c
byç wyjàtkowo trwa∏e.

Fizycy wiedzà dziÊ, ˝e nietrwale

klastery w odpowiednio wysokich
temperaturach szybko pozbywajà
si´ nadmiarowych atomów i ulega-
jà transformacji do struktur bardziej

stabilnych. Dla goràcych

atomów sodu za-

uwa˝ono kolej-

ne magiczne

wartoÊci: 92,

138, 198, 264, 344, 442, 554 i jeszcze
wy˝sze. Klastery sodowe (a tak˝e kilku
innych metali) z∏o˝one z tylu elemen-
tów pozostajà trwa∏e – nawet wówczas,
gdy sà zbyt goràce, by zakrzepnàç, i
istniejà wy∏àcznie jako kropelki ato-
mowej cieczy.

Tendencja do tworzenia klasterów

o pewnych szczególnych liczbach ato-
mów wynika z regu∏ mechaniki kwan-
towej, zgodnie z którà elektrony zwiàza-
ne muszà mieç ÊciÊle okreÊlone energie.
Elektrony nadmiarowe (w stosunku do
konfiguracji atomu szlachetnego) zwià-
zane sà s∏abo; w odosobnionych ato-
mach b∏àdzà z dala od jàdra. Nazywa-
my je walencyjnymi i to one decydujà
o w∏aÊciwoÊciach chemicznych pier-
wiastków.

W klasterze metalicznym (lub wi´k-

szym kawa∏ku metalu) elektrony wa-
lencyjne nie sà ju˝ przypisane do kon-
kretnego atomu, z którego pochodzà -
stosunkowo swobodnie w´drujà pomi´-
dzy wszystkimi. OkreÊlamy je jako
„zdelokalizowane”. Pozostajà one jed-
nak w granicach klastera przyciàgane
przez dodatni ∏adunek, który pozosta-
wi∏y, od∏àczajàc si´ od jàder. (Po usu-
ni´ciu elektronów walencyjnych dodat-
ni ∏adunek protonów jàdrowych nie jest
ju˝ dok∏adnie bilansowany ∏adunkami
ujemnymi; atom, który dotychczas by∏
elektrycznie oboj´tny, staje si´ jonem
dodatnim.)

Aby zrozumieç, dlaczego konkretne

liczby atomów nadajà trwa∏oÊç klaste-
rom, fizycy muszà poznaç szczegó∏owà
konfiguracj´ wszystkich jonów i elek-
tronów walencyjnych. Jest to zadanie
nies∏ychanie trudne. Okazuje si´ jednak,
˝e wielu odpowiedzi mo˝e dostarczyç
modelowanie klastera jako g∏adkiej „ga-

laretki” dodatniego ∏adunku, z którà
powiàzane sà elektrony walencyjne
(uproszczenie znane jako model ga-
laretowy – jellium model) .

Energie tych elektronów zgodnie z re-

gu∏ami mechaniki kwantowej sà skwan-
towane, tzn. mogà przybieraç wy∏à-
cznie ÊciÊle okreÊlone wartoÊci. W
klasterze metalicznym, podobnie jak
w izolowanym atomie, dost´pne pozio-
my energetyczne nie sà równo roz-
mieszczone, pojawiajà si´ raczej w gru-
pach oddzielonych od siebie wi´kszymi
przerwami. Takie „wiàzki” atomowych
poziomów energetycznych nazywamy,
z przyczyn historycznych, pow∏okami
elektronowymi (choç obszary, w któ-
rych mogà przebywaç elektrony, nie
majà w∏aÊciwie kszta∏tu pow∏ok). Re-
gu∏y kwantowomechaniczne ogranicza-
jà maksymalnà liczb´ elektronów w ka˝-
dej z nich. Natomiast po ca∏kowitym
wype∏nieniu jednej pow∏oki lub wi´k-
szej ich liczby atom przestaje reagowaç
z innymi, uzyskuje wi´c szczególnà
trwa∏oÊç. Pojawianie si´ liczb magicz-
nych w opisie klasterów wyglàda za-
tem sensownie: odpowiadajà one licz-
bom elektronów walencyjnych, które
ca∏kowicie zape∏niajà jednà lub kilka
elektronowych pow∏ok atomowego
zlepka, czyniàc go szczególnie odpor-
nym. (Podobny mechanizm dzia∏a przy
wype∏nianiu protonami i neutronami
pow∏ok jàdrowych; wyjaÊnia te˝ odpo-
wiednie liczby magiczne.)

Klastery metaliczne wykazujàce naj-

wi´kszà trwa∏oÊç majà kszta∏t niemal
sferyczny. Gdy dost´pne elektrony nie
mogà ca∏kowicie wype∏niç najwy˝szej
pow∏oki, wówczas klaster sp∏aszcza si´
lub wyd∏u˝a i zaczyna przypominaç
placek lub pi∏k´ do rugby. Mo˝e te˝

przybieraç postaç bardziej skompliko-
wanej bry∏y – gruszki, cytryny, rogatej
poduchy – lub nie mieç szczególnej sy-
metrii. Takie kszta∏ty oznaczajà, ˝e ener-
gia klastera si´ obni˝y∏a, zwi´kszajàc je-

go trwa∏oÊç. Struktury te b´dà jednak
zawsze mniej stabilne ni˝ klastery o ca∏-
kowicie wype∏nionych pow∏okach elek-

WIÑZKA DROBIN METALU tworzonych w goràcym êródle
atomów przemierza d∏ugà komor´ pró˝niowà. Klastery te mo-

gà byç ma∏ymi czàsteczkami o sztywnych wiàzaniach, jednak

po zmianie warunków eksperymentu stajà si´ wi´kszymi sku-

piskami atomów upakowanych w foremne bry∏y lub bezkszta∏t-

ne galaretowate krople. Te trzy formy, ∏atwe do zaobserwowa-

nia, zwykle nie wyst´pujà razem.

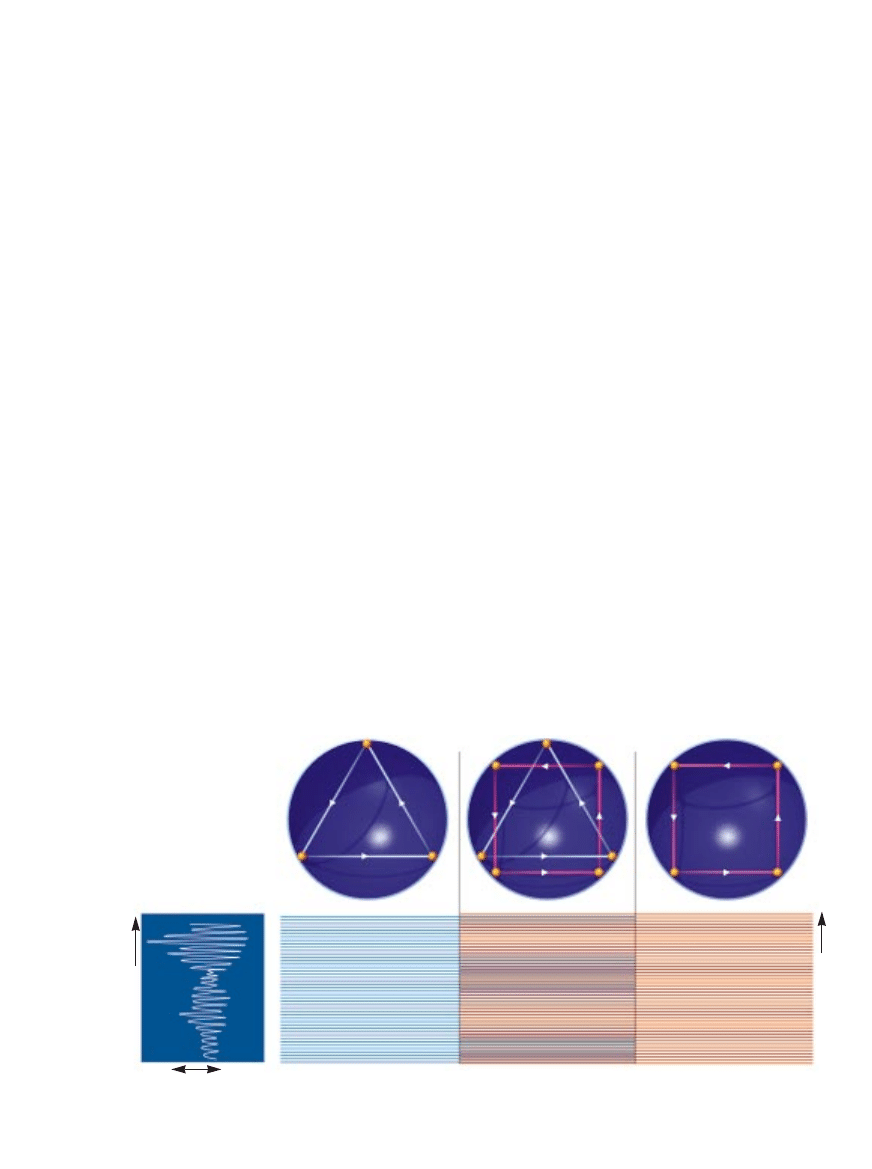
tronowych. Fizycy ju˝ dawno zauwa-
˝yli, ˝e wiele trwa∏ych jàder atomo-
wych równie˝ przybiera zdeformowane
kszta∏ty. Niektóre narz´dzia teoretycz-
ne przydatne do opisu klasterów zapo-
˝yczono wi´c z wczeÊniejszych prac
w dziedzinie fizyki jàdrowej.

Superpow∏oki

Formalizm mechaniki kwantowej po-

zwala opisaç elektronowe pow∏oki kla-
sterów i zrozumieç, skàd pochodzà licz-
by magiczne. Wielu niespecjalistom
wnioskowanie takie wyda si´ jednak
trudne do wyobra˝enia i niekiedy
sprzeczne z intuicjà. Na szcz´Êcie istnie-
je sposób wyprowadzenia liczb magicz-
nych z klasycznych rozwa˝aƒ, które na-
wiàzujà do codziennych doÊwiadczeƒ
z makroskopowymi obiektami.

Punktem wyjÊcia jest tu tzw. teoria

orbit okresowych opracowana na po-
czàtku lat siedemdziesiàtych jako po-
most pomi´dzy mechanikà kwantowà
i klasycznà. Teoria ta pozwala fizykom
stosunkowo ∏atwo ustaliç energie g∏ów-
nych pow∏ok w uk∏adach zawierajàcych
elektrony lub inne ma∏e czàstki.

Aby zrozumieç zastosowanie teorii

orbit okresowych, wystarczy wyobra-
ziç sobie klaster metaliczny jako pustà
kul´ z elektronami walencyjnymi, które
poruszajà si´ ze sta∏à pr´dkoÊcià wzd∏u˝
linii prostych. Elektrony odbijajà si´ od
wewn´trznej powierzchni sfery pod kà-

tem równym kàtowi padania; jest to re-
gu∏a ogólna, prawdziwa zarówno dla
czàstek uderzajàcych w Êcian´, jak dla
fali Êwietlnej odbijanej przez zwiercia-
d∏o. Ten zgrubny model dzia∏a, elektro-
ny walencyjne sà bowiem wewnàtrz
atomowego zlepka praktycznie swobod-
ne, nie mogà go jedynie opuÊciç.

Orbity okresowe wewnàtrz kulistej

wn´ki to po prostu mo˝liwe trajektorie
czàstek. Elektrony Êmigajà w t´ i z po-
wrotem wzd∏u˝ Êrednicy albo kreÊlà
wielokàty – o trzech lub wi´cej wierz-
cho∏kach. Fizycy uzyskujà przybli˝ony
rozk∏ad dost´pnych poziomów energe-
tycznych, rozwa˝ajàc tylko te orbity, któ-
re majà najmniejszà d∏ugoÊç i najcz´Êciej
wyst´pujà. Trzy najkrótsze trajektorie to
Êrednica, trójkàt i kwadrat. Z bardziej
subtelnych rozwa˝aƒ geometrycznych
wynika jednak, ˝e orbity Êrednicowe po-
jawiajà si´ stosunkowo rzadko.

Natomiast obliczenia dla samych trój-

kàtów i kwadratów prowadzà do okre-
sowej (w pewnym sensie) konfiguracji
dost´pnych poziomów. Po wykreÊle-
niu w funkcji energii poziomy te poja-
wiajà si´ w regularnych odst´pach. Po-
wtórzenia nie sà jednak obserwowane
ze sta∏à „cz´stotliwoÊcià”. Widaç raczej
dwie ró˝ne cz´stotliwoÊci, które odpo-
wiadajà dwóm dominujàcym rodzajom
orbit: trójkàtnym i kwadratowym. Co
wi´cej, pojawiajà si´ „dudnienia” (po-
dobnie jak podczas nak∏adania fal
dêwi´kowych o zbli˝onych cz´stotli-
woÊciach); dwa zbiory pow∏ok interfe-
rujà ze sobà, tworzàc wielkoskalowe
zgrupowania poziomów energetycz-
nych – „superpow∏oki”.

Superpow∏oki w zasadzie mog∏yby

równie˝ wyst´powaç w modelach jàder
atomowych. Tak si´ jednak nie dzieje,
jàdra bowiem nigdy nie sà wystarcza-
jàco du˝e, by je utrzymaç. Pierwsze
dudnienia superpow∏okowe powstajà
dopiero dla 800–1000 czàstek, podczas
gdy najwi´ksze z utworzonych dotàd
jàder liczà mniej ni˝ 200 neutronów i 120
protonów. Superpow∏oki obserwowa-
no jednak w wielkich klasterach metali.
W 1991 roku fizycy z Niels Bohr Institu-
tet w Kopenhadze i z Max-Planck-In-
stitut für Festkörperforschung w Stut-
tgarcie zaobserwowali to zjawisko w
goràcych klasterach sodu. Wkrótce po-
tem badacze z Institut Aimé Cotton
w Orsay (Francja) znaleêli argumenty
Êwiadczàce o wyst´powaniu superpow-
∏ok w klasterach litu, natomiast na Uni-
versité Claude Bernard Lyon 2 zauwa-
˝ono je w klasterach galu.

Teoria orbit okresowych modelu

wn´ki sferycznej przewiduje, ˝e pier-
wiastek szeÊcienny z liczby magicznej
(odpowiadajàcy z grubsza promienio-
wi konkretnego klastera) powinien
zmieniaç si´ o sta∏à wartoÊç podczas
przechodzenia z jednej pow∏oki na in-
nà. Po wykreÊleniu dla ró˝nych klaste-
rów pierwiastków szeÊciennych z od-
powiadajàcych im liczb magicznych
w funkcji liczby pow∏ok, naukowcy
otrzymali lini´ prostà o nachyleniu 0.61.
Wynik ten jest zgodny z przewidywa-
niami teorii orbit okresowych (0.603)
z dok∏adnoÊcià oko∏o 1%. Pe∏niejszy opis
kwantowomechaniczny, wykorzystujà-
cy model galaretowy, mo˝na zrealizo-
waç dla klasterów zawierajàcych nie

36 Â

WIAT

N

AUKI

Luty 1998

UPROSZCZONY MODEL traktuje
klaster atomów metalu jak wy-
drà˝onà kul´, wewnàtrz której odbi-
jajà si´ elektrony (z prawej). Fizycy
pos∏ugujà si´ z teorià orbit okreso-
wych, aby obliczyç przybli˝one ener-
gie elektronowych poziomów (pozio-
me linie). Dwa najwa˝niejsze typy
zamkni´tych trajektorii (trójkàty i
kwadraty) wzajemnie interferujà,
tworzàc zgrupowania pow∏ok, tzw.
superpow∏oki. Ten charakterystycz-
ny wzór (poni˝ej) daje si´ zaobser-
wowaç doÊwiadczalnie; przewidujà
go tak˝e bardziej zaawansowane mo-
dele teoretyczne.

WIELKOÂå KLASTERA

NISKA

WYSOKA

TRWA¸OÂå

TRÓJKÑT

INTERFERENCJA

KWADRAT

ENERGIA ELEKTRONOWA

SLIM FILMS

wi´cej ni˝ kilka tysi´cy atomów (wi´k-
sze uk∏ady wymaga∏yby zbyt d∏u-
gotrwa∏ych obliczeƒ) . Otrzymuje si´
wówczas wartoÊç nachylenia zgodnà
z doÊwiadczeniem.

WieloÊciany foremne

Materia, zgodnie z wizjà greckiego

filozofa Platona, mia∏a si´ sk∏adaç
z „cegie∏ek” majàcych form´ regular-
nych wieloÊcianów, tzw. bry∏ platoƒ-
skich. Ciekawe, ˝e w przypadku zim-
nych klasterów poglàd ten nie odbiega
daleko od prawdy. Gdy du˝a liczba ato-
mów metalu podlega wolnej agregacji
w stosunkowo niskiej temperaturze,
wówczas przyjmujà one kszta∏t regular-
nych bry∏ o strukturze ciasnej – jak
w stosie pomaraƒczy u∏o˝onym na la-
dzie sklepowej.

Fizycy mogà przewidywaç geome-

tryczny kszta∏t takich zimnych zlep-
ków, badajàc zale˝noÊç ich trwa∏oÊci
od rozmiarów. W 1991 roku badacze
z Max-Planck-Institut für Festkörper-
forschung pozwalali atomom sodu ∏à-
czyç si´ w niskich temperaturach i
stwierdzili, ˝e najtrwalsze klastery mia-
∏y zupe∏nie inne rozmiary ni˝ w tempe-
raturach wysokich. Innymi s∏owy, obo-
wiàzywa∏ zupe∏nie inny zestaw liczb
magicznych. Niemiecki zespó∏ szybko
ustali∏, ˝e te nowe liczby odpowiadajà
atomom upakowanym w ikosaedry fo-
remne, czyli bry∏y o dwudziestu trój-
kàtnych Êcianach.

OkreÊlony zbiór liczb magicznych

ulega rozbudowie w miar´ dodawania
jednoatomowych warstw sodu i wytwa-
rzania kolejnych dwudziestoÊcianów.
Te „atomowe pow∏oki” przywodzà na
myÊl warstwowà budow´ cebuli. Pro-
ste wieloÊcienne kszta∏ty klasterów sà
trwalsze od struktur nieregularnych,
poniewa˝ energia potrzebna do zwià-
zania atomów maleje wraz ze zmniej-
szaniem si´ liczby kraw´dzi tworzonej
bry∏y. Wyglàda na to, ˝e przyroda
upodoba∏a sobie oszcz´dne kszta∏ty wie-
loÊcianów foremnych.

Dla zimnych klasterów metalicznych

pierwiastki szeÊcienne z magicznych
liczb wzrastajà proporcjonalnie do licz-
by pow∏ok atomowych. Nachylenie od-
powiedniej prostej jest jednak inne ni˝
na wykresach ilustrujàcych zale˝noÊç

liczb magicznych goràcych klasterów
od liczby elektronowych pow∏ok ener-
getycznych. Wydaje si´ to równie˝ za-
le˝ne od rodzaju klasterów, co sygna-
lizuje obecnoÊç rozmaitych kszta∏tów
wieloÊciennych. Na przyk∏ad zimne
klastery sodu lub wapnia, które dajà
nachylenie oko∏o 1.5, odpowiadajà
przypuszczalnie dwudziestoÊcianom.
Natomiast klastery zawierajàce te same
iloÊci sodu i jodu lub sodu i chloru cha-
rakteryzujà si´ nachyleniem wyno-
szàcym dok∏adnie 1.0, co wskazuje na
kszta∏t szeÊcienny. Uprzywilejowanie
pewnych bry∏ pozostaje w∏aÊciwoÊcià
nieco tajemniczà.

Szczególnie zagadkowe jest powsta-

wanie zimnych klasterów glinu i indu.
Po wykreÊleniu szeÊciennego pierwiast-
ka z ich liczb magicznych w funkcji licz-
by pow∏ok atomowych stwierdzono na-
chylenie 0.220 – znacznie mniejsze ni˝
dla trwa∏ych pow∏ok elektronowych
(0.6) , a zarazem inne od spodziewane-
go dla czworoÊcianów (0.550) , oÊmio-
Êcianów (0.874) , dwudziestoÊcianów
(1.493) lub szeÊcianów (1.0) . Niemo˝li-
we okaza∏o si´ znalezienie jakiegokol-
wiek wieloÊcianu foremnego, który
w miar´ pokrywania kolejnymi war-
stwami atomowymi odtwarza∏by zbiór
liczb magicznych obserwowany dla tych
klasterów.

Badacze ze Stuttgartu zaproponowa-

li mo˝liwe rozwiàzanie – klastery glinu
lub indu mia∏yby rozbudowywaç si´ ja-
ko oÊmioÊciany, jednak zwi´kszeniu
liczby magicznej odpowiada∏oby pokry-
cie zaledwie jednej trójkàtnej Êcianki.
Konsekwencjà by∏oby ma∏e nachylenie
wykreÊlanej linii. Propozycja ta wyglà-
da rozsàdnie, choç rodzi nast´pne py-
tanie: dlaczego foremne („dokoƒczone”)
oktaedry nie sà wyraênie trwalsze od
tych, którym rozbudowano tylko jednà
lub dwie trójkàtne Êciany?

Co ciekawe, liczby magiczne wyni-

k∏e z mo˝liwoÊci upakowania atomów
nie wyznaczajà jednoznacznie kszta∏tu
tworzonych wieloÊcianów. Na przyk∏ad
liczby zwiàzane z dwudziestoÊcianami
sà zbie˝ne z tymi, które znajdujemy dla
kubooktaedrów (szeÊcianów o Êci´tych
naro˝ach) . Wnikliwe badania sugeru-
jà, ˝e zimne klastery sodowe przybie-
rajà jednak postaç dwudziestoÊcianów.
Ale pewnoÊci nie mamy – nikt nie wi-

dzia∏ tych tworów. Wi´ksze klastery, je-
Êli pozostawa∏yby w spoczynku, w za-
sadzie powinno daç si´ zaobserwowaç
pod mikroskopem elektronowym. Nie-
stety izolowane klastery powstajà
w wiàzkach szybko poruszajàcych si´
atomów. Zlepków tych nie mo˝na za-
trzymaç „do zdj´cia” bez naruszenia ich
w∏aÊciwego kszta∏tu.

Mistrzowskie wspó∏zawodnictwo

W staraniach o nadanie du˝ym me-

talicznym klasterom kszta∏tu i trwa-
∏oÊci wspó∏zawodniczà dwa rodzaje
pow∏ok: energii elektronowej oraz ato-
mowe. O tym, które przewa˝ajà, decy-
duje temperatura i rozmiar tworzonej
drobiny. Jednak pomiar temperatury
oddzielnych klasterów w wiàzce mole-
kularnej nie jest ∏atwy. Mo˝na by nawet
zapytaç, czy temperatura naszych zlep-
ków w ogóle jest zdefiniowana, skoro
poj´cie to, w Êcis∏ym uj´ciu, odnosi si´
wy∏àcznie do wieloczàstkowych uk∏a-
dów w równowadze termodynamicz-
nej. Warunek równowagi z regu∏y nie
jest spe∏niany w wiàzkach molekular-
nych. Nale˝y raczej przyjàç, ˝e ka˝dy
klaster porusza si´ samodzielnie, nieza-
le˝nie od sàsiadów. Takie odosobnione
zlepki nie osiàgajà równowagi termo-
dynamicznej. Nie ma zatem ∏atwego
sposobu okreÊlenia temperatury (nie
wetkniemy przecie˝ termometru w
pojedynczy twór o mikroskopowych
rozmiarach) .

Podstawowe zale˝noÊci sà jednak wy-

raêne. Po ostro˝nym ogrzaniu dyszy
obserwujemy zanikanie eleganckich
dwudziestoÊciennych pow∏ok typowych
dla zimnych klasterów sodu. Zjawi-
sko to nale˝y interpretowaç jako rodzaj
przejÊcia fazowego – topnienie sta∏ych

Â

WIAT

N

AUKI

Luty 1998 37

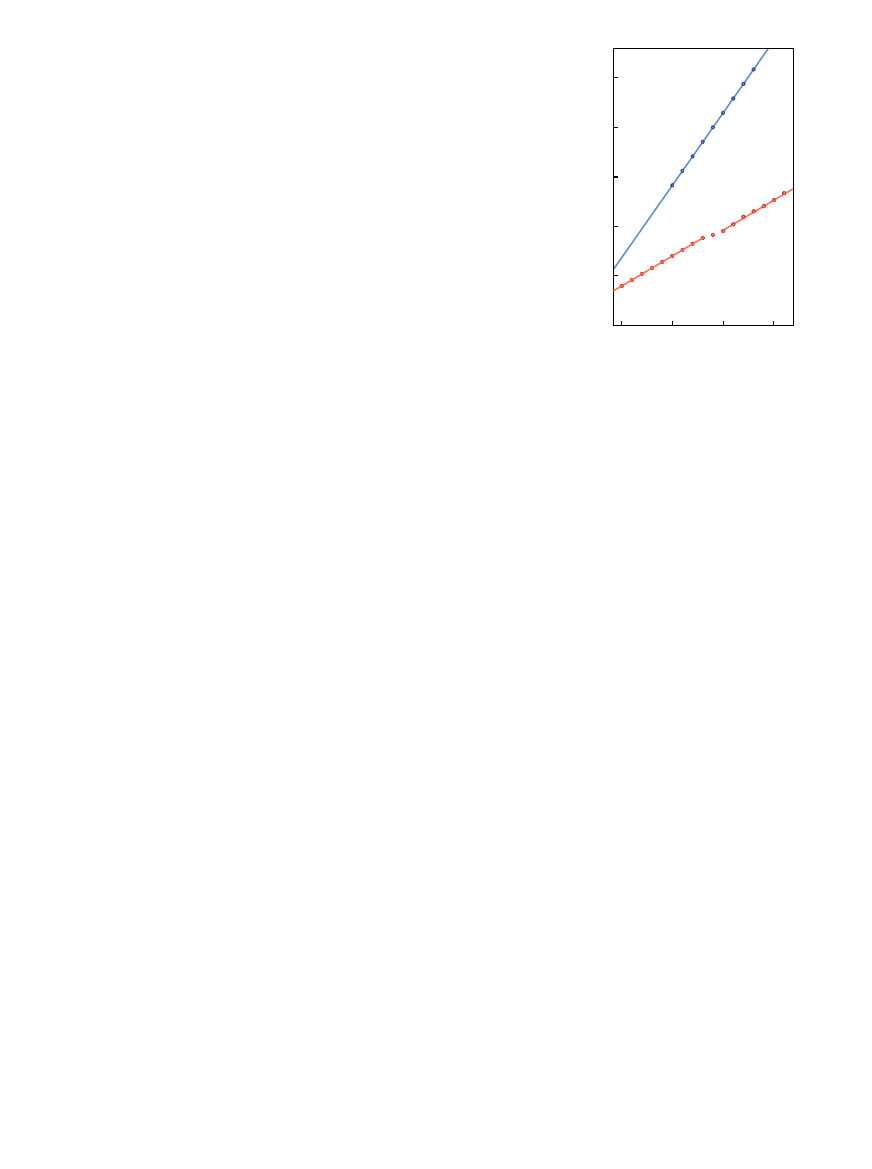
25

20

15

10

5

0

5

10

15

20

WIELKOÂå KLASTERA

(PIERWIASTEK SZEÂCIENNY Z LICZBY ATOMÓW)

LICZBA POW¸OK

ZIMNE
KLASTERY
SODU

GORÑCE
KLASTERY
SODU

WIELKOÂå KLASTERA, wyra˝ona jako pierwiastek szeÊcienny z liczby atomów, mu-
si rosnàç wraz ze zwi´kszaniem liczby pow∏ok. Jednak szybkoÊç tego wzrostu (nachyle-
nie prostej na wykresie obok) zale˝y od temperatury wiàzki klasterów. Zimne klastery
sodowe zbudowane sà z 20-Êciennych warstw ciasno upakowanych atomów; geometria
ta prowadzi do nachylenia 1.5. Natomiast kszta∏t goràcych klasterów determinowany
jest przez pow∏oki elektronowe, które generujà nachylenie 0.6. Defekt (przesuni´cie
prostych) dla czternastej pow∏oki (widoczny na wykresie) jest konsekwencjà efektu
superpow∏ok; dobrze opisanà przez teori´ orbit okresowych.

ARTHUR CHRISTIE

klasterów. Temperatura topnienia oka-
zuje si´ zale˝na od ich rozmiarów.

Podobny proces zaobserwowano dla

klasterów glinu. Gdy temperatura êró-
d∏a przekroczy 500 K (jest to znacznie
mniej ni˝ potrzeba do stopienia makro-
skopowych próbek glinu), wówczas wy-
kresy pierwiastka szeÊciennego z liczb
magicznych w funkcji liczby pow∏ok nie

wykazujà ju˝ nachylenia 0.220, które
Êwiadczy∏o o upakowaniu atomów na
Êciankach foremnego oktaedru. Pojawia
si´ natomiast nachylenie oko∏o 0.6, ty-
powe dla pow∏ok elektronowych. Roz-
sàdnie jest za∏o˝yç, ˝e klastery uleg∏y
stopieniu mimo niezbyt wysokiej tem-
peratury dyszy. Taki wniosek mo˝e byç
jednak zbytnim uproszczeniem: dla ma-

∏ych tworów odró˝nienie fazy sta∏ej od
ciek∏ej stanowi problem sam w sobie.
Byç mo˝e klastery doÊwiadczajà „lokal-
nego” topnienia swych powierzchni, co
burzy ich wewn´trznà struktur´ deter-
minowanà upakowaniem jonów. Kon-
trol´ nad trwa∏oÊcià drobin przejmuje
wówczas dà˝enie do ca∏kowitego zape∏-
niania pow∏ok elektronowych.

38 Â

WIAT

N

AUKI

Luty 1998

N

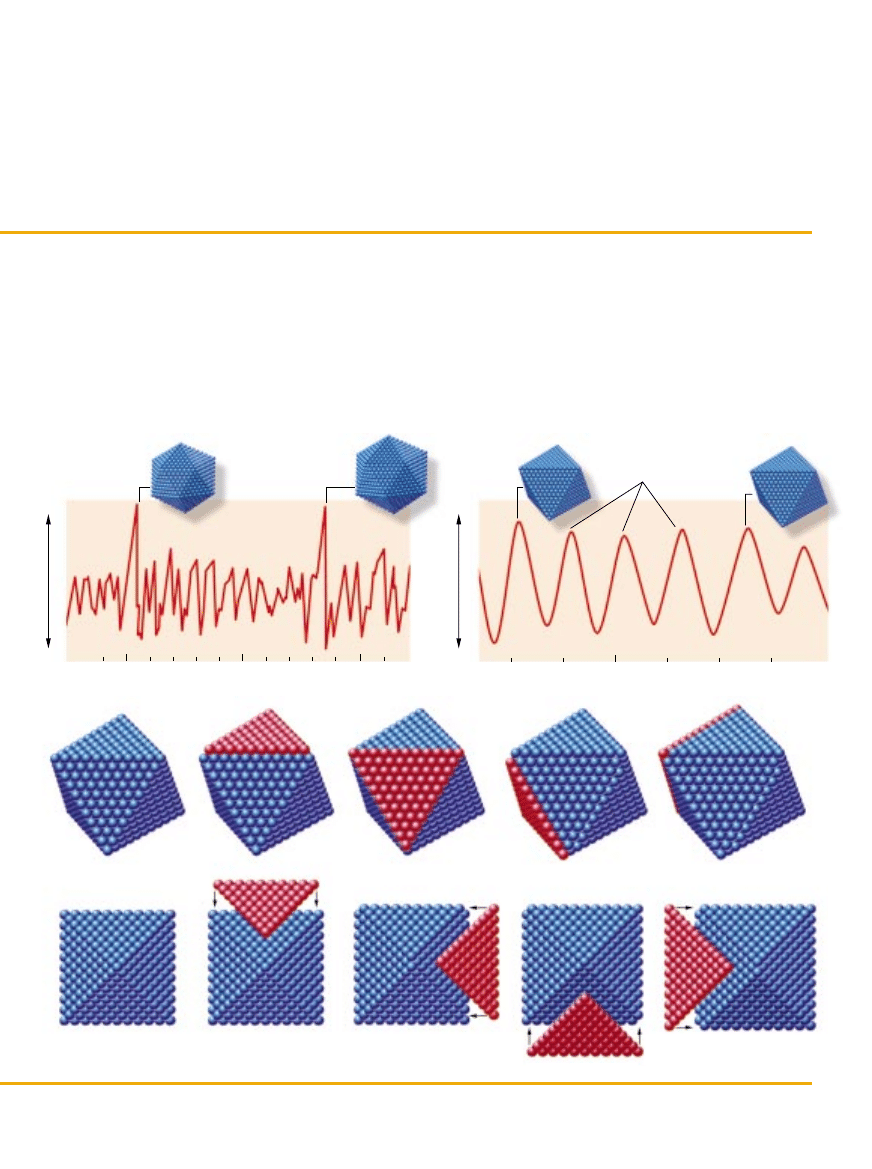
aukowcy t∏umaczà wyjàtkowà trwa∏oÊç niektórych zimnych
klasterów ich szczególnà geometrià. Zlepki atomów sodu

stajà si´ na przyk∏ad szczególnie trwa∏e po upakowaniu w kszta∏t
ikosaedru, czyli w bry∏´ o dwudziestu Êcianach. Wykresy trwa∏o-
Êci jako funkcji rozmiarów klasterów ujawniajà wi´c wyraêne mak-
sima, gdy liczba atomów odpowiada mo˝liwoÊci utworzenia dwu-
dziestoÊcianu foremnego (z lewej). Zimne klastery glinu charak-
teryzujà si´ oÊmioÊciennym u∏o˝eniem atomów, co troch´ trud-

niej zrozumieç. Maksima trwa∏oÊci pojawiajà si´ tu nie tylko dla
oktaedrów foremnych, lecz równie˝ dla bry∏ o poÊrednich rozmia-
rach (z prawej). Mo˝liwe, ˝e zwi´kszona stabilnoÊç wyst´puje
równie˝ w wyniku pokrycia pojedynczej Êciany nast´pnà warstwà
atomów (czerwone warstwy poni˝ej). Nowe warstwy na czterech
dodatkowych Êcianach oznaczajà przejÊcie do kolejnego okta-
edru, tak wi´c mi´dzy maksimami g∏ównymi mo˝na si´ spodzie-
waç trzech poÊrednich.

Upakowanie na zimno

2000

2500

3000

LICZBA ATOMÓW

TRWA¸OÂå

WYSOKA

NISKA

LICZBA ATOMÓW

MAKSIMA POÂREDNIE

1800

1900

2000

2100

2200

2300

TRWA¸OÂå

WYSOKA

NISKA

SLIM FILMS; èród∏o: T. P. Martin,

Max

-Planck

-Institut für Festköperforschung

OKTAEDR 891-ATOMOWY

DODANIE JEDNEJ ÂCIANY

DODANIE DWÓCH ÂCIAN

DODANIE TRZECH ÂCIAN

OKTAEDR 1156-ATOMOWY

Fizycy z Uniwersytetu we Fryburgu

zaobserwowali ostatnio nieco inne, choç
pokrewne zjawisko. Skorzystali z po-
mys∏owego triku, aby lepiej zapanowaç
nad temperaturà ma∏ych klasterów so-
dowych: badane czàstki otoczyli gazo-
wym helem, którego temperatur´ ∏a-
two ustaliç. W mieszaninie takiej
dochodzi do wielu zderzeƒ. Hel jest
jednak gazem szlachetnym (czyli nie-
aktywnym chemicznie), zachowuje za-
tem struktur´ klasterów – przynaj-
mniej dopóki temperatura nie jest zbyt
wysoka. W takim Êrodowisku mo˝li-
we wi´c by∏o osiàgni´cie równowagi
termodynamicznej.

Naukowców, którzy przeprowadza-

li to doÊwiadczenie, nie interesowa∏y
liczby magiczne, lecz sposób, w jaki
okreÊlone klastery absorbujà Êwiat∏o la-
serowe. Wykres prawdopodobieƒstwa
poch∏aniania promieniowania w funkcji
d∏ugoÊci fali (widmo absorpcji) cz´sto
wzbogaca naszà wiedz´ o fizycznych
w∏aÊciwoÊciach oÊwietlanych obiektów.
W szczególnoÊci ró˝nie wyglàdajà wid-
ma zimnych, sztywnych czàsteczek i go-
ràcych kropelek cieczy. Przy tempera-
turach ni˝szych od 100 K zarejestro-
wano wiele ostrych linii, co jest typowe
dla uk∏adów sztywnych, natomiast

powy˝ej 380 K widoczne by∏y jedynie
dwa ob∏e pasma o po∏o˝eniu zgodnym
z przewidywaniami dla bezkszta∏tnej
„galarety”.

Wewn´trzna struktura najmniejszych

klasterów zawsze jest wa˝na. Mo˝na
dla nich przeprowadziç dok∏adne obli-
czenia kwantowomechaniczne, które
uwzgl´dniajà wszystkie elektrony ka˝-
dego atomu. Odkrywamy w ten sposób
szczegó∏y budowy atomowych zlepków
i precyzyjnie przewidujemy ich trwa-
∏oÊç. W przypadku agregatów o kilku-
set atomach dok∏adne obliczenie nie jest
mo˝liwe i fizycy muszà korzystaç z mo-
delu galaretowego. Natomiast du˝e
uk∏ady, liczàce wiele tysi´cy atomów,
zmuszajà nas do porzucenia Êcis∏ych
metod i korzystania z prostego mode-
lu orbit okresowych lub informacji po-
Êrednich, których êród∏em sà doÊwiad-
czalnie znalezione liczby magiczne.

Badacze, którzy si´ tym zajmujà, prze-

byli od 1984 roku d∏ugà drog´. Znacznie
lepiej rozumiemy dziÊ sekwencje liczb
magicznych; potrafimy te˝ przewidy-
waç kolejne liczby. Wykonywano ju˝
eksperymenty z dwudziestoÊciennymi
klasterami sodu, które liczy∏y a˝ 21 tys.
atomów. Jest jednak oczywiste, ˝e w ob-
j´toÊciowej strukturze metalicznego so-

du podobne dwudziestoÊciany nie wy-
st´pujà. Co wi´cej, ˝aden materia∏ nie
mo˝e byç formowany przez upakowa-
nie takich jednostek strukturalnych.
DwudziestoÊciany nie majà po prostu
w∏aÊciwych elementów symetrii, aby
tworzyç z nich trójwymiarowe kryszta-
∏y i szczelnie wype∏niaç przestrzeƒ (po-
dobnie jak nie da si´ pokryç p∏aszczy-
zny pi´ciokàtnymi p∏ytkami) . Tak wi´c
nawet najwi´ksze z wytwarzanych dziÊ
klasterów sodu zorganizowane sà zu-
pe∏nie inaczej ni˝ makroskopowe prób-
ki tego metalu.

Jednym z pierwszych powodów zain-

teresowania mikroskopijnymi zlepka-
mi by∏a ch´ç sprawdzenia, ile muszà
mieç atomów, zanim przyjmà struktur´
makroskopowej materii. Fizycy sporo
ju˝ wiedzà o klasterach i magicznych
liczbach, które wyznaczajà ich trwa∏oÊç,
nie znaleêli jednak odpowiedzi na pyta-
nie podstawowe: kiedy i w jaki sposób
dokonuje si´ przejÊcie do substancji
o normalnej strukturze krystalicznej.
Mo˝emy jedynie stwierdziç, ˝e zbadane
mikroobiekty ujawni∏y osobliwy spo-
sób organizacji materii, i oczekiwaç wie-
lu jeszcze niespodzianek.

T∏umaczy∏

Robert Ko∏os

Â

WIAT

N

AUKI

Luty 1998 39

Informacje o autorze

MATTHIAS BRACK zdoby∏ wykszta∏cenie fizycz-

ne w kopenhaskim Niels Bohr Institutet oraz na

Uniwersytecie w Bazylei, gdzie w 1972 roku uzy-

ska∏ doktorat. Badania w zakresie fizyki jàdrowej

prowadzi∏ zarówno w Kopenhadze, jak i w State

University of New York w Stony Brook oraz w In-

stitut Laue-Langevin (Grenoble). Od 1978 roku

jest profesorem fizyki teoretycznej na Uniwersy-

tecie w Regensburgu w Niemczech.

Literatura uzupe∏niajàca

SEMICLASSICAL PHYSICS

. Mattias Brack i Rajat K. Bhaduri; Addison-Wesley, 1997.

CLUSTERS, CONDENSED MATTER IN EMBRYONIC FORM

. Sven Bj¿rnholm, Contemporary Physics,

vol. 31, nr 5, ss. 309-324, IX/ 1997.

THE PHYSICS OF METAL CLUSTERS

. M. L. Cohen i W. D. Knight, Physics Today, vol. 43, nr 12,

ss. 42-50, XII/1990.

THE PHYSICS OF SIMPLE METAL CLUSTERS: EXPERIMENTAL ASPECTS AND SIMPLE MODELS

. Walt A. de

Heer, Reviews of Modern Physics, vol. 65, nr 3, cz. I, VII/1993, ss. 611-676;

SELF-CONSISTENT

JELLIUM MODEL AND SEMICLASSICAL APPROACHES

, Matthias Brack, tam˝e ss. 677-732,.

SHELLS OF ATOMS

. T. P. Martin, Physics Reports, vol. 273, nr 4, ss. 199-242, VIII/1996.

WIDMA ABSORPCJI ÂWIAT¸A LASEROWEGO wskazujà, ˝e wraz ze wzrostem temperatury klastery ulegajà transformacji od sztyw-
nych czàsteczek do bezkszta∏tnej masy. W pierwszym przypadku, dla zimnych klasterów sodu, prawdopodobieƒstwo poch∏oni´cia fo-
tonu bardzo wyraênie zale˝y od cz´stotliwoÊci promieniowania laserowego (niebieskie odcienie). Jednak w wy˝szych temperaturach
(pomaraƒczowe odcienie) widma ulegajà wyg∏adzeniu i sk∏adajà si´ wy∏àcznie z dwóch ob∏ych pasm przewidzianych przez tzw. model
galaretowy. Fizycy stosujà ten model do opisu klasterów pozbawionych wewn´trznej struktury.

CZ¢

STOTLIWO

Âå Â

WIAT

¸A LASEROWEGO

(x 10

14

Hz)

5 6

7

8

35

100

120

142

164

188

209

229

249

269

380

TEMPERATURA (STOPNIE KELVINA)

ABSORPCJA

Â

WIAT

¸A

WYSOKA

NISKA

ARTHUR CHRISTIE; èRÓD¸O: MARTIN SCHMIDT

iHELMUT HABERLAND,

Uniwersytet we Fryburgu