Matematyka nansowa
1. Procent, Stopa Procentowa
De nicja 1.1 Procentem nazywamy setn¡ cz¦±¢ caªo±ci.
Przykªad 1.1 Mamy na inwestycji 5000 zª. zarobi¢ 8%, tzn.
8%
· 5000 = 0, 08 · 5000 = 400zª.
Przykªad 1.2 Cena produktu ulegªa podwy»ce o 25% i wynosi 250 j.p. (jednostek
pieni¦»nych). Wyznaczy¢ poprzedni¡ cen¦ tego produktu.
Ustalamy proporcje
x
− 100%
250
− 125%
Wtedy x =
250
125%
· 100% = 200 j.p.
Przykªad 1.3 Cena produktu ulegªa obni»ce o 25%. Wyznaczyc pierwotn¡ cen¦
towaru, je±li cena obecna wynosi 250 j.p.
x
− 100%
250
− 75%
A wi¦c x =
250
75%
· 100% = 333, 33 j.p.
De nicja 1.2 Okresowa stopa procentowa jest to stosunek ceny po»yczonego ka-
pitaªu na dany okres do warto±ci tego kapitaªu.
W praktyce najcz¦±ciej mamy do czynienia ze stopami ustalonymi dla okresu roczne-
go i wtedy mówimy o rocznej stopie procentowej. Stosuje si¦ równie» stopy póªroczne,
kwartalne i miesi¦czne.
1
Stopa procentowa zale»y od poziomu in acji, ryzyka po»yczenia pieni¦dzy i od mar-
»y (zysku) po»yczaj¡cego.
De nicja 1.3 Odsetkami uzyskanymi z kwoty K
0
jednostek pieni¦»nych za dany
okres (rok, kwartaª, miesi¡c) przy okresowej stopie procentowej r nazywamy iloczyn
O = r
· K
0
.
De nicja 1.4 Punktem procentowym (pp.) nazywamy bezwzgl¦dn¡ ró»nic¦ mi¦-
dzy wielko±ciami wyra»onymi procentowo.
Zakªadaj¡c, »e stopa bezrobocia wynosi 10%, a kilka lat wcze±niej wynosiªa 20%
mo»na powiedzie¢, »e obni»yªa si¦ ona o poªow¦, a wi¦c o 50%. Mo»na równie» po-
wiedzie¢, »e obni»yªa sie o 10 pp.
Rodzaje stóp procentowych.
De nicja 1.5 Nominalna stopa procentowa (r) jest to stopa podawana przez banki
lub inne instytucje nansowe.
Obserwowany w rzeczywisto±ci poziom stóp procentowych zale»y od poziomu in-
acji. Po wyeliminowaniu czynnika in acji otrzymamy stop¦ realn¡.
De nicja 1.6 Stopa realna (r
r
) jest to stopa nominalna pomniejszona o wpªyw
in acji.
Zachodzi nast¦puj¡cy wzór Fishera:
r = r
r
+ r
i
+ r
r
· r
i
lub
r
r
=
r
− r
i
1 + r
i
gdzie r
i
oznacza stop¦ in acji.
Przykªad 1.4 Wyznaczy¢ realna stop¦ procentow¡, je»eli stopa nominalna banku
wynosi 5%, a roczna stopa in acji 3%.
Rozwi¡zanie. r
r
=
0,05
−0,03
1+0,03
=
0,02
1,03
= 0, 0194
.
Realna stopa procentowa wynosi r
r
= 1, 94%
.
De nicja 1.7 Faktyczna stopa procentowa r
f
jest to stopa uwzgl¦dniaj¡ca podatek
dochodowy od zysków z inwestycji kapitaªowych.
2
r
f
= r
· (1 − T ), gdzie T jest stop¡ podatku dochodowego od zysków z inwestycji
kapitaªowych i w Polsce T = 19%.
Przykªad 1.5 Obliczy¢ faktyczna stop¦ procentow¡, je±li r = 4%.
Rozwi¡zanie. r
f
= 4%
· (1 − 0, 19) = 3, 24%.
De nicja 1.8. Oprocentowanie jest to czynno±¢ okresowa polegaj¡ca na dodawaniu
odsetek z posiadanego kapitaªu do tego kapitaªu.
De nicja 1.9 Oprocentowanie proste polega na tym, »e odsetki uzyskane w okre-
sach poprzednich nie podlegaj¡ oprocentowaniu w okresie nast¦pnym, s¡ tylko do-
dawane w ka»dym okresie do kapitaªu.
Oprocentowanie proste stosuje si¦ w obliczeniach dotycz¡cych bankowych trans-
akcji krótkoterminowych oraz umów zawieranych poza sfer¡ bankow¡.
Kapitaª przyszªy K
p
n
oraz kwot¦ odsetek O
n
po n okresach naliczania odsetek
obliczamy ze wzorów:
K
p
n
= K
0
· (1 + n · r),
O
n
= K
0
· n · r,
K
p
n
= K
0
+ O
n
.
Gdy stopy procentowe s¡ zmienne wtedy stosujemy wzór:
K
p
n
1
+n
2
+...+n
m
= K
0
· (1 + n
1
· r
1
+ n
2
· r
2
+ . . . n
m
· r
m
)
Przykªad 1.6 W banku, w którym roczna stopa procentowa r = 4% zªo»ono kwot¦
5000
zª. Obliczy¢ warto±¢ kapitaªu po a) roku, b) dwóch latach, c)póª roku, d) 9-ciu
miesi¡cach, e) 108-miu dniach.
Rozwi¡zanie.
Obliczamy faktyczn¡ stop¦ procentow¡ r
f
= 4%
· (1 − 0, 19) = 3, 24%.
a)
K
p
1
= 5000(1 + 1
· 0, 0324) = 5162 zª.
b)
K
p
2
= 5000(1 + 2
· 0, 0324) = 5324 zª.
c)
K
p
1/2
= 5000(1 +
1
2
· 0, 0324) = 5081 zª.
d)
K
p
9/12
= 5000(1 +
9
12
· 0, 0324) = 5121, 5 zª.
Warto±ci
1
2
· 0, 0324 oraz
9
12
· 0, 0324 nosz¡ nazwy stóp sródokresowych (lub pod-
okresowych) odpowiednio póªrocznej i miesi¦cznej.
3
Ogólnie stopa ±ródokresowa i
k
= a
·r, gdy r jest na ogóª roczn¡ stop¡ procentow¡
oraz a cz¦±ci¡ roku.
e) W praktyce bankowej przyjmuje si¦, »e rok ma 360 dni, a ka»dy miesi¡c 30 dni.
K
p
= 5000(1 +
108
360
· 0, 0324) = 5048, 6 zª.
Przykªad 1.7 Obliczy¢ stan kapitaªu po roku, je±li warto±¢ kapitaªu pocz¡tkowe-
go wynosi 1000 zª. przy zaªo»eniu, »e roczna stopa procentowa w pierwszych 4-ch
miesi¡cach wynosi 12%, w dwóch kolejnych m-cach 10%, a w 6-ciu nast¦pnych 9%.
Rozwi¡zanie. Obliczamy faktyczne stopy procentowe.
r
1
= 12%
· 0, 81 = 9, 72%
r
2
= 10%
· 0, 81 = 8, 1%
r
3
= 9%
· 0, 81 = 7, 29%
Poszczególne ±ródokresy s¡ równe n
1
=
4
12
,
n
2
=
2
12
,
n
3
=
6
12
.
Zatem
K
p
= 1000(1 +
1
3
· 0, 0972 +
1
6
· 0, 081 +
6
12
· 0, 0729) = 1082, 35zª
De nicja 1.10 Przeci¦tn¡ stop¡ procentow¡ (r) w okresie n = n
1
+ n
2
+ . . . + n
m
nazywamy tak¡ roczn¡ stop¦ procentow¡, przy której dowolny kapitaª pocz¡tkowy
osi¡gnie po okresie n tak¡ sam¡ warto±¢ przyszª¡, któr¡ osi¡ga przy zró»nicowanych
stopach procentowych r
1
, r
2
, . . . , r
m
, tzn. musi by¢ speªnione poni»sze równanie
K
0
(1 + rn) = K
0
(1 + n
1
r
1
+ n
2
r
2
+ . . . + n
m
r
m
)
Przeci¦tna stopa procentowa
r =
1
n
m
∑
j=1
n
j
r
j
=
n
1
r
1
+ n
2
r
2
+ . . . + n
m
r
m
n
1
+ n
2
+ . . . + n
m
Przykªad 1.8 Na podstawie danych z poprzedniego przykªadu obliczy¢ r.
Rozwi¡zanie.
r =
1
3
· 0.12 +
1
6
· 0, 10 +
1
2
· 0, 09
1
3
+
1
6
+
1
2
= 0, 1017
A wi¦c r = 10, 17%.
4
De nicja 1.11 Dyskontowanie proste jest to obliczanie warto±ci kapitaªu pocz¡t-
kowego K
0
na podstawie warto±ci kapitaªu ko«cowego K
n
. Stosujemy wzór
K
0
=
K
p
n
1 + nr
Dyskontem prostym nazywamy ró»nic¦ D = K
n
− K
0
.
Przykªad 1.9 Za 30 dni mamy otrzyma¢ zapªat¦ za dostarczone towary w wyso-
ko±ci 2000 zª. Obliczy¢ bie»¡c¡ warto±¢ tej kwoty przy zaªo»eniu nominalnej stopy
procentowej r = 32%.
Rozwi¡zanie. K
0
=
2000
1+
30
360
·0,32
= 1948, 05
zª.
De nicja 1.12 Dyskontem handlowym nazywamy opªat¦ pobieran¡ z góry za prawo
korzystania z cudzego kapitaªu naliczan¡ w stosunku do kapitaªu ko«cowego.
Stosunek dyskonta handlowego do kwoty nale»nej wierzycielowi po upªywie roku
nazywamy roczn¡ stop¡ dyskontow¡ i oznaczamy przez d.
Warto±¢ dyskonta handlowego za czas n jest okre±lona wzorem
D
H
= K
n
· d · n
Kwota kapitaªu, któr¡ dªu»nik otrzymuje "do r¦ki" stanowi warto±¢ zdyskontowan¡:
K
0
= K
n
− D
H
= K
n
(1
− dn)
Przykªad 1.13 Bior¡c K
n
i K
0
z przykªadu poprzedniego obliczmy stop¦ dyskon-
tow¡ d.
Rozwi¡zanie. Najpierw obliczamy dyskonto handlowe
D
H
= K
n
− K
0
= 2000
− 1948, 05 = 51, 95.
d =
D
H
K
n
· n
=
51, 95
2000
·
30
360
= 0, 3117
Stopa dyskontowa wynosi 31, 17%, a wi¦c jest ni»sza (w tym przypadku) od stopy
procentowej.
5
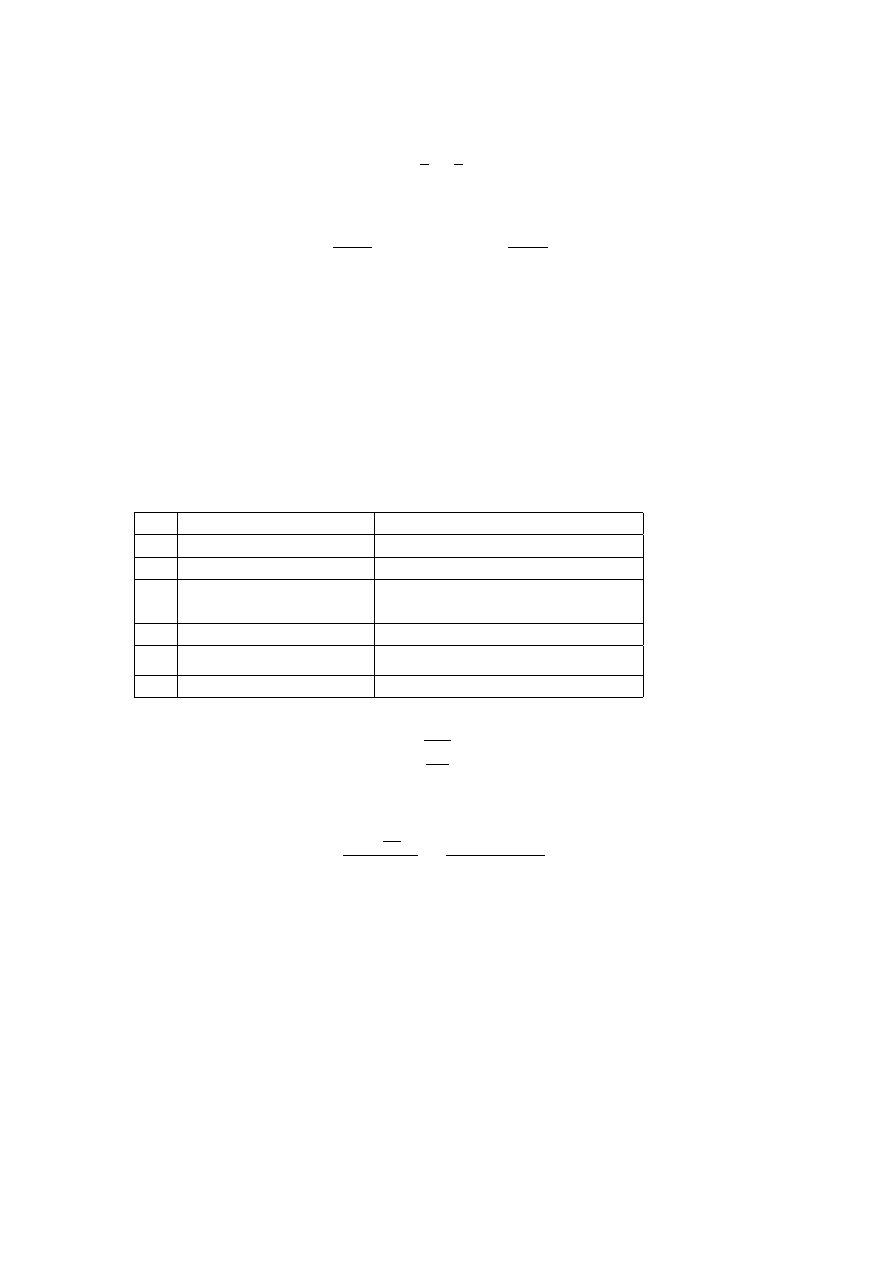
Uwaga. Równo±¢ D = D
H
zachodzi wtedy, gdy prawdziwe jest równanie
n =
1
d
−
1
r
.
Przyjmuj¡c n = 1 mamy dwa równowa»ne wzory
d =
r
1 + r
lub
r =
d
1
− d
.
Wynika z nich, »e d < r. W tym przypadku r oznacza, o ile procent zwi¦ksza si¦
pocz¡tkowa warto±¢ kapitaªu po roku. Natomiast d oznacza, o ile zmniejsza si¦ ko«-
cowa warto±¢ kapitaªu w efekcie rocznego dyskontowania.
2. Procent skªadany.
De nicja 2.1 Oprocentowanie skªadane polega na tym, »e odsetki uzyskane w
okresach poprzednich podlegaj¡ oprocentowaniu wraz z kapitaªem pocz¡tkowym w
okresie nast¦pnym.
Doliczanie odsetek do kapitaªu nazywamy kapitalizacj¡ odsetek.
rok
odsetki
warto±¢ kapitaªu
0
0
K
0
1
K
0
r
K
1
= K
0
+ K
0
r = K
0
(1 + r)
2
K
1
r = K
0
(1 + r)r
K
2
= K
1
+ K
1
r = K
1
(1 + r) =
= K
0
(1 + r)(1 + r) = K
0
(1 + r)
2
3
K
2
r = K
0
(1 + r)
2
r
K
3
= K
0
(1 + r)
3
...
...
...
n
K
n
−1
r = K
0
(1 + r)
n
−1
r
K
s
n
= K
0
(1 + r)
n
Wzór na stop¦ procentow¡:
r =
n
√
K
s
n
K
0
− 1
oraz na ilo±¢ okresów oprocentowania:
n =
log
K
n
K
0
log(1 + r)
=
lnK
n
− lnK
0
ln(1 + r)
Ci¡g {K
n
} jest ci¡giem geometrycznym.
6
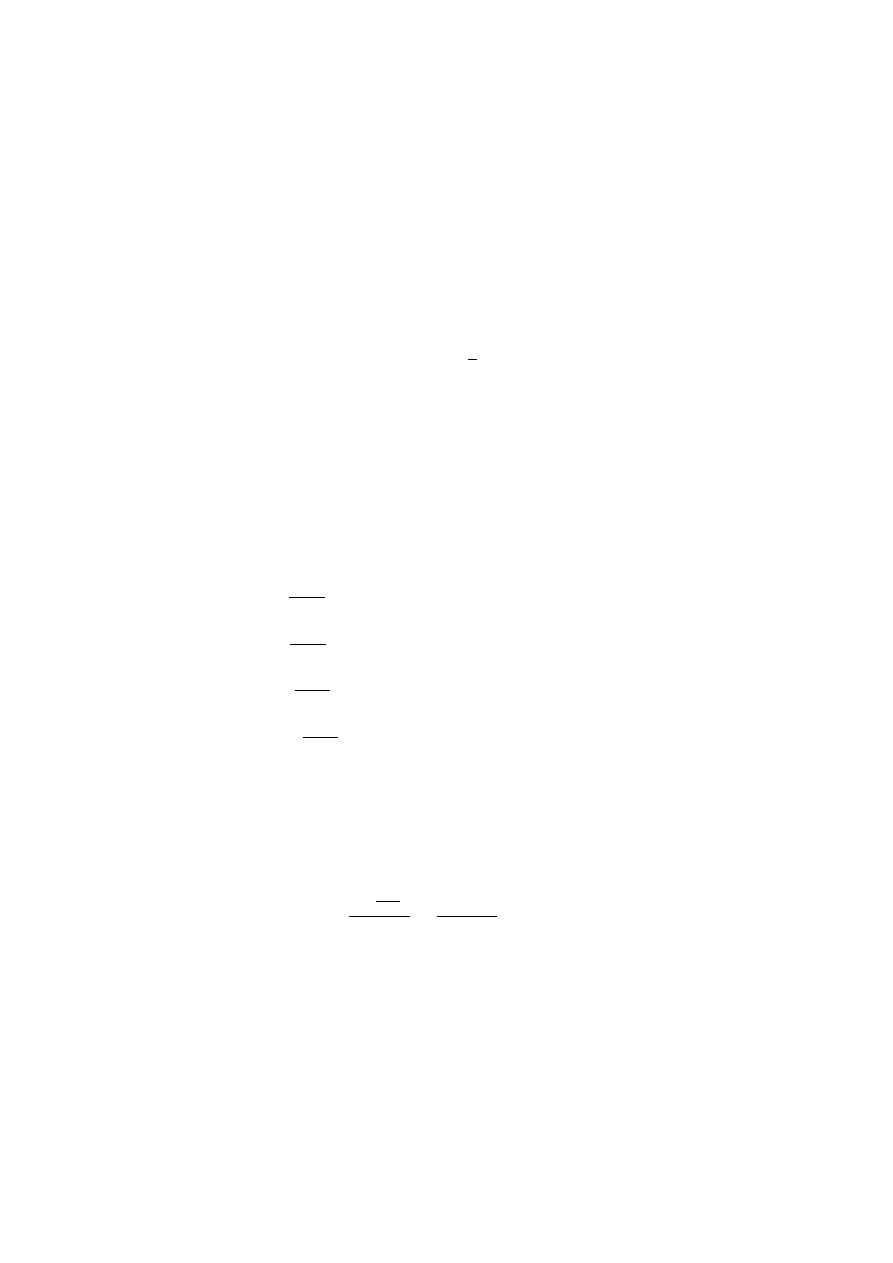
Przykªad 2.1 Znale¹¢ warto±¢ kapitaªu po a) 1 roku, b) 3 latach, je±li kapitaª
pocz¡tkowy K
0
= 2000
zª, a stopa procentowa r = 8%.
Rozwi¡zanie. Obliczamy stop¦ faktyczn¡ r
f
= 8%
· 0, 81 = 6, 48%.
a) K
s
1
= 2000
· (1 + 0, 0648) = 2129, 6 zª.
b) K
s
3
= 2000
· (1 + 0, 0648)
3
= 2414, 53
zª.
Warto±¢ przyszªa kapitaªu przy kapitalizacji odsetek k razy w roku wynosi:
K
s
nk
= K
0
(
1 +
r
k
)
nk
Wraz ze wzrostem liczby okresów kapitalizacji w ci¡gu roku zwi¦ksza si¦ wysoko±¢
odsetek.
Przykªad 2.2 Jak¡ warto±¢ osi¡gnie kapitaª pocz¡tkowy 1000 zª. po 2 latach w
banku oferuj¡cym stop¦ 6% w skali roku przy kapitalizacji odsetek a)póªrocznej, b)
kwartalnej, c) miesi¦cznej, d) dziennej ?
Rozwi¡zanie. r
f
= 6%
· 0.81 = 4, 86%
a) K
s
2
·2
= 1000
(
1 +
0.0486
2
)
2
·2
= 1100, 8
zª.
b) K
s
2
·4
= 1000
(
1 +
0.0486
4
)
2
·4
= 1101, 43
zª.
c) K
s
2
·12
= 1000
(
1 +
0.0486
12
)
2
·12
= 1101, 86
zª.
d) K
s
2
·360
= 1000
(
1 +
0.0486
360
)
2
·360
= 1102, 07
zª.
Przykªad 2.3 Wyznaczy¢ okres trwania depozytu, po okresie którego posiadany
kapitaª K
0
zostanie podwojony, wiedz¡c , »e roczna faktyczna stopa procentowa
r = 7, 1%
i kapitalizacja odsetek nast¦puje raz do roku.
Rozwi¡zanie. Korzystamy ze wzoru na ilo±¢ okresów kapitalizacji:
n =
ln
2K
0
K
0
ln 1, 071
=
ln 2
ln 1, 071
≈ 10
7
Uwaga. Do przybli»onej oceny okresu n, w którym kapitaª podwaja swoj¡ warto±¢
i przy zaªo»eniu rocznej stopy r (podanej w %) stosuje si¦ tzw. reguª¦ 70:
n
≈
70
r
lat
Faktycznie, warto±¢ n z ostatniego przykªadu mo»na policzy¢ szybciej
n =
70
7, 1
≈ 10lat
De nicja 2.2 Ci¡gªa kapitalizacja odsetek zachodzi gdy odsetki naliczane s¡ w
ka»dym momencie trwania lokaty. Liczba okresów kapitalizacji jest niesko«czona.
K
s
k
→∞
= lim
k
→∞
K
0
(
1 +
r
k
)
nk
= K
0
lim
k
→∞
[(
1 +
r
k
)
k
r
]
nr
= K
0
e
nr
De nicja 3. Dwie stopy oprocentowania skªadanego s¡ równowa»ne, je±li przy ka»-
dej z nich odsetki skªadane od kapitaªu pocz¡tkowego po czasie n maj¡ t¡ sam¡
warto±¢ tzn.
K
s
nk
1
= K
s
nk
2
K
0
(
1 +
r
1
k
1
)
nk
1
= K
0
(
1 +
r
2
k
2
)
nk
2
(
1 +
r
1
k
1
)
k
1
=
(
1 +
r
2
k
2
)
k
2
Równowa»no±¢ stóp nie zale»y od:
- kapitaªu pocz¡tkowego
- czasu oprocentowania
Przykªad 2.4 Bank A oferuje roczn¡ stop¦ 8% i kwartalne oprocentowanie od-
setek. Bank B oferuje roczn¡ stop¦ 9% i roczn¡ kapitalizacj¦ odsetek. Który bank
wybra¢?
Rozwi¡zanie. Obliczamy stopy efektywne:
r
1f
= 8%
· 0, 81 = 6, 48%,
r
2f
= 9%
· 0, 81 = 7, 29%.
(
1 +
0,0648
4
)
4
= 1, 0664
,
(
1 +
0,0729
1
)
1
= 1, 0729
.
Z ostatnich oblicze« wnioskujemy, »e bank B oferuje lepsze warunki oprocentowania
lokat.
8
Uwaga. Przy wy»szych stopach procentowych cz¦stsza kapitalizacja ma wi¦ksze
znaczenie.
Przykªad 2.5 Zaªó»my, »e bank A oferuje faktyczn¡ (dla uproszczenia oblicze«)
stop¦ procentow¡ 11% w jednym roku, a w kolejnym 12% i kwartaln¡ kapitalizacj¦.
Bank B oferuje w tych samych latach stopy równe odpowiednio 11, 5% i12, 5% ale
kapitalizacj¦ roczn¡. Który bank wybra¢?
Rozwi¡zanie. Po obliczeniach
(
1 +
0,11
4
)
4
= 1, 1146
,
(
1 +
0,115
1
)
1
= 1, 115
,
(
1 +
0,12
4
)
4
= 1, 1255
,
(
1 +
0,125
1
)
1
= 1, 12
.
stwierdzamy, »e w pierwszym roku lepiej wybra¢ bank B, a w nast¦pnym bank A.
Warto±¢ przyszª¡ kapitaªu dla zmiennej stopy procentowej liczymy ze wzoru:
K
s
n
1
+n
2
+...+n
m
= K
0
(1 + r
1
)
n
1
(1 + r
2
)
n
2
. . . (1 + r
m
)
n
m
Przeci¦tna stopa procentowa r w okresie n speªnia równanie:
K
0
(1 + r)
n
= K
0
(1 + r
1
)
n
1
(1 + r
2
)
n
2
. . . (1 + r
m
)
n
m
,
z którego obliczamy
r =
n
√
(1 + r
1
)
n
1
(1 + r
2
)
n
2
. . . (1 + r
m
)
n
m
− 1
Przykªad 2.6 Roczna stopa procentowa banku w 1-szym roku wynosi 7%, a w
dwóch nast¦pnych 6%. Ustali¢ warto±¢ kapitaªu po 3-ch latach, je±li warto±¢ pocz¡t-
kowa kapitaªu K
0
= 1000
zª. Kapitalizacja odsetek jest roczna. Znale¹¢ r.
Rozwi¡zanie. Obliczamy stopy efektywne:
r
1f
= 7%
· 0, 81 = 5, 67%,
r
2f
= 6%
· 0, 81 = 4, 86%.
Warto±¢ przyszªa kapitaªu wynosi
K
s
1+2
= 1000(1 + 0, 0567)(1 + 0, 0486)
2
= 1161, 90
Z oblicze« r =
3
√
1, 07
· 1, 06
2
− 1 = 0, 0633 otrzymujemy warto±¢ 6, 33%, która
jest przeci¦tn¡ stop¡ procentow¡.
9
De nicja 2.4 Efektywn¡ stop¡ procentow¡ r
e
nazywamy stop¦ oprocentowania
rocznego, która przynosi ten sam efekt kapitalizacji rocznej co kapitalizacja o danej
nominalnej stopie procentowej w krótszych okresach ni» rok.
r
e
=
(
1 +
r
k
)
k
− 1
gdzie k - ilo±¢ kapitalizacji w ci¡gu roku,
r
- nominalna stopa procentowa.
Uwaga. Je±li kapitalizacja odsetek zachodzi raz do roku to stopa efektywna jest
równa stopie nominalnej.
Uwaga. Je±li uwzgl¦dnimy podatek dochodowy od zysków z inwestycji kapitaªo-
wych to otrzymamy tak zwan¡ faktyczn¡ efektywn¡ stop¦ procentow¡.
Uwaga. r
e
umo»liwia porównanie ró»nych warunków oprocentowania
Przykªad 2.7 Bank A oferuje nominaln¡ stop¦ procentow¡ 24% przy miesi¦cznej
kapitalizacji odsetek, bank B stop¦ 25%, przy kwartalnej kapitalizacji odsetek. Któ-
ry bank oferuje wy»sz¡ efektywn¡ stop¦ procentow¡?
Rozwi¡zanie. Dla banku A otrzymujemy r
e
=
(
1 +
0,24
12
)
12
− 1 = 0, 268,
a dla banku B r
e
=
(
1 +
0,25
4
)
4
− 1 = 0, 274. Bank B oferuje lepsze warunki lokaty
kapitaªu.
Odwrotno±ci¡ poj¦cia stopy efektywnej jest okresowa stopa równowa»na .
De nicja 2.5 Okresowa stopa równowa»na r
d
jest stopa procentowa, przy której
±ródokresowa (podokresowa) kapitalizacja odsetek przynosi ten sam efekt co kapi-
talizacja okresowa o danej stopie % w ci¡gu tego samego czasu trwania depozytu.
r
d
= k
(
k
√
1 + r
− 1
)
gdzie k - liczba dziel¡ca okres na ±ródokresy.
Przykªad 2.8 Bank proponuje kapitalizacj¦ roczn¡ przy rocznej stopie równej 8%.
Jaka powinna by¢ a) póªroczna, b) kwartalna stopa równowa»na.
10
Rozwi¡zanie. a) r
d
= 2(
√
1 + 0, 08
− 1) = 0, 0785.
b) r
d
= 4(
4
√
1 = 0, 08
− 1) = 0, 0777.
Póªroczna stopa równowa»na wynosi 7, 85%, a kwartalna 7, 77%.
De nicja 2.6 Dyskontowanie skªadane jest to obliczanie warto±ci kapitaªu pocz¡t-
kowego K
0
na podstawie znanej warto±ci kapitaªu ko«cowego K
s
n
.
K
0
=
K
s
n
(1 + r)
n
Ró»nic¦ K
n
− K
0
= D
nazywamy dyskontem skªadanym.
Przykªad 2.9 Jak¡ kwot¦ nale»y wpªaci¢ do banku by po 3-ch latach uzyska¢ kwo-
t¦ 5000 zª. je±li r = 5% przy kapitalizacji rocznej.
Rozwi¡zanie. K
0
=
5000
(1+0,05)
3
= 4319, 19
zª.
3. Kredyty
De nicja 3.1 Kredyt bankowy jest to zale»no±¢ nansowo-prawna mi¦dzy bankiem-
kredytodawc¡, a inwestorem-kredytobiorc¡, która polega na:
-oddaniu kredytobiorcy okre±lonej kwoty ±rodków pªatniczych do czasowej dyspozy-
cji na realizacj¦ okre±lonego celu
-spªaceniu kredytu wraz z odsetkami i prowizj¡ - najcz¦±ciej naliczan¡ do odsetek
zgodnie z zawart¡ umow¡ kredytow¡
- kontroli realizacji umowy i wykonania przez kredytobiorców przyznanych ±rodków
pªatniczych.
Raty kredytowe, którymi spªacamy zaci¡gni¦ty kredyt skªadaj¡ si¦ na ogóª z
dwóch cz¦±ci - raty kapitaªowej oraz raty odsetkowej. Mog¡ zawiera¢ równie» np.
rat¦ ubezpieczenia.
Rata kapitaªowa to cz¦±¢ kredytu, któr¡ spªacamy w danym okresie (najcz¦±ciej
miesi¡cu), i która pomniejsza nasz dªug wobec banku.
Rata odsetkowa zawiera naliczane za dany okres odsetki od pozostaªej do spªaty
cz¦±ci kredytu.
Najcz¦±ciej banki stosuj¡ raty malej¡ce lub raty równe.
Omówimy kolejno ka»d¡ z nich.
11
Rata malej¡ca charakteryzuje si¦ staª¡ rat¡ kapitaªow¡ oraz malej¡c¡ rat¡ odset-
kow¡.
Wówczas rata kapitaªowa
T =
S
N
,
gdzie S to kwota zaci¡gni¦tego kredytu, a N - ilo±¢ rat.
Wprowad¹my oznaczenia.
S
n
= S
− nT - kwota pozostaªego do spªacenia kredytu po wpªaceniu n-tej raty.
O
n
= S
n
−1
· r = S
(
1
−
n
−1
N
)
r
- wysoko±¢ odsetek za n-ty okres (rata odsetkowa).
r
- stopa procentowa kredytu.
A
n
= T + O
n
= T [1 + (N
− n + 1)r] - n-ta kwota pªatno±ci (n-ta rata).
W powy»szych oznaczeniach zmienna n przyjmuje warto±ci ze zbioru {1, 2, . . . , N}.
Suma wszystkich odsetek wynosi
O = O
1
+ O
2
+ . . . + O
N
= r
· S ·
N + 1
2
¡czna kwota pªatno±ci
A = A
1
+ A
2
+ . . . + A
N
= S
(
1 + r
N + 1
2
)
Przykªad 3.1 Klient zaci¡gn¡ª kredyt w wysoko±ci 24000 zª. na okres 4 lat wg.
stopy procentowej 25%. Kredyt ten nale»y spªaci¢ w 4-ch ratach przy zaªo»eniu rów-
no±ci rat kapitaªowych.
Rozwi¡zanie. Sporz¡dzamy tabel¦.
12
Kwota kredytu
Rata
Odsetki od
Kwota
Kwota kredytu
Rok
na pocz¡tku
kapitaªowa
pozostaªego do
pªatno±ci na koniec roku
roku
T
spªacenia kapitaªu
A
n
1
24000
6000
6000
12000
18000
2
18000
6000
4500
10500
12000
3
12000
6000
3000
9000
6000
4
6000
6000
1500
7500
0
∑
24000
15000
39000
Suma wszystkich odsetek wynosi
O = r
· S ·
N + 1
2
= 0, 25
· 24000 ·
5
2
= 15000
¡czna kwota pª¡tno±ci
A = S
(
1 + r
N + 1
2
)
= 24000
(
1 + 0, 25
·
5
2
)
= 39000
Równe raty kapitaªowe. Okresy spªat i kapitalizacji takie same ale inny
okres stopy procentowej.
Mamy m rat kapitaªowych w jednym okresie procentowym czyli mN rat w ogó-
le. Obliczamy ±ródokresow¡ stop¦ procentow¡ r
m
=
r
m
. We wzorach okre±laj¡cych
koszty kredytu nale»y zast¡pi¢ liczb¦ okresów procentowych N przez mN oraz r
przez r
m
. Rata kapitaªowa
T =
S
mN
Kwota kredytu do spªacenia
S
n
= S
− nT
n = 1, 2, . . . , mN.
Kwota odsetek naliczana od faktycznie pozostaªego do spªaty dªugu
O
n
= S
n
−1
· r
m
= S
(
1
−
n
− 1
mN
)
·
r
m
n = 1, 2, . . . , mN.
Suma wszystkich odsetek wynosi
O = O
1
+ O
2
+ . . . + O
mN
=
r
m
· S ·
mN + 1
2
13
n-ta kwota pªatno±ci
A
n
= T + O
n
n = 1, 2, . . . , mN.
¡czna kwota pªatno±ci
A = A
1
+ A
2
+ . . . + A
mN
= S
(
1 + r
m
mN + 1
2
)
Przykªad 3.2 Dane jak w przykªadzie 3.1 ale spªata kredytu i kapitalizacja odsetek
odbywa si¦ co póª roku.
Rozwi¡zanie. m=2, wi¦c ilo±¢ rat wynosi 2 · 4 = 8
Rata kapitaªowa
T =
24000
8
= 3000
,
stopa ±ródokresowa r
m
=
0,25
2
= 0125
Kwota kredytu
Rata
Odsetki od
Kwota
Kwota kredytu
Póªrocze
na pocz¡tku
kapitaªowa
pozostaªego do
pªatno±ci
na koniec
póªrocza
T
spªacenia kapitaªu
A
n
póªrocza
1
24000
3000
3000
6000
21000
2
21000
3000
2625
5625
18000
3
18000
3000
2250
5250
15000
4
15000
3000
1875
4875
12000
5
12000
3000
1500
4500
9000
6
9000
3000
1125
4125
6000
7
6000
3000
750
3750
3000
8
3000
3000
375
3375
0
∑
24000
13500
37500
Suma wszystkich odsetek wynosi
O = 0, 125
· 24000 ·
8 + 1
2
= 13500
¡czna kwota pª¡tno±ci
A = 24000
(
1 + 0, 125
·
8 + 1
2
)
= 37500
14
Odsetki od kredytu mog¡ by¢ naliczane nie od faktycznie pozostaªego do spªa-
cenia dªugu ale od dªugu istniej¡cego na pocz¡tku okresu procentowego. Wówczas
klient ma sytuacj¦ mniej korzystn¡.
Raty odsetkowe maj¡ nast¦puj¡ce warto±ci
O
k,n
=
r
m
S
(
1
−
n
− 1
N
)
k = 1, 2, . . . , m,
n = 1, 2, . . . , N.
Suma wszystkich odsetek wynosi
O = r
· S ·
N + 1
2
¡czna kwota pª¡tno±ci
A = S
(
1 + r
N + 1
2
)
Przykªad 3.3 Dane jak w przykªadzie 3.2 ale odsetki naliczane s¡ od salda na
pocz¡tku roku.
Kwota kredytu
Rata
Odsetki od
Kwota
Kwota kredytu
Póªrocze
na pocz¡tku
kapitaªowa
pozostaªego do
pªatno±ci
na koniec
póªrocza
T
spªacenia kapitaªu
A
n
póªrocza
1
24000
3000
3000
6000
21000
2
21000
3000
3000
6000
18000
3
18000
3000
2250
5250
15000
4
15000
3000
2250
5250
12000
5
12000
3000
1500
4500
9000
6
9000
3000
1500
4500
6000
7
6000
3000
750
3750
3000
8
3000
3000
750
3750
0
∑
24000
15000
39000
Suma wszystkich odsetek wynosi
O = 0, 25
· 24000 ·
4 + 1
2
= 15000
¡czna kwota pªatno±ci
A = 24000
(
1 + 0, 25
·
4 + 1
2
)
= 39000
15
W tym wypadku strata kredytobiorcy wynosi
∆O = rS
N + 1
2
− r
m
S
mN + 1
2
= r
m
S
m
− 1
2
= 0, 125
· 24000 ·
1
2
= 1500
Spªata kredytu w równych ratach kapitaªowych m razy w roku, odsetki
naliczane i pªacone na koniec roku.
Odsetki naliczane s¡ od pozostaªego do spªacenia kredytu w ka»dym ±ródokresie i
sumuje si¦ na koniec roku.
Warto±¢ odsetek po kolejnych okresach kapitalizacji wynosi
O
n
=
S
N
· r ·
(
N
− n +
m + 1
2m
)
n = 1, 2, . . . , N.
¡czna suma odsetek
O = O
1
+ O
2
+ . . . + O
N
=
r
m
· S ·
mN + 1
2
Kwota kredytu do spªacenia po n okresach kapitalizacji
S
n
= S
− n
S
mN
n = 1, 2, . . . , N.
Kwoty pªatno±ci w okresach, w których byªy naliczane odsetki
A
n
=
S
mN
+ O
n
n = 1, 2, . . . , N.
Kwoty pªatno±ci w okresach, w których nie naliczano odsetek s¡ równe racie kapita-
ªowej:
A =
S
mN
Przykªad 3.4 Klient pobiera kredyt 24000 zª. ze spªat¡ w ci¡gu 4-ch lat w o±miu
ratach ze stop¡ 25% w trzech pierwszych latach i stop¡ 26% w roku ostatnim. Ka-
pitalizacja odsetek nast¦puje raz do roku. Dodatkowo bank pobiera prowizj¦ w wy-
soko±ci 1% za udzielenie kredytu.
16
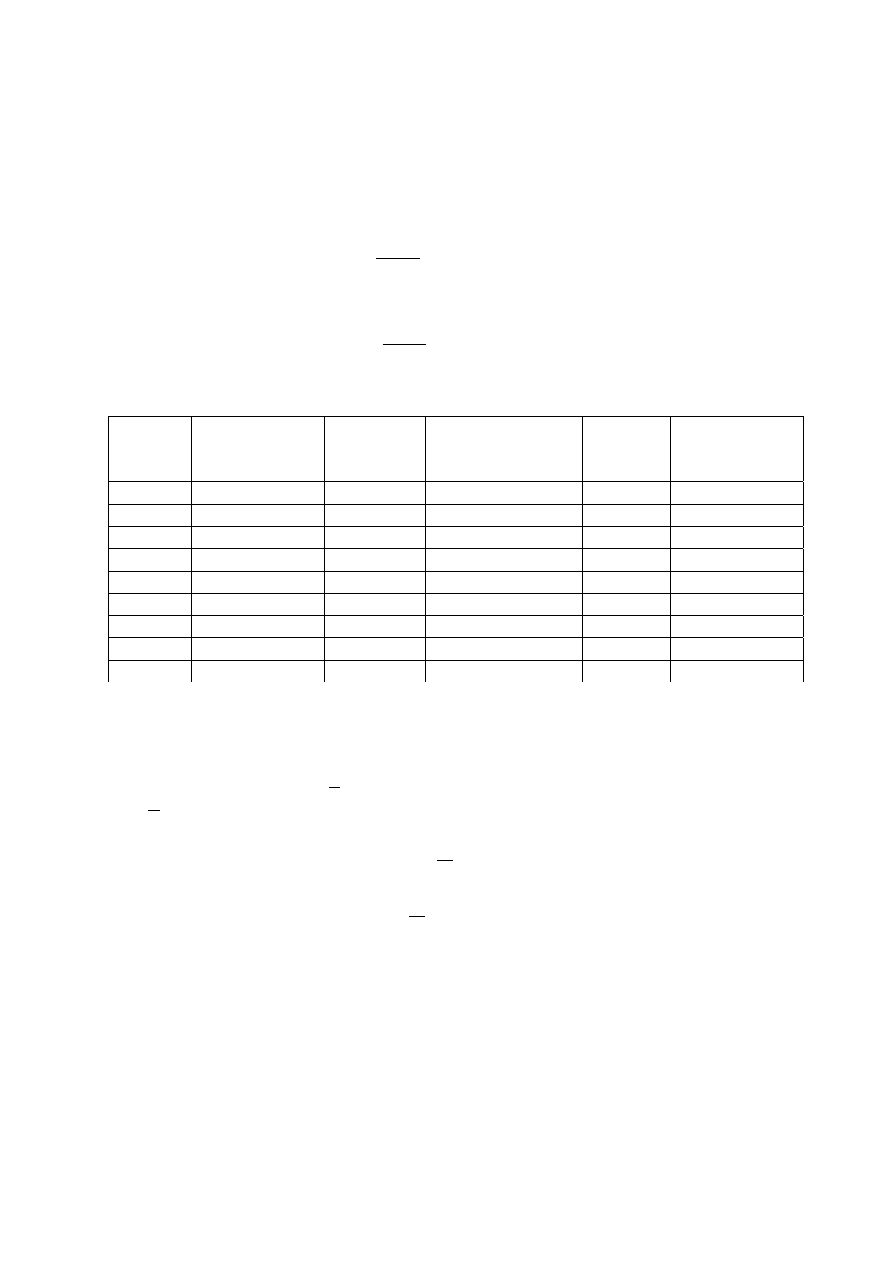
Rozwi¡zanie. Poniewa» potrzebujemy kwoty 24000, wi¦c z uwagi na prowizj¦ musimy
wyliczy¢ faktyczn¡ kwot¦ pobieranego kredytu x.
x
− 1% · x = 24000
x
· 99% = 24000
x =
24000
0, 99
= 24242
zª.
Rata kapitaªowa równa si¦
T =
24242
8
= 3030.25
Ukªadamy plan amortyzacji
Kwota kredytu
Rata
Odsetki od
Kwota
Kwota kredytu
Póªrocze
na pocz¡tku
kapitaªowa
pozostaªego do
pªatno±ci
na koniec
póªrocza
T
spªacenia kapitaªu
A
póªrocza
1
24242
3030
,25
3030
,25
21211
,75
2
21211
,75
3030
,25
3030, 25 + 2651
,47
8711
,97
18181
,5
3
18000
3030
,25
3030
,25
15151
,25
4
15000
3030
,25
2272, 69 + 1893
,91
7196
,85
12121
,25
5
12000
3030
,25
3030
,25
9090
,75
6
9000
3030
,25
1515, 13 + 1136
,35
5681
,73
6060
,5
7
6000
3030
,25
3030
,25
3030
,25
8
3000
3030
,25
787, 87 + 393
,94
4211
,06
0
∑
242420
13681
,61 37923,61
Równe raty kapitaªowe. Kapitalizacja odsetek cz¦stsza ni» spªata odsetek.
Mamy m kapitalizacji odsetek mi¦dzy kolejnymi spªatami. Mo»emy wi¦c zast¡pi¢
m-krotn¡ kapitalizacj¦ stop¡
r
m
przez jednokrotn¡ kapitalizacj¦ stop¡ efektywn¡ r
e
=
(
1 +
r
m
)
m
− 1. Wówczas poszczególne warto±ci kosztów kredytu s¡ równe:
T =
S
N
S
n
=
S
N
(N
− n)
17
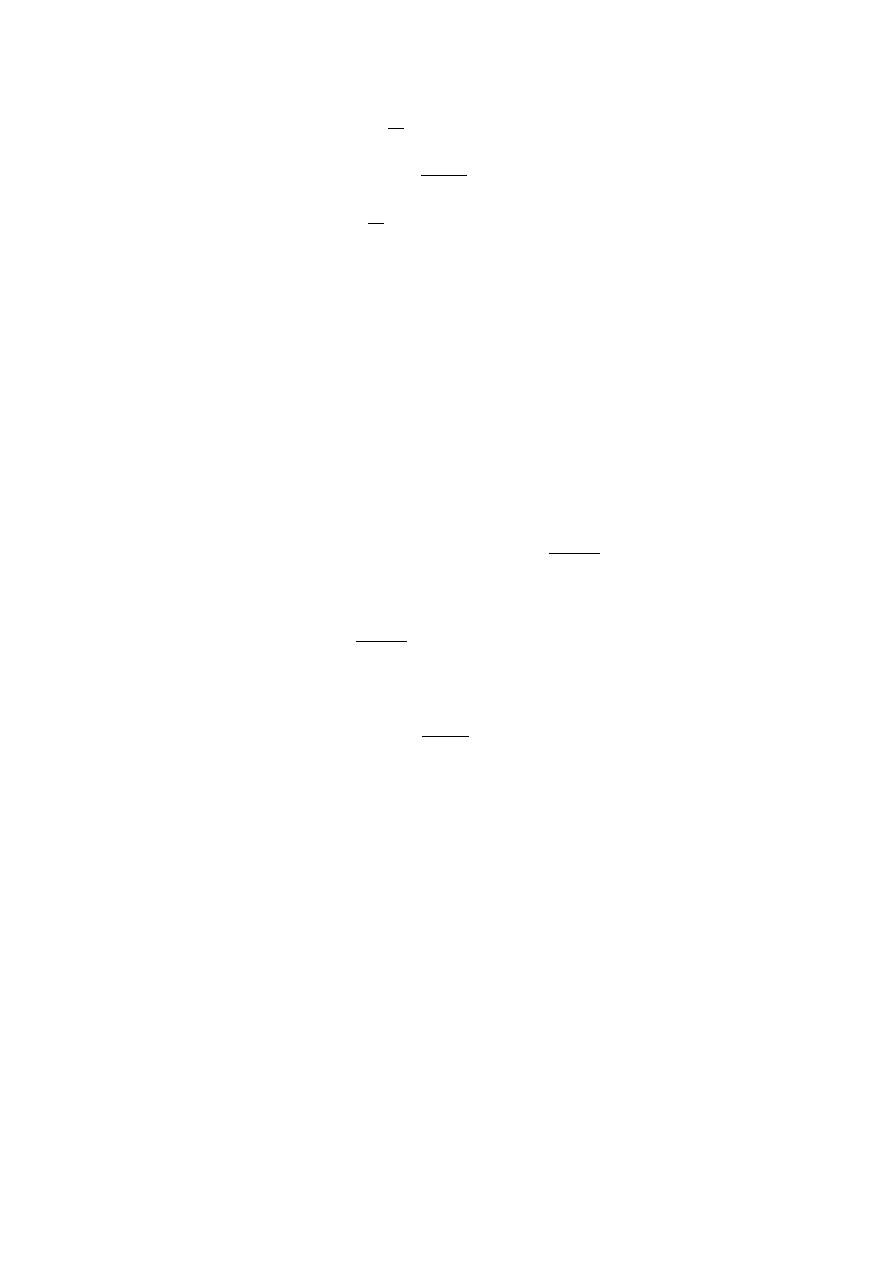
O
n
=
S
N
(N
− n + 1)r
e
O = S
N + 1
2
r
e
A
n
=
S
N
[1 + (N
− n + 1)r
e
]
Raty równe.
Kredyt jest spªacany w N równych kwotach pªatno±ci, tzn.
A
1
= A
2
= . . . = A
N
= A
Gdyby kredyt nie byª spªacany to po upªywie N lat kwota S wzrosªaby do poziomu
S(1 + r)
N
= Sq
N
,
q = 1 + r
(1)
Natomiast, gdyby kredyt byª spªacany w równych ratach A, to raty te utworzyªyby
kapitaª
A + A(1 + r) + . . . + A(1 + r)
N
−1
= A
q
N
− 1
q
− 1
(2)
Z porównania wielko±ci (1) i (2) otrzymujemy wzór na staª¡ rat¦
A = Sq
N
q
− 1
q
N
− 1
gdzie q = 1 + r.
Kwota kredytu pozostaªa do spªacenia:
S
n
= S
n
−1
· q − A = Sq
n
− A
q
n
− 1
q
− 1
n = 1, 2, . . . , N
Kwota odsetek naliczana na koniec kolejnego roku:
O
n
= S
n
−1
· r
n = 1, 2, . . . , N
Rata kapitaªowa:
T
n
= A
− O
n
= S
n
−1
− S
n
n = 1, 2, . . . , N
18
¡czna kwota odsetek:
O = N A
− S = S
(
N q
N
q
− 1
q
N
− 1
− 1
)
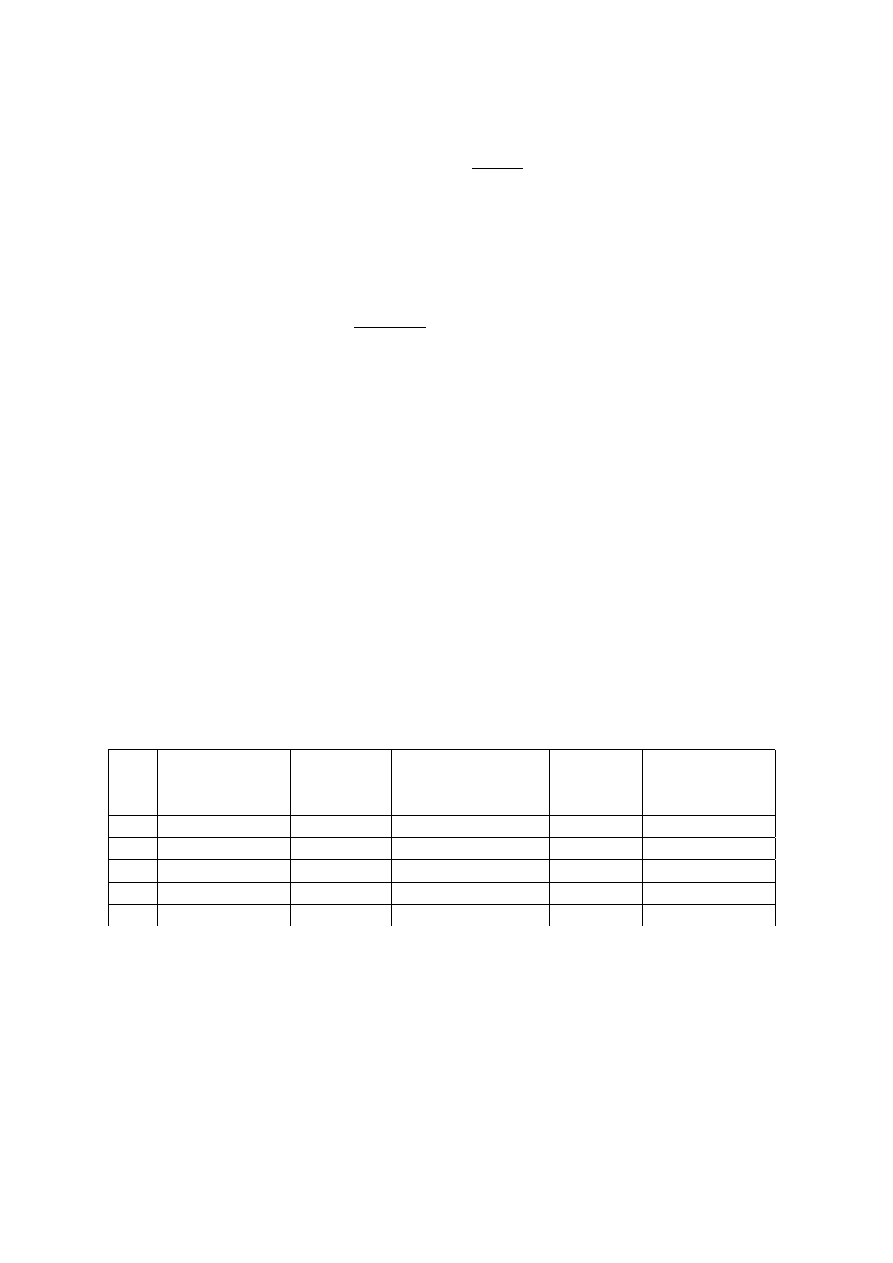
Przykªad 3.5 Dane jak w przykªadzie 1. Kredyt ma by¢ spªacany w 4-ch równych
ratach.
Rozwi¡zanie. wielko±¢ raty wynosi.
A = 24000
· 1, 25
4
·
1, 25
− 1
1, 25
4
− 1
= 10162, 60163
≈ 10162, 602
Obliczamy "r¦cznie" kolejne raty odsetkowe i kapitaªowe:
O
1
= S
· r = 24000 · 0, 25 = 6000
T
1
= A
− O
1
= 4162, 602
S
1
= S
− T
1
= 24000
− 4162, 602 = 19837, 398
O
2
= S
1
· r = 4959, 35
T
2
= A
− O
2
= 10162, 602
− 4959, 35 = 5203, 26
S
2
= S
1
− T
2
= 19837, 398
− 5203, 26 = 14634, 146
O
3
= S
2
· r = 14634, 13 · 0, 25 = 3658, 537
T
3
= A
− O
3
= 10162, 602
− 3658, 537 = 6504, 065
S
3
= S
2
− T
3
= 14634, 146
− 6504, 065 = 8130, 081
O
4
= S
3
· r = 8130, 081 · 0, 25 = 2032, 52
T
4
= A
− O
4
= 10162, 602
− 2032, 52 = 8130, 082
S
4
= S
3
− T
4
= 0
Wyniki umieszczamy w tabeli.
Kwota kredytu
Rata
Odsetki od
Kwota
Kwota kredytu
Rok
na pocz¡tku
kapitaªowa
pozostaªego do
pªatno±ci na koniec roku
roku
T
n
spªacenia kapitaªu
A
1
24000
4162
,602
6000
10162
,602
19837
,398
2
19837
,39
5203
,252
4959
,35
10162
,602
14634
,146
3
14634
,13
6504
,065
3658
,537
10162
,602
8130
,081
4
8130
,081
8130
,082
2032
,52
10162
,602
0
∑
24000
,001
16650
,407
40650
,408
19
Zauwa»my, »e w przypadku staªych kwot spªaty dªugu, kolejne raty kapitaªowe rosn¡,
a raty odsetkowe malej¡. Poza tym koszt kredytu o staªych spªatach jest wi¦kszy,
poniewa» wi¦ksze kwoty kredytu pozostaj¡ do spªacenia w pó¹niejszych okresach
pªatno±ci.
Je»eli równe raty miaªyby by¢ wpªacane m razy cz¦±ciej ni» kapitalizacja odsetek
(liczona od pozostaªego do spªaty dªugu), to staªa rata równa si¦
A = Sq
N
2
2m + (m
− 1)r
·
q
− 1
q
N
− 1
Je»eli kapitalizacja odsetek odbywaªaby si¦ m razy cz¦±ciej ni» spªata kolejnych rat,
to
A = Sq
N
q
− 1
q
N
− 1
= S
·
(
1 +
r
m
)
mN
·
(1 +
r
m
)
m
− 1
(1 +
r
m
)
mN
− 1
gdzie q = 1 + r
e
, r
e
=
(
1 +
r
m
)
m
− 1
jest efektywn¡ stop¡ procentow¡ w okresie
mi¦dzy dwiema wpªatami rat.
Czasami zdarza si¦, »e kredytobiorca ma problemy ze spªat¡ kredytu i wynego-
cjowuje spªat¦ odsetek caªych lub cz¦±ciowych po pewnym czasie.
W przypadku odroczenia wszelkich pªatno±ci na okres p lat, to po tym czasie
kredyt zwi¦ksza si¦ do sumy
S(1 + r)
p
W przypadku odroczenia spªacania jedynie rat kapitaªowych przy zachowaniu spªat
rat odsetkowych O
p
= Sr
po okresie p lat pozostaje do spªacenia ta sama kwota
kredytu S.
Przykªad 3.6 Dane jak w przykªadzie 3.1. Spªata zaci¡gni¦tego kredytu ma rozpo-
cz¡¢ si¦ po upªywie 3-letniego okresu karencji a) caªego kredytu, b) rat kapitaªowych.
Rozwi¡zanie. a) Po 3-ch latach warto±¢ dªugu ro±nie do kwoty
S = 24000(1 + 0, 25)
3
= 46875
zª.
Plan amortyzacji dªugu przedstawia poni»sza tabela.
20
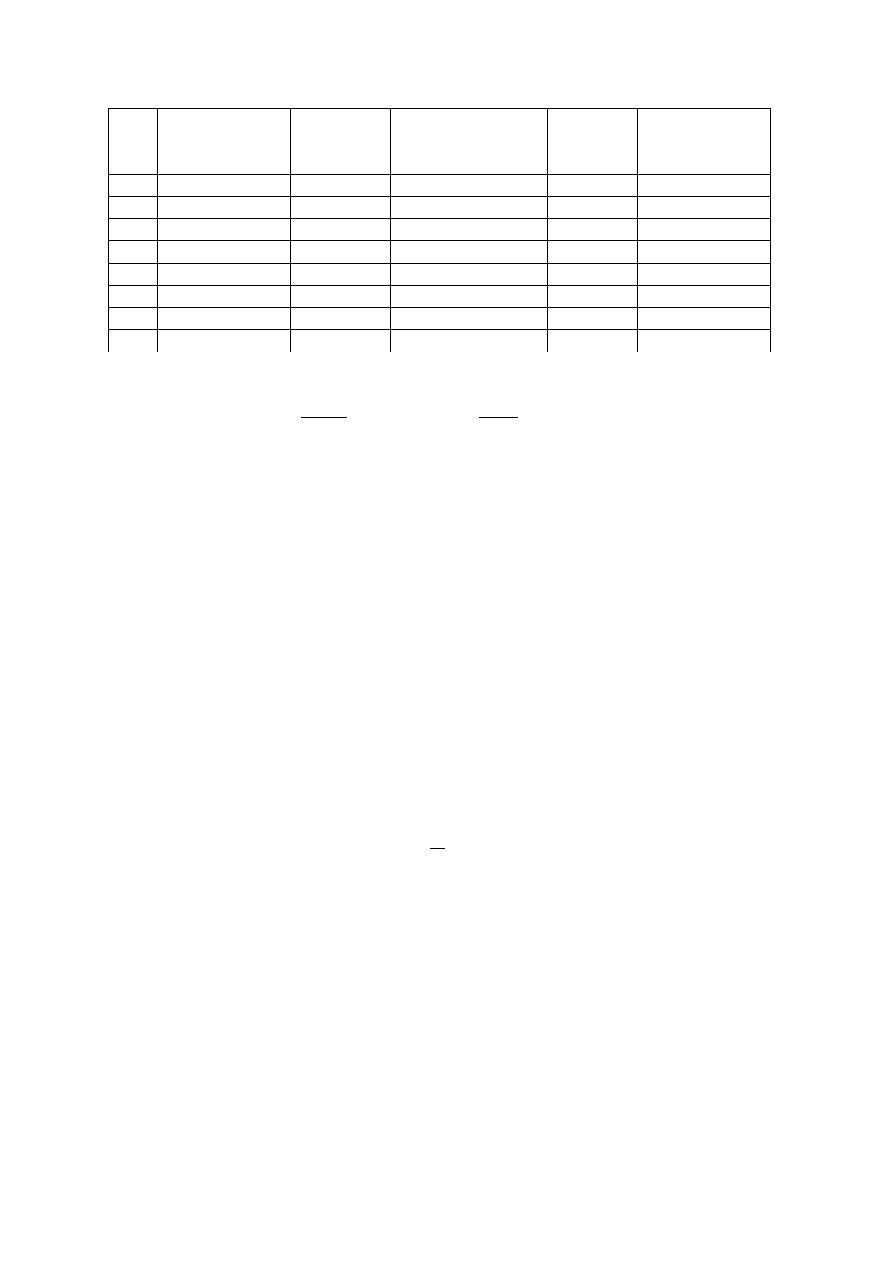
Kwota kredytu
Rata
Odsetki od
Kwota
Kwota kredytu
Rok
na pocz¡tku
kapitaªowa
pozostaªego do
pªatno±ci na koniec roku
roku
T
spªacenia kapitaªu
A
1
24000
−
−
−
30000
2
30000
−
−
−
37500
3
37500
−
−
−
46875
4
46875
11718
,75
11718
,75
23437
,5
35156
,25
5
35156
,25
11718
,75
8789
,06
20507
,81
23437
,5
6
23437
,5
11718
,75
5859
,38
17578
,13
11718
,75
7
11718
,75
11718
,75
2929
,69
14648
,44
0
∑
46875
29296
,88
76171
,88
Kwota odsetek wynosi
O = Sr
N + 1
2
= 46875
· 0, 25 ·
4 + 1
2
= 29296, 88
b) W ci¡gu kolejnych 3 lat b¦d¡ spªacane odsetki od zaci¡gni¦tego kredytu w wy-
soko±ci
S
· r = 24000 · 0, 25 = 6000 zª.
Pozostaªe dane w nast¦pnych latach takie jak w tabeli przykªadu 1.
W efekcie caªkowita suma spªacanych odsetek wynosi
3
· 6000 + 15000 = 33000 zª.
Do oceny kosztu kredytu nale»y wzi¡¢ ró»nic¦ pomi¦dzy przyszª¡ warto±ci¡ sumy
wszystkich pªatno±ci, a warto±ci¡ pobranego kredytu. Jest to tzw. efektywny koszt
kredytu.
K
e
= [A
1
(1 + r)
N
−1
+ A
2
(1 + r)
N
−2
+ . . . + A
N
−1
(1 + r) + A
N
]
− S
Miar¡ jednostkowego kosztu kredytu jest warto±¢
r
e
=
(
1 +
r
m
)
m
− 1,
gdzie m oznacza cz¦sto±¢ kapitalizacji odsetek przy stopie procentowej r w ci¡gu
roku.
21
4. Wkªady okresowe.
Wkªadami okresowymi nazywamy jednostkowe kwoty pieni¦»ne skªadane w rów-
nych odst¦pach czasu w celu ich kapitalizacji.
Wkªad okre±lony jest przez
- liczb¦ rat,
- wysoko±¢ raty,
- dªugo±¢ okresu mi¦dzy kolejnymi ratami,
- dat¦ pªatno±ci 1-szej raty.
Wkªady zgodne s¡ to raty dokonywane w terminach zgodnych z okresem stopy
procentowej i okresem kapitalizacji odsetek.
Oprocentowanie proste.
Wkªady okresowe w wysoko±ci K j.p. przy okresowej stopie procentowej r i okreso-
wym oprocentowaniu tworz¡ kwot¦:
- przy wpªatach dokonywanych z góry - na pocz¡tku ka»dego z n kolejnych okresów
P
+
n
= K
· n ·
(
1 +
n + 1
2
r
)
- przy wpªatach dokonywanych z doªu - pod koniec ka»dego z n kolejnych okresów
P
−
n
= K
· n ·
(
1 +
n
− 1
2
r
)
Przykªad 4.1 W banku roczna nominalna stopa% depozytów pieni¦»nych przy
rocznej kapitalizacji wynosi 12%. Wyznaczy¢ kwot¦ jak¡ nale»y wpªaca¢ z góry przez
3 kolejne kwartaªy, aby na koniec 3-go kwartaªu uzyska¢ kwot¦ 2000 zª.
Rozwi¡zanie. Z równania
P
+
3
= K
· 3 · (1 +
3 + 1
2
r)
mamy wyznaczy¢ K:
K =
2000
3
· (1 + 2 · 0, 12)
= 537, 64
zª.
22
Uwaga. W caªym tym rozdziale dotycz¡cym wkªadów okresowych stopy procentowe
traktujemy jako stopy faktyczne, a wi¦c uwzgl¦dniaj¡ce ju» podatek od inwestycji
kapitaªowych, je±li taki podatek musimy zapªaci¢.
Oprocentowanie skªadane.
Wkªady okresowe w wysoko±ci K j.p. przy okresowej stopie procentowej r i okreso-
wym oprocentowaniu tworz¡ kwot¦:
- przy wpªatach dokonywanych z góry - na pocz¡tku ka»dego z n kolejnych okresów
Q
+
n
= K(1 + r)
(1 + r)
n
− 1
r
- przy wpªatach dokonywanych z doªu - pod koniec ka»dego z n kolejnych okresów
Q
−
n
= K
(1 + r)
n
− 1
r
Przykªad 4.2 Jak¡ kwot¦ uzyskamy wpªacaj¡c do banku rocznie 12000 zª. przez
5 lat. Roczna stopa procentowa wynosi 6% przy rocznej kapitalizacji odsetek. Roz-
patrzy¢ dokonywanie wpªat a) na pocz¡tku roku, b) na koniec roku
Rozwi¡zanie.
Q
+
5
= 12000(1 + 0, 06)
(1 + 0, 06)
5
− 1
0, 06
= 71703, 82
Q
−
5
= 12000
(1 + 0, 06)
5
− 1
0, 06
= 67645, 16
Warto±ci¡ pocz¡tkow¡ K
0
wkªadów zªo»nych z n rat nazywamy sum¦ warto±ci
tych rat zaktualizowanych na pocz¡tek okresu.
Dla wpªat dokonywanych z góry:
K
0
= K(1 + r)
1
− (1 + r)
−n
r
= K
(1 + r)
n
− 1
r(1 + r)
n
−1
23
Dla wpªat dokonywanych z doªu:
K
0
= K
1
− (1 + r)
−n
r
= K
(1 + r)
n
− 1
r(1 + r)
n
Przykªad 4.3 Nowy telewizor wart 10000 zª. mo»na kupi¢ na raty wpªacaj¡c przez
2 lata na koniec kwartaªu 1622 zª. lub zaci¡gn¡¢ kredyt w wysoko±ci 10000 zª. w
banku oferuj¡cym oprocentowanie 16% przy kwartalnej kapitalizacji odsetek. Który
wariant bardziej si¦ opªaca?
Rozwi¡zanie. Stopa kwartalna kredytu wynosi r
m
=
16%
4
= 4%
.
Policzmy jakiej wysoko±ci kredyt S musieliby±my spªaca¢ równymi kwartalnymi ra-
tami w wysoko±ci 1622 zª przez dwa lata.
Ze wzoru na staª¡ rat¦:
1622 = S
· 1, 04
8
·
1, 04
− 1
1, 04
8
− 1
obliczamy
S = 1622
1, 04
8
− 1
0, 04
· 1, 04
8
= 10920, 51
Zauwa»my, »e obliczona warto±¢ S jest wªa±nie warto±ci¡ pocz¡tkow¡ K
0
. Poniewa»
K
0
> 10000
, wi¦c lepiej wzi¡¢ kredyt 10000 zª.
Przykªad 4.4 Stan konta w banku wynosi 10000 zª. Wyznaczy¢ kwot¦ jak¡ nale»y
wpªaca¢ pod koniec roku, by przy danej stopie procentowej 5% i rocznej kapitalizacji
stan konta po 5-ciu latach podwoiª si¦.
Rozwi¡zanie.
Q
5
= K
0
(1 + r)
5
+ K
(1 + r)
5
− 1
r
20000 = 10000(1 + 0, 05)
5
+ K
(1 + 0, 05)
5
− 1
0, 05
K =
20000
− 10000(1, 05)
5
(1, 05)
5
− 1
· 0, 05 = 1309, 75
24
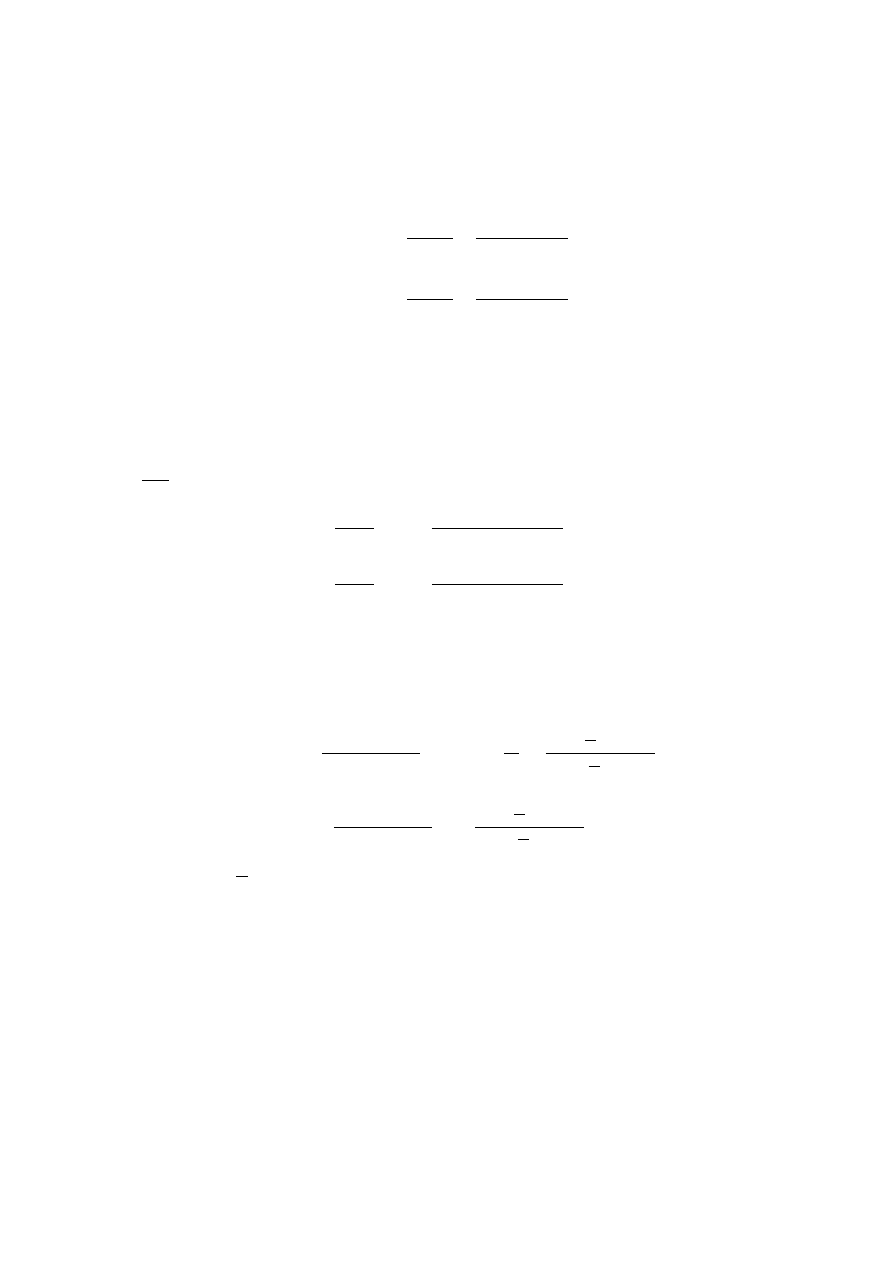
Wkªady niezgodne.
I. Wpªaty dokonywane s¡ m · n razy , gdy kapitalizacja nast¦puje n razy. Wówczas
przy wpªatach dokonywanych
- z góry
Q
+
nm
= K
(
m +
m + 1
2
r
)
(1 + r)
n
− 1
r
- z doªu
Q
−
nm
= K
(
m +
m
− 1
2
r
)
(1 + r)
n
− 1
r
Przykªad 4.5 Wpªacamy 200 zª. miesi¦cznie przez 3 lata na lokacie oprocentowa-
nej 4, 8% rocznie przy kwartalnej kapitalizacji odsetek. Znale¹¢ kwot¦ jak¡ udaªo si¦
uzbiera¢ przy wpªatach a) z góry, b) z doªu.
Rozwi¡zanie. Liczymy stop¦ procentow¡ kwartaln¡.
r =
4,8%
4
= 1, 2%
,
m = 3
,
n = 4
· 3 = 12.
Q
+
3
·12
= 200
(
3 +
3 + 1
2
0, 012
)
(1 + 0, 012)
12
− 1
0, 012
= 7756, 29
Q
−
3
·12
= 200
(
3 +
3
− 1
2
0, 012
)
(1 + 0, 012)
12
− 1
0, 012
= 7725, 51
II. Kapitalizacja odbywa si¦ m razy w ci¡gu kolejnych wpªat. Przy czym okres wpªat
pokrywa si¦ z okresem stopy procentowej.
Warto±¢ przyszªa wkªadów przy wpªatach dokonywanych
- z góry
Q
+
n
= K(1 + r
e
)
(1 + r
e
)
n
− 1
r
e
= K
(
1 +
r
m
)
m
(1 +
r
m
)
mn
− 1
(1 +
r
m
)
m
− 1
- z doªu
Q
−
n
= K
(1 + r
e
)
n
− 1
r
e
= K
(1 +
r
m
)
mn
− 1
(1 +
r
m
)
m
− 1
gdzie r
e
=
(
1 +
r
m
)
m
− 1 jest efektywn¡ stop¡ procentow¡ w okresie mi¦dzy kolej-
nymi wpªatami.
25
Przykªad 4.6 Wpªaty dokonywane s¡ raz w roku w wysoko±ci 1000 zª. do ban-
ku, który oferuje kwartaln¡ kapitalizacj¦ odsetek z kwartaln¡ stop¡ procentow¡ 4%.
Obliczy¢ warto±¢ przyszª¡ wkªadów po upªywie 4-ch lat przy wpªatach a) z góry, b)
z doªu.
Rozwi¡zanie. Obliczamy r
e
= (1 + 0, 04)
4
− 1 = 0, 1699.
Q
+
4
= 1000(1 + 0, 1699)
(1 + 0, 1699)
4
− 1
0, 1699
= 6013, 01
Q
−
4
= 1000
(1 + 0, 1699)
4
− 1
0, 1699
= 5139, 76
Przykªad 4.7 Jak¡ kwot¦ nale»y wpªaca¢ przez 8 lat na pocz¡tku ka»dego póªrocza
na konto bankowe, je»eli chcemy uzyska¢ po upªywie tego czasu kwot¦ 20000 zª. Sto-
pa procentowa jest staªa i wynosi 4% rocznie, a kapitalizacja odsetek jest kwartalna.
Rozwi¡zanie. Stopa kwartalna r =
4%
4
= 1%
.
Efektywna stopa póªroczna
r
e
= (1 + 0, 01)
2
− 1 = 0, 0201
Z równania
20000 = K
·
(1 + 0, 0201)
16
− 1
0, 0201
Znajdujemy rozwi¡zanie.
K =
20000
· 0, 0201
(1, 0201)
16
− 1
= 1072, 17
Literatura.
Adamczak A., Majerowska E., Matematyka nansowa w przykªadach, Wydawnictwo
Wiedzy Gospodarczej, Sopot 2003.
Dynus M., Prewysz-Kwinto P., Matematyka nansowa, Wydawnictwo "Dom orga-
nizatora", Toru« 2005.
Podgórska M., Klimkowska J., Matematyka nansowa, PWN, Warszawa 2005.
26
Sobczyk M., Matematyka nansowa. Podstawy teoretyczne, przykªady, zadania, Agen-
cja Wydawnicza "Placet", Warszawa 2000.
Borowski J., Gola«ski R., Kasprzyk K., Melon M., Podgórska M., Matematyka -
nansowa. Przykªady, zadania, testy, rozwi¡zania, wydanie 3, Warszawa 2002.
27