
Podstawy logiki i teorii mnogości Ćwiczenie 1
---------------------------------------------------------------------------------------------------------------------------------------
– 1 –
ĆWICZENIE 1
Klasyczny Rachunek Zdań (KRZ): zdania w sensie logicznym, wartości logiczne, spójniki
logiczne, zmienne zdaniowe, tabele prawdziwościowe dla spójników logicznych, formuły,
wartościowanie zbioru zmiennych zdaniowych, wartość logiczna formuły przy danym
wartościowaniu, tautologia, kontrtautologia.
Wartości logiczne
: Prawda ( 1 ), Fałsz ( 0 )
DEF.
Zdanie w sensie logicznym
jest to zdanie oznajmujące, które jest prawdziwe lub
fałszywe.
Np. Olsztyn leży nad Łyną
- zdanie prawdziwe, wartość logiczna
1
4 jest większe od 5 - zdanie fałszywe, wartość logiczna 0
DEF.
Spójniki logiczne
są to wyrażenia służące do budowy zdań złożonych ze zdań prostych.
Podstawowe spójniki logiczne:
nazwa
wyrażenie
symbol
kontekst
negacja
nieprawda, że
¬
p
¬
koniunkcja
i
∧
q
p ∧
alternatywa
lub
∨
q
p ∨
implikacja
jeżeli ..., to
→
q
p →
równoważność
wtedy i tylko wtedy
↔
q
p ↔
Symbole p, q, r, s (także z indeksami) reprezentują dowolne zdania i nazywamy je
zmiennymi
zdaniowymi.
Własność ekstensjonalności:
Wartość logiczna zdania złożonego, zbudowanego za pomocą spójnika logicznego, zależy
wyłącznie od rodzaju spójnika logicznego i wartości logicznych zdań prostych
Tę zależność opisują
tablice prawdziwościowe
spójników logicznych:
p
p
¬
1
0
0
1
Negacja zdania prawdziwego jest zdaniem fałszywym.
Negacja zdania fałszywego jest zdaniem prawdziwym.

Podstawy logiki i teorii mnogości Ćwiczenie 1
---------------------------------------------------------------------------------------------------------------------------------------
– 2 –
Zdanie p nazywamy
argumentem
negacji w zdaniu
p
¬
.
p
q
q
p ∧
q
p ∨
q
p →
q
p ↔
1
1
1
1
1
1
1
0
0
1
0
0
0
1
0
1
1
0
0
0
0
0
1
1
Zdania
p
,
q
nazywamy
argumentami
koniunkcji w zdaniu
q
p ∧
i podobnie dla ∨, →, ↔.
W zdaniu
q
p →
, zdanie
p
nazywamy
poprzednikiem
a zdanie
q
następnikiem
implikacji.
Poprawnie zbudowane schematy zdań nazywamy
formułami
KRZ.
Wyrażenia
są to skończone ciągi symboli (zmiennych zdaniowych i spójników logicznych).
DEF.
Formułami
KRZ nazywamy wyrażenia określone przez następujące warunki
indukcyjne:
a) każda zmienna zdaniowa jest formułą,
b) jeżeli wyrażenia
A
,
B
są formułami, to wyrażenia
(((( )))) ((((
)))) ((((
)))) ((((
)))) ((((
))))
B
A
B
A
B
A
B
A
A
↔
↔
↔
↔
→
→
→
→
∨
∨
∨
∨
∧
∧
∧
∧
¬
¬
¬
¬
,
,
,
,
są formułami.
Przykład:
p
,
q
(a)
( )
p
¬
,
(
)
q
p →
(b)
( ) (
)
(
)
q
p
p
→
→
¬
(b)
W praktyce opuszczamy niektóre nawiasy:
1) Opuszczamy parę zewnętrznych nawiasów
Np.
( ) (
)
q
p
p
→
→
¬
zamiast
( ) (
)
(
)
q
p
p
→
→
¬
2) przyjmujemy, że „siła wiązania” spójników maleje od lewej do prawej
¬
∨
∧
↔
→
Np.
(
)
q
p
p
→
→
¬
zamiast
( ) (
)
q
p
p
→
→
¬
p
q
q
p
∧
↔
∧
zamiast
(
) (
)
p
q
q
p
∧
↔
∧
.

Podstawy logiki i teorii mnogości Ćwiczenie 1
---------------------------------------------------------------------------------------------------------------------------------------
– 3 –
DEF. Niech
V
będzie pewnym zbiorem zmiennych zdaniowych.
Wartościowaniem
nazywamy dowolną funkcję
{{{{ }}}}
1
,
0
:
→
→
→
→
V
w
.
Mniej formalnie: wartościowanie jest to przyporządkowanie wartości logicznych pewnym
zmiennym zdaniowym
Zamiast
(((( ))))
(((( ))))
1
,
0
=
==
=
=
==
=
p
w
p
w
piszemy
1
,
0
=
==
=
=
==
=
p
p
.
Każde wartościowanie w zbioru V jednoznacznie określa wartość logiczną dowolnej formuły
KRZ, której wszystkie zmienne zdaniowe należą do V.
Literami A, B, C, ... oznaczamy dowolne formuły KRZ. Wartość logiczną formuły A dla
wartościowania w oznaczamy przez w(A) i wyznaczamy korzystając z tabel
prawdziwościowych. Podobnie, jak dla zmiennych zdaniowych, zamiast
(((( ))))
(((( ))))
1
,
0
=
==
=
=
==
=
A
w
A
w
,
piszemy
1
,
0
=
==
=
=
==
=
A
A
.
Wyznaczanie wartości logicznej zdania złożonego.
Jeżeli nieprawda, że 5 < 4, to jeżeli 5< 4, to 2 < 1 lub 2 < 3.
I. Tworzymy schemat logiczny tego zdania
p: 5 < 4
q: 2 < 1
r: 2 < 3
(
)
r
q
p
p
∨
→
→
¬
II. Ustalamy wartości logiczne zdań prostych.
p = 0, q = 0, r = 1
III. Podstawiamy te wartości za zmienne p, q, r i przeprowadzamy obliczenia zgodnie z
tablicami prawdziwościowymi
(
)
(
)
1
1
1
1
0
1
1
0
0
0
=
→
=
→
→
=
∨
→
→
¬
Odp. Zdania jest prawdziwe.
Podstawy logiki i teorii mnogości Ćwiczenie 1
---------------------------------------------------------------------------------------------------------------------------------------
– 4 –
Tablica prawdziwościowa formuły.
Niech
{{{{
}}}}
n
p
p
p
,
,
,
2
1
K
będzie zbiorem zmiennych zdaniowych występujących w formule A.
Istnieje
n
2 różnych wartościowań tego zbioru. Dla formuły A wyznaczamy jej wartość
logiczną dla każdego z tych wartościowań tworząc tabelę prowdziwościową formuły A
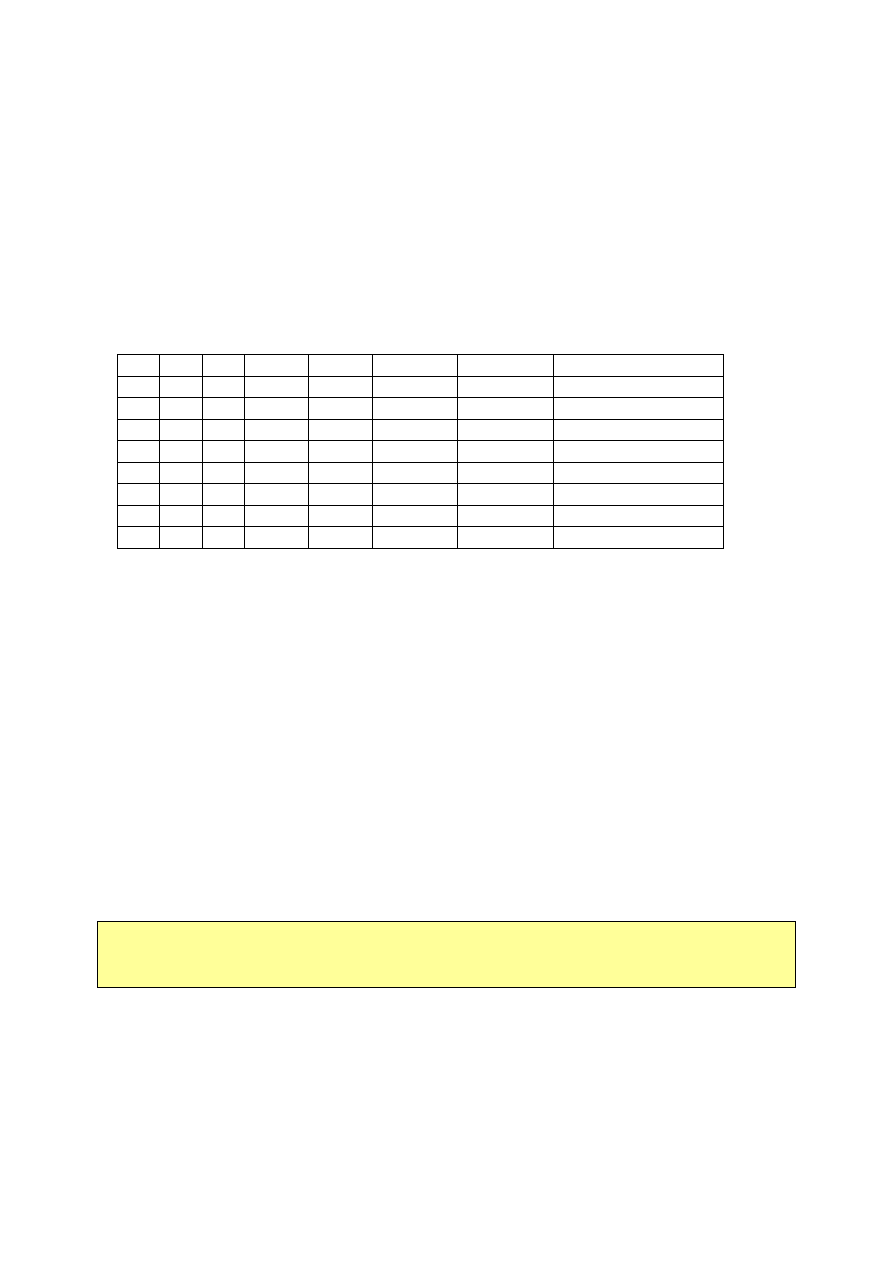
Przykład:
r
p
q
p
A
∧
∧
∧
∧
¬
¬
¬
¬
→
→
→
→
¬
¬
¬
¬
∨
∨
∨
∨
=
=
=
=
{{{{
}}}}
r
q
p
V
,
,
=
==
=
Liczba wartościowań =
8
2
3
====
p
q
r
p
¬
¬
¬
¬
q
¬
¬
¬
¬
q
p
¬
¬
¬
¬
∨∨∨∨
r
p
∧∧∧∧
¬
¬
¬
¬
r
p
q
p
∧
∧
∧
∧
¬
¬
¬
¬
→
→
→
→
¬
¬
¬
¬
∨
∨
∨
∨
1
1
1
0
0
1
0
0
1
1
0
0
0
1
0
0
1
0
1
0
1
1
0
0
1
0
0
0
1
1
0
0
0
1
1
1
0
0
1
1
0
1
0
1
0
0
0
1
0
0
1
1
1
1
1
1
0
0
0
1
1
1
0
0
DEF.
Tautologią
KRZ nazywamy formułę KRZ, która przyjmuje wartość logiczną 1 dla
każdego wartościowania zmiennych występujących w tej formule.
Tautologie KRZ są schematami zdań logicznie prawdziwych, tzn. prawdziwych na mocy
samej logiki, niezależnie od rzeczywistej wartości logicznej zdań składowych.
DEF.
Kontrtautologią
KRZ nazywamy formułę KRZ, która przyjmuje wartość logiczną 0 dla
każdego wartościowania zmiennych występujących w tej formule.
TW. O podstawianiu w tautologiach
Jeżeli A jest tautologią KRZ, a formuła A
′′′′ powstaje z A przez podstawienie za wszystkie
wystąpienia pewnej zmiennej zdaniowej dowolnej formuły, to formuła A
′′′′ jest tautologią.
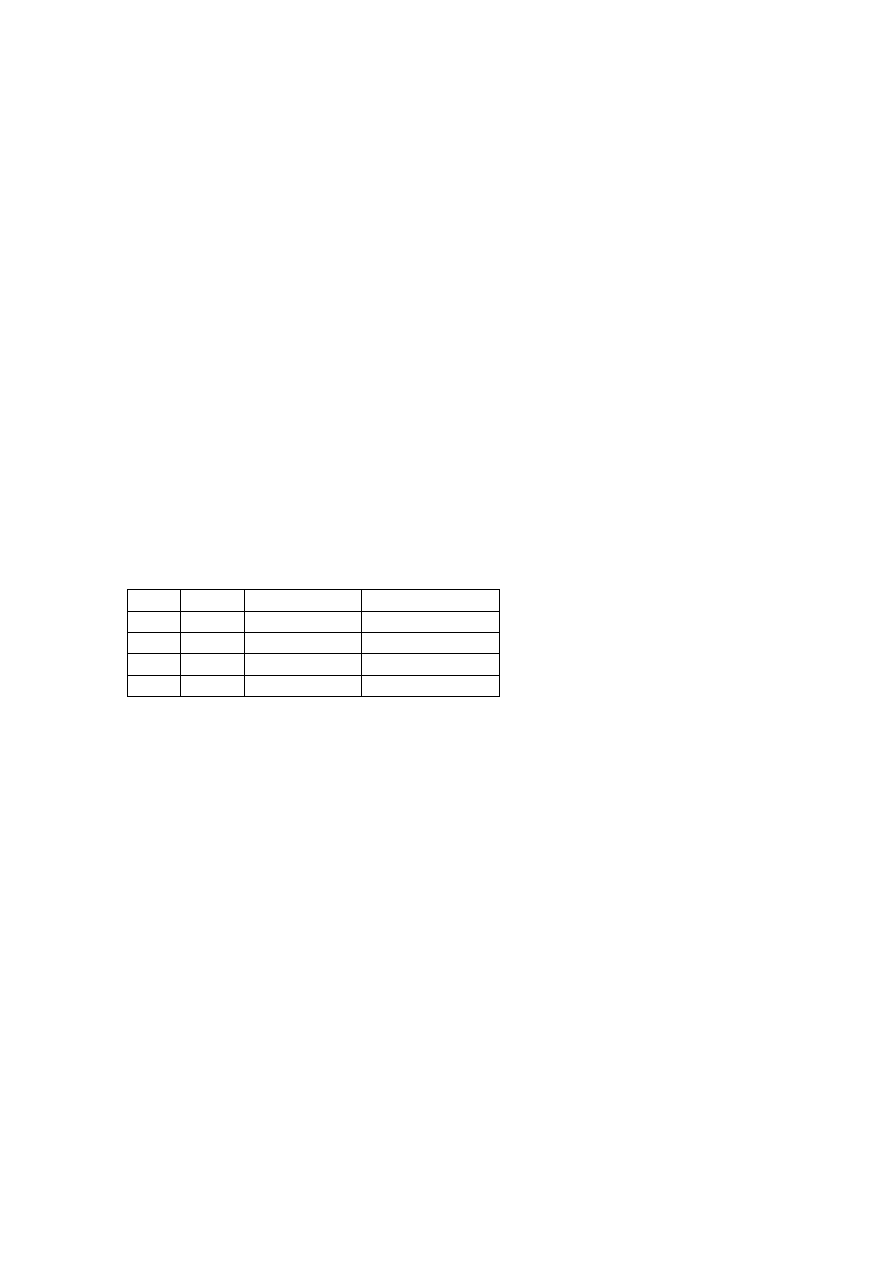
Podstawy logiki i teorii mnogości Ćwiczenie 1
---------------------------------------------------------------------------------------------------------------------------------------
– 5 –
Przykład. 1
Olsztyn leży nad Łyną lub nieprawda, że Olsztyn leży nad Łyną. – zdanie logicznie
prawdziwe
schemat:
p
p
¬
∨
0
=
=
=
=
p
1
1
0
0
0
====
∨∨∨∨
====
¬
¬
¬
¬
∨∨∨∨
====
¬
¬
¬
¬
∨∨∨∨ p
p
1
====
p
1
0
1
1
1
====
∨∨∨∨
====
¬
¬
¬
¬
∨∨∨∨
====
¬
¬
¬
¬
∨∨∨∨ p
p
Przykład. 2
Niech
((((
))))
q
p
p
A
∨
∨
∨
∨
→
→
→
→
=
==
=
. Wykażemy, że A jest tautologią.
Sposób 1. Wprost
. Tworzymy tabelę prawdziwościową formuły A.
((((
))))
q
p
p
A
∨
∨
∨
∨
→
→
→
→
=
=
=
=
{{{{ }}}}
q
p
V
,
=
==
=
Liczba wartościowań =
4
2
2
=
==
=
p
q
q
p
∨∨∨∨
q
p
p
∨
∨
∨
∨
→
→
→
→
1
1
1
1
1
0
1
1
0
1
1
1
0
0
0
1
Dla każdego wartościowania zmiennych p i q formuła A jest prawdziwa, zatem jest
tautologią.
Sposób 2. Nie wprost
.
Zakładamy, że formuła A nie jest tautologią. Wtedy istnieje wartościowanie, dla którego
0
=
==
=
A
. Szukamy tego wartościowania.
1)
((((
))))
0
=
==
=
∨
∨
∨
∨
→
→
→
→
q
p
p
Implikacja jest fałszywa tylko w przypadku, gdy poprzednik jest prawdziwy, a następnik
fałszywy.
2)
1
=
==
=
p
i
0
====
∨∨∨∨ q
p
Alternatywa jest fałszywa, gdy oba zdania składowe są fałszywe

Podstawy logiki i teorii mnogości Ćwiczenie 1
---------------------------------------------------------------------------------------------------------------------------------------
– 6 –
3)
0
=
==
=
p
i
0
=
==
=
q
Otrzymaliśmy sprzeczność:
1
=
==
=
p
i
0
=
==
=
p
. Oznacza to, że nie istnieje wartościowanie, przy
którym
0
=
==
=
A
. Zatem A jest tautologią.
Schematycznie:
q
p
p
∨
∨
∨
∨
→
→
→
→
↓
↓
↓
↓
1) ↓
↓
↓
↓ 0 ↓↓↓↓
2) 1 ↓
↓
↓
↓ 0 ↓↓↓↓
3) 0 0
|______|
sprzeczność

Podstawy logiki i teorii mnogości Ćwiczenie 1
---------------------------------------------------------------------------------------------------------------------------------------
– 7 –
Ważne tautologie KRZ
Prawo wyłączonego środka
p
p
∨ ¬
(tertium non datur)
Prawo sprzeczności
¬ ∧ ¬
(
)
p
p
Prawo podwójnej negacji
¬¬ ↔
p
p
Prawo transpozycji
(
) (
)
p
q
q
p
→
↔ ¬ → ¬
Prawo sylogizmu warunkowego
(
) (
) (
)
p
q
q
r
p
r
→
∧
→
→
→
Prawa algebraiczne .
Prawa łączności
((
)
)
(
(
))
p
q
r
p
q
r
∧
∧
↔
∧
∧
((
)
)
(
(
))
p
q
r
p
q
r
∨
∨
↔
∨
∨
((
)
)
(
(
))
p
q
r
p
q
r
↔
↔
↔
↔
↔
Prawa przemienności
(
)
(
)
p
q
q
p
∧
↔
∧
(
)
(
)
p
q
q
p
∨
↔
∨
(
)
(
)
p
q
q
p
↔
↔
↔
Prawa rozdzielczości
(
(
))
((
)
(
))
p
q
r
p
q
p
r
∧
∨
↔
∧
∨
∧
(
(
))
((
)
(
))
p
q
r
p
q
p
r
∨
∧
↔
∨
∧
∨
Prawa idempotentności
(
)
p
p
p
∧
↔
(
)
p
p
p
∨
↔
Prawa de Morgana
¬
∧
↔ ¬ ∨ ¬
(
)
(
)
p
q
p
q
¬
∨
↔ ¬ ∧ ¬
(
)
(
)
p
q
p
q
Prawa definiowania
)
(
)
(
q
p
q
p
∨
∨
∨
∨
¬
¬
¬
¬
↔
↔
↔
↔
→
→
→
→
((((
)))) ((((
)))) ((((
))))
p
q
q
p
q
p
→
→
→
→
∧
∧
∧
∧
→
→
→
→
↔
↔
↔
↔
↔
↔
↔
↔
((((
)))) ((((
)))) ((((
))))
q
p
q
p
q
p
¬
¬
¬
¬
∧
∧
∧
∧
¬
¬
¬
¬
∨
∨
∨
∨
∧
∧
∧
∧
↔
↔
↔
↔
↔
↔
↔
↔
Prawa z ustalonym argumentem
p
p
↔
↔
↔
↔
∧
∧
∧
∧ 1
1
1 ↔
↔
↔
↔
∨
∨
∨
∨
p
((((
))))
p
p ↔
↔
↔
↔
→
→
→
→
1
((((
))))
1
1 ↔
↔
↔
↔
→
→
→
→
p
0
0 ↔
↔
↔
↔
∧
∧
∧
∧
p
p
p
↔
↔
↔
↔
∨
∨
∨
∨ 0
((((
))))
1
0
↔
↔
↔
↔
→
→
→
→ p
((((
))))
p
p
¬
¬
¬
¬
↔
↔
↔
↔
→
→
→
→ 0

Podstawy logiki i teorii mnogości Ćwiczenie 1
---------------------------------------------------------------------------------------------------------------------------------------
– 8 –
Ćwiczenie 1: wiadomości i umiejętności
1.
Po ćwiczeniu 1 student powinien znać definicje pojęć podanych w nagłówku ćwiczenia
2.
Student powinien posiadać następujące umiejętności:
•
zapisywać konkretne zdania języka naturalnego za pomocą symboliki logicznej KRZ oraz
odczytywać zdania zapisane z użyciem tej symboliki;
•
sprawdzać, czy dane wyrażenie zapisane w języku KRZ, tzn. z użyciem zmiennych
zdaniowych i spójników zdaniowych jest poprawną formułą KRZ;
•
wyznaczać wartość logiczną formuły dla danego wartościowania zmiennych zdaniowych
występujących w tej formule;
•
wyznaczać wartości logiczne konkretnych zdań złożonych według schematu:
- utworzyć schemat logiczny zdania
- wyznaczyć wartości logiczne prostych zdań składowych (na podstawie posiadanej
wiedzy przedmiotowej)
- wyznaczyć wartość całego zdania korzystając z tablic prawdziwościowych
•
sprawdzać, czy dana formuła (schemat zdaniowy) jest tautologią (kontrtautologią):
a) wprost - poprzez utworzenie tablicy prawdziwościowej tej formuły (inaczej: metodą
tablicową lub zero-jedynkową),
b) nie wprost – zakładając, że badana formuła nie jest tautologią i dochodząc do
sprzeczności.
Wyszukiwarka
Podobne podstrony:
Cwiczenie 01 id 98935 Nieznany
Antropologia Cwiczenia 01 id 65 Nieznany (2)
CwiczenieArcGIS 01 id 125936 Nieznany
2012 Skrypt cwiczenia 01 10 201 Nieznany
cwiczenie 01 id 125027 Nieznany
Pediatria Cwiczenia 01 id 35420 Nieznany
Fizjologia Cwiczenia 01 id 1743 Nieznany
Cwiczenie 01 id 98935 Nieznany
01 aeid 3052 Nieznany (2)
NLP Magazine 01 id 320421 Nieznany
I CKN 316 01 1 id 208193 Nieznany
domowe2 01 id 140222 Nieznany
CHORZOW1 TRAGEDIA 28 01 2006 id Nieznany
Choroby skory koni cwiczenie id Nieznany
01 Uprawnienia w budownictwieid Nieznany
cwiczenia zestaw2(1) Nieznany
CwiczenieNr1 WprowadzenieDoProg Nieznany
HUR2006 01 id 207254 Nieznany
więcej podobnych podstron