1. Konstrukcje obciążone dynamicznie:
konstrukcje duże, wiotkie, lekkie;
mosty wiszące i podwieszane;
kładki dla pieszych;
maszty;
wieże;
kominy;
wysokie budynki;
kolejki linowe;
niektóre konstrukcje wsporcze pod maszyny;
platformy wiertnicze;
budowle wodne.
Obciążenia dynamiczne działające na konstrukcje:
porywy (turbulencje) wiatru;
obciążenia ruchome spowodowane przejazdem pojazdów drogowych, kolejowych, pieszych,
ruchem podwieszonych gondoli pasażerskich;
oddziaływania maszyn (młoty, kruszarki, młyny, silniki, turbogeneratory, maszyny tkackie,
pralki);
obciążenia spowodowane falowaniem wody (w obiektach hydrotechnicznych).
2. Schemat dynamiczny - jest to schemat statyczny uzupełniony o dodatkowe informacje
istotne z punktu widzenia dynamiki, takie jak:
opis wielkości i rozkład masy;
opis charakteru i rozkładu oporów ruchu (tłumienia);
opis zewnętrznych sił czynnych jako funkcji miejsca i czasu (opis obciążenia
dynamicznego).
3. Liczba dynamicznych stopni swobody „d” – jest to liczba niezależnych współrzędnych
uogólnionych, koniecznych do określenia w danej chwili położenia wszystkich punktów
masowych układu.
Dynamicznym stopniom swobody odpowiadają przemieszczenia, które nazywamy
współrzędnymi uogólnionymi Lagrange’a.
Liczbę d oblicza się po myślowym usunięciu nieważkich więzi odkształcalnych, jako sumę
współrzędnych uogólnionych swobodnych elementów masowych (lokalnych stopni
swobody), od której odejmuje się liczbę warunków nałożonych przez więzi nieodkształcalne.
4. Dyskretny układ dynamiczny – układ dynamiczny z dyskretnym rozkładem masy 𝑑 < ∞;
Ciągły układ dynamiczny – układ dynamiczny z ciągłym rozkładem masy 𝑑 = ∞;
Układ zachowawczy – układ niezmieniający się w czasie ???, układ w którym siły zewnętrzne
czynne i oddziaływania zewnętrzne oraz wewnętrzne nie zmieniają się w czasie. Układ,
którego suma energii potencjalnej i kinetycznej jest stała; brak wymiany energii z
otoczeniem; nie występuje tarcie mechaniczne i czynny opór.
Układ dyssypacyjny – układ dynamiczny, w którym zjawiska dynamiczne takie jak fale czy
oscylacje zatracają energię wraz z upływem czasu z powodu tarcia lub turbulencji (na
podstawie wikipedii).
5. Układ równao w postaci macierzowej:
𝑑
𝑑𝑡
𝑔𝑟𝑎𝑑
𝑞
𝐸
𝑘
𝑞 +
𝑔𝑟𝑎𝑑
𝑞
𝜙 𝑞 + 𝑔𝑟𝑎𝑑
𝑞
𝐸
𝑝
𝑞 = 𝑔𝑟𝑎𝑑
𝑞
𝐿(𝑞 )
𝐿 = 𝐿(𝑞 ) - praca zewnętrznych sił czynnych
𝑞 = 𝑐𝑜𝑙 𝑞
1
, … , 𝑞
𝑛
- wektor (macierz jednokierunkowa przemieszczeo uogólnionych;
𝑞 = 𝑐𝑜𝑙(𝑞
1
, … , 𝑞
𝑛
) - wektor prędkości uogólnionych;
Jeśli ustrój wykonuje małe drgania, to 𝐸
𝑘
= 𝐸
𝑘
𝑞 i wtedy
𝑑𝐸
𝑘
𝑑𝑞
𝑖
= 0;
𝜙 = 𝜙(𝑞 ) - moc tłumienia (funkcja dyssypacji)
𝐸
𝑝
= 𝐸
𝑝
𝑞
1
, … , 𝑞
𝑛
= 𝐸
𝑝
(𝑞 )
6.
7.Omówić rodzaje współrzędnych stosowanych w analizie dynamicznej układów
dyskretnych.
Trzy rodzaje współrzędnych:
a) współrzędne zewnętrzne: x
i
(np. kartezjańskie) - niezależne od czasu, opisują
geometrię układu w stanie odniesienia, czyli stanie równowagi statycznej.
b) współrzędne lokalne: u
i
(x
i
,t) - zależne od czasu i współrzędnych zewnętrznych;
opisują przemieszczenia lokalne dowolnych punktów układu (np. punktów masowych,
punktów zamocowania więzi, itp.)
c) współrzędne uogólnione Lagrange'a: q
j
(t) - zależne tylko od czasu, opisują
przemieszczenia uogólnione punktów masowych układu, odpowiadają dynamicznym
stopniom swobody
8.
Podać i omówić wzory określające ogólną postać macierzy bezwładności układu
dyskretnego i wektora uogólnionych sił wzbudzających.
Macierz bezwładności układu dyskretnego
Dla układu materialnego, który tworzą punkt masowy m
A
i masa skupiona m
B
z
bezwładnością obrotową J
B
m
sumujemy energią kinetyczną:
Obieramy przemieszczenie lokalne (wsp. lokalne) mas - zestawiamy je w wektor:
𝑢 = [𝑢
1
, 𝑢
2
, … , 𝑢
𝑖
, … ]
𝑇
Transformacja współrzędnych:
𝑢 = 𝐴𝑚𝑞
𝐸
𝑘
=
1
2
𝑖
𝑚
𝑖
𝑢
𝑖
2
𝐸
𝑘
=
1
2
𝑢
𝑇
𝑚 𝑢
gdzie:
𝑚 = 𝑑𝑖𝑎𝑔 𝑚
𝐴
, 𝑚
𝐴
, 𝑚
𝐵
, 𝑚
𝐵
, 𝐽
𝐵
𝑚
- macierz diagonalna, w której masy układu są
zestawione zgodnie z uporządkowaniem przemieszczeń lokalnych.
𝑢 = 𝐴
𝑚
𝑞 , 𝑢
𝑇
= 𝐴
𝑚
𝑞
𝑇
= 𝑞
𝑇
∙ 𝐴
𝑚
𝑇
𝐸
𝑘
=
1
2
𝑢
𝑇
𝑚 𝑢 =
1
2
𝑞
𝑇
𝐴
𝑚
𝑇
𝑚 𝐴
𝑚
𝑞 =
1
2
𝑞
𝑇
𝐵𝑞
macierz
funkcja skalarowa
bezwładności
(jednorodna forma
kwadratowa)
Energia kinetyczna jest jednorodna formą kwadratową prędkości uogólnionych. Jądrem
formy jest macierz bezwładności:
TO MI SIĘ WYDAJE NAJBARDZIEJ ISTOTNE:
𝑚 = 𝑑𝑖𝑎𝑔 𝑚
1
, 𝑚
2
, … , 𝑚
𝑖
, …
𝐴
𝑚
− 𝑗ą𝑑𝑟𝑜 𝑓𝑜𝑟𝑚𝑦 𝑘𝑤𝑎𝑑𝑟𝑎𝑡𝑜𝑤𝑒𝑗 (? )
𝐵 = 𝐴
𝑚
𝑇
𝑚 𝐴
𝑚
macierz bezwładności (kwadratowa, symetryczna)
𝐵 = 𝑏
𝑖𝑗
→ 𝑏
𝑖𝑗
= 𝑏
𝑗𝑖
→ 𝐵 = 𝐵
𝑇
nieosobliwa i dodatnio określona:
det B > 0, jeśli mamy bazę minimalną n = d
osobliwa i określona nieujemnie:
det B = 0, jeśli n > d
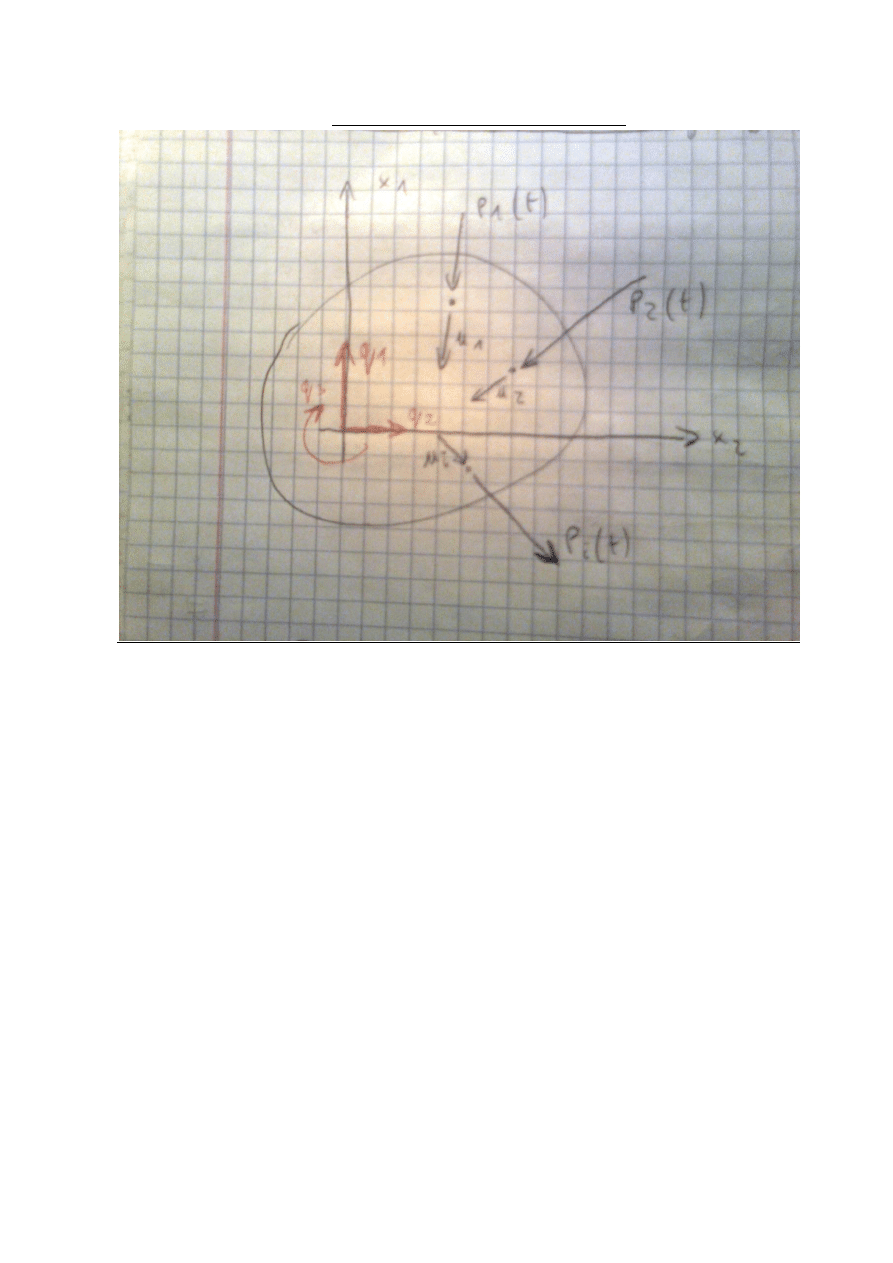
Wektor uogólnionych sił wzbudzających
Analizując prace zewnętrznych sił zewnętrznych czynnych
określamy wektory:
𝑢 = [𝑢
1
, 𝑢
2
, … , 𝑢
𝑖
, … ]
𝑇
𝑃 = [𝑃
1
, 𝑃
2
, … , 𝑃
𝑖
, … ]
𝑇
𝑢 = 𝐴
𝑝
𝑞 , 𝑢
𝑇
= 𝑞
𝑇
𝐴
𝑝
𝑇
𝑝𝑟𝑧𝑒𝑚𝑖𝑒𝑠𝑧𝑐𝑒𝑛𝑖𝑒 𝑙𝑜𝑘𝑎𝑙𝑛𝑒 → 𝐿 = 𝑃
1
𝑢
1
+ 𝑃
2
𝑢
2
+ ⋯ + 𝑃
𝑖
𝑢
𝑖
+ ⋯ = 𝑃
𝑖
𝑢
𝑖
=
𝑖
𝑢
𝑇
𝑃 = 𝑃
𝑇
𝑢
Obieramy przemieszenie lokalne punktów przyłożenia siły, zgodnie z kierunkiem i zwrotem
przyłożenia sił.
𝐿 = 𝑢
𝑇
𝑃 = 𝑞
𝑇
𝐴
𝑝
𝑇
𝑃
𝑇
= 𝑞
−𝑇
𝐹
macierz
praca sił
transformacji
wewnętrznych
𝐹 = 𝐴
𝑝
𝑇
𝑃
Wektor uogólnionych sił wzbudzających
9. Podać i omówić wzory określające ogólną postać macierzy sztywności i macierzy
tłumienia układu dyskretnego zawierającego jawne więzi sprężyste i wiskotyczne
więzi tłumiące.
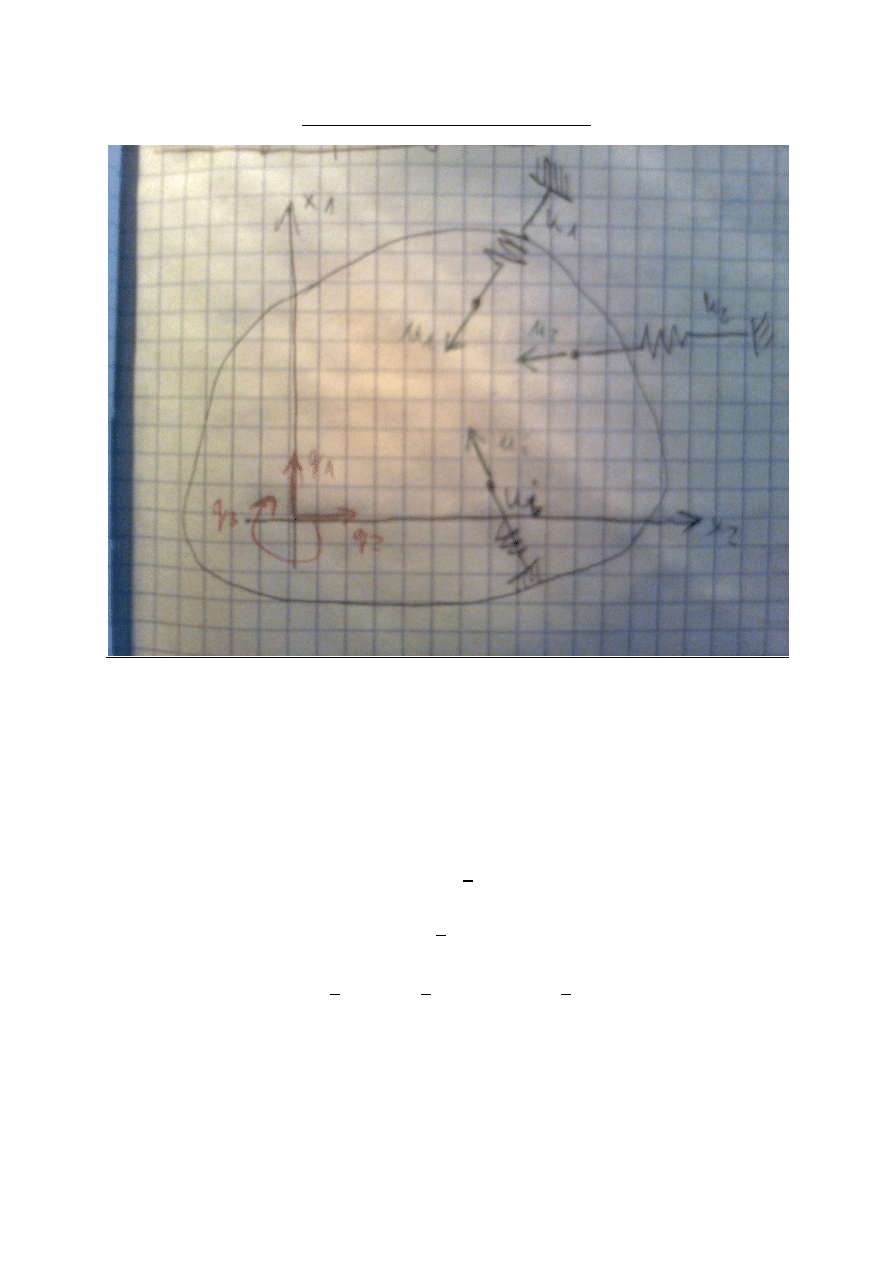
Macierz sztywności układu dyskretnego
Obieramy przemieszczenie lokalne na kierunkach - zestawiamy je w wektor:
𝑢 = [𝑢
1
, 𝑢
2
, … , 𝑢
𝑖
, … ]
𝑇
𝑘 = 𝑑𝑖𝑎𝑔 𝑘
1
, 𝑘
2
, … , 𝑘
𝑖
, …
Transformacja współrzędnych:
𝑢 = 𝐴
𝑘
𝑞
𝐸
𝑝
=
1
2
𝑖
𝑘
𝑖
𝑢
𝑖
2
𝐸
𝑝
=
1
2
𝑢
𝑇
𝑘 𝑢
𝐸
𝑝
=
1
2
𝑢
𝑇
𝑘 𝑢 =
1
2
𝑞
𝑇
𝐴
𝑘
𝑇
𝑘 𝐴
𝑘
𝑞 =
1
2
𝑞
𝑇
𝐾𝑞
macierz
sztywności
TO MI SIĘ WYDAJE NAJBARDZIEJ ISTOTNE:
𝑘 = 𝑑𝑖𝑎𝑔 𝑘
1
, 𝑘
2
, … , 𝑘
𝑖
, …
𝐴
𝑘
− 𝑗ą𝑑𝑟𝑜 𝑓𝑜𝑟𝑚𝑦 𝑘𝑤𝑎𝑑𝑟𝑎𝑡𝑜𝑤𝑒𝑗 (? )
𝐾 = 𝐴
𝑘
𝑇
𝑘 𝐴
𝑘
macierz sztywnośći (kwadratowa, symetryczna)
𝐾 = 𝑘
𝑖𝑗
→ 𝑘
𝑖𝑗
= 𝑘
𝑗𝑖
→ 𝐾 = 𝐾
𝑇
dodatnio określona:
det K > 0, jeśli postać równowagi statycznej jest zachowawcza
Macierz odwrotną nazywamy macierzą podatności.
𝐷 = 𝐾
−1
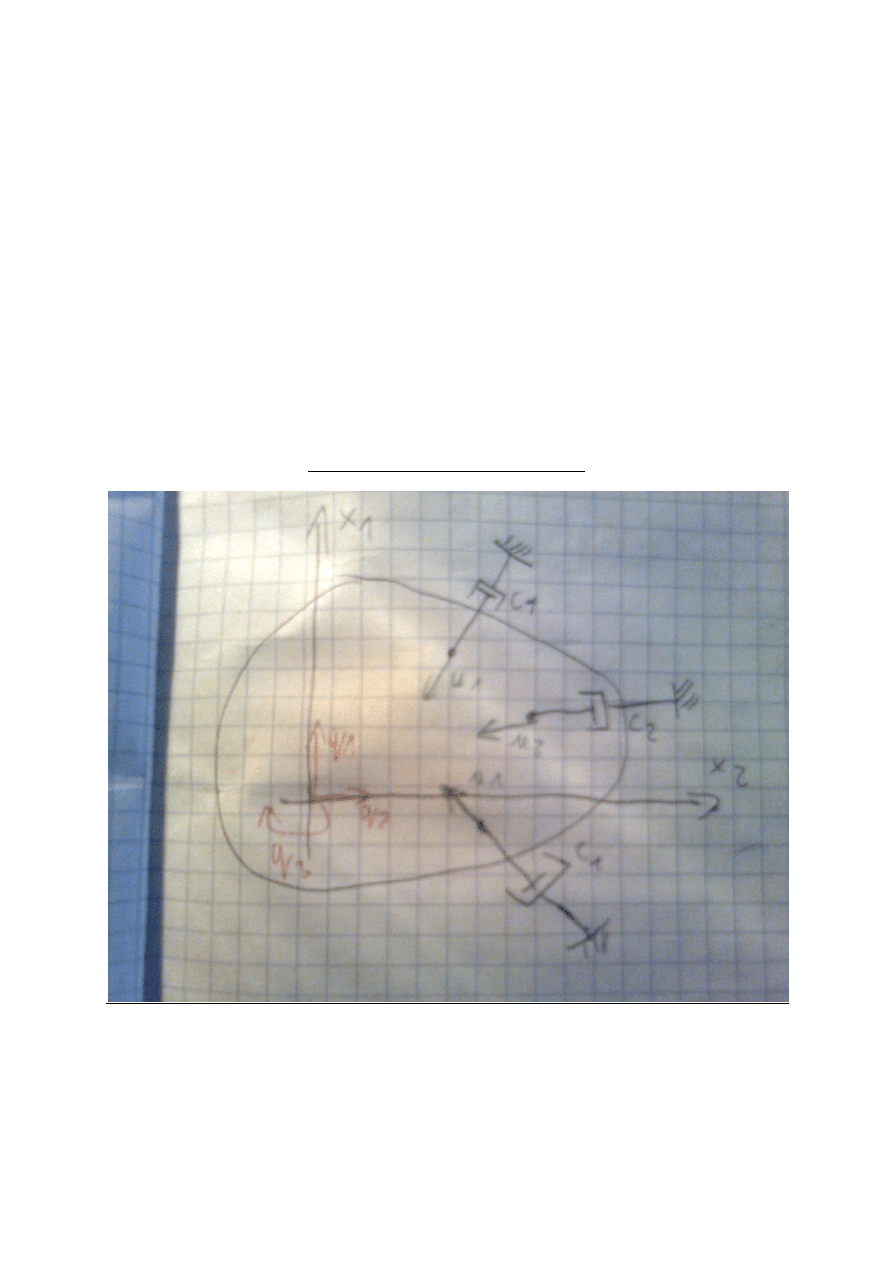
Macierz tłumienia układu dyskretnego
Obieramy przemieszczenie lokalne na kierunkach - zestawiamy je w wektor:
𝑢 = [𝑢
1
, 𝑢
2
, … , 𝑢
𝑖
, … ]
𝑇
𝑐 = 𝑑𝑖𝑎𝑔 𝑐
1
, 𝑐
2
, … , 𝑐
𝑖
, …
Transformacja współrzędnych:
𝑢 = 𝐴
𝑐
𝑞 ,
𝑢 = 𝐴
𝑐
𝑞
Φ =
1
2
𝑖
𝑐
𝑖
𝑢
𝑖
2
Φ =
1
2
𝑢
𝑇
𝑐 𝑢
Φ =
1
2
𝑢
𝑇
𝑐 𝑢 =
1
2
𝑞
𝑇
𝐴
𝑐
𝑇
𝑐 𝐴
𝑐
𝑞 =
1
2
𝑞
𝑇
𝐶𝑞
macierz
tłumienia
TO MI SIĘ WYDAJE NAJBARDZIEJ ISTOTNE:
𝑐 = 𝑑𝑖𝑎𝑔 𝑐
1
, 𝑐
2
, … , 𝑐
𝑖
, …
𝐴
𝑐
− 𝑗ą𝑑𝑟𝑜 𝑓𝑜𝑟𝑚𝑦 𝑘𝑤𝑎𝑑𝑟𝑎𝑡𝑜𝑤𝑒𝑗 (? )
𝐾 = 𝐴
𝑐
𝑇
𝑐 𝐴
𝑐
macierz tłumienia (kwadratowa, symetryczna)
𝑐 = 𝑐
𝑖𝑗
→ 𝑐
𝑖𝑗
= 𝑐
𝑗𝑖
→ 𝑐 = 𝑐
𝑇
określona nieujemnie:
det C ≥ 0
10.
Wyprowadzić z zasady d’Alamberta ogólną postać równania ruchu układu o jednym
dynamicznym stopniu swobody.
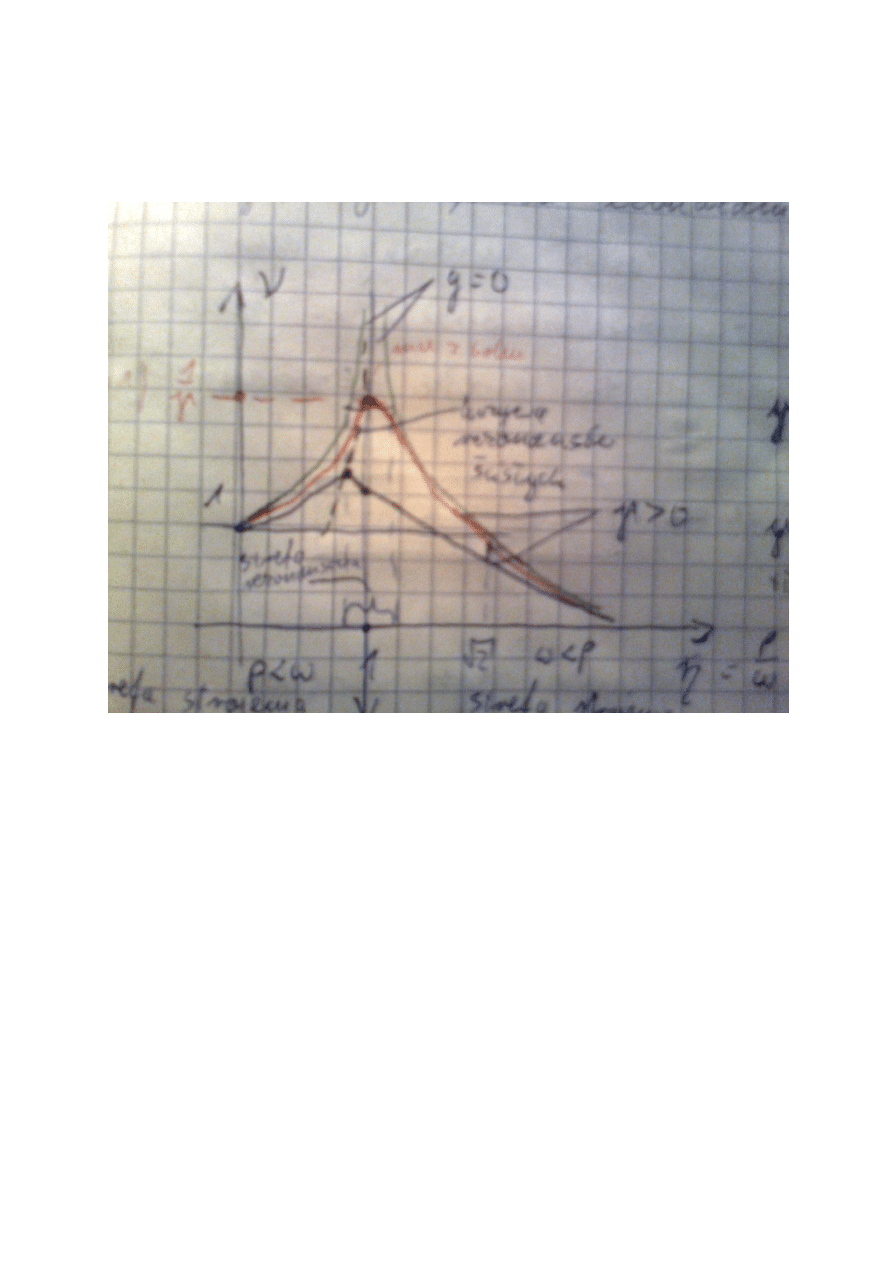
22.Co oznacza określenie "krzywa rezonansów ścisłych":
Jest to krzywa łącząca wierzchówki wykresów krzywych rezonansowych dla
𝛾 > 0 w
zależnośći od współczynnika dynamicznego
𝜈 oraz względnej częstości wzbudzania 𝜂.
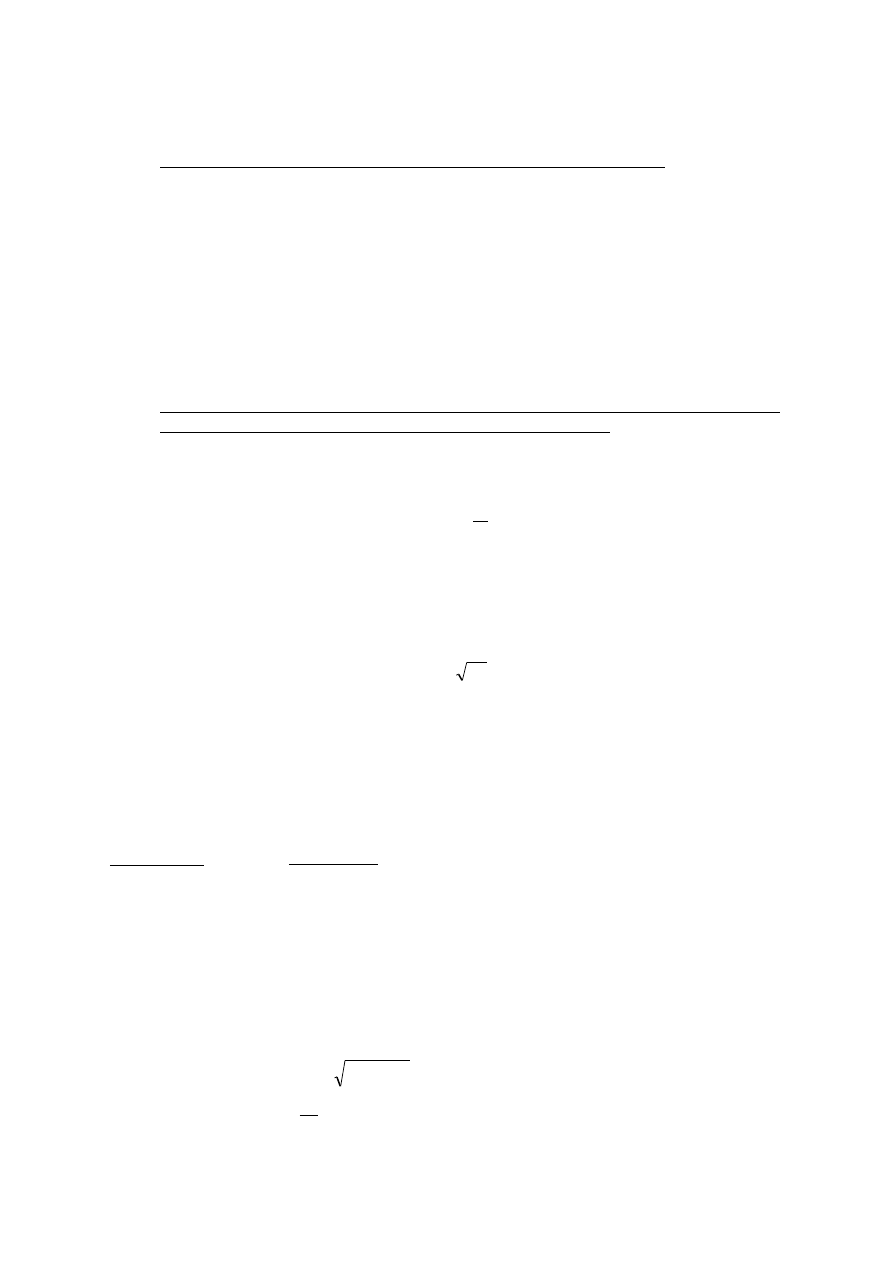
11.
Określid pojęcia: drgania własne, drgania swobodne, drgania wymuszone.
Drgania własne jest to rozwiązanie ogólne jednorodnego równania ruchu, które stanowi
matematyczny opis możliwości ustroju do wykonywania drgao. Nie jest to proces fizyczny, czyli
zachodzący w rzeczywistości.
Drgania swobodne są procesem fizycznym spowodowanym wyłącznie początkowym zaburzeniem
stanu równowagi opisanym warunkami początkowymi.
Drgania wymuszone to proces fizyczny, spowodowany siłą wymuszającą przy określonych warunkach
początkowych. Jeżeli warunki początkowe są zerowe, to nie ma początku stanu zaburzenia.
12.
Napisad równanie drgao własnych układu zachowawczego o jednym dynamicznym stopniu
swobody i podad postad rozwiązania. Wymienid parametry drgao.
Układ zachowawczy, czyli nie jest tłumiony c=0, zachowujący energię.
Równanie drgao własnych
0
2
q
q
gdzie ,
m
k
2
Zakładamy równanie w postaci:
t
e
t
q
)
(
Równanie charakterystyczne :
0
2
2
t
t
e
e
0
2
2
2 pierwiastki zespolone sprzężone :
i
w
2
,
1
,
1
i
Całki szczególne równania ruchu:
t
i
e
,
t
i
e
Korzystając ze wzorów Eulera zaprowadzamy 2 nowe całki szczególne, które są liniowymi wzajemnie
niezależnymi kombinacjami całek poprzednich:
t
z
e
e
i
t
i
t
i
sin
,
t
z
e
e
i
t
i
t
i
cos
Rozwiązanie ogólne :
t
q
t
q
t
q
c
s
cos
sin
)
(
Zapis zwinięty:
f
t
a
t
q
sin
)
(
Parametry drgao :
2
2
)
(
_
c
s
q
q
t
q
am
a
s
c
q
q
arctg
f
m
k
13.
Napisad równanie drgao własnych układu tłumionego o jednym dynamicznym stopniu
swobody i podad postad rozwiązania. Wymienid parametry drgao.
Układ tłumiony czyli
0
c
Równanie drgao własnych
0
2
2
q
q
q
gdzie
km
c
2
,
m
k
Zakładamy równanie w postaci:
t
e
t
q
)
(
Równanie charakterystyczne :
0
2
2
2
Rozwiązanie ogólne :
t
q
t
q
e
t
q
c
s
t
'
cos
'
sin
)
(
Funkcja quasi-harmoniczna:
)
'
sin
)
(
t
ae
t
q
t
Funkcja modulacji amplitudy:
t
ae
t
a
)
(
Parametry drgao układu tłumionego:
częstośd drgao własnych układu tłumionego (i swobodnych)
2
1
'
, [rad/s]
T
T
T
2
2
1
1
2
'
2
'
, [s]
liczba tłumienia, wyraża ułamek (procent) krytycznego
km
c
2
, [-]
bezwymiarowy współczynnik tłumienia, stosowany głownie w normach
km
c
2
14.
Wyznaczyd funkcję opisującą drgania swobodne układu zachowawczego o jednym
dynamicznym stopniu swobody przy następujących warunkach początkowych: ....... .
Warunki początkowe :
o
q
q
)
0
(
,
o
q
q
)
0
(
Równanie drgao swobodnych :
0
2
q
q
Rozwiązanie :
t
q
t
q
t
q
c
s
cos
sin
)
(
,
m
k
Wyznaczamy stałe
c
s
q
q ,
z warunków początkowych:
t
q
t
q
t
q
c
s
cos
sin
)
(
o
c
q
q
q
)
0
(
t
q
t
q
t
q
c
s
sin
cos
)
(
o
s
q
q
q
)
0
(
o
s
q
q
Rozwiązanie :
t
q
t
q
t
q
o
o
cos
sin
)
(
15.
Wyznaczyd funkcję opisującą drgania swobodne układu tłumionego o jednym dynamicznym
stopniu swobody przy następujących warunkach początkowych: ....... .
𝑞 + 2 ∗ 𝛼 ∗ 𝜔 ∗ 𝑞 + 𝜔
2
∗ 𝑞 = 0
Warunki początkowe: 𝑞 0 = 𝑞
0
; 𝑞 0 = 𝑞
0
𝑞 𝑡 = 𝑒
−𝛼∗𝜔∗𝑡
∗ (𝑞
𝑠
∗ sin 𝜔
′
∗ 𝑡 + 𝑞
𝑐
∗ 𝑐𝑜 𝑠 𝜔
′
∗ 𝑡 )
𝑞 0 = 𝑞
0
= 𝑞
𝑐
𝑞 𝑡 = −𝛼 ∗ 𝜔 ∗ 𝑒
−𝛼∗𝜔∗𝑡
∗ 𝑞
𝑠
∗ 𝑠𝑖𝑛 𝜔
′
∗ 𝑡 + 𝑞
𝑐
∗ 𝑐𝑜 𝑠 𝜔
′
∗ 𝑡 +
+𝑒
−𝛼∗𝜔∗𝑡
∗ 𝑞
𝑠
∗ 𝜔
′
∗ 𝑐𝑜𝑠 𝜔 ∗ 𝑡 + 𝑞
𝑐
∗ 𝜔 ∗ 𝑠𝑖𝑛 𝜔
′
∗ 𝑡
𝑞 0 = 𝑞
0
= −𝛼 ∗ 𝜔 ∗ 𝑞
𝑐
+ 𝜔
′
∗ 𝑞
𝑠
→ 𝑞
𝑠
=
𝑞
0
𝜔
′
+
𝛼 ∗ 𝑞
0
1 − 𝛼
2
Drgania swobodne są rzeczywistym procesem opisanym funkcją quasi-harmoniczną
𝑞 𝑡 = 𝑎 ∗ 𝑒
−𝛼∗𝜔∗𝑡
∗ 𝑠𝑖𝑛 𝜔
′
∗ 𝑡 + 𝜑
o amplitudzie:
𝑎 =
1
𝜔
′
∗ 𝜔
2
∗ 𝑞
0
2
+ 𝑞
0
2
+ 2 ∗ 𝛼 ∗ 𝜔 ∗ 𝑞
0
∗ 𝑞
0
𝜑 = 𝑎𝑟𝑐𝑡𝑔
𝜔
′
∗ 𝑞
0
𝛼 ∗ 𝜔 ∗ 𝑞
0
+ 𝑞
0
16. Określid pojęcia: tłumienie podkrytyczne, krytyczne i nadkrytyczne.
Tłumienie podkrytyczne, krytyczne i nadkrytyczne występuje przy drganiach własnych układu
dyspersyjnego (tłumionego) gdzie 𝐶 ≠ 0.
𝑚 ∗ 𝑞 + 𝑐 ∗ 𝑞 + 𝑘 ∗ 𝑞 = 0 → 𝑞 + 2 ∗ 𝛼 ∗ 𝜔 ∗ 𝑞 + 𝜔
2
∗ 𝑞 = 0
𝜔
2
=
𝑘
𝑚
; 𝛼 =
𝑐
2 ∗ 𝑘 ∗ 𝑚
zakładamy równanie postaci: 𝑞 𝑡 = 𝑒
𝜆∗𝑡
równanie charakterystyczne: 𝜆
2
+ 2 ∗ 𝛼 ∗ 𝜔 ∗ 𝜆 + 𝜔
2
= 0
wyróżnik rów. charakterystycznego: ∆= 4 ∗ 𝛼
2
∗ 𝜔
2
− 4 ∗ 𝜔
2
= 4 ∗ 𝜔
2
𝛼
2
− 1 = −4 ∗ 𝜔
2
1 − 𝛼
2
Rozwiązani mogą byd różne w zależności od poziomu tłumienia:
Tłumienie nadkrytyczne 𝛼 > 1 → ∆> 0
W układach budowlanych na ogół nie występuje bo liczba tłumienia 𝛼 < 1
Ruch nie jest oscylacyjny, bo są 2 pierwiastki rzeczywiste rów. charakterystycznego
𝜆
1,2
= −𝛼 ∗ 𝜔 ± 𝜔 ∗ 𝛼
2
− 1
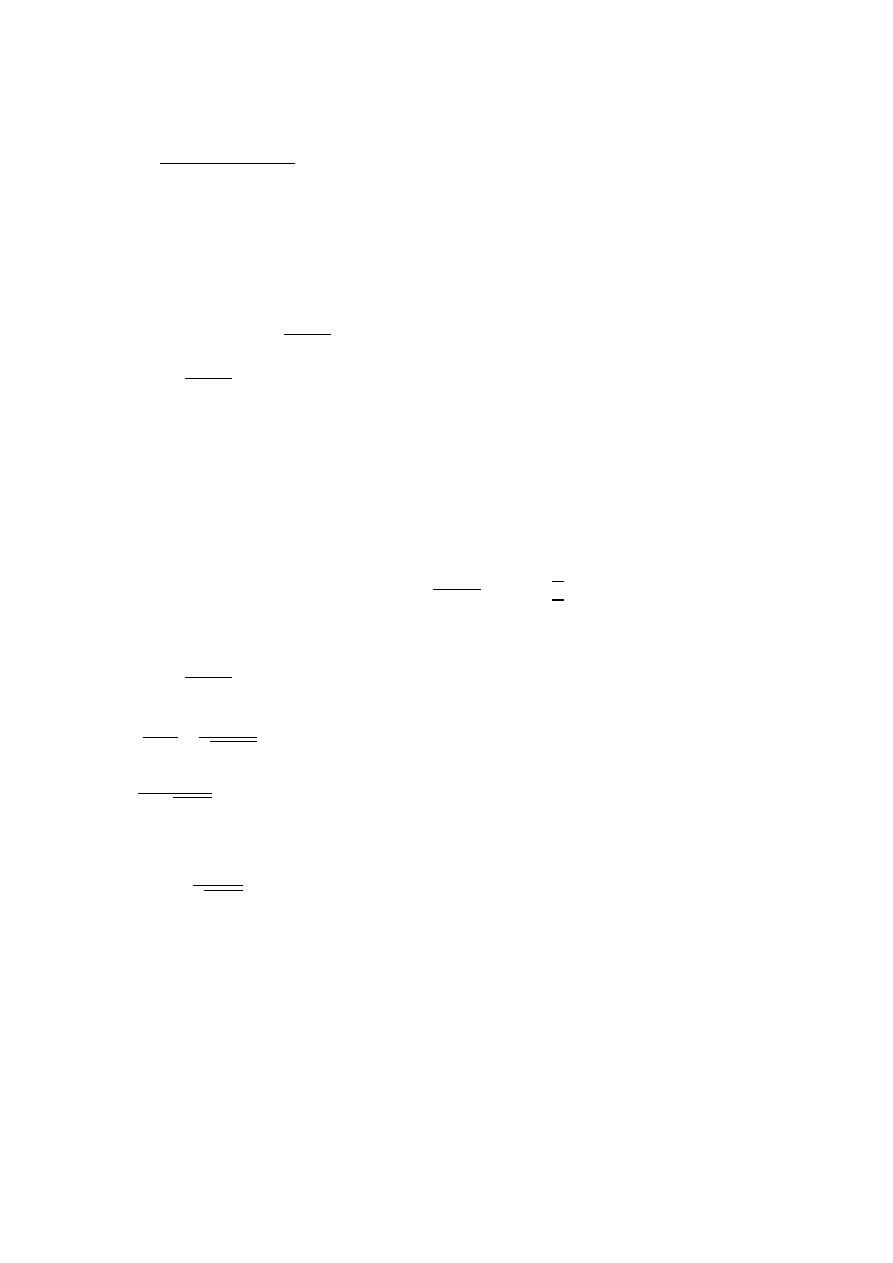
Wychylenie układu po przekroczeniu max asymptotycznie maleje do 0.
Tłumienie krytyczne 𝛼 = 1 → ∆= 0
Ruch nie jest oscylacyjny bo są 2 pierwiastki rów. charakterystycznego
𝜆
1,2
= −𝛼 ∗ 𝜔
Na ogół nie występuje w ustrojach budowlanych.
Tłumienie podkrytyczne 𝛼 < 1 → ∆< 0
Ruch oscylacyjny bo są 2 pierwiastki zespolone, sprzężone
𝜆
1,2
= −𝛼 ∗ 𝜔 ± 𝑖 ∗ 𝜔 ∗ 1 − 𝛼
2
= −𝛼 ∗ 𝜔 ± 𝑖 ∗ 𝜔′
𝜔
′
= 𝜔 ∗ 1 − 𝛼
2
− 𝑐𝑧ę𝑠𝑡𝑜ś𝑐 𝑤ł𝑎𝑠𝑛𝑎 𝑢𝑘ł𝑎𝑑𝑢 𝑡ł𝑢𝑚𝑖𝑜𝑛𝑒𝑔𝑜
Przypadek najczęstszy w ustrojach budowlanych
Całka ogólna równania wyjściowego ma postad:
𝑞 𝑡 = 𝑒
−𝛼∗𝜔∗𝑡
∗ (𝑞
𝑠
∗ sin 𝜔
′
∗ 𝑡 + 𝑞
𝑐
∗ 𝑐𝑜 𝑠 𝜔
′
∗ 𝑡 )
Opis zwinięty: 𝑞 𝑡 = 𝑎 ∗ 𝑒
−𝛼∗𝜔∗𝑡
∗ 𝑠𝑖𝑛 𝜔
′
∗ 𝑡 + 𝜑
Drgania własne układu harmonicznego są funkcją quasi-harmoniczną, zanikającą w czasie
ekspotencjalnie, o częstości kołowej: 𝜔
′
= 𝜔 ∗ 1 − 𝛼
2
; 𝜔 =
𝑘
𝑚
Parametry drgao własnych układu tłumionego:
𝜔
′
= 𝜔 ∗ 1 − 𝛼
2
< 𝜔 − 𝑐𝑧ę𝑠𝑡𝑜ś𝑐 𝑘𝑜ł𝑜𝑤𝑎 𝑑𝑟𝑔𝑎ń 𝑢𝑘łą𝑑𝑢 𝑡ł𝑢𝑚𝑖𝑜𝑛𝑒𝑔𝑜
𝑇
′
=
2 ∗ 𝜋
𝜔
′
=
𝑇
1 − 𝛼
2
> 𝑇 − 𝑑ł𝑢𝑔𝑜ść 𝑐𝑦𝑘𝑙𝑢 𝑑𝑟𝑔𝑎ń 𝑢𝑘ł𝑎𝑑𝑢 𝑡ł𝑢𝑚𝑖𝑜𝑛𝑒𝑔𝑜
𝛼 =
𝑐
2 ∗ 𝑘 ∗ 𝑚
− 𝑙𝑖𝑐𝑧𝑏𝑎 𝑡ł𝑢𝑚𝑖𝑒𝑛𝑖𝑎, 𝑐𝑧ę𝑠𝑡𝑜 𝑤𝑦𝑟𝑎ż𝑎𝑛𝑎 𝑤 %, 𝑜𝑘𝑟𝑒ś𝑙𝑎 % 𝑡ł𝑢𝑚𝑖𝑒𝑛𝑖𝑎
𝑘𝑟𝑦𝑡𝑦𝑐𝑧𝑛𝑒𝑔𝑜
𝛾 = 2 ∗ 𝛼 =
𝑐
𝑘 ∗ 𝑚
− 𝑏𝑒𝑧𝑤𝑧𝑔𝑙ę𝑑𝑛𝑦 𝑤𝑠𝑝ół𝑐𝑧𝑦𝑛𝑛𝑖𝑘 𝑡ł𝑢𝑚𝑖𝑒𝑛𝑖𝑎
17. Podad zakresy wartości bezwymiarowego współczynnika tłumienia zalecane dla konstrukcji
stalowych i żelbetowych.
Dla konstrukcji stalowych: 0,01 ≤ 𝛾 ≤ 0,025
Dla konstrukcji drewnianych: 0,03 ≤ 𝛾 ≤ 0,05
Dla konstrukcji murowych: 0,04 ≤ 𝛾 ≤ 0,08
Dla konstrukcji żelbetowych: 0,05 ≤ 𝛾 ≤ 0,1
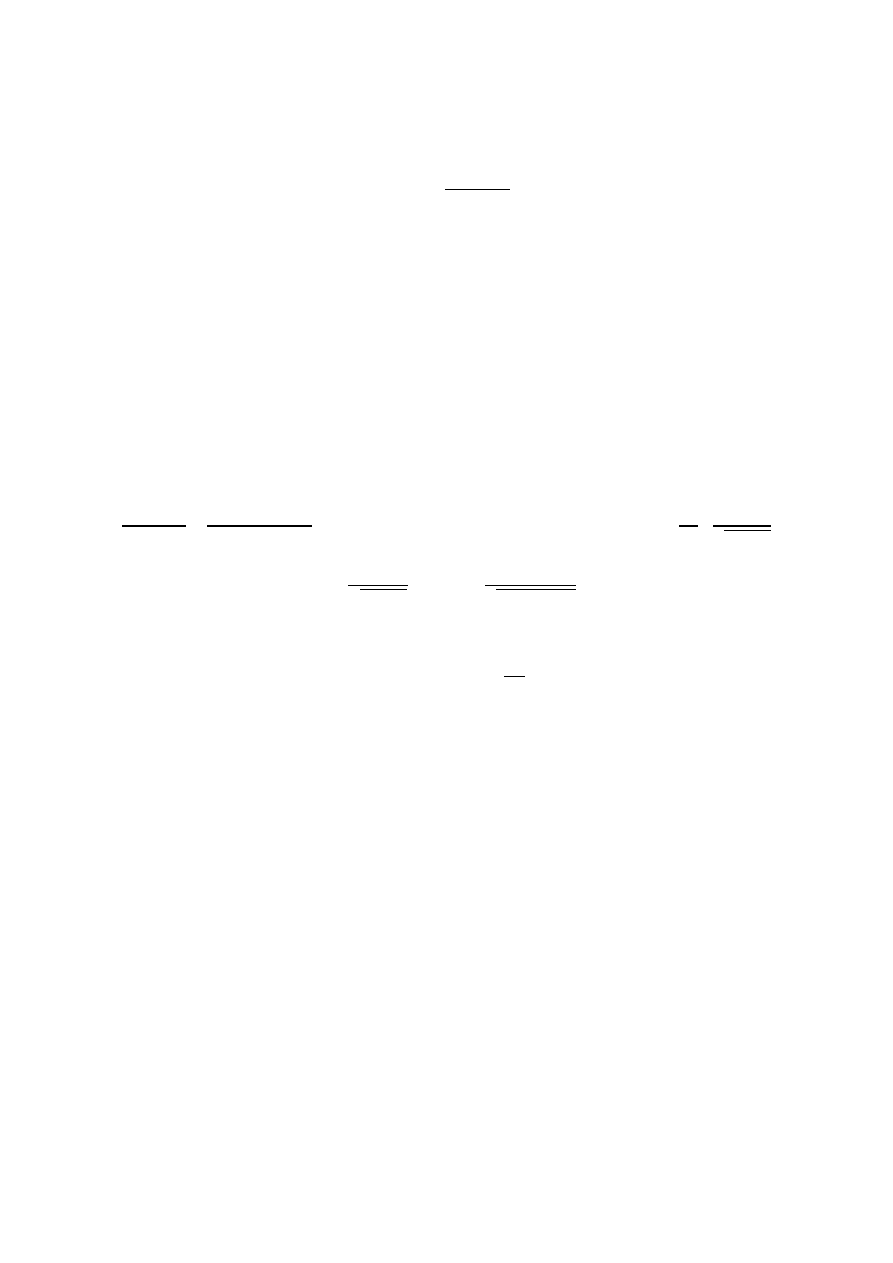
18.
Zdefiniowad pojęcie logarytmicznego dekrementu tłumienia i określid jego związek z liczbą
tłumienia.
𝜗 = 𝑙𝑛 ∗
𝑞(𝑡)
𝑞(𝑡 + 𝑇
′
)
Logarytmiczny dekrement tłumienia jest to parametr, który można wyznaczad na podstawie
pomiarów drgao swobodnych, badając stosunek wychylenia po okresie t do wychylenia po okresie T’.
Określa odwrotnośd liczny cykli, po której amplituda drgao zmniejszy się e-razy.
Związek między 𝜗 a 𝛼.
𝛼 − 𝑙𝑖𝑐𝑧𝑏𝑎 𝑡ł𝑢𝑚𝑖𝑒𝑛𝑖𝑎
𝑞 𝑡 = 𝑎 ∗ 𝑒
−𝛼∗𝜔∗𝑡
∗ 𝑠𝑖𝑛 𝜔
′
∗ 𝑡 + 𝜑
𝑞 𝑡 + 𝑇′ = 𝑎 ∗ 𝑒
−𝛼∗𝜔∗(𝑡+𝑇
′
)
∗ 𝑠𝑖𝑛 𝜔
′
∗ 𝑡 + 𝑇′ + 𝜑 = 𝑎 ∗ 𝑒
−𝛼∗𝜔∗(𝑡+𝑇
′
)
∗ 𝑠𝑖𝑛 𝜔
′
∗ 𝑡 + 𝜑
𝑞 𝑡
𝑞 𝑡 + 𝑇′
=
𝑒
−𝛼∗𝜔∗𝑡
𝑒
−𝛼∗𝜔∗𝑡−𝛼∗𝜔∗𝑇′
= 𝑒
𝛼∗𝜔∗𝑇′
→ 𝜗 = 𝑙𝑛(𝑒
𝛼∗𝜔∗𝑇′
) = 𝛼 ∗ 𝜔 ∗ 𝑇
′
= 𝛼 ∗
2𝜋
𝑇
∗
𝑇
1 − 𝛼
2
𝜗 =
2 ∗ 𝜋 ∗ 𝛼
1 − 𝛼
2
→ 𝛼 =
𝜗
4 ∗ 𝜋
2
+ 𝜗
2
Wzory są ważne gdy zanikanie drgao jest ekspotencjalne (wykładnicze).
Dla małego tłumienia 𝛼 ≪ 1 → 𝜗 ≈ 2 ∗ 𝜋 ∗ 𝛼 ; 𝛼 ≈
𝜗
2∗𝜋
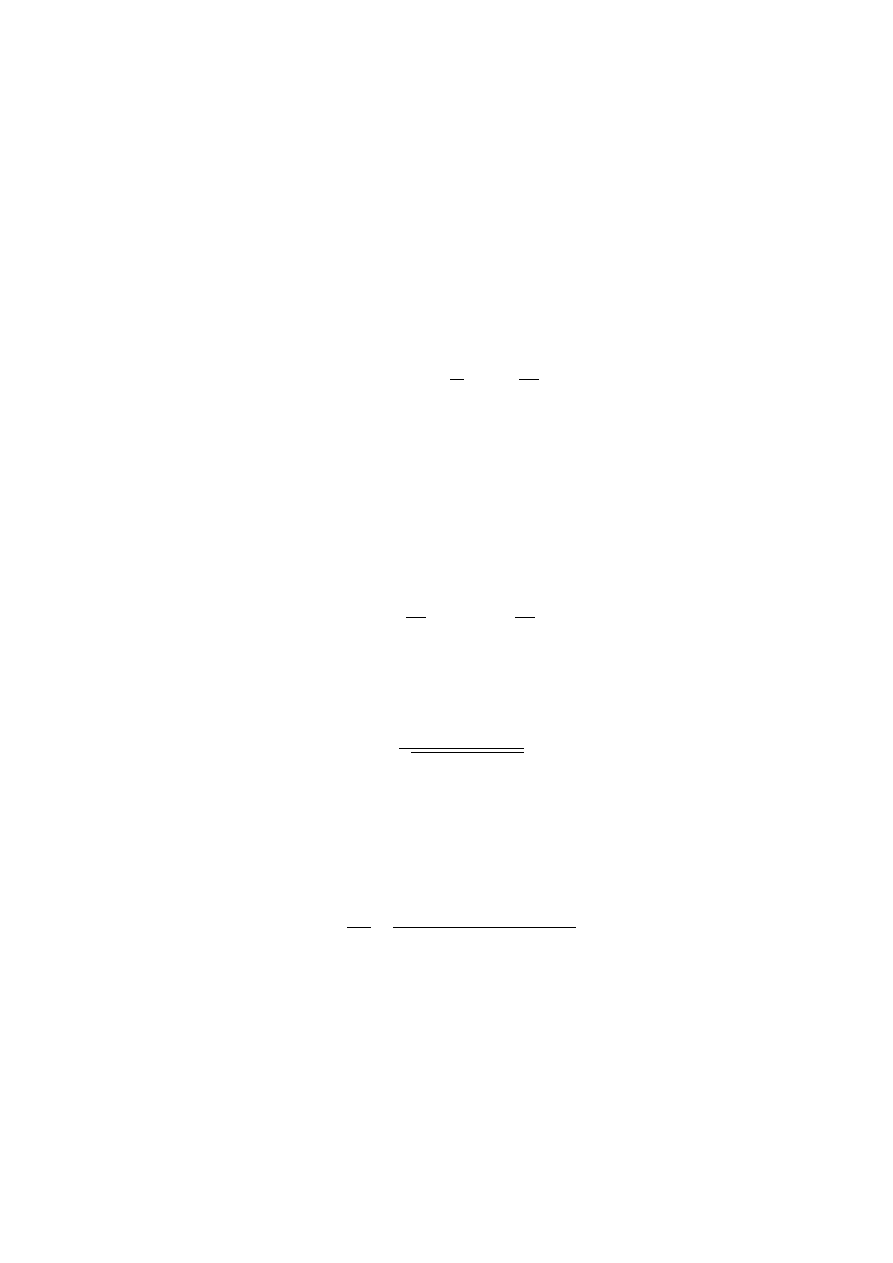
19. Napisad równanie drgao wymuszonych harmonicznie układu o jednym dynamicznym stopniu
swobody, przedstawid ustalone rozwiązanie równania.
𝑪𝑶𝑹𝑵 = 𝑪𝑶𝑹𝑱 + 𝑪𝑺𝑹𝑵
Rozwiązanie ustalone gdy CORJ = 0. Wtedy:
𝑪𝑶𝑹𝑵 = 𝑪𝑺𝑹𝑵
𝑞 𝑡 = 𝑞
𝑠
sin 𝑝𝑡 + 𝑞
𝑐
cos 𝑝𝑡
Równanie ruchu (chyba ;p )
𝑞 + 𝛾𝜔𝑞 + 𝜔
2
𝑞 =
1
𝑚
𝐹 𝑡 =
𝜔
2
𝑘
𝐹(𝑡)
Rozwiązanie:
𝑞 𝑡 = 𝑞
𝑠
sin 𝑝𝑡 + 𝑞
𝑐
cos 𝑝𝑡
𝑞 𝑡 = 𝑝𝑞
𝑠
sin 𝑝𝑡 − 𝑝𝑞
𝑐
cos 𝑝𝑡
𝑞 𝑡 = −𝑝
2
𝑞
𝑠
sin 𝑝𝑡 − 𝑝
2
𝑞
𝑐
cos 𝑝𝑡
Podstawienie:
−𝑝
2
𝑞
𝑠
sin 𝑝𝑡 − 𝑝
2
𝑞
𝑐
cos 𝑝𝑡 + 𝛾𝜔𝑝𝑞
𝑠
sin 𝑝𝑡 − 𝛾𝜔𝑝𝑞
𝑐
cos 𝑝𝑡 + 𝜔
2
𝑞
𝑠
sin 𝑝𝑡
+ 𝜔
2
𝑞
𝑐
cos 𝑝𝑡 =
𝜔
2
𝑘
𝐹
𝑠
sin 𝑝𝑡 +
𝜔
2
𝑘
𝐹
𝑐
cos 𝑝𝑡
20. Zdefiniowad i omówid pojęcie współczynnika dynamicznego przy wymuszeniu harmonicznym
𝜈 =
1
1 − 𝜂
2
+ 𝛾
2
𝜂
2
Współczynnik dynamiczny jest miarą efektów dynamicznych wymuszenia
Im v większe tym większa jest amplituda drgao
Uogólnienie pojęcia współczynnika dynamicznego:
𝜈 =
𝑦𝑑
𝑦𝑠𝑡
=
𝑜𝑑𝑝𝑜𝑤𝑖𝑒𝑑ź 𝑑𝑦𝑛𝑛𝑎𝑚𝑖𝑐𝑧𝑛𝑎
𝑜𝑑𝑝𝑜𝑤𝑖𝑒𝑑ź 𝑠𝑡𝑎𝑡𝑦𝑐𝑧𝑛𝑎
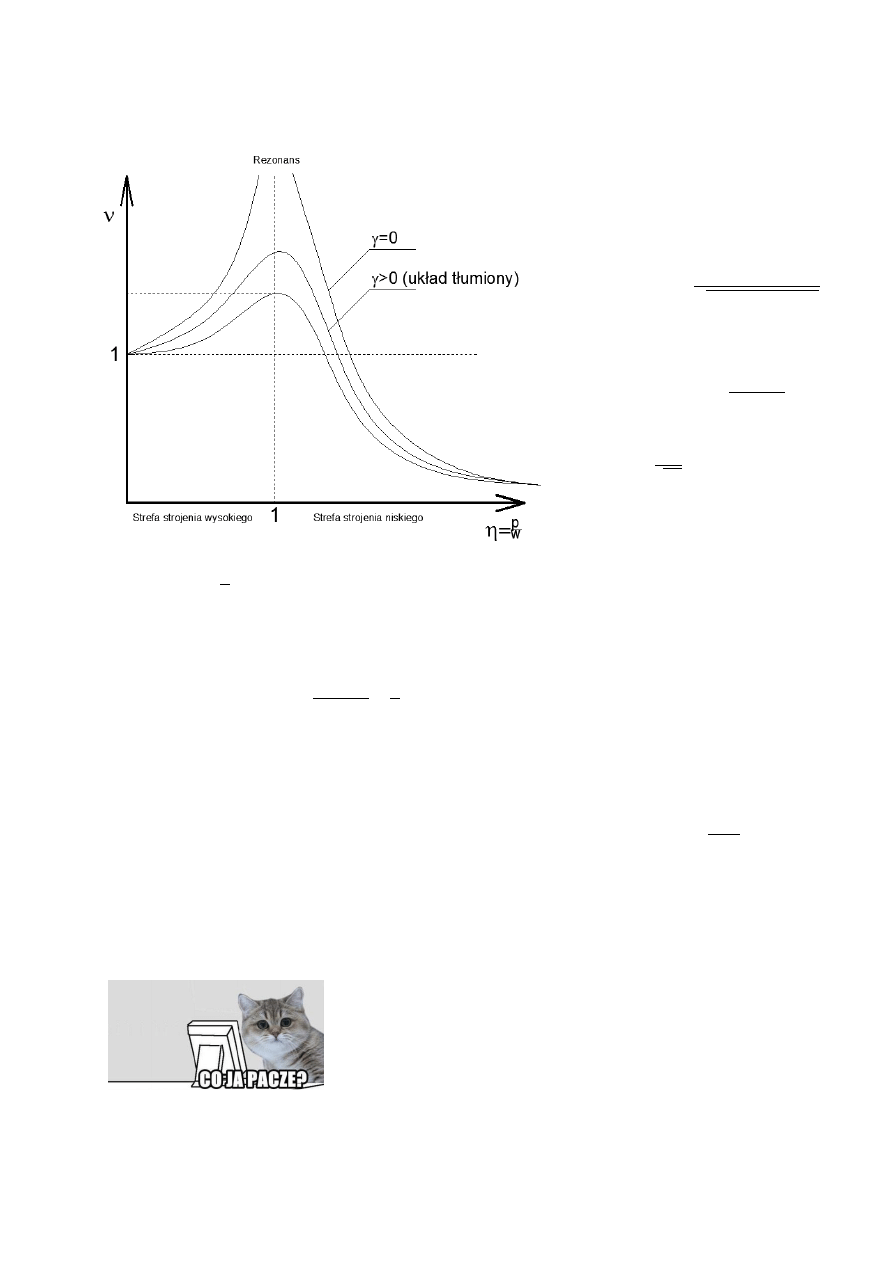
21. Naszkicowad wykres krzywej rezonansowej i omówid wykres.
Układ tłumiony:
𝛾 > 0 → 𝜈 =
1
1 − 𝜂
2
+ 𝛾
2
𝜂
2
Układ nietłumiony:
𝛾 = 0 → 𝜈 =
1
1 − 𝜂
2
Gdzie:
𝛾 =
𝑐
𝑘𝑚
- Bezwymiarowy
współczynnik tłumienia
Wykres ten przedstawia zależnośd współczynnika dynamicznego 𝑣 od względnej częstości
wzbudzania 𝜂 =
𝑝
𝜔
. Z wykresu możemy wywnioskowad, że jeśli częstośd drgao własnych 𝜔 jest równa
częstości kołowej wzbudzania 𝑝, to mamy do czynienia z rezonansem.
Strefa rezonansu :
1
|1 − 𝜂
2
|
≤
1
𝛾
→ 1 − 𝛾 ≤ 𝜂
𝑟𝑒𝑧 .
≤ 1 + 𝛾
Konstrukcję należy projektowad tak, aby nie pracowała w strefie rezonansu
Im mniejsze tłumienie 𝛾, tym współczynnik dynamiczny 𝜈 jest większy
Poza strefą rezonansową wpływ tłumienia jest bardzo mały, bo krzywe rezonansowe zbiegają
się do siebie. Tłumienie poza tą strefą pomija się.
Gdy mamy narzucony parametr p, możemy odpowiednio dobrad parametr 𝜔 =
𝑘/𝑚
Optymalne jest takie projektowanie konstrukcji, aby pracowały w strefie strojenia wysokiego,
wówczas podczas ustalania reżimu pracy (np. rozruch maszyny), nie przechodzi się przez
rezonans.
22. Co oznacza określenie „krzywa rezonansów ścisłych”?
:P