The Glass Transition

• On cooling, some polymer melts don't crystallize
rather they form a glass;

Vitrify

Tg

Force

Temperature

Soft -- above Tg

Hard -- below Tg

F

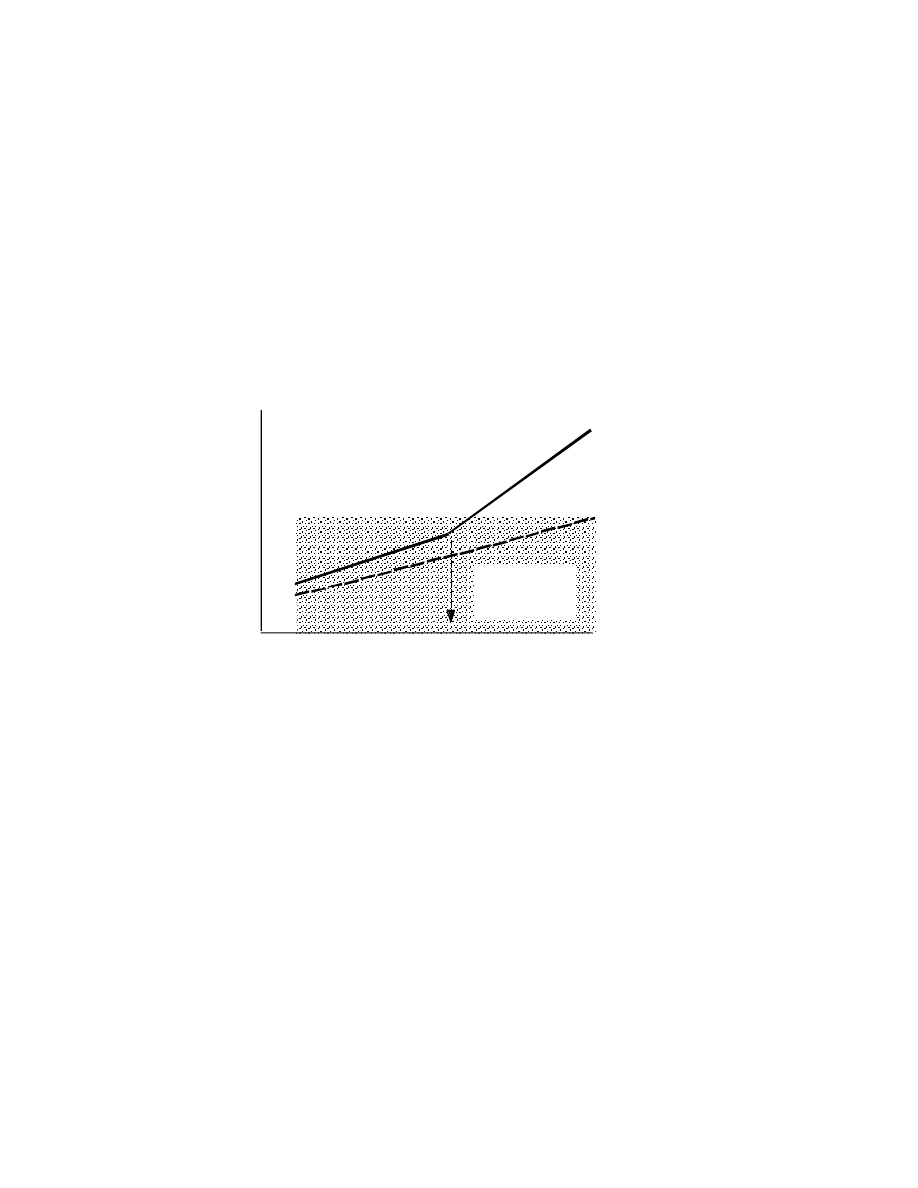
α

g

Specific Vol.

Tg

Temperature

α

l

α

g

2

≈

Total

Volume

Occupied

Volume

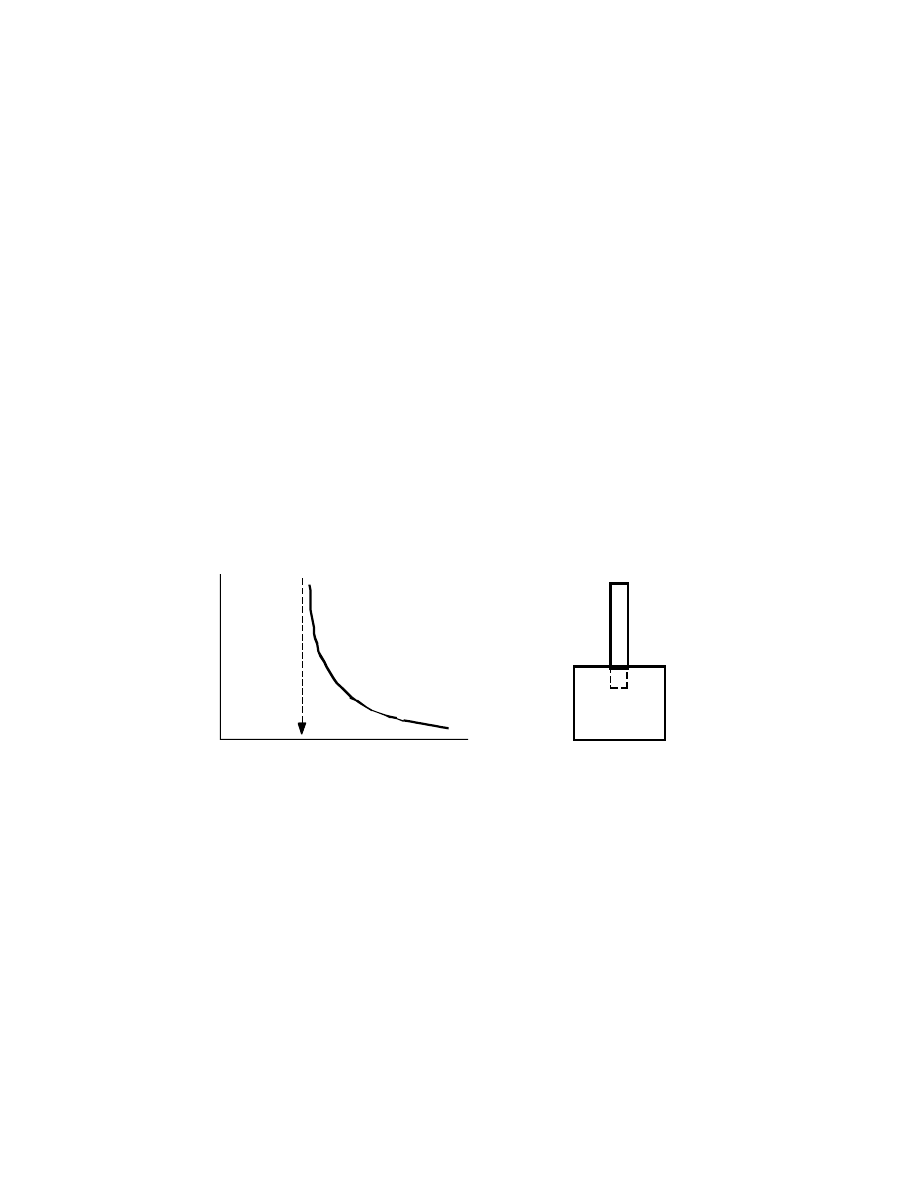
• Coefficient of expansion of the polymer liquid (melt)

is approximately twice that of the glass.

Free Volume

• Total system volume =

Volume occupied by
chains; physically or
effectively

+

Unoccupied volume;
space between chains
(free volume)

Volume

Temperature

Fast

Slow

• Tg is rate dependent; higher heating/cooling rates

or higher frequencies test rates give higher values
for Tg.

• Both cooling and heating rates should be specified

when measuring and reporting Tg.

• After fast cooling a polymer below Tg, the sample

will try and find the most thermodynamically stable
state through reorganization.

• Possible 'Aging' and embrittlement of polymer held

at up to 50° below Tg.

Practical determination of Tg

• DSC or DTA; use large samples and as high a
heating rate as possible to amplify poor signals.

∆

T or

∆

H

Temperature

• Several thermal 'definitions' of Tg including;

Onset + (Extrapolated);

Mid line intersection;

Return + (Extrapolated);

Inflection point;

Derivative.

• With semicrystalline polymers having moderate to

high crystallinity Tg may be poorly resolved.

• Other STATIC methods used to measure Tg:-

Refractive index (OM); Gas Diffusion/Solubility;
Thermal conductivity;

Chain mobility (NMR);

Specific volume (Dilatometer).

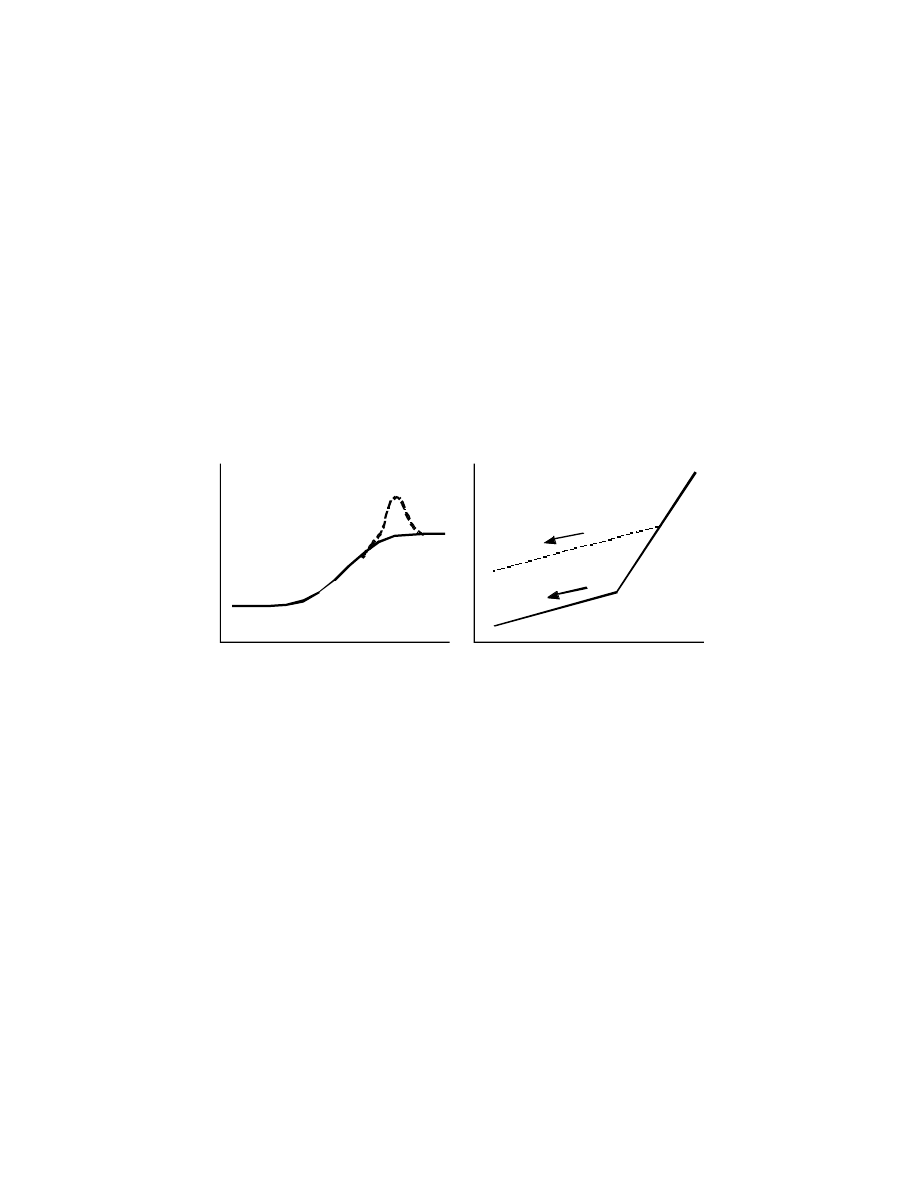
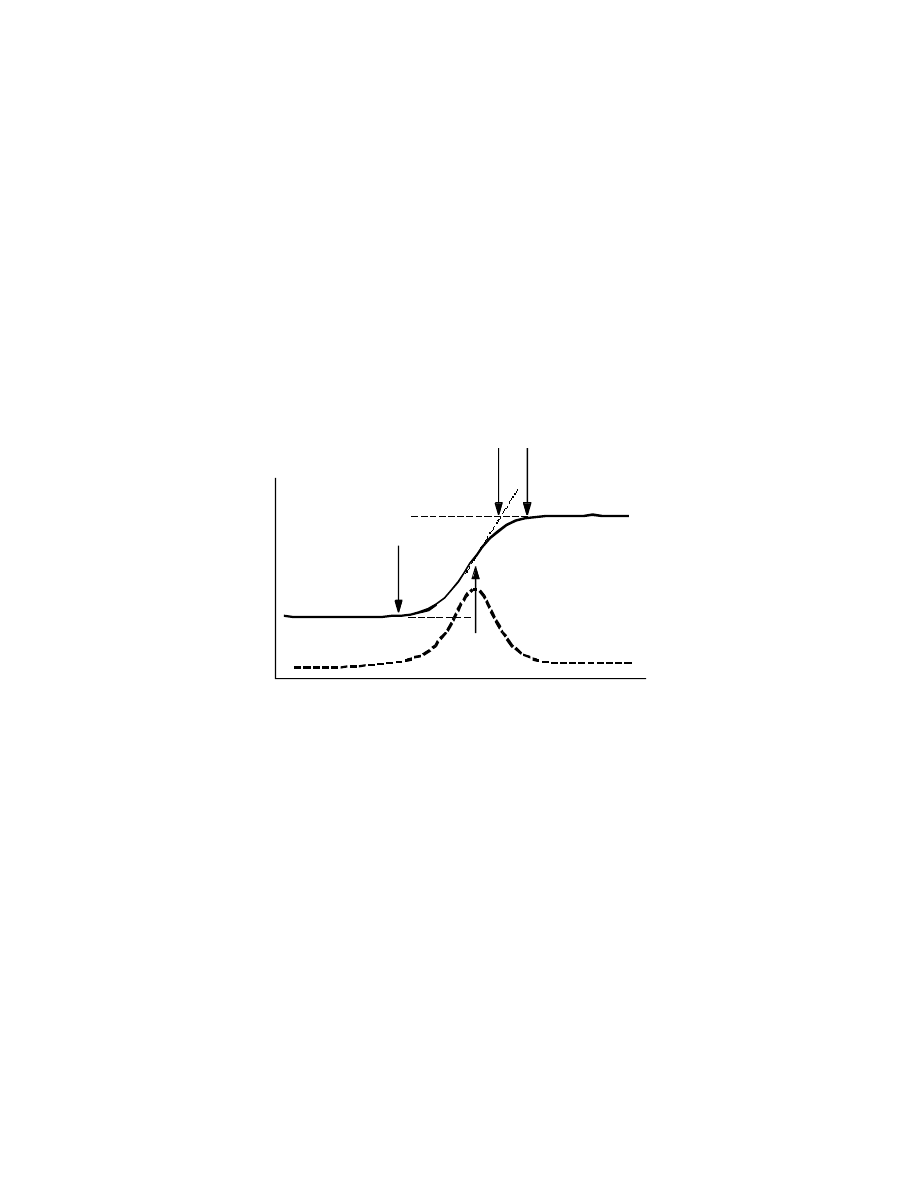
• Tg as measured by thermal methods often show
'peaks' near the transition.

Fast

Slow

∆

T or

∆

H

Temperature

Specific Vol.

Temperature

• Exotherm near Tg explained as the 'melting out' of

holes or of frozen in 'free volume".

• Experimentally observed Tg is a function of several

variables including :-

Molecular weight

Plasticizer content

Test Rate/Frequency

Sample size

Copolymers/Blends

Cross-linking

Crystallinity

Tacticity

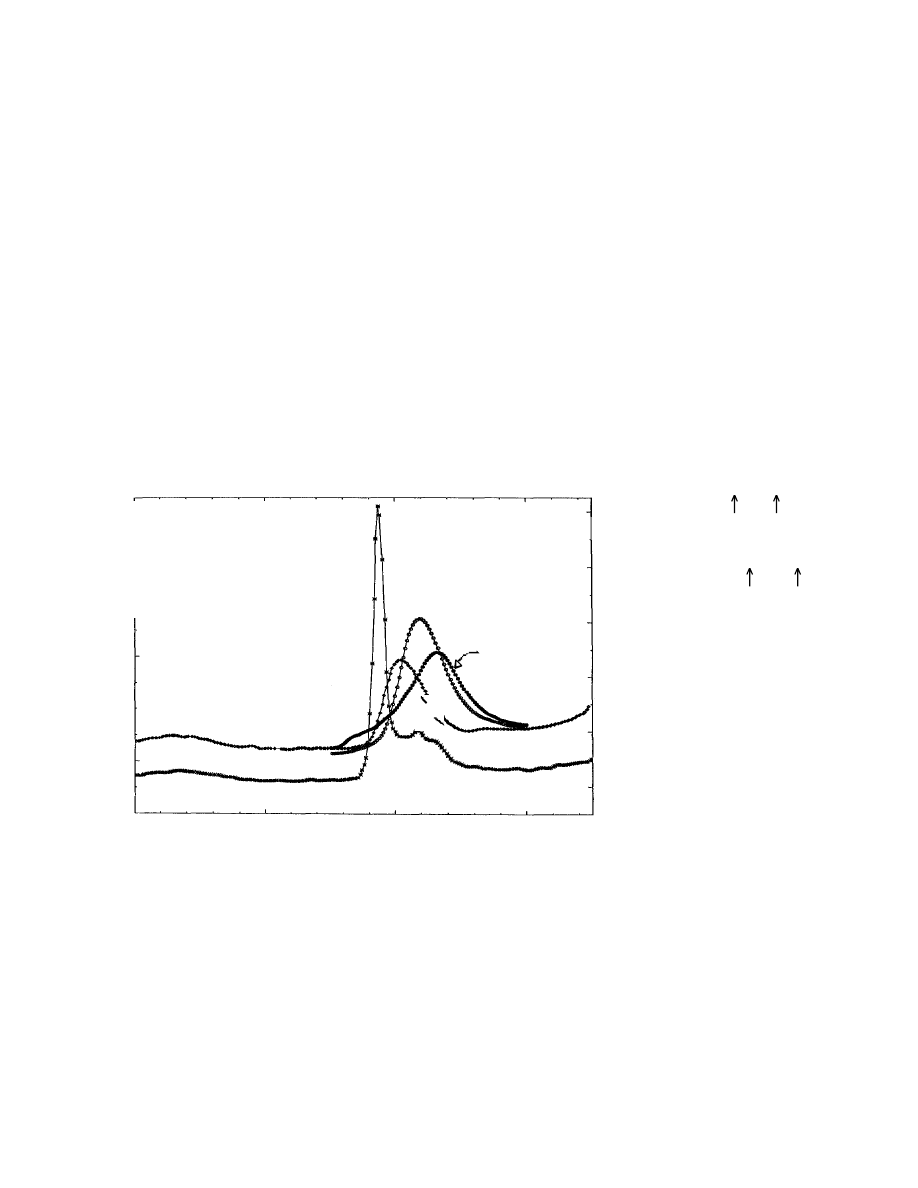
Influence of Crystallinity and Orientation

• Ratio of energy dissipated by viscous component

vs. energy stored by the elastic component;
Tan

δ

(Loss Tangent) is maximum near Tg.

a)

Drawn (x3.5)

b)

Drawn (x5.4)

c)

Crystalline

d)

Amorphous

Tan

δ

or

Loss Tangent

0

Temperature (°C)

a

b

c

d

• Crystallinity

,

Tg ;

restrain amorphous chains.

• Cold drawing , Tg ;
tension in amorphous
chains.

Influence of Molecular Weight

• Experimentally, Tg is a fn. of molecular weight.

• Major changes in Tg at low molecular weights and

small changes at high molecular weights.

More free volume at the
ends of a chain, so more
chain ends per volume
means lower Tg.

• Fox-Flory equation:-

Tg = Tg

∞

-K/Mn (K

≈

25x103)

Tg

Mn -1

Mn

Tg

Tg

∞

Tg

∞

≈

25x10 3

• Situation regarding molecular weight dependence is

experimentally more complicated, some systems
show 2 or 3 straight line regions.

• Transition from entangled coils to isolated coils to

rod like systems. Rods pack more efficiently than
coils so free volume associated with chain end is
lower for rods.

10

3

10

4

Isolated
coils

Rod-like

molecules

Tg

Mn-1

Tangled

coils

• Different K's for different molecular weights;

K from one region can't predict Tg in another.

Note

•

Some RING compounds follow Fox-Flory!!!

•

Hydroxyl terminated PPO has no mol.wt.

dependence of Tg; K=0.!! CH3 terminated K>0.

•

Tg(upper) - restrained amorphous; folds.

Tg(lower) - free amorphous; cilia, loose loops.

Influence of Branching and Cross-links

• Intuitively, adding cross-links increases Tg; restrain

chains more than in uncrosslinked state.

• However, consider joining two chains together

whose molecular weights are M1 and M2.

Type of Join

# of

Ends

End to end

"T" junction

Middles as

"X" joint

2

3

4

• All joined chains have the same molecular weight.

• For the SAME molecular weight Tg is depressed

more for branched polymers vs. linear molecules.

• If chains are crosslinked anticipate increase in Tg.

Decrease free volume. Inhibit chain motion.
Increase average size of moving units.

Tg = Tg

∞

-K/M + Kx.(# crosslinks/gm)

Predicted

Observed

Tg

% Cross-Links

• Network is a copolymer. If cross-link agent is ‘like’

the polymer the equation above works. If the
chemistry of the cross-link is different could see a
maximum in Tg vs. # of cross-links.

• At very high cross-link densities Tg rises faster than

predicted.

Influence of Copolymerization, Blending and

Plasticization

• Equations developed for these systems depend on

the assumption that free volume is additive.

• General form of the equation for diluents

(plasticizers) is given by :-

α

p.Vp.Tgp +

α

d.(1 - Vp).Tgd

Tgs = –––––––––––––––––––––––

α

p.Vp +

α

d.(1 - Vp)

Where

Vp

= Volume fraction of polymer.

α

p

= Coefficient of expansion of

free polymer volume.

Tgp

= Tg of the polymer.

• How do we find

α

d and Tgp for a low molecular

weight liquid.

Remember;

α

l

≈

2.

α

g; so,

α

(free volume)

≈

α

l;

assume

α

p or

α

d to be

≈

10-3 for many liquids.

• Make up one or two mixtures and measure Tgs;

then derive Tgd using the above equation.

• For copolymers and blends simplify the previous

equation with some assumptions:-

Tg(copolymer or miscible blend) =

α

p1.Vp1.Tgp1 +

α

p2.(1 - Vp1).Tgp2

–––––––––––––––––––––––––––

α

p1.Vp1 +

α

p2.(1 - Vp1)

Now,

α

p1

≈

α

p2

and Vp1 + Vp2 =1

and many polymer have

≈

the same density so

Vp1

≈

Xp1 - Mole fraction or weight fraction.

so,

Tg(cop/blend)

≈

X1.Tg1 + X2.Tg2

alternatively, 1/Tg(cop)

≈

(W1/Tg1) + (W2/Tg2)

Tg1

Tg2

Composition

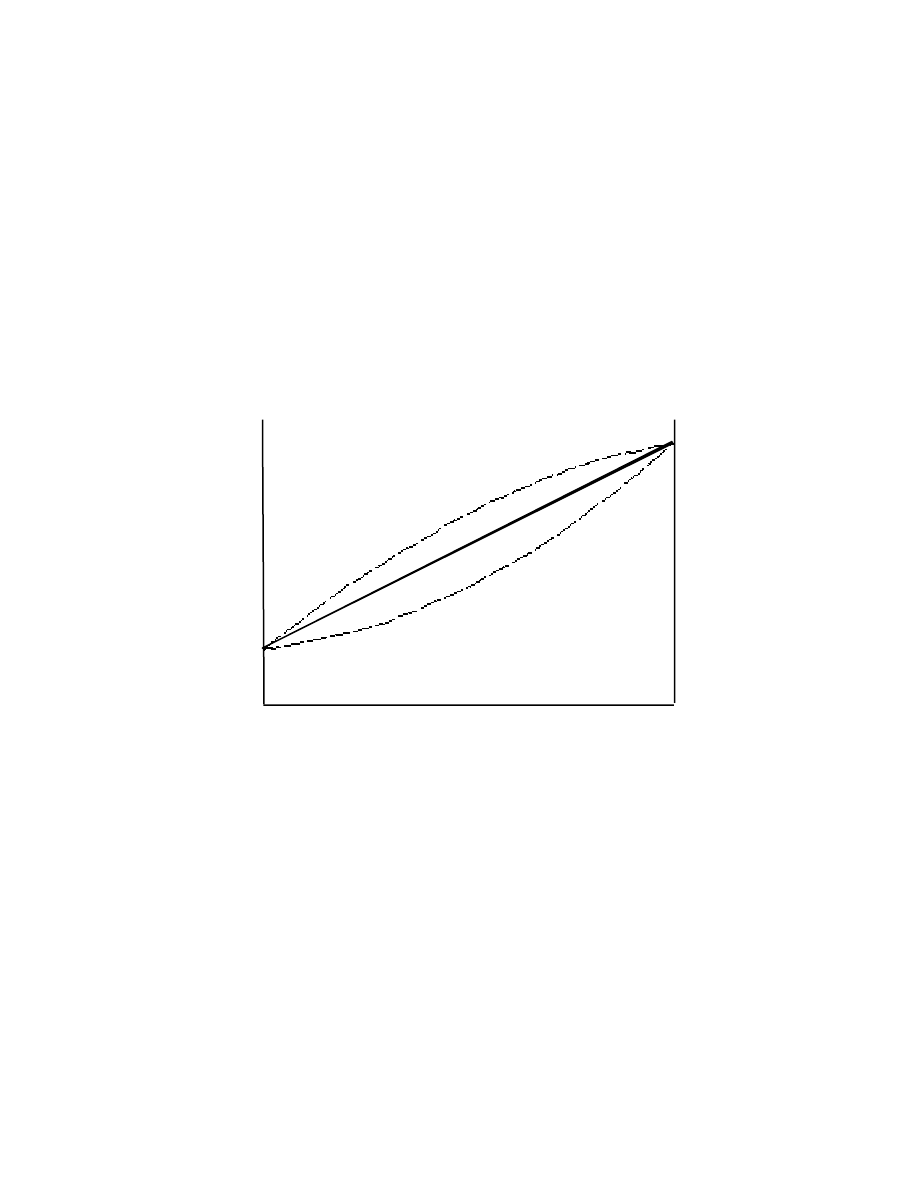
• The above equations hold for immiscible blends and

random copolymers.

• Block copolymers and Immiscible blends phase

separate and show individual Tg's for each phase.

Tg1

Tg2

Composition

Blocks and

Immiscible blends

Random

copolymers

• For crystallizable copolymers Tg depends on the

composition of the amorphous phase. This could
be different from overall copolymer composition;
polymer chains rich in the most crystallizable
component will preferentially crystallize.

2

-CH -CH -

2

2

-CH -CH

-

|

CH

3

|

2

-CH

C-

|

-

CH

3

CO

2

CH

3

|

2

-CH

C-

-

|

CH

3

2

-CH -CH

-

|

CH

3

+ CH

3

+ CH

3

Influence of Structural Parameters

• Explanations based on the concept of free volume.

CH

3

|

2

-CH

C-

|

-

CH

3

CO

2

2

CH

CH

3

|

2

-CH

C-

|

-

CH

3

CO

2

(

)

3

-

• Flexible side groups introduce more free volume.

• More 'linear' Trans chain can pack better reduces

free volume and raises Tg.

-CH

2

CH -

2

C=C

CH -

2

-CH

2

C=C

Trans

Cis

Tg

≈

-120 Tg

≈

-48

72

x

x

x

x

x

x

x

x

x x

x

x

x

x

x

x

x

x

• Tg (iso) PS

≈

Tg (atactic) PS;

but, for most polymers Tg (iso) < Tg (atactic)

Rotation is 'easier' in Isotactic materials, favors
changes in conformation chain mobility.
Energy minima are deeper in less crowded
syndiotactic form.

Chain-chain interactions and backbone flexibility

CH

3

|

CH

3

|

|

CH

3

|

CH

3

CH

3

|

CH

3

|

- C - CH - C - CH -

2

2

|

CH

3

|

CH

3

Cl

|

Cl

|

- C - CH - C - CH -

2

2

|

Cl

|

Cl

≈

≈

• Increase in backbone flexibility lowers T

g.

• Increase in chain-chain interactions increases Tg.

Summary

• Intermolecular interactions pull chains together -

decrease free volume -and raise Tg.

• Chain side substituents

Stiff and bulky groups -inhibit rotation -raise Tg.
Flexible side groups -hold chains apart

-increase free volume -lower Tg.

• Chain backbone substituents

Flexibilize the chain; -thio, ether, Si-O; -lower Tg.
Bulky groups stiffen chain; rings; -raise Tg.

• Easier to rationalize Tg; much more difficult to

predict; some attempts at group contribution
methods.

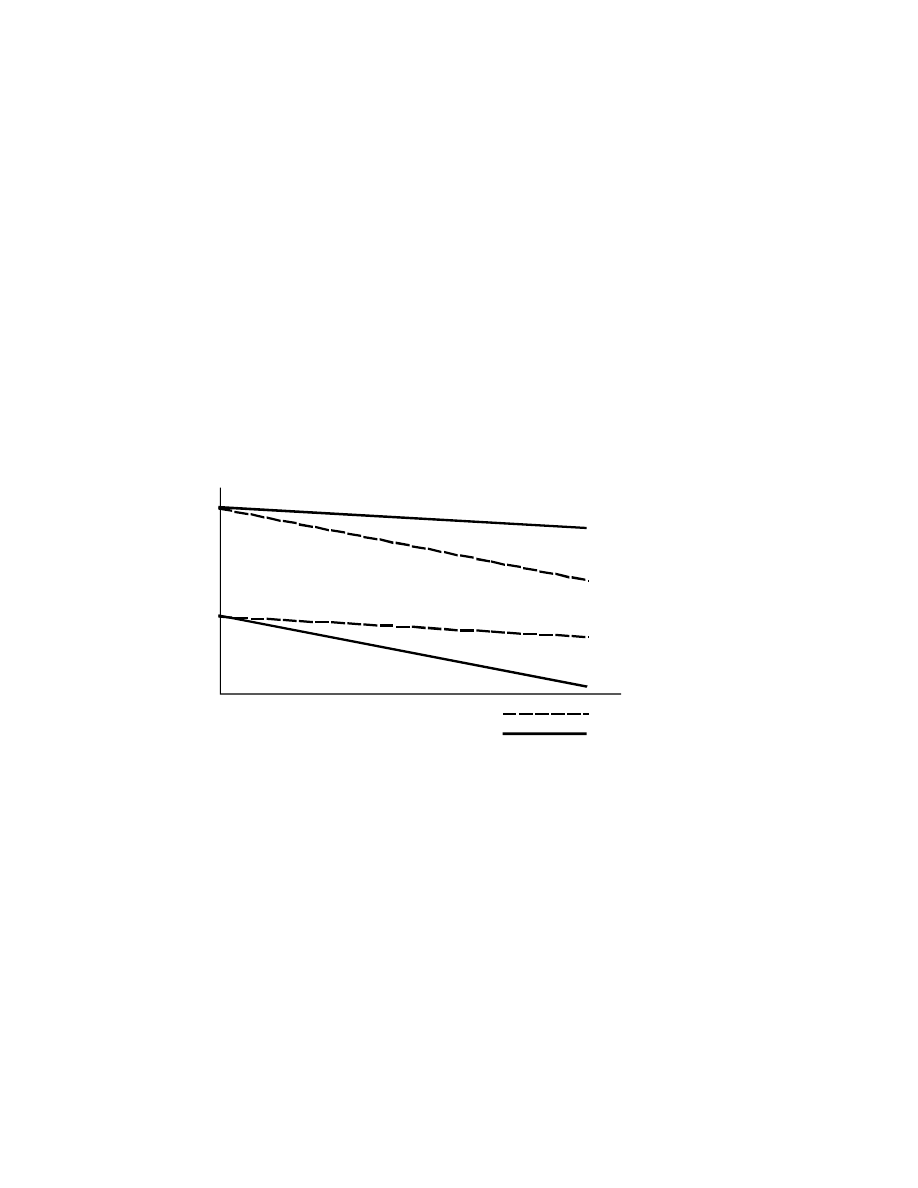
Compatible blends

or

Random copolymers

Tm

Incompatible blends

or

Block copolymers

Homo

polymers

Tg

0.5

0.7

PE, PVDC

PS, PP

Temp

Tg

% comonomer
or plasticizer

Tm

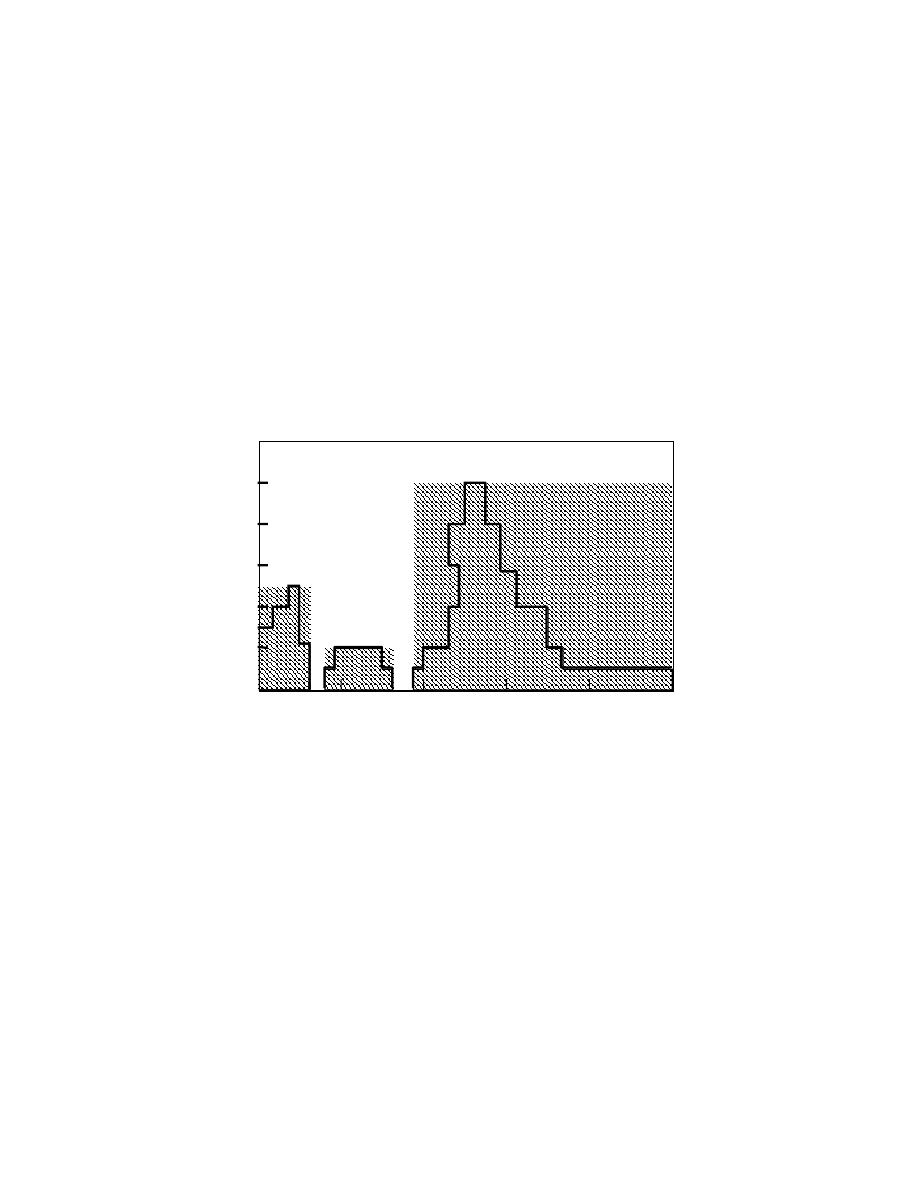
Number of times

Tg reported

140 220 300

2

6

10

Temperature °K