EGZAMIN Z FIZYKI

Zadanie 1

Samolot leci między dwoma miastami A i B odległymi od siebie o D. Załóżmy, że wiatr wieje z jednostajną prędkością V

w

od

miasta A w kierunku miasta B. Prędkość samolotu względem powietrza wynosi V

o

i jest stała.

(a) Jak długo będzie poruszał się samolot pomiędzy miastami od miasta B do miasta A.
(b) Ile wynosi średnia prędkość samolotu w podróży od miasta A do miasta B i z powrotem.

Zadanie 2

Dziecko o masie m

d

= 35 kg stoi u podnóża wzniesienia o kącie nachylenia α=15

o

. W pewnym momencie dziecko nadało sankom

o masie M

S

= 2 kg prędkość V

o

= 2 m/s skierowaną w wzdłuż wzniesienia. Współczynnik tarcia pomiędzy płozami sanek a

śniegiem wynosi f = 0,01. Przyjmij, że g = 10 m/s

2

.

(a) Narysuj siły działające na sanki poruszające się pod górę.
(b) Zapisz treść II zasady dynamiki Newtona i zastosuj ją dla sanek.
(c) Oblicz drogę przebędą sanki do momentu zatrzymania się.
(d) Następnie dziecko podbiegło do miejsca w którym sanki się zatrzymały, wsiadło na sanki a następnie sanki wraz z

dzieckiem zaczęły zjeżdżać ze wzniesienia. Czy sanki dojadą do podstawy wzniesienia? Odpowiedź uzasadnij.

(e) Kiedy spełniona jest zasada zachowania energii mechanicznej.

Zadanie 3

Wiadomo, że Księżyc porusza się wokół Ziemi w ten sposób, że co 27,3 dnia znajduje się w tym samym miejscu. Odległość
pomiędzy środkiem Ziemi a Księżycem wynosi 384 tys km. Masa Księżyca wynosi 7,35 x 10

22

kg. Przyjmij, że g = 10 m/s

2

.

(a) Oblicz przyspieszenie z jakim porusza się Księżyc.
(b) Przyspieszenie dośrodkowe kulki jest związane ze zmianą

A: kierunku prędkości liniowej. B. wartości prędkości liniowej. C. kierunku i wartości prędkości liniowej.

(c) Księżyc porusza się ruchem:

A: jednostajnym prostoliniowym
B: jednostajnym krzywoliniowym
C: przyspieszonym, przy czym przyspieszenie zależy od czasu
D: przyspieszonym, przy czym wartość prędkości zmienia się w czasie.

(d) Oblicz pracę wykonaną przez siłę grawitacji pochodzącą od Ziemi w czasie jednego obiegu Księżyca wokół Ziemi?
(e) Oblicz moment siły grawitacji pochodzącej od Ziemi a działającej na Księżyc.
(f) Wyjaśnij dlaczego Księżyc porusza się po krzywej płaskiej?
(g) Z powierzchni Księżyca startuje pojazd kosmiczny o masie 1 tony. Jak zmienia się energia potencjalna układu Księżyc-

pojazd kosmiczny, jeśli pojazd kosmiczny oddala się od Księżyca?
A: rośnie B: maleje C: nie zmienia się D: nie mam zdania

Zadanie 4

Sprężynę o stałej sprężystości k = 65 N/m zamocowano jednym końcem do sufitu, a na jej drugim końcu przymocowano ciężarek
o masie m = 680g. Przyjmij, że g = 10 m/s

2

.

(a) O ile wydłużyła się sprężyna?
(b) Ciężarek odciągnięto na odległość d = 11 mm od położenia równowagi a następnie puszczono. Zapisz równanie ruchu

ciężarka, jeśli zaniedbamy opory ruchu.

(c) Masę ciężarka zwiększono dziewięciokrotnie. Jak zmienia się okres jego drgań i ile razy się zmieni?
(d) Ile wynosi energia potencjalna odpowiadająca sile sprężystości w odległości a = 5,5 mm od położenia równowagi?
(e) Sprężynę wraz z masą m wkładamy do ośrodka w którym stała tłumienia b = 70 g/s. Czy możemy mówić o słabym

tłumieniu? Ile wynosi okres drgań.

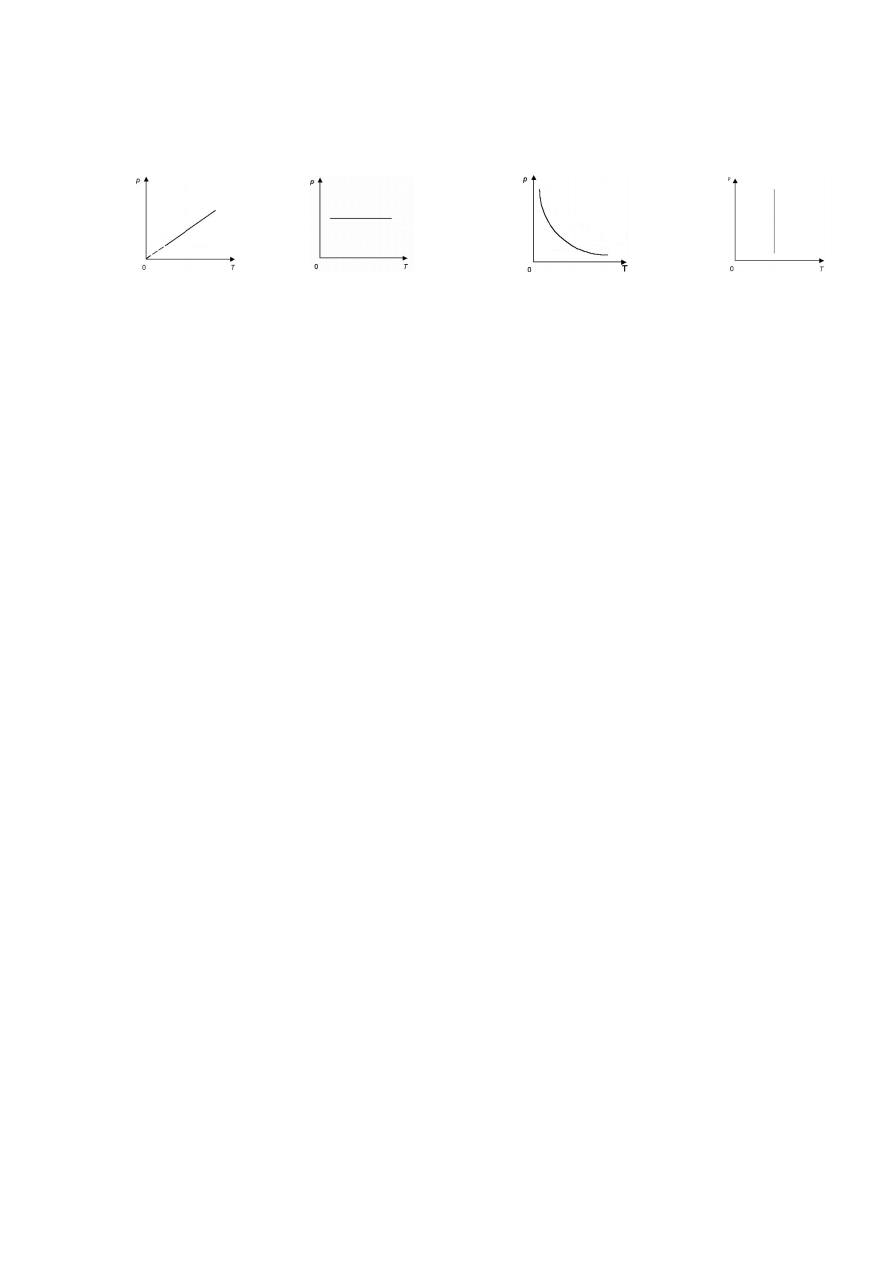
Zadanie 5

Pierwsza zasada termodynamiki dla pewnej przemiany gazu doskonałego ma postać ∆U = Q. Masa gazu nie uległa zmianie
podczas przemiany.

(a) Który z wykresów przedstawia poprawnie zależność ciśnienia od temperatury dla tej przemiany?

A.

B.

C.

D.

(b) W naczyniu o objętości 2 dm3 znajduje się gaz doskonały pod ciśnieniem 5

.

10

5

N/m

2

. Znaleźć sumaryczną energię

kinetyczną ruchu postępowego cząsteczek tego gazu.

Zadanie 6

Wyjaśnij, przy pomocy odpowiednich praw, dlaczego łyżwiarka figurowa wykonująca piruet ściąga ręce ku sobie?

Zadanie 7

Na czym polega zjawisko rezonansu mechanicznego? (Podaj stosowny przykład, zapisz równanie, rozwiąż równanie, wyznacz
częstość rezonansu, narysuj zależność amplitudy od częstości w przypadku różnych wartości stałych tłumienia.)