Zadanie 1
Oblicz WACC firmy wiedząc, że struktura kapitałowa wygląda następująco:

a) 10.000 akcji zwykłych na okaziciela o wartości rynkowej 1.000 każda.
b) 5.000 akcji uprzywilejowanych o wartości nominalnej 1.000. których właściciele co roku

pobierają dywidendę niezależnie od sytuacji spółki, w wysokości 35%. Rynkowa cena akcji to
1.600.

c) Kredyt bankowy w wysokości 20.000.000, którego rzeczywisty roczny koszt wynosi 14% p.a.
d) Zobowiązania z tytułu dostaw i usług w wysokości 15.000.000 PLN (dostawcy nie udzielają

rabatu w przypadku wcześniejszej płatności, jednak faktura na kwotę 2.000.000 została
przeterminowana o 2 miesiące i zapłacono 20.000 tytułem odsetek karnych)

Współczynnik β dla akcji zwykłych spółki wynosi 2., a oprocentowanie bonów skarbowych 5,5%.
Główny indeks giełdowy wzrósł w ciągu ostatnich 10 lat z poziomu 15.000 punktów do 46.588 punktów.

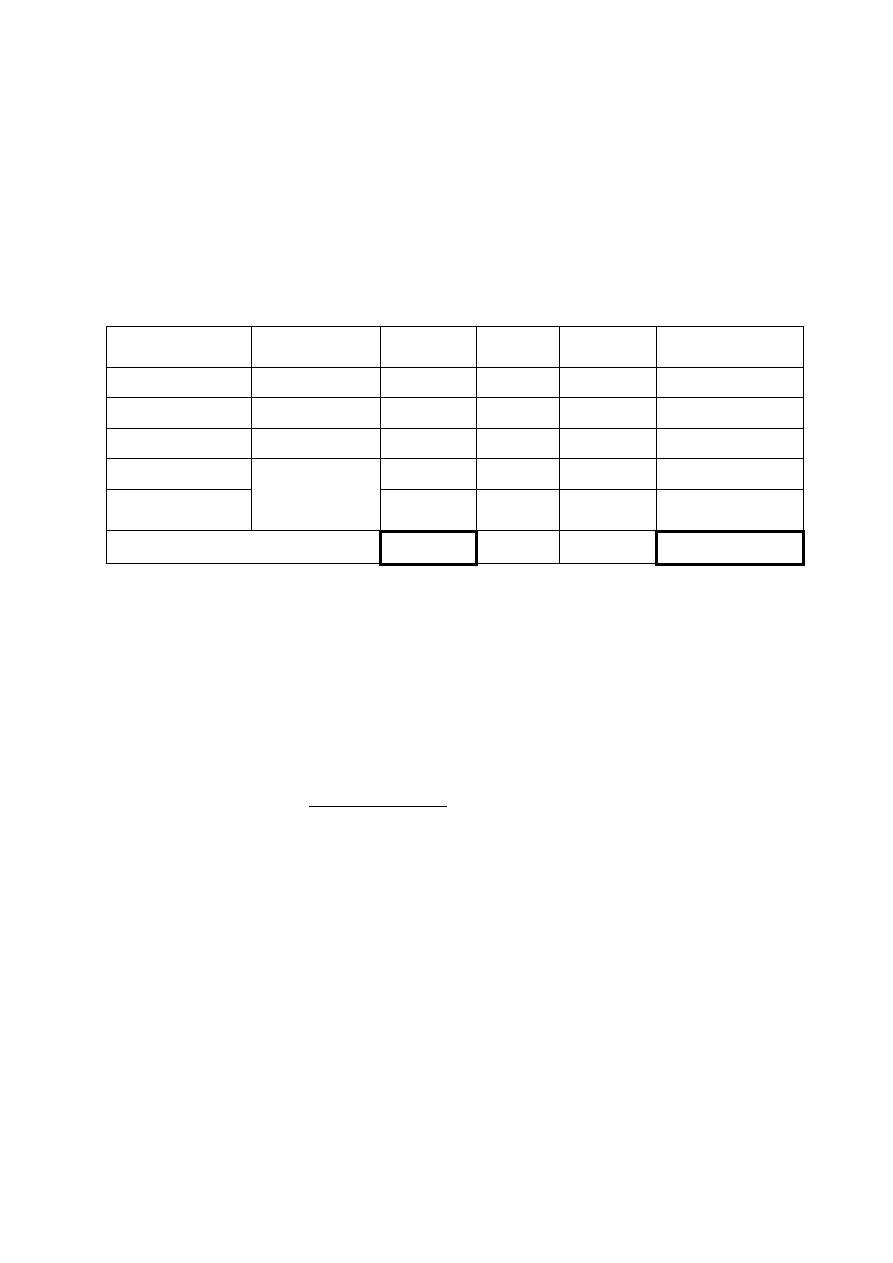
Rodzaj kapitału

Obliczenia

Wartość

(mln)

Udział %

Koszt

kapitału

Udział%*koszt

kapitału

Akcje zwykłe

10.000*1.000

10

20%

0,185

0,0370

Akcje uprzywil.

5.000*1.600

8

16%

0,21875

0,0350

Kredyt bankowy

27

54%

0,1134

0,0612

Kredyt kupiecki

Rozbijamy na
dwie grupy

13

26%

0

0,0000

Kredyt kupiecki
(przeterminowany)

2

4%

0,06

0,0024

RAZEM:

50

100%

WACC:

0,1356

a)

Korzystamy z SML :

k=r

f

+β(r

m

-r

f

)

musimy obliczyć

r

m

wiadomo, że WIG wzrósł w ciągu 10 lat do 46.588 z 15.000 punktów co daje wzrost o

i=(46.588/15.000)-1=2,1058(6) czyli o 211%

obliczamy średnioroczną stopę zwrotu z indeksu
(jeżeli pojawiają się problemy odsyłam do zadań dotyczących kapitalizacji i dyskontowania – temat nr 2)

r

m

= √

(1 + 2,1058(6)

10

− 1 = 0,12

k=0,055+2(0,12-0,055) = 0,185

b) Wykorzystujemy model stałej dywidendy

D= 0,35*1.000 = 350

K= D/P = 350/1.600 =0, 21875

c) Kredyt bankowy k=r(1-T) = 0,14*(1-0,19)=0,1134

d) Część zobowiązań niezwiązaną z odsetkami karnymi i rabatem (nic nie ma o rabatach)

wyceniamy na 0 pozostałą część musimy odnieść do płaconych odsetek karnych

k= 20.000/2.000.000=0,01 (czyli 1% w ciągu dwóch miesięcy)
zatem koszt w skali roku wynosi 6* 0,01 = 0,06

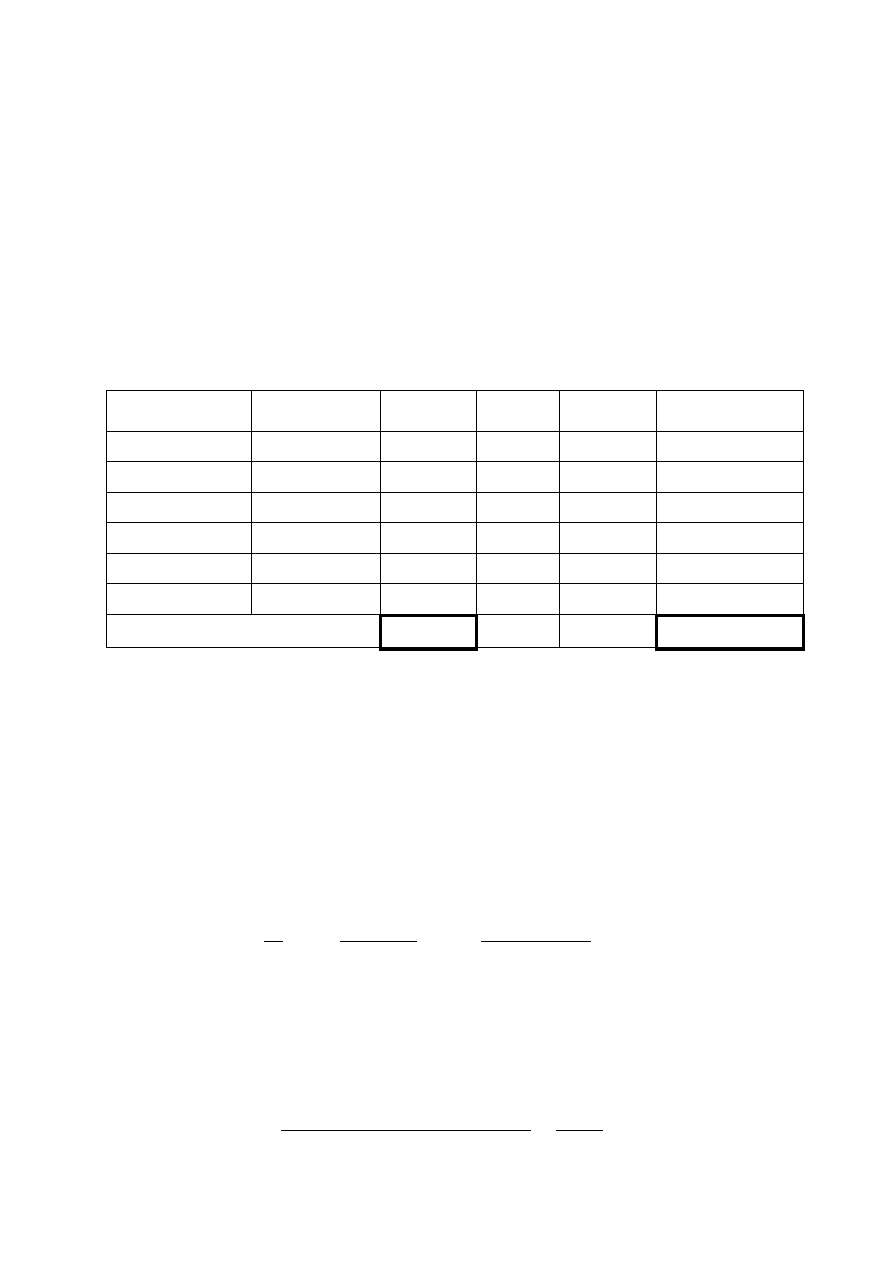
nie ma tarczy podatkowej, bo odsetki karne nie podlegają zaliczeniu jako koszt uzyskania
przychodu.

Zadanie 2
Oblicz WACC firmy wiedząc, że struktura kapitałowa wygląda następująco:

a) 30.000 akcji zwykłych na okaziciela, w obrocie giełdowym, o wartości 1.000 każda
b) 5.000 imiennych akcji uprzywilejowanych, dających prawo do dwóch głosów na jedną akcję o

wartości 1.500 każda

c) 3.000 akcji uprzywilejowanych, z dywidendą która co roku wzrasta o 3%. Ostatnia dywidenda

wyniosła 200 PLN, a rynkowa wartość akcji uprzywilejowanej kształtuje się na poziomie 1.500.

d) Rezerwy w wysokości 7.500.000
e) Kredyt bankowy 15.000.000 oprocentowany na 10%
f) Zobowiązania z tytułu dostaw i usług w wysokości 12.000.000 PLN (dostawcy udzielają rabatu

1/7net 21)

Współczynnik β wynosi 2,5. Średnia rentowność WIG wynosi 11% , a oprocentowanie bonów
skarbowych 5%.

Rodzaj kapitału

Obliczenia

Wartość

Udział %

Koszt

kapitału

Udział%*koszt

kapitału

Akcje zwykłe

30.000*1.000

30m

40,00%

0,2

0,0800

Akcje uprzywil. 1

5.000*1.500

7,5m

10,00%

0,2

0,0200

Akcje uprzywil. 2

3.000*1.000

3m

4,00%

0,1673

0,0067

Rezerwy

7,5m

10,00%

0,2

0,0200

Kredyt bankowy

15m

20,00%

0,081

0,0162

Kredyt kupiecki

12m

16,00%

0,2426

0,0388

RAZEM:

75m

100,00%

WACC:

0,1817

a) Korzystamy z SML

k=r

f

+β(r

m

-r

f

)

k=0,05+2,5(0,11-0,05) = 0,2

b) Akcje są uprzywilejowane co do głosu a nie co do dywidendy więc traktujemy je jak

akcje zwykłe

c) Korzystamy z modelu rosnącej dywidendy

𝑘 =

𝐷

1

𝑃

+ 𝑔 =

𝐷

0

(1 + 𝑔)

𝑃

+ 𝑔 =

200(1 + 0,03)

1.500

+ 0,03 = 0,167(3)

d) Rezerwy wyceniamy tak jak kapitał akcyjny zwykły = 0,2

e) Kredyt bankowy k=r(1-T) = 0,10*(1-0,19)=0,081

f) Musimy oszacować koszt utracenia rabatu

𝑎 =

365

𝑜𝑘𝑟𝑒𝑠 𝑜𝑑𝑟𝑜𝑐𝑧𝑒𝑛𝑖𝑎 − 𝑜𝑘𝑟𝑒𝑠 𝑢𝑝𝑢𝑠𝑡𝑢

=

365

21 − 7

= 26,07

𝑘

𝑛

=

𝑢𝑝𝑢𝑠𝑡

1 − 𝑢𝑝𝑢𝑠𝑡

∗ 𝑎 =

0,01

1 − 0,01

∗ 26,07 = 0,263(3)

𝑘

𝑒

= (1 +

𝑘

𝑛

𝑎

)

𝑎

− 1 = 0,2995

𝑘 = 𝑘

𝑒

(1 − 𝑇) = 0,2995(1 − 0,19) = 0,2426

Zadanie 3
Oblicz WACC firmy wiedząc, że struktura kapitałowa wygląda następująco:

a) 10.000 akcji zwykłych na okaziciela o wartości 1.000 każda. (Beta=1,7)
b) 2.000 akcji uprzywilejowanych o wartości 2.000. Ostatnia dywidenda wyniosła 200 PLN, a

poprzednia 196 PLN

c) Rezerwy w łącznej wielkości 6.000.000 PLN
d) Trzyletnie obligacje nowej emisji (w cenie emisyjnej równej cenie nominalnej) o łącznej wartości

4.000.000, których oprocentowanie wynosi 15% rocznie

e) 10.000 szt. obligacji dwuletnich o łącznej wartości księgowej 4.000.000 PLN. Oprocentowanie

wynosi 10%p.a. Ostatnia płatność odsetek miała miejsce pół roku temu. Jedną obligację można
kupić na rynku za 425 PLN. W poprzednim roku obligacje były o 12 punktów procentowych
mniej rentowne niż akcje zwykłe spółki.

f) Zobowiązania z tytułu dostaw i usług w wysokości 12.000.000 PLN (dostawcy nie udzielają

rabatu w przypadku wcześniejszej płatności)

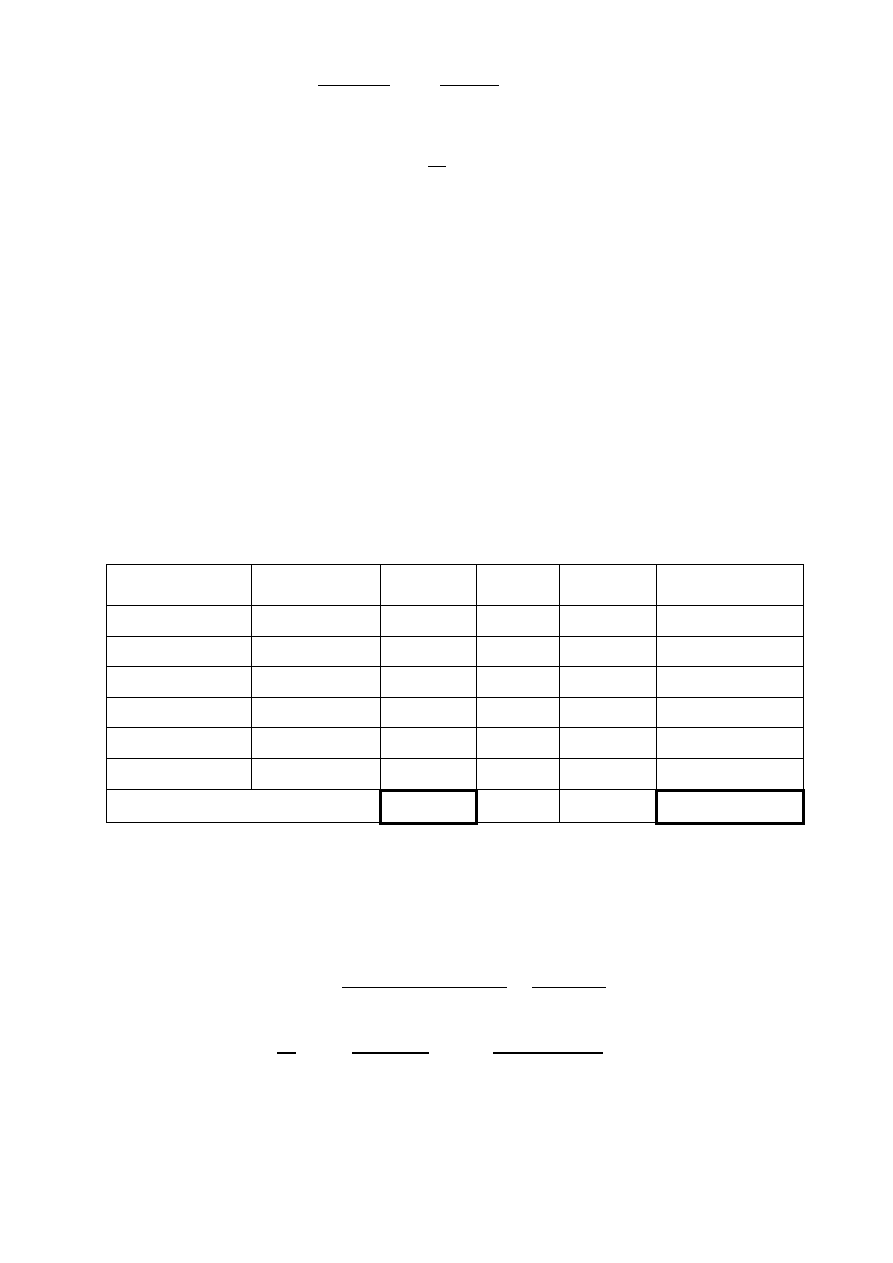
Rodzaj kapitału

Obliczenia

Wartość

Udział %

Koszt

kapitału

Udział%*koszt

kapitału

Akcje zwykłe

10.000*1.000

10m

25,00%

0,2191

0,0548

Akcje uprzywil.

2.000*2.000

4m

10,00%

0,1220

0,0122

Rezerwy

6m

15,00%

0,2191

0,0329

Obligacje (3)

4m

10,00%

0,1215

0,0122

Obligacje (2)

4m

10,00%

0,0802

0,0080

Kredyt kupiecki

12m

30,00%

0

0,0000

RAZEM:

40m

100,00%

WACC:

0,1201

a) Pomimo faktu, że podano betę w nawiasie, brakuje danych do skorzystania z modelu SML.

Interesującą jest natomiast informacja w punkcie „e”
Dlatego do tego punktu wrócimy później.

b) Skorzystamy z modelu stałego wzrostu dywidendy

Potrzebujemy „g”

𝑔 =

𝐷

𝑜𝑠𝑡𝑎𝑡𝑛𝑖𝑎

− 𝐷

𝑝𝑜𝑝𝑟𝑧𝑒𝑑𝑛𝑖𝑎

𝐷

𝑝𝑜𝑝𝑟𝑧𝑒𝑑𝑛𝑖𝑎

=

200 − 196

196

= 0,02

𝑘 =

𝐷

1

𝑃

+ 𝑔 =

𝐷

0

(1 + 𝑔)

𝑃

+ 𝑔 =

200(1 + 0,02)

2000

+ 0,02 = 0,122

c) Do tego punktu wrócimy później.
d)

Obligacje nowej emisji więc k=r(1-T) = 0,15*(1-0,19)=0,1215

e)

Obligacje „w toku”

Nominalna cena obligacji = 4.000.000/10.000=400

𝑉 = 𝑃 (1 −

𝑚

12

∗ 𝑟) = 425 (1 −

6

12

∗ 0,1) = 403,75

𝑘 =

𝐼

𝑉

(1 − 𝑇) =

0,1 ∗ 400

403,75

(1 − 0,19) = 0,0802

a) Teraz można powrócić do punktu a

Rentowność obligacji z punktu e to:

𝑟 =

𝐼

𝑉

=

0,1 ∗ 400

403,75

= 0,0991

Skorzystamy z modelu rentowność obligacji + premia, bo mamy podaną premię = 12 pp

k= bieżąca rentowność obligacji + premia za ryzyko

k= 0,0991+0,12=0,2191

c) teraz możemy wpisać wycenę dla rezerw = 0,2191

f) Brak informacji o rabatach, brak informacji o odsetkach karnych więc wpisujemy 0