Przechodzenie sygnałów przez układ liniowy

u(t)

y(t)

w dziedzinie czasu

G(j

ω

ω

ω

ω)

u(t)
R

uu

(

τ

)

S

u

(

ω

)

y(t)
R

yu

(

τ

)

S

y

(

ω

)

w dziedzinie czasu

i w dziedzinie częstotliwości

Związki w dziedzinie czasowej

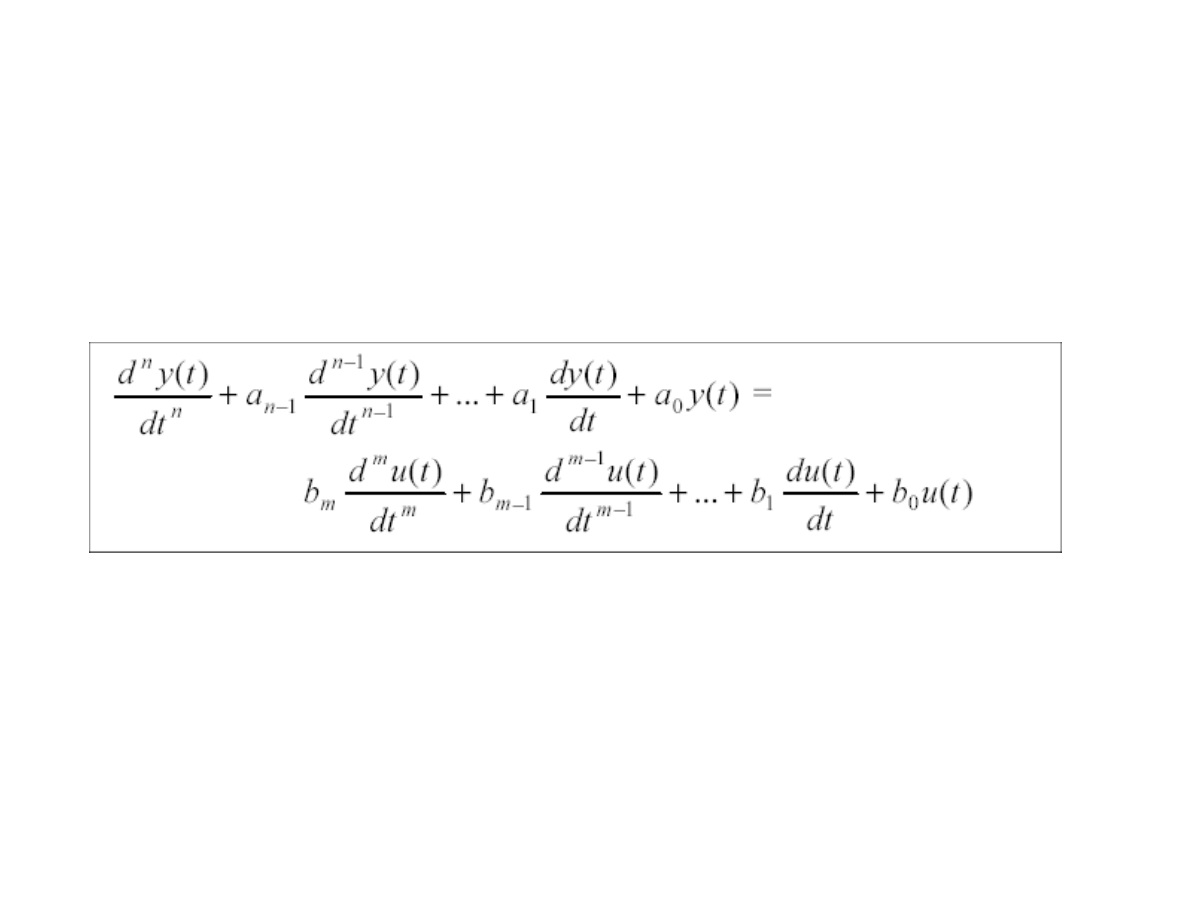
Równanie różniczkowe opisujące układ liniowy (model liniowy o stałych
skupionych) o wejściu u(t) i wyjściu y(t) ma postać

(1)

a

n

Rząd równania n będącego modelem rzeczywistego układu
musi spełniać warunek n

≥

m, wynikający z ograniczeń energetycznych.

Transmitancja układu ma postać

b

m

s

m

+ b

n-1

s

(n-1)

+ …+ b

1

s + b

0

a

n

s

n

+ a

n-1

s

(n-1)

+ … + a

1

s + a

0

G(s) = —————————————— ,

(2)

a wyjście y(t) z układu na wymuszenie u(t), przy zerowych warunkach
Początkowych wyznacza się z zależności

)}

(

)

(

{

)

(

1

s

U

s

G

L

t

y

−

=

. (3)

Odpowiedzią impulsową nazywamy wynik

{

}

,

)

(

)

(

1

s

G

L

t

g

−

=

(4)

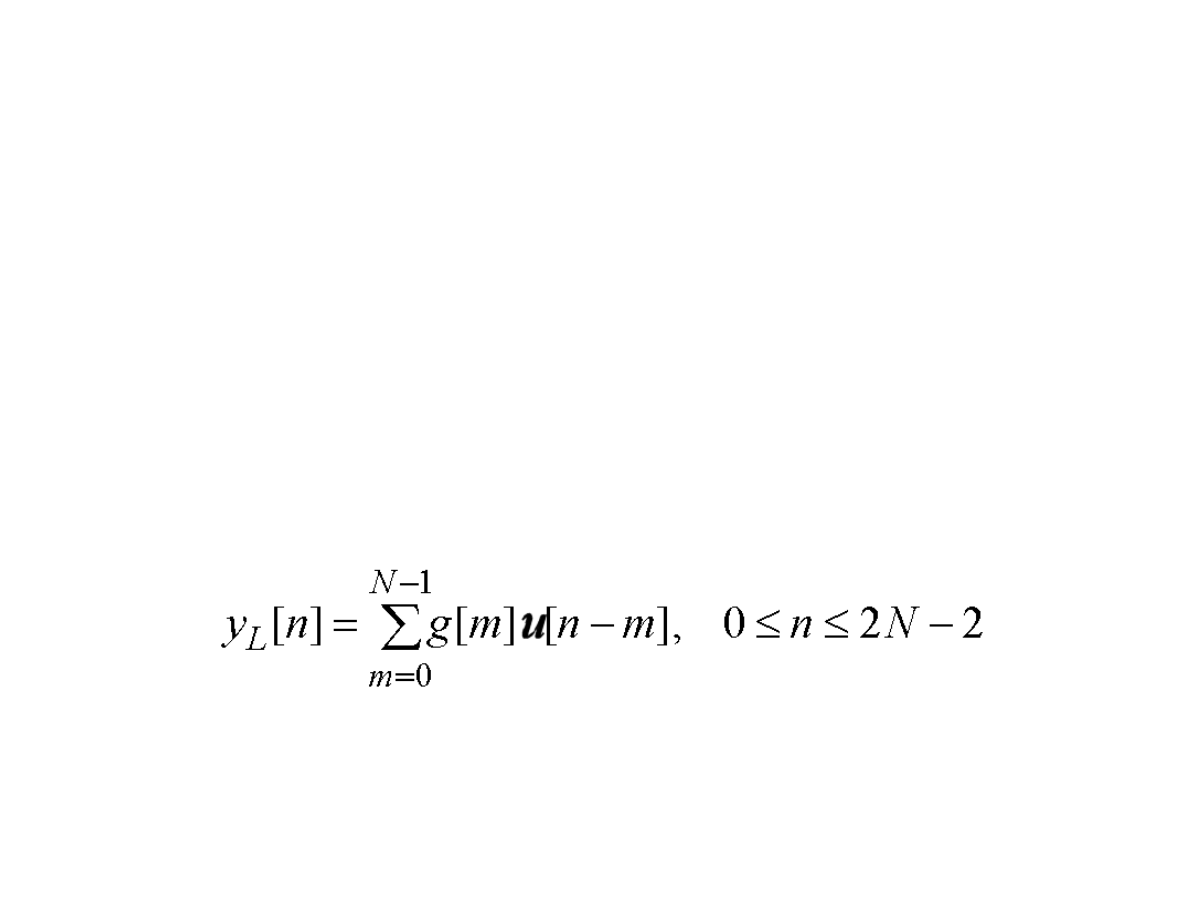
Wejście u(t) i wyjście y(t) wiąże równanie splotowe, wykorzystujące
w splocie funkcję odpowiedzi impulsowej

y(t) = g(

τ

)u(t-

τ

)d

τ

= u(

τ

) g(t-

τ

)d

τ

(5)

∫

0

t

∫

0

t

Dyskretny splot liniowy y

L

(n) skończonych ciągów g(n) i u(n)

o długościach N próbek ma postać

(6)

Długość splotu liniowego to L= 2N - 1

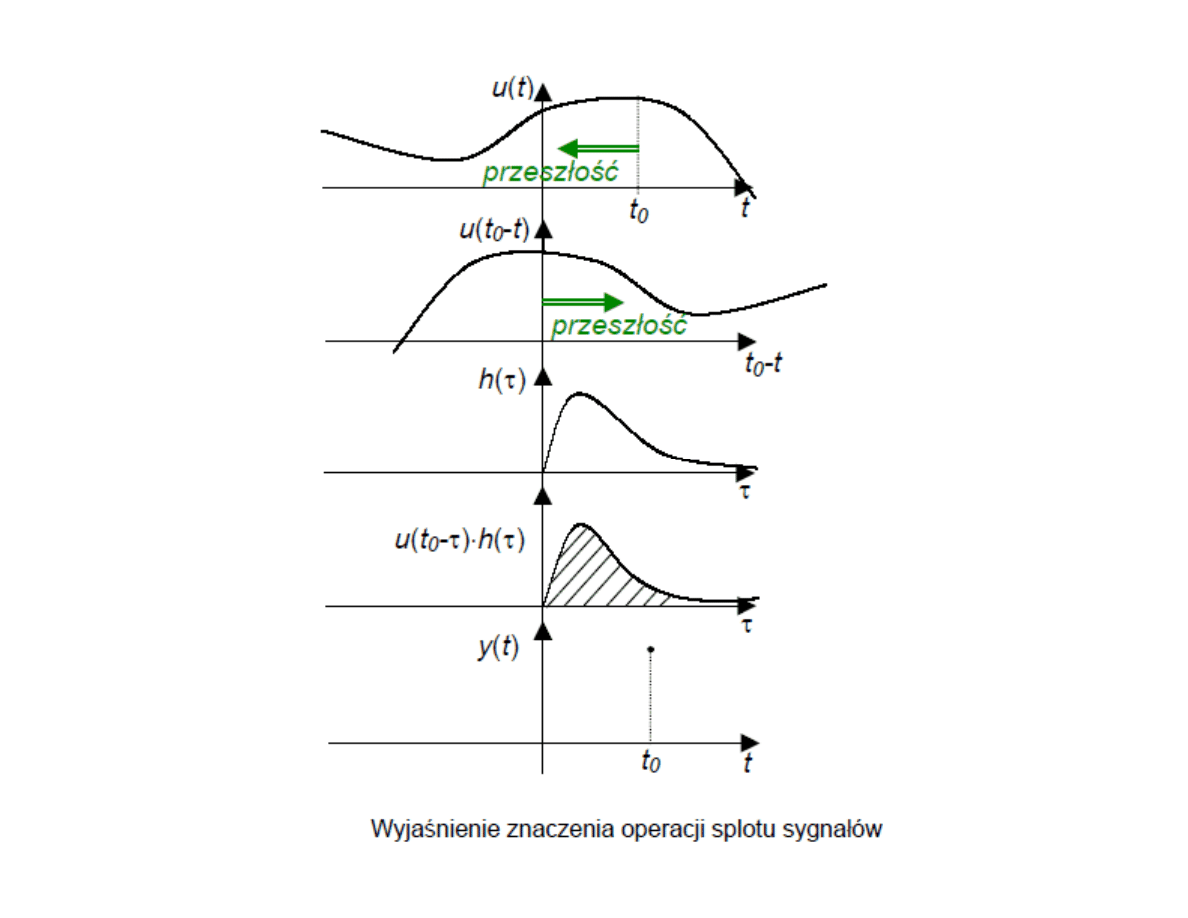
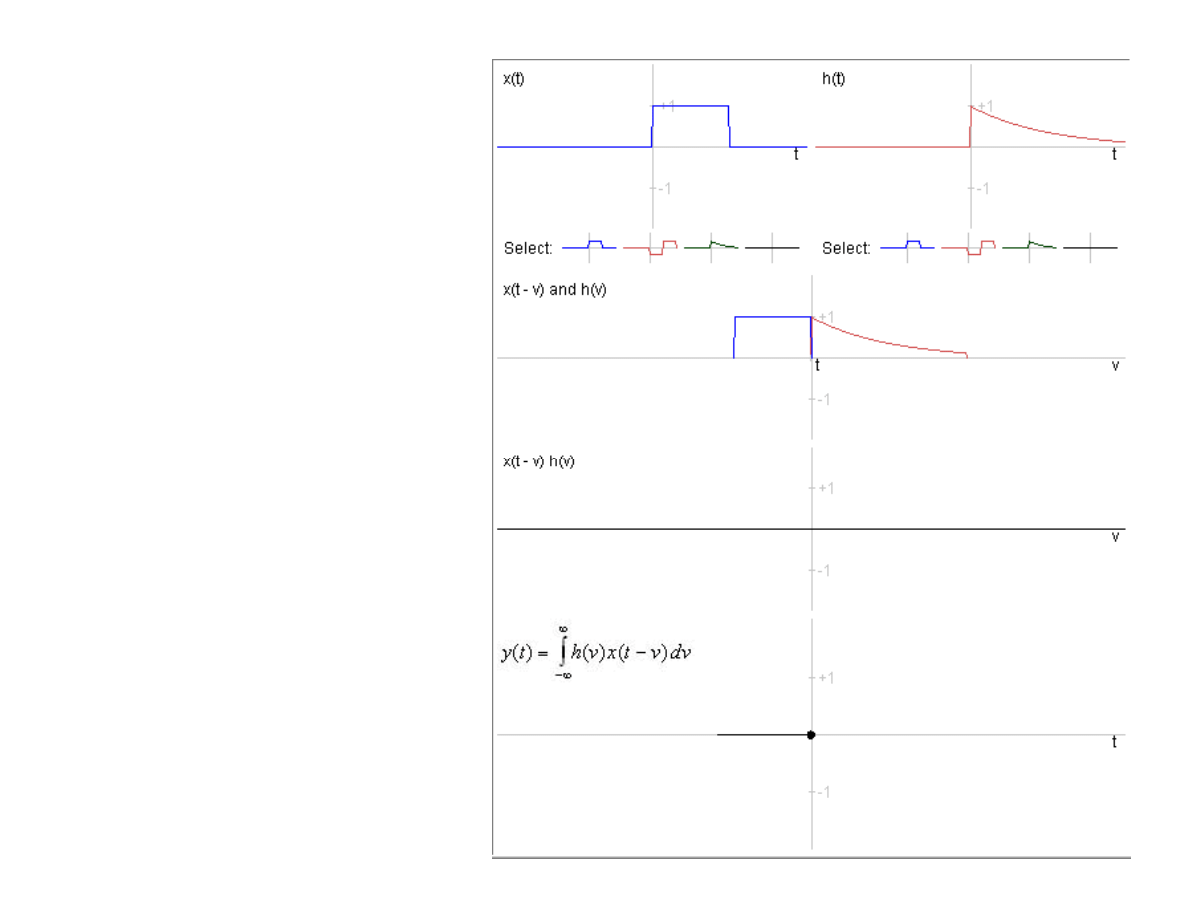
Interpretacja

geometryczna

splotu liniowego

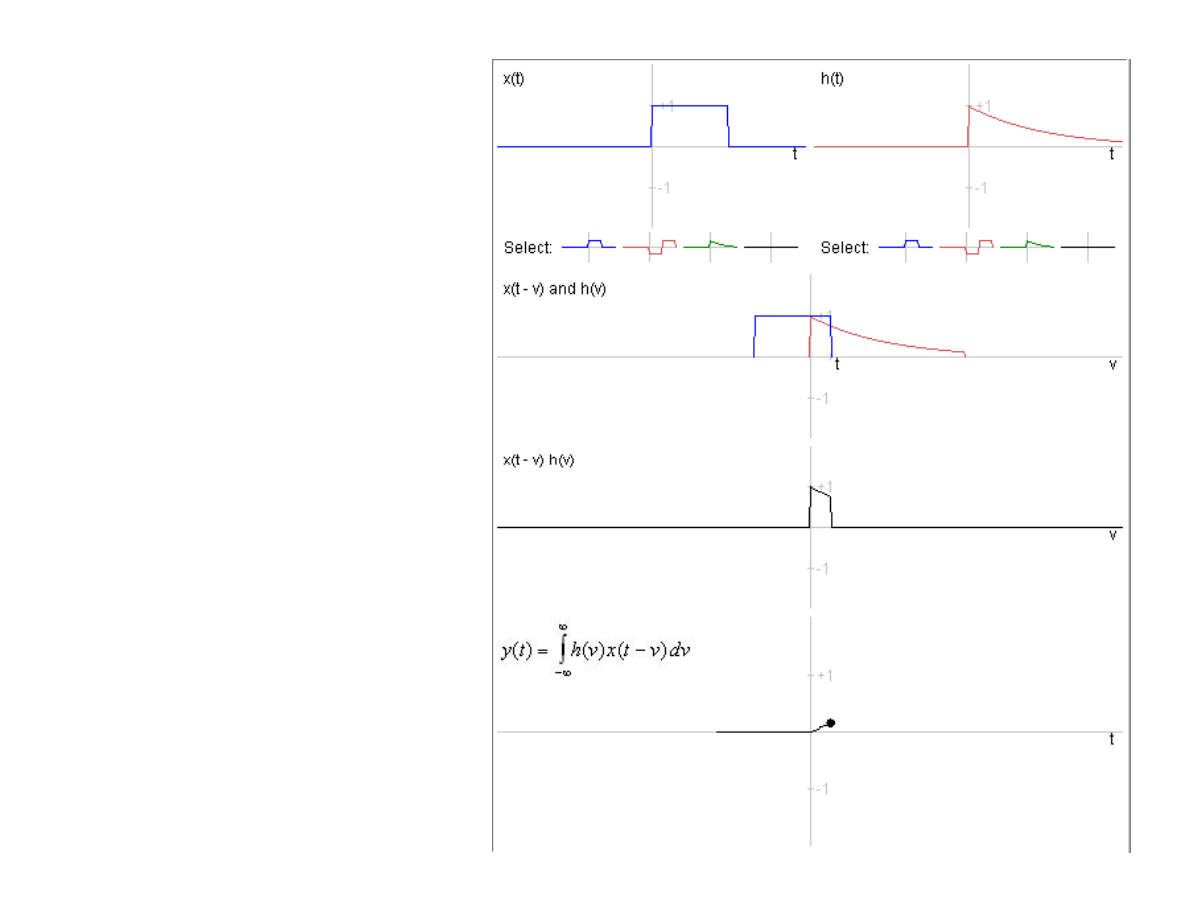
Interpretacja

geometryczna

splotu liniowego

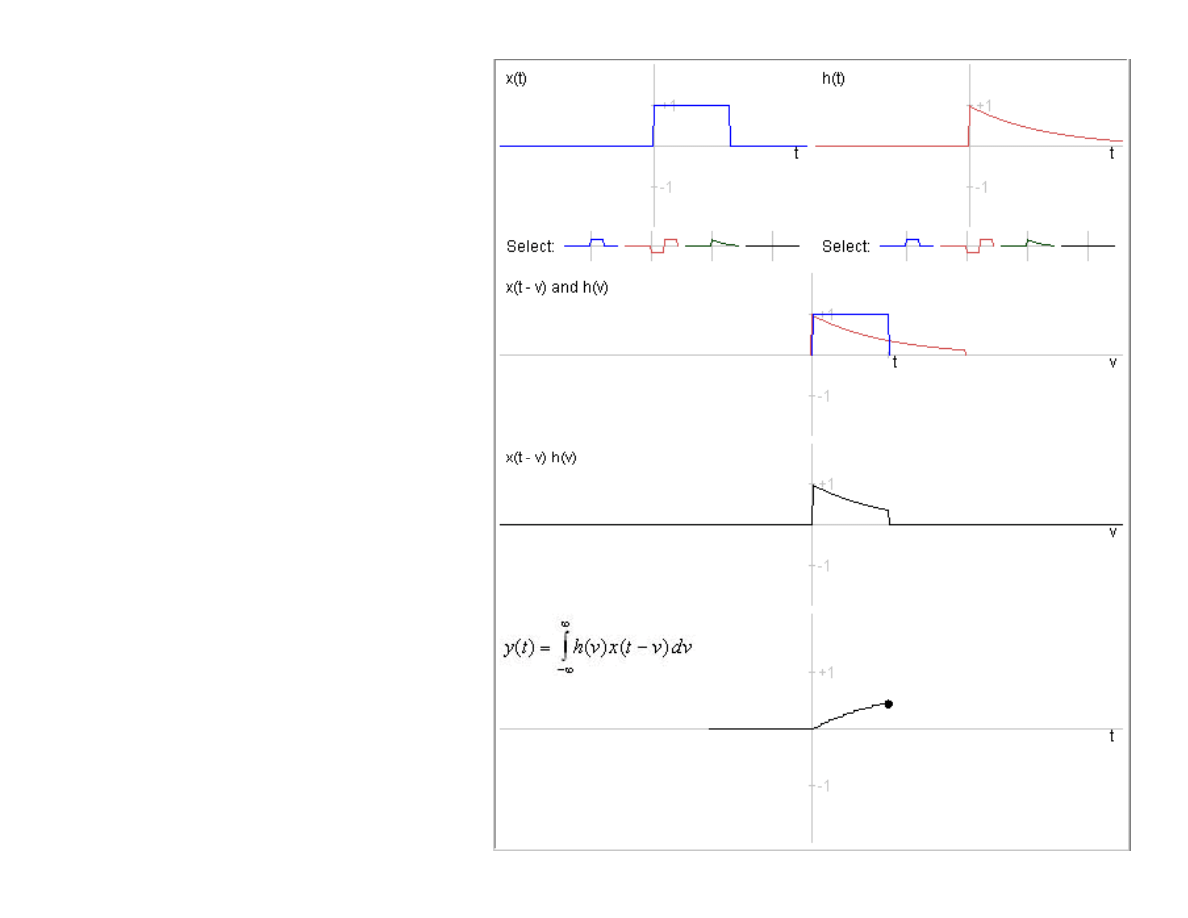
Interpretacja

geometryczna

splotu liniowego

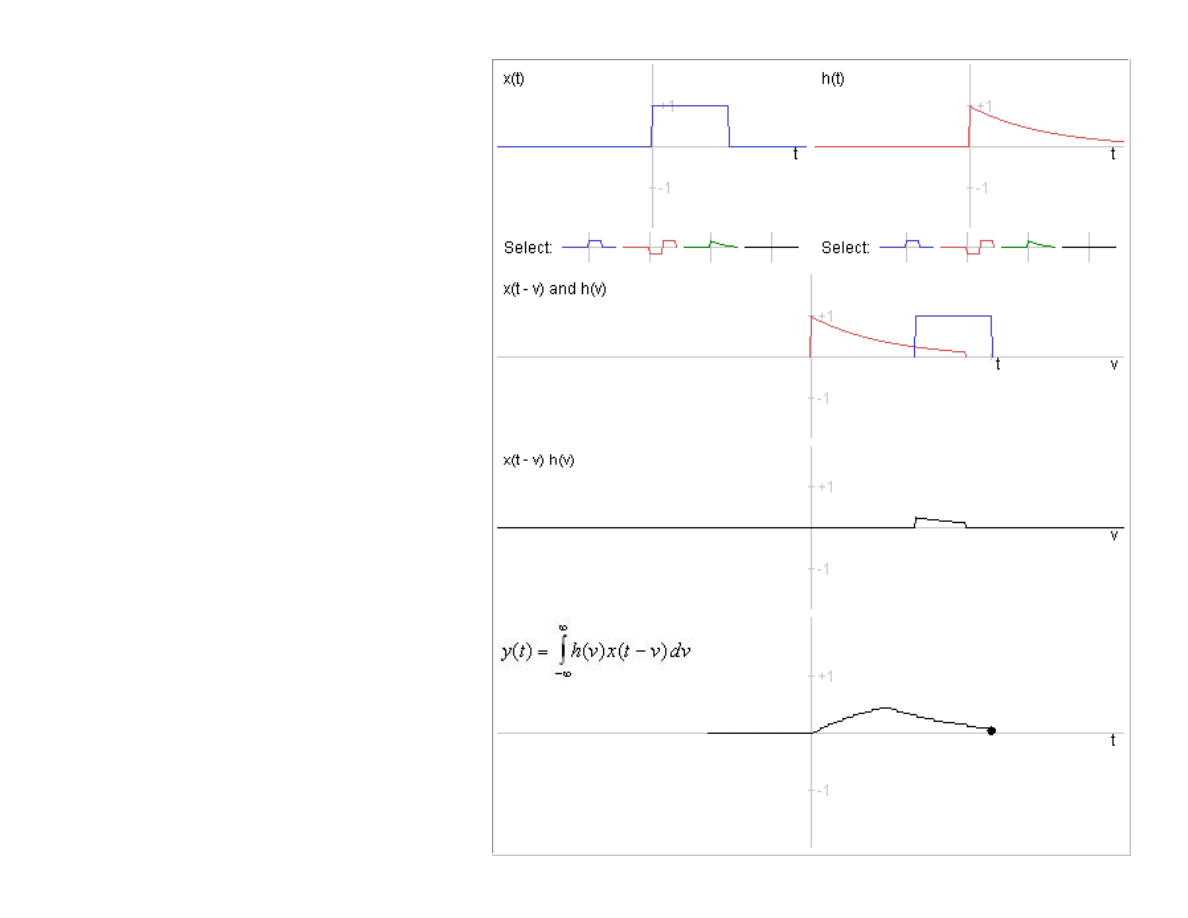
Interpretacja

geometryczna

splotu liniowego

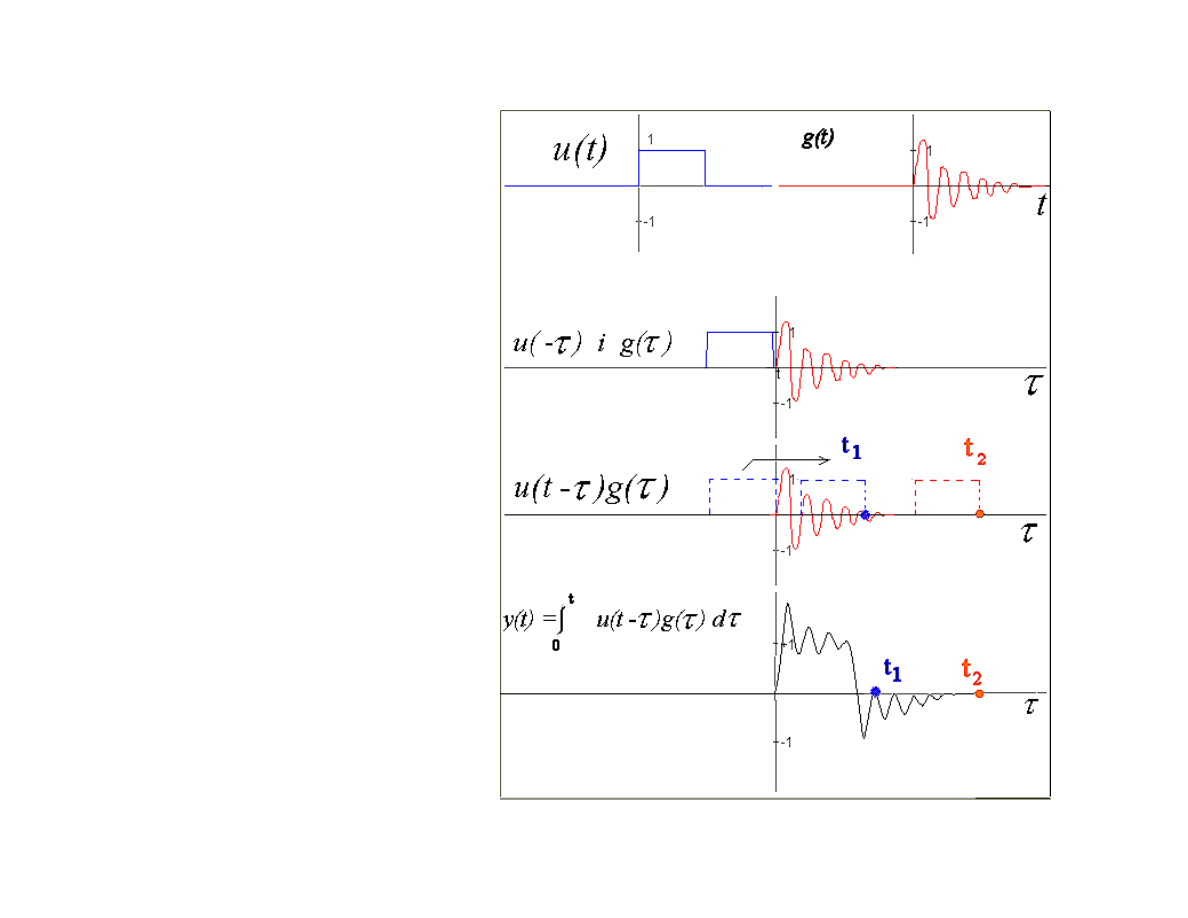
Interpretacja

geometryczna

splotu liniowego

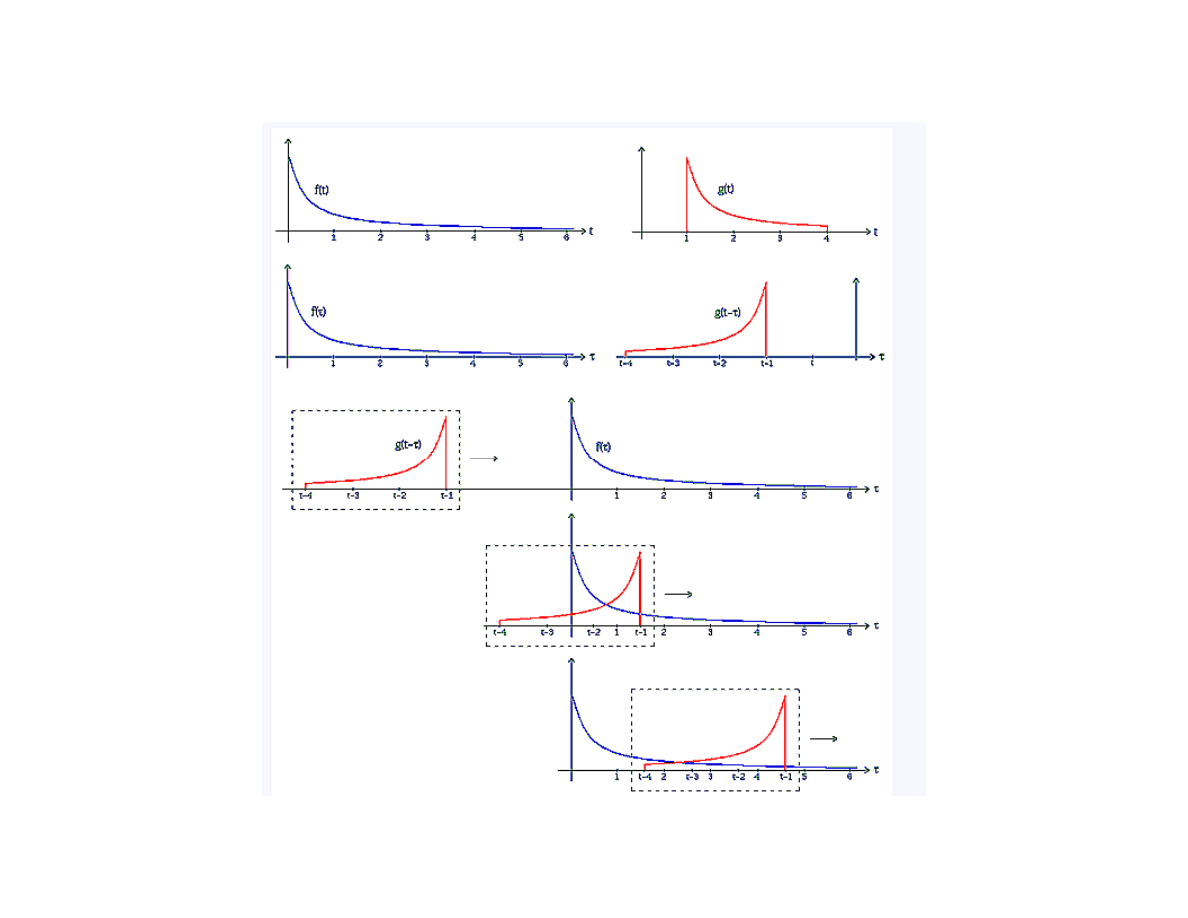
Odwracać możemy też odpowiedź impulsową – przemienność splotu

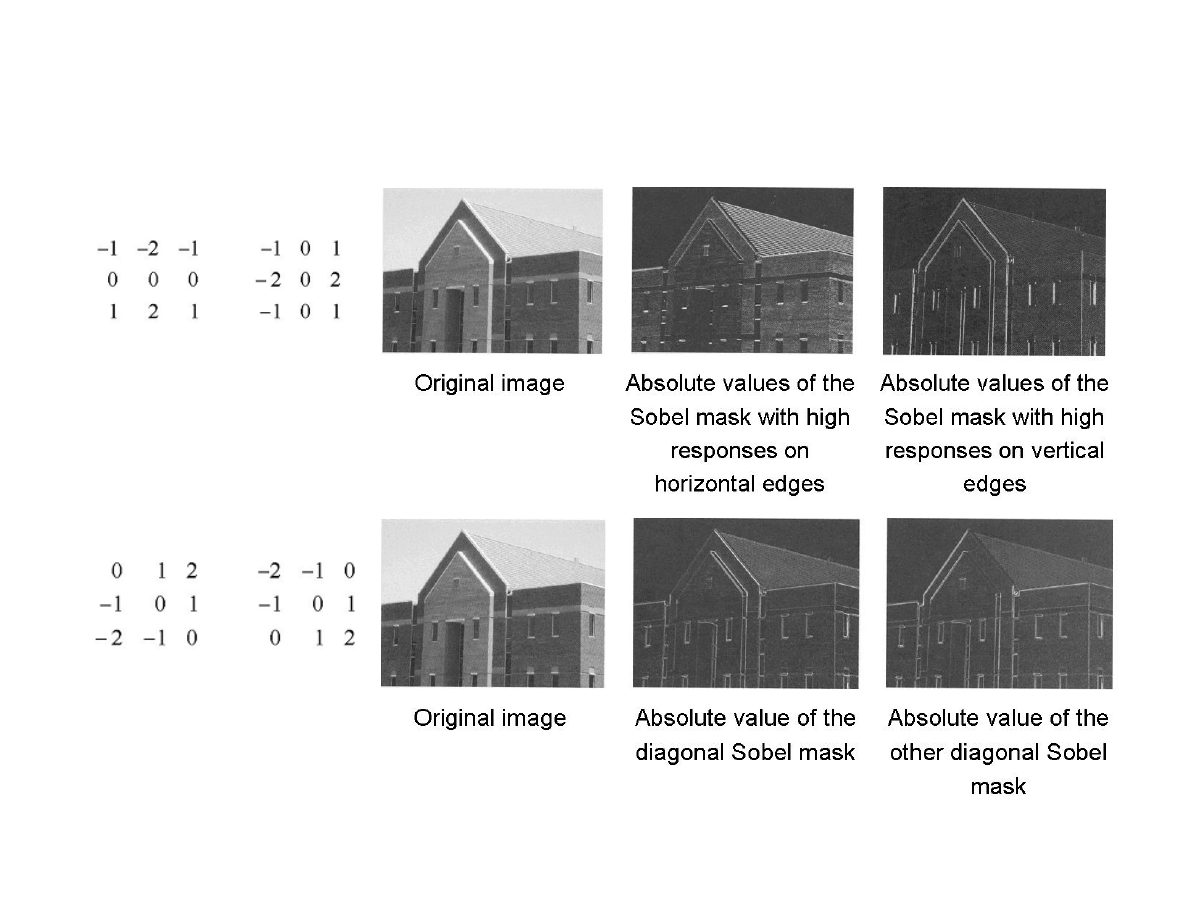
Splot dwuwymiarowy – przetwarzanie obrazów

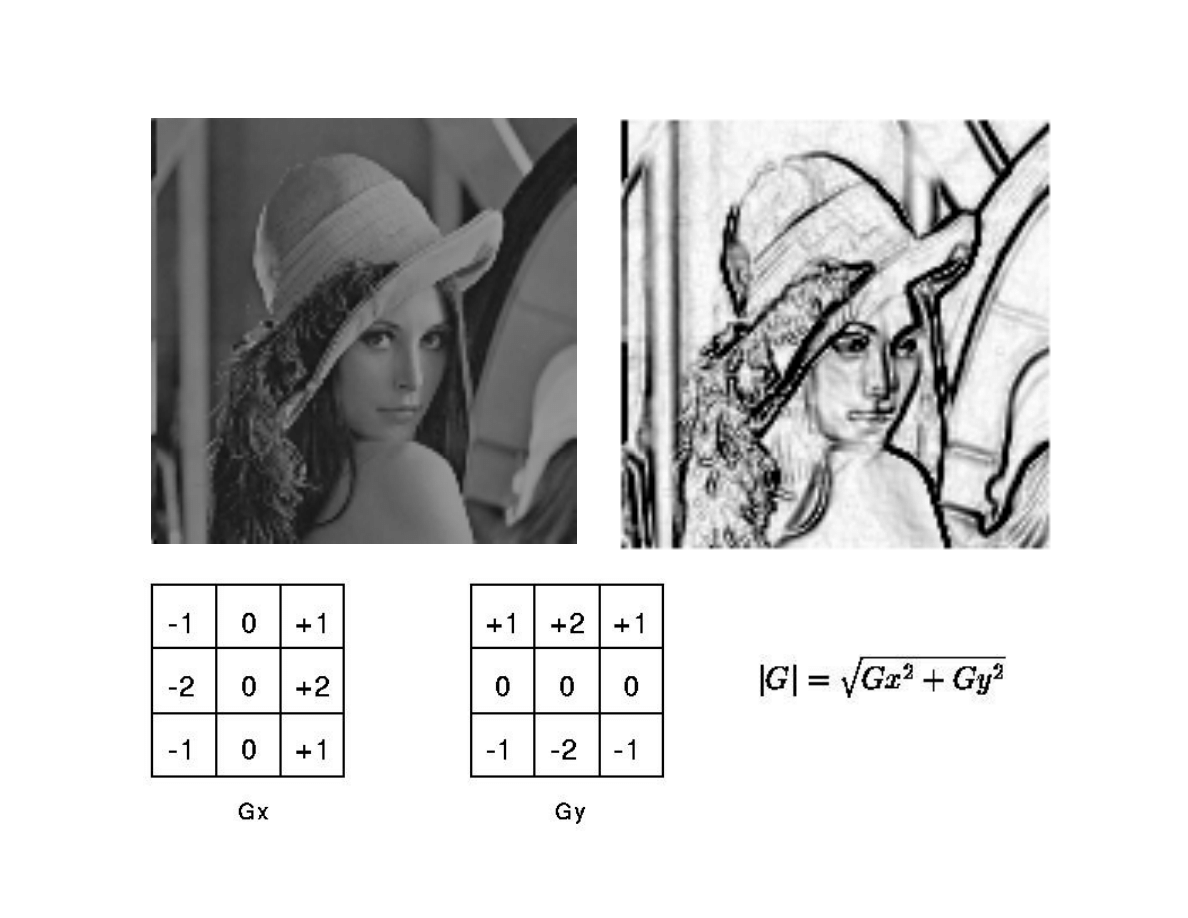
Negatyw gradientu

Odpowiedź impulsowa a funkcje korelacji

R

UU

(

τ

) = E[u(t +

τ

)u(t)] = E[u(t)u(t -

τ

)]

R

YU

(

τ

) = E[y(t +

τ

)u(t)] = E[y(t)u(t -

τ

)]

Skoro

(9)

(10)

y(t)= u(t)

∗g(t)

(11)

to

R

YU

(

τ

) = E{[u(t)

∗g(t)]u(t -

τ

)} = g

(τ)

∗E[u(t)u(t -

τ

)] ,

R

YU

(

τ

) = R

UU

(

τ

)

∗ g

(

τ

)

(12)

Równanie (12) nosi nazwę

Wienera-Hopfa.

R

yu

(

τ

)=

∫

y(t)u(t-

τ

)dt

Jeśli bowiem przyjąć, że estymaty funkcji korelacji, to

T

→ ∞

(dokładniej lim 1/2T

∫

zamiast symbolu

∫

) i licząc całki

∫

w granicach (-

∞, ∞), otrzymamy (12)

-T

T

R

yu

(

τ

)=

∫ ∫

g(

λ

)u(t-

λ

)d

λ

u(t-

τ

)dt =

∫

g(

λ

)

∫

u(t-

λ

)u(t-

τ

)dt d

λ

=

∫

g(

λ

)R

uu

(

τ

-

λ

)d

λ

= g

(τ)

∗ R

uu

(

τ

)

Dla funkcji autokorelacji uważanej jako pobudzenie układu o odpowiedzi
impulsowej g(t) i funkcji korelacji wzajemnej sygnału wyjściowego z układu
z sygnałem wejściowym, obowiązuje analogiczna zależność splotowa (11)
jak dla samych sygnałów y(t) i u(t) .

W przypadku, gdy na wyjściu układu sumuje się szum n(t), nieskorelowany
z wejściem układu, zależność (11) również pozostaje w mocy, gdyż

E{[y(t)+n(t)]u(t-

τ

)} = E[y(t)u(t-

τ

)] + E[n(t)u(t-

τ

)] = R

yu

(τ

)

,

0

co pozwala na stosowanie równania równania Wienera-Hopfa do
wyznaczania estymaty odpowiedzi impulsowej w przypadku występowania
zakłóceń. Ponadto, przy pobudzeniu układu szumem białym, którego
autokorelacja ma postać

R

uu

(τ

)

= σ

u

2

δ(τ)

,

(13)

otrzymujemy z (12)

R

yu

(

τ

) = g

(

τ

) .

Norbert Wiener

(1894 – 1964)

matematyk amerykański,

twórca cybernetyki

Heinz Hopf

(1894 – 1971)

matematyk szwajcarski,

(poch. niemieckie, żydowskie,
ur. w Grabiszynie / Wrocław)

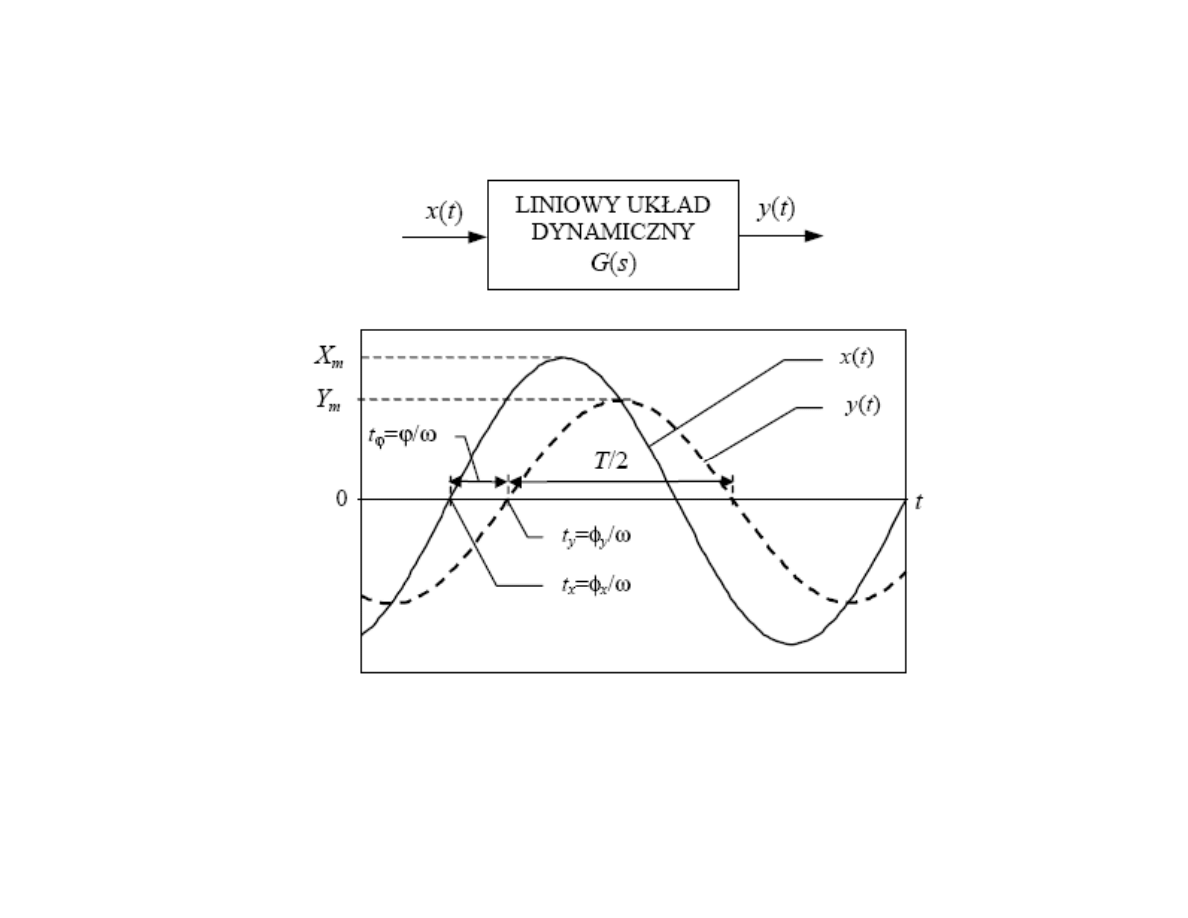
Związki w dziedzinie częstotliwości

Odpowiedź liniowego układu stacjonarnego na wymuszenie

u(t) = U sin (ωt) jest w stanie ustalonym wielkością sinusoidalną

Wprowadzając oznaczenia

).

sin(

)

(

ϕ

ω

+

=

t

Y

t

y

Transmitancję widmową można wyrazić następująco:

,

)

(

)

(

ϕ

ω

ω

j

Ye

j

Y

U

j

U

=

=

),

(

)

(

)

(

)

(

)

(

)

(

ω

ω

ω

ω

ω

ω

ϕ

ϕ

jQ

P

e

j

G

U

Ye

j

U

j

Y

j

G

j

j

+

=

=

=

=

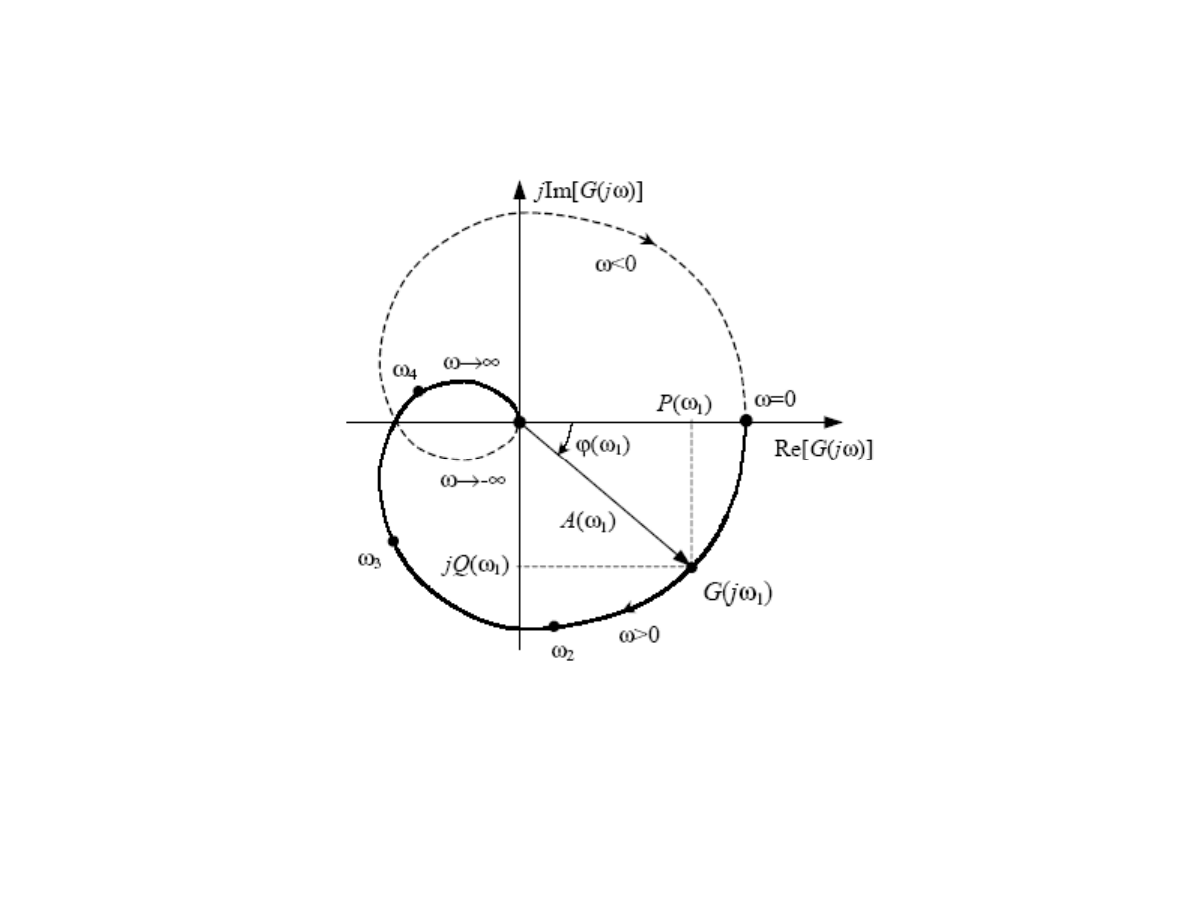
P(

ω

)

jQ(

ω

)

Charakterystyka amplitudowo-fazowa na płaszczyźnie zmiennej zespolonej

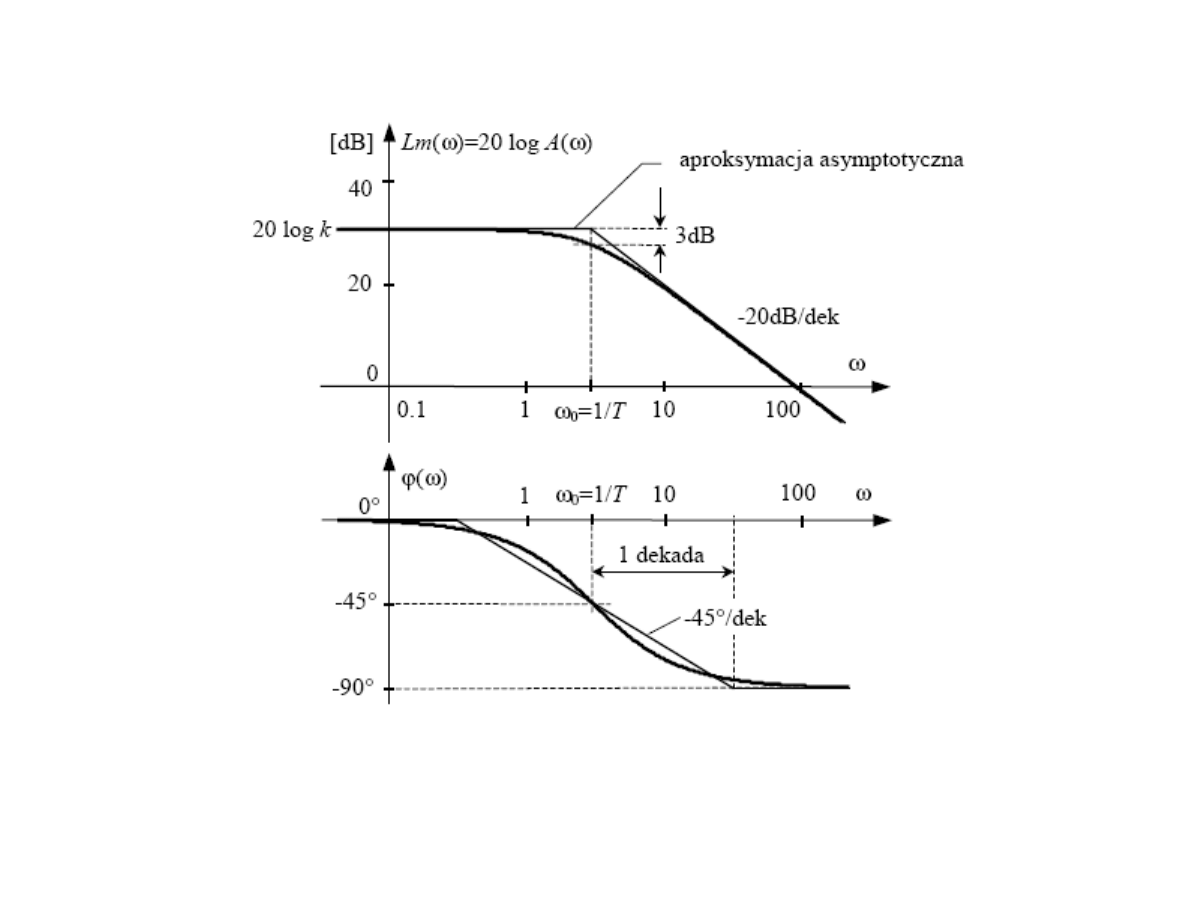
Charakterystyki Bodego

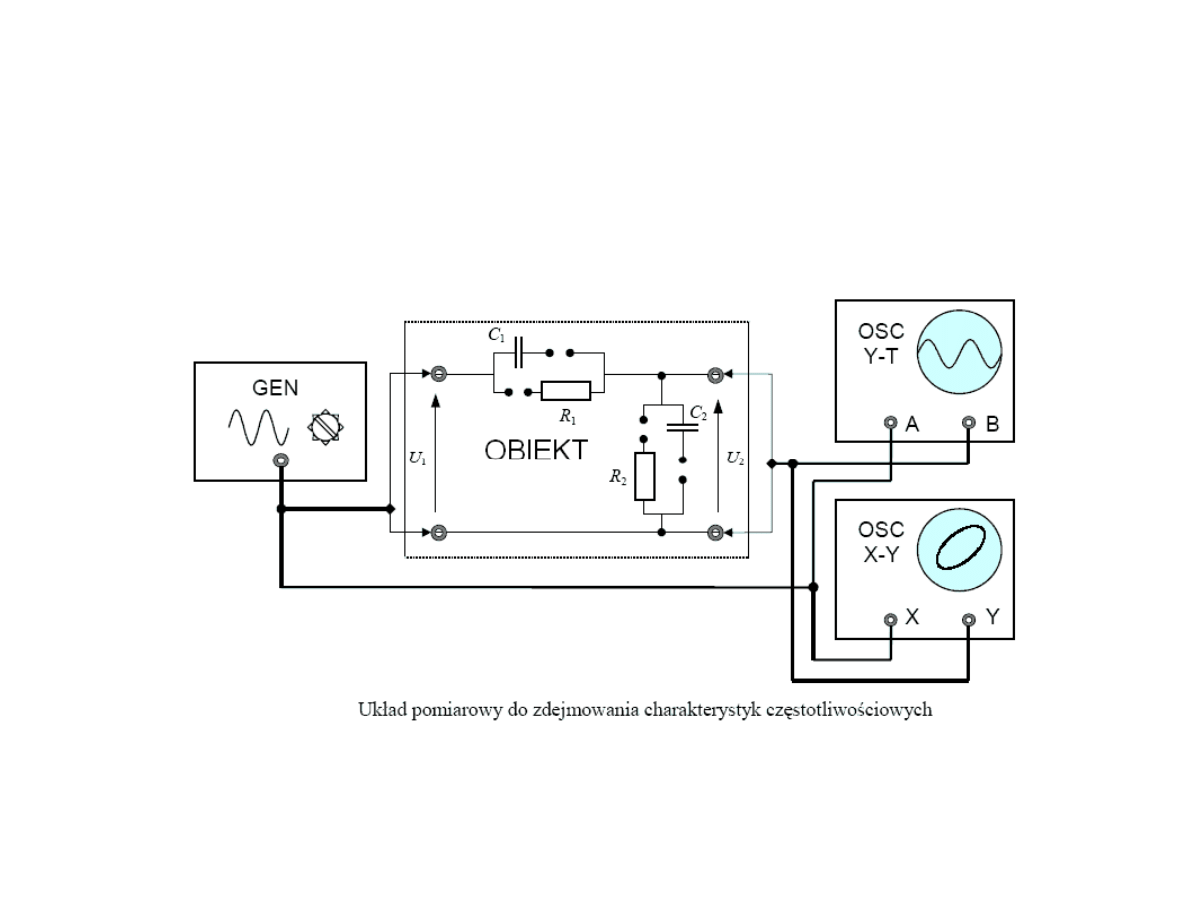
Pomiar charakterystyki amplitudowo-fazowej

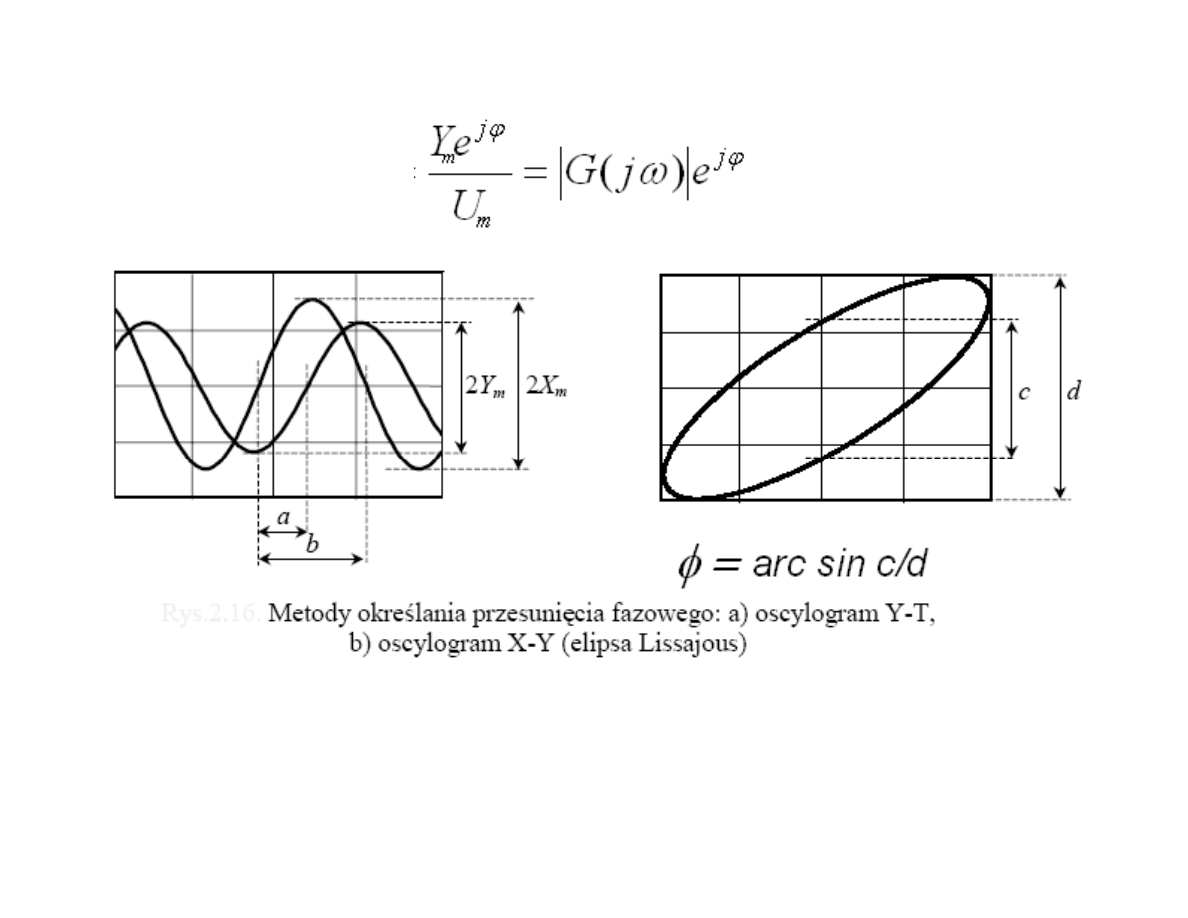
Generator

sin (

ω

0

t)

cos (

ω

0

t)

××××

××××

Obiekt

|G ( j

ω

0

) | sin (ω

0

t +

φ)

Dla czasów uśredniania T

>

>

T

0

zachodzi

~P(

ω

0

)

~Q(

ω

0

)

∫

∫

1/T

1/T

0

0

T

T

•

dt

•

dt

|G(j

ω

0

)|sin(

ω

0

t)sin(

ω

0

t+

φ

)dt = |G(j

ω

0

)| (cos(

φ

) – cos(2

ω

0

t+

φ

)dt

≈≈≈≈

Dla czasów uśredniania T

>

>

T

0

zachodzi

∫

1/T

∫

0

0

T

T

½ |G(j

ω

0

)| (cos(

φ

) ~

2T

__

1

Re[G(j

ω

)] = P(

ω

0

)

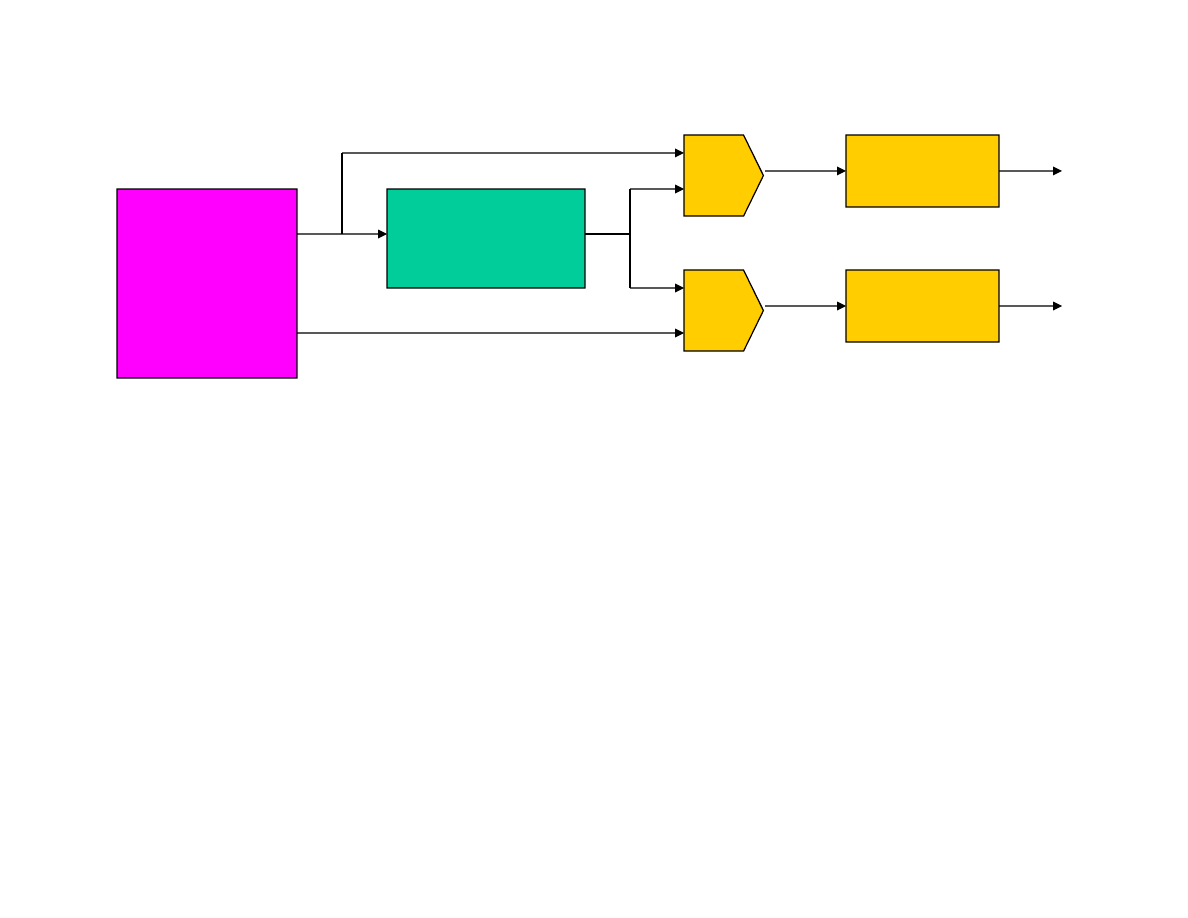
Schemat blokowy analizatora widmowego do pomiaru G(j

ω

) = P(

ω

)+jQ(

ω

)

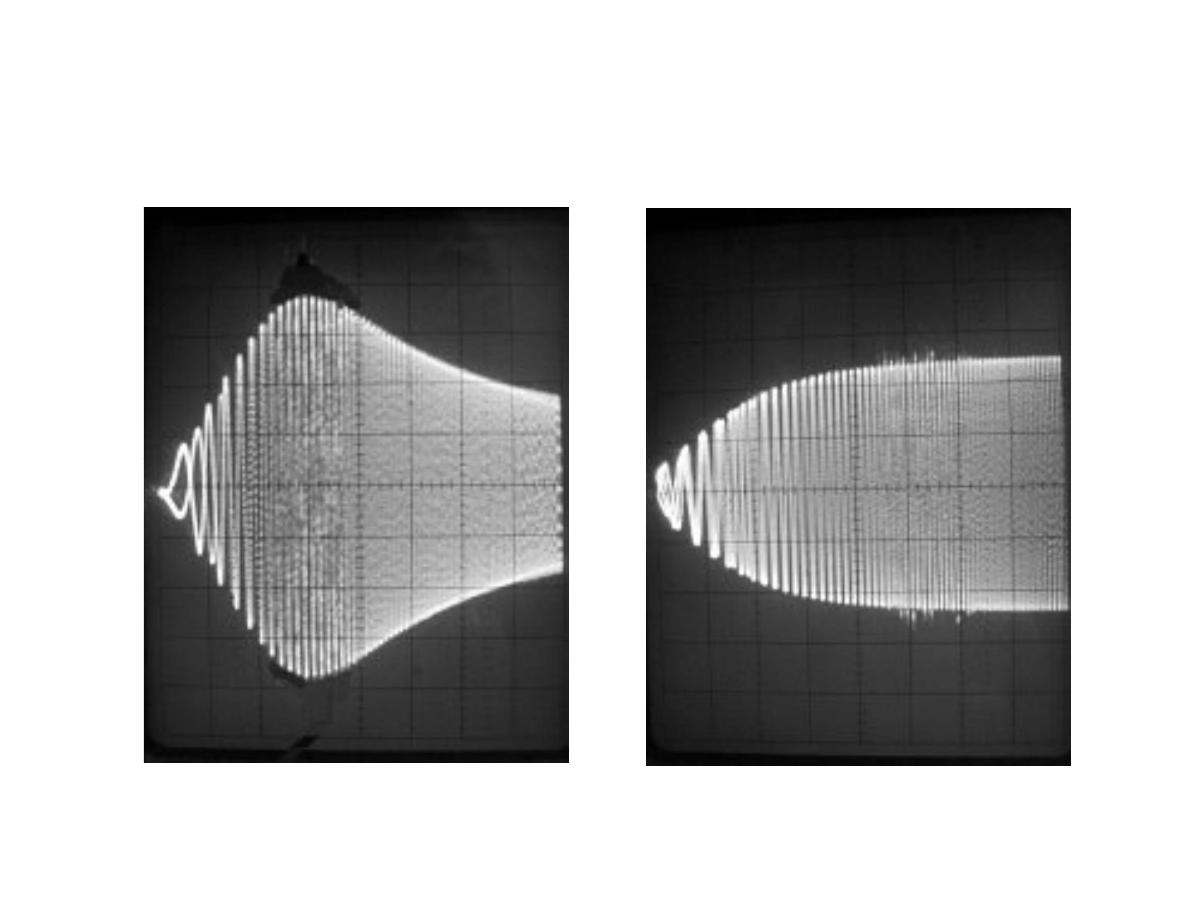
Pomiar charakterystyki amplitudowej

Filtr środkowoprzepustowy

Filtr górnoprzepustowy

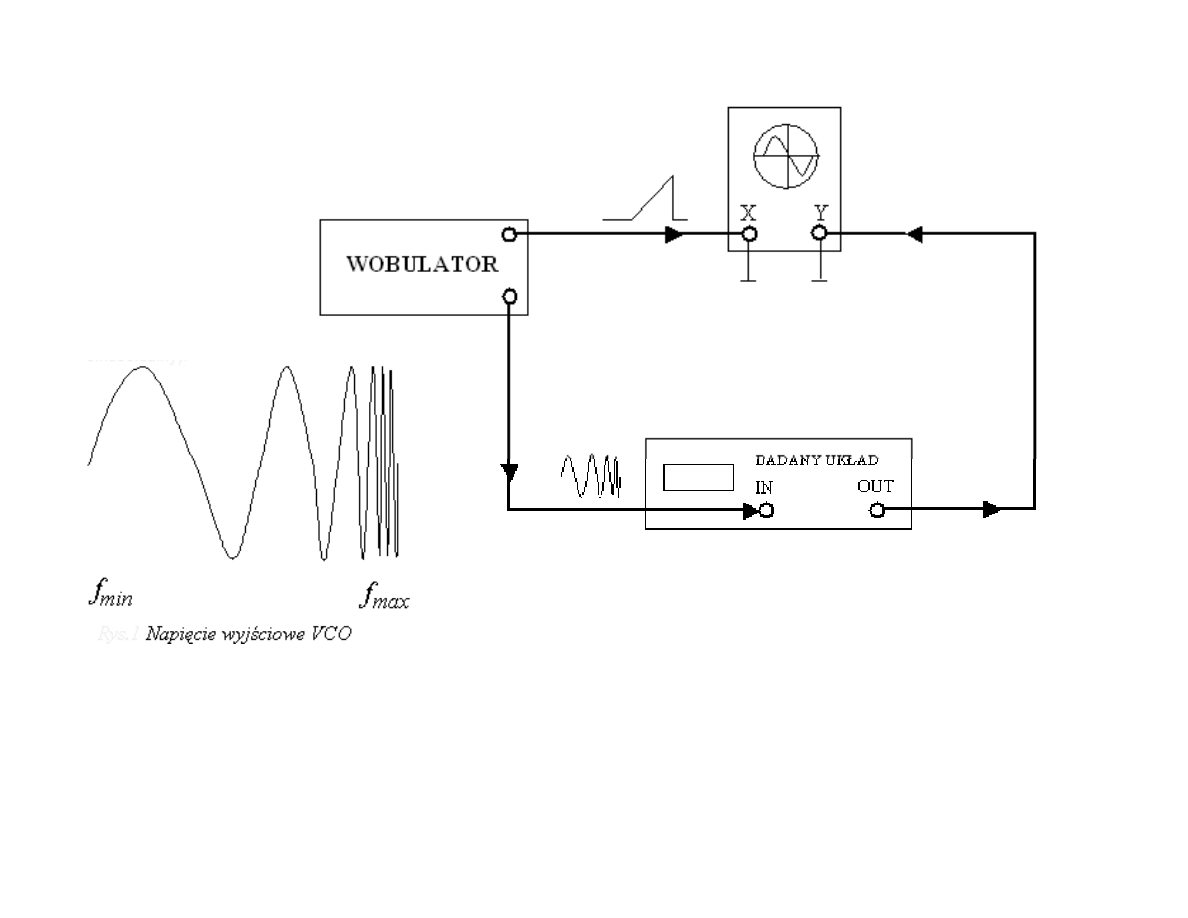
Schemat blokowy wobuloskopu do wyznaczania charakterystyki amplitudowej

VCO - Voltage Controlled Oscillator

Związki pomiędzy gęstościami widmowymi mocy

Transformata Fouriera estymaty funkcji korelacji wynosi

F[R

xx

(

τ

)] =

∫

lim

∫

x(t)x(t-

τ

)dt e d

τ

=

lim

∫

x(t) e dt

∫

x(t-

τ

) e d

τ

= lim X(j

ω

)X*(j

ω

) .

-j

ωτ

(14)

-T

T

-

∞

∞

1

__

2T

-j

ω

t

2T

__

1

T

→ ∞

T

→ ∞

-

∞

-

∞

∞

j

ω

(t-

τ

)

2T

1

__

T

→ ∞

∞

Ostatnie wyrażenie w (14) nazywamy

gęstością widmową mocy

S

x

(

ω

) = lim

X(j

ω

)



2

i jest ona również definiowana jako transformata Fouriera funkcji korelacji.

-

∞

-

∞

1

2T

__

T

→ ∞

(15)

def

Kwadrat modułu widma sygnału

X(j

ω

)



2

nazywamy

widmem energii.

F

–1

[S

x

(

ω

)] =

∫

S

x

(

ω

)e d

ω

= R

xx

(

τ

)

Ze wzoru na odwrotną transformatę Fouriera z gęstości S

x

(

ω

)

1

__
2

π

j

ωτ

∞

-

∞

i dla

τ = 0 otrzymujemy

∫

S (

ω

)d

ω

= R (0) = E[x

2

],

(16)

2

π

__

1

∞

a ponieważ wzór (16) oznacza moc sygnału x(t) ,stąd nazwa wielkości S

x

.

∫

S

x

(

ω

)d

ω

= R

x

(0) = E[x

2

],

(16)

2

π

-

∞

Gęstość widmowa sygnału, jako transformata Fouriera funkcji parzystej
jest wielkością rzeczywistą. Jest też dla każdej częstotliwości nieujemna
(patrz(15)).

Dla sygnału u(t) podanego na układ liniowy o transmitancji G(j

ω

)

otrzymujemy na wyjściu sygnał y(t), a ich transformaty Fouriera
łączą zależności

Y(j

ω

) = G(j

ω

)U(j

ω

)

oraz

|Y(j

ω

)|

2

= |G(j

ω

)|

2

|U(j

ω

)|

2

(17)

a zatem, mając na uwadze definicję (15), gęstości widmowe obu sygnałów
wiąże zależność

S

y

(

ω

) = |G(j

ω

)|

2

S

u

(

ω

)

(18)

Twierdzenie Parsevala

( )

∞

+

∞

+

∞

+

∈

t

x

R

R

R

R

Zależność na energie sygnału x(t) dana jest wzorem

( )

( )

( )

∫

∫

∫

∞

+

∞

+

∞

−

∞

+

∞

−

=

=

=

0

2

2

2

1

2

1

ω

ω

π

ω

ω

π

d

X

d

X

dt

t

x

E