1st INTERNATIONAL CONFERENCE OF LOGISTICS
INTLOG 2006
„LOGISTICS IN GLOBAL ECONOMY – Challenges and trends”
1
CALCULATION THE MINIMAL NUMBER OF BUSES
WYZNACZANIE MINIMALNEJ LICZBY AUTOBUSÓW
Wùodzimierz Choromañski, prof. nzw. dr hab. in¿.
Politechnika Warszawska (Wydzia
ù Transportu)
Wojciech Napieraùa, mgr in¿.
Politechnika Warszawska (Wydzia
ù Transportu)
ABSTRACT
This paper shows a simulation way of calculation the minimal number of buses utilization purpose
to provide continuity of transport with given probability. For given buses utilization system and requisition
there is set time of continuity of transport, which can value empirical probability. This way of treatment is
in first and second method problem
’s solving. Third m
ethod is about analyzing weight function, which
contain two factors. First one is costs factor and second retain continuity of transport factor.
ABSTRAKT
Autobusy jak ka
¿de urz¹dzenia mog¹ w sposób losowy ulegaã uszkodzeniom. Utrata zdatnoœci
nie jest, wi
êc
zdeterminowane
i
mamy
doczynienia
z
procesem
losowym.
Parametrem
deterministycznym obok prawdopodobie
ñstwa uszkodzenia autobusu je
st resurs pojazdu oraz
zapotrzebowanie na autobusy. Resurs rozumiany jest jako warto
ϋ pracy przewoz
owej (liczonej w
przejechanych km) autobusu po wykonaniu, kt
órej kierowany jest on na prz
egl
¹d stanu technicznego.
Utraty zdatno
œci autobusów, okresowe prz
egl
¹dy stanu technicznego wynikaj¹ce z wartoœci
resurs
ów oraz koniecznoœã zachowania ci¹gùoœci zaspokojenia zapotrzebowania powoduj¹, ¿e
decydenci w przedsi
êbiorstwie stoj¹ przed problemem okreœlenia minimalnej liczby eksploatowanego
taboru, aby m
óc na zad
awalaj
¹cym poziomie zaspokoiã zapotrzebowanie komunikacyjne. Dla okreœlenia
racjonalnej, wymaganej liczby taboru wprowadza si
ê wspóùczynnik istotnoœci zachowania ci¹gùoœci
realizacji prac przewozowych, kt
óry
dopuszcza
wyst¹pienie
utraty
ci¹gùoœci
realizacj
i prac
przewozowych.
Minimalna liczba eksploatowanych autobus
ów
jest
wa¿nym
czynnikiem
okreœlaj¹cym
konkurencyjno
œã przedsiêbiorstwa na rynku. Wiêksza ich liczba w stosunku do wymagañ stawianych, o
kt
órych wspomniano wy¿ej powoduje, i¿ przedsiêbiorstwo po
nosi nadmiarowe koszty. Wyznaczanie
minimalnej liczby autobus
ów zawiera, zatem czynnik ekonomiczny, który zostaù uwzglêdniony w jednej z
metod rozwi
¹zania problemu.
id14586500 pdfMachine by Broadgun Software - a great PDF writer! - a great PDF creator! - http://www.pdfmachine.com http://www.broadgun.com
1st INTERNATIONAL CONFERENCE OF LOGISTICS
INTLOG 2006
„LOGISTICS IN GLOBAL ECONOMY – Challenges and trends”
2
1. Wstêp
Przeobra
¿enia
, jakie zachodz
¹ w Polsce od roku 1989 roku widoczne s¹ w
prawie wszystkich
elementach gospodarki. Wdra
¿any system rynkowy powoduje wzrost konkurencyjnoœci podmiotów
gospodarczych a transport tak jak i inne dzia
ùy gospodarki nie stanowi wyj¹tku. Przedsiêbiorstwa, firmy
transportowe musz
¹ ci¹gle poprawiaã efekty f
inansowe, aby utrzyma
ã siê na rynku i by nie stanowiùy
balastu finansowego dla spo
ùeczeñstwa.
W otwartej gospodarce rynkowej istotnym i nieodzownym elementem jest konkurencja. Na rynku
konkurencja pozwala na obni
¿enie cen, podnoszenie jakoœci. Podnoszenie
konkurencyjno
œci
przedsi
êbiorstwa transportowego wi¹¿e siê z podniesieniem jakoœci usùug oferowanych co zwi¹zane jest
z usprawnianiem ca
ùego systemu eksploatacji autobusów. Mechanizm taki powoduje wiêc selekcje i
eliminuje z rynku firmy o niskiej skuteczno
œci [12]. Przedsiêbiorstwa musz¹ dostosowywaã swoje
dzia
ùania do wymagañ rynku, na którym dzi
a
ùaj¹. W zwi¹zku z tym wùaœciciele przedsiêbiorstw
, aby nimi
efektywnie zarz
¹dzaã, musz¹ odpowiadaã sobie ci¹gle na szereg pytañ. Jednym z takich pytañ jest: Czy
posiadam wystarczaj
¹ca liczbê œrodków transportu do realizacji przewozów transportowych? Czy nie
posiadam zbyt du
¿ej liczby œrodków transportu? Czy rozmiar posiadanej floty œrodków transportu jest
optymalny do zada
ñ które realizuje?
Problem zarz
¹dzania œrod
kami transportowymi, wyznaczenia optymalnej ich liczby jest szeroko
poruszany w literaturze polskiej m.in. [6, 7, 8, 9, 13] jak i zagranicznej, m.in. w [10, 11]. W wielu
przedstawianych problemach wyznaczania optymalnej liczby pojazd
ów, rozmiaru floty tran
sportowej
oraz podej
œciach do rozwi¹zania tych problemów m.in. w [6, 7, 8] autorzy prac rozpatrywali modele
deterministyczne, kt
óre mogùy byã okreœlone analitycznie jak i rozwi¹zane w ten sam sposób. Zaùo¿enia
(ograniczenia) jakie przyj
êli autorzy ró¿ni¹ s
i
ê od zaùo¿eñ niniejszej pracy. W opisywanym w tej pracy
podej
œciu
do problemu, podstawow
¹ ró¿nic¹ jest wprowadzenie parametrów stochastycznych w postaci
poziomu istotno
œci zachowania ci¹gùoœci pracy przewozowej zwi¹zanego z wystêpowaniem awarii i
uszkodze
ñ [1] autobusów w czasie wykonywania pracy przewozowej. Wprowadzony poziom istotnoœci
zwany, tak
¿e prawdopodobieñstwem, wystêpuje w tym modelu w postaci empirycznej i zaù
o
¿onej.
Warto
œã prawdopodobieñstwa zachowania ci¹gùoœci jest okreœlon
a na pocz
¹tku
a prawdopodobie
ñstwo
empiryczne zachowania ci
¹gùoœci wyznaczane jest na podstawie prz
eprowadzonej symulacji. Symulacja
takiego systemu powala na dok
ùadniejsze przyjrzenie siê czynnikom wystêpuj¹cym w rzeczywistym
systemie eksploatacji autobus
ów [5].
Aby przyst
¹piã do rozwa¿añ wyliczania minimalnej liczby autobusów eksploatowanych nale¿y
rozpatrzy
ã jak zbudowany jest system eksploatacji.
2. System eksploatacji autobusów
Autobusy dzia
ùaj¹c w strukturach przedsiêbiorstw transportu miejskiego eksploatowane s¹
zgodnie z przyj
êtym systemem eksploatacji (zwany dalej ‘systemem’).
(1)
U
ÝYTKO W ANIE
(3)
REZERWA
(2)
OBS
£UGA
(4)
KOLEJKA DO
OBS
£UGI
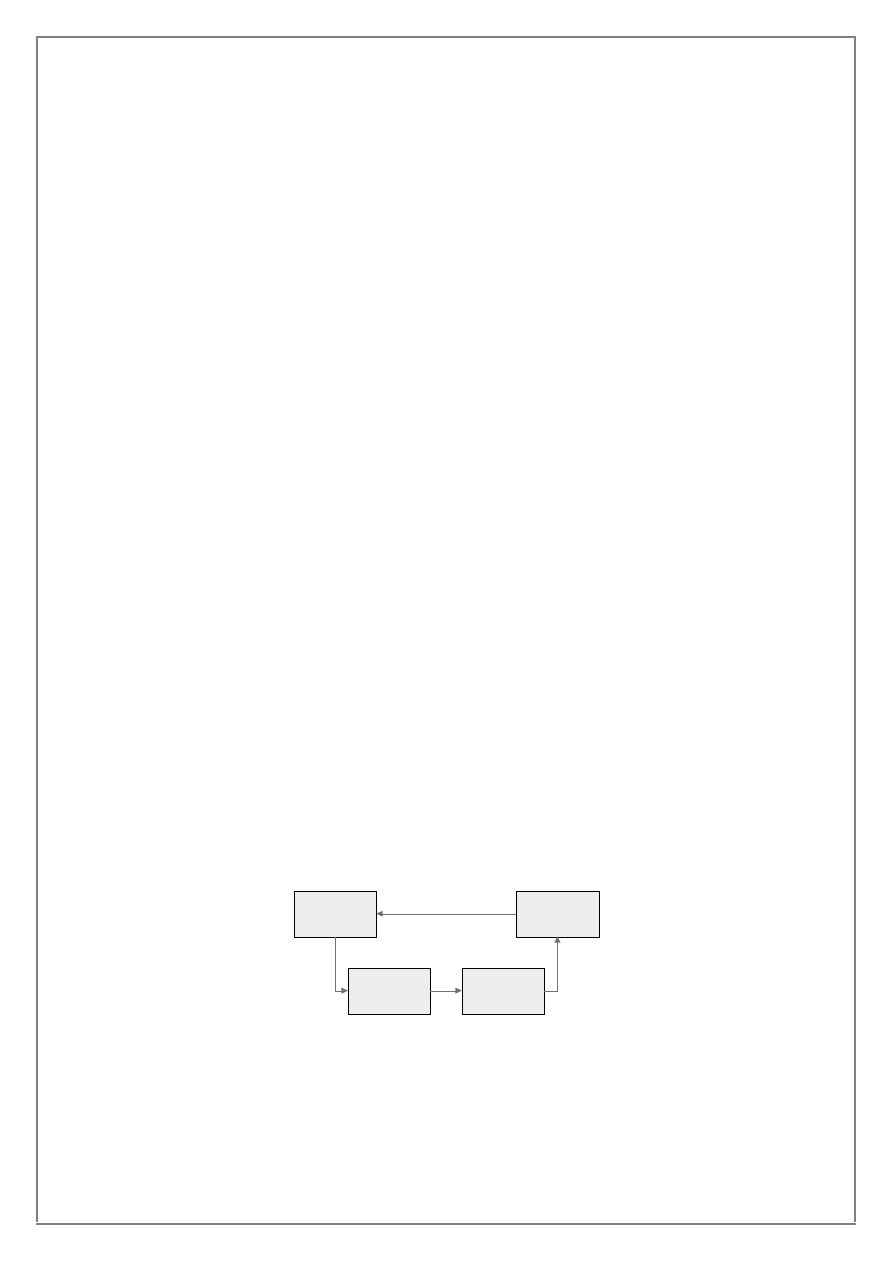
Rysunek 1. System eksploatacji w postaci blokowej.
Model symulacyjny zosta
ù zaprojektowany zgodnie ze struktur¹ systemu przedstawion¹ na rys
unku 1.
System sk
ùada siê z trzech podstawowych bloków, charakteryzuj¹cych siê stanami
eksploatacyjnymi: u
¿ytkowanie, kolejka do obsùugi, obsùuga
oraz rezerwa. W uj
êciu bardziej
szczeg
óùowym mo¿na wyró¿niã dalsze elementy bloku Obsùuga jak kanaùy obsùugi
i stanowiska obs
ùugi.
1st INTERNATIONAL CONFERENCE OF LOGISTICS
INTLOG 2006
„LOGISTICS IN GLOBAL ECONOMY – Challenges and trends”
3
3. Model symulacyjny systemu eksploatacji autobusów
W niniejszym rozdziale zostan
¹ scharakteryzowane podstawowe zaùo¿enia i
struktura modelu
symulacyjnego zwanego dalej modelem.
3.1.
Zaùo¿enia do modelu symulacyjnego
W modelu przyj
êto z
a jednostk
ê czasu godzinê (
=1 godzina) i jest ona jednakowa dla
wszystkich element
ów modelu. Model posiada horyzont czasowy w postaci Caùkowitego Symulowanego
Czasu Eksploatacji (CSCE), kt
óry liczony jest w dobach (T) a na ka¿d¹ z nich przypadaj¹ ô = 24 g
odzin,
a wi
êc:
T
Tg
(1)
wyznacza CSCE wyra
¿ony w jednostkach czasu, godzinach.
Podstawowe za
ùo¿enia w badaniu modelu
mo
¿na sformuùo
wa
ã nastêpuj¹co:
Okre
œlona jest macierz N =
{
n
ij
};
i
=1,2,
…,7; j
=1,2,
…,ô; ô = 24,
zapotrzebowania godzinowego na
autobusy u
¿ytkowane w kolejnych dniach tygodnia, przy czym przyjmuje siê, ¿e i
=1 odpowiada
poniedzia
ùkowi, i
=2 wtorkowi, itd. Do
i
=7 odpowiadaj
¹
cego niedzieli. Chwilowa liczba autobus
ów
u
¿ytkowanych
(autobusy przebywaj
¹ce w stanie eksploatacyjnym ‘u¿ytkowanie’)
w dniu tygodnia
i
i
godzinie
j
N
chij
nie mo
¿e byã mniejsza od n
ij
a wi
êc dla ka¿dej godziny dnia tygodnia musi byã
zachowana nier
ównoœã (
wz
ór 2):
N
chij
≥ n
ij
(2)
Niepo
¿¹dana jest sytuacja, w której liczba autobusów faktycznie u¿ytkowanych w godzinie j
i w
dniu tygodnia
i
jest mniejsza od liczby autobus
ów, któr
a wynika z zapotrzebowania dla
j
godziny i
i
dnia tygodnia. okre
œlonej poni¿sz¹ nierównoœci¹ (wzór 3):
N
chij
<
n
ij
(3)
Eksploatowany jest jeden typ autobus
ów.
Model jest modelem dyskretnym w czasie.
Zak
ùada siê trzy rodzaje resursu. Resurs obsùugi technicznej pierwszego rodzaju (OT
-1), resurs
obs
ùugi technicznej drugiego rodzaju (OT
-2), resurs ca
ùkowity po którym autobus kierowany jest na
napraw
ê gùówn¹ (NG). Resurs rozumiany jest jako liczba kilometrów
po przejechaniu kt
órej
autobus kierowany jest do Systemu Obs
ùugi (blok nr.2, rysunek 1).
Ka
¿dy autobus ma do wykonania pracê przewozow¹ Pp
okre
œlon¹ dùugoœci¹ trasy w km.
Zak
ùada siê prawdopodobieñstwo utraty zdatnoœci puz
zaù
w czasie u
¿ytkowania.
3.2.
Metoda
symulacji
przebywania
autobusu
w
wyodrêbnionych
stanach
eksploatacyjnych
Elementem, kt
óry determinuje liczbê autobusów wymaganych d
o zaspokojenia popytu
transportowego wyra
¿ony zostaù zapotrzebowaniem godzinowym. Zapotrzebowanie na autobusy
u
¿ytkowane jest wyra¿one poprzez wektor zapotrzebowania godzinowego N
, w kt
órym dla ka¿dej
przyj
êtej jednostki czasu (godzin
y) w jednej dobie wyst
êpuje wartoœã liczbowa wyra¿aj¹ca minimaln¹
liczb
ê autobusów u¿ytkowanych potrzebnych do
zaspokojenia zapotrzebowania przewozowego.
Elementy wektora zapotrzebowania wyra
¿one s¹ przez n
ij
, gdzie (
i
= 1,2,
…,7; j
= 1,2
… ô). Wielkoœã
zapotrzebowania godzinowego okre
œlona jest dla siedmiu dni tygodnia i
a ze wzgl
êdu na ró¿nice ksztaùtu
popytu w dniach weekendowych, tj. sobocie i niedzieli wprowadzono dwa wektory zapotrzebowania.
1st INTERNATIONAL CONFERENCE OF LOGISTICS
INTLOG 2006
„LOGISTICS IN GLOBAL ECONOMY – Challenges and trends”
4
Zapotrzebowania godzinowe, okre
œlone dla siedmiu dni tygodnia przyjêto jako niezmien
ne w ca
ùej
symulacji. Przyjmuje si
ê, iê zapotrzebowanie jest niezale¿ne od czasu. Przykùadow
e wektory
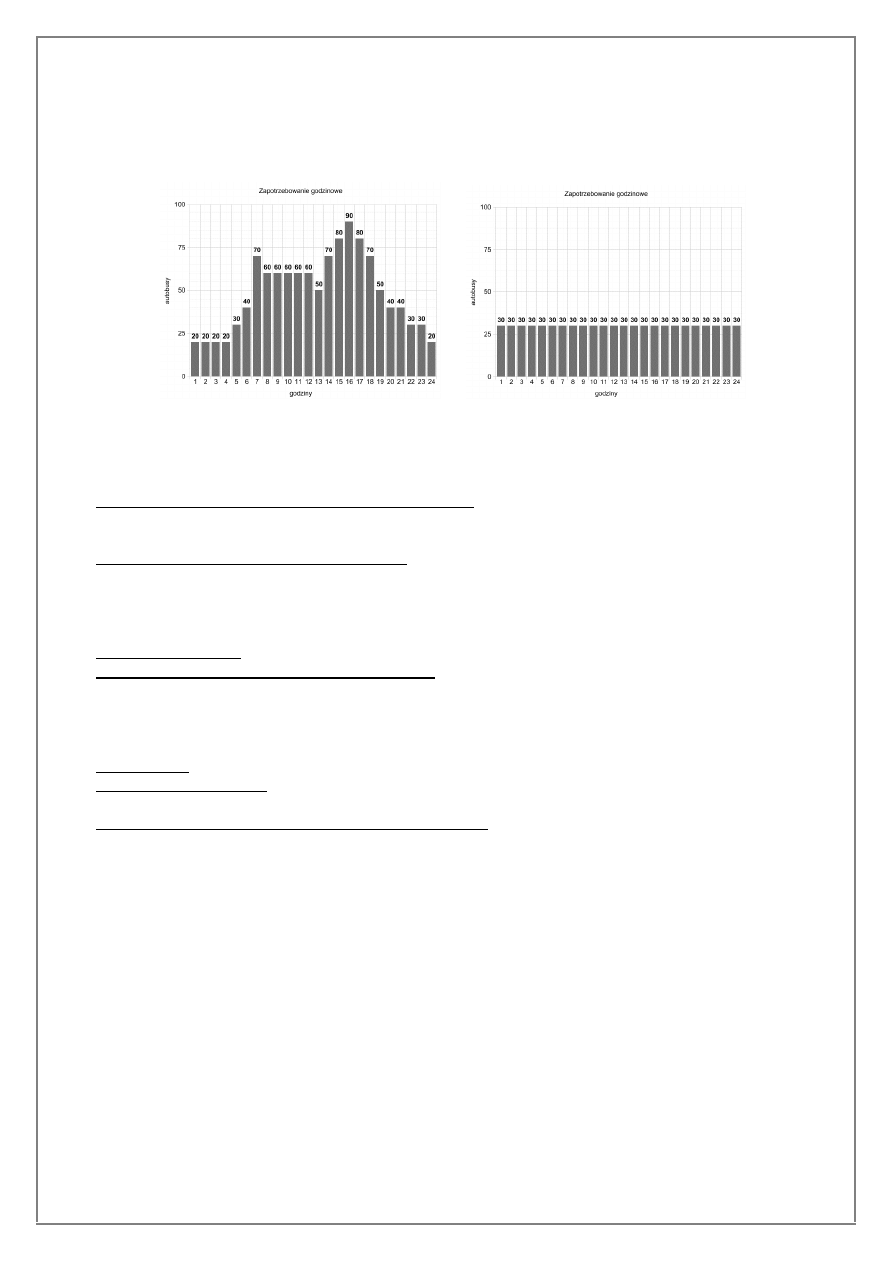
zapotrzebowania przedstawiono w postaci graficznej na rysunku 2.
a)
b)
Rysunek 2 Przyk
ùadowe zapotrzebowan
ie godzinowe na autobusy u
¿ytkowane dla okreœlonych dni
tygodnia:
a) dla i=1,2,
…,5
; b) dla i=6,7
W procesie symulacji wykonywane s
¹ m.in. procedury:
1. Wycofywanie autobus
ów z zakoñczonym zadaniem
–
zmniejszenie liczby u
¿ytkowanych autobusów
o te jednostki, kt
óre prz
ejecha
ùy zaùo¿on¹ liczbê kilometrów Pp
.
2. Wycofywanie nadmiarowych autobus
ów
–
zmniejszanie liczby u
¿ytkowanych autobusów w
przypadku mniejszego zapotrzebowania.
N
chij >
n
ij
dla
i
=1,2,
…,7; j
= 1,2,
…,ô ; ô = 24
(4)
3. Obs
ùuga techniczna
–
wykonywane s
¹ czynnoœci diagnostyczno
-naprawcze.
4. Uzupe
ùnianie grupy pojazdów u¿ytkowanych
–
zwi
êkszanie liczby u¿ytkowanych autobusów w
przypadku konieczno
œci zaspokojenia zapotrzebowania w godzinie i
.
N
chij <
n
ij
dla
i
=1,2,
…,7; j
= 1,2,
…,ô ; ô = 24 (5)
5. U
¿ytkowanie
–
wykonywany jest proces transportowy [3].
6. Sprawdzanie resurs
ów
–
analiza warto
œci resursów chwilowych w celu wyszukania autobusów
wymagaj
¹cych przegl¹du technicznego w syste
mie obs
ùugi.
7. Generator utraty zdatno
œci, kontrola zdatnoœci –
generator wyst
¹pienia utraty zdatnoœci.
Wykorzystywany jest generator liczb losowych o rozk
ùadzie jednostajnym [4].
4. Wyznaczanie minimalnej liczby autobusów
W niniejszym rozdziale zostan
¹ op
isane metody wyznaczania minimalnej liczby autobus
ów.
4.1. Opis metody I
Proponowana metoda polega na por
ównaniu prawdopodobieñstw: empirycznego (obliczonego
na podstawie wynik
ów symulacji) oraz zaùo¿o
nego. Aby m
óc okreœliã empirycznie prawdopodobieñstwo
zachowania ci
¹gùoœci do modelu symulacyjnego wprowadzono parametr wyznaczaj¹cy czas utraty
ci
¹gùoœci Tuc
i
jest on okre
œlany jako liczba godzin, w których liczba autobusów u¿ytkowanych byùa
mniejsza od liczby autobus
ów wynikaj¹ca z zapotrzebowania dla danej godziny (niespeùniona
nier
ównoœã ze wz
oru 3).
1st INTERNATIONAL CONFERENCE OF LOGISTICS
INTLOG 2006
„LOGISTICS IN GLOBAL ECONOMY – Challenges and trends”
5
T
d
d
uc
Tuc
1
(6)
Tuc
Tg
Tzc
(7)
gdzie:
d
uc
- liczba godzin w dobie
d
(
d
=1
…T
), w kt
órych nast¹piùa utrata
ci
¹gùoœci prac przewozowych.
Dla opisanego modelu symulacyjnego eksploatacji autobus
ów i dla przyjêtej liczby N
autobus
ów
eksploatowanych wykonywana jest symulacja. Po wykonaniu symulacji wyznaczane jest empiryczne
prawdopodobie
ñstwo zachowania ci¹gùoœci
pzc
zgodnie ze wzorem 8
.
Mo
¿na uznaã, ¿e empiryczne
prawdopodobie
ñstwo zachowania ci¹gùoœci jest funkcj¹ liczby eksploatowanych autobusów.
Tg
Tuc
Tg
Tg
Tzc
pzc
(8)
gdzie:
Tzc
–
liczba godzin zachowania ci
¹gùoœci,
Tg
–
ca
ùkowity symulowany c
zas eksploatacji w godzinach (wz
ór 3).
Nast
êpnie sprawdzana jest ró¿nica pr. empirycznego p
zc
i pr. za
ùo¿onego p
zaù
.
Gdy spe
ùniona jest nierównoœã:
p
zaù
>
p
zc
(9)
zwi
êkszana jest wartoœã zmiennej decyzyjnej
N (liczby pojazd
ów eksploatowanych domyœ
lnie
zwi
êkszana jest jednostkowo). Model z now¹ wartoœci¹ parametru
N poddawany jest ponownie
procesowi symulacji.
Warto
ϋ zmiennej decyzyjnej
N, przy kt
órej:
p
zaù
≤
p
zc
(10)
stanowi rozwi
¹zanie
optymalne.
Okreœlona
jest
wiêc
wtedy
minimalna
liczba
a
utobus
ów
eksploatowanych (N*) z prawdopodobie
ñstwem p
zc
zachowania ci
¹gùoœci realizacji prac przew
ozowych.
Algorytm
sprawdzania
prawdopodobie
ñstwa
empirycznego
zachowania
ci¹gùoœci
i
prawdopodobie
ñstwa zaùo¿onego zachowania ci¹gùoœci zostaù przedstawiony
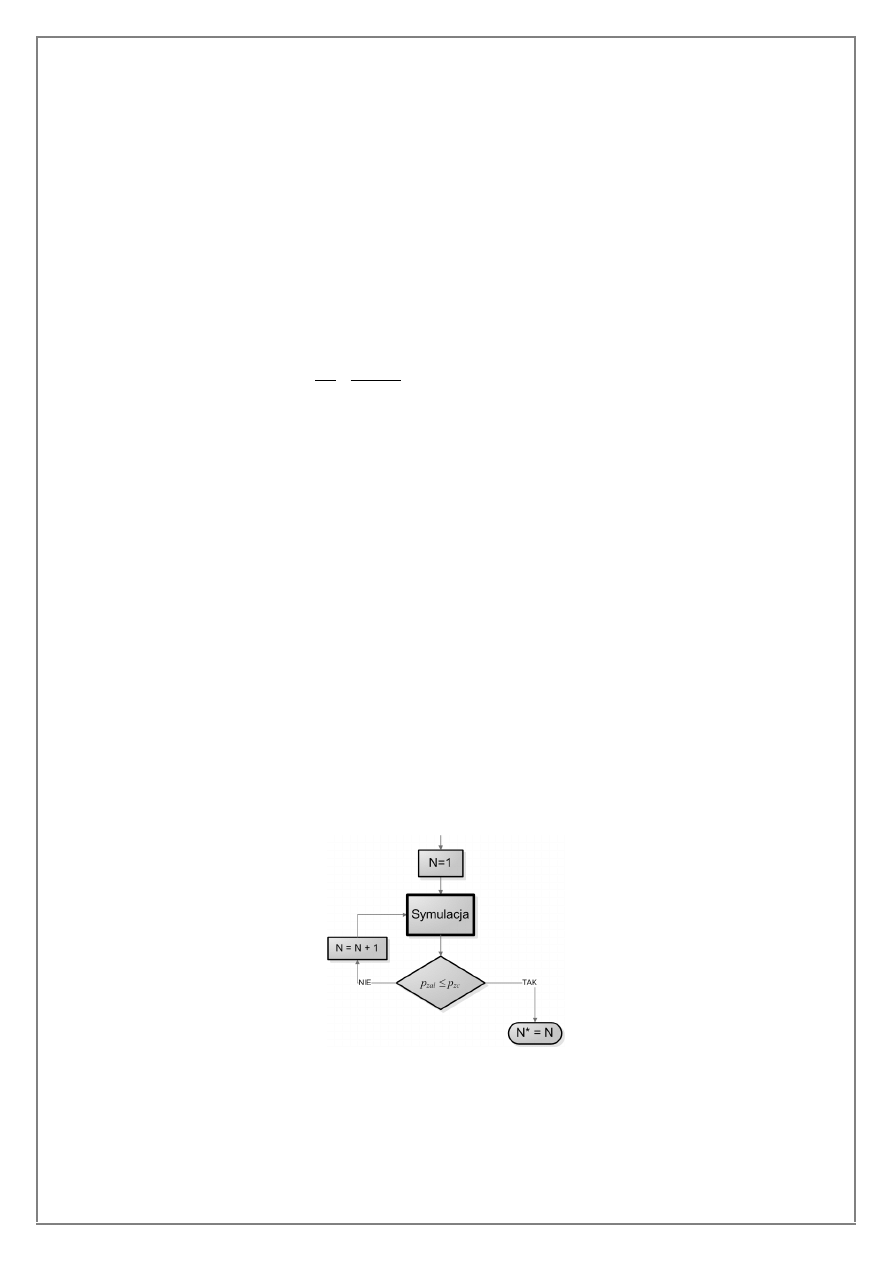
w postaci schematu
blokowego na rys. 3.
Rysunek 3. Schemat blokowy obrazuj
¹cy sprawdzanie warunku zachowania ci¹gùoœci
1st INTERNATIONAL CONFERENCE OF LOGISTICS
INTLOG 2006
„LOGISTICS IN GLOBAL ECONOMY – Challenges and trends”
6
4.2. Opis metody II
Metoda druga jest bardzo podobna do metody om
ówionej w podrozdziale 4.1. a ró¿ni
ca zawarta
jest w sposobie wyznaczania prawdopodobie
ñstwa empirycznego zachowania ci¹gùoœci.
Prawdopodobie
ñstwo empiryczne wyznaczane jest w tej metodzie jako stosunek liczby utrat
ci
¹gùoœci oraz liczby mo¿liwych utrat ci¹gùoœci w caùym procesie symulacji
(wz
ór 11). Liczba utrat
ci
¹gùoœci jest liczb¹ wszystkich sytuacji, w których nie byùo mo¿liwe zast¹pienie autobusów, które utraciùy
zdatno
œã w procesie u¿ytkowania.
1
1
1
1
1
1
]
[
g
g
T
d
g
dg
g
g
T
d
g
dg
g
uc
n
T
s
n
T
u
n
p
(11)
gdzie:
n
g
–
liczba autobus
ów u¿ytkowanych w godzinie g
wynikaj
¹ca z zapotrzebowania
godzinowego
u
dg
–
liczba autobus
ów u¿ytkowanych w godzinie g,
dobie
d
s
dg
–
liczba utrat ci
¹gùoœci w godzinie g
, dobie
d
W metodzie tej wa
¿ne s¹ wszystkie pojedyncze utraty ci¹gùoœci a nie tylko te godziny, w których
nast
¹piùy utraty tak jak to ma miejsce w metodzie pierwszej (podrozdziaù 4.1
.)
4.3. Opis metody III
Trzecim podej
œciem do rozwi¹zania tego zadania jest metoda wagowej funkcji celu, która
uwzgl
êdnienia dwa czynniki:
1. Koszt eksploatacji
Ke
;
2. Warto
ϋ strat Tuc
.
Wagowa funkcja celu przedstawia si
ê nastêpuj¹co (suma iloczynów odpowiednich wag i czynników):
f(N) = W
1
Tuc(N)+W
2
Ke(N)
(12)
gdzie:
W
1
i
W
2
–
wagi. (W
1
,W
2
(0,1) i W
1
+W
2
=1)
Tuc
–
warto
œã strat (liczba godzin utracenia ci¹gù
o
œci)
Ke
–
koszty eksploatacji floty autobus
ów (m.in. koszty przegl¹du, naprawy, paliwa)
Dla tak zbudowanej funkcji celu proces symulacji modelu eksploatacji pozwala na wyznaczenie
dopuszczalnej liczby autobus
ów eksploatowanych
N
*
dla kt
órych wartoœã funk
cji osi
¹ga minimum.
Wa
¿noœã czynników okreœlana jest poprzez wagi. Rozwi¹zanie zadania przy u¿yciu tej metody mo¿e byã
podyktowane r
ó¿nymi wzglêdami, które bêd¹ miaùy swoje odniesienie w wagach W
1
oraz W
2
.
Przyk
ùadowy wykres wagowej funkcji celu przedstaw
iono na rys. 4.
1st INTERNATIONAL CONFERENCE OF LOGISTICS
INTLOG 2006
„LOGISTICS IN GLOBAL ECONOMY – Challenges and trends”
7
W ykres w agow ej funkcji celu
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
90
95
100
105
110
115
120
125
130
135
140
N
W
a
rt
o
œ
f
u
n
k
c
ji
Rysunek 4. Przyk
ùadowy wykres wagowej funkcji celu.
Zadanie wyznaczania optymalnej liczby autobus
ów eksploatowanych wymaga operowania
prawdopodobie
ñstwami ze wzglêdu na losowy charakter opisanego procesu ekspl
oatacji.
5. Wyniki symulacji
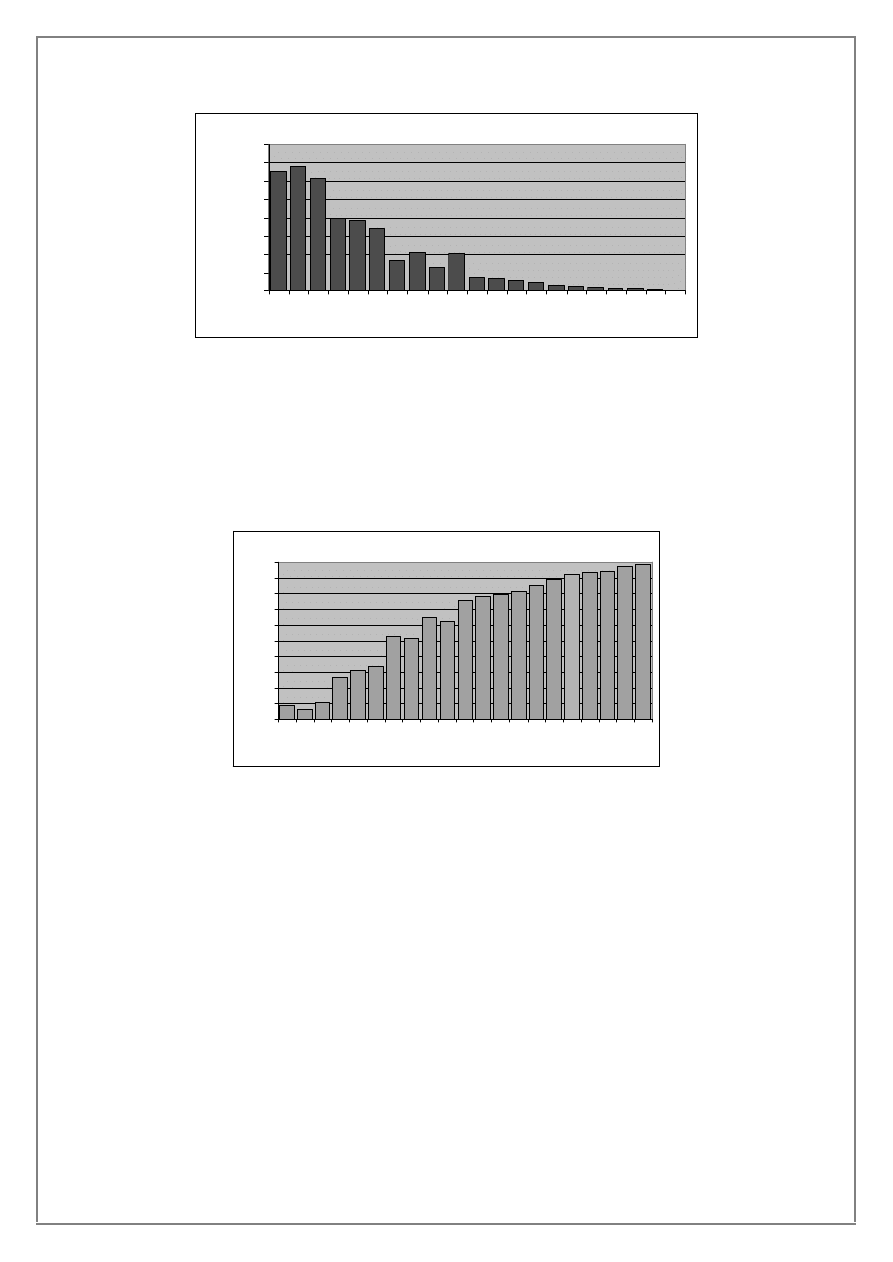
Rysunki 5 i 6 przedstawiaj
¹ wyniki symulacji, odpowiednio wielkoœã utraty ci¹gùoœci oraz
prawdopodobie
ñstwo zachowania ci¹gùoœci z zaznaczon¹ optymaln¹ liczb¹ autobusów przy której
zapotrzebowanie
zrealizowane
zosta
ùo
z
zaùo¿
onym
prawdopodobie
ñstwem
p
zaù
= 0,98. Poni
¿ej przedstawione s¹ zaùo¿enia i parametry symulacji dla przykùadowego systemu
eksploatacji.
Zapotrzebowanie godzinowe dla dni tygodnia 1,2,3,4,5 by
ùo jednakowe i wynosiùo:
N =
[20, 20, 20, 20, 30, 40, 70, 60, 60, 60, 60, 60, 50, 70, 80, 90, 80, 70, 50, 40, 40, 30, 30, 20] dla
i
=1,2,
…,5
Zapotrzebowanie godzinowe dla dni tygodnia 6 i 7 by
ùo jednakowe i wynosiùo:
N =
[30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30] dla
i
=6,7
Strategi
¹ wybierania pojazdów z zapasu do u¿ytkowania byùa strategi¹ maksymalnego przebiegu
ca
ùkowitego; strategia wycofywania z u¿ytkowania ze wzglêdu na zmniejszone zapotrzebowanie byùa
strategi
¹ maksymalnego procentu wykonania z
adania przewozowego, liczonego w km, wyst
êpowaù
jeden typ autobus
ów Q=1, pojemnoœã systemu obsùugi wynosiùa 10 autobusów jednoczeœnie
obs
ùugiwanych, wyjœcie z kolejki oczekuj¹cych autobusów do rozpoczêcie obsùugi zrealizowano w
oparciu o teori
ê kolejki FIF
O (First-In-First-Out), zadanie przewozowe okre
œlono na 100km, wyù¹czono
kierowanie do Naprawy G
ùównej (NG = 0), wektor resursów byù jednakowy dla wszystkich pojazdów:
resurs OT-1 wynosi
ù 1000 km, resurs OT
-2 wynosi
ù 10000 km, resurs caùkowity wynosiù 200
00 km. W
przypadku wyczerpania resursu ca
ùkowitego autobus byù wycofywany z eksploatacji. Autobusy wycofane
z eksploatacji zmniejsza
ùy liczbê autobusów eksploatowanych a na ich miejsce generowane byùy n
owe
obiekty.
1st INTERNATIONAL CONFERENCE OF LOGISTICS
INTLOG 2006
„LOGISTICS IN GLOBAL ECONOMY – Challenges and trends”
8
Wielkoœã utraty ci¹gùoœci
3266
3410
3081
1963 1916
1694
828
1046
645
1024
342 333 296
227
142
106
73
46
40
20
8
0
500
1000
1500
2000
2500
3000
3500
4000
90 91 92 93 94 95 96 97 98 99 10
0
10
1
10
2
10
3
10
4
10
5
10
6
10
7
10
8
10
9
11
0
Liczba autobusów eksploatowanych
L
ic
z
b
a
u
tr
a
t
c
i¹
g
ùo
œ
c
i
Rysunek 5. Wielko
œã utraty ci¹gùoœci z 21 symulacji przeprowadzonych dla T=60 dni.
Przy tak za
ùo¿onych wartoœciach resursów czas symulowanej eksploatacji autobusów (T
=60 dni)
powodowa
ù byù na tyle dùugi, ¿e nastêpowaùo wycofywanie autobusów do obsùugi profilaktyczn
ej OT-1 jak
i OT-2 z powodu wyczerpywanych resurs
ów. System obsùugi byù obci¹¿any autobusami, które ulegùy
awarii b
¹dê wypadkowi oraz przebywaùy w Obsùudze Codziennej, której poddawane byùy wszystkie
autobusy wycofywane z u
¿ytkowania i koñcz¹ce zadanie prz
ewozowe. Autobusy, kt
óre wyczerpaùy
resurs ca
ùkowity byùy wycofywane z eksploatacji a na ich miejscu eksploatacjê rozpoczynaùy autobusy
nowe.
Prawdopodobieñstwo zachowania ci¹gùoœci
0,8
0,82
0,84
0,86
0,88
0,9
0,92
0,94
0,96
0,98
1
90 91 92 93 94 95 96 97 98 99 10
0
10
1
10
2
10
3
10
4
10
5
10
6
10
7
10
8
10
9
11
0
Liczba autobusów e ksploatowanych
p
z
c
Rysunek 6. Prawdopodobie
ñstwo zachowania ci¹gùoœci (21 symulacji; T=60 dni)
.
Na rysunku 4 wida
ã jest jak zmienia siê wielkoœã utraty ci¹gùoœci, która rozumiana jest jako
liczba
brakuj
¹cych autobusów ze wzglêdy na niespeùnienie zapotrzebowania, które to wynikaã mo¿e z kilku
przyczyn. Taka sytuacja wynika z przebywania autobus
ów w Systemie
Obs
ùugi (oczekuj¹cych w kolejce
na obs
ùugê lub obsùugiwanych) i nie mog¹cych w ten sposób zrealizowaã zapotrzebowania
wynikaj
¹cego z wekt
ora
N
.
Rysunek 5 obrazuje jak zmienia
ùo siê prawdopodobieñstwo zachowania ci¹gùoœci w trakcie symulacji,
kt
óre dla pot
rzeb tej symulacji liczone by
ùo zgodnie ze wzorem 10 (metoda I). Przy przyjêciu p
zaù
=0,98 to
ju
¿ w 17 symulacji, w której N=107 nastêpuje speùnienie warunku z wzoru 12 i N*
=107 odpowiada
minimalnej liczbie autobus
ów.
W rzeczywisto
œci warunek ze wzoru 10 n
ie jest wystarczaj
¹cy i w dalszych badaniach nale¿y uœciœliã
za
ùo¿enia wyboru minimum poprzez analizê prawdopodobieñstwa speùnienia zapotrzebowania
godzinowego n
ij
dla
i
=1,2,
…,7; j
= 1,2,
…,ô.
1st INTERNATIONAL CONFERENCE OF LOGISTICS
INTLOG 2006
„LOGISTICS IN GLOBAL ECONOMY – Challenges and trends”
9
5. Wnioski
System eksploatacji autobus
ów uwzglêdniaj¹cy wy
st
êpowanie uszkodzeñ i awarii zrealizowany
zosta
ù poprzez wprowadzenie losowej utraty zdatnoœci. W procesie symulacji generowane jest
prawdopodobie
ñstwo uszkodzenia oraz awarii. Utrata zdatnoœci eksploatowanych œrodków transportu w
prezentowanym modelu jest zdarzeniem losowym i czyni z niego modelem stochastyczny (losowy).
Wyst
êpowanie zdarzeñ losowych z natury rzeczy nie da siê jednoznacznie przewidzieã i chc¹ ustaliã
minimaln
¹ liczbê eksploatowanych aut
obus
ów nale¿y zaùo¿yã poziom istotnoœci realizacji pr
acy
przewozowej. Bez tego za
ùo¿enia dochodzi siê do wniosku, i¿ aby zapewniã caùkowite zaspokojenie
popytu transportowego nale
¿aùoby dysponowaã nieskoñczon¹ liczb¹ autob
us
ów.
Opisana w tej pracy metoda symulacji eksploatacji systemu o parametrach losowych jest
narz
êdziem pozwalaj¹cym w ùatwy sposób wyznaczenie wymaganej liczby autobusów, których
u
¿ytkowanie okreœlone jest przez popyt przewozowy.
LITERATURA
[1] Wa
¿yñska
-Fiok K.: Podstawy teorii eksploatacji i niezawodno
œci systemów transportowych. WPW.
Warszawa 1993.
[2] Okulewicz J
ózef: Badanie symulacyjne utrzymania parku samochodów w przedsiêbiorstwie
transportowym. Rozprawa doktorska. Warszawa 1985
[3] Piasecki Stanis
ùaw: Analiza systemowa transportu: Transport XXI Wieku. Warszawa 2004
[4] Woch Janusz: Statystyka proces
ów transportowych. Gliwice 2001
[5] Napiera
ùa Wojciech, Choromañski Wùodzimierz: Wyznaczanie minimalnej liczby autobusów
eksploatowanych w celu zapewnienia ci
¹gùoœci realizacji prac transportowych. Tran
sport XXI Wieku,
Warszawa 2004
[6] Piasecki S.: Optymalizacja system
ów obsùugi technicznej. WNT, Warszawa 1972
[7] Piasecki S.: Optymalizacja system
ów przewozowych. WK£, Warszawa 1973
[8] Pyza Dariusz: Metoda wyboru optymalnej struktury organizacyjno-technologicznej systemu obs
ùugi
technicznej. Transport XXI Wieku, Warszawa 2004
[9] Napiera
ùa W., Choromañski W.:
Suboptymalizacja liczby
œrodków transportu w ci¹gùym systemie
transportowym. Transcomp, Zakopane 2005.
[10] George J. Beaujon, Mark A. Turnquist: A Model for Fleet Sizing and Vehicle Allocation.
Transportation science. Vol. 25
[11] I. Gertsbach, Yu . Gurecvich: Constructing an Optimal Fleet for a Transportation Schedule
Transportation science. Vol. 11
[12] Wyszomirski Olgierd: Gospodarowanie w komunikacji miejskiej, Wydawnictwo Uniwersytetu
Gda
ñskiego 2002
[13]
Ýak J.: Modelowanie i optymalizacja wielokryterialna funkcjonowania systemów transportowych
.
Rozprawa habilitacyjna. 2005