Prof. Edmund Wittbrodt

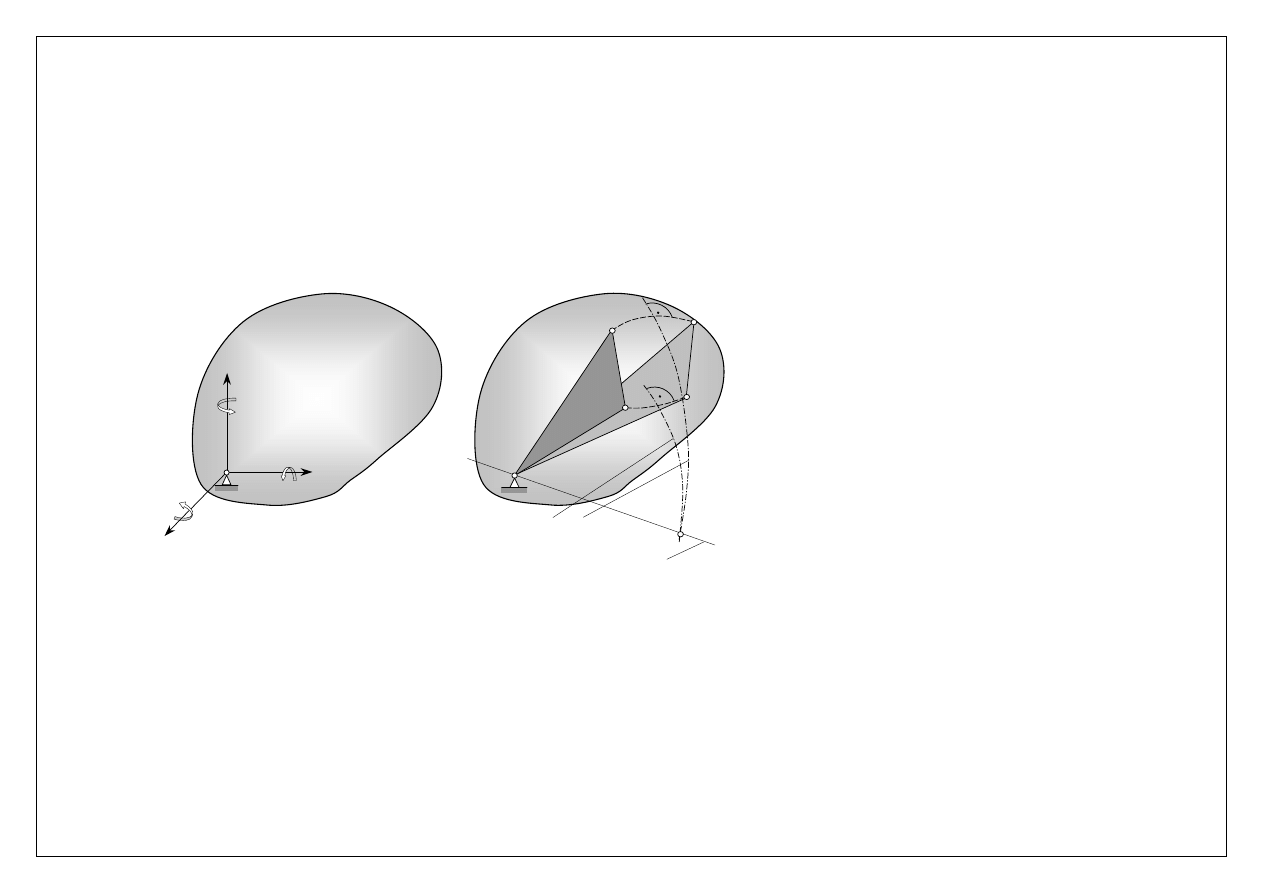
Ruch kulisty bryły. Kinematyka

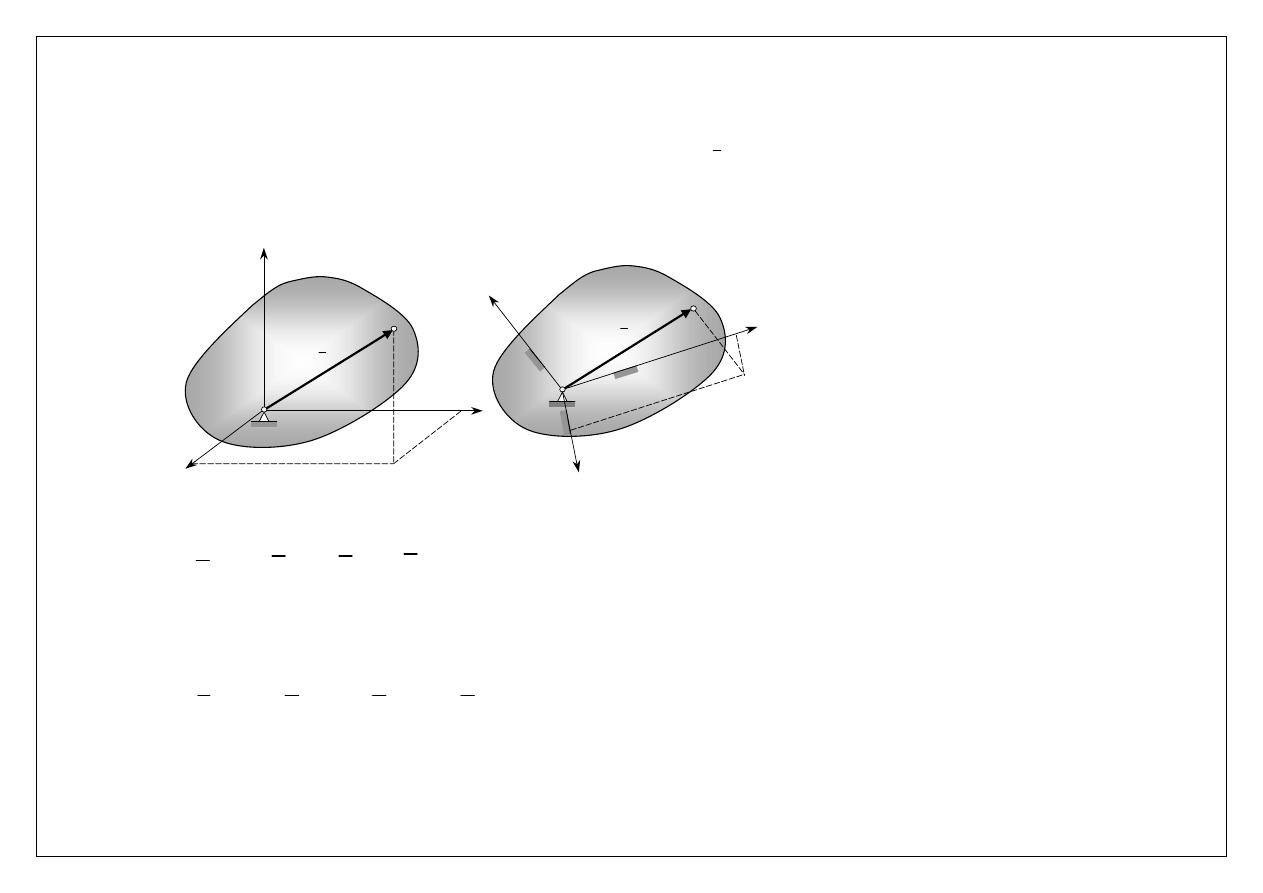
Ruchem kulistym nazywamy ruch, w czasie którego jeden z punktów bryły jest stale nieruchomy. Ruch kulisty jest obrotem
dookoła chwilowej osi obrotu (oś ta zmienia swoje położenie w czasie).

Ruch kulisty bryły: a) obrót wokół punktu, b) obrót dookoła chwilowej osi obrotu

Symetralne, le

żą

ce

na kołach du

ż

ych

A’

∆

OAB=

∆

OA’B’

O

1

Chwilowa
o

ś

obrotu

B’

A

B

O

b)

O

a)

y

x

z

ϕ

x

ϕ

y

ϕ

z

Prof. Edmund Wittbrodt

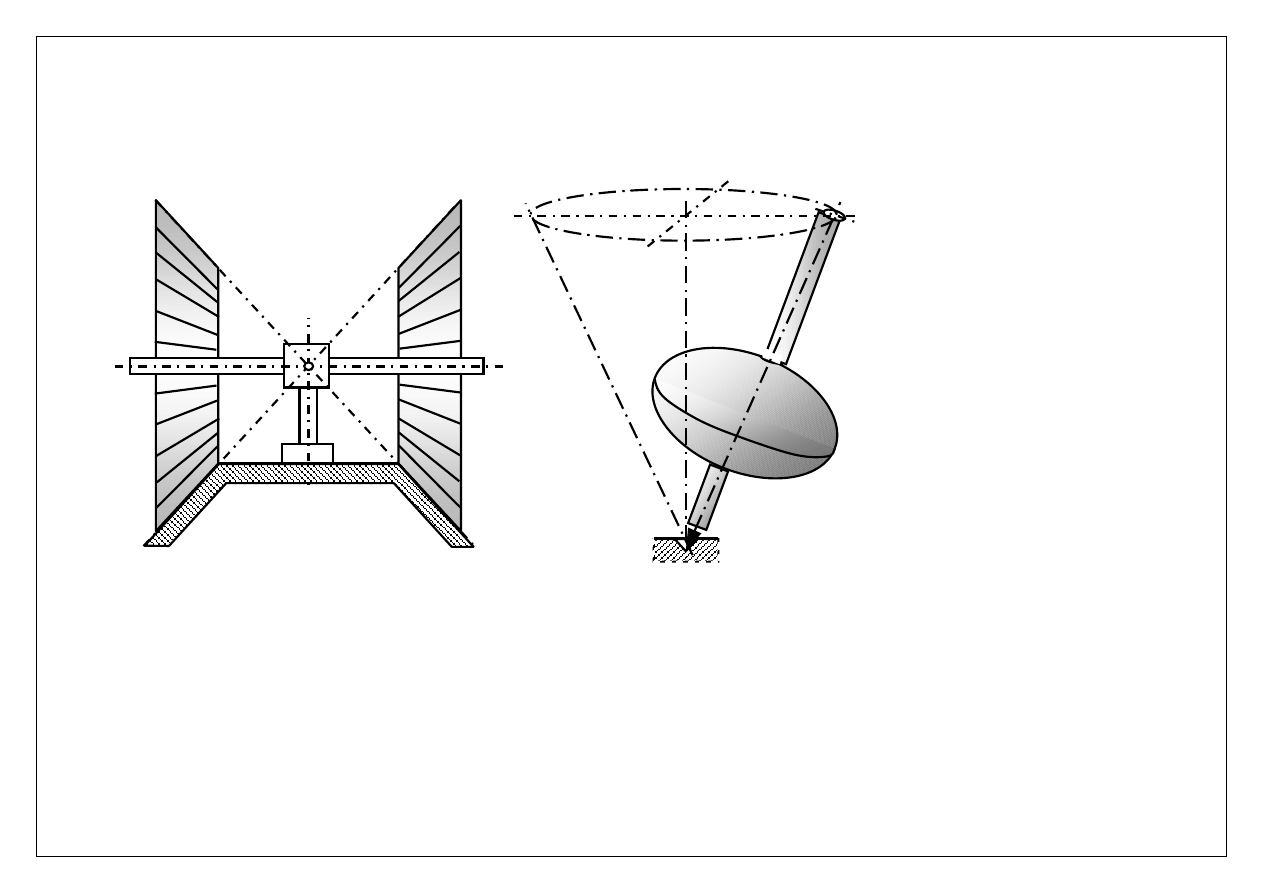
Przykłady brył w ruchu kulistym

Prof. Edmund Wittbrodt

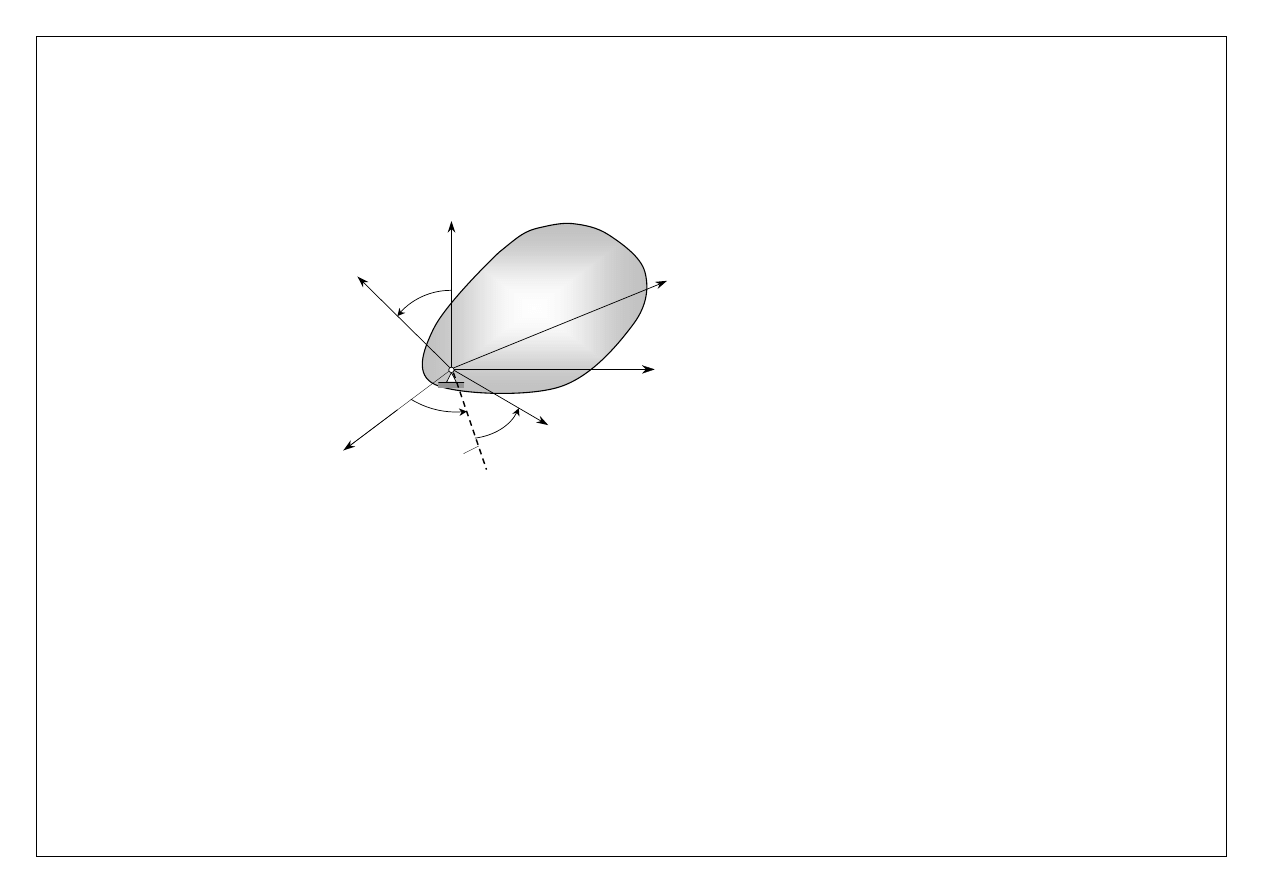
Położenie. Bryła, której jeden punkt jest unieruchomiony ma 3 stopnie swobody. Jej położenie jest opisane w sposób
jednoznaczny jedynie za pomocą kątów, zwanych

kątami Eulera

. Dla określenia tych kątów wprowadzamy układ

współrzędnych związanych z bryłą

ξ

,

η

,

ζ

.

Opis ruchu kulistego bryły za pomocą kątów Eulera

Wyobraźmy sobie, że początkowo osie układu nieruchomego x, y, z pokrywają się z osiami układu

ξ

,

η

,

ζ

. Następnie bryła

wykonuje obroty:

•

wokół osi nieruchomej

z

o kąt

ψ

(kąt

precesji

), po wykonaniu tego obrotu oś

ξ

znajdzie się na linii zwanej linią

węzłów

w

,

•

wokół osi

ξ

o kąt

θ

(kąt

nutacji

), ściśle wokół linii węzłów

w

,

•

wokół osi

ζ

o kąt

ϕ

(kąt

obrotu własnego

).

Kolejność „wykonywania” powyższych obrotów jest dowolna i nie ma ona wpływu na położenie końcowe bryły.

y

ξ

ψ

x

η

z

ζ

θ

ϕ

linia
w

ę

złów w

O

Prof. Edmund Wittbrodt

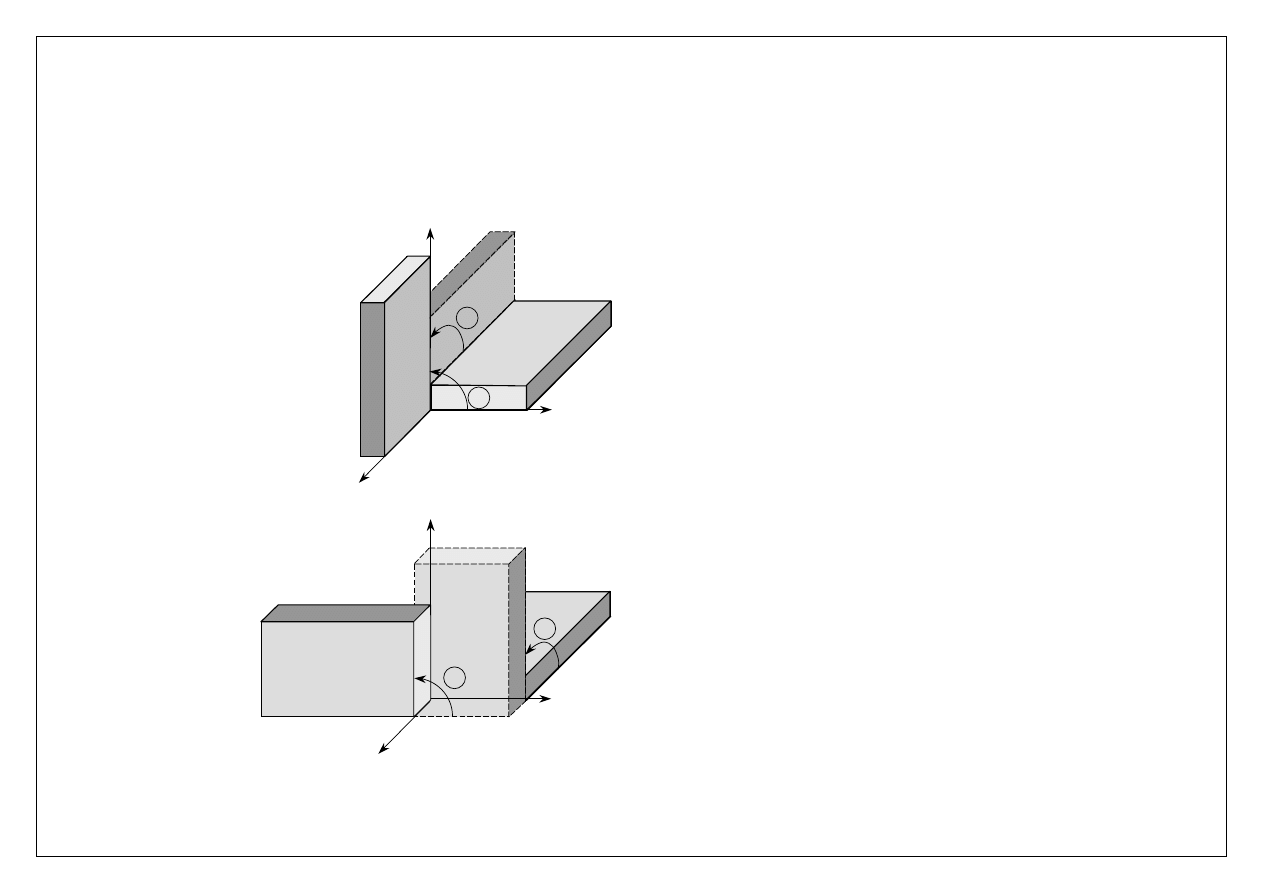
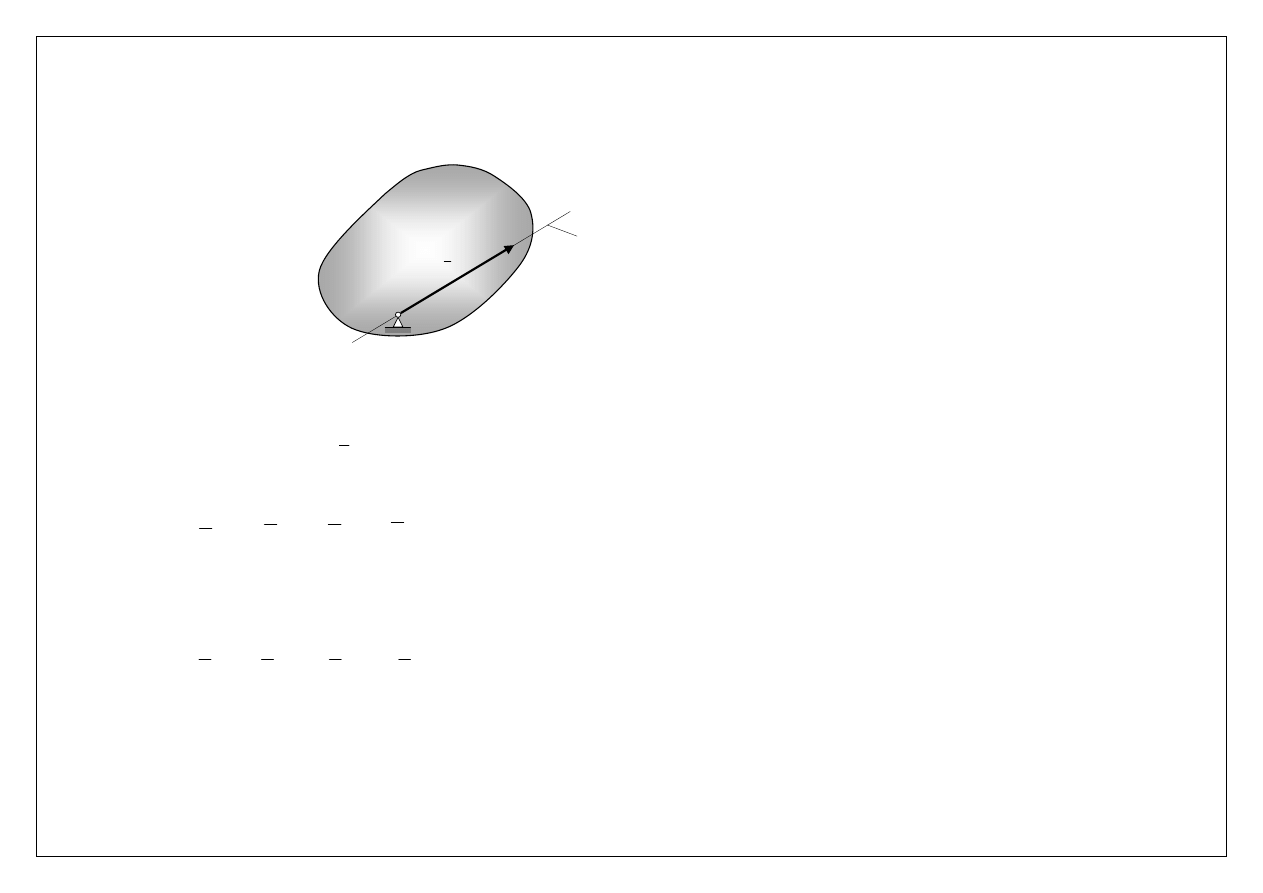
Gdybyśmy chcieli za współrzędne bryły przyjąć kąty będące obrotami wokół osi układu nieruchomego x, y, z, wówczas
kolejność wykonywania obrotów decydowałaby o położeniu końcowym bryły. Kąty

ϕ

x

,

ϕ

y

,

ϕ

z

nie opisują więc

jednoznacznie położenia bryły (można je przyjąć tylko dla małych obrotów).

Wpływ kolejności „wykonywania” obrotów bryły na położenie

końcowe: a) obroty w kolejności – wokół osi x potem y, b)

obroty w kolejności – wokół osi y potem x

Zatem kąty:

ψ

=

ψ

(t),

θ

=

θ

(t),

( )

t

ϕ ϕ

=

są współrzędnymi bryły w ruchu kulistym.

x

z

y

1

2

b)

x

z

y

1

2

a)

Prof. Edmund Wittbrodt

Położenie dowolnego punktu A bryły określamy za pomocą wektora

r

(o stałej długości), którego współrzędne możemy

podać w nieruchomym układzie osi x, y, z

Położenie punktu A bryły w ruchu kulistym:

a) w układzie nieruchomym x, y, z,

b) w układzie

ξ

,

η

,

ζ

związanym z bryłą

A

A

A

A

r

x i

y j

z k

=

+

+

lub w układzie związanym z bryłą

ξ

,

η

,

ζ

ζ

η

ξ

ζ

η

ξ

e

e

e

r

A

A

A

A

+

+

=

,

gdzie

ξ

A

,

η

A

,

ζ

A

są wielkościami stałymi.

z

A

x

y

A

O

x

A

y

z

A

r

A

a)

O

A

r

A

ξ

η

ζ

ζ

A

ξ

A

η

A

b)

Prof. Edmund Wittbrodt

Prędkość. Ponieważ ruch kulisty jest obrotem wokół chwilowej osi obrotu, wektor prędkości kątowej leży na tej osi.

Chwilowa oś obrotu bryły w ruchu kulistym

Wektor prędkości kątowej

ω

możemy podać zarówno w nieruchomym układzie osi x, y, z

x

y

z

i

j

k

ω ω

ω

ω

=

+

+

,

jak i w układzie związanym z bryłą

e

e

e

ξ ξ

η η

ζ ζ

ω ω

ω

ω

=

+

+

.

0

chwilowa o

ś

obrotu

ω

Prof. Edmund Wittbrodt

Znając prędkości:

ϕ

&

– obrotu własnego,

ψ

&

– precesji oraz

θ

&

– nutacji,

Wektory prędkości kątowych: obrotu własnego

ϕ

&

, precesji

ψ

&

i nutacji

θ

&

Składowe wektora

ω

, w układzie nieruchomym

z

y

x

,

,

oraz ruchomym

ξ

,

η

,

ζ

obliczamy z zależności:





















⋅





















−

=





















=

θ

ψ

ϕ

θ

ψ

ψ

θ

ψ

ψ

θ

ω

ω

ω

ω

&

&

&

0

1

cos

sin

0

cos

sin

cos

0

sin

sin

z

y

x

.





















⋅





















−

=





















=

θ

ψ

ϕ

θ

ϕ

ϕ

θ

ϕ

ϕ

θ

ω

ω

ω

ω

ζ

η

ξ

&

&

&

0

cos

1

sin

cos

sin

0

cos

sin

sin

0

natomiast:

ϕ

ω

ϕ

&

=

,

ψ

ω

ψ

&

=

,

θ

ω

θ

&

=

- prędkości zmian kątów Eulera.

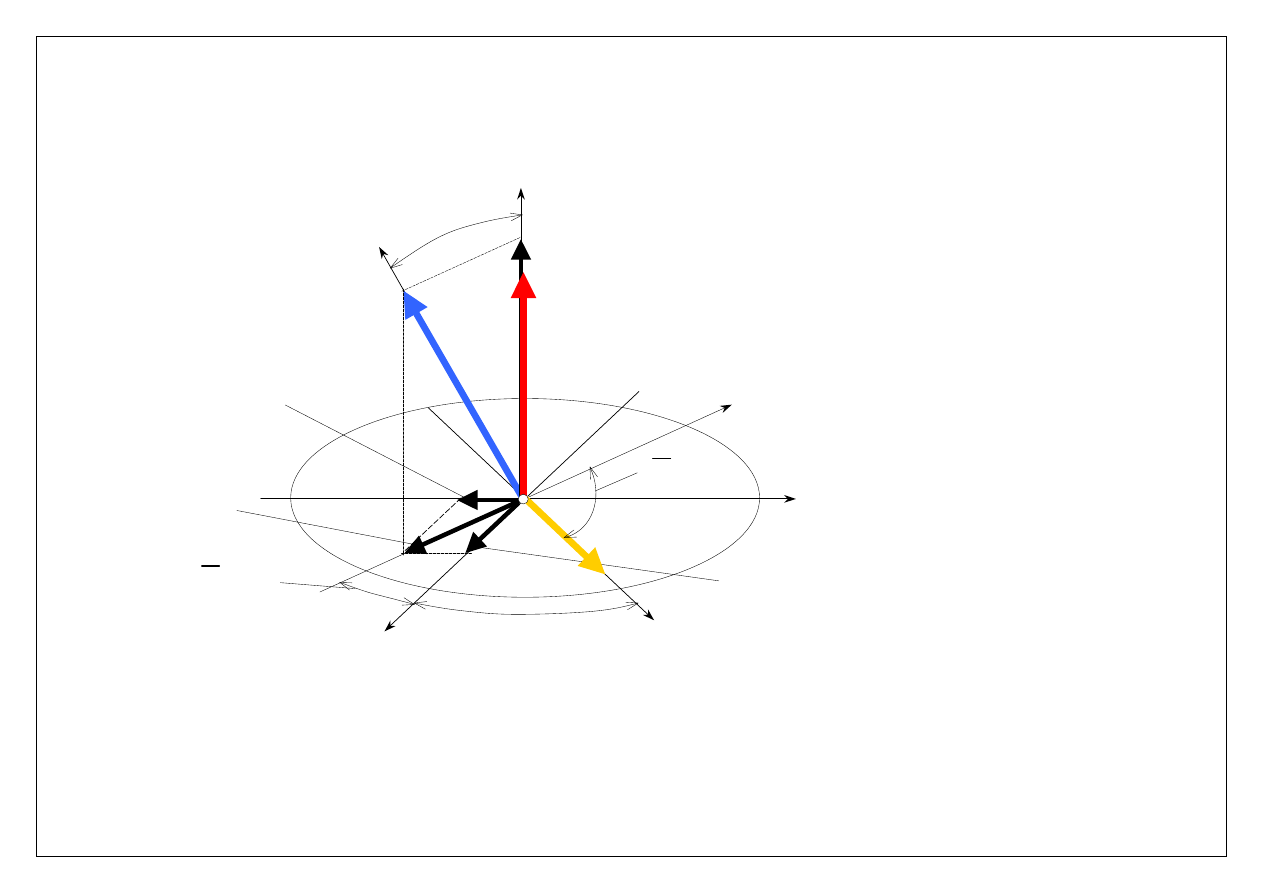
Możemy też wektor prędkości kątowej bryły w ruchu kulistym przedstawić w postaci

w

e

k

e

⋅

+

⋅

+

⋅

=

θ

ψ

ϕ

ω

ζ

&

&

&

ϕ

y

ξ

ψ

x

η

z

ζ

O

ψ

&

ϕ

&

θ

&

θ

w

Prof. Edmund Wittbrodt

W celu znalezienia składowych prędkości kątowej w układzie x,y,z obliczamy poszczególne jej składowe sumując

algebraicznie odpowiednie składowe wektorów prędkości kątowych w układzie x’,y’,z’

z’

O

z

y

w

x

n

θθθθ

2

ϕ

′

=

ω

k

r

r

&

2

π ψ

−

ψ

1

ψ

=

ω

k

r

r

&

3

e

θ

=

r

r

&

w

ω

2

π

cos

ϕ

θ

&

sin sin

ϕ

θ ψ

&

sin cos

ϕ

θ

ψ

−

&

sin

ϕ

θ

&

Prof. Edmund Wittbrodt

Transformacja do układu nieruchomego:

x,y,z

k

⋅

=

ψ

ω

&

1

'

2

k

⋅

=

ϕ

ω

&

w

e

⋅

=

θ

ω

&

3

x

ω

0

ψ

θ

ϕ

sin

sin

⋅

⋅

&

ψ

θ

cos

⋅

&

y

ω

0

ψ

θ

ϕ

cos

sin

⋅

⋅

−

&

ψ

θ

sin

⋅

&

z

ω

ψ

&

θ

ϕ

cos

⋅

&

0

Transformacja do układu ruchomego:

ζ

η

ξ

,

,

k

⋅

=

ψ

ω

&

1

'

2

k

⋅

=

ϕ

ω

&

w

e

⋅

=

θ

ω

&

3

ξ

ω

ϕ

θ

ψ

sin

sin

⋅

⋅

&

0

ϕ

θ

cos

⋅

&

η

ω

ϕ

θ

ψ

cos

sin

⋅

⋅

&

0

ϕ

θ

sin

⋅

−

&

ζ

ω

θ

ψ

cos

⋅

&

ϕ

&

0

Prędkość liniową punktu A bryły, w układzie nieruchomym x, y, z, obliczamy z zależności

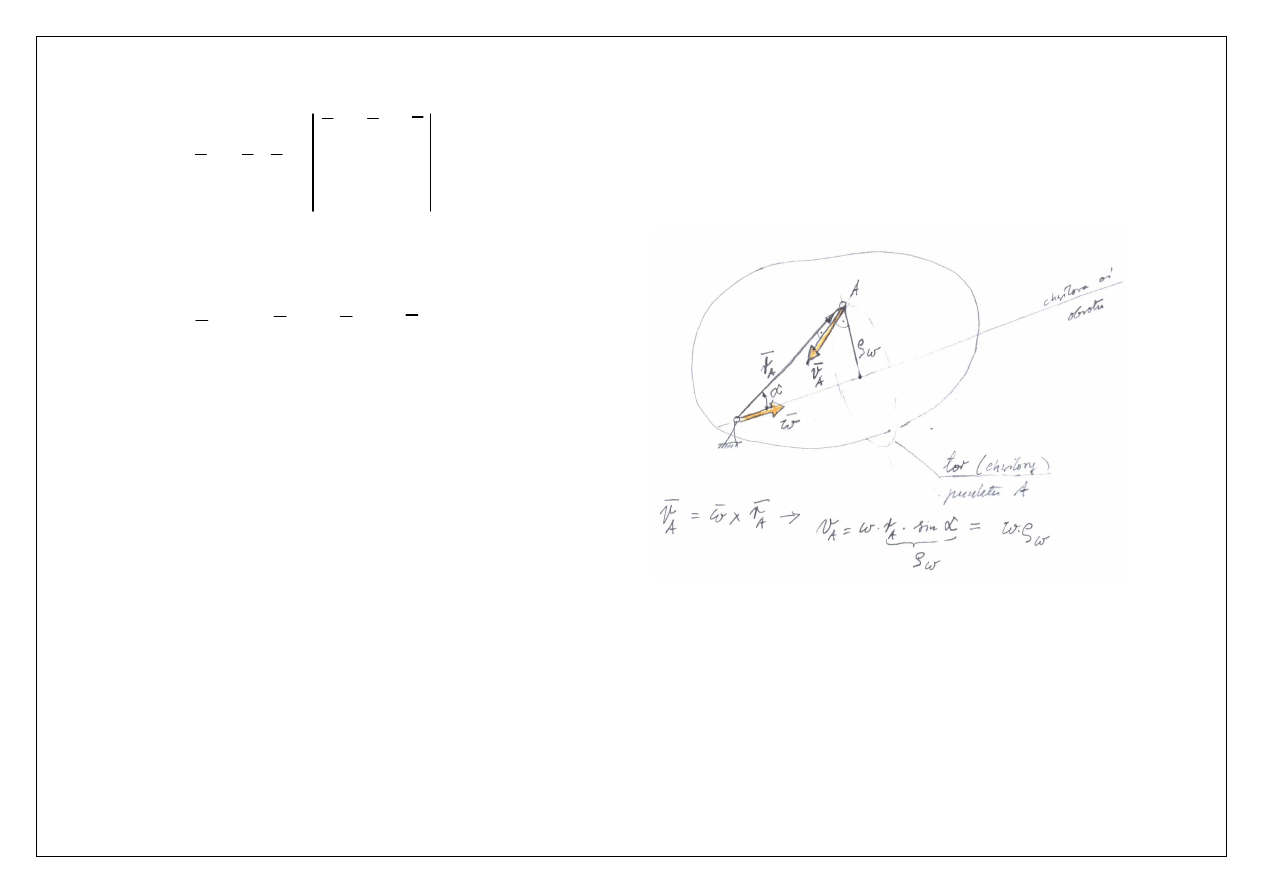
Prof. Edmund Wittbrodt

A

A

x

y

z

A

A

A

i

j

k

v

r

x

y

z

ω

ω

ω

ω

= × =

,

co stanowi wektor

A

Ax

Ay

Az

v

v

i

v

j

v k

=

+

+

,

gdzie:

Ax

y A

z

A

v

z

y

ω

ω

=

−

,

Ay

z A

x A

v

x

z

ω

ω

=

−

,

Az

x

A

y A

v

y

x

ω

ω

=

−

.

Natomiast wektor prędkości punktu A w układzie związanym z bryłą obliczamy

Prof. Edmund Wittbrodt

ξ

η

ζ

ξ

η

ζ

ω

ω

ω

ω

ξ

η

ζ

= × =

A

A

A

A

A

e

e

e

v

r

,

co zapisujemy

ς

ς

η

η

ξ

ξ

e

v

e

v

e

v

v

A

A

A

A

+

+

=

,

gdzie:

A

A

A

v

ξ

η

ζ

ω ζ

ω η

=

−

,

A

A

A

v

η

ζ

ξ

ω ξ

ω ζ

=

−

,

A

A

A

v

ζ

ξ

η

ω η ω ξ

=

−

.

Prof. Edmund Wittbrodt

Przyspieszenie. Wektor przyspieszenia kątowego bryły w ruchu kulistym leży na chwilowej osi przyspieszenia.

Chwilowa oś przyśpieszenia bryły w ruchu kulistym

Wektor przyspieszenia kątowego możemy podać tak w nieruchomym układzie osi x, y, z

x

y

z

i

j

k

ε ω ε

ε

ε

= =

+

+

&

,

jak i w ruchomym układzie osi

ξ

,

η

,

ζ

e

e

e

ξ ξ

η η

ζ ζ

ε ω ε

ε

ε

= =

+

+

&

.

O

chwilowa

oś

przyśpieszenia

ε

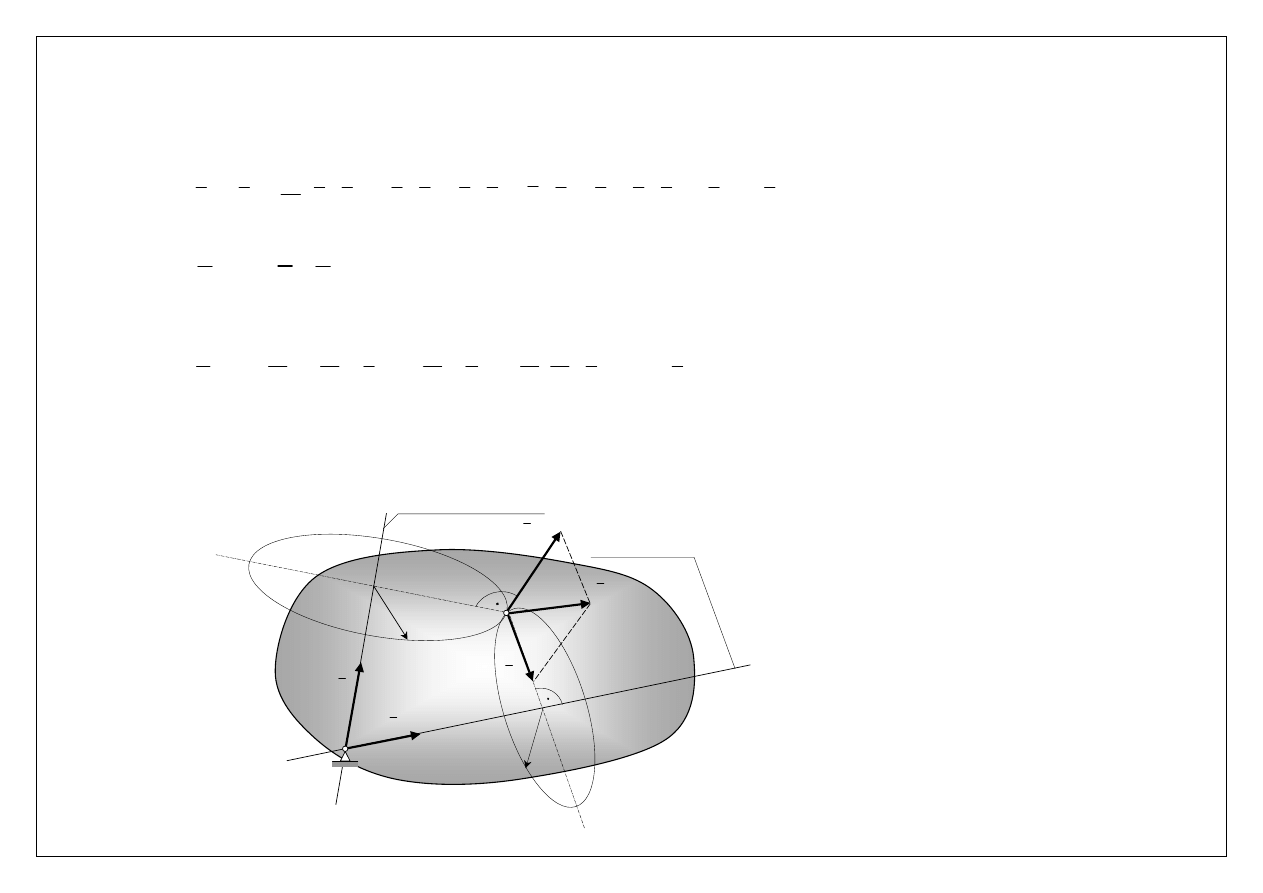
Prof. Edmund Wittbrodt

Przyspieszenie liniowe dowolnego punktu A bryły określamy różniczkując względem czasu wyrażenie na prędkość
liniową tego punktu

(

)

(

)

A

A

A

A

A

A

A

Aob

Ado

d

a

v

r

r

r

r

r

a

a

dt

ω

ω

ω

ε

ω ω

=

=

×

= × + × = × + × ×

=

+

&

&

&

,

gdzie:

Aob

A

a

r

ε

= ×

–

przyspieszenie obrotowe

,

A

A

A

A

Ado

r

r

v

r

a

2

)

(

)

(

ω

ω

ω

ω

ω

ω

−

⋅

=

×

=

×

×

=

–

przyspieszenie doosiowe

.

Przyśpieszenie doosiowe i obrotowe bryły w ruchu kulistym

Znając

położenie

chwilowych

osi

prędkości i przyspieszenia, wartości
przyspieszeń obrotowego i doosiowego
możemy obliczać ze wzorów:

Aob

a

ε

ερ

=

,

2

ω

ω ρ

=

Ado

a

.

chwilowa o

ś

obrotu

ρ

ε

ρ

ω

chwilowa o

ś

przy

ś

pieszenia

O

ω

ε

A

a

Ado

a

Aob

a

A

Prof. Edmund Wittbrodt

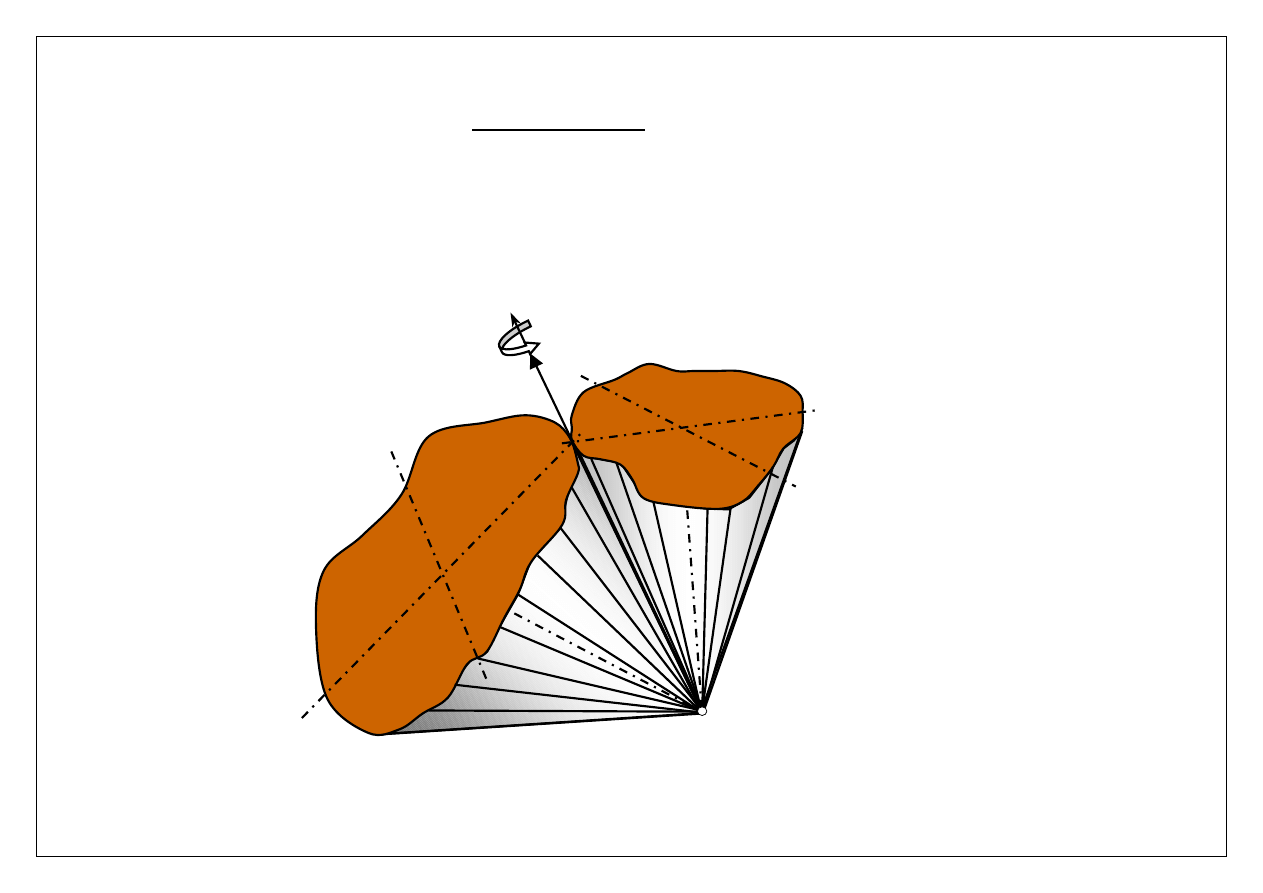
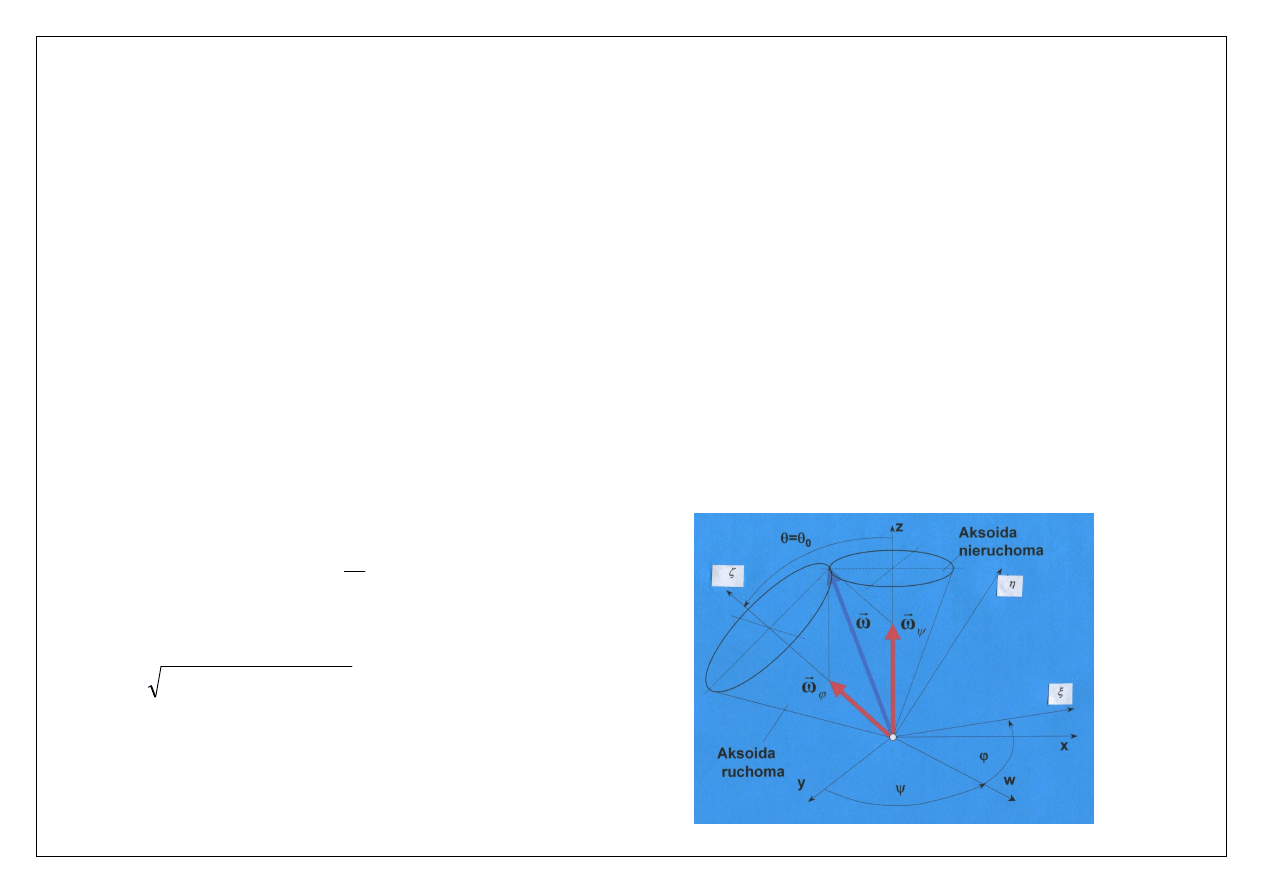
W czasie ruchu kulistego bryły sztywnej chwilowa oś obrotu zmienia swoje położenie względem nieruchomego układu

odniesienia U oraz względem poruszającej się bryły. Przechodzi ona jednak zawsze przez środek O ruchu kulistego. Z tego

względu chwilowe osie obrotu muszą leżeć na pewnej powierzchni stożkowej o wierzchołku w punkcie O. Podobnie,

miejscem geometrycznym chwilowych osi obrotu w układzie ruchomym U’ jest powierzchnia innego stożka, o wierzchołku

w punkcie O. Powierzchnie te nazywają się

aksoidami (aksioida ruchoma i aksioida nieruchoma)

.

aksioida nieruchoma

aksioida ruchoma

ω

ωω

ω

l

O=O’

Prof. Edmund Wittbrodt

Precesja regularna

(szczególny przypadek ruchu kulistego)

Precesja regularna ma miejsce, gdy spełnione są warunki:

const

=

θ

, stąd

0

=

θ

&

const

=

ϕ

&

const

=

ψ

&

Dla precesji regularnej ruchy obrotowy precesji i obrotu własnego są jednostajnymi ruchami wokół osi

z

oraz

ζ

.

Precesję regularną można zinterpretować jako sumę dwóch obrotowych ruchów jednostajnych: ruchu wokół osi związanej z

bryłą

ζ

, nachylonej stale pod kątem

θ

, z prędkością kątową

const

=

ϕ

&

oraz ruchu wokół osi

z

, z prędkością kątową

precesji

const

=

ψ

&

.

Wektor prędkości kątowej

ω

leży w płaszczyźnie z,

ζ

,

a jego długość wynosi (tw. cosinusów)

0

2

2

cos

2

θ

ψ

ϕ

ψ

ϕ

ω

&

&

&

&

+

+

=

gdzie:

const

=

ω

,

const

=

0

θ

Prof. Edmund Wittbrodt

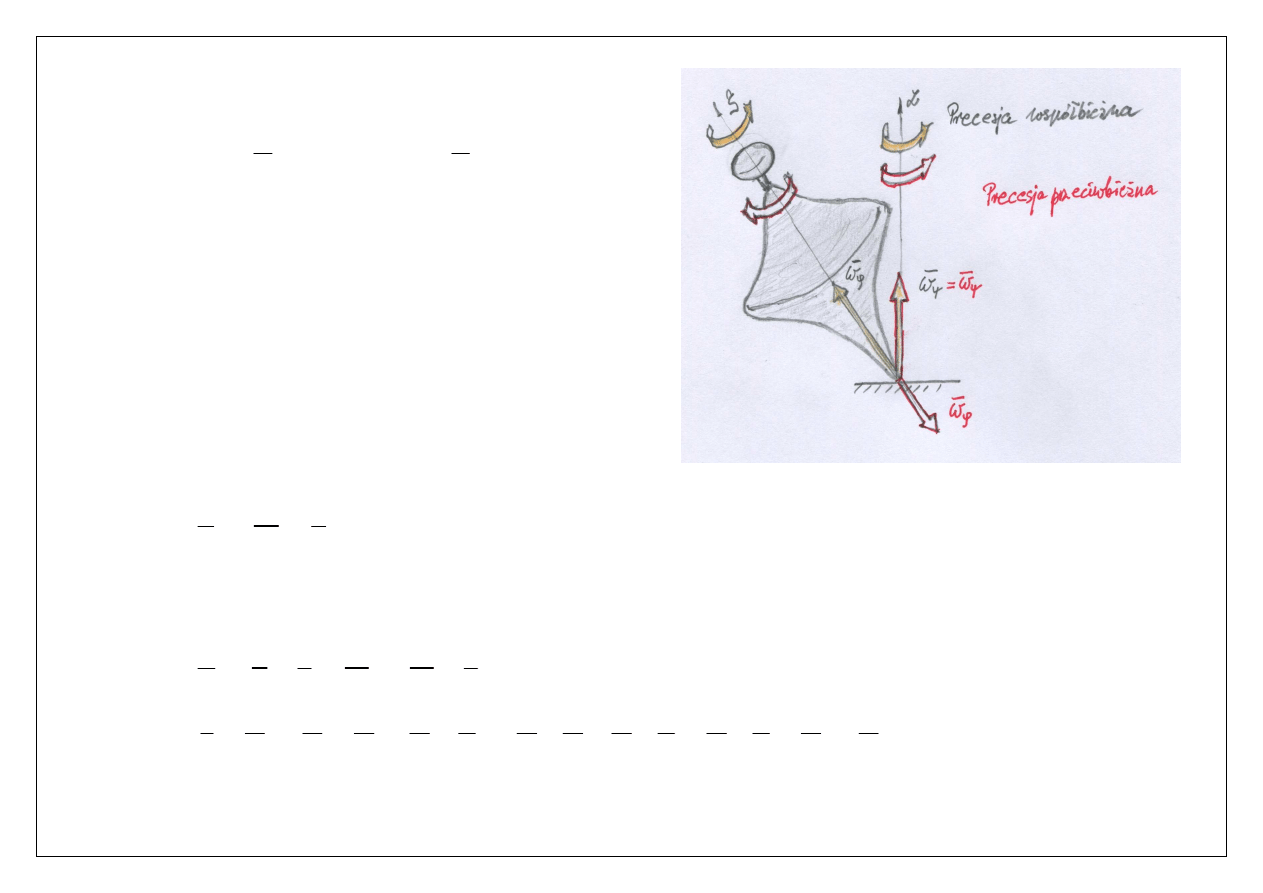
W zależności od wartości kąta pomiędzy wektorami prędkości

kątowej precesji

ψ

ω

i obrotu własnego

ϕ

ω

, mamy do czynienia

z precesją prostą (

współbieżną

), gdy

0

0

90

≤

θ

(kąt ostry), lub

precesją odwrotną (

przeciwbieżną

), gdy

0

0

90

>

θ

(kąt rozwarty).

Dla precesji regularnej prędkość punktu obliczamy z zależności

r

v

×

=

ω

natomiast przyspieszenie z zależności

)

(

r

r

a

×

×

+

×

=

ω

ω

ε

,

gdzie

ϕ

ψ

ψ

ω

ω

ϕ

ψ

ϕ

ψ

ψ

ψ

ϕ

ψ

ψ

ω

ω

ε

×

=

×

=

×

+

×

=

+

×

=

×

=

&

&

&

&

&

&

&

&

&

)

(

Prof. Edmund Wittbrodt

Ruch kulisty bryły. Dynamika

Rozważmy bryłę będącą w ruchu kulistym, której prędkość kątowa wynosi

ω

. W punkcie A tej bryły wyróżniamy

elementarną masę dm, której prędkość wynosi

v

.

Dynamika ruchu kulistego

Kręt bryły

względem nieruchomego punktu O obliczamy z zależności

( )

( )

(

)

O

m

m

K

r

vdm

r

r dm

ω

=

×

=

× ×

∫

∫

,

(4.98)

co przy

[ , , ]

r x y z

oraz

[

,

,

]

x

y

z

ω ω ω ω

daje wektor krętu w postaci

=

+

+

O

x

y

z

K

K i

K j

K k

,

(4.99)

gdzie:

x

x

x

xy

y

xz

z

K

J

D

D

ω

ω

ω

=

−

−

,

y

yx

x

y

y

yz

z

K

D

J

D

ω

ω

ω

= −

+

−

,

(4.100)

z

zx

x

zy

y

z

z

K

D

D

J

ω

ω

ω

= −

−

+

.

x

O

y

z

r

dm

ω

vdm

A

Prof. Edmund Wittbrodt

Wzory (4.100) w zapisie macierzowym mają następującą postać

[ ]





















⋅

=





















z

y

x

xyz

z

y

x

J

K

K

K

ω

ω

ω

,

(4.101)

gdzie

[ ]





















−

−

−

−

−

−

=

z

zy

zx

yz

y

yx

xz

xy

x

xyz

J

D

D

D

J

D

D

D

J

J

(4.102)

- macierz (tensor) bezwładności.

Prof. Edmund Wittbrodt

Dowód:

dm

r

r

dm

v

r

K

m

m

O

∫

∫

×

×

=

×

=

)

(

)

(

)

(

ω

)

(

)

(

)

(

z

y

y

x

z

x

x

z

y

z

z

y

z

y

x

z

y

x

r

r

k

r

r

j

r

r

i

r

r

r

k

j

i

r

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

−

+

−

+

−

=

=

×

+

−

−

+

=

−

−

−

=

×

×

]

)

(

[

)

(

2

2

z

x

z

y

x

y

z

y

x

x

y

y

x

z

x

x

z

y

z

z

y

z

y

x

r

r

r

r

r

r

i

r

r

r

r

r

r

r

r

r

k

j

i

r

r

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

=

+

+

−

−

+

−

+

+

−

+

)]

(

[

]

)

(

[

2

2

2

2

y

x

z

y

z

y

x

z

x

z

y

z

z

x

y

x

y

x

r

r

r

r

r

r

k

r

r

r

r

r

r

j

ω

ω

ω

ω

ω

ω

)

(

)

(

)

(

2

2

2

z

z

y

z

y

x

z

x

z

y

z

y

y

x

y

x

z

x

z

y

x

y

x

x

r

r

r

r

k

r

r

r

r

j

r

r

r

r

i

ρ

ω

ω

ω

ω

ρ

ω

ω

ω

ω

ρ

ω

+

−

−

+

−

+

−

+

−

−

=

Prof. Edmund Wittbrodt

Po scałkowaniu po masie bryły otrzymujemy:

)

(

)

(

)

(

z

z

yz

y

xz

x

yz

z

y

y

xy

x

xz

z

xy

y

x

x

O

J

D

D

k

D

J

D

j

D

D

J

i

K

ω

ω

ω

ω

ω

ω

ω

ω

ω

+

−

−

+

−

+

−

+

−

−

=

Powyższe równanie zapisać możemy właśnie w postaci:

[ ]





















⋅

=





















z

y

x

xyz

z

y

x

J

K

K

K

ω

ω

ω

,

gdzie

[ ]





















−

−

−

=

z

yz

y

xz

xy

x

xyz

J

sym

D

J

D

D

J

J

.

- macierz (tensor) bezwładności

.

Co było do udowodnienia.

Prof. Edmund Wittbrodt

Równanie ogólne

ruchu kulistego otrzymamy z twierdzenia o pochodnej względem czasu krętu bryły

O

O

K

M

=

&

,

(4.103)

co można zapisać w postaci układu trzech równań:

x

Ox

K

M

=

&

,

y

Oy

K

M

=

&

,

z

Oz

K

M

=

&

.

(4.104)

W równaniach (4.104) występują składowe wektora prędkości kątowej oraz masowe momenty bezwładności (4.100).
Ponieważ w nieruchomym układzie odniesienia zmieniają się wraz z położeniem ciała wartości masowych momentów
bezwładności, rozwiązanie równania (4.103) napotyka na ogromne trudności.

Dla pokonania powyższych trudności wyrażamy kręt w układzie ruchomym

, ,

ξ η ζ

, związanym z bryłą

[

,

,

]

O

K

J

J

J

ξ ξ

η η

ζ ζ

ω

ω

ω

.

W układzie tym wektor krętu w zapisie macierzowym ma postać

[ ]





















⋅

=





















ζ

η

ξ

ξηζ

ζ

η

ξ

ω

ω

ω

J

K

K

K

, (4.105)

gdzie:

[ ]

)

,

,

(

ζ

η

ξ

ξηζ

J

J

J

diag

J

=

.

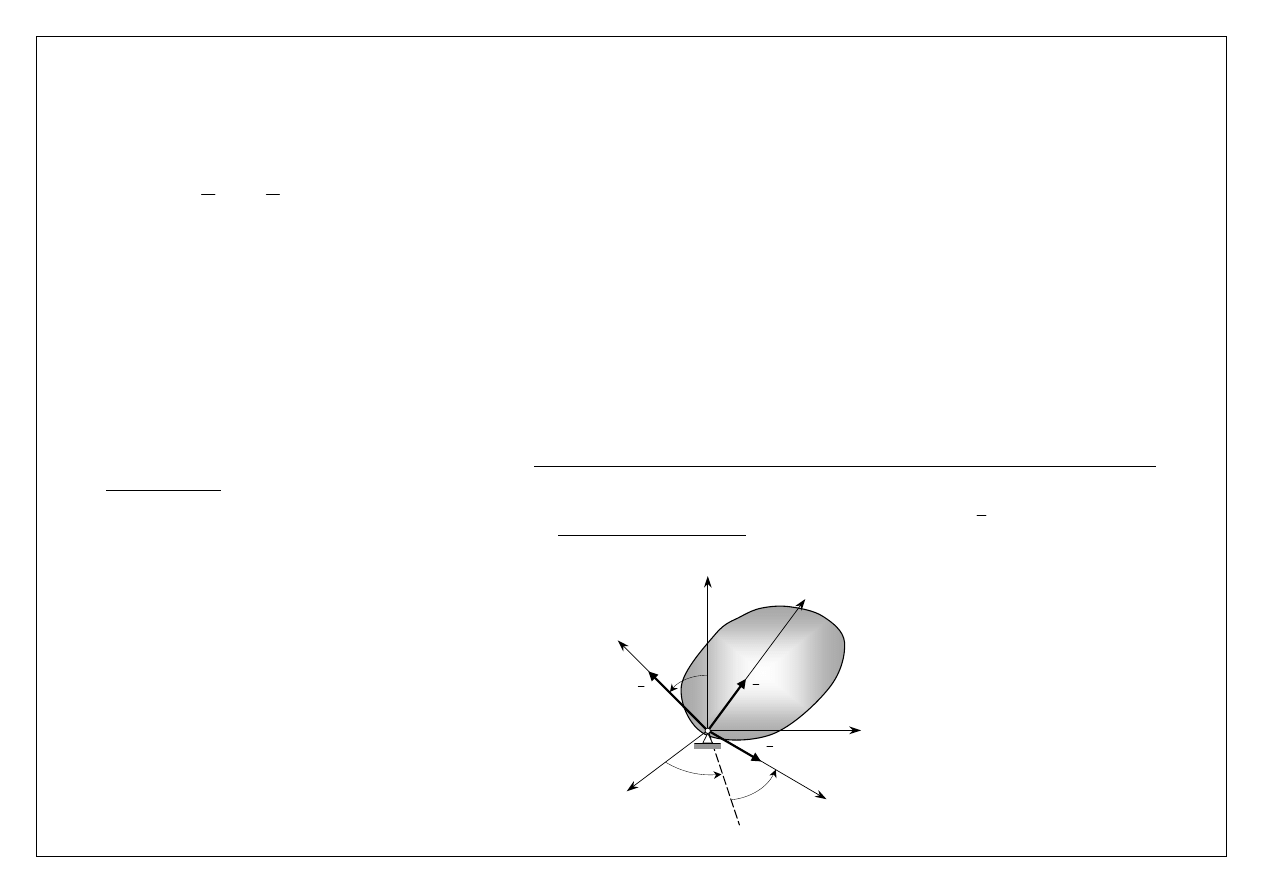
Bryła w ruchu kulistym

we współrzędnych prostokątnych i Eulera

ϕ

y

ξ

ψ

x

η

z

ζ

O

θ

ζ

ω

η

ω

ξ

ω

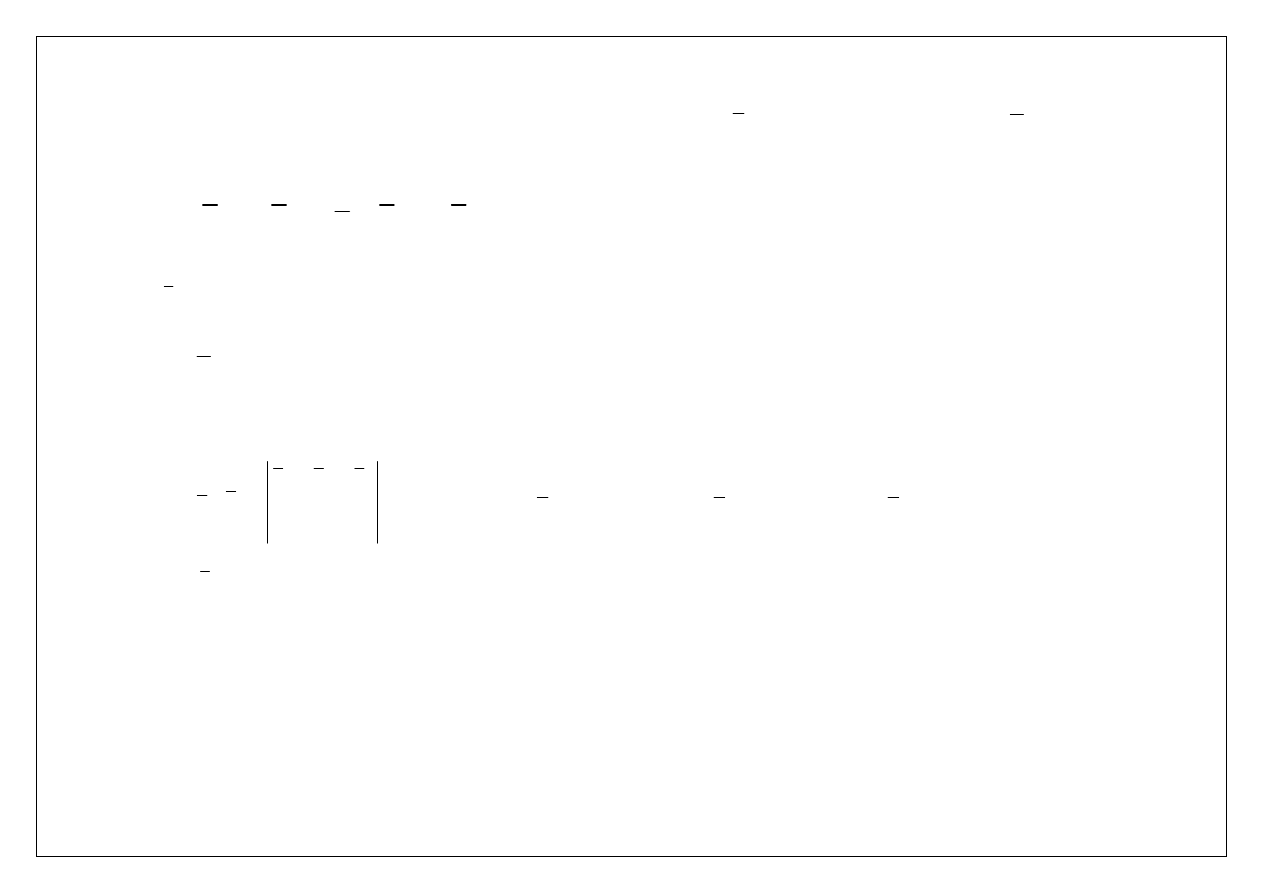
Prof. Edmund Wittbrodt

Następnie różniczkujemy względem czasu (4.103), pamiętając że wektor

O

K

wiruje z prędkością kątową

ω

. Zatem mamy

*

O

O

O

O

K

K

K

M

ω

=

+ ×

=

&

&

,

(4.106)

gdzie

*

O

K

&

– pochodna lokalna, której składowe

*

*

*

,

,

K

K

K

ξ

η

ζ

&

&

&

obliczamy z zależności macierzowej

[ ]





















⋅

=





















=

∗

∗

∗

∗

ζ

η

ξ

ξηζ

ζ

η

ξ

ω

ω

ω

&

&

&

&

&

&

&

J

K

K

K

K

O

,

(4.107)

zaś:

ξ

η

ζ

ξ

η

ζ

ξ

η

ζ

ω

ω

ω

ω

×

=

O

e

e

e

K

K

K

K

=

(

) (

) (

)

ζ η

η ζ

ξ

ζ ξ

ξ ζ

η

η ξ

ξ η

ζ

ω

ω

ω

ω

ω

ω

−

+

−

+

−

K

K

e

K

K

e

K

K

e

,

(4.108)

,

,

O

M

M

M

M

ξ

η

ζ





=





(4.109)

– moment wyrażony w układzie ruchomym.

Prof. Edmund Wittbrodt

Po podstawieniu (4.105), (4.107)–(4.109) do (4.106) otrzymujemy układ równań w postaci:

(

)

J

J

J

M

ξ ξ

η

ζ

η ζ

ξ

ω

ω ω

−

−

=

&

,

(

)

J

J

J

M

η η

ζ

ξ

ζ ξ

η

ω

ω ω

−

−

=

&

,

(4.110)

(

)

J

J

J

M

ζ ζ

ξ

η

ξ η

ζ

ω

ω ω

−

−

=

&

.

Równania (4.110) noszą nazwę

równań dynamicznych Eulera

. Po rozwiązaniu tych równań i podstawieniu rozwiązań do

(3.50) możemy określić zmiany kątów Eulera w funkcji czasu.

Zatem

wektor krętu obliczamy

względem nieruchomego układu odniesienia z zależności (4.99) lub (4.101), albo względem

ruchomego układu związanego z bryłą z zależności (4.105).

Prof. Edmund Wittbrodt

Energia kinetyczna

. Energia kinetyczna bryły w ruchu kulistym jest równa

2

2

2

1

(

)

2

x

x

y

y

z

z

yz

y

z

zx

z

x

xy

x

y

E

J

J

J

D

D

D

ω

ω

ω

ω ω

ω ω

ω ω

=

+

+

−

−

−

,

(4.111)

co można zapisać w postaci macierzowej

{ }

[ ]

{ }

ω

ω

⋅

⋅

=

xyz

T

J

E

2

1

,

(4.112)

gdzie

{ }

)

,

,

(

z

y

x

col

ω

ω

ω

ω

=

.

Jeżeli znamy położenie

chwilowej osi obrotu

l

i masowy moment bezwładności względem tej osi, to energię kinetyczną

możemy też obliczyć z zależności

2

1

2

l

E

J

ω

=

,

(4.113)

gdzie

J

l

– masowy moment bezwładności względem chwilowej osi obrotu.

Ruch kulisty bryły wokół chwilowej osi obrotu

O

l

ω