E

st

y

m

a

to

ry

.

E

st

y

m

a

cj

a

p

u

n

k

to

w

a

i

p

rz

ed

zi

a

ło

w

a

.

•

Z

a

d

a

n

ie

m

s

ta

ty

st

y

k

i

m

a

te

m

a

ty

cz

n

ej

j

es

t

u

zy

sk

a

n

ie

i

n

fo

rm

a

cj

i

o

c

a

łe

j

p

o

p

u

la

cj

i

n

a

p

o

d

st

a

w

ie

p

ró

b

y

p

o

ch

o

d

zą

ce

j

z

te

j

p

o

p

u

la

cj

i.

•

Z

ał

ó

żm

y

,

że

w

zr

o

st

d

o

ro

sł

y

ch

m

ęż

cz

y

zn

w

p

o

p

u

la

cj

i

o

p

is

y

w

an

y

j

es

t

p

rz

ez

r

o

zk

ła

d

n

o

rm

al

n

y

N

(

m

=

?

,

s

2

=

5

2

).

•

m

je

st

w

t

y

m

p

rz

y

p

ad

k

u

n

ie

zn

an

y

m

p

ar

am

et

re

m

r

o

zk

ła

d

u

n

o

rm

al

n

eg

o

.

•

In

ac

ze

j

m

ó

w

ią

c,

m

je

st

n

ie

zn

an

y

m

p

ar

am

et

re

m

p

o

p

u

la

cj

i,

w

k

tó

re

j

ro

zk

ła

d

c

ec

h

y

j

es

t

o

p

is

y

w

an

y

p

rz

ez

p

o

w

y

żs

zy

r

o

zk

ła

d

.

•

Z

a

m

ie

rz

a

m

y

o

sz

a

co

w

a

ć

te

n

n

ie

zn

a

n

y

p

a

ra

m

et

r

w

o

p

a

rc

iu

o

i

n

fo

rm

a

cj

e

z

p

ró

b

y

l

o

so

w

ej

p

o

b

ra

n

ej

z

p

o

p

u

la

cj

i.

•

P

o

n

ie

w

aż

p

ar

am

et

r

m

je

st

w

ar

to

śc

ią

śr

ed

n

ią

ro

zk

ła

d

u

n

o

rm

al

n

eg

o

,

to

w

y

d

aj

e

si

ę

n

at

u

ra

ln

e,

ż

e

m

o

żn

a

o

sz

a

co

w

a

ć

(i

n

a

cz

ej

:

es

ty

m

o

w

a

ć)

t

en

p

a

ra

m

et

r

za

p

o

m

o

cą

śr

ed

n

ie

j

z

p

ró

b

y

.

•

P

ro

b

le

m

:

w

r

ó

żn

y

ch

p

ró

b

ac

h

p

o

b

ra

n

y

ch

z

p

o

p

u

la

cj

i

te

ś

re

d

n

ie

m

o

g

ą

b

y

ć

ró

żn

e,

n

p

.

p

ró

b

a

n

r

1

:

1

7

8

1

7

8

1

7

8

1

7

4

1

7

6

1

7

9

1

7

5

1

7

4

1

7

6

p

ró

b

a

n

r

2

:

1

7

2

1

7

5

1

7

6

1

7

2

1

7

2

1

7

5

1

7

7

1

8

3

1

7

1

p

ró

b

a

n

r

3

:

1

7

7

1

8

0

1

7

0

1

7

2

1

7

7

1

7

9

1

7

4

1

8

0

1

7

5

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

.

śr

ed

n

ia

z

p

ró

b

y

n

r

1

:

1

7

6

,4

śr

ed

n

ia

z

p

ró

b

y

n

r

2

:

1

7

4

,8

śr

ed

n

ia

z

p

ró

b

y

n

r

3

:

1

7

6

,0

•

T

ak

ie

w

ie

lk

o

śc

i,

k

tó

re

m

o

żn

a

o

b

li

cz

y

ć

n

a

p

o

d

st

aw

ie

d

an

y

ch

z

p

ró

b

y

,

n

az

y

w

a

si

ę

st

a

ty

st

y

k

a

m

i

.

•

Ś

re

d

n

ia

z

p

ró

b

y

j

es

t

p

rz

y

k

ła

d

em

s

ta

ty

st

y

k

i.

•

In

n

y

p

rz

y

k

ła

d

s

ta

ty

st

y

k

i:

w

ar

ia

n

cj

a

z

p

ró

b

y

p

ró

b

a

n

r

1

:

1

7

8

1

7

8

1

7

8

1

7

4

1

7

6

1

7

9

1

7

5

1

7

4

1

7

6

p

ró

b

a

n

r

2

:

1

7

2

1

7

5

1

7

6

1

7

2

1

7

2

1

7

5

1

7

7

1

8

3

1

7

1

p

ró

b

a

n

r

3

:

1

7

7

1

8

0

1

7

0

1

7

2

1

7

7

1

7

9

1

7

4

1

8

0

1

7

5

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

..

.

w

ar

ia

n

cj

a

z

p

ró

b

y

n

r

1

:

3

,5

3

w

ar

ia

n

cj

a

z

p

ró

b

y

n

r

2

:

1

3

,9

4

w

ar

ia

n

cj

a

z

p

ró

b

y

n

r

3

:

1

2

,5

0

(

)

1

1

2

2

−

−

=

∑

=

n

x

x

S

n

i

i

•

W

ar

to

ść

d

an

ej

s

ta

ty

st

y

k

i

za

le

ży

o

d

d

an

y

ch

w

p

ró

b

ie

i

d

la

r

ó

żn

y

ch

p

ró

b

p

rz

y

jm

u

je

r

ó

żn

e

w

ar

to

śc

i.

•

S

ta

ty

st

y

k

a

j

es

t

za

te

m

z

m

ie

n

n

ą

l

o

so

w

ą

i

m

a

s

w

ó

j

ro

zk

ła

d

p

ra

w

d

o

p

o

d

o

b

ie

ń

st

w

a

.

•

P

rz

y

k

ła

d

o

w

o

,

zn

an

y

j

es

t

ro

zk

ła

d

p

ra

w

d

o

p

o

d

o

b

ie

ń

st

w

a

śr

ed

n

ie

j

z

p

ró

b

y

:

J

eś

li

p

ró

b

y

ro

zm

ia

ru

n

p

o

ch

o

d

zą

z

ro

zk

ła

d

u

n

o

rm

a

ln

eg

o

N

(m

,

s

2

),

to

ś

re

d

n

ie

z

p

ró

b

m

a

ją

ro

zk

ła

d

n

o

rm

a

ln

y

z

w

a

rt

o

śc

ią

śr

ed

n

ią

m

o

ra

z

w

a

ri

a

n

cj

ą

s

2

/

n

.

•

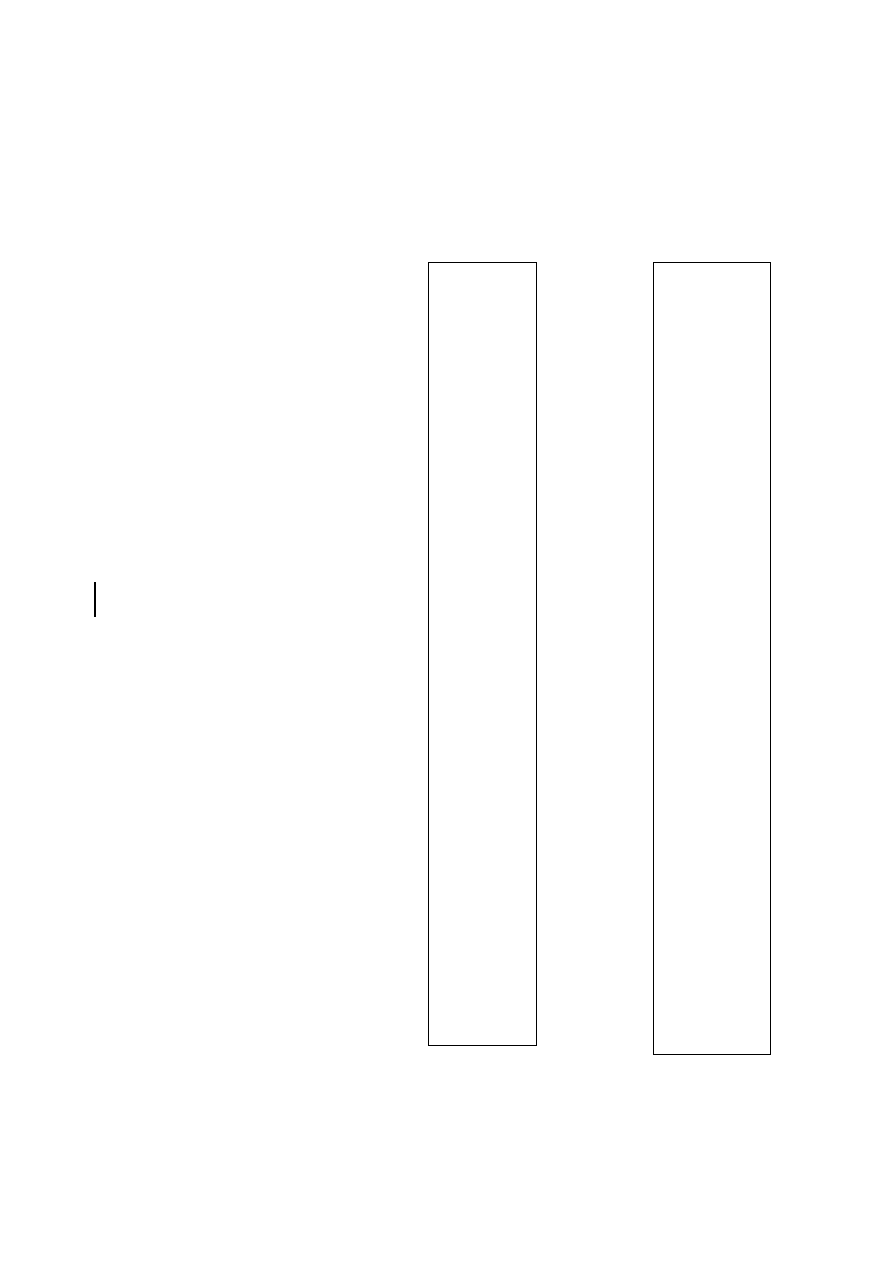
Ś

re

d

n

ią

z

p

ró

b

y

o

zn

ac

za

m

y

p

rz

ez

•

N

al

eż

y

w

y

ra

źn

ie

r

o

zr

ó

żn

ić

ś

re

d

n

ią

z

p

ró

b

y

,

k

tó

ra

j

es

t

zm

ie

n

n

ą

lo

so

w

ą

o

d

w

ar

to

śc

i

te

j

zm

ie

n

n

ej

l

o

so

w

ej

w

k

o

n

k

re

tn

ej

p

ró

b

ie

(

ta

w

ar

to

ść

je

st

k

o

n

k

re

tn

ą

li

cz

b

ą)

.

•

D

la

r

o

zr

ó

żn

ie

n

ia

,

zm

ie

n

n

e

lo

so

w

e

są

o

zn

ac

za

n

e

d

u

ży

m

i

li

te

ra

m

i,

z

aś

ic

h

w

ar

to

śc

i

(l

ic

zb

y

)

m

ał

y

m

i

li

te

ra

m

i.

•

T

ak

ą

st

at

y

st

y

k

ę,

k

tó

ra

s

łu

ży

d

o

o

sz

ac

o

w

an

ia

d

an

eg

o

p

ar

am

et

ru

,

n

az

y

w

a

si

ę

es

ty

m

a

to

re

m

te

g

o

p

ar

am

et

ru

.

•

Ś

re

d

n

ia

z

p

ró

b

y

j

es

t

es

ty

m

a

to

re

m

p

a

ra

m

et

ru

m

(w

ar

to

śc

i

śr

ed

n

ie

j

ro

zk

ła

d

u

n

o

rm

al

n

eg

o

)

•

P

ro

ce

s

sz

ac

o

w

an

ia

n

ie

zn

an

ej

w

ar

to

śc

i

p

ar

am

et

ru

p

o

p

u

la

cj

i

n

a

p

o

d

st

aw

ie

p

ró

b

y

n

az

y

w

a

si

ę

es

ty

m

a

cj

ą

.

X

•

R

o

zr

ó

żn

ia

s

ię

d

w

a

r

o

d

za

je

e

st

y

m

a

cj

i:

es

ty

m

ac

ję

p

u

n

k

to

w

ą

i

p

rz

ed

zi

a

ło

w

ą

.

•

W

y

n

ik

ie

m

e

st

y

m

a

cj

i

p

u

n

k

to

w

ej

d

a

n

eg

o

p

a

ra

m

et

ru

j

es

t

k

o

n

k

re

tn

a

li

cz

b

a

,

k

tó

ra

s

ta

n

o

w

i

o

sz

a

co

w

a

n

ie

t

eg

o

p

a

ra

m

et

ru

.

•

P

rz

y

k

ła

d

o

w

o

,

g

d

y

b

y

b

y

ła

w

y

lo

so

w

an

a

p

ró

b

a

n

r

1

:

1

7

8

1

7

8

1

7

8

1

7

4

1

7

6

1

7

9

1

7

5

1

7

4

1

7

6

to

j

ak

o

p

u

n

k

to

w

e

o

sz

ac

o

w

an

ie

p

ar

am

et

ru

m

p

rz

y

ję

to

b

y

ś

re

d

n

ią

z

p

ró

b

y

,

w

t

y

m

p

rz

y

p

ad

k

u

w

y

n

o

si

1

7

6

,4

c

m

.

•

Ś

re

d

n

ia

z

p

ró

b

y

j

es

t

es

ty

m

a

to

re

m

p

u

n

k

to

w

y

m

p

a

ra

m

et

ru

m

.

•

O

zn

ac

za

t

o

,

że

n

a

p

o

d

st

aw

ie

w

ar

to

śc

i

w

k

o

n

k

re

tn

ej

p

ró

b

ie

w

y

zn

ac

za

m

y

w

ar

to

ść

te

g

o

e

st

y

m

at

o

ra

i

w

ar

to

ść

ta

j

es

t

p

o

je

d

y

n

cz

ą

li

cz

b

ą.

•

W

y

n

ik

ie

m

e

st

y

m

a

cj

i

p

rz

ed

zi

a

ło

w

ej

j

es

t

p

rz

ed

zi

a

ł

li

cz

b

o

w

y

n

a

zy

w

a

n

y

p

rz

ed

zi

a

łe

m

u

fn

o

śc

i.

•

Is

tn

ie

ją

w

zo

ry

,

k

tó

re

p

o

zw

al

aj

ą

w

y

zn

ac

zy

ć

p

rz

ed

zi

ał

u

fn

o

śc

i

d

la

d

an

eg

o

p

ar

am

et

ru

.

•

P

rz

y

k

ła

d

o

w

o

,

g

d

y

b

y

b

y

ła

w

y

lo

so

w

an

a

p

ró

b

a

n

r

1

:

1

7

8

1

7

8

1

7

8

1

7

4

1

7

6

1

7

9

1

7

5

1

7

4

1

7

6

to

j

ak

o

p

rz

ed

zi

ał

o

w

e

o

sz

ac

o

w

an

ie

p

ar

am

et

ru

m

n

a

p

o

zi

o

m

ie

u

fn

o

śc

i

9

5

%

p

rz

y

ję

to

b

y

p

rz

ed

zi

ał

[

1

7

3

,1

c

m

;

1

7

9

,7

c

m

]

p

ró

b

a

n

r

2

:

1

7

2

1

7

5

1

7

6

1

7

2

1

7

2

1

7

5

1

7

7

1

8

3

1

7

1

to

j

ak

o

p

rz

ed

zi

ał

o

w

e

o

sz

ac

o

w

an

ie

p

ar

am

et

ru

m

n

a

p

o

zi

o

m

ie

u

fn

o

śc

i

9

5

%

p

rz

y

ję

to

b

y

p

rz

ed

zi

ał

[

1

7

1

,5

c

m

;

1

7

8

,1

c

m

]

P

ro

b

le

m

zw

ią

za

n

y

z

e

st

y

m

ac

ją

p

u

n

k

to

w

ą

i

p

rz

ed

zi

ał

o

w

ą:

•

o

sz

ac

o

w

an

ie

n

ie

zn

an

eg

o

p

ar

am

et

ru

u

st

al

a

si

ę

w

o

p

ar

ci

u

o

d

an

e

z

k

o

n

k

re

tn

ej

p

ró

b

y

•

w

i

n

n

ej

p

ró

b

ie

t

o

o

sz

ac

o

w

an

ie

p

rz

y

ję

ło

b

y

z

ap

ew

n

e

in

n

ą

w

ar

to

ść

•

w

y

st

ęp

u

je

z

at

em

r

o

zr

zu

t

o

sz

ac

o

w

ań

,

k

tó

re

m

o

żn

a

b

y

u

zy

sk

ać

w

o

p

ar

ci

u

o

ró

żn

e

p

ró

b

y

.

Ja

k

ie

m

o

żn

a

m

ie

ć

w

o

b

ec

t

eg

o

z

au

fa

n

ie

d

o

o

sz

ac

o

w

an

ia

,

k

tó

re

u

zy

sk

al

iś

m

y

w

o

p

ar

ci

u

o

k

o

n

k

re

tn

ą

w

y

lo

so

w

an

ą

p

ró

b

ę?

•

W

p

rz

y

p

ad

k

u

e

st

y

m

ac

ji

p

u

n

k

to

w

ej

p

ro

b

le

m

t

en

c

zę

śc

io

w

o

r

o

zw

ią

zu

je

si

ę

p

o

d

aj

ąc

t

zw

.

b

łą

d

s

ta

n

d

a

rd

o

w

y

e

st

y

m

a

to

ra

(l

u

b

o

sz

ac

o

w

an

ie

t

eg

o

b

łę

d

u

u

zy

sk

an

e

n

a

p

o

d

st

aw

ie

p

ró

b

y

).

•

B

łą

d

s

ta

n

d

a

rd

o

w

y

e

st

y

m

a

to

ra

to

o

d

ch

y

le

n

ie

s

ta

n

d

a

rd

o

w

e

te

g

o

es

ty

m

a

to

ra

.

•

W

a

n

al

iz

o

w

an

y

m

p

rz

y

k

ła

d

zi

e

es

ty

m

at

o

re

m

p

ar

am

et

ru

m

i

b

y

ła

ś

re

d

n

ia

z

p

ró

b

y

.

W

ia

d

o

m

o

,

ja

k

i

je

st

r

o

zk

ła

d

p

ra

w

d

o

p

o

d

o

b

ie

ń

st

w

a

te

g

o

es

ty

m

at

o

ra

:

J

eś

li

p

ró

b

y

ro

zm

ia

ru

n

p

o

ch

o

d

zą

z

ro

zk

ła

d

u

n

o

rm

a

ln

eg

o

N

(m

,

s

2

),

to

ś

re

d

n

ie

z

p

ró

b

m

a

ją

ro

zk

ła

d

n

o

rm

a

ln

y

z

w

a

rt

o

śc

ią

śr

ed

n

ią

m

o

ra

z

w

a

ri

a

n

cj

ą

s

2

/

n

.

•

O

d

ch

y

le

n

ie

s

ta

n

d

ar

d

o

w

e

śr

ed

n

ie

j

z

p

ró

b

y

j

es

t

w

o

b

ec

t

eg

o

r

ó

w

n

e

•

B

łą

d

s

ta

n

d

a

rd

o

w

y

ś

re

d

n

ie

j

z

p

ró

b

y

j

es

t

ró

w

n

y

n

σ

n

σ

•

W

a

n

al

iz

o

w

an

y

m

p

rz

y

k

ła

d

zi

e

m

am

y

z

ał

o

że

n

ie

,

że

p

ró

b

a

p

o

ch

o

d

zi

z

ro

zk

ła

d

u

N

(

m

=

?

,s

2

=

5

2

)

•

W

o

b

ec

t

eg

o

b

łą

d

s

ta

n

d

ar

d

o

w

y

j

es

t

ró

w

n

y

o

k

o

ło

1

,6

7

c

m

.

•

W

p

rz

y

p

ad

k

u

e

st

y

m

ac

ji

p

rz

ed

zi

ał

o

w

ej

,

p

re

cy

zj

ę

es

ty

m

a

cj

i

o

k

re

śl

a

d

łu

g

o

ść

p

rz

ed

zi

ał

u

u

fn

o

śc

i.

•

Ja

k

o

m

a

k

sy

m

a

ln

y

b

łą

d

s

za

cu

n

k

u

p

rz

y

e

st

y

m

a

cj

i

p

rz

ed

zi

a

ło

w

ej

p

rz

y

jm

u

je

s

ię

p

o

ło

w

ę

d

łu

g

o

śc

i

p

rz

ed

zi

a

łu

u

fn

o

śc

i.

•

N

ie

ch

a

b

ęd

zi

e

p

ew

n

ą

li

cz

b

ą

z

p

rz

ed

zi

ał

u

(

0

,

1

).

(1

–

a

)·

1

0

0

%

p

r

ze

d

zi

a

ł

u

fn

o

śc

i

d

la

n

ie

zn

an

eg

o

p

ar

am

et

ru

p

o

p

u

la

cj

i

to

p

rz

ed

zi

ał

l

ic

zb

o

w

y

[

a,

b

],

k

tó

ry

s

p

eł

n

ia

n

as

tę

p

u

ją

ce

w

ar

u

n

k

i

1

.

K

o

ń

ce

a

,

b

te

g

o

p

rz

ed

zi

ał

u

p

rz

y

jm

u

ją

w

ar

to

śc

i

za

le

żn

e

o

d

t

eg

o

,

co

o

b

se

rw

o

w

an

o

w

p

ró

b

ie

.

2

.

Z

p

ra

w

d

o

p

o

d

o

b

ie

ń

st

w

em

r

ó

w

n

y

m

(

1

–

a

)

p

rz

ed

zi

ał

te

n

p

o

k

ry

w

a

p

ra

w

d

zi

w

ą

w

ar

to

ść

p

o

sz

u

k

iw

an

eg

o

p

ar

am

et

ru

p

o

p

u

la

cj

i.

•

W

sp

ó

łc

zy

n

n

ik

(1

–

a

)

n

az

y

w

a

si

ę

p

o

zi

o

m

em

u

fn

o

śc

i

.

•

N

a

o

g

ó

ł

p

rz

y

jm

u

je

s

ię

,

że

1

–

a

=

0

,9

5

(

co

o

d

p

o

w

ia

d

a

9

5

%

p

rz

ed

zi

ał

o

w

i

u

fn

o

śc

i)

l

u

b

1

–

a

=

0

,9

9

(

co

o

d

p

o

w

ia

d

a

9

9

%

p

rz

ed

zi

ał

o

w

i

u

fn

o

śc

i)

.

•

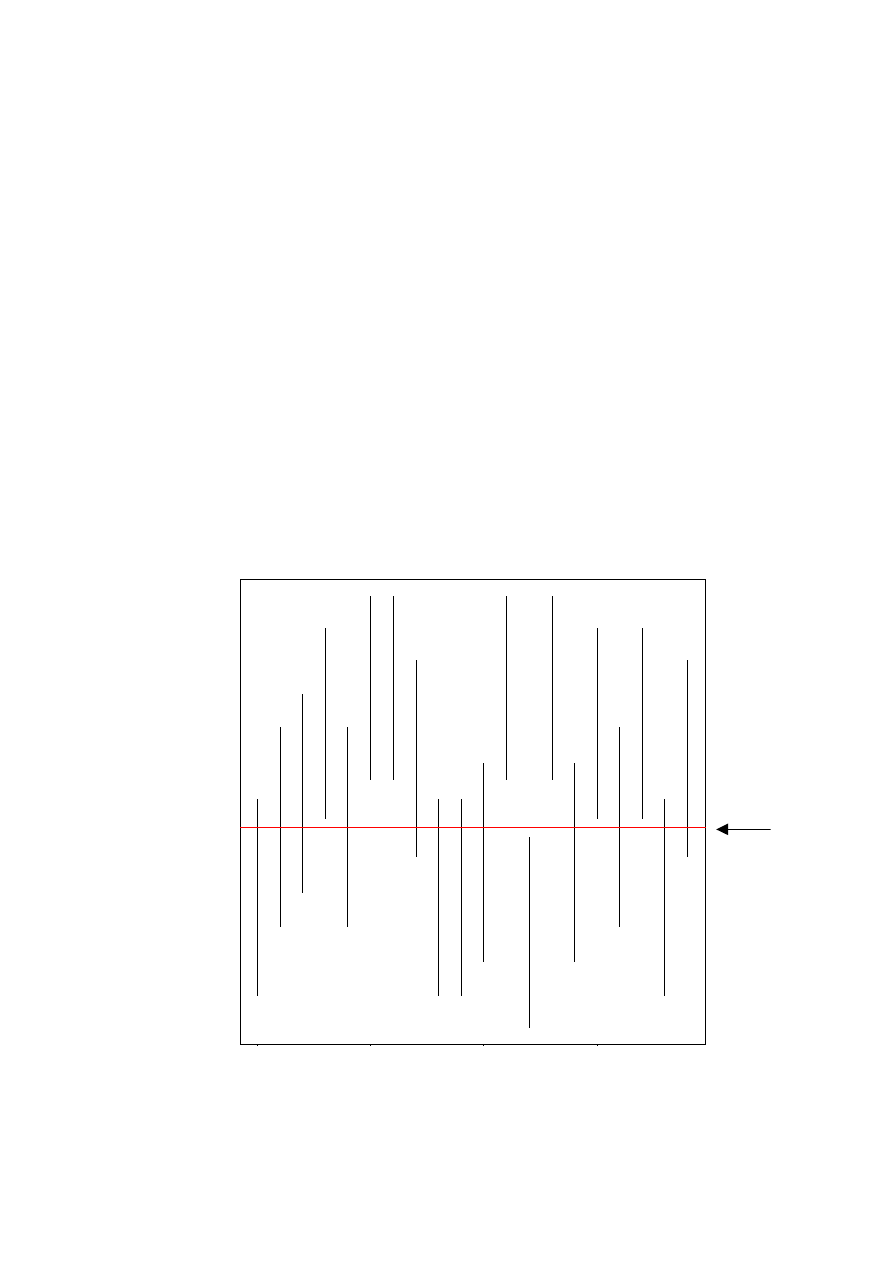
M

ó

w

ią

c

in

ac

ze

j,

p

rz

ed

zi

a

ł

u

fn

o

śc

i

d

la

d

a

n

eg

o

p

a

ra

m

et

ru

p

o

p

u

la

cj

i

to

p

rz

ed

zi

a

ł

o

k

o

ń

ca

ch

z

a

le

żn

y

ch

o

d

p

ró

b

y

i

t

a

k

i,

k

tó

ry

z

z

a

d

a

n

y

m

z

g

ó

ry

d

u

ży

m

p

ra

w

d

o

p

o

d

o

b

ie

ń

st

w

em

p

o

k

ry

w

a

p

ra

w

d

zi

w

ą

n

ie

zn

a

n

ą

w

a

rt

o

ść

p

a

ra

m

et

ru

p

o

p

u

la

cj

i.

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

P

rz

ed

zi

ał

y

u

fn

o

śc

i

u

zy

sk

an

e

d

la

r

ó

żn

y

ch

p

ró

b

t

eg

o

s

am

eg

o

ro

zm

ia

ru

:

(1

–

a

)·

1

0

0

%

z

t

y

ch

p

r

ze

d

zi

a

łó

w

p

o

k

ry

w

a

p

ra

w

d

zi

w

ą

w

a

rt

o

ść

n

ie

zn

a

n

eg

o

p

a

ra

m

et

ru

.

p

ra

w

d

zi

w

a

w

a

rt

o

ść

p

a

ra

m

et

ru

•

Ja

k

o

ść

e

st

y

m

ac

ji

z

al

eż

y

o

d

n

ar

zę

d

zi

a,

p

rz

y

p

o

m

o

cy

k

tó

re

g

o

d

o

k

o

n

u

je

m

y

e

st

y

m

ac

ji

.

T

y

m

n

ar

zę

d

zi

em

j

es

t

es

ty

m

at

o

r

d

an

eg

o

p

ar

am

et

ru

.

•

W

a

n

al

iz

o

w

an

y

m

p

rz

y

k

ła

d

zi

e

es

ty

m

at

o

re

m

p

ar

am

et

ru

m

je

st

ś

re

d

n

ia

z

p

ró

b

y

,

al

e

m

o

żn

a

w

y

o

b

ra

zi

ć

so

b

ie

i

n

n

y

e

st

y

m

at

o

r

p

ar

am

et

ru

m

,

n

p

.

m

ed

ia

n

ę

z

p

ró

b

y

.

U

za

sa

d

n

ie

n

ie

:

z

za

ło

że

n

ia

p

ró

b

a

p

o

ch

o

d

zi

z

r

o

zk

ła

d

u

n

o

rm

al

n

eg

o

.

R

o

zk

ła

d

n

o

rm

al

n

y

j

es

t

ro

zk

ła

d

em

s

y

m

et

ry

cz

n

y

m

,

a

d

la

r

o

zk

ła

d

ó

w

sy

m

et

ry

cz

n

y

ch

z

ac

h

o

d

zi

,

że

ś

re

d

n

ia

a

ry

tm

et

y

cz

n

a

=

m

ed

ia

n

a.

•

P

o

w

st

aj

e

za

te

m

k

w

es

ti

a

w

y

b

o

ru

n

aj

le

p

sz

eg

o

m

o

żl

iw

eg

o

e

st

y

m

at

o

ra

d

la

d

an

eg

o

p

ar

am

et

ru

.

•

Ja

k

ie

k

ry

te

ri

a

st

o

so

w

ać

d

o

o

ce

n

y

e

st

y

m

at

o

ró

w

?

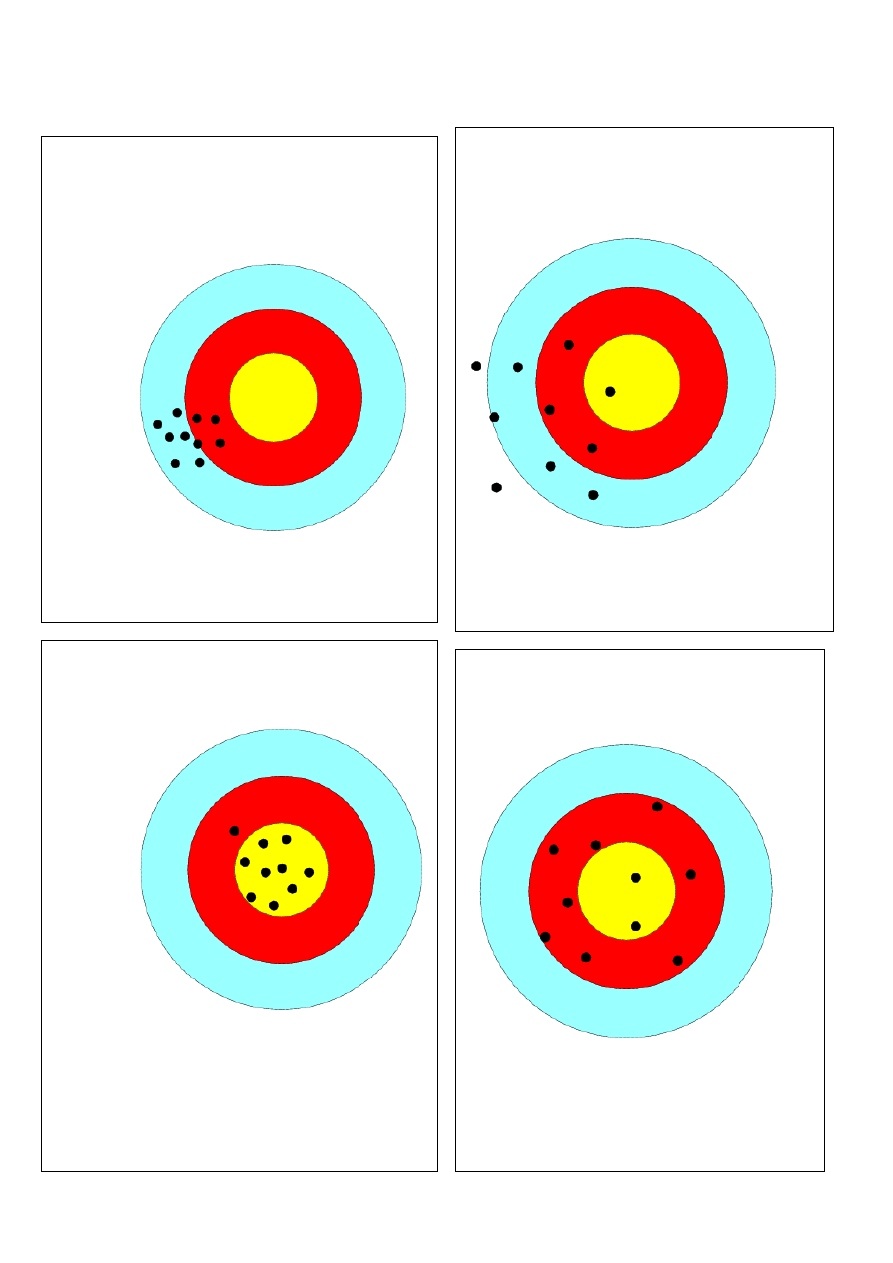
E

st

y

m

at

o

r

o

b

ci

ąż

o

n

y

,

o

m

ał

ej

w

ar

ia

n

cj

i

E

st

y

m

at

o

r

o

b

ci

ąż

o

n

y

,

o

d

u

że

j

w

ar

ia

n

cj

i

E

st

y

m

at

o

r

n

ie

o

b

ci

ąż

o

n

y

,

o

d

u

że

j

w

ar

ia

n

cj

i

E

st

y

m

at

o

r

n

ie

o

b

ci

ąż

o

n

y

,

o

m

ał

ej

w

ar

ia

n

cj

i