Rozkłady statystyk

Własności estymatorów

Estymacja punktowa

 

Odchylenie standardowe z

próby

Wariancja z próby

Dla małych prób 

Jeżeli znana jest średnia rozkładu generalnego (a priori )
m to używamy następującej postaci wariancji z próby:

2

S

S 















n

i

i

X

X

n

S

n

n

S

1

2

2

2

)

(

1

1

1

ˆ









n

i

i

m

X

n

S

1

2

2

*

)

(

1

















n

i

i

n

i

i

X

X

n

X

X

n

S

1

2

2

1

2

2

1

)

(

1

Wyznaczanie rozkładów statystyk

Wektor losowy X =(X

1

,X

2

,...,X

n

) oznacza n-

elementową próbę. Dowolna statystyka Z

n

=g(X) –jest

zmienną losową, której rozkład jest zależny od:


    

Liczebności próby



    

Schematu losowania



    

Rozkładu populacji, z której pochodzi próba X

Postaci funkcji g określającej statystykę

Ze względu na liczebność próby:

Rozkład dokładny statystyki – rozkład wyznaczony dla
każdej (dowolnej) liczby naturalnej traktowanej jak
znany parametr rozkładu.

Rozkład graniczny - taki rozkład prawdopodobieństwa
tej statystyki, który otrzymuje się przy założeniu
nieograniczenie dużej próby

Rozkład graniczny często nie zależy od rozkładu
populacji, z której losujemy próbę.

Konsekwencje centralnego twierdzenia granicznego:

Dla niektórych statystyk dokładny rozkład Z

n

dla n>30

na tyle mało różni się od rozkładu granicznego, że w
praktyce wnioskowanie statystyczne przeprowadza się
dla rozkładu granicznego dla każdej próby n>30 .
Niekiedy jednak dopiero dla próbek o liczebności >100
rozkład graniczny daje dobre przybliżenie dokładnego
rozkładu statystyki Z

n

.

Twierdzenie 1

Jeżeli dana ciągła zmienna losowa X ma znany rozkład o
funkcji gęstości f(x) i jeżeli g jest pewną monotoniczną
i różniczkowalną funkcją a h jest funkcją do niej
odwrotną to zmienna losowa Y = g(X) ma rozkład
określony funkcją gęstości:

)

(

gdzie

))

(

[

)

(

y

h

x

dy

dx

y

h

f

x









Przykła
d



















2

2

2

)

(

exp

2

1

)

(







m

x

x

f



m

X

U











m

x

u

g

e

u

u









:

2

1

)

(

2

2

1



u

m

x

h





:





du

dx

Dana jest zm. losowa o rozkładzie N(m,

), i gęstości

:

Zmienna losowa
unormowana:

ma gęstość:

Przekształcenie
odwrotne:

Twierdzenie 2

Jeżeli dla dwuwymiarowej zmiennej losowej (X,Y) o
znanym rozkładzie określonym funkcją gęstości f(x,y)
dane są ciągłe, monotoniczne i różniczkowalne
przekształcenia u = g

1

(x,y) i

v = g

2

(x,y) do których przekształceniami odwrotnymi są

x = h

1

(u,v) i y = h

2

(u,v) , to zmienna losowa (U,V) na

rozkład o funkcji gęstości

 
gdzie J jest jakobianem przekształcenia odwrotnego
określonym jako

J

v

u

h

v

u

h

f

v

u





))

,

(

),

,

(

(

)

,

(

2

1



v

y

u

y

v

x

u

x

J



















Z wyznaczonego w ten sposób dwuwymiarowego
rozkładu (U,V) łatwo jest uzyskać jednowymiarowy
rozkład samej, np. zmiennej V za pomocą całkowania
względem U:

 
To twierdzenie łatwo uogólnić dla n-wymiarym
zmiennych losowych (wektorów losowych) X,Y.
Znajdując gęstość f(x) rozkładu wektor X oraz funkcję
(wektor) y = g(x), do którego przekształceniem
odwrotnym jest (wektor) x = h(y) , otrzymujemy gęstość



(y) wektora losowego Y jako:











du

v

u

v

)

,

(

)

(

1





J

f





)

(

)

(

x

y



gdzie
oraz jakobian

)

(y

x h



y

x







J

Rozkład średniej arytmetycznej z

próby







n

i

i

X

n

X

1

1

Często posługujemy się różnicą
średnich arytmetycznych z dwu
prób wylosowanych niezależnie z
dwu populacji, tzn. statystyką
postaci

2

1

X

X 

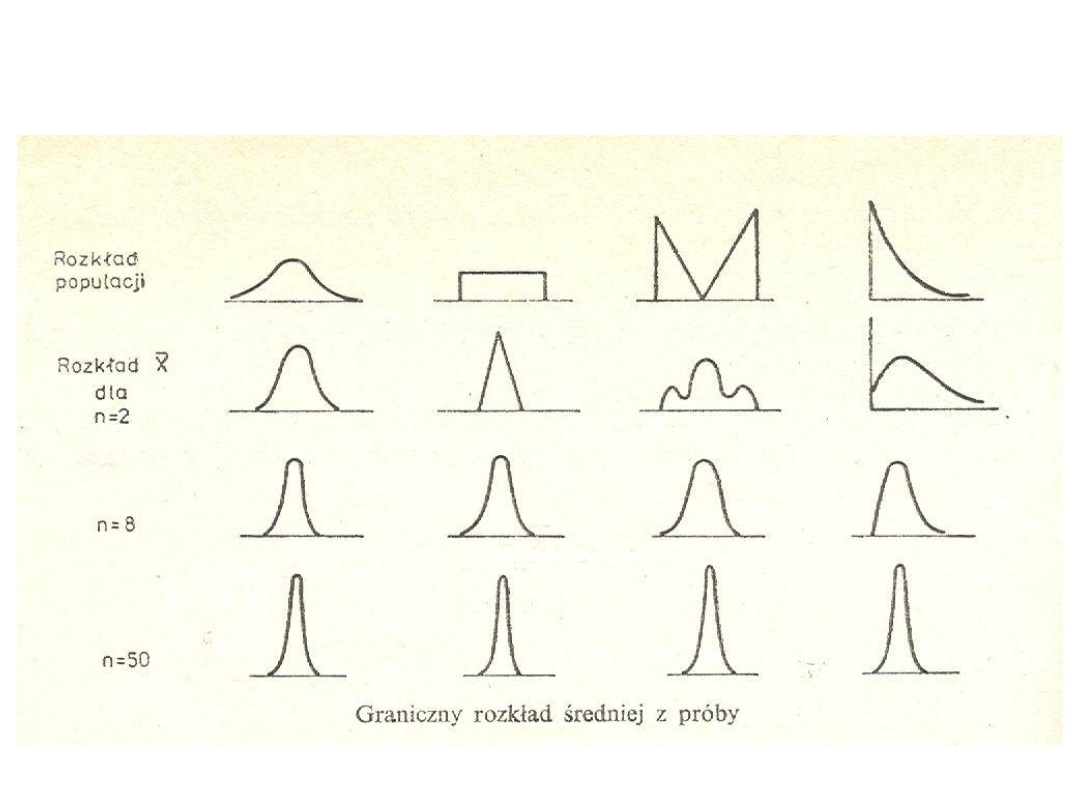
Dokładny rozkład statystyki tj. średniej arytmetycznej z n-elementowej
próby prostej, zależy oczywiście od rozkładu populacji generalnej, z której
losujemy próby proste, zależy oczywiście od rozkładu populacji generalnej, z
której losujemy próbę.
Można wykazać, że średnia arytmetyczna z próby prostej, wylosowana z
populacji o takich rozkładach jak

dwumianowy, Poissona, normalny

ma

odpowiednio taki sam rozkład jak populacja, ale o innych parametrach.
Ze względu na dużą częstość występowania w praktyce (zwłaszcza w
zagadnieniach przyrodniczych i technicznych) populacji o rozkładzie
normalnym, znajdziemy rozkład średniej arytmetycznej z próby prostej
wylosowanej z populacji o rozkładzie normalnym N(m,

) ze znanymi

parametrami.

X

X

X

Rozkład średniej z próby

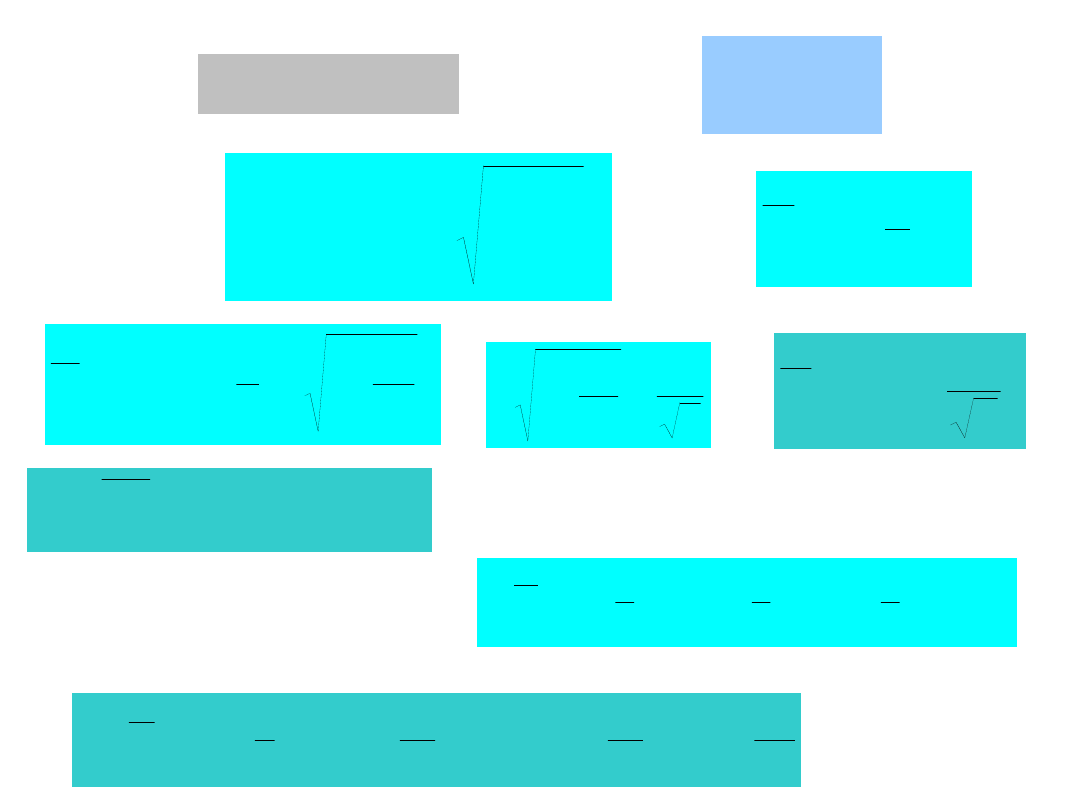
Jeżeli to

)

,

(

~



m

N

X







n

i

i

i

X

a

Y

1























n

i

i

n

i

i

a

a

m

N

1

2

1

,



ma rozkład







n

i

i

X

n

X

1

1























n

i

n

i

n

n

m

N

X

1

1

2

1

,

1

~



n

n

n

i









1

2

1













n

m

N

X



,

~

 
 

EX

m

X

E





)

(

m

m

n

X

E

n

X

n

E

X

E

n

i

i

n

i

i





























1

1

1

)

(

1

1

)

(

n

n

X

D

n

X

n

D

X

D

n

i

n

i

i

n

i

i

2

1

2

2

1

2

2

1

2

2

1

)

(

1

1

)

(





































poprawka na skończoność

populacji

Gdy próbę losujemy z populacji skończonej bez zwracania
to można wykazać, że wprawdzie zachodzi

Ale wariancja średniej z próby jest dana wzorem

 
Ten ostatni czynnik jest nazywany poprawką na
skończoność populacji

EX

m

X

E





)

(

1

)

(

2

2









N

n

N

n

X

D



Twierdzenie 3

Jeżeli z populacji o rozkładzie normalnym N(m,σ)
losujemy
n-elementową próbę prostą, to statystyka

ma unormowany rozkład normalny N(0,1).
 

Twierdzenie 4

Jeżeli z populacji o rozkładzie normalnym N(m,σ) gdzie
jest nieznane, σ losujemy n-elementową próbę prostą, to
statystyka

 
ma rozkład

t-Studenta o n-1

stopniach swobody

n

m

X

U







1







n

S

m

X

t

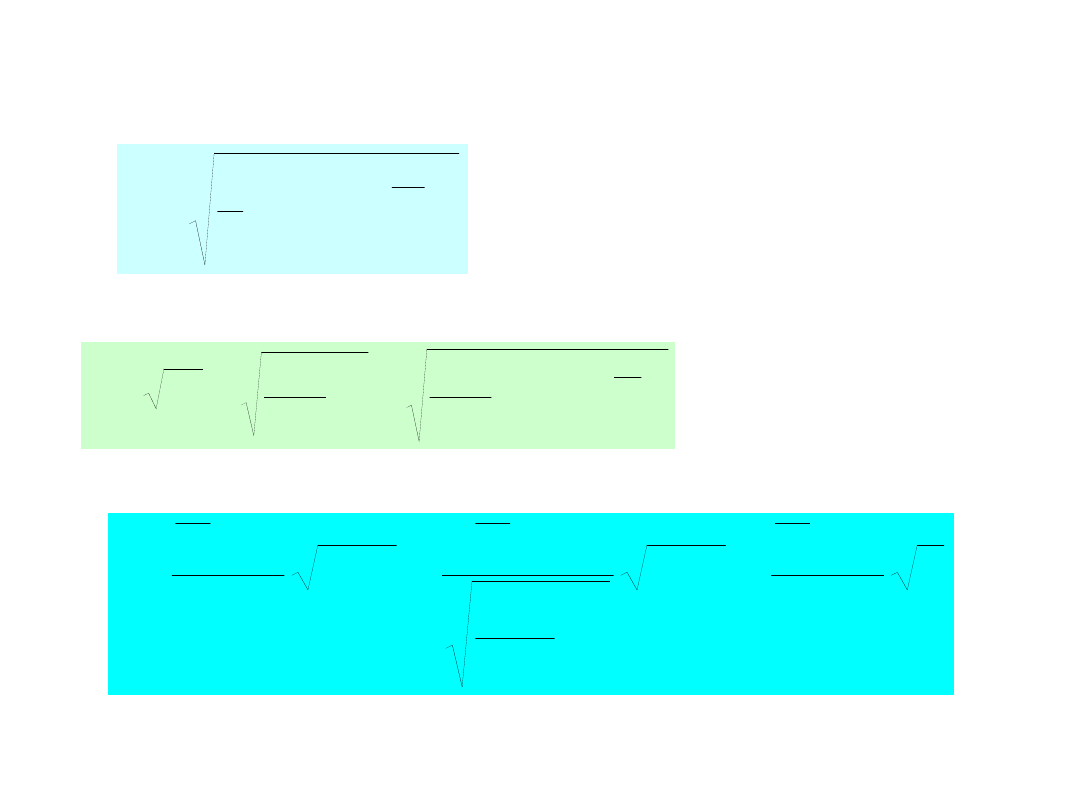
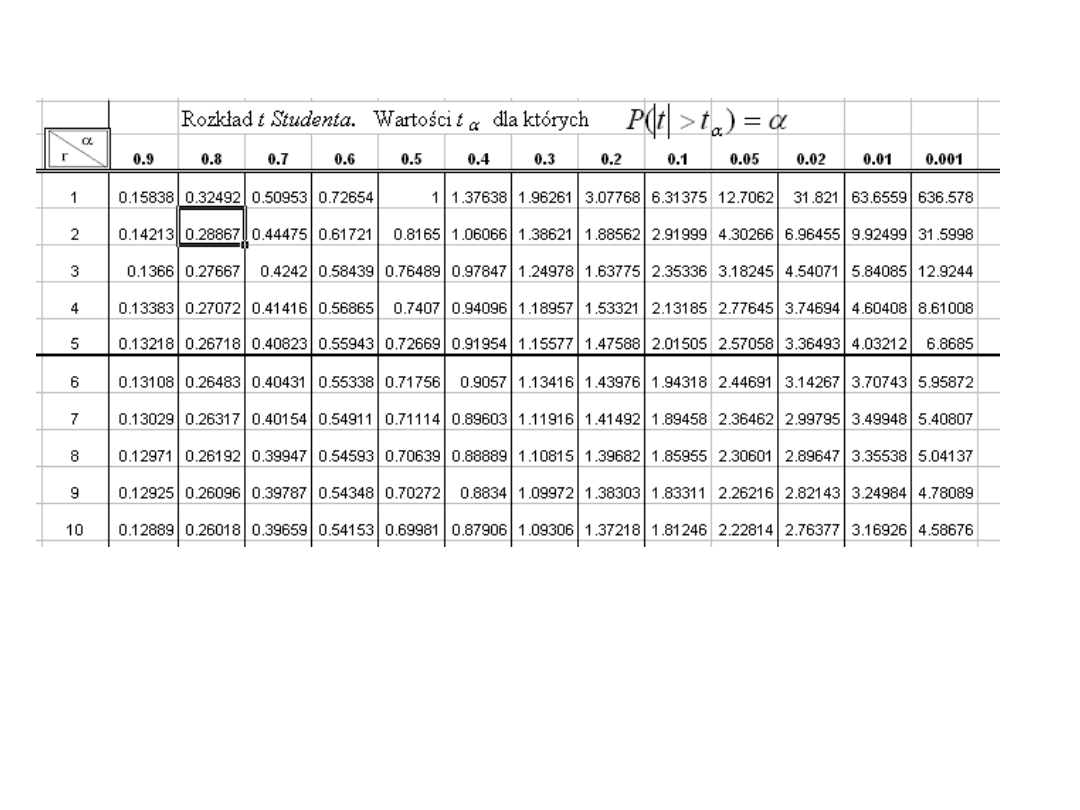
rozkład t-Studenta cd.

 
 













n

i

i

X

X

n

S

1

2

1





















n

i

i

X

X

n

S

n

n

S

S

1

2

2

2

1

1

1

ˆ

ˆ

n

S

m

X

n

S

n

n

m

X

n

S

m

X

t

ˆ

1

ˆ

1

1

2



















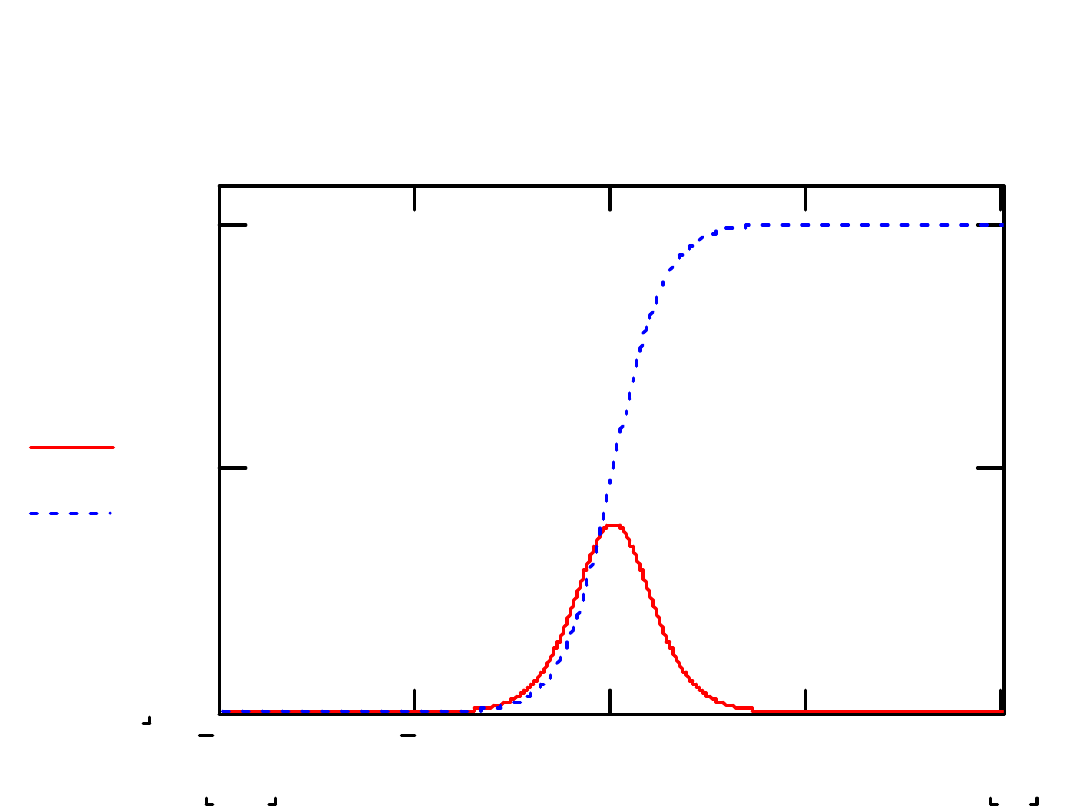
Gęstość i dystrybuanta rozkładu t-

Studenta

10

5

0

5

10

0

0.5

1

1.08

7.05210

6





dt x 7



(

)

pt x 7



(

)

10

10



x x



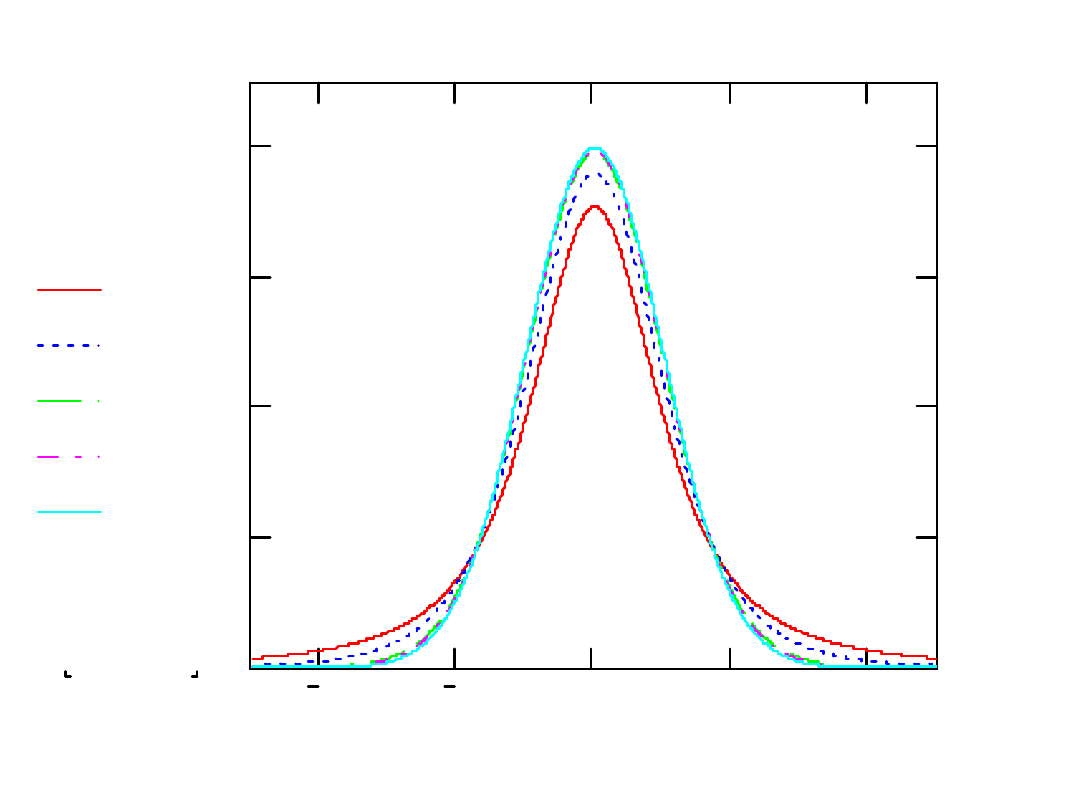
4

2

0

2

4

0

0.1

0.2

0.3

0.4

0.45

1.48710

6





dt x 2



(

)

dt x 5



(

)

dt x 25



(

)

dt x 40



(

)

dnormx 0

 1



(

)

5

5



x

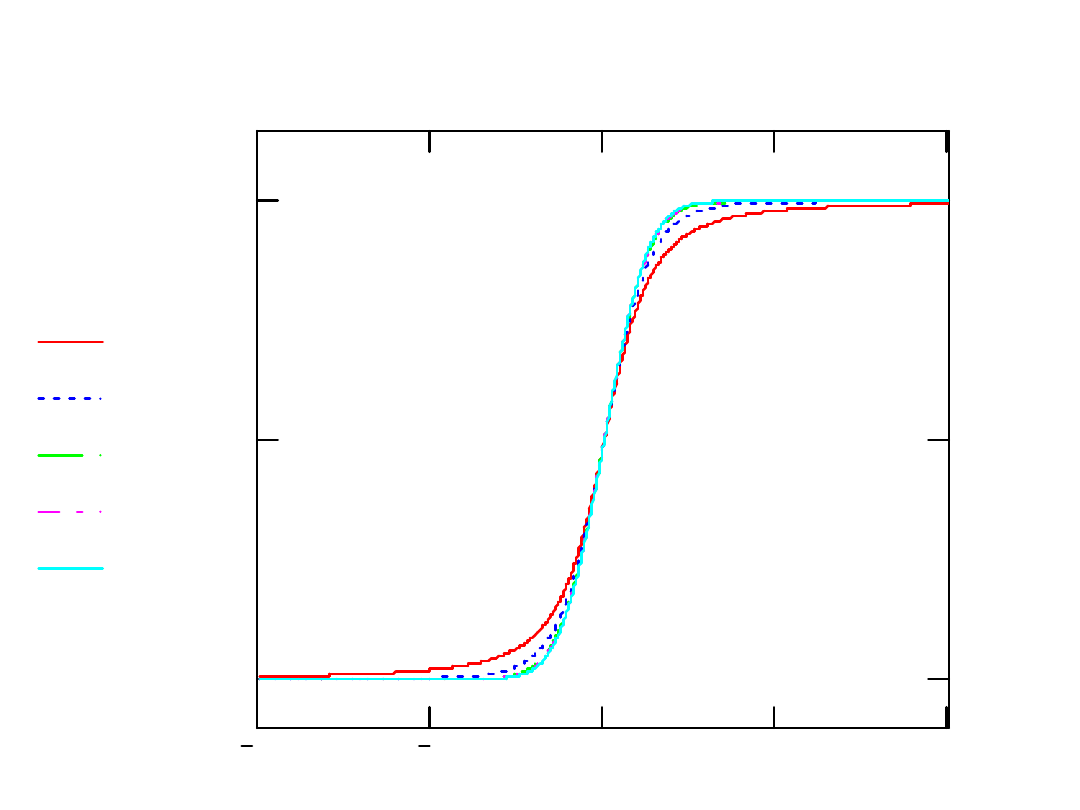
Dystrybuanty t-Studenta i N(0,1)

10

5

0

5

10

0

0.5

1

1.15

0.1



pt x 2



(

)

pt x 5



(

)

pt x 25



(

)

pt x 40



(

)

pnormx 0

 1



(

)

10

10



x

Porównywanie wartości

oczekiwanych

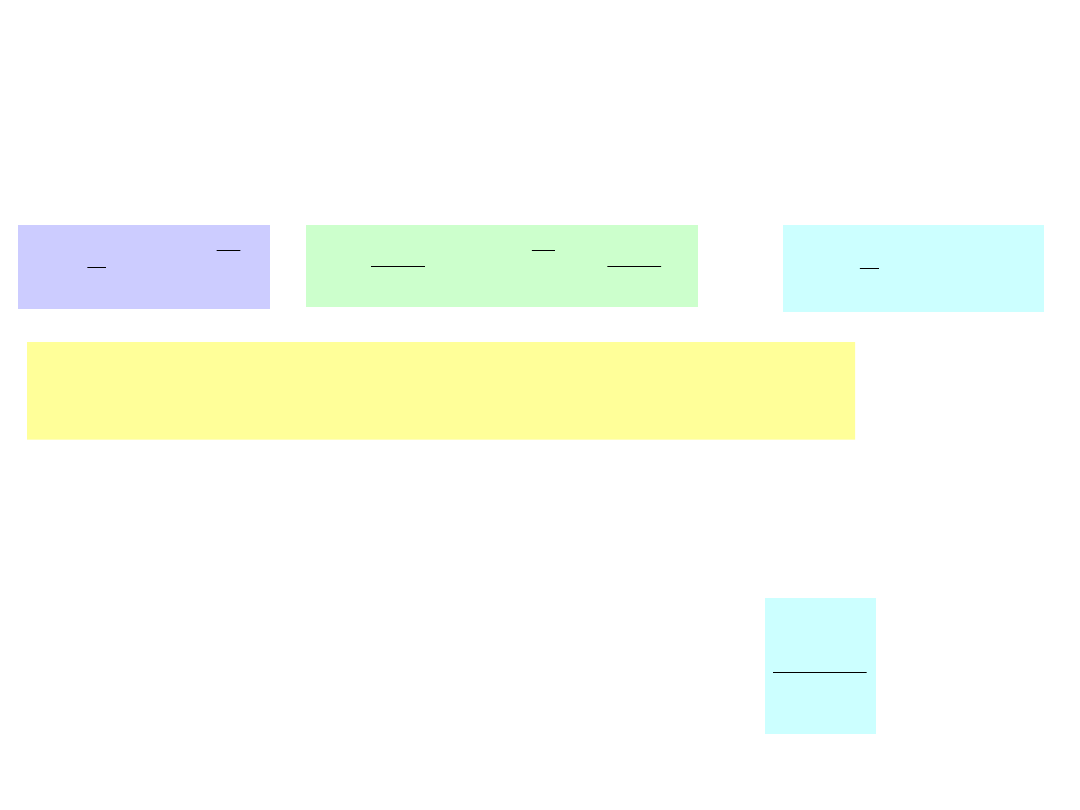
Twierdzenie 5.

Dane są dwie populacje generalne o niezależnych
rozkładach normalnych N(m

1

,σ

1

) N(m

2

,σ

2

)

Z populacji tych wylosowano dwie próby proste o
liczebnościach n

1

,n

2

elementów. Niech będą

średnimi arytmetycznymi z tych prób.

Wówczas statystyka ma też rozkład
normalny

2

1

i

X

X

2

1

X

X

Z























2

2

2

1

2

1

2

1

,

n

n

m

m

N





Porównywanie wartości

oczekiwanych cd.

Twierdzenie 6.

 
Jeżeli są dwiema średnimi z dwóch
niezależnych prób o liczebnościach n

1

,n

2

wylosowanych

niezależnie z dwóch populacji o odpowiednio rozkładach
normalnych N(m

1

,σ

1

) N(m

2

,σ

2

) to statystyka

2

1

i

X

X

2

2

1

1

2

1

2

1

)

(

n

n

m

m

X

X

U















ma standardowy (unormowany ) rozkład normalny
N(0,1).

Porównywanie wartości

oczekiwanych cd.

Twierdzenie 7.

Jeżeli są odpowiednio średnimi i
wariancjami z dwu prób o liczebnościach n

1

, n

2

wylosowanych z dwóch populacji o niezależnych
rozkładach normalnych N(m

1

,σ) , N(m

2

,σ) z nieznaną

wspólną wariancją σ

2

, to statystyka

2

2

2

2

1

1

,

oraz

,

S

X

S

X





























2

2

2

1

2

2

2

2

1

1

2

1

2

1

1

1

2

)

(

n

n

n

n

S

n

S

n

m

m

X

X

t

ma rozkład t-Studenta o

n

1

+ n

2

– 2

stopniach swobody

Uwagi o rozkładach granicznych

Granicznym rozkładem średniej z próby jest
zawsze rozkład normalny, nie zależnie od tego, jaki
rozkład ma populacja.
Wynika to z twierdzeń granicznych (Lindeberga-
Levy’ego).

X

Fakt, że niezależnie od typu populacji granicznej
rozkładem średniej z próby jest zawsze rozkładem
normalnym N(m,σ) , oznacza, że gdy tylko próba jest
dostatecznie duża (praktycznie n>30 ) wnioskowanie
statystyczne o średniej m dowolnej populacji można
oprzeć na granicznym rozkładzie normalnym
statystyki













n

m

N



,

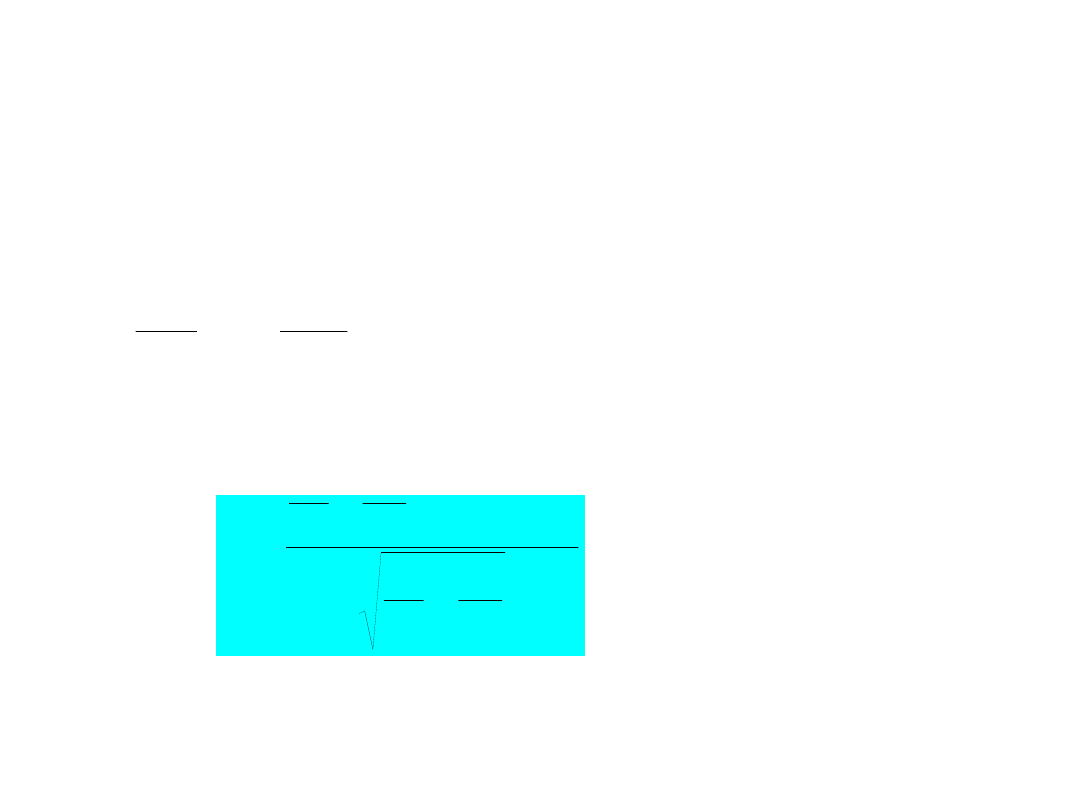
Rozkład wariancji z próby













n

i

i

X

X

n

S

1

2

2

1





2

1

2

2

1

1

1

ˆ

S

n

n

X

X

n

S

n

i

i



























n

i

i

m

X

n

S

1

2

2

*

1

Twierdzenie

Rozkład tych statystyk zależy od rozkładów
populacji.

Jeżeli populacja generalna ma rozkład normalny N(m,

) i

wylosowano z niej

n-elementową próbę prostą, z której wyznaczamy statystykę S

*2

To liniowe jej przekształcenie , a mianowicie
statystyka

ma rozkład



2

o n stopniach swobody.

2

2

*



nS

2

1

2

2

2

2

ˆ

)

1

(









n

S

n

nS







Rozkład wariancji z
próby cd.

Dla statystyk S

2

i

2

ˆ

S

Bardzo często korzysta się z szybkiej zbieżności
do rozkładu normalnego

1

2

2

2







k

U



2

2







1

,

1

2 

k

N

Dla k>30 zmienna
losowa

ma rozkład normalny
N(0,1)

Graniczne rozkłady samych statystyk S

2

i S, tzn. wariancji i

odchylenia standardowego z próby pochodzących z populacji
normalnych są też normalne





n































n

N

S

n

N

S

2

,

2

,

4

2

2









Gdy

Rozkład



2

Jeżeli U

1

, U

2

, ...,U

k

są niezależnymi zmiennymi

losowymi o standardowym rozkładzie normalnym
N(0,1) każda, to zmienna losowa będąca sumą ich
kwadratów:





k

i

i

U

1

2

ma rozkład



2

o k stopniach swobody.

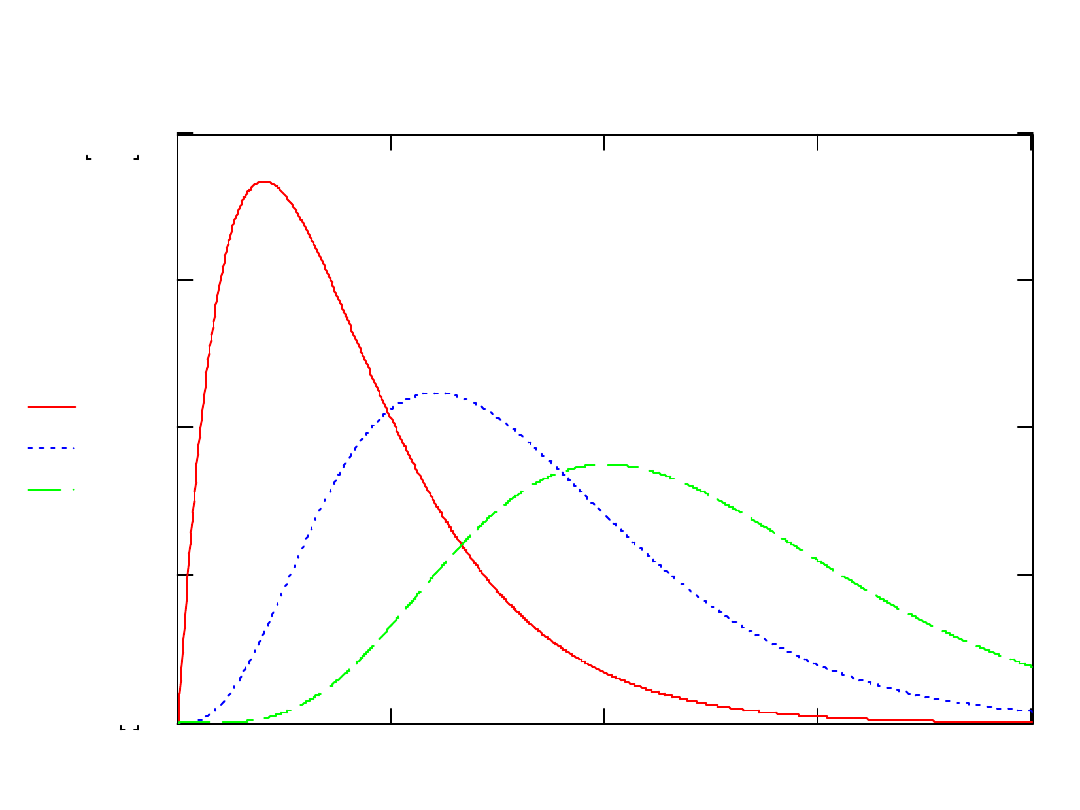
Gęstość rozkładu



2

0

5

10

15

20

0

0.05

0.1

0.15

0.2

0.184

0

dchisqx 4



(

)

dchisqx 8



(

)

dchisqx 12



(

)

20

0

x

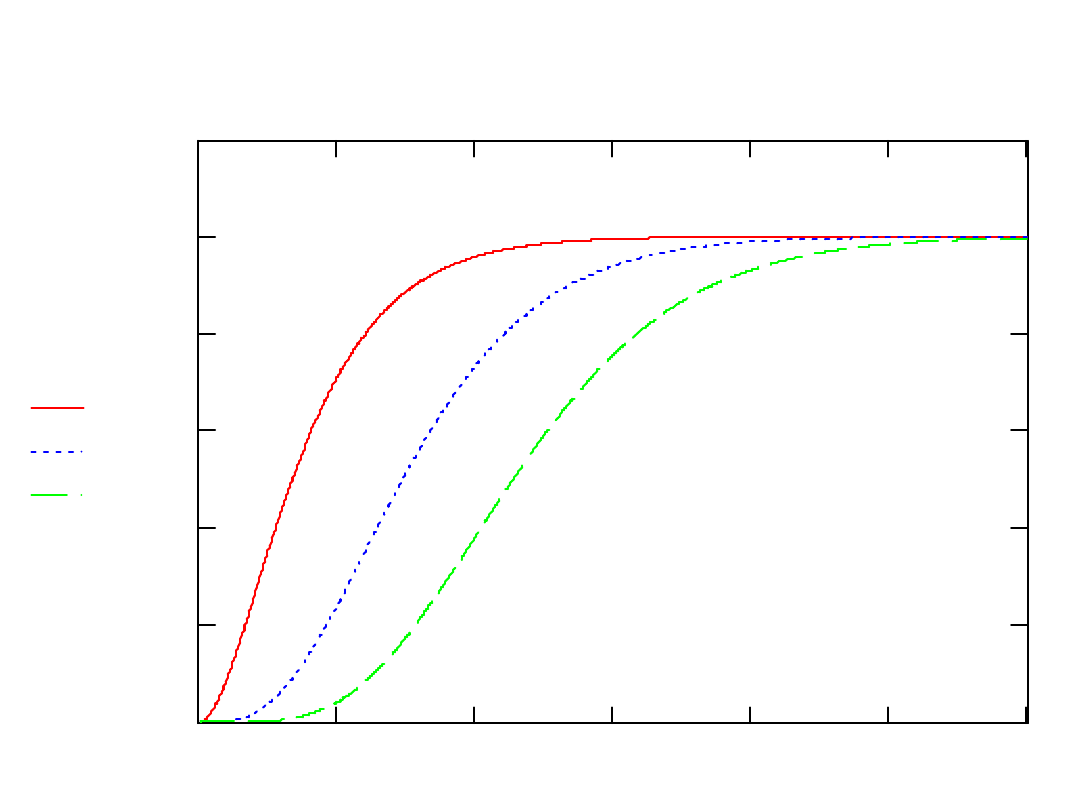
Dystrubuanta rozkładu



2

0

5

10

15

20

25

30

0

0.2

0.4

0.6

0.8

1

1.2

0

pchisqx 4



(

)

pchisqx 8



(

)

pchisqx 12



(

)

30

0

x x

 x



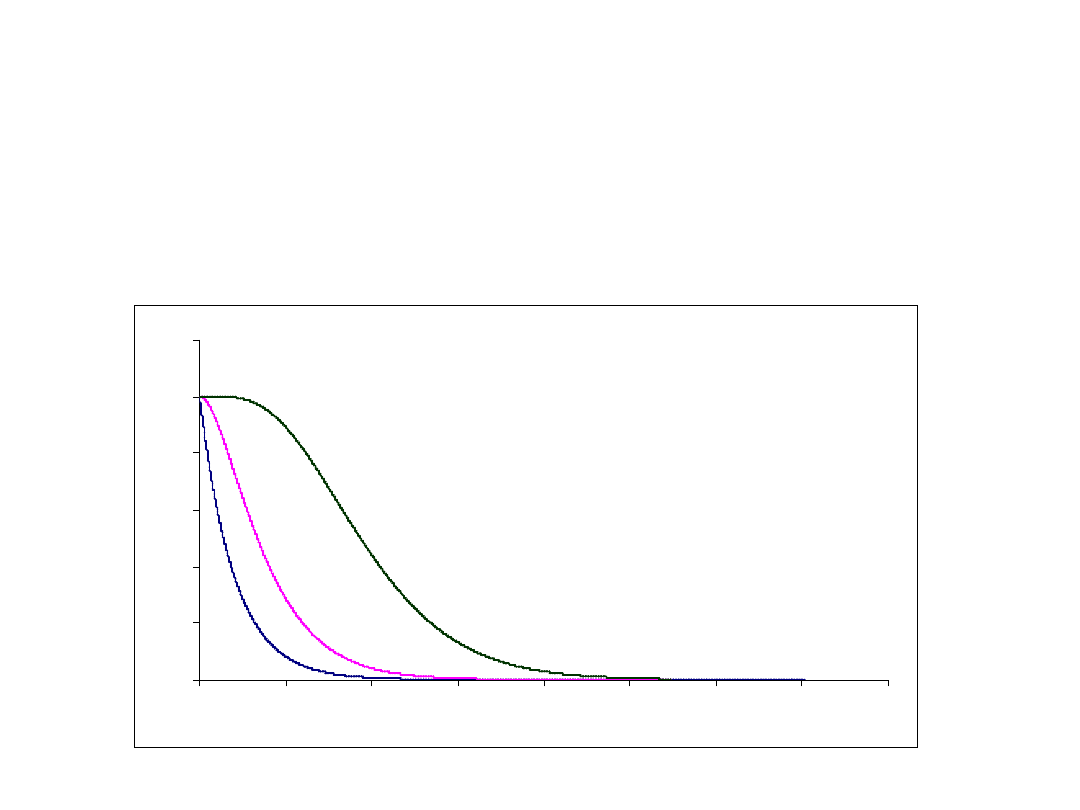
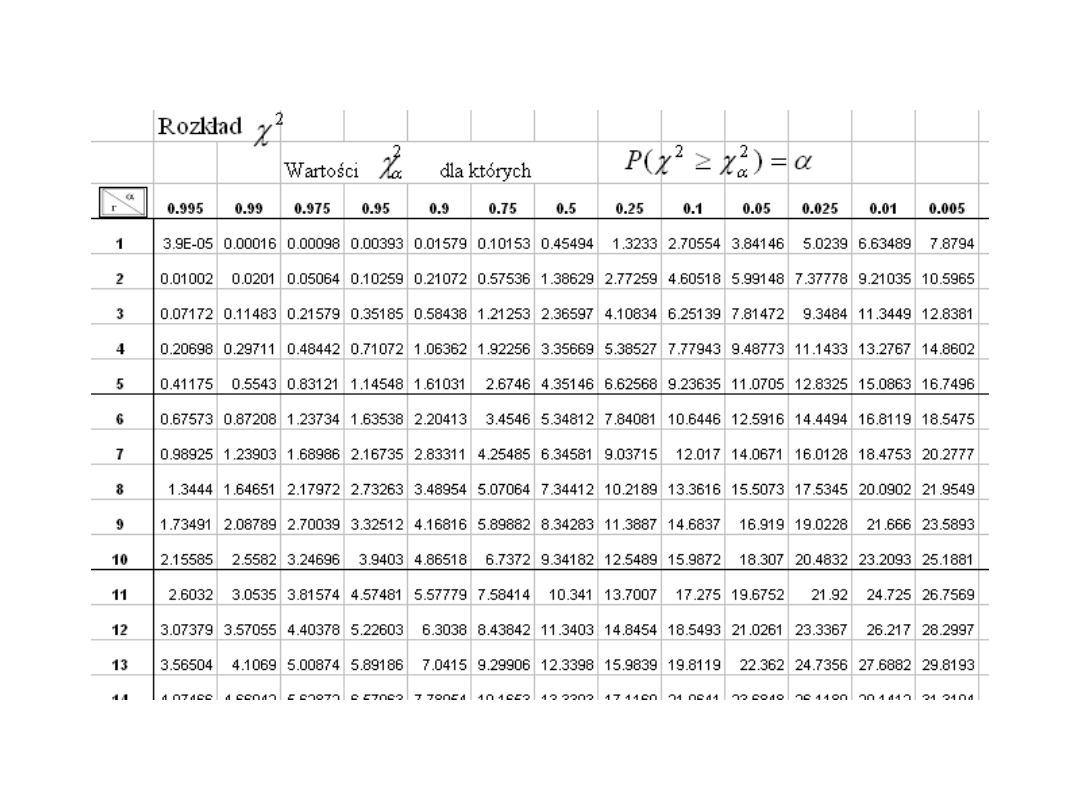
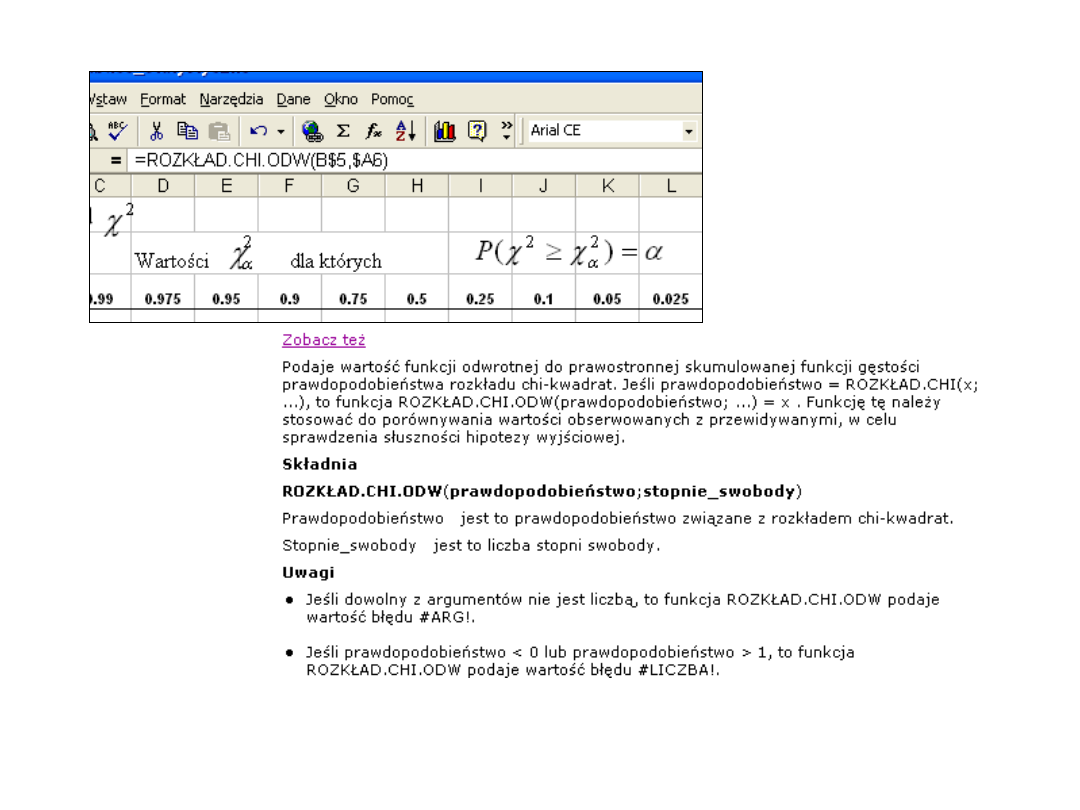
Rozkład



2

(Excel)

•Wartość funkcji ROZKŁAD.CHI wyznacza się
jako ROZKŁAD.CHI = P(X >x ), gdzie X jest zmienną losową χ

2

.

0

0.2

0.4

0.6

0.8

1

1.2

0

5

10

15

20

25

30

35

40

Punktowa estymacja

parametrów

• Estymacja parametryczna – estymacja nieparametryczna
• Szacowanie parametrów rozkładu populacji
• Szacowanie postaci funkcyjnej tego rozkładu.
• Estymacja punktowa - estymacja przedziałowa

 

Celem punktowej estymacji parametrycznej jest podanie
jednej oceny wartości parametru



na podstawie wyników

próby losowej.

Ocena parametru



Estymator szacowanego parametru.

Niech będzie n-elementową
próbą prostą wylosowaną z populacjui o rozkładzie
F(x,



). Niech Z

n

=g(X) będzie dowolną statystyką.

Jest to zmienna losowa.

Estymatorem szacowanego parametru



nazywamy każdą statystykę służącą do
oszacowania parametru



, której rozkład zależy

od parametru



.

Jeżeli populacja ma rozkład normalny N(m,



) i

nieznane są wartości obu parametrów

m

i



2

, to

średnia arytmetyczna oraz wariancja z próby S

2

mają rozkłady zależne od odpowiednich
parametrów populacji, mogą być zatem ich
estymatorami.

Punktowa estymacja polega na tym, że ze zbioru
możliwych wartości parametru



podaje się tylko

jedną liczbę (punkt) jako ocenę parametru.





n

X

X

X

,...,

,

2

1



X

W teorii statystyki matematycznej wysuwa
się pod adresem statystyki

Z

n

mającej być

estymatorem jakiegoś parametru



pewne

postulaty, których spełnienie gwarantuje
małe błędy szacunku,

tzn. żąda się, by estymator charakteryzował
się pewnymi pożądanymi własnościami.

Nieobciążoność

Efektywność

Zgodność

Dostateczność

.

Nieobciążoność

Estymator parametru



nazywa się

estymatorem nieobciążonym

jeżeli zachodzi:





)

(

n

Z

E

n

n

b

Z

E











)

(

to taki estymator nazywa się estymatorem
obciążonym

b

n

nazywa się obciążeniem estymatora

Jeżeli

 Obciążenie jest miarą błędu systematycznego, jakim
obarczone są oceny uzyskane za pomocą estymatora
obciążonego.

Jeżeli estymator jest obciążony, to jego obciążenie,
zależne od wielkości próby n może maleć wraz ze
zwiększaniem się próby:

Estymator obciążony, dla którego obciążenia b

n

spełnia równość:















)

(

zn.

t

0

lim

lim

n

n

n

n

Z

E

b

nazywa się estymatorem asymptotycznie
nieobciążonym.

Przykład 1.

Dla dowolnego rozkładu populacji, niech
statystyka będzie estymatorem
wartości średniej m populacji generalnej
z n-elementowej próby prostej.

m

m

n

X

E

n

X

n

E

X

E

n

i

n

i

i

n

i

i













































1

1

1

1

1

1

)

(

Przykład 2.

Dla dowolnego rozkładu populacji z wariancją



2

oraz średnią m i niech statystyki:











































n

i

i

n

i

i

n

i

i

X

X

n

S

n

n

S

X

X

n

S

m

X

n

S

1

2

2

2

1

2

1

2

2

2

*

1

1

1

ˆ

1

1

będą estymatorami wariancji



2

populacji z n-

elementowej próby prostej. Zachodzi:

2

2

2

2

1

2

2

1

2

2

)

1

(

)

(

)

(

)

(

)

(

)

(





































n

n

n

n

X

nD

X

D

m

X

nE

m

X

E

nS

E

n

i

i

n

i

i

















2

1

2

1

2

1

2

1

2

1

2

)

(

)

(

2

)

(

)

(

)

(

m

X

m

X

m

X

n

nm

X

m

X

m

X

m

X

m

X

X

m

m

X

n

i

i

n

i

n

i

i

i

n

i

i

n

i

i







































































Otrzymuje się więc :

E
s
t
y
m
a
t
o
r
y

n
i
e
o
b
i
ą
ż
o
n
e

i

a
s
y
m
p
t
o
t
y
c
z
n
i
e

n
i
e
o
b
c
i
ą
ż
o
n
e
.

 

Estymatory nieobiążone i asymptotycznie
nieobciążone.

2

2

2

2

2

2

2

*

)

ˆ

(

1

1

1

)

(

)

(





















 









S

E

n

n

n

S

E

S

E

Błąd standardowego szacunku

W punktowej estymacji parametrycznej gdy
używa się estymatora nieobciążonego Z

n

, to

wynik estymacji czyli ocena uzyskana z
konkretnej próby dla estymatora uzupełnia
się podaniem tzw. błędu standardowego
szacunku D(Z

n

) . Wynik estymacji pisze się

jako

)

(

n

Z

D

z

Błąd standardowego szacunku będący
odchyleniem standardowym D(Z

n

) estymatora

nieobciążonego Z

n

wyraża przeciętny (in plus lub

in minus ) błąd , jaki popełniamy przy
wielokrotnym szacowaniu parametru



za pomocą

estymatora nieobciążonego Z

n ,

gdyż









2

2

2

)

(

)

(

)

(













n

n

n

n

n

Z

E

Z

E

Z

E

Z

D

Z

D

Efektywność

Jeżeli są dwoma estymatorami
nieobciążonymi tego samego parametru



pewnej populacji , to mówimy, że estymator
jest efektywniejszy od estymatora ,
jeżeli zachodzi nierówność:

 

 

Dwa estymatory są tak samo efektywne jeżeli:

)

2

(

)

1

(

n

n

Z

Z

)

1

(

n

Z

)

2

(

n

Z

)

(

)

(

)

2

(

2

)

1

(

2

n

n

Z

D

Z

D



)

(

)

(

)

2

(

2

)

1

(

2

n

n

Z

D

Z

D



Zgodność estymatora

Estymator Z

n

parametru



nazywa się

estymatorem zgodnym jeżeli spełnia on
równość:





0

każażde

dla

1

lim



















n

n

Z

P

Twierdzenie.

Dane są dwie populacje generalne o niezależnych rozkładach

normalnych
N(m

1

, σ

1

), N(m

2

, σ

2

) z jednakowymi wariancjami σ

1

= σ

1

= σ . Z

populacji tych
wylosowano dwie próby proste o liczebności n

1

i n

2

elementów.

Niech

2

2

2

2

2

1

2

1

1

1

2

1

1

ˆ

oraz

1

ˆ

S

n

n

S

S

n

n

S









będą odpowiednio wariancjami z tych prób.
Wówczas statystyka :

 

 

ma rozkład F Snedecora o n

1

– 1 i n

2

– 1

stopniach swobody.

2

2

2

1

ˆ

ˆ

S

S

F 