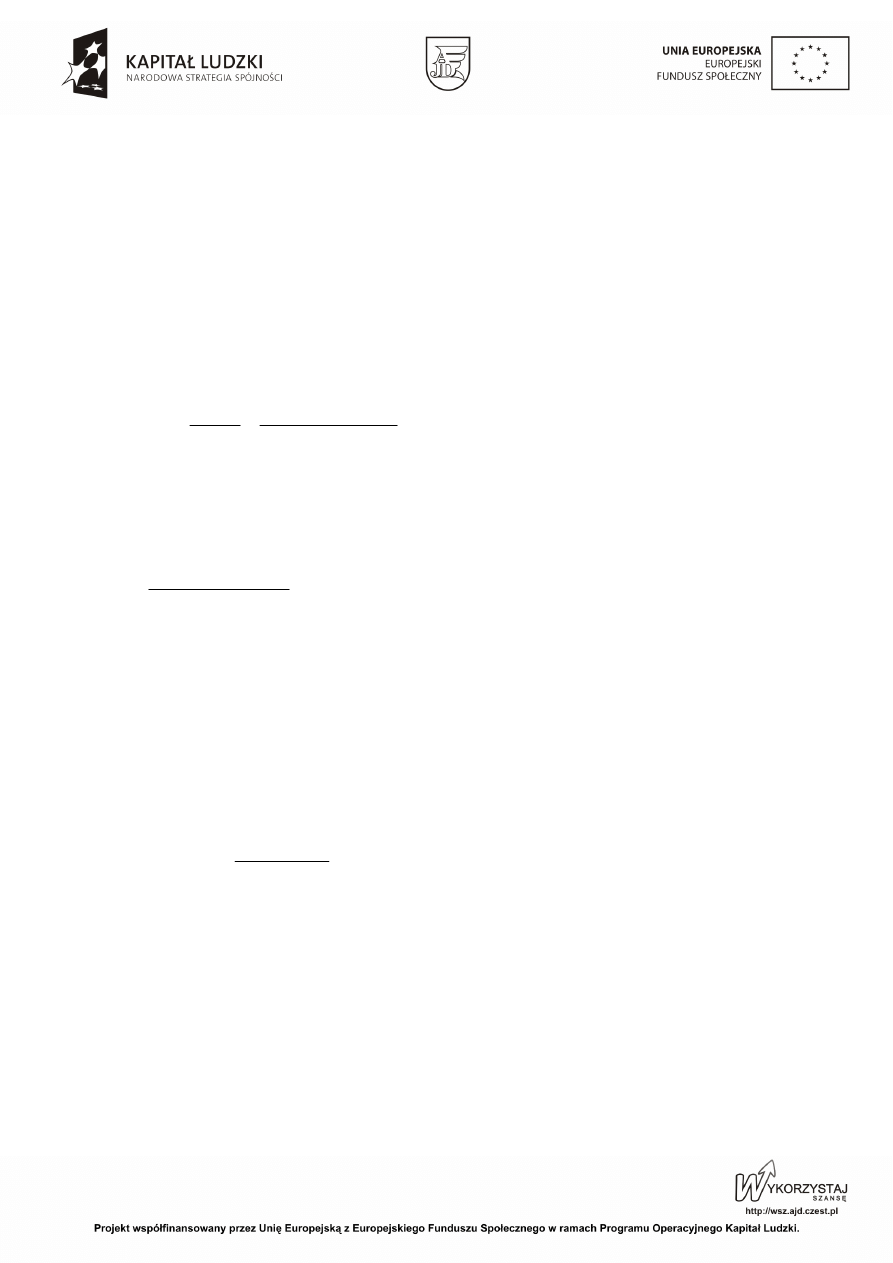
BLOK I
RACHUNEK RÓŻNICZKOWY I CAŁKOWY
1.1
Pochodna funkcji w punkcie
Zakładamy, że funkcja f jest określona w przedziale
)
,
( b
a
oraz, że
),
,
(
0
b
a
x
∈
a x
∆
jest
liczbą, dla której
).
,
(
)
(
0
b
a
x
x
∈
∆
+
Liczbę
x
∆
nazywamy
przyrostem argumentu
w punkcie
,
0
x
natomiast różnicę
)
(
)
(
0
0
x
f
x
x
f
−
∆
+
nazywamy
przyrostem wartości
funkcji f w punkcie
0
x
i oznaczamy
).
(
0
x
f
∆
Stosunek
x
x
f
x
x
f
x
x
f
∆
−
∆
+
=
∆
∆
)
(
)
(
)
(
0
0
0
nazywamy
ilorazem różnicowym funkcji
f
w punkcie
0
x .
Definicja 1.1.1
Jeżeli funkcja f jest określona w przedziale
)
,
( b
a
i
)
,
(
0
b
a
x
∈
oraz istnieje skończona granica
0
lim
→
∆
x
x
x
f
x
x
f
∆
−
∆
+
)
(
)
(
0
0
, to tę granicę nazywamy
pochodną funkcji w punkcie
0
x
i oznaczamy
).
(
0
'
x
f
W tym przypadku mówimy również, że funkcja f jest
różniczkowalna w punkcie
.
0
x
A zatem pochodna
)
(
0
'
x
f
jest granicą ilorazu różnicowego funkcji f w punkcie
0
x , gdy
przyrost x
∆
zmiennej x dąży do zera.
Uwaga 1.1.1 Pochodną funkcji f w punkcie
0
x można w sposób równoważny określić
następująco:
=
)
(
0
'
x
f
0
lim
x
x
→
0
0
)
(
)
(
x
x
x
f
x
f
−
−
.
1.2
Interpretacje pochodnej
I.
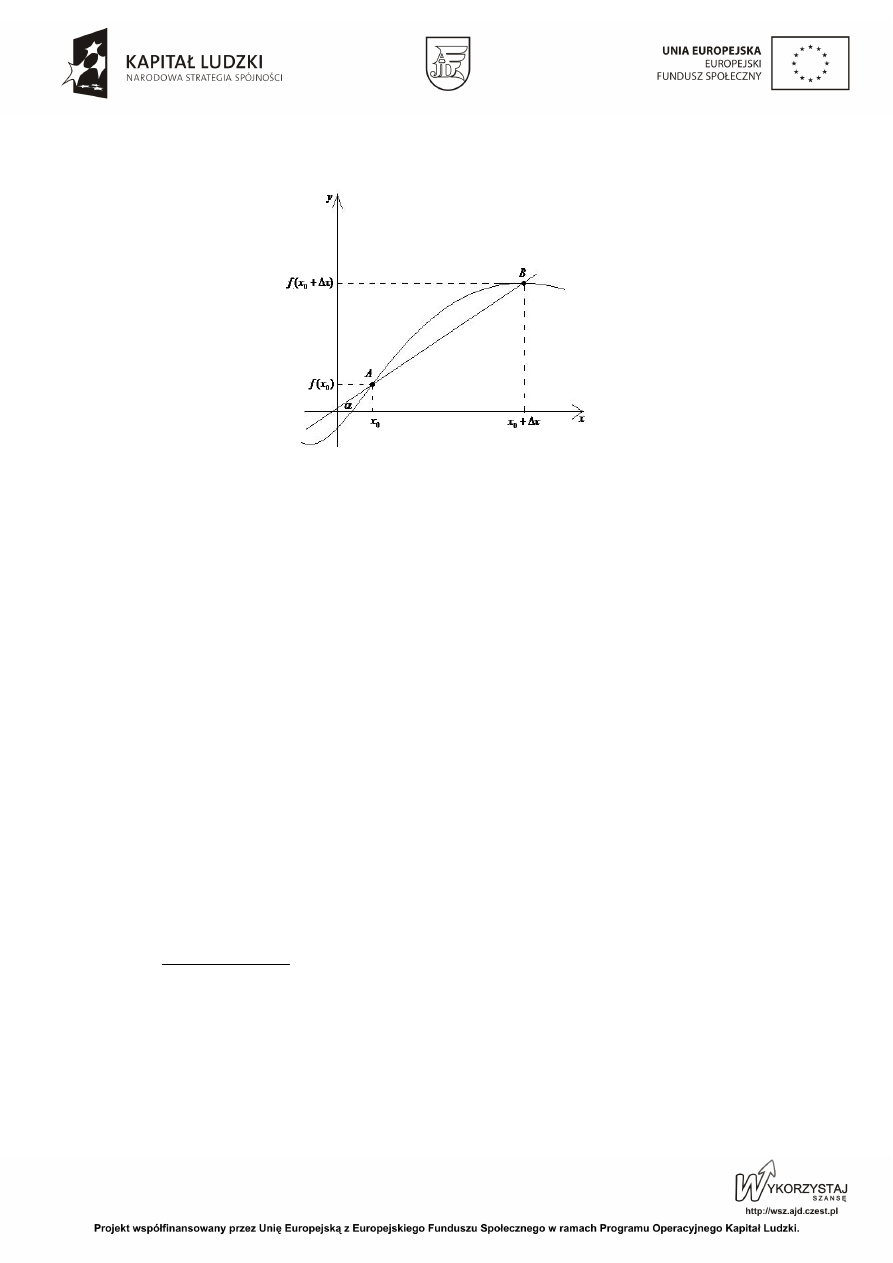
Interpretacja geometryczna
Jeżeli funkcja f jest określona w punkcie
0
x i w pewnym przedziale, którego środkiem jest
0
x , a także jest różniczkowalna w
0
x , to zachodzi związek:
,
)
(
0
'
α
tg
x
f
=
gdzie
α
jest kątem
nachylenia do osi x stycznej do wykresu funkcji w punkcie
)).
(
,
(
0
0
x
f
x
P
Styczna do wykresu funkcji f w punkcie
))
(
,
(
0
0
x
f
x
P
jest prostą o równaniu:
).
)(
(
)
(
0
0
'
0
x
x
x
f
x
f
y
−
=
−
Spójrzmy na rysunek.
Jeżeli x
∆
dąży do zera, to punkt
B dąży, po wykresie funkcji f, do punktu A. Każdemu
położeniu punktu
B odpowiada sieczna przechodząca przez B i przez A. Zatem styczną do
wykresu funkcji
f w punkcie
))
(
,
(
0
0
x
f
x
A
=
możemy traktować jako graniczne położenie
siecznej
AB, gdy B dąży po wykresie do A.
Stąd wynika, że pochodną funkcji
f w punkcie
0
x można interpretować geometrycznie jako
współczynnik kierunkowy stycznej do wykresu funkcji
f w punkcie
)).
(
,
(
0
0
x
f
x
A
=
II.
Interpretacja fizyczna
Niech
)
(t
f
oznacza długość drogi jaką przebył punkt materialny P do chwili t licząc od
pewnej chwili początkowej
0
t .
Różnica
)
(
)
(
0
0
t
f
t
t
f
−
∆
+
jest długością drogi przebytej przez punkt materialny w przedziale czasu
).
,
(
0
0
t
t
t
∆
+
A zatem iloraz
t
t
f
t
t
f
∆
−
∆
+
)
(
)
(
0
0
jest średnią prędkością punktu materialnego P w przedziale
).
,
(
0
t
t
∆
Dodajmy, że mówimy
o prędkości średniej, ponieważ na ogół prędkość ta może być zmienna, w odróżnieniu od
przypadku, gdy prędkość ta jest stała i niezależna zarówno od
0
t jak i t
∆
(ruch jednostajny).
Granicę

0
lim
→
∆
t
t
t
f
t
t
f
∆
−
∆
+
)
(
)
(
0
0
)
(
0
'
t
f
=
nazywamy prędkością (chwilową) punktu materialnego
P w chwili
.
0
t Zatem pochodną
)
(
0
'
t
f
interpretujemy jako prędkość (chwilową) punktu materialnego
P w chwili .
0
t
Przedstawmy jeszcze inną fizyczną interpretację pochodnej.
Jeśli
)
(t
f
oznacza ilość kalorii jaka jest potrzebna do ogrzania 1 grama pewnego ciała od
temperatury
0
t
C
o
do
t
t
∆
+
0
C
o
, to iloraz
t
t
f
t
t
f
∆
−
∆
+
)
(
)
(
0
0
wyraża średnie ciepło właściwe
tego ciała między temperaturami:
0
t i
.
0
t
t
∆
+
Pochodną
)
(
0
'
t
f
=
0
lim
→
∆
t
t
t
f
t
t
f
∆
−
∆
+
)
(
)
(
0
0
nazywamy ciepłem właściwym ciała przy temperaturze
III.
Interpretacja ekonomiczna
Załóżmy, że funkcja
)
(
x
K
przyjmuje wartości dodatnie dla
x
> 0. Funkcję
)
(
x
K
będziemy
interpretować jako funkcję tzw. kosztów całkowitych. Mówiąc dokładniej przyjmujemy, że
)
(
x
K
wyraża całkowity koszt wyprodukowania
x
jednostek pewnego dobra. Oznaczmy
przez
h bezwzględną wielkość przyrostu produkcji. Przyrostowi produkcji od
0
x do
h
x
+
0
odpowiada przyrost funkcji kosztów
).
(
)
(
0
0
x
K
h
x
K
−
+
Iloraz
h
x
K
h
x
K
)
(
)
(
0
0
−
+
daje przeciętny koszt wyprodukowania jednej jednostki pewnego dobra licząc od poziomu
0
x .
W konsekwencji granica
0
lim
→
h
h
x
K
h
x
K
)
(
)
(
0
0
−
+
=
)
(
0
'
x
K
czyli pochodna
)
(
0
'
x
K
jest tzw. kosztem krańcowym w punkcie
.
0
x
1.3
Pochodna jako funkcja

Definicja 1.3.1
Jeśli funkcja
)
(x
f
jest określona w zbiorze X i w każdym punkcie
D
x
∈
0
(
X
D
⊆
) istnieje
pochodna
)
(
0
'
x
f
, to funkcję
)
(
'
x
f
x a
, która każdemu
D
x
∈
przyporządkowuje
)
(
'
x
f
,
nazywamy
pochodną funkcji f i oznaczamy
'
f
.
Uwaga 1.3.1
Pochodna funkcji f jest funkcją, natomiast pochodna funkcji f w punkcie
0
x
jest liczbą. Te
dwa pojęcia należy rozróżniać.
W praktyce, wyznaczając pochodną funkcji, korzystamy z odpowiednich wzorów i twierdzeń
ułatwiających obliczenia.
Twierdzenie 1.3.1
Jeżeli funkcje f, g są określone i różniczkowalne w każdym punkcie przedziału
)
,
( b
a
, to
w tym przedziale są również różniczkowalne funkcje: cf, gdzie c oznacza ustaloną liczbę
rzeczywistą,
g
f
g
f
g
f
g
f
,
,
,
⋅
−
+
(pod warunkiem, że
0
)
(
≠
x
g
) i prawdziwe są wzory:
1)
),
(
)]
(
[
'
'
x
f
c
x
cf
⋅
=
2)
),
(
)
(
)]
(
)
(
[
'
'
'
x
g
x
f
x
g
x
f
+
=
+
3)
),
(
)
(
)]
(
)
(
[
'
'
'
x
g
x
f
x
g
x
f
−
=
−
4)
),
(
)
(
)
(
)
(
)]
(
)
(
[
'
'
'
x
g
x
f
x
g
x
f
x
g
x
f
⋅
+
⋅
=
⋅
5)
.
)]
(
[
)
(
)
(
)
(
)
(
)
(
)
(
2
'
'
'
x
g
x
g
x
f
x
g
x
f
x
g
x
f
⋅
−
⋅
=
Twierdzenie 1.3.2
Funkcje: funkcja stała, funkcja potęgowa, funkcje trygonometryczne są różniczkowalne
w swoich dziedzinach. Pochodne tych funkcji wyrażają się wzorami:
1)
,
0
'
=
c
c – ustalona liczba rzeczywista,
2)
,
)
(
1
'
−
⋅
=
α
α
α
x
x
,
R
∈
α
3)
,
cos
)
(sin
'
x
x
=
4)
,
sin
)
(cos
'
x
x
−
=

5)
,
cos
1
)
(
2
'
x
tgx
=
6)
.
sin
1
)
(
2
'
x
ctgx
−
=
Twierdzenie 1.3.3
Jeżeli funkcja
h jest złożeniem funkcji f z funkcją g i funkcja g jest różniczkowalna w punkcie
x
, natomiast funkcja
g jest różniczkowalna w punkcie
),
(x
f
y
=
to funkcja h jest
różniczkowalna w punkcie x i zachodzi wzór
).
(
)]
(
[
)
(
'
'
'
x
f
x
f
g
x
h
⋅
=
Twierdzenie 1.3.3 nazywa się twierdzeniem o pochodnej funkcji złożonej i można je
wypowiedzieć krótko, choć niezbyt ściśle, tak: pochodna funkcji złożonej równa się
iloczynowi pochodnej jej funkcji zewnętrznej i pochodnej funkcji wewnętrznej. Należy przy
tym pamiętać, że argumentem pochodnej funkcji zewnętrznej nie jest x, lecz
).
(x
f
Podstawą do wyprowadzenia wzorów na pochodną funkcji wykładniczej i logarytmicznej jest
następujące twierdzenie:
Twierdzenie 1.3.4
Jeżeli
0
>
a
i
1
≠
a
, to
,
ln
1
lim
0
a
x
a
x
x
=
−
→
gdzie
a
ln
oznacza logarytm liczby
a
przy
podstawie
e
i nazywa się logarytmem naturalnym liczby
.
a
Twierdzenie 1.3.5
Funkcja wykładnicza i logarytmiczna są różniczkowalne w swoich dziedzinach. Prawdziwe są
wzory:
7)
,
)
(
'
x
x
e
e
=
8)
,
ln
)
(
'
a
a
a
x
x
=
+
∈
R
a
\{1},
9)
,
1
)
(ln
'
x
x
=
10)
,
ln
1
)
(log
'
a
x
x
a
=
+
∈
R
a
\{1}.
Twierdzenie 1.3.6
Jeżeli f jest ściśle monotoniczna i ciągła na przedziale
)
,
( b
a
, różniczkowalna w
)
,
( b
a
x
∈
i
,
0
)
(
'
≠
x
f
to funkcja odwrotna
1
−
f
(określona w zbiorze wartości funkcji f ) jest
różniczkowalna w
)
(x
f
y
=
i zachodzi wzór

.
)
(
1
))
(
(
'
'
1
x
f
y
f
=
−
Podamy jeszcze pochodne funkcji cyklometrycznych.
11)
,
1
1
)
(arcsin
2
'
x
x
−
=
),
1
,
1
(
−
∈
x
12)
,
1
1
)
(arccos
2
'
x
x
−
−
=
),
1
,
1
(
−
∈
x
13)
(arctgx)
'
=
1
1
2
+
x
,
,
R
x
∈
14)
(arcctg)
'
=
,
1
1
2
+
−
x
.
R
x
∈
1.4
Monotoniczność funkcji różniczkowalnej
Twierdzenie 1.4.1
Jeżeli funkcja f jest określona i różniczkowalna w przedziale
)
,
( b
a
i przy tym jest funkcją
rosnącą w tym przedziale, to jej pochodna
'
f jest, w każdym punkcie przedziału
)
,
( b
a
nieujemna.
Twierdzenie 1.4.2
Jeżeli funkcja f jest określona i różniczkowalna w przedziale
)
,
( b
a
i przy tym jest funkcją
malejącą w tym przedziale, to jej pochodna
'
f jest, w każdym punkcie przedziału
)
,
( b
a
niedodatnia.
Twierdzenie 1.4.3
Jeżeli funkcja f jest określona i różniczkowalna w przedziale
),
,
( b
a
a jej pochodna
'
f
przyjmuje, w co najwyżej skończonej liczbie punktów przedziału, wartość zero, a we
wszystkich pozostałych punktach przedziału jest dodatnia, to funkcja f jest w przedziale
)
,
( b
a
rosnąca.
Twierdzenie 1.4.4
Jeżeli funkcja f jest określona i różniczkowalna w przedziale
),
,
( b
a
a jej pochodna
'
f
przyjmuje, w co najwyżej skończonej liczbie punktów przedziału, wartość zero, a we
wszystkich pozostałych punktach przedziału jest ujemna, to funkcja f jest w przedziale
)
,
( b
a
malejąca.

1.5
Ekstrema lokalne
Niech f będzie funkcją określoną w pewnym otoczeniu punktu
.
0
x
Definicja 1.5.1
Mówimy, że funkcja f ma w punkcie
0
x maksimum lokalne (krótko: maksimum), jeśli
).
(
)
(
0
)
,
(
0
0
0
x
f
x
f
r
x
r
x
x
r
≤
∀
∃
+
−
∈
>
(tzn. dla x dostatecznie bliskich
0
x funkcja f przyjmuje wartości mniejsze lub równe od
wartości f w punkcie
0
x .)
Definicja 1.5.2
Mówimy, że funkcja f ma w punkcie
0
x minimum lokalne (krótko: minimum), jeśli
).
(
)
(
0
)
,
(
0
0
0
x
f
x
f
r
x
r
x
x
r
≥
∀
∃
+
−
∈
>
(tzn. dla x dostatecznie bliskich
0
x funkcja f przyjmuje wartości większe lub równe od
wartości f w punkcie
0
x .)
Definicja 1.5.3
Mówimy, że funkcja f ma w punkcie
0
x ekstremum lokalne, jeśli ma w tym punkcie
maksimum lokalne lub minimum lokalne.
Uwaga 1.5.1
W przypadku występowania ekstremum funkcji f w punkcie
0
x jest ważne zachowanie się
funkcji wyłącznie dostatecznie blisko
0
x . To jak funkcja zachowuje się dla x „dalekich” od
0
x nie jest tu ważne.
Uwaga 1.5.2
Zwróćmy uwagę, że w definicji ekstremum nic nie mówimy o pochodnej funkcji f w punkcie
0
x . Funkcja f może mieć ekstremum w
0
x , natomiast pochodna
)
(
0
'
x
f
może istnieć lub nie
istnieć.
Wyznaczając ekstremum lokalne funkcji na ogół korzystamy z pewnych twierdzeń. Poniższe
twierdzenie podaje warunek dostateczny na to, aby funkcja f miała ekstremum lokalne
w punkcie
0
x .
Twierdzenie1.5.1 (Warunek dostateczny istnienia ekstremum)
Niech f będzie funkcją ciągłą określoną przynajmniej w pewnym otoczeniu
)
,
(
0
0
r
x
r
x
+
−

punktu
0
x oraz różniczkowalną w zbiorze
)
,
(
)
,
(
0
0
0
0
r
x
x
x
r
x
+
∪
−
(pochodna
)
(
0
'
x
f
nie
musi istnieć).
Wówczas
1.
Jeśli
0
)
(
'
>
x
f
dla
)
,
(
0
0
x
r
x
x
−
∈
i
0
)
(
'
<
x
f
dla
),
,
(
0
0
r
x
x
x
+
∈
to funkcja f ma
w
0
x maksimum lokalne.
2.
Jeśli
0
)
(
'
<
x
f
dla
)
,
(
0
0
x
r
x
x
−
∈
i
0
)
(
'
>
x
f
dla
),
,
(
0
0
r
x
x
x
+
∈
to funkcja f ma
w
0
x minimum lokalne.
Powstaje pytanie, jak dla danej funkcji f wyznaczyć punkty, należące do jej dziedziny,
w których może ona mieć ekstremum lokalne.
Odpowiedź na to pytanie (dla pewnej klasy funkcji) zawarta jest w następującym twierdzeniu.
Twierdzenie 1.5.2 (Warunek konieczny istnienia ekstremum funkcji różniczkowalnej)
Jeśli f jest różniczkowalna w punkcie
0
x i ma w tym punkcie ekstremum lokalne, to
.
0
)
(
0
'
=
x
f
Uwaga 1.5.3
Z faktu, że
0
)
(
0
'
=
x
f
nie wynika jeszcze, że f ma w
0
x ekstremum.
Uwaga 1.5.4
Funkcja może mieć w
0
x ekstremum lokalne, ale nie musi być w tym punkcie
różniczkowalna, np. funkcja
|
|
)
(
x
x
f
=
ma w punkcie
0
x = 0 minimum lokalne, ale
)
0
(
'
f
nie istnieje.
Twierdzenie 1.5.3
Niech f będzie funkcją posiadającą pochodne
'
f i
''
f w pewnym otoczeniu punktu
0
x , przy
czym
)
(
''
x
f
jest ciągła w
0
x i
.
0
)
(
0
'
=
x
f
Wówczas
1.
Jeśli
,
0
)
(
0
''
>
x
f
to f ma w punkcie
0
x minimum lokalne.
2.
Jeśli
,
0
)
(
0
''
<
x
f
to f ma w punkcie
0
x maksimum lokalne.

1.6
Funkcja pierwotna. Całka nieoznaczona
Niech f będzie funkcją określoną na przedziale P.
Definicja 1.6.1
Mówimy, że funkcja F określona na P jest funkcją pierwotną funkcji f, jeśli
).
(
)
(
'
x
f
x
F
P
x
=
∀
∈
Zauważmy, że jeśli F(x) jest funkcją pierwotną funkcji f, to także F(x) + c, gdzie c jest stałą,
jest funkcją pierwotną funkcji f.
Twierdzenie 1.6.1
Niech
0
F będzie funkcją pierwotną funkcji f. Wówczas F jest też funkcją pierwotną funkcji f
wtedy i tylko wtedy, gdy
,
)
(
)
(
0
c
x
F
x
F
+
=
gdzie c jest pewną stałą.
Zatem funkcja pierwotna funkcji f (o ile istnieje) nie jest wyznaczona jednoznacznie. Jeśli
istnieje jedna taka funkcja, to tym samym istnieje tych funkcji nieskończenie wiele.
Definicja 1.6.2
Niech
0
F będzie funkcją pierwotną funkcji f. Wyrażenie
,
0
c
F
+
będące ogólną postacią
funkcji pierwotnej funkcji f nazywamy jej całką nieoznaczoną i piszemy
.
)
(
)
(
0
c
x
F
dx
x
f
+
=
∫
Po prawej stronie powyższej równości mamy wyrażenie oznaczające dowolną funkcję
pierwotną funkcji f. Całkowanie jest więc operacją (określoną na pewnej klasie funkcji)
niejednoznaczną, bowiem wynikiem całkowania jest nie jedna funkcja, a pewna klasa
(rodzina) funkcji.
Nadmieniamy dla przypomnienia, że pochodna danej funkcji f (w pewnym zbiorze), o ile
istnieje, jest wyznaczona jednoznacznie.
Definicja 1.6.3
Mówimy, że funkcja f, określona na przedziale P, jest na tym przedziale
całkowalna, jeśli
całka
∫
dx
x
f
)
(
istnieje.
Całki nieoznaczone istnieją dla dość licznej klasy funkcji. Jednakże pewne funkcje nie mają
całki nieoznaczonej.
Dla przykładu funkcja
R
R
f
→
:
określona następująco:
−
=
1
1
)
(x
f
dla
dla
0
0
<
≥
x
x
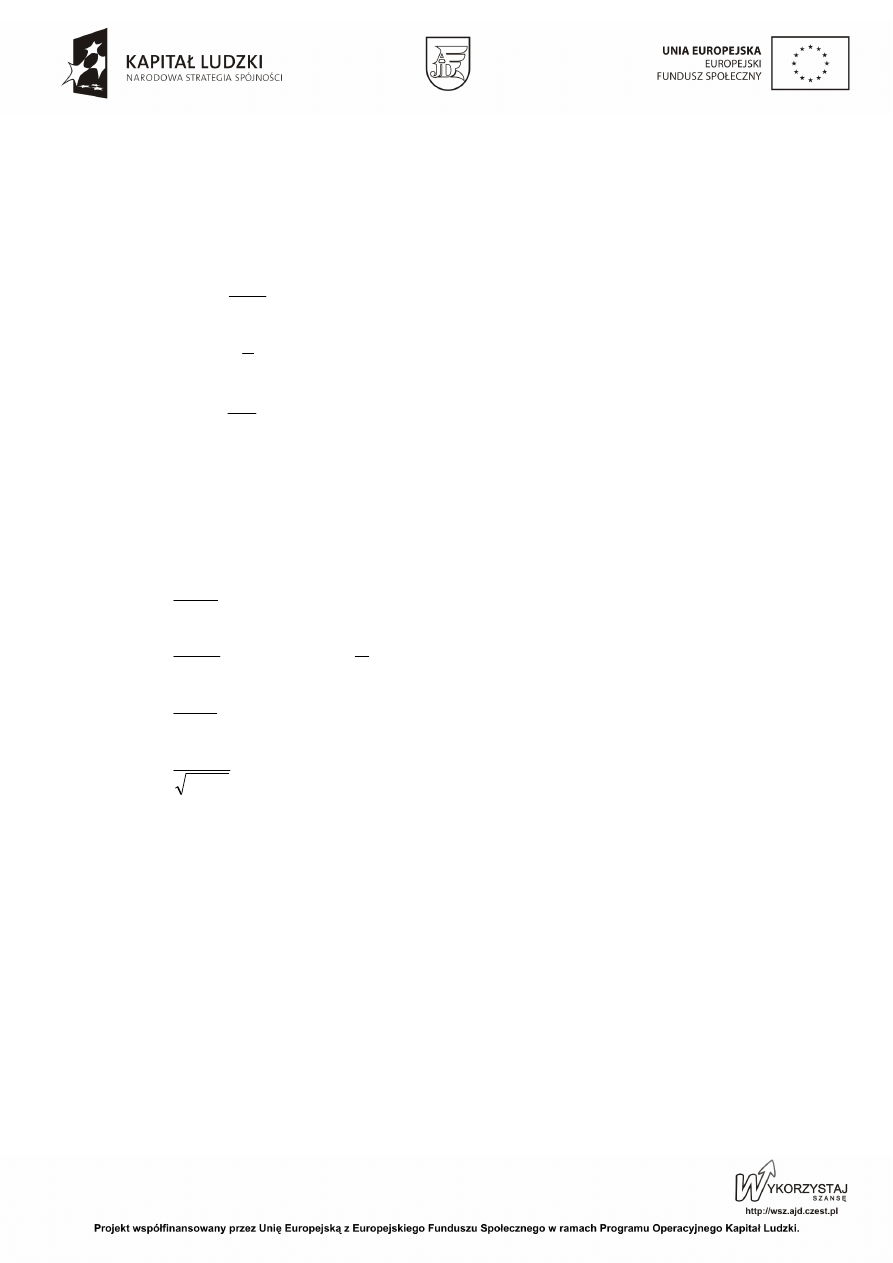
nie ma funkcji pierwotnej, tzn. nie istnieje funkcja
R
R
F
→
:
taka, że
),
(
)
(
'
x
f
x
F
=
.
R
x
∈
Podamy poniżej całki funkcji elementarnych:
1)
∫
=
,
0
c
dx
c – stała;
2)
∫
∫
+
=
=
;
1
c
x
dx
dx
3)
,
1
1
c
x
dx
x
+
+
=
+
∫
α
α
α
;
0
,
1
>
−
≠
x
α
4)
c
x
dx
x
dx
x
+
=
=
∫
∫
−
|
|
ln
1
1
,
0
≠
x
;
5)
c
a
a
dx
a
x
x
+
=
∫
ln
,
;
,
1
,
0
R
x
a
a
∈
≠
>
6)
c
e
dx
e
x
x
+
=
∫
;
7)
∫
+
−
=
,
cos
sin
c
x
xdx
;
R
x
∈
8)
∫
+
=
,
sin
cos
c
x
xdx
;
R
x
∈
9)
∫
+
−
=
,
sin
1
2
c
ctgx
dx
x
;
Z
k
k
x
∈
∧
≠
π
10)
∫
+
=
c
tgx
dx
x
2
cos
1
,
;
2
Z
k
k
x
∈
∧
+
≠
π
π
11)
,
1
1
1
2
c
arcctgx
c
arctgx
dx
x
+
−
=
+
=
+
∫
;
R
x
∈
12)
1
2
arccos
arcsin
1
1
c
x
c
x
dx
x
+
−
=
+
=
−
∫
,
).
1
,
1
(
−
∈
x
1.7
Elementarne własności całki nieoznaczonej
Twierdzenie 1.7.1
Jeżeli f i g są funkcjami ciągłymi na przedziale P, to dla dowolnych
,
,
R
R
∈
∈
β
α
∫
∫
∫
+
=
+
.
)
(
)
(
))
(
)
(
(
dx
x
g
dx
x
f
dx
x
g
x
f
β
α
β
α
(1.7.1)
Z twierdzenia 1.7.1 wynika w szczególności, że
∫
∫
=
,
)
(
)
(
dx
x
f
dx
x
f
α
α
(1.7.2)
tzn. stałą można wyłączyć przed znak całki
oraz, że
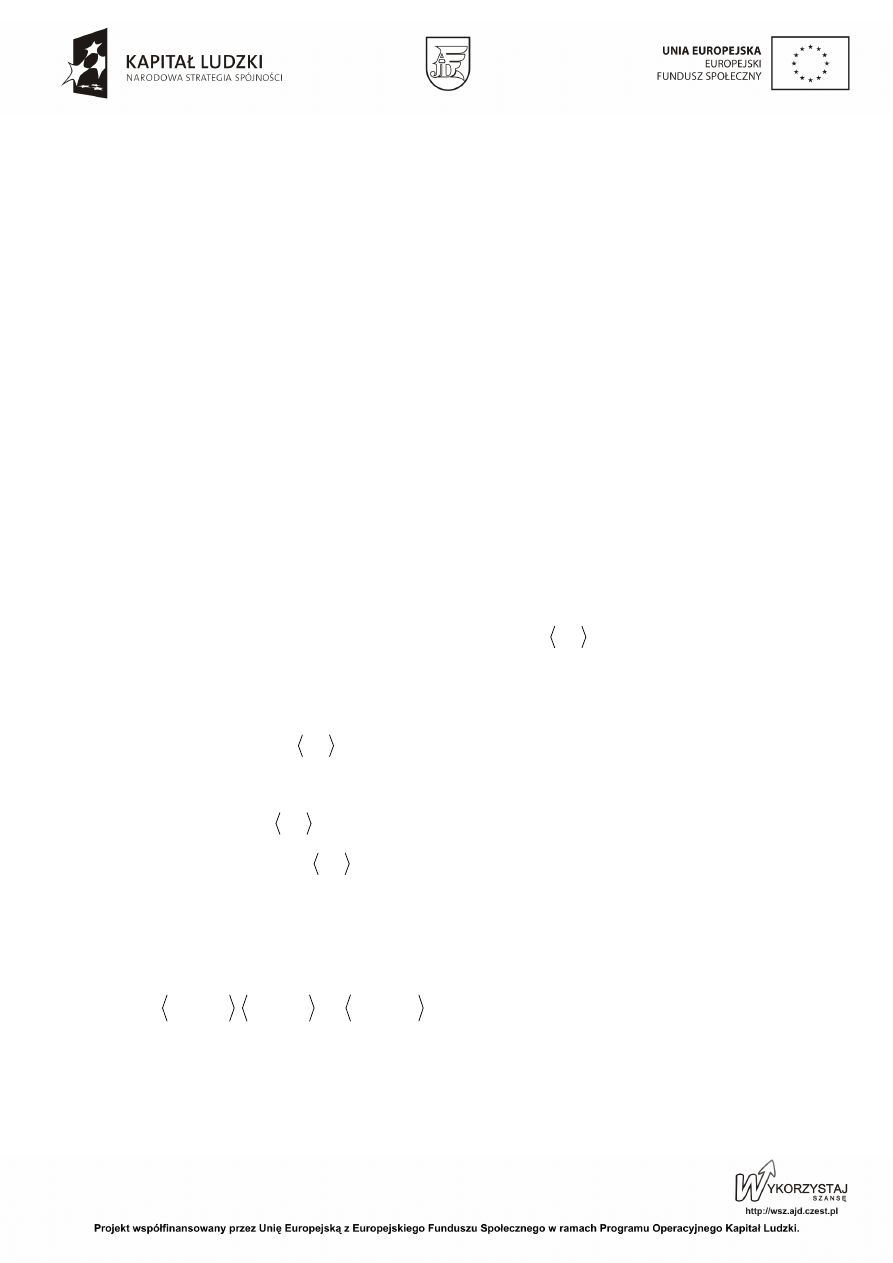
∫
∫
∫
±
=
±
,
)
(
)
(
))
(
)
(
(
dx
x
g
dx
x
f
dx
x
g
x
f
(1.7.3)
tzn. całka sumy (różnicy) dwóch funkcji
f i g jest równa sumie (różnicy) całek – całki funkcji
f i całki funkcji g.
Twierdzenie 1.7.2 (O całkowaniu przez części)
Jeżeli funkcje
f i g są ciągłe i mają ciągłe pochodne na przedziale P, to
∫
∫
⋅
−
=
⋅
.
)
(
)
(
)
(
)
(
)
(
)
(
'
'
dx
x
g
x
f
x
g
x
f
dx
x
g
x
f
(1.7.4)
Wzór (1.7.4) jest wzorem na
całkowanie przez części.
Drugą ważną metodą całkowania jest całkowanie przez podstawienie.
Twierdzenie 1.7.3 (O całkowaniu przez podstawienie)
Jeżeli
f jest funkcją ciągłą wraz ze swoją pochodną na przedziale P, zaś g jest funkcją ciągłą
na zbiorze wartości funkcji
f, to
∫
∫
=
⋅
,
)
(
)
(
))
(
(
'
dt
t
g
dx
x
f
x
f
g
)).
(
(
x
f
t
=
(1.7.5)
Wzór (1.7.5) nazywa się wzorem na
całkowanie przez podstawienie.
1.8
Całka oznaczona
Niech f będzie funkcją określoną na przedziale domkniętym
b
a,
.
Definicja 1.8.1
Mówimy, że liczby rzeczywiste
n
x
x
x
x
,
,
,
,
2
1
0
K
(punkty na prostej) wyznaczają
podział
przedziału domkniętego
,
, b
a
jeśli
.
2
1
0
b
x
x
x
x
a
n
=
<
<
<
<
=
K
Dla danego przedziału
b
a,
rozważmy ciąg (
)
n
π
podziałów tego przedziału. Załóżmy,
ż
e n-ty podział przedziału
b
a,
jest wyznaczony przez punkty
,
,
,
,
)
(
)
(
2
)
(
1
)
(
0
n
k
n
n
n
n
x
x
x
x
K
przy
czym zgodnie z definicją 1.8.1 mamy:
.
:
)
(
)
(
2
)
(
1
)
(
0
b
x
x
x
x
a
n
k
n
n
n
n
n
=
<
<
<
<
=
K
π
W n – tym podziale spośród odcinków
)
(
)
(
1
)
(
2
)
(
1
)
(
1
)
(
0
,
,
,
,
,
,
n
k
n
k
n
n
n
n
n
n
x
x
x
x
x
x
−
K
wybieramy ten, który ma największą długość.
Niech
)
,
2
,
1
(
K
=
∆
n
n
oznacza długość największego odcinka.

Definicja 1.8.2
Mówimy, że ciąg podziałów (
)
n
π
jest normalny, jeśli
,
0
lim
=
∆
∞
→
n
n
(długość największego odcinka wraz ze wzrostem
n zmierza do zera).
Niech (
)
n
π
będzie ciągiem normalnym podziałów przedziału
b
a,
. Oznaczmy przez
)
(
n
γ
ciąg liczbowy, którego
n – ty wyraz jest określony następująco:
∑
=
−
−
=
n
k
i
n
i
n
i
n
i
n
x
x
c
f
1
)
(
1
)
(
)
(
),
)(
(
γ
,
,
2
,
1
K
=
n
gdzie
.
,
2
,
1
,
.
,
2
,
1
,
,
)
(
)
(
1
)
(
K
K
=
=
∈
−
n
k
i
x
x
c
n
n
i
n
i
n
i
Definicja 1.8.3
Jeżeli granica ciągu
)
(
n
γ
jest skończona oraz nie zależy ona ani od wyboru normalnego ciągu
podziałów przedziału
b
a,
, ani od wyboru punktów
,
)
( n
k
c
to mówimy, że f jest całkowalna
w sensie Riemanna na przedziale
b
a,
, zaś granicę
γ
ciągu
)
(
n
γ
oznaczamy symbolem
∫
b
a
dx
x
f
)
(
i nazywamy
całką Riemanna (całką oznaczoną ) funkcji f na przedziale
b
a,
.
A zatem
.
lim
:
)
(
n
n
b
a
dx
x
f
γ
+∞
→
=
∫
Twierdzenie 1.8.1
Jeżeli f jest funkcją ciągłą na przedziale domkniętym
b
a,
, to
1)
Istnieje na
b
a,
funkcja pierwotna F funkcji f;
2)
f jest całkowalna na
b
a,
i zachodzi wzór:
∫
−
=
=
b
a
b
a
a
F
b
F
x
F
dx
x
f
).
(
)
(
)]
(
[
)
(
(1.8.1)
Uwaga 1.8.1
We wzorze (1.8.1) F jest jakąkolwiek funkcją pierwotną funkcji f.
Twierdzenie 1.8.2
Funkcja całkowalna na
b
a,
jest na tym przedziale ograniczona.

Wniosek
Jeżeli f nie jest ograniczona na
b
a,
, to całka
∫
b
a
dx
x
f
)
(
nie istnieje.
Twierdzenie 1.8.3
Jeżeli f i g są funkcjami całkowalnymi na przedziale
b
a,
, to dla dowolnych
α
i
β
funkcja
)
(
)
(
x
g
x
f
β
α
+
też jest całkowalna na
b
a,
i zachodzi wzór:
∫
∫
∫
+
=
+
b
a
b
a
b
a
dx
x
g
dx
x
f
dx
x
g
x
f
.
)
(
)
(
))
(
)
(
(
β
α
β
α
Twierdzenie 1.8.4
Niech f będzie funkcją określoną na przedziale
b
a,
i niech
.
b
c
a
<
<
Wówczas całka
∫
b
a
dx
x
f
)
(
istnieje wtedy i tylko wtedy, gdy istnieją całki
∫
c
a
dx
x
f
)
(
,
∫
b
c
dx
x
f
)
(
i zachodzi
równość:
∫
∫
∫
+
=
b
a
c
a
b
c
dx
x
f
dx
x
f
dx
x
f
.
)
(
)
(
)
(
Twierdzenie 1.8.5
Jeżeli
0
)
(
≥
x
f
dla
b
a
x
,
∈
i całka
∫
b
a
dx
x
f
)
(
istnieje, to
∫
b
a
dx
x
f
)
(
.
0
≥
Tak więc całka z funkcji nieujemnej na
b
a,
o ile istnieje, jest liczbą nieujemną.
1.9
Całka oznaczona jako pole
Niech
0
)
(
≥
x
f
dla
b
a
x
,
∈
.

Wprost z definicji całki oznaczonej (definicja 1.8.3) wynika, że całka oznaczona
∫
b
a
dx
x
f
)
(
jest polem obszaru
)}.
(
0
:
)
,
{(
x
f
y
b
x
a
y
x
P
≤
≤
∧
≤
≤
=
Całkę
∫
b
a
dx
x
f
)
(
można interpretować jako pole bez założenia, że
0
)
(
≥
x
f
dla
.
, b
a
x
∈
Bowiem, jeśli
0
)
(
≤
x
f
dla
,
, b
a
x
∈
to przyjmujemy, że pole obszaru jest równe
∫
−
=
b
a
dx
x
f
P
.
)
(
|
|
Wyszukiwarka
Podobne podstrony:
matematyka dyskretna w 2 id 283 Nieznany
matematyka wzory id 284044 Nieznany
Matematyka dyskretna id 283281 Nieznany
Matematyka lista1 id 283685 Nieznany
Matematyka 17 id 283105 Nieznany
Matematyka dyskretna 3 id 28329 Nieznany
Cwiczenie 3A id 99454 Nieznany
matematyka dyskretna w id 28343 Nieznany
ekonomia 3a id 155736 Nieznany
matematyka model 1 id 766047 Nieznany
Matematyka 13 id 283096 Nieznany
matematyka 1 odp(3) id 284049 Nieznany
Matematyka 16 id 283104 Nieznany
klasa 2 LO Matematyka doc id 23 Nieznany
Projekt 3A id 398296 Nieznany
mech 3a id 290417 Nieznany
Matematyka 15 id 283098 Nieznany
więcej podobnych podstron