Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/1
piwicki@pg.gda.pl
Wykład nr 6.
Linie wpływu w układach statycznie niewyznaczalnych
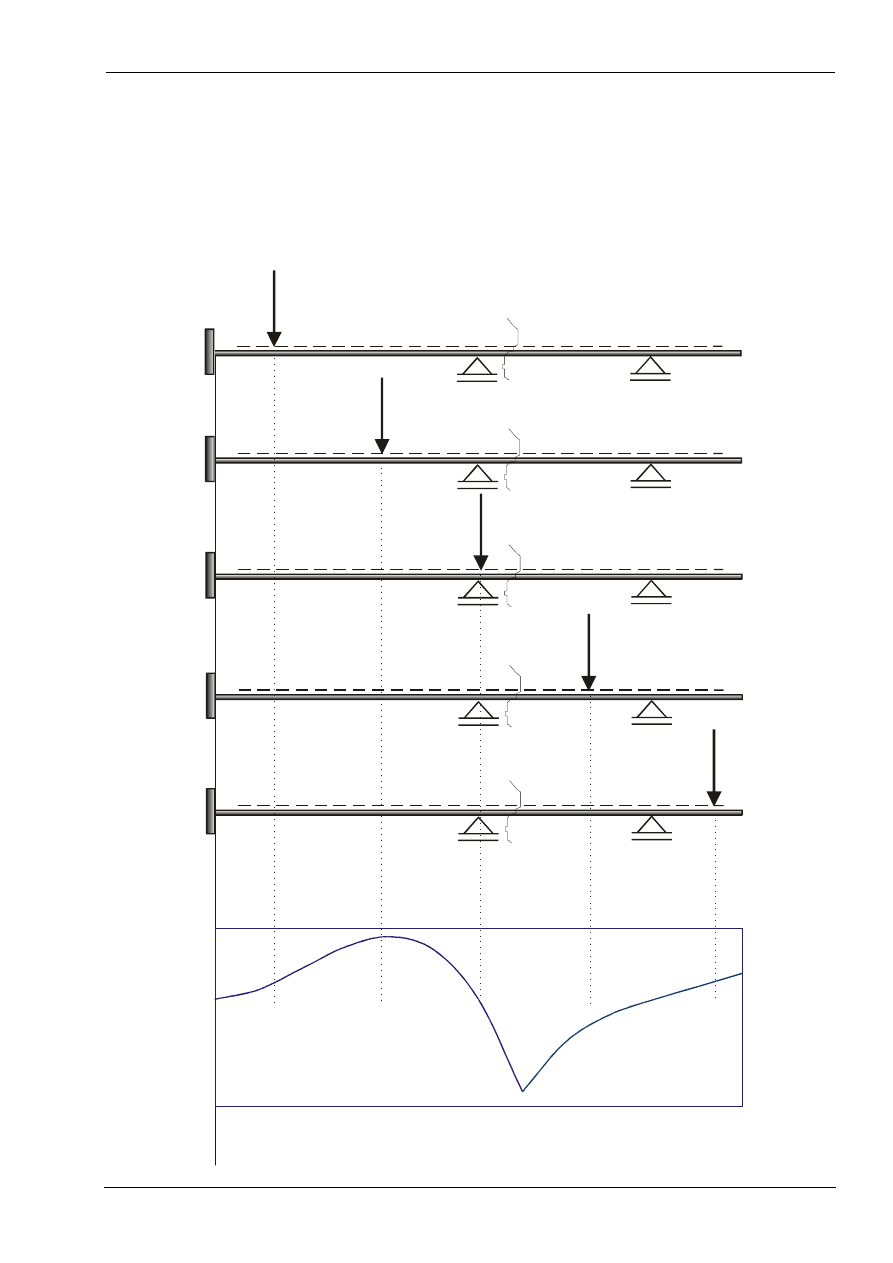
Linią wpływu pewnej wielkości statycznej Z (reakcja, moment zginający, siła tnąca,
siła normalna) nazywamy wykres przedstawiający zależność pomiędzy wartością Z a
położeniem poruszającej się po układzie siły jednostkowej o określonym kierunku.
L i n i a w p ł y w u s i ł y t n ą c e j M a
- 0 . 4
- 0 . 3
- 0 . 2
- 0 . 1
0 . 0
0 . 1
0 . 2
0 . 3
0 . 4
0 . 5
0 . 6
0 . 0
1 . 0
2 . 0
3 . 0
4 . 0
5 . 0
6 . 0
7 . 0
8 . 0
9 . 0
1 0 .
1 1 .
1 2 .
P=1
P=1
P=1
P=1
P=1
A
A
A
A
A
C
C
C
C
C
D
D
D
D
D
B -
α
B -
α
B -
α
B -
α
B -
α
Linia wpływu momentu M
α
L i n i a w p ł y w u s i ł y t n ą c e j M a
- 0 . 4
- 0 . 3
- 0 . 2
- 0 . 1
0 . 0
0 . 1
0 . 2
0 . 3
0 . 4
0 . 5
0 . 6
0 . 0
1 . 0
2 . 0
3 . 0
4 . 0
5 . 0
6 . 0
7 . 0
8 . 0
9 . 0
1 0 .
1 1 .
1 2 .
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/2
piwicki@pg.gda.pl
Linie wpływu mają zastosowanie do ustalania najbardziej niekorzystnych dla
konstrukcji położeń obciążeń zmiennych takich jak na przykład obciążenie pojazdem,
obciążenie tłumem ludzi, obciążenie zmienne użytkowe. Projektant powinien tak
zaplanować ustawienie obciążenia zmiennego aby wynikające z niego siły i
przemieszczenia były maksymalne. Bez znajomości linii wpływu trudno jest to
określić.
X
Y
Z
123456
123456
3
23
123
23
13
3
94.
94.
6.
6.
14.
14.
86.
86. 34.
34.
66.
66.
26.
26.
74.
74.
6.
6.
94.
94.
14.
14.
86.
86. 66.
66.
34.
34.
26.
26.
74.
74.
6.
6.
14.
14.
86.
86.
94.
94.
74.
74.
26.
26.
34.
34.
66.
66.
6.
6.
14.
14.
94.
94.
86.
86.
74.
74.
26.
26.
34.
34.
66.
66.
6.
6.94.
94.
14.
14.
86.
86.
74.
74.
26.
26.
34.
34.
66.
66.
6.
6.
14.
14.
86.
86.
74.
74.
26.
26.
34.
34.
66.
66.
94.
94.
6.
6.
14.
14.
94.
94.
86.
86. 66.
66.
34.
34.
26.
26.
74.
74.
6.94.
14.
86.74.
26.
34.
66.
66.
34.
26.
74.86.
14.
14.
14.
86.
86.
74.
74.
26.
26.
34.
34.
66.
66.
6.
94.
V11
L21
C2
Na przykład które położenie obciążenia samochodem jest najbardziej niekorzystne dla
wyznaczenia sił wewnętrznych w łuku, poprzecznicach i podłużnicach mostu?
Czasami problem ten można rozwiązać ustawiając obciążenie w wielu różnych
pozycjach i analizując wszystkie uzyskane wyniki. Jest to jednak podejście bardzo
pracochłonne i wydłuża czas obliczeń.
X
Y
Z
123456
123456
3
23
123
23
13
3
6.
6.
14.
14.
94.
94.
86.
86.
74.
74.
26.
26.
34.
34.
66.
66.
0.00728
0.00395
0.000632
-0.00269
-0.00601
-0.00933
-0.0127
-0.016
-0.0193
-0.0226
-0.0259
-0.0293
-0.0326
-0.0359
-0.0392
-0.0426
-0.0459
V11
L16
C2
Output Set: MSC/ NASTRAN Case 16
Deformed(0.0472): Total Translation
Contour: T3 Translation
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/3
piwicki@pg.gda.pl
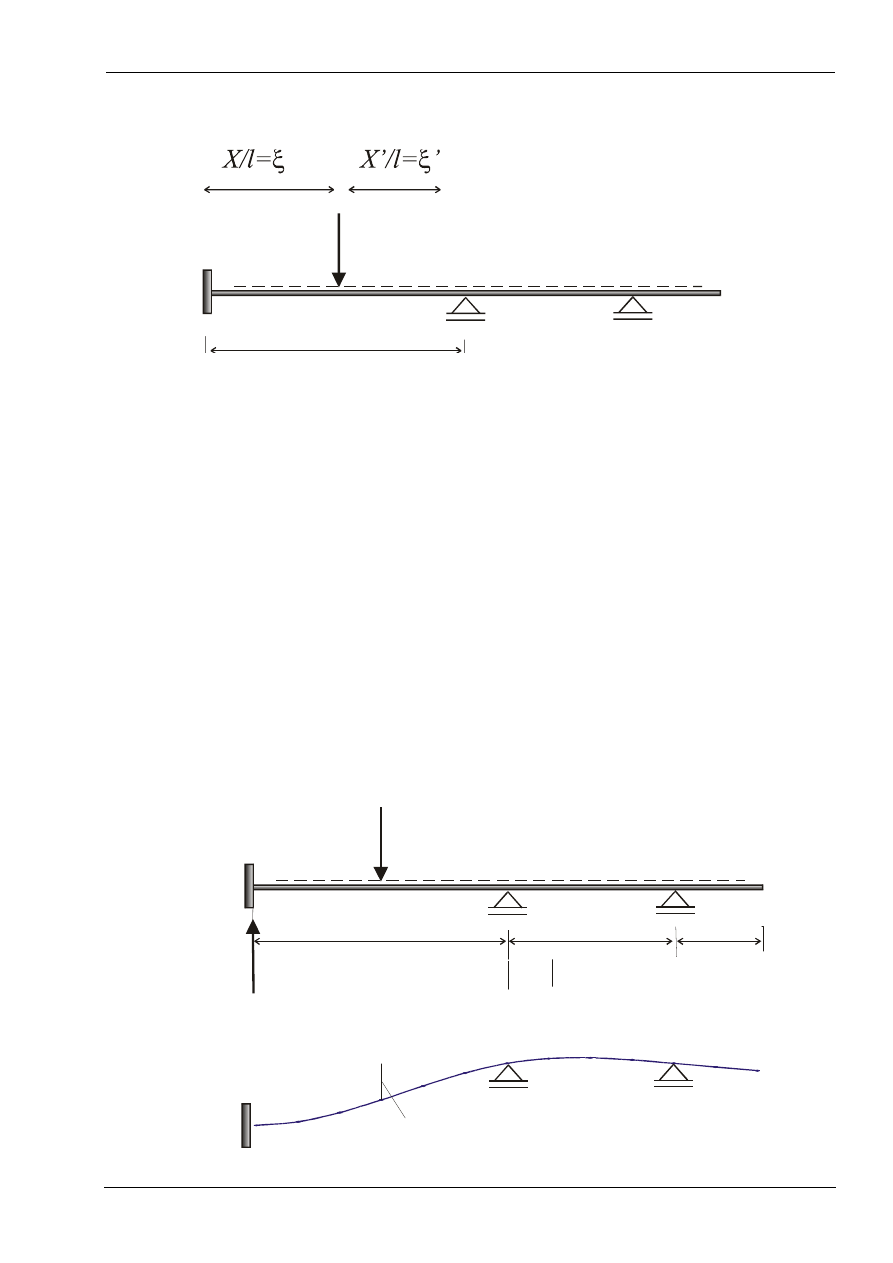
• Linie wpływu można wyznaczać wprost z definicji. W tym celu należy
wyrazić wielkości statyczne w funkcji położenia siły jednostkowej (x, x’).
L
P=1
A
C
D
B -
α
• Drugi sposób wyznaczania linii wpływu sił wewnętrznych lub reakcji polega na
wykorzystaniu twierdzenia o wzajemności reakcji i przemieszczeń.
Z twierdzenia o wzajemności prac Betti-Maxwell’a wiemy, że:
∑
∑
=
I
ki
II
k
II
ik
I
i
P
P
δ
δ
zakładając, że w I układzie działa siła P a podpory nie ulegają przemieszczeniom, a w
drugim układzie mamy przemieszczenia a siły są równe zeru
0
II
I
k
ki
P
δ
=
∑
otrzymamy:
0
=
Δ
−
II
k
I
k
II
ik
I
i
R
P
δ
zakładając ponadto, że:
1
,
1
=
Δ
=
II
k
I
i
P
otrzymujemy twierdzenie Mullera Breslaua:
II
ik
I
k
R
δ
=
L
i n
i a
w
p
ł y w
u
r e
a
k
c j i
R
A
- 0
. 2
0
. 0
0
. 2
0
. 4
0
. 6
0
. 8
1
. 0
1
. 2
0
1
2
3
4
5
6
7
8
9
1
0
1
1
1
2
P =1
i
I
R
k
I
Δ
k
II
=1
−− δ
ik
II
Układ “I”
Układ “II”
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/4
piwicki@pg.gda.pl
Reakcja na podporze k od obciążenia jednostkowego w punkcje i jest
równa liczbowo przemieszczeniu punktu i (w kierunku tego obciążenia)
wywołanemu jednostkowym przemieszczeniem podpory k przeciwnie do
zwrotu reakcji. (zasada Mullera-Breslau’a).
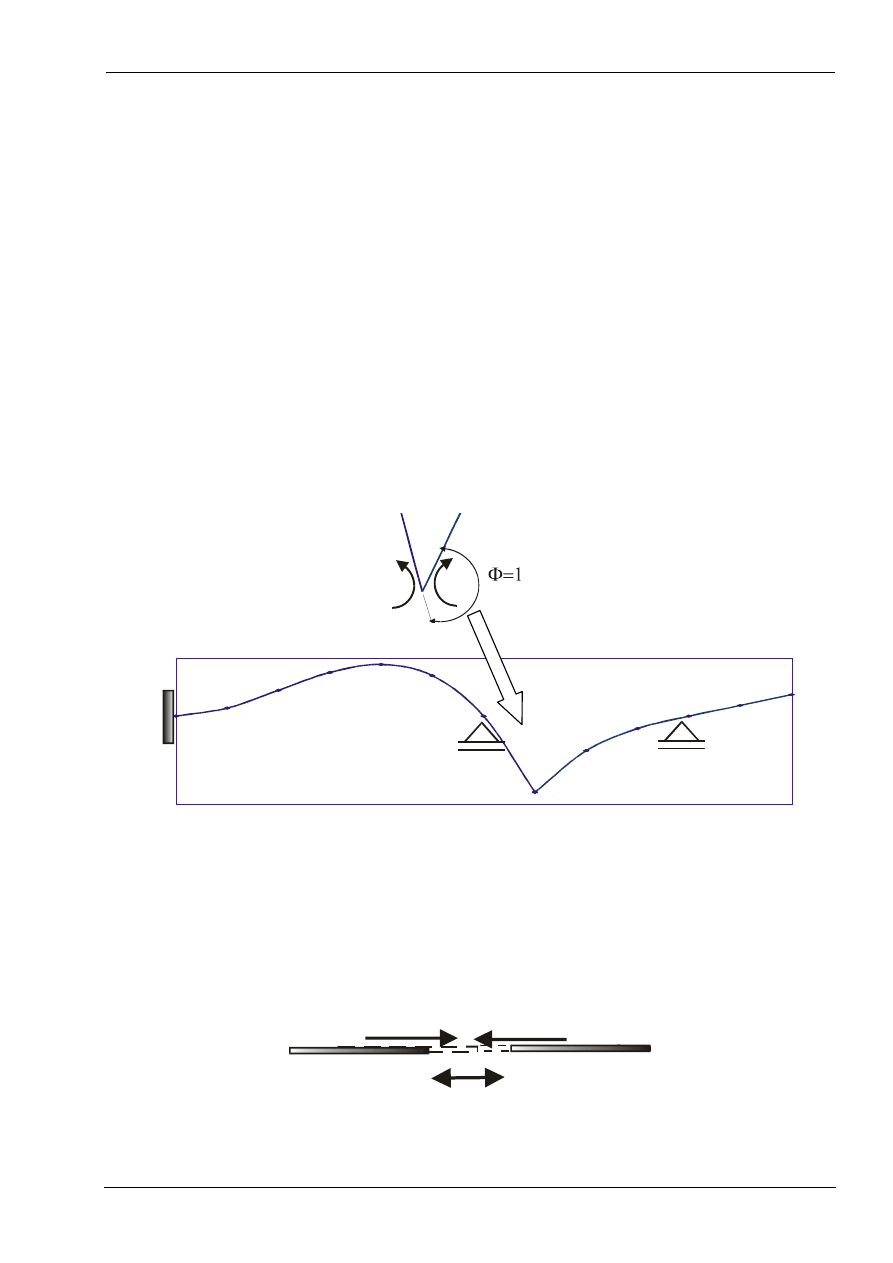
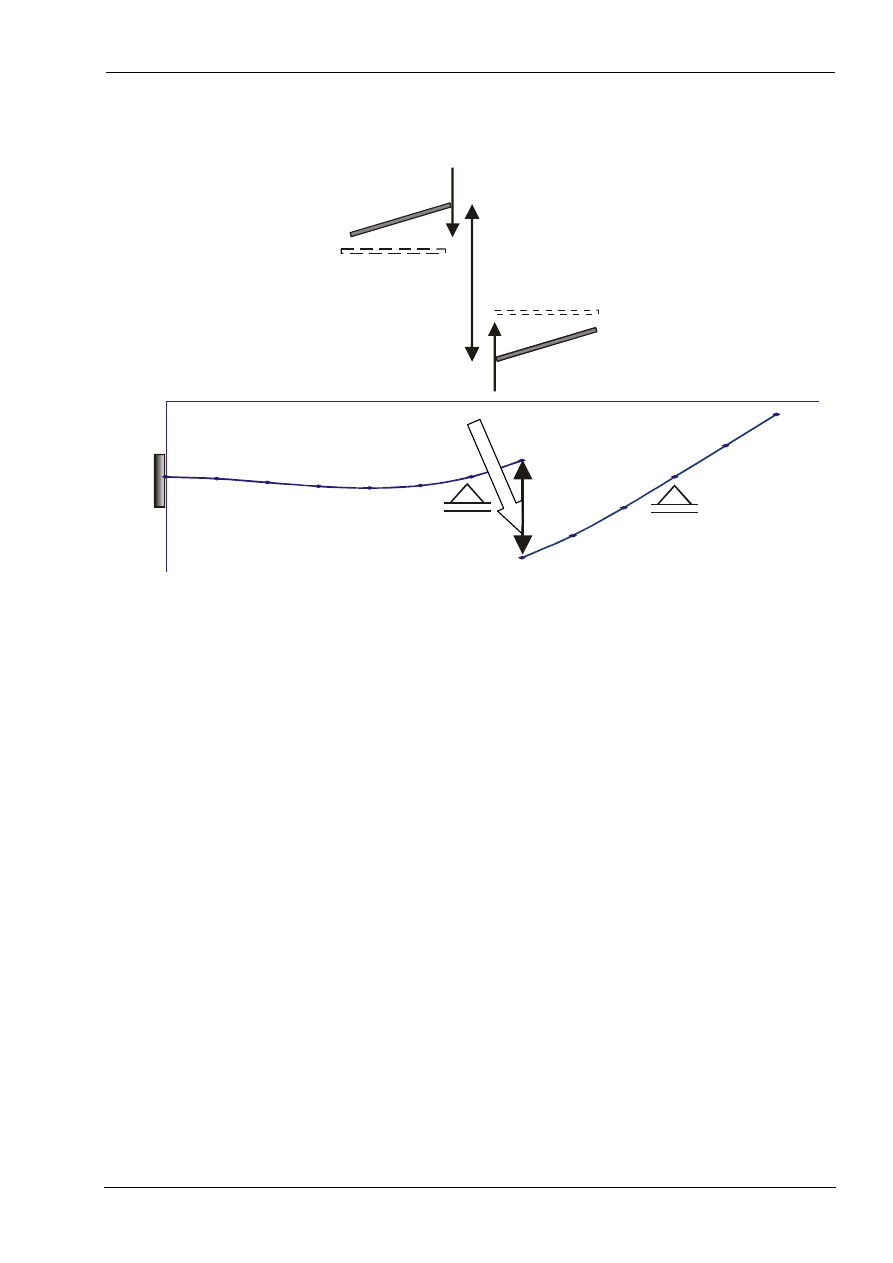
Twierdzenie to może służyć do kinematycznego wyznaczania linii
wpływu. Linia wpływu danej wielkości statycznej Z pokrywa się z linią
ugięcia części konstrukcji (po których porusza się siła jednostkowa)
wywołaną odpowiednim jednostkowym wymuszeniem kinematycznym
skierowanym przeciwnie do wielkości Z
.
Wymuszenia kinematyczne nałożone na konstrukcję zależą od tego jakiej
linii wpływu szukamy.
•
Wyznaczanie linii wpływu momentu zginającego:
W celu wyznaczenia linii wpływu momentu zginającego wprowadzamy
jednostkowe wymuszenie kinematyczne na kącie obrotu przekrojów.
L i n i a
w
p ł y w
u
s i ł y
t n ą c e j M
a
- 0 . 4
- 0 . 3
- 0 . 2
- 0 . 1
0 . 0
0 . 1
0 . 2
0 . 3
0 . 4
0 . 5
0 . 6
0 . 0
1 . 0
2 . 0
3 . 0
4 . 0
5 . 0
6 . 0
7 . 0
8 . 0
9 . 0
1 0 .
1 1 .
1 2 .
•
Linia wpływu siły normalnej
W celu wyznaczenia linii wpływu siły normalnej wprowadzamy
jednostkowe rozsunięcie przekrojów.
N
N
Δ=1
M
M
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/5
piwicki@pg.gda.pl
•
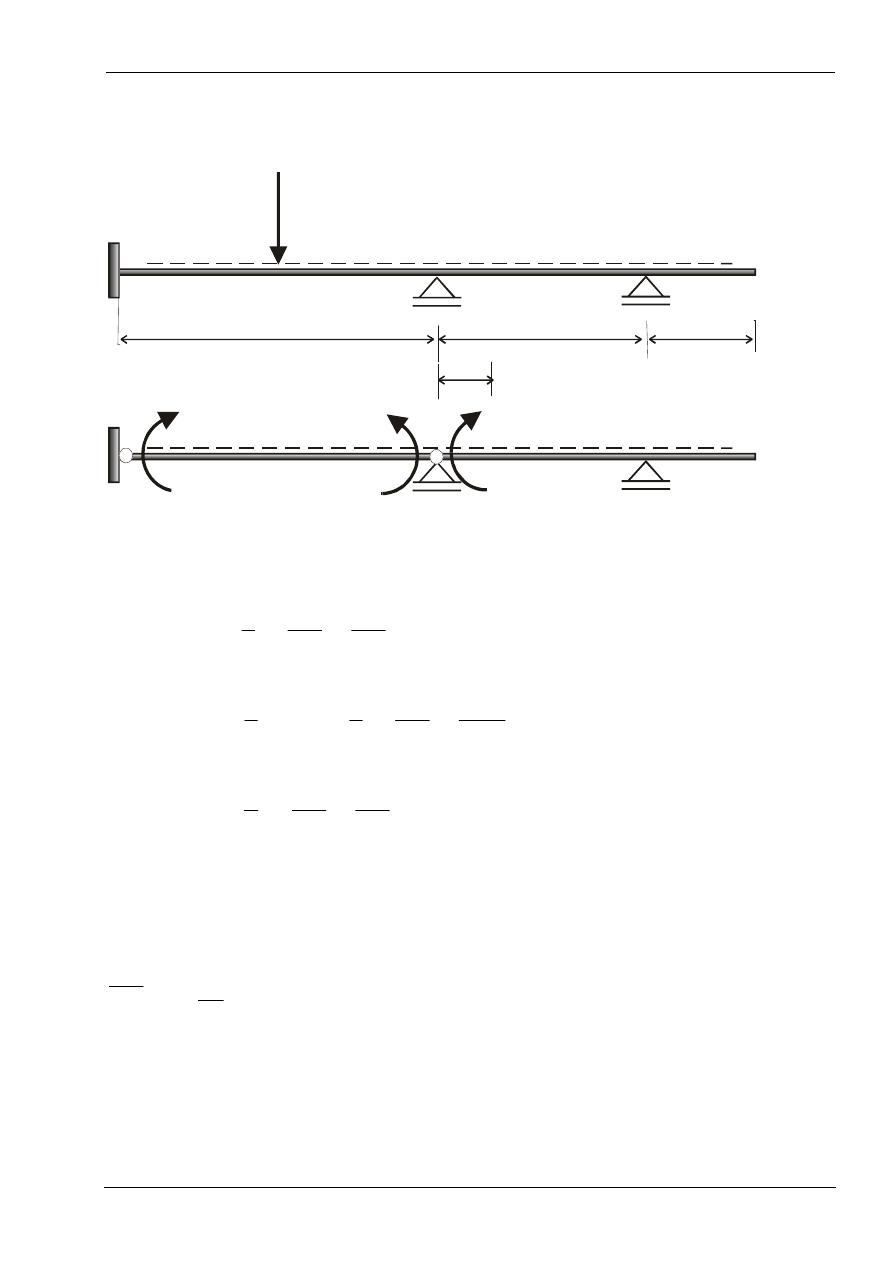
Wyznaczanie linii wpływu siły tnącej:
Wprowadzamy wymuszenie kinematyczne w postaci rozsunięcia
przekrojów pręta w kierunku siły tnącej.
T
T
Δ=1
Δ
k
II
=1
L i n i a
w p ł y w u
s i ł y
t n ą c e j T a
- 0 . 8
- 0 . 6
- 0 . 4
- 0 . 2
0 . 0
0 . 2
0 . 4
0 . 6
0 . 8
1 . 0
0 . 0
1 . 0
2 . 0
3 . 0
4 . 0
5 . 0
6 . 0
7 . 0
8 . 0
9 . 0
1 0 .
1 1 .
1 2 .
Δ
k
II
=1
•
Linia wpływu reakcji: przesunięcie podpory o 1 przeciwnie
skierowane do zwrotu reakcji.
•
Linia wpływu momentu podporowego : obrót podpory o kąt
jednostkowy przeciwnie skierowany do działającego momentu.
Własności linii wpływu:
•
Tam gdzie kierunek przemieszczenia powstałego przy wymuszeniu
kinematycznym jest zgodny z kierunkiem działania siły jednostkowej
znak linii wpływu jest dodatni.
•
W układzie statycznie niewyznaczalnym linie wpływu są liniami
gładkimi (nie mają załamań i nieciągłości) za wyjątkiem przekroju w
którym nastąpiło wymuszenie oraz przegubów.
•
W obrębie wspornika linia wpływu jest linią prostą
•
W układach statycznie wyznaczalnych również można wyznaczać
linię wpływu w sposób kinematyczny. W układach statycznie
wyznaczalnych linia wpływu jest linią prostą lub składa się z linii
prostych.
•
Przy podporach kształt linii wpływu jest zgodny z warunkami
brzegowymi (na przykład w utwierdzeniu styczna pozioma)
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/6
piwicki@pg.gda.pl
Przykład.
Wyznaczanie linii wpływu metodą bezpośrednią – wprost z definicji.
Wyznaczyć za pomocą metoda sił linie wpływu: R
A
R
B
M
A
M
α
T
α.
6m
4m
1m
2m
P=1
I
I
I
A
C
D
B -
α
X
1
X
2
X
2
A
C
D
B -
α
Dla podanego schematu podstawowego metody sił obliczamy:
EJ
EJ
2
1
)
3
1
6
1
(
11
=
×
×
×
=
δ
EJ
EJ
3
10
1
)
3
1
4
1
3
1
6
1
(
22
=
×
×
×
+
×
×
=
δ
EJ
EJ
1
1
)
6
1
6
1
(
12
=
×
×
×
=
δ
Powyższe współczynniki równania zgodności przemieszczeń metody sił nie zależą od
obciążenia zewnętrznego. Równanie zgodności przemieszczeń ma postać:
,
3
10
1
1
2
1
20
10
2
1
2
1
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
⎥
⎦
⎤
⎢
⎣
⎡
×
=
⎥
⎦
⎤
⎢
⎣
⎡
×
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
δ
δ
X
X
F
X
X
EJ
Z powyższego równania możemy wyznaczyć równania linii wpływu nadliczbowych
metody sił. W tym celu wyznaczamy wartości współczynników
20
10
,
δ
δ
w zależności
od położenia siły P, zakładając że siła ta znajduje się w kolejnych przęsłach belki
ciągłej.
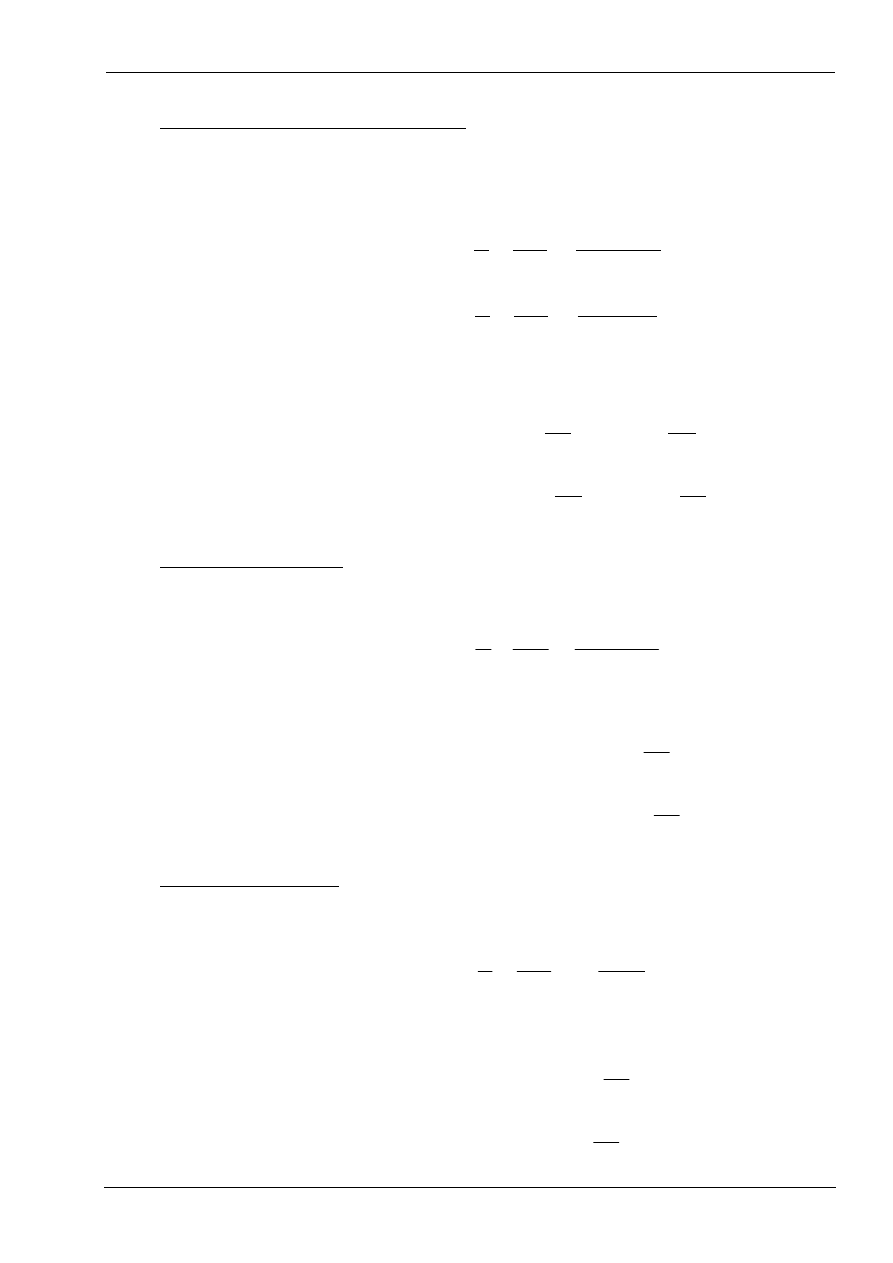
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/7
piwicki@pg.gda.pl
• Siła P znajduje się w przedziale AB.
Wprowadzamy oznaczenia:
3
)
(
ξ
ξ
ξ
ω
−
=
T
,
3
)
(
ξ
ξ
ξ
ω
′
−
′
=
′
T
.
Współczynniki
20
10
,
δ
δ
możemy zapisać następującymi wzorami:
EJ
EJ
l
T
T
)
(
6
1
6
1
)
(
2
1
10
ξ
ω
ξ
ω
δ
′
=
×
×
×
′
=
EJ
EJ
l
T
T
)
(
6
1
6
1
)
(
2
1
20
ξ
ω
ξ
ω
δ
=
×
×
×
=
Następnie możemy wyznaczyć równania linii wpływu nadliczbowych:
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
′
+
−
′
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
×
=
⎥
⎦
⎤
⎢
⎣
⎡
−
17
18
)
(
17
36
)
(
17
60
)
(
17
18
)
(
20
10
1
2
1
ξ
ω
ξ
ω
ξ
ω
ξ
ω
δ
δ
T
T
T
T
F
X
X
• Siła w przedziale BC.
10
0
δ
=
2
20
2
8
( )
1
1
( )
6
3
T
T
l
EJ
EJ
ω ξ
δ
ω ξ
′
′
=
× × ×
=
równania linii wpływu nadliczbowych
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
′
−
′
=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
×
×
=
⎥
⎦
⎤
⎢
⎣
⎡
−
17
16
)
(
17
8
)
(
20
10
1
2
1
ξ
ω
ξ
ω
δ
δ
T
T
F
EJ
X
X
• Siła w przedziale CD
0
10
=
δ
EJ
EJ
l
l
3
4
1
6
1
2
3
20
ξ
ξ
δ
−
=
×
×
×
×
−
=
równania linii wpływu nadliczbowych:
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
×
×
=
⎥
⎦
⎤
⎢
⎣
⎡
−
ξ
ξ
δ
δ
17
8
17
4
20
10
1
2
1
F
EJ
X
X
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/8
piwicki@pg.gda.pl
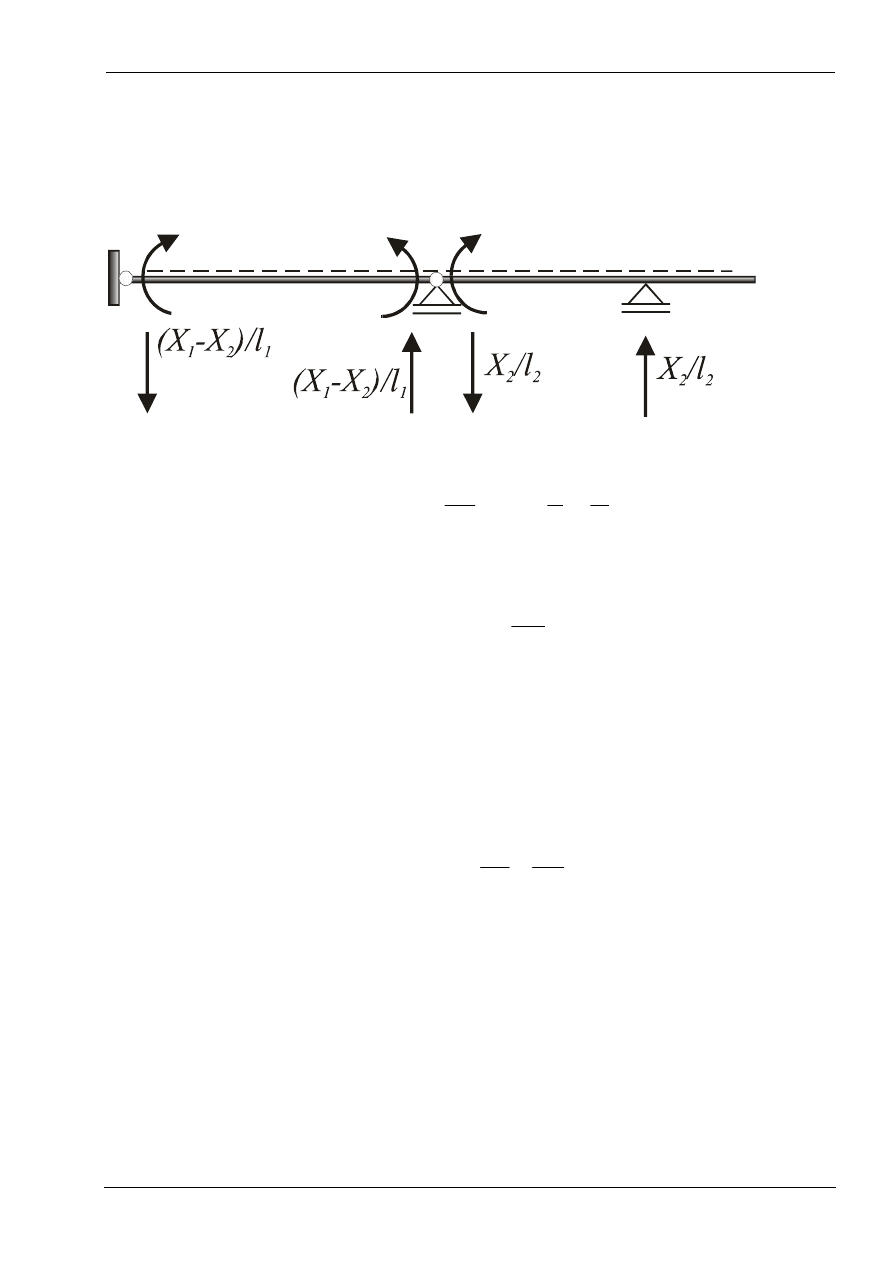
Wyznaczenie linii wpływu sił wewnętrznych i reakcji odbywa się przez zsumowanie
odpowiednich linii wpływu nadliczbowych oraz linii wpływu danej wielkości
statycznej dla układu podstawowego – statycznie wyznaczalnego.
X
1
X
2
X
2
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
−
+
=
2
1
2
1
1
1
1
]
[
l
l
X
l
X
R
R
B
B
2
2
]
[
l
X
T
T
−
=
α
α
2
]
[
X
M
M
′
+
=
α
α
α
ξ
Dla przekroju
β
znajdującego się w pierwszym przęśle:
1
2
1
2
[ ]
X
X
T
T
l
l
α
β
=
−
+
1
2
[
]
M
M
X
X
β
β
β
β
ξ
ξ
′
=
+
+
Na podstawie przedstawionych zależności wyznaczono wykresy poszczególnych linii
wpływu.
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/9
piwicki@pg.gda.pl
6m
4m
1m
2m
P=1
I
I
I
A
C
D
B -
α
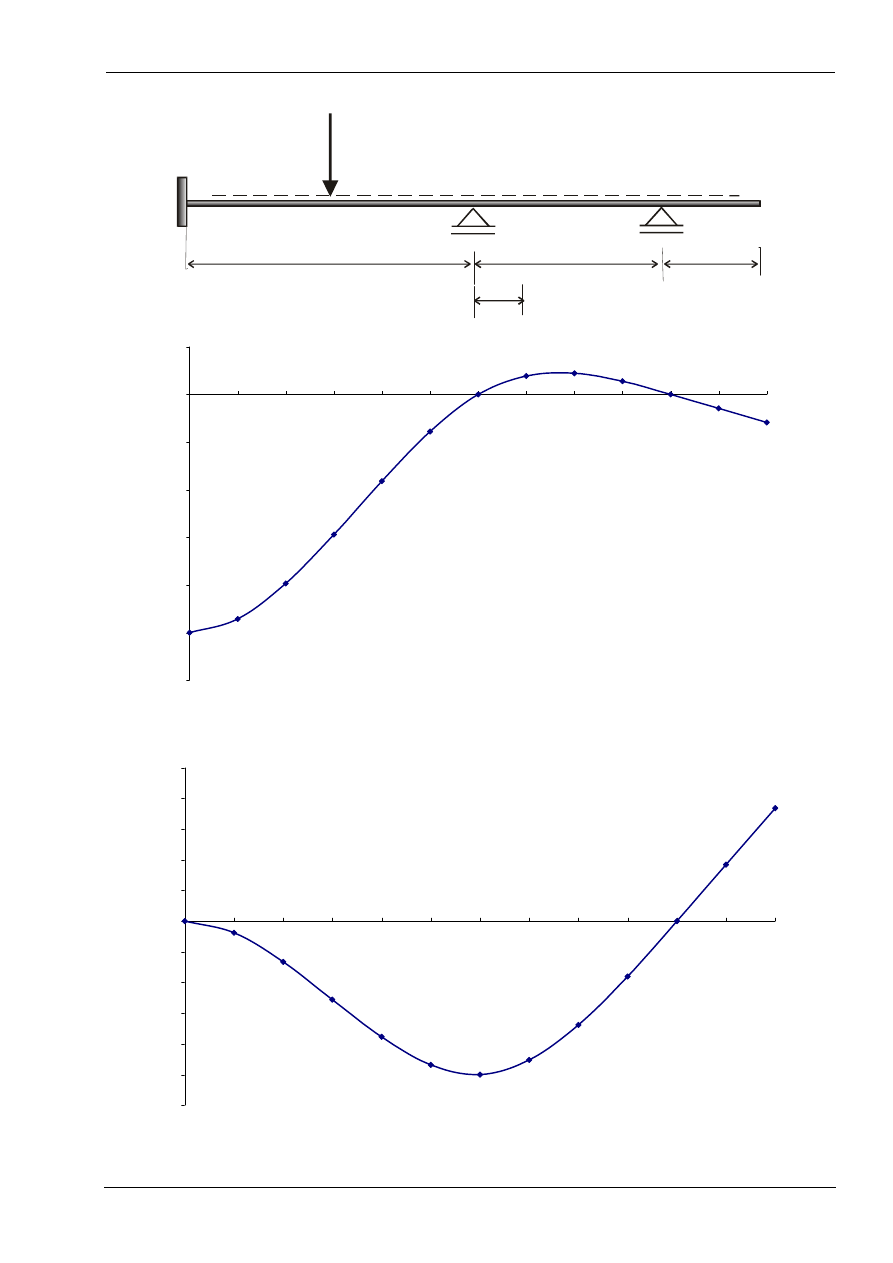
Linia wpływu reakcji RA
-0.2
0.0
0.2
0.4
0.6
0.8
1.0
1.2
0
1
2
3
4
5
6
7
8
9
10
11
12
linia wpływu R
A
Linia wpływu reakcji RB
-1.0
-0.8
-0.6
-0.4
-0.2
0.0
0.2
0.4
0.6
0.8
1.0
1.2
0
1
2
3
4
5
6
7
8
9
10
11
12
linia wpływu R
B
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/10
piwicki@pg.gda.pl
6m
4m
1m
2m
P=1
I
I
I
A
C
D
B -
α
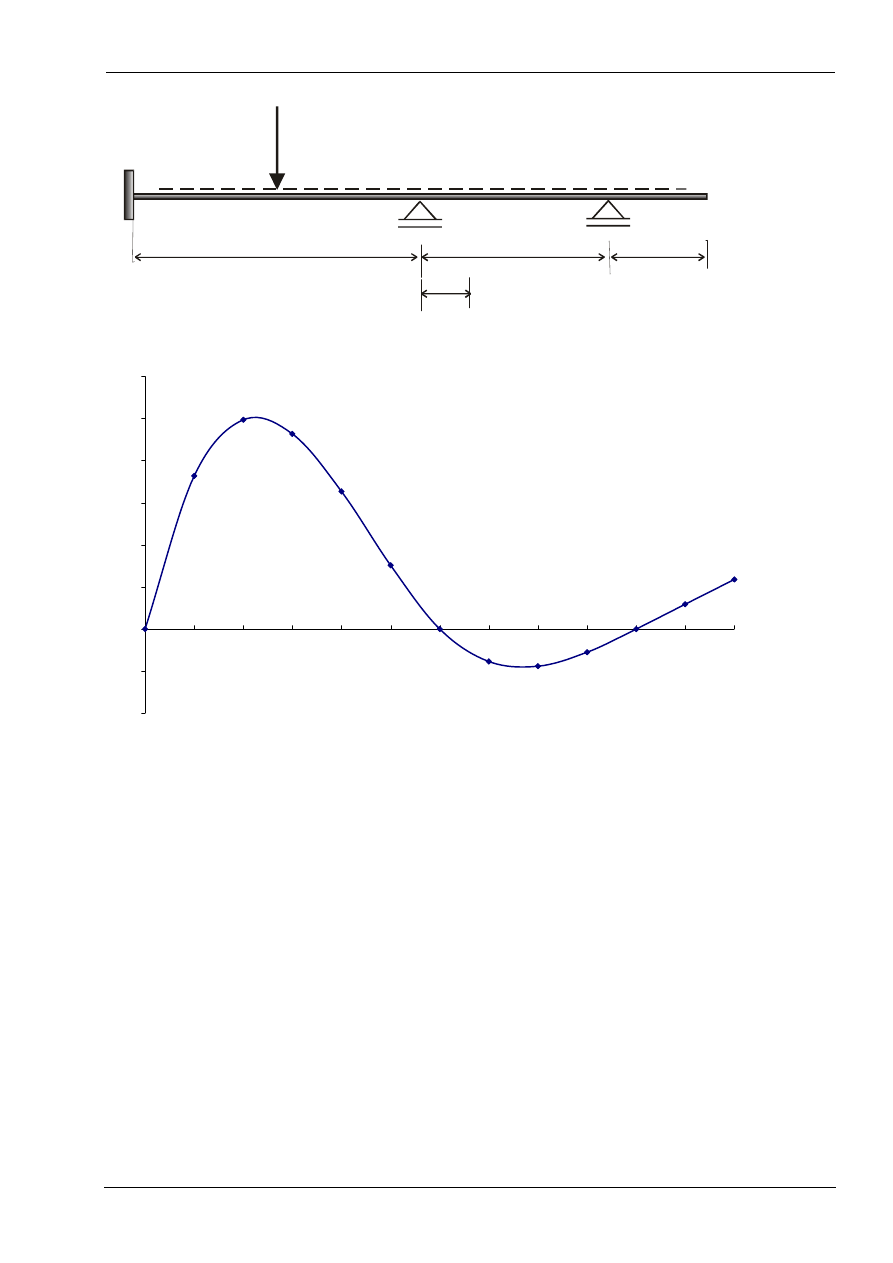
Linia wpływu reakcji Ma
-1.2
-1.0
-0.8
-0.6
-0.4
-0.2
0.0
0.2
0.4
0
1
2
3
4
5
6
7
8
9
10
11
12
Linia wpływu nadliczbowej X
1
= linia wpływu momentu M
A
.
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/11
piwicki@pg.gda.pl
6m
4m
1m
2m
P=1
I
I
I
A
C
D
B -
α
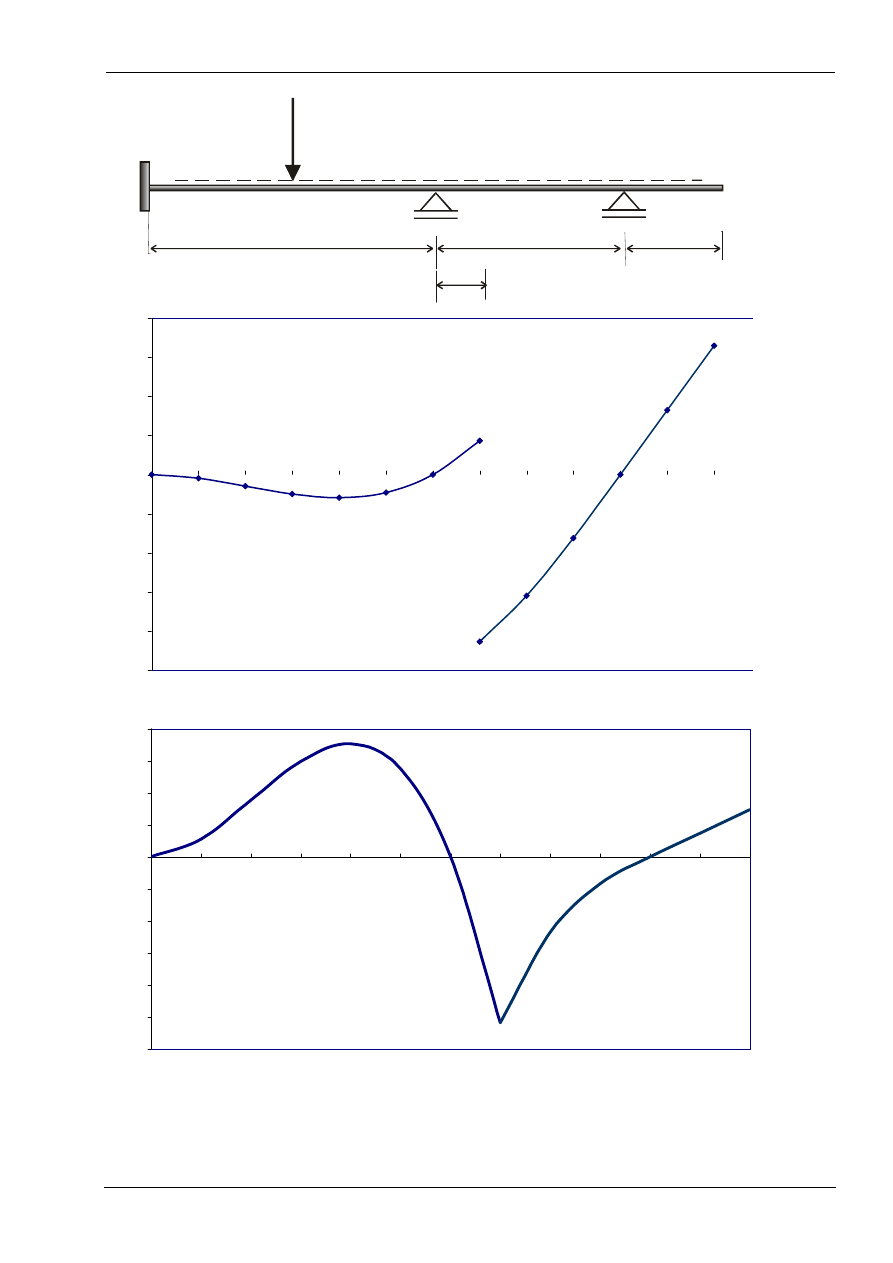
Linia wpływu siły tnącej Ta
-0.8
-0.6
-0.4
-0.2
0.0
0.2
0.4
0.6
0.8
1.0
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
9.0
10.
11.
12.
l
Linia wpływu momentu Ma
-0.4
-0.3
-0.2
-0.1
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
9.0
10.
11.
12.
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/12
piwicki@pg.gda.pl
Obciążanie linii wpływu.
Linia wpływu danej wielkości statycznej Z przedstawia wartość tej
wielkości w zależności od położenia jednostkowej siły poruszającej się po
konstrukcji. Jeżeli na konstrukcję działają inne obciążenia to linia wpływu
może być wykorzystana do wyznaczenia danej wielkości statycznej Z od
tych obciążeń.
P
1
P
2
P
i
q
1
η
Rzędna:
1
η
Rzędna:
2
η
Rzędna:
i
Pole: A
Linia wpływu wielkości statycznej Z.
Jeżeli na układ działają siły skupione P, i obciążenie ciągłe q to wielkość
statyczną Z możemy wyznaczyć z następującego wzoru:
dx
x
x
q
P
Z
n
i
i
b
a
i
i
)
(
)
(
1
η
η
∑
∫
=
=
×
+
×
=
Jeżeli obciążenie q jest stałe na pewnym odcinku konstrukcji to powyższy
wzór przyjmie postać:
∑
=
=
×
+
×
=
n
i
i
i
i
x
q
A
P
Z
1
)
(
η
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/13
piwicki@pg.gda.pl
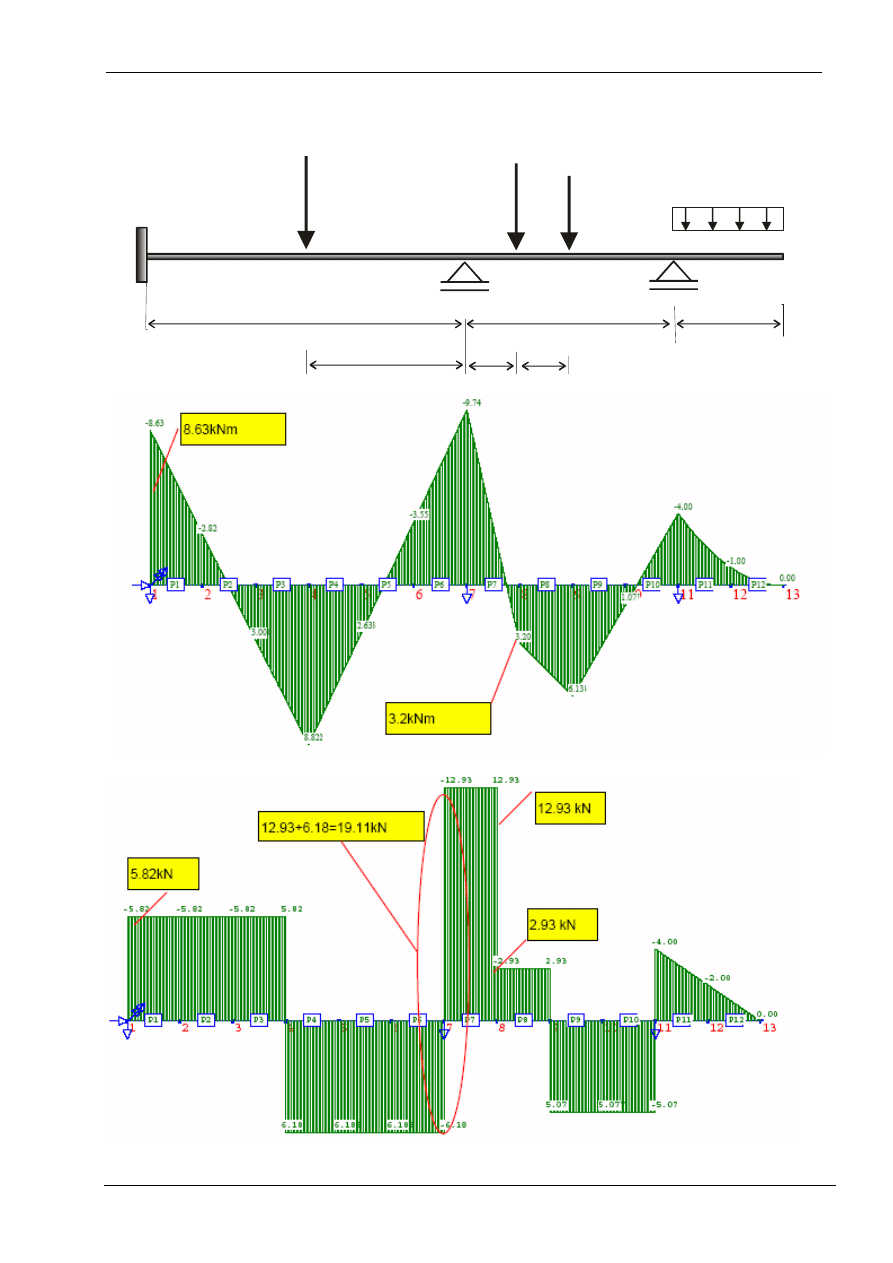
Przykład
Sprawdzić rozwiązanie belki za pomocą obciążania linii wpływu. Dla podanego
obciążenia obliczyć wartość M
α
, T
α
, R
A
, R
B
, M
A
.
6m
4m
1m
1m
3m
2m
12kN
10kN
8kN
2kN/m
HE140A
A
C
D
B -
α
geometria układu
wykres momentów zginających M [kNm]
wykres sił tnących T [kN]
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/14
piwicki@pg.gda.pl
x[m]
Linia wpływu
reakcji R
B
1
0.000
2
0.076
3
0.266
4
0.511
5
0.754
6
0.936
7
1.000
8
0.904
9
0.677
10
0.360
11
0.000
12
-0.368
13
-0.735
Wartości sił wewnętrznych uzyskane z rozwiązania statyki belki:
M
α
= 3.20kNm, T
α
L
=12.93kN, R
A
= 5.820 kN, R
B
= 19.12 kN, M
A
= 8.63 kNm
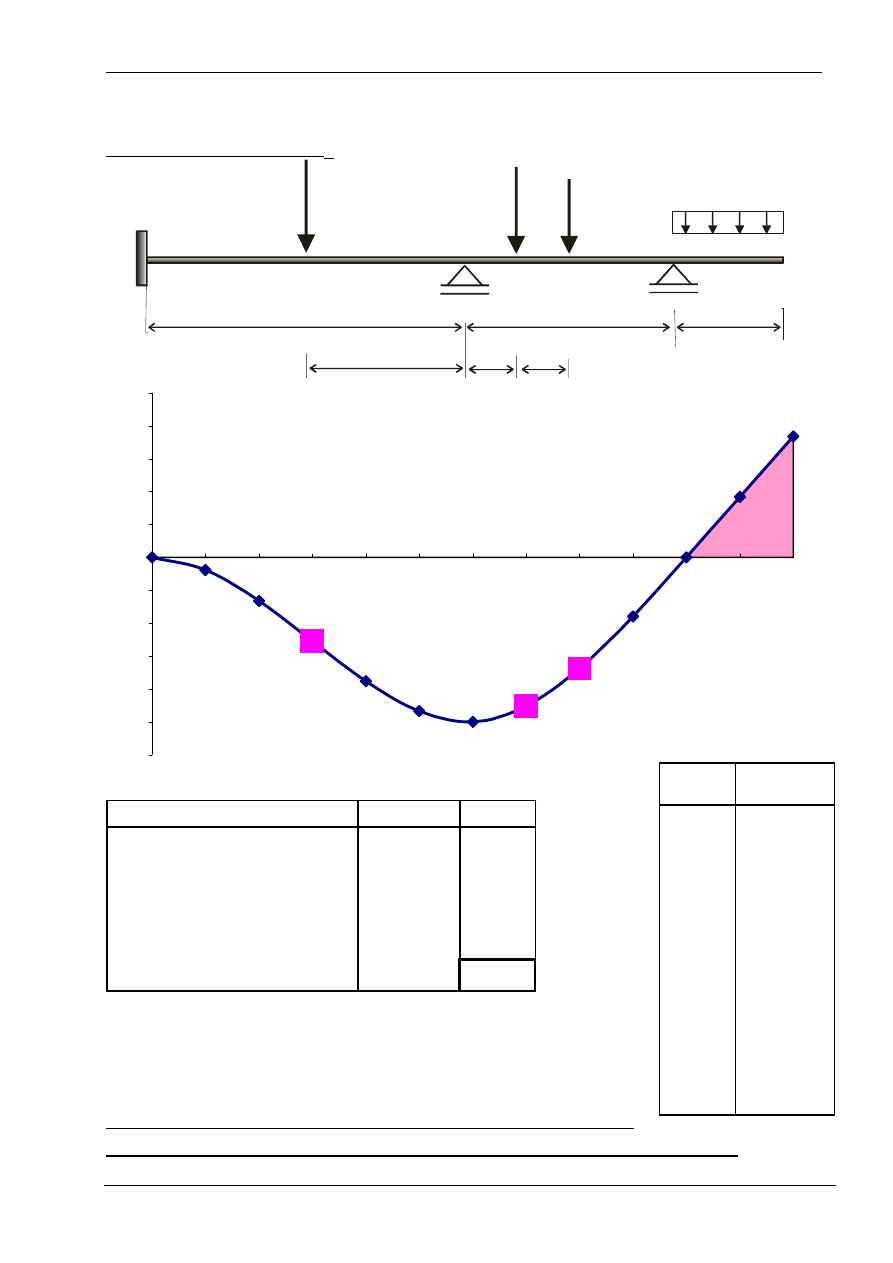
Sprawdzenie reakcji R
B
6m
4m
1m
1m
3m
2m
12kN
10kN
8kN
2kN/m
HE140A
A
C
D
B -
α
Linia wpływu reakcji RB
-1.0
-0.8
-0.6
-0.4
-0.2
0.0
0.2
0.4
0.6
0.8
1.0
1.2
0
1
2
3
4
5
6
7
8
9
10
11
12
Przyjeto, że reakcja jest dodatnia gdy jest skierowana w
górę. Dodatnie rzędne linii wpływu dla sił skupionych
świadczą, że siły te wywołują reakcję dodatnią,
obciążenie ciągłe natomiast powoduje reakcję ujemną
- odrywanie belki od podpory. Poprzez obciążenie linii
wpływu uzyskano tą samą reakcję co z rozwiązania statyki belki.
rzędne linii wpływu
η
siła P [kN] P x
η
0.5110
12
6.1
0.9044
10
9.0
0.6765
8
5.4
pole pod linią wpływu
-0.7353
2
-1.5
reakcja R
B
19.1
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/15
piwicki@pg.gda.pl
x[m]
Linia
wpływu
reakcji RA
0
1
1
0.9423
2
0.793
3
0.5882
4
0.3638
5
0.1558
6
0
7
-0.0772
8
-0.0882
9
-0.0551
10
0
11
0.0588
12
0.1176
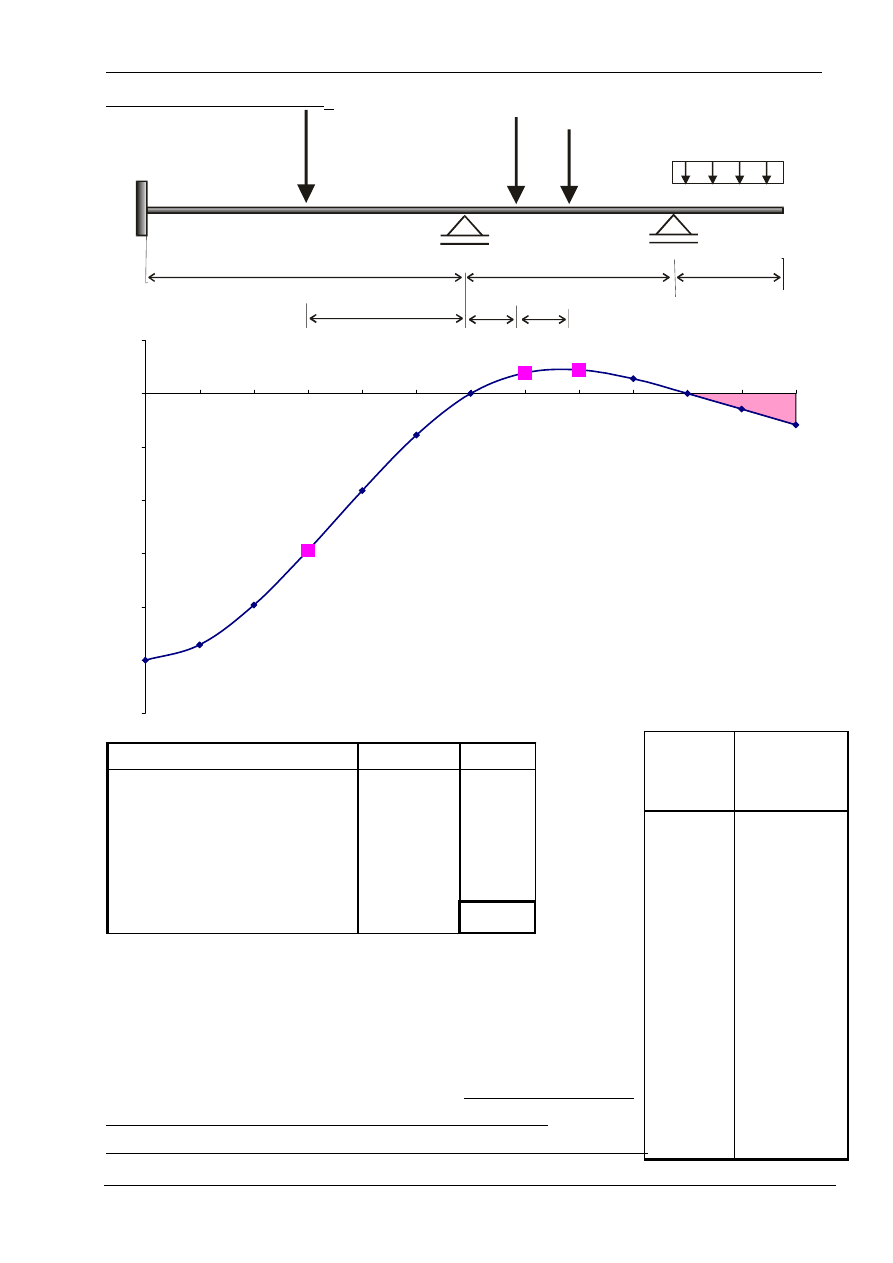
Sprawdzenie reakcji R
B
6m
4m
1m
1m
3m
2m
12kN
10kN
8kN
2kN/m
HE140A
A
C
D
B -
α
Linia wpływu reakcji RB
-0.2
0.0
0.2
0.4
0.6
0.8
1.0
1.2
0
1
2
3
4
5
6
7
8
9
10
11
12
Przyjeto, że reakcja jest dodatnia gdy jest skierowana w
górę. Dodatnie rzędne linii wpływu dla siły 12kN
i obciążenia ciągłego świadczą, że siły te wywołują
reakcję dodatnią, obciążenie środkowego przęsła,
natomiast powoduje reakcję ujemną - odrywanie belki
od podpory. Poprzez obciążenie linii wpływu
uzyskano tą samą reakcję co z rozwiązania statyki belki.
rzędne linii wpływu
η
siła P [kN] P x
η
0.5882
12
7.1
-0.0772
10
-0.8
-0.0882
8
-0.7
pole pod linią wpływu
0.1176
2
0.2
reakcja R
A
5.82
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/16
piwicki@pg.gda.pl
x[m]
Linia wpływu
reakcji MA
0
0
1
-0.7271
2
-0.9935
3
-0.9265
4
-0.6536
5
-0.3023
6
0
7
0.1544
8
0.1765
9
0.1103
10
0
11
-0.1176
12
-0.2353
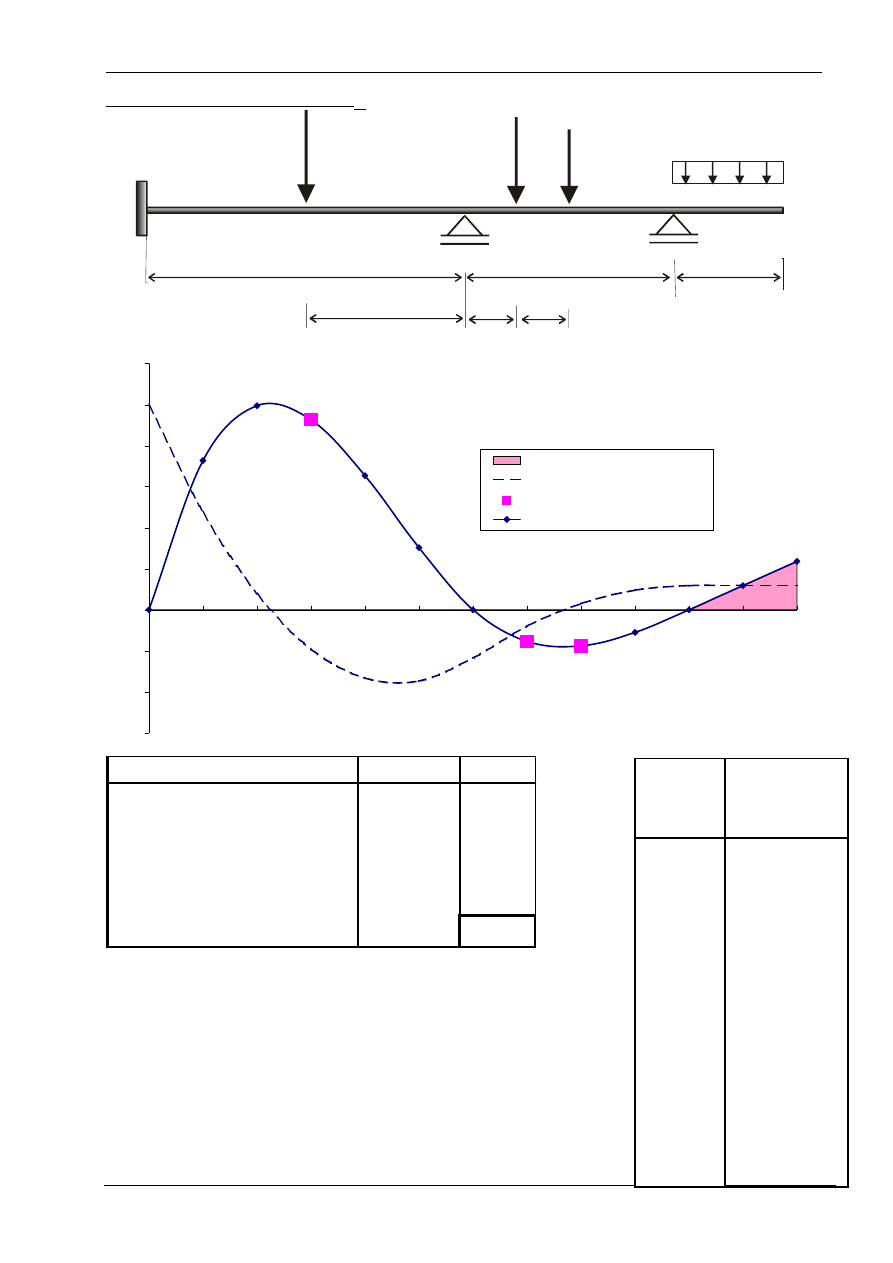
Sprawdzenie momentu M
A
6m
4m
1m
1m
3m
2m
12kN
10kN
8kN
2kN/m
HE140A
A
C
D
B -
α
Linia wpływu reakcji Ma
-1.2
-1.0
-0.8
-0.6
-0.4
-0.2
0.0
0.2
0.4
0.6
0
1
2
3
4
5
6
7
8
9
10
11
12
pole pod obciążeniem ciągłym
linia kątów obrotu
rzędne pod siłami skupionymi
Linia wpływu reakcji RB
założono, że moment M
A
jest dodatni gdy działa w prawo,
siła 12kN wywołuje ujemny moment przy podporze A,
podobnie obciążenie ciągłe, siły z przęsła środkowego
wywołują moment dodatni. Na rysunku przedstawiono
również linię kątów obrotu. Na tej linii występuje skok o 1,
przy podporze A co odpowiada zakładanemu wymuszeniu
kinematycznemu-obrotowi podpory.
rzędne linii wpływu
η
siła P [kN] P x
η
-0.9265
12
-11.1
0.1544
10
1.5
0.1765
8
1.4
pole pod linią wpływu
-0.2353
2
-0.5
reakcja M
A
-8.63
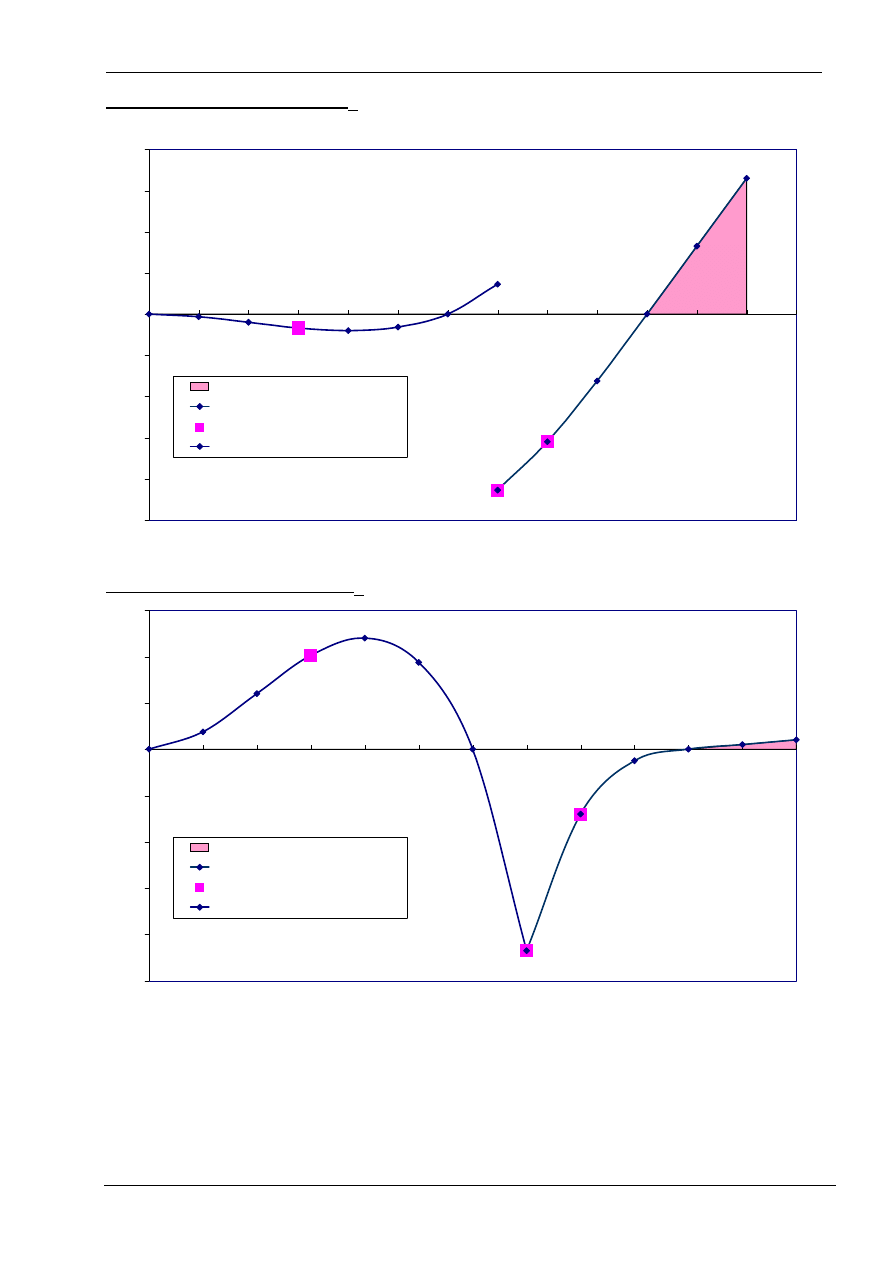
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/17
piwicki@pg.gda.pl
Sprawdzenie momentu T
α
Linia wpływu siły tnącej Ta
-0.8
-0.6
-0.4
-0.2
0.0
0.2
0.4
0.6
0.8
1.0
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
9.0
10.
11.
12.
pole pod obciążeniem ciągłym
linia wpływu Ta
rzędne pod siłami skupionymi
linia wpływu Ta
Sprawdzenie momentu M
α
Obliczamy siłę M
α
=3.2kNm
Obliczamy siłę
T
α
L
=12.93kN
Linia wpływu siły tnącej Ta
-0.3
-0.2
-0.1
0.0
0.1
0.2
0.3
0.4
0.5
0.0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
9.0
10.
11.
12.
pole pod obciążeniem ciągłym
linia wpływu Ta
rzędne pod siłami skupionymi
linia wpływu Ta
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/18
piwicki@pg.gda.pl
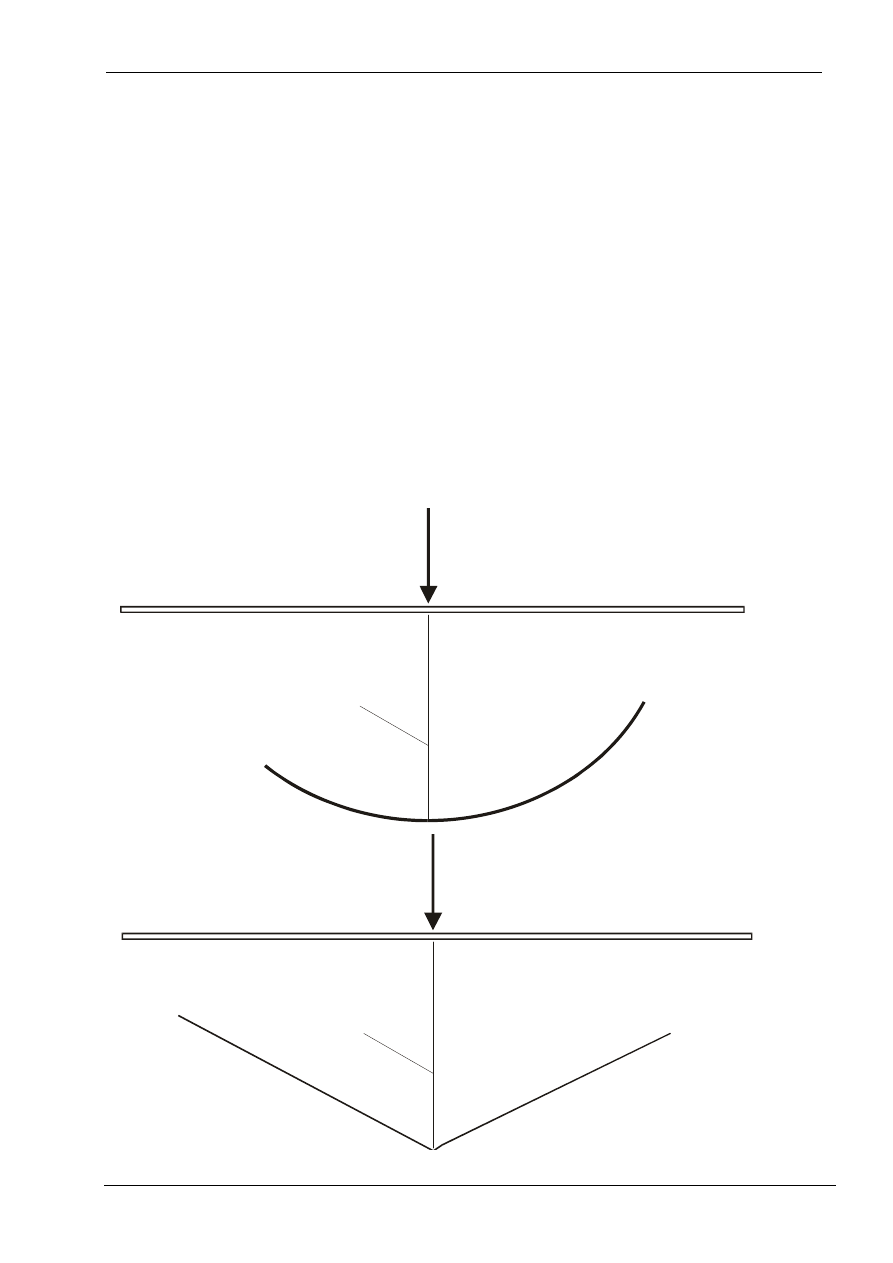
Ekstremalne obciążanie linii wpływowych.
Obwiednie wielkości statycznych.
Obciążenia konstrukcji możemy podzielić na obciążenia stałe i obciążenia
zmienne. Do obciążeń stałych możemy zaliczyć na przykład obciążenie
ciężarem własnym. Obciążenie zmienne to obciążenia śniegiem, wiatrem,
obciążenia użytkowe, obciążenia pojazdami, suwnicami. Przy analizie
konstrukcji często powtaje problem takiego ustawienia obciążeń
zmiennych aby uzyskać ekstremalne wielkości sił wewnętrznych, które są
najbardziej niekorzystne dla konstrukcji. Przy poszukiwaniu takich
ekstremalnych położeń sił wewnętrznych przydatna jest znajomość linii
wpływu.
Dla pojedynczej siły skupionej najbardziej niekorzystna wartość wielkości
statycznej Z powstanie przy ustawieniu siły w ekstremalnych miejscach
linii wpływu:
P
η
Rzędna:
max
max
max
η
×
=
i
P
Z
P
η
Rzędna:
max
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/19
piwicki@pg.gda.pl
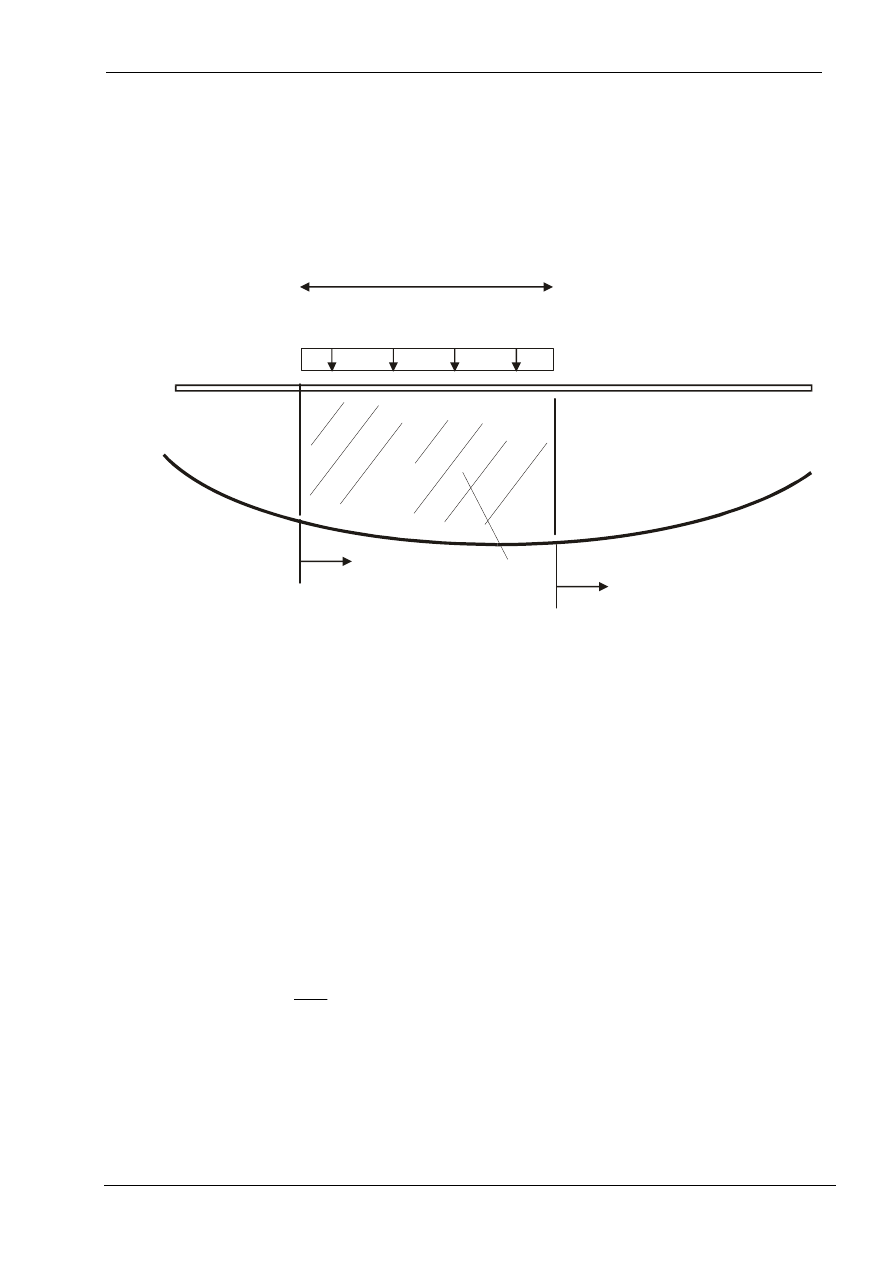
W przypadku obciążenia ciągłego o skończonej długości wartość Z jest równa:
)
(x
q
A
Z
×
=
q
a
dx
dx
η
Rzędna:
1
η
Rzędna:
2
Pole: A
jeżeli założymy przesunięcie odcinka obciążenia o dx to nastąpi zmiana
wielkości Z:
)
(
2
1
dx
z
dx
z
q
q
dA
dZ
×
+
×
−
×
=
×
=
ponieważ poszukujemy takiego położenia obciążenia aby Z osiągało
ekstremum z warunku zerowania się pochodnej możemy wyznaczyć:
2
1
2
1
0
)
(
z
z
z
z
q
dx
dZ
=
⇔
=
+
−
×
=
ekstremalna wielkość Z będzie wtedy gdy rzędne z
1
= z
2
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/20
piwicki@pg.gda.pl
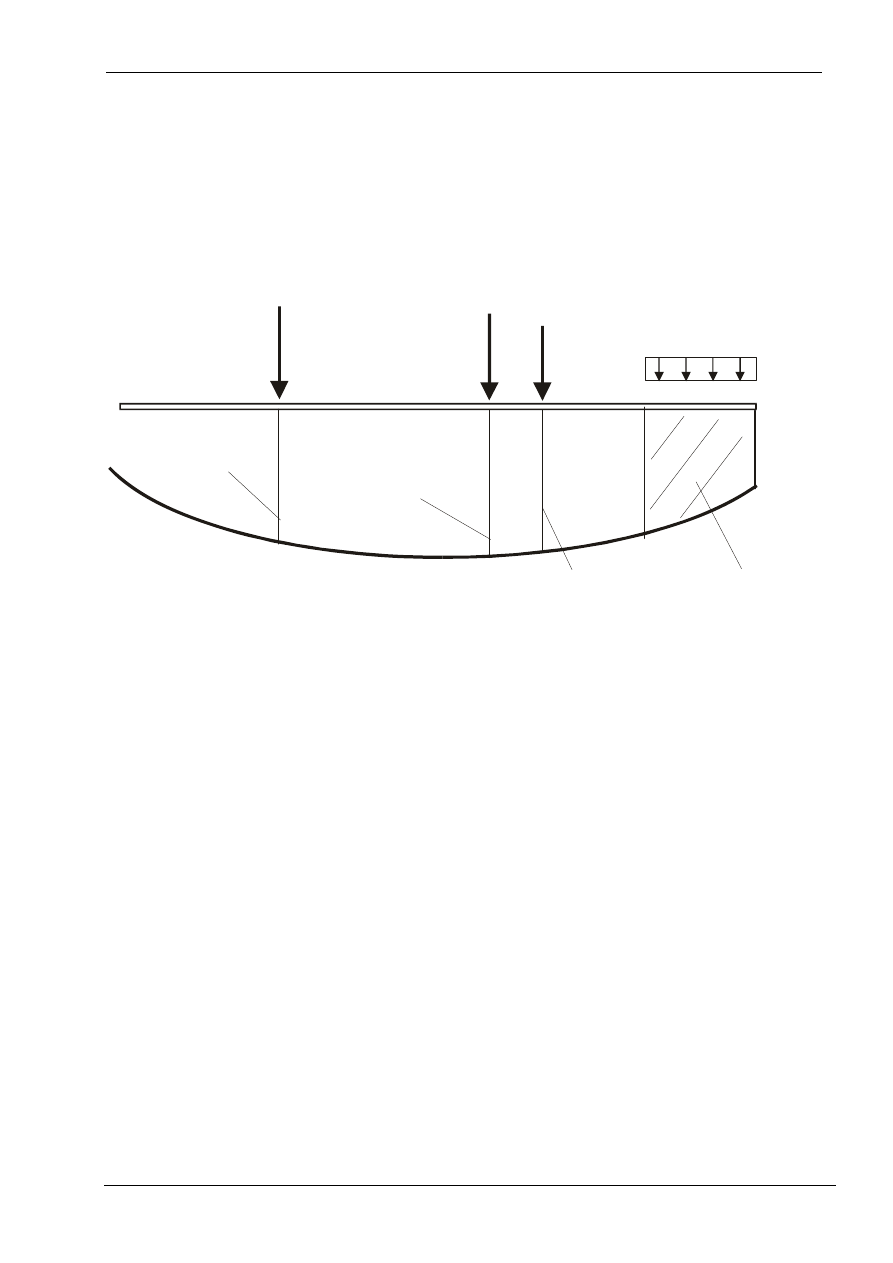
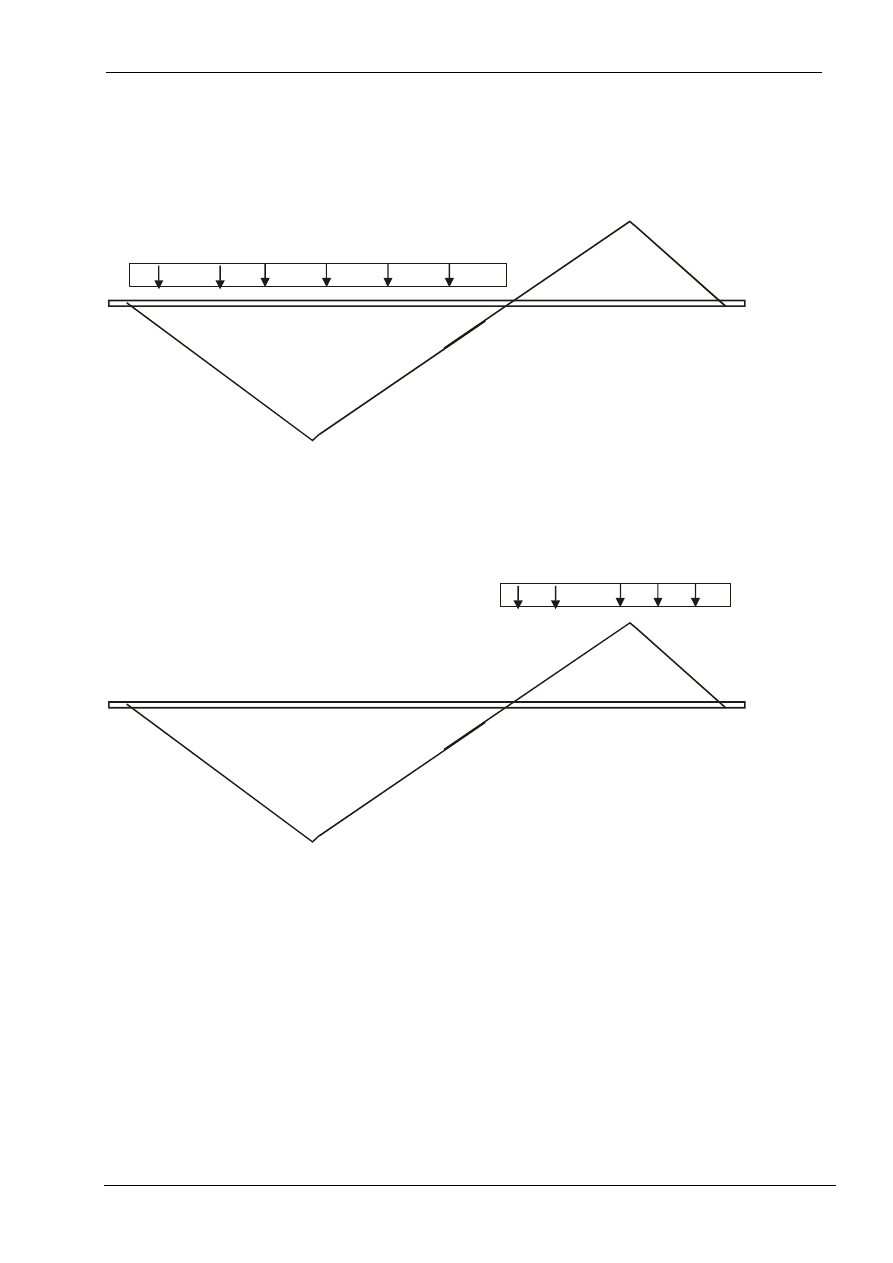
W przypadku obciążeń o dowolnej długości ekstremalną wartość wielkości
statycznej wyznaczymy przyjmując długość obciążenia tak aby się ona
pokrywała z dodatnnią częścią linii wpływu
q
Z
max
+
_
Aby uzyskać minimalne wartości danej wielkości statycznej możemy ustawić
obciążenie tak aby pokrywało się z ujemną częścią linii wpływu wielkości Z.
q
Z
min
+
−
Jeżeli we wszystkich przekrojach poprzecznych wyznaczymy wartość
maksymalną danej wielkości statycznej i wartość minimalną tej wielkości
od zadanego obciążenia to uzyskany wykres wielkości ekstremalnych
nazywamy obwiednią Z.
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/21
piwicki@pg.gda.pl
Przykład
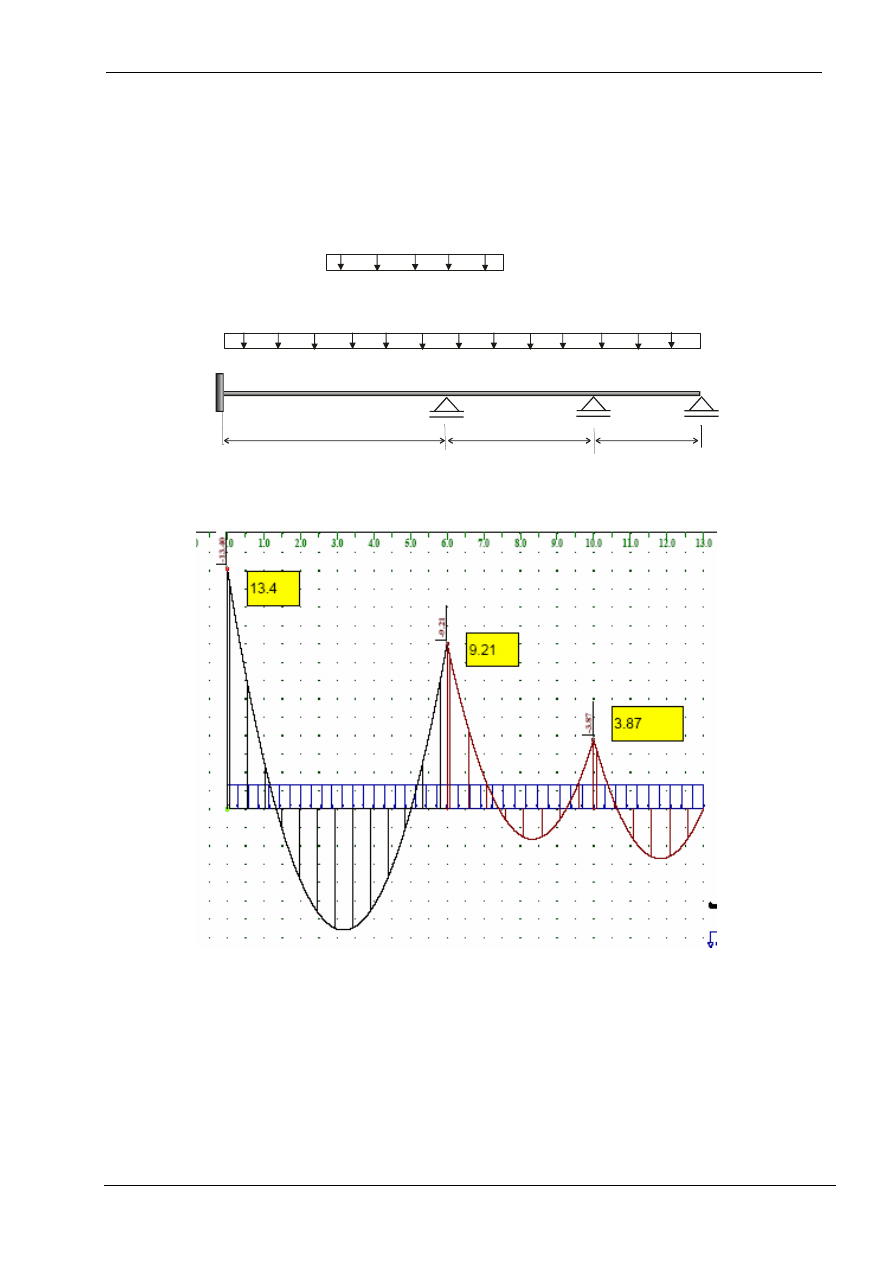
Wyznaczyć obwiednię momentów zginających M dla belki obciążonej ciężarem
własnym i obciążeniem zmiennym o dowolnej długości
.
6m
4m
3m
4kN/m=q
2kN/m=p
HE160A
D
B
β
C
γ
A
α
Przypadek 1. Momenty zginające od obciążeń stałych.
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/22
piwicki@pg.gda.pl
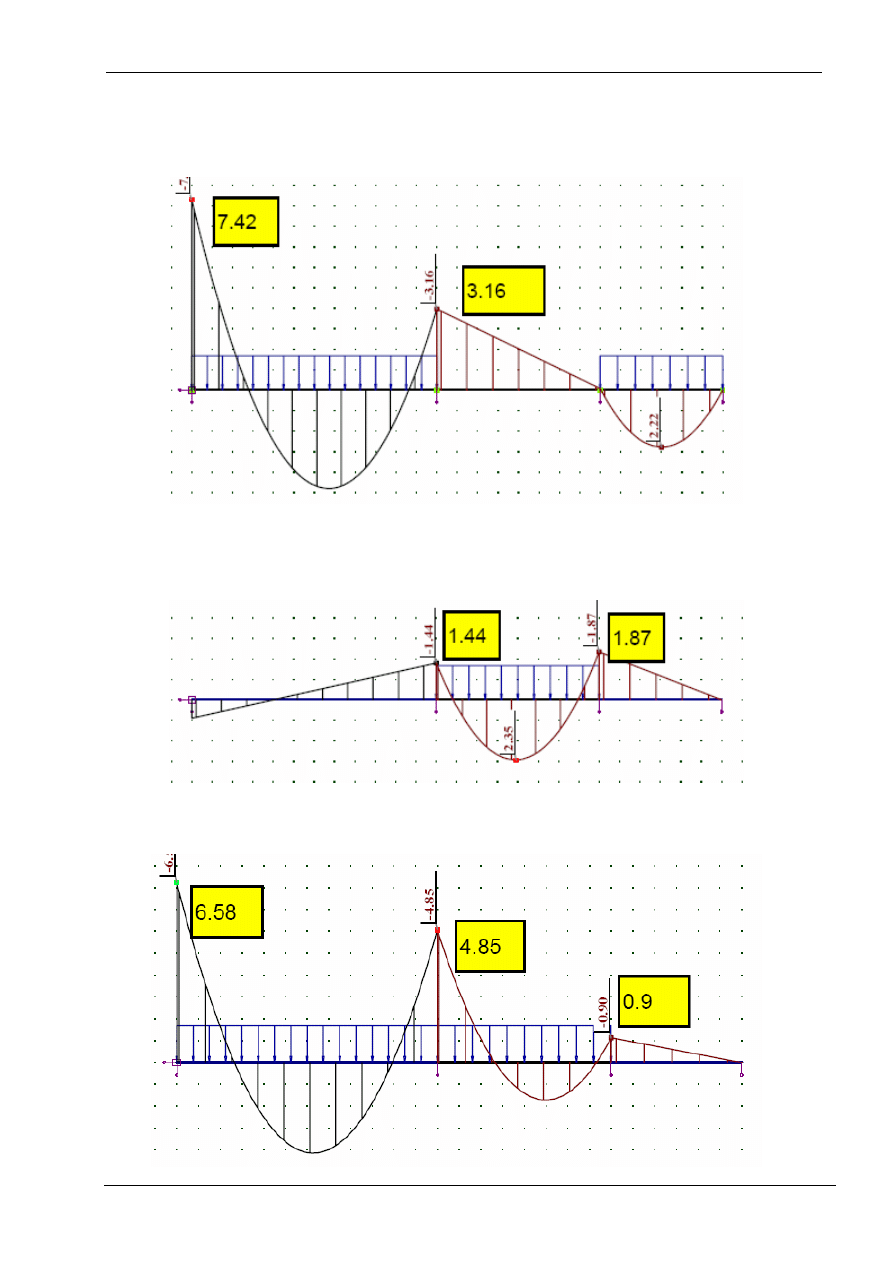
Przypadek 2. obciążenie zmienne w przęśle AB i CD (max moment przęsłowy w przęśle
AB i CD przęśle, maksymalny moment na podporze A, minimalny moment w przęśle
BC.
Przypadek 3. obciążenie zmienne w przęśle BC (max moment przęsłowy w przęśle BC,
minimalny moment na podporze A, w przęśle AB i CD
Przypadek 4. obciążenie zmienne w przęśle AB i BC przęśle (min moment nad podporą
B)
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/23
piwicki@pg.gda.pl
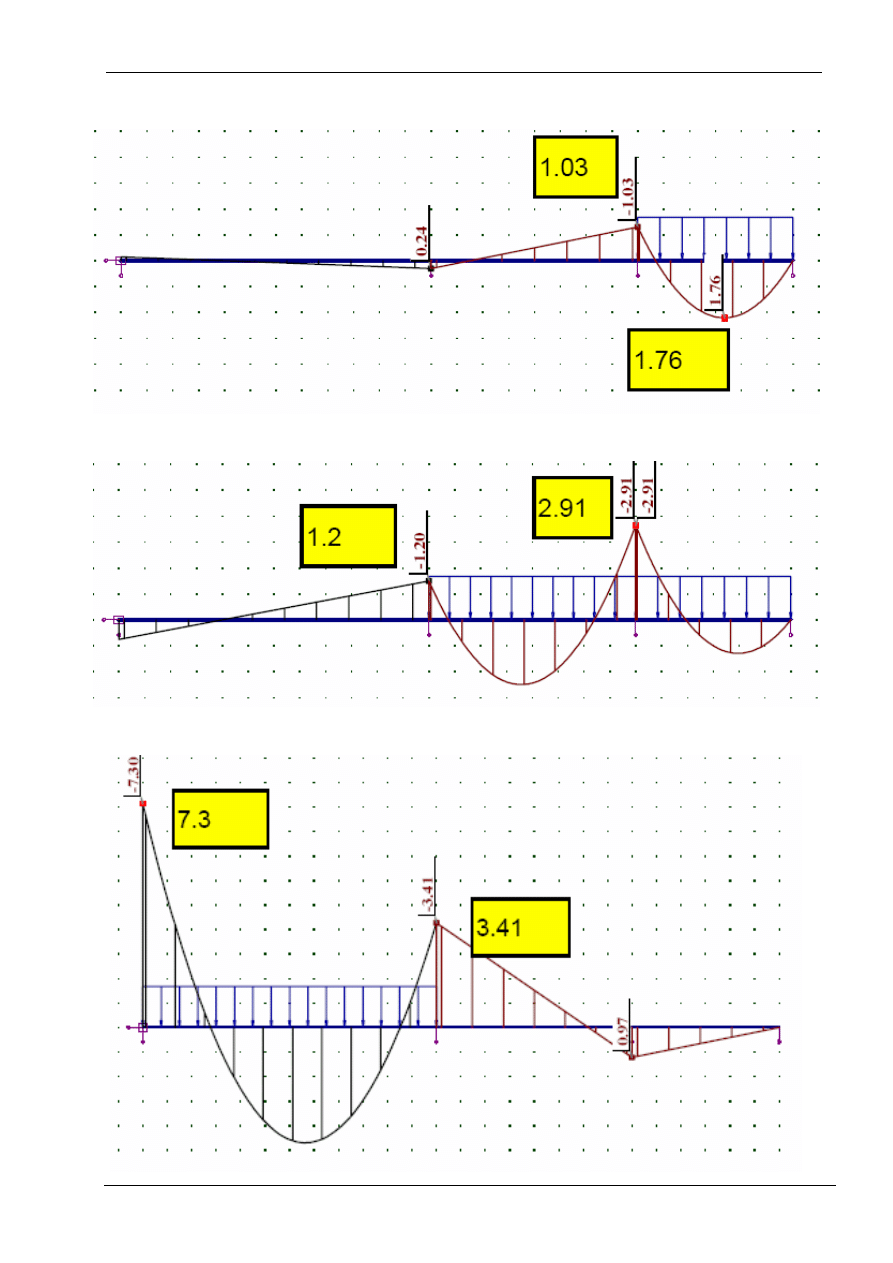
Przypadek 5. Obciążenie zmienne w przęśle CD (max moment nad podporą B)
Przypadek 6. Obciążenie zmienne w przęśle BC i CD (min moment nad podporą C)
Przypadek 7. Obciążenie zmienne w przęśle AB (max moment nad podporą C)
Mechanika Budowli (C16)
Piotr Iwicki
http://www.okno.pg.gda.pl
wykład
6/24
piwicki@pg.gda.pl
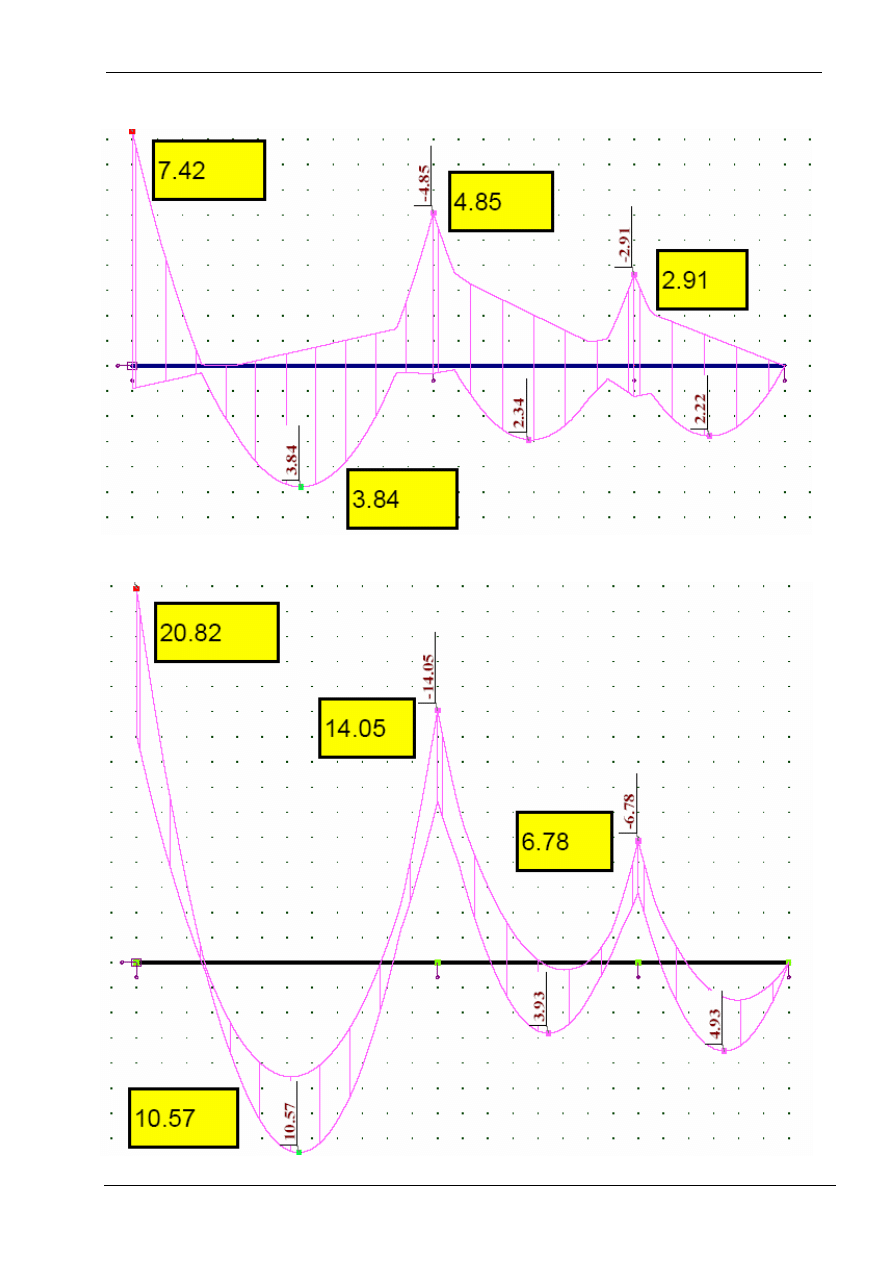
OBWIEDNIA MOMENTÓW ZGINAJĄCYCH OD OBCIĄŻEŃ ZMIENNYCH-
NA JEDNYM RYSUNKU WYKRESY Z PRZYPADKÓW 2-7
OBWIEDNIA MOMENTÓW ZGINAJĄCYCH OD OBCIĄŻEŃ STAŁYCH I
ZMIENNYCH – NA JEDNYM RYSUNKU WYKRESY 1-7
Document Outline