Zestaw 1

 

Trygonometria Strona

1

Zadanie 1. Wyrażenie

(

)(

)

cos30

cos 45

cos30

cos 45

−

+

D

D

D

D

przyjmuje wartość:

A. 0,25

B. l

C. –1

D. 0,5

Zadanie 2. Na poniższym rysunku

2

cos

3

α

= . Wówczas bok AB trójkąta ABC ma długość:

A.2

B.

22,5

C.

10

D.

l

Zadanie 3. Jeżeli

4

sin

5

α

= i

α

jest kątem ostrym, to:

A.

3

cos

5

α

= − B.

1

cos

5

α

= C.

3

cos

5

α

= D.

16

cos

25

α

=

Zadanie 4. W którym przypadku istnieje kąt o mierze x spełniający warunki:
A.

B.

si

sin

0,6, cos

0,4

x

x

=

=

n

0,5, tg

1

x

x

=

=

C.

D. si

sin

0,6, cos

0,8

x

x

=

=

n

1, tg

2,4

x

x

=

=

Zadanie 5. Drabina nachylona jest do podłoża pod kątem

i oddalona od ściany o 6 dm. Jaka jest długość

drabiny?

60

D

A. 4 3 dm

B. 12 dm

C. 6 3 dm

D. 6 dm

Zadanie 6. Jeżeli długości przyprostokątnych trójkąta prostokątnego są w stosunku

3 : 3 , to jeden z kątów

ostrych ma miarę:
A.

B.

C.

75

D

D.

35

45

D

60

D

D

Zadanie 7. Jeżeli

α jest kątem ostrym i tg

2

α

= , to:

A.

5

sin

2

α

=

B

2 5

sin

5

α

=

C.

5

sin

5

α

=

D.

sin

5

α

=

Zadanie 8. Jeżeli

α jest kątem ostrym i

1

cos

4

α

= , to:

A.

B.

76

α

=

C.

75

α

>

D

D.

75

α

<

D

75

α

=

D

D

Zadanie 9. W trójkącie prostokątnym

ABC o kącie prostym przy wierzchołku C i kącie ostrym

α przy

wierzchołku A dane są długości boków:

4

AB

= i

3

BC

= . Wtedy:

A.

3

cos

4

α

= B.

3

cos

5

α

= C.

4

cos

5

α

= D.

7

cos

4

α

=

Zadanie 10. Jeżeli

α jest kątem ostrym, to tożsamością trygonometryczną nie jest:

A.

B.

(

)

2

sin

cos

1

α

α

+

=

2

2

1 cos

sin

2cos

2

α

α

α

+

−

=

C.

2

1

cos

cos tg

cos

α

α

α

α

+

=

D.

sin

cos

1 tg

cos

α

α

α

α

+

= +

Zadanie 11. Liczba 1 jest wartością wyrażenia:

A.

sin 30

1 cos 45

+

D

D

B.

(

)

2

tg30

cos 45

D

D

C. D.

(

2

sin 45

cos60

+

D

D

)

2

1 sin 90

+

D

Zadanie 12. Sinus kąta ostrego

α jest równy

4
5

. Wynika stąd, że:

A. tg

0,75

α

=

B.

3

co

α

= C.

s

5

1

4

tg

3

α

= D.

54

α

≈

D

Zestaw 1

 

Trygonometria Strona

2

Zadanie 13. Człowiek o wysokości 1,8 m rzuca cień o długości 2,4 m. Ile wynosi kąt padania promieni
słonecznych na powierzchnię ziemi?
A.

B.

C.

D.

37

35

D

34

D

36

D

D

Zadanie 14. Liczba

jest:

cos75

D

A. całkowita

B. równa

2

2

C.

mniejsza

od

1
2

D.

większa od

3

3

Zadanie 15. Wartość wyrażenia

, dla

2

a

b

−

sin

cos

a

α

α

=

+

i

2sin cos

b

α

α

=

wynosi:

A. 2

B. 1

C. –1

D.

1
2

Zadanie 16. Liczba

1
6

jest dla

wartością wyrażenia:

30

α

=

D

A.

1

sin cos

tg

α

α

α

+

B.

2

1

sin

tg

2sin

α

α

α

−

⋅

C.

sin

cos

tg

α

α

α

⋅

⋅

D.

2

2

1

sin

cos

6

α

α

+

Zadanie 17. Która z podanych liczb jest największa?
A.

B.

t

C.

c

D.

si

sin 30

D

g 45

D

os75

D

n 20

D

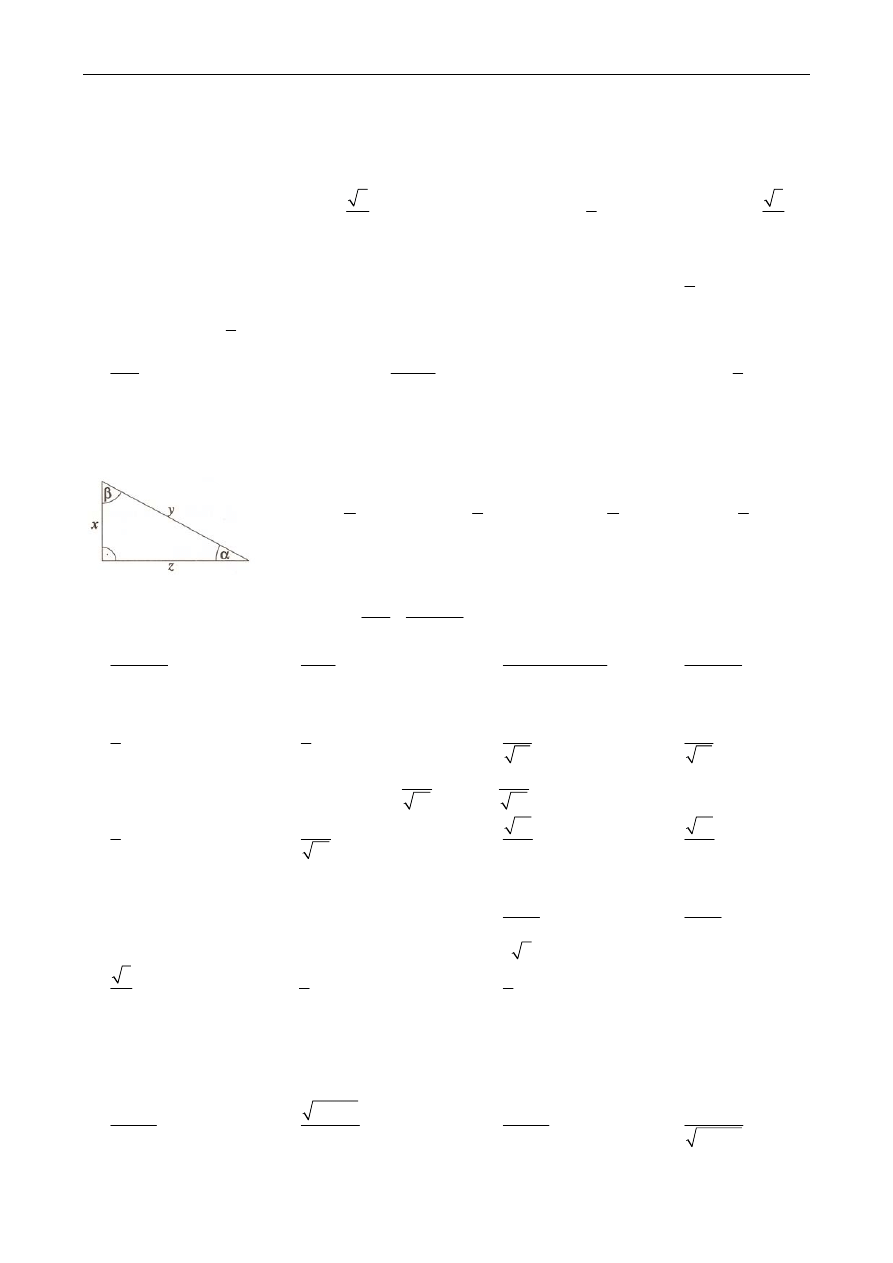
Zadanie 18. Wskaż zapis zgodny z rysunkiem:

A. sin

z

y

α

= B. tg

z

x

β

= C.

tg

y

z

α

=

D. cos

z

x

β

=

Zadanie19. Upraszczając wyrażenie

1

sin

tg

1 cos

x

α

α

α

=

+

+

otrzymujemy:

A.

1

cos

1

α

+

B.

1

sin

α

C.

(

)

1

sin

1 cos

α

α

+

D.

2 tg

1 cos

α

α

+

Zadanie 20. W trójkącie prostokątnym o przyprostokątnych 2 i 3 tangens większego kąta ostrego jest równy:

A.

3
2

B.

2
3

C.

3
13

D.

2
13

Zadanie 21. W trójkącie prostokątnym

4

sin

41

α

=

,

5

cos

41

α

=

. Wówczas tg

α

jest równy:

A.

4
5

B.

9

41

C.

41

4

D.

41

5

Zadanie 22. Wyrażenie cos

tg

α

α

⋅

jest równe:

A.

sin

α

B.

cos

α

C.

sin

cos

α

α

D.

cos

sin

α

α

Zadanie 23. Dla pewnego kąta ostrego

α

mamy sin

cos

2

α

α

+

=

. Wtedy sin

cos

α

α

⋅

równa się:

A.

3

4

B.

1
2

C.

1
4

D.

1

Zadanie 24. Dla kąta ostrego

fałszywą nierównością jest:

45

α

<

D

A.

sin

cos

α

α

<

B.

tg

1

α

< C.

cos

sin

α

α

<

D.

sin

1

α

< sina < 1

Zadanie 25. Jeśli dla pewnego kąta ostrego

α

mamy sin

M

α

=

, to tg

α

równa się:

A.

2

1

M

M

−

B.

2

1 M

M

−

C.

2

1 M

M

−

D.

2

1

M

M

−

Zestaw 1

 

Trygonometria Strona

3

ZADANIA OTWARTE KRÓTKIEJ ODPOWIEDZI

Zadanie 1. Wiedząc, że

α

jest kątem ostrym i

5

sin

5

α

=

, oblicz tg

α

.

Zadanie 2. Wiedząc, że

1

tg

3

α

= , oblicz wartość wyrażenia

(

)

2

5 2sin

1

α

− .

Zadanie 3. Wiedząc, że tg

5

α

= oblicz

sin

cos

sin

cos

α

α

α

α

−
+

.

Zadanie 4. Czy istnieje kąt ostry

α

taki, że

3

sin

3

α

=

i

2

tg

3

α

= ? Odpowiedź uzasadnij.

Zadanie 5. W trójkącie prostokątnym o kątach ostrych

α

i

β

spełniony jest warunek

5

sin

sin

2

α

β

+

=

.

Oblicz iloczyn cosinusów tych kątów.

Zadanie 6. Posługując się wzorem:

(

)

sin

sin

cos

cos

sin

α β

α

β

α

+

=

⋅

+

⋅

β

oblicz

.

sin15

D

Zadanie 7. Dany jest trapez równoramienny, w którym długości podstaw wynoszą 3 i 5, a ramię ma długość 4,
Oblicz tangens kąta ostrego tego trapezu.

ZADANIA OTWARTE ROZSZERZONEJ ODPOWIEDZI

Zadanie 8. Zapoznaj się z rysunkiem i wyznacz długość

x.

Zadanie 9. Udowodnij tożsamość trygonometryczną:

3

3

cos

cos

tg

sin

sin

α

α

α

α

α

−

=

−

Zadanie 10. Konstruktor stworzył projekt, w którym maszt radiowy o wysokości 30 m ma być wspierany
dwiema linami jednakowej długości łączącymi wierzchołek masztu z ziemią pod katem

. Oblicz, jakiej

długości liny są potrzebne do wykonania projektu oraz w jakiej odległości od masztu należy przygotować
mocowania do lin.

55

D

Zadanie 11. Dla pewnego kąta ostrego

α

prawdziwa jest równość

1

5

tg

tg

cos

α

α

α

+

=

.

Oblicz wartość sin , cos

α

α

i tg

α

.