2012

Wykład 3

1

Fizyka laserów

LASER czyli Light Amplification by

Stimulation Emission of Radiation

Literatura:

1.

A. Kujawski, P. Szczepański – LASERY, podstawy fizyczne – Oficyna Wyd. P.W. Warszawa 1999

2.

B. Ziętek - Lasery wyd. UMK Toruń 2009

3.

B. Ziętek – Optoelektronika – Wyd. UMK Toruń 2011

Podstawowe zasady działania laserów zostały po raz pierwszy sformułowane przez
Charlesa Townesa i Arthura Schalowa z Bell Telephone Laboratories w 1958 r.,
a pierwszy laser na bazie kryształu rubinu zademonstrował w 1960 r. Theodor Maiman
z Hughes Research Laboratories.

Lasery

2

Rodzaje laserów

• Gazowe (np. HeNe, CO

2

), ciekłe (barwniki), stałe (np. Nd:YAG,

Yb:YAG, rubin, Ti:szafir), światłowodowe (specjalny rodzaj laserów z
c. stałego), półprzewodnikowe, chemiczne (HF), na wolnych
elektronach, rentgenowskie X-Ray

• X-Ray (λ ~1 nm) do dalekiej podczerwieni ( ~1 mm)
• CW (mocy ciągłej) ~ 1-mW (telekomunikacja, zapis pamięci,

wskaźniki laserowe)
do ~ 100 kW (obróbka laserowa)
do ~ 5 MW (wojskowe)

• Implusowe do ~ 1015 W

• Czas impulsu ~ 5 fs
• Długość rezonatora ~ 1µm (VCSEL) zasięg do 6,5 km

Lasery

3

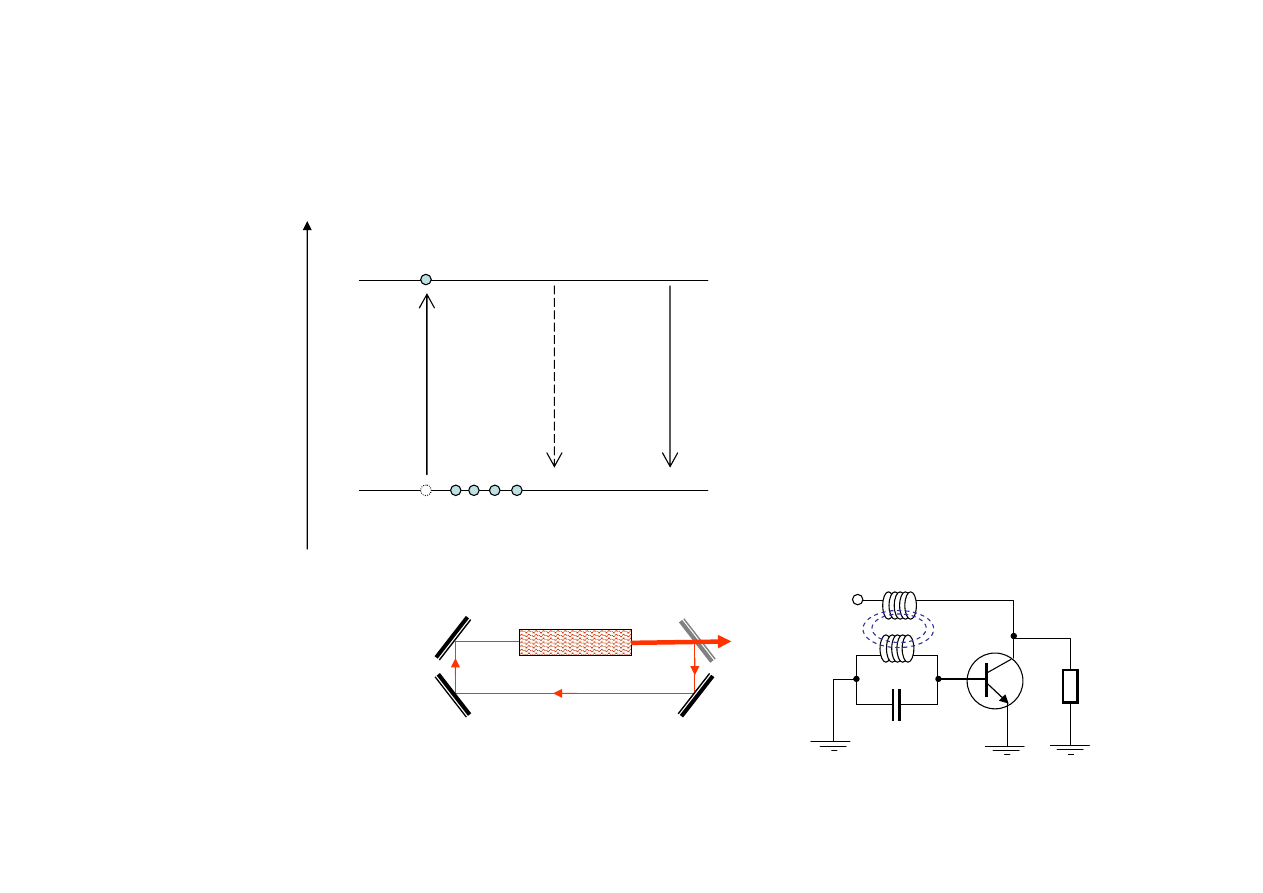
Ogólna zasada działania

- schemat dwupoziomowy

E

Górny laserowy poziom energii elektronów

Dolny laserowy poziom energii elektronów

E

1

E

2

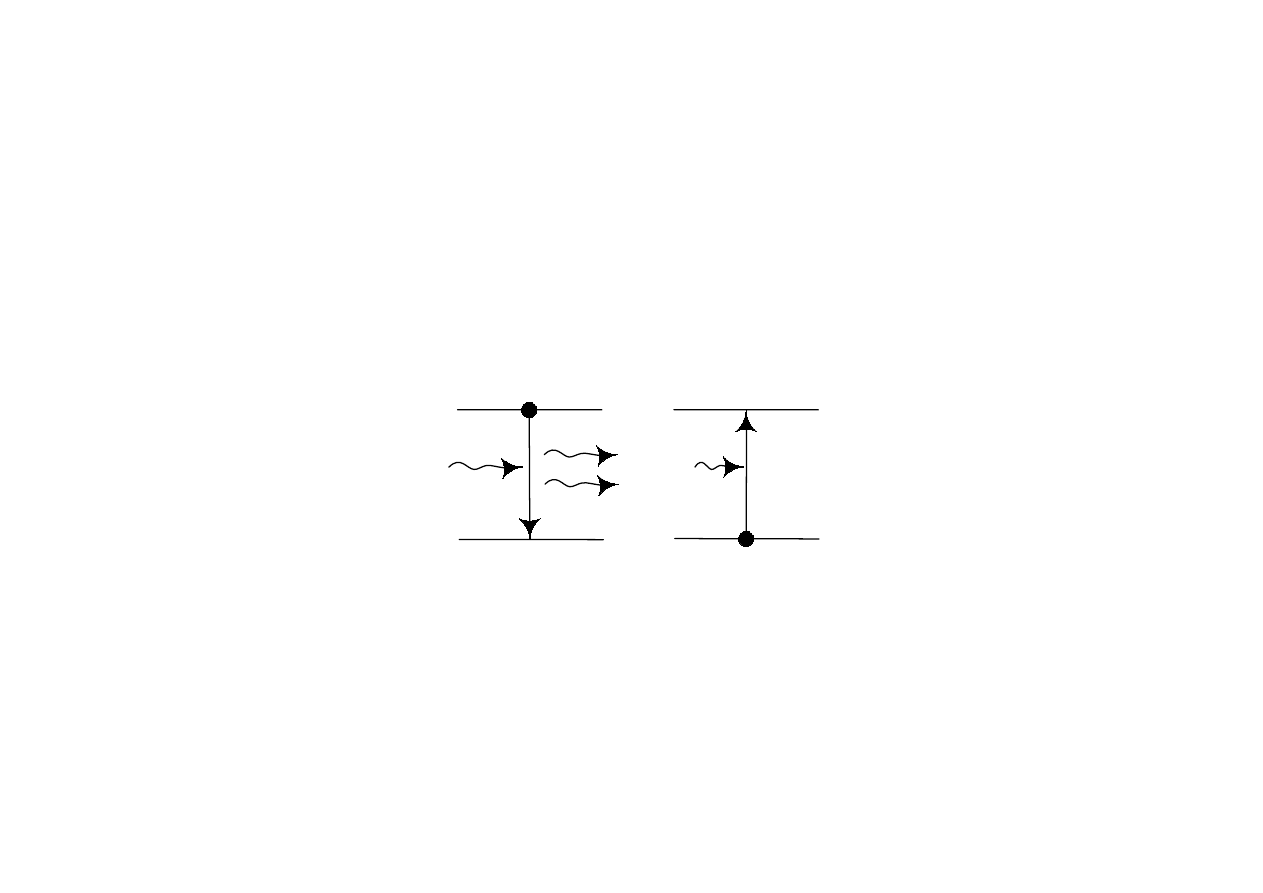
Absorp

cja

Emisja

spon

tanic

zna

Emisja

wym

uszona

(sty

mulow

ana)

N

2

N

1

N

1

, N

2

- obsadzenie poziomów [cm

-3

]

Laser to oscylator
i wzmacniacz zarazem!

Zwierciadło

półprzepuszczalne

Rezonator

Ośrodek czynny,

wzmacniacz

Lasery

4

Warunki akcji laserowej

1.

Ośrodek wzmacniający

•

Może być nim gaz (plazma), ciecz lub ciało stałe.

•

Musi mieć określoną inwersję obsadzeń N

2

> N

1

•

Jeżeli ośrodek jest inwersyjny, to proces „stymulowanej emisji”
jest mocniejszy niż proces absorpcyjny“ .

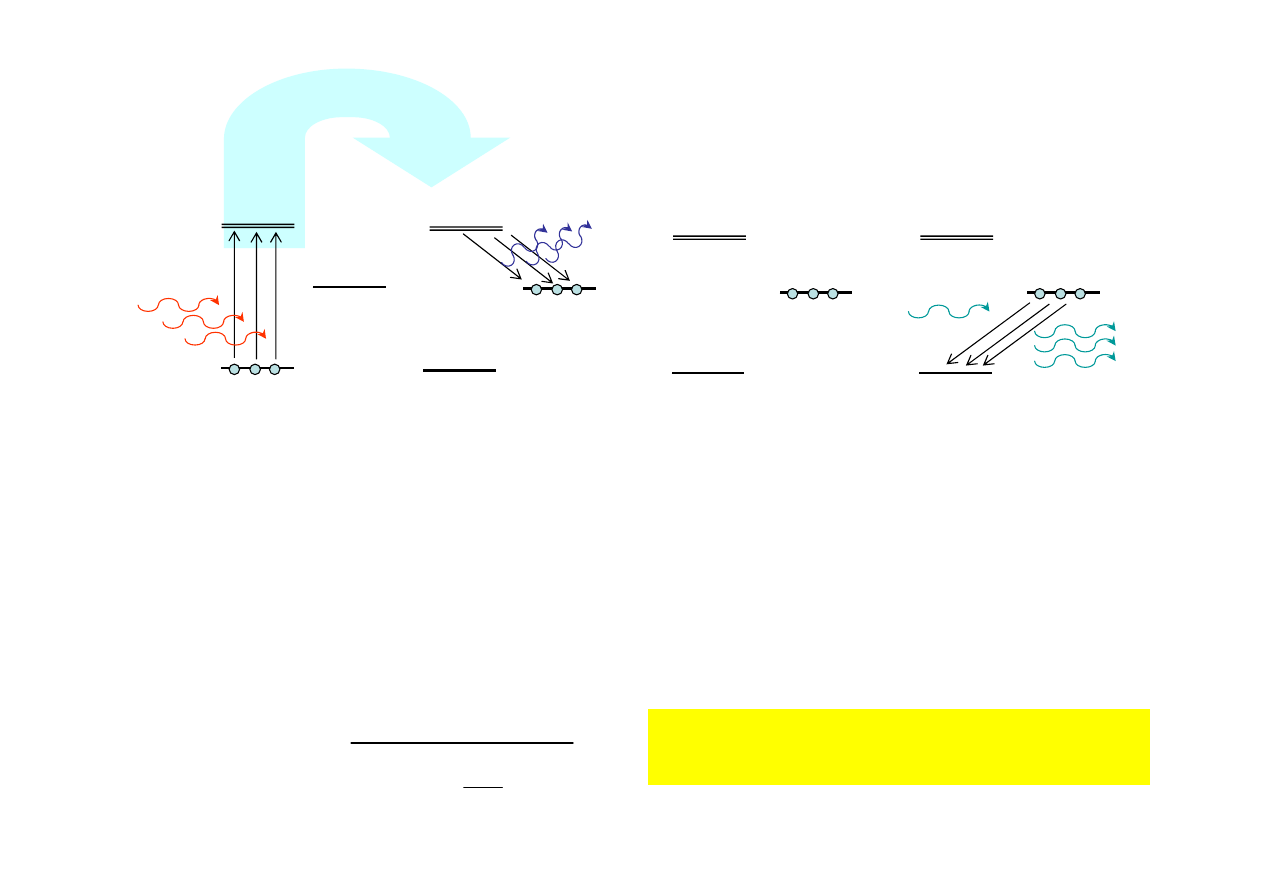
2.

Mechanizm wzbudzania albo „pompowanie” :

•

„pompowanie” jest procesem, szeregiem procesów albo metodą
wzbudzania atomów na wyższy poziom energetyczny,

•

pompowanie może nie być bezpośrednie, ale odbywać się poprzez
poziom pośredni albo kilka takich poziomów.

h

h

2

2

1

1

Lasery

5

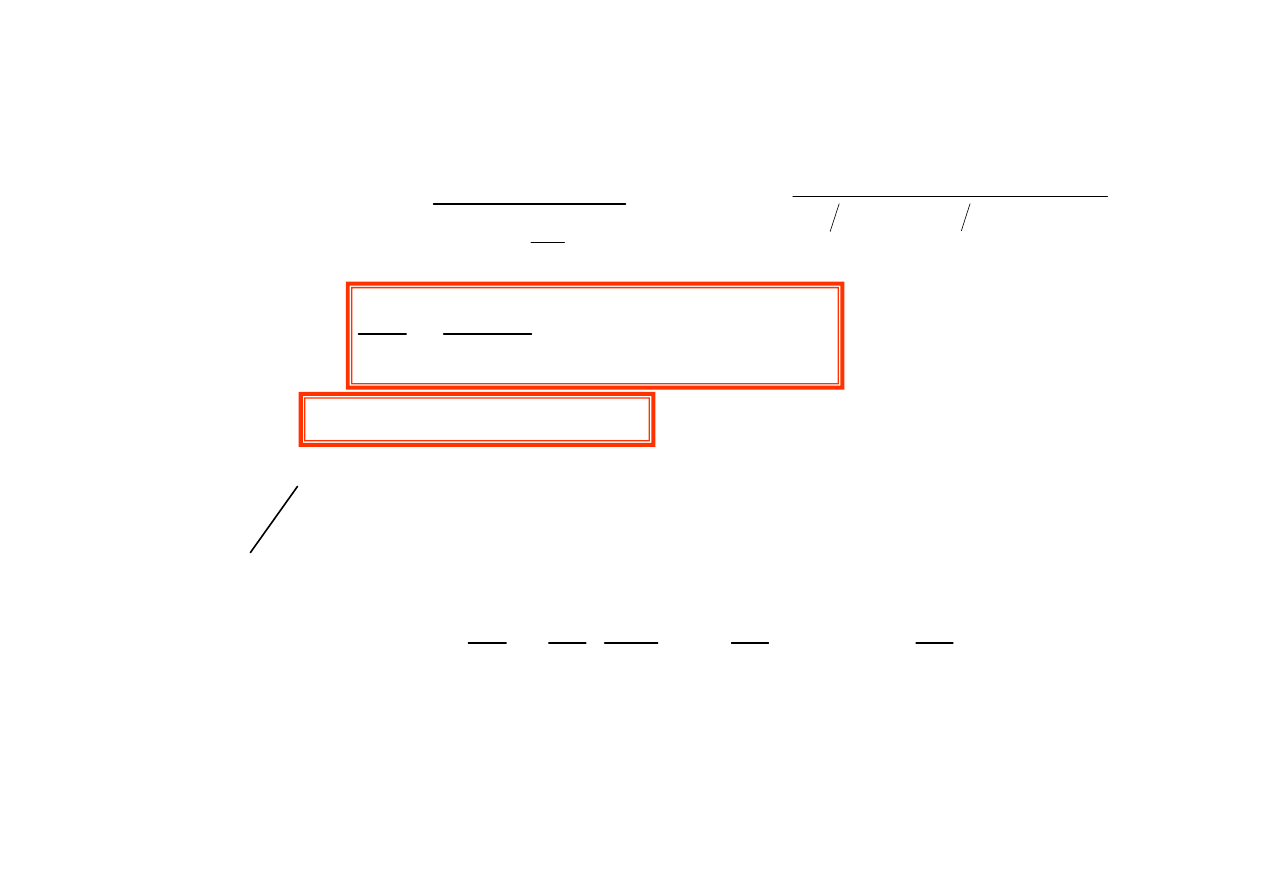
Analiza działania lasera

- schemat trójpoziomowy

E

1

; N

1

hv

13

metastabilny

E

1

E

2

E

3

metastabilny

hv

32

E

1

E

3

E

1

E

3

E

2

E

2

hv

21

hv

21

koherentne

fotony

E

2

; N

2

E

3

; N

3

N

i

– koncentracja atomów o energii E

i

Szybkość przejść

w górę (absorpcji):

 

12

12

1

B N

h

 



R

gdzie: B

12

– stała proporcjonalności

(współczynnik absorpcji Einsteina)



(hv) – gęstość częstotliwościowa

energii fotonów [#/cm

-3

Hz

-1

],

wg prawa Plancka o radiacji c. czarnego:

 

21

21

2

21

2

A N

B N

h

 





R

Szybkość przejść w dół (emisji):

gdzie A

21

– współczynnik emisji (Einsteina)

spontanicznej,

B

21

– współczynnik emisji (Einsteina)

stymulowanej

W warunkach równowagi termodynamicznej:

R

12

= R

21

 

3

3

8π

exp

1

eq

h

h

h

c

kT





































Lasery

6

W warunkach równowagi termodynamicznej:

R

12

= R

21



  

12

1

21

2

21

2

0

B N

B N

h

A N

 







czyli

stąd

 

21

2

12

1

21

2

A N

h

B N

B N

 





Teraz stosując statystykę Boltzmanna
i uwzględniając, że poziomy E

1

i E

2

są zdegenerowane

w stopniu g

1

i g

2

– odpowiednio - mamy

E

2

g

2

- podpoziomów

(o tej samej energii E

2

)

E

1

g

1

- podpoziomów

(o tej samej energii E

1

)

2

1

1

2

1

2

1

1

exp

exp

N

N

N

E

E

h

g

g

kT

g

kT





































Podstawiając to równanie do powyższego, otrzymamy

 









21

1

2

13

21

exp

A

h

g g

h kT B

B

 







, a wg teorii

 

3

3

8π

exp

1

eq

h

h

h

c

kT









































1

2

1

1 e

h

kT

N

N

N

N















Lasery

7

Relacje Einsteina

 

3

3

8π

exp

1

eq

h

h

h

c

kT





































Z porównania

oraz

 









21

1

2

13

21

exp

A

h

g g

h kT B

B

 







otrzymamy, że

3

21

3

21

8π

A

h

B

c





1

12

2

21

g B

g B



Jeżeli g

1

= g

1

=1,

to

12

21

B

B



Wnioski z powyższych wzorów:

1. Zauważmy, że

3

21

21

A

B





czyli gdy częstotliwość rośnie, to wzrasta emisja spontaniczna,
a zatem światło staje się mniej koherentne.
Dlatego trudniej jest zbudować X-laser.

2. Stosunek szybkości opróżniania poziomu E

2

– w wyniku emisji spontanicznej

i stymulowanej - wynosi

i

2 3

sp

21

3

st

21

exp

1

exp

1

A

v

B

kT

kT

































































R

R







Dla optycznych







rad/s i w T=500K mamy zatem

R

sp

>>

R

st

. Zatem światło na wyjściu lasera jest niekoherentne!

3. Wzmocnienie światła koherentnego może nastąpić nawet w powyższych
okolicznościach, jeżeli szybkość stymulowanej emisji przewyższy absorpcję.
Różnica pomiędzy nimi wynosi .



  

st

abs

21

2

1

B

N

N

 







R

R

Lasery

8

Warunki równowagi termodynamicznej

- Wg statystyki Boltzmanna:





2

1

2

1

exp

E

E

N

N

kT



















Równowagowy rozkład energii fotonów wg Plancka

(promieniowanie doskonałego ciała czarnego):

 

3

3

8π

exp

1

eq

h

h

h

c

kT





































Zakładając stan równowagi termodynamicznej (korzystając z prawa Plancka)
oraz z faktu, że B

12

=B

21

można wykazać, że

3

21

3

21

8π

A

h

B

c





Teraz rozważając proporcję emisji stymulowanej do spontanicznej, mamy









 

 

21

21

2

21

21

21

2

21

stym

spon

B N

h

B

h

A N

A

 

 





R
R

a uwzględniając
powyższe równanie









 

3

21

3

21

stym

spon

8π

c

h

h

 





R
R

Ponadto, uwzględniamy relację stymulowanej emisji do absorpcji:









21

2

21

1

stym

absorp

N

N



R

R

[**]

Lasery

9

Dalsze dwa wnioski:

1. Aby stymulowana emisja fotonów przekroczyła absorpcję (wg ostatniego równania),

musimy osiągnąć inwersję obsadzeń, czyli

2

1

N

N



2. Aby stymulowana emisja fotonów była dużo większa od spontanicznej emisji,

musimy mieć dużą koncentrację fotonów, którą uzyskamy, tworząc wnękę optyczną
gromadzącą fotony.

Wymagania o dużej inwersji N

2

>N

1

, oznaczają, że odeszliśmy od stanu równowagi

termodynamicznej. Bowiem stosując statystkę Bolzmanna przy nierówności uzyskujemy

z równania ujemną temperaturę!

[**]

Zasada pracy lasera jest zatem oparta na osiągnięciu stanu

nierównowagi termodynamicznej!

Lasery

10

W nierównowadze …

2

1

2

2

1

1

e

E

E

kT

N

g

N

g







<1

2

2

1

1

1

N g

N g



2

1

2

1

0

g N

N

g





- czyli absorpcja.

Zatem jest stanem nierównowagowym, nazywanym

inwersją obsadzeń!

2

1

2

1

0

g N

N

g





Lasery

11

Szybkość absorpcji

1

12

1

12

1

abs

dN

N

N

dt

 

 

 

R

N

1

- ilość atomów albo cząsteczek z dolnym poziomem energetycznym, typowe 10

20

cm

-3



12

- przekrój czynny centrów absorpcyjnych, typowy 10

-18

cm

-2

,



– strumień fotonów #/cm

2

s

Lasery

12

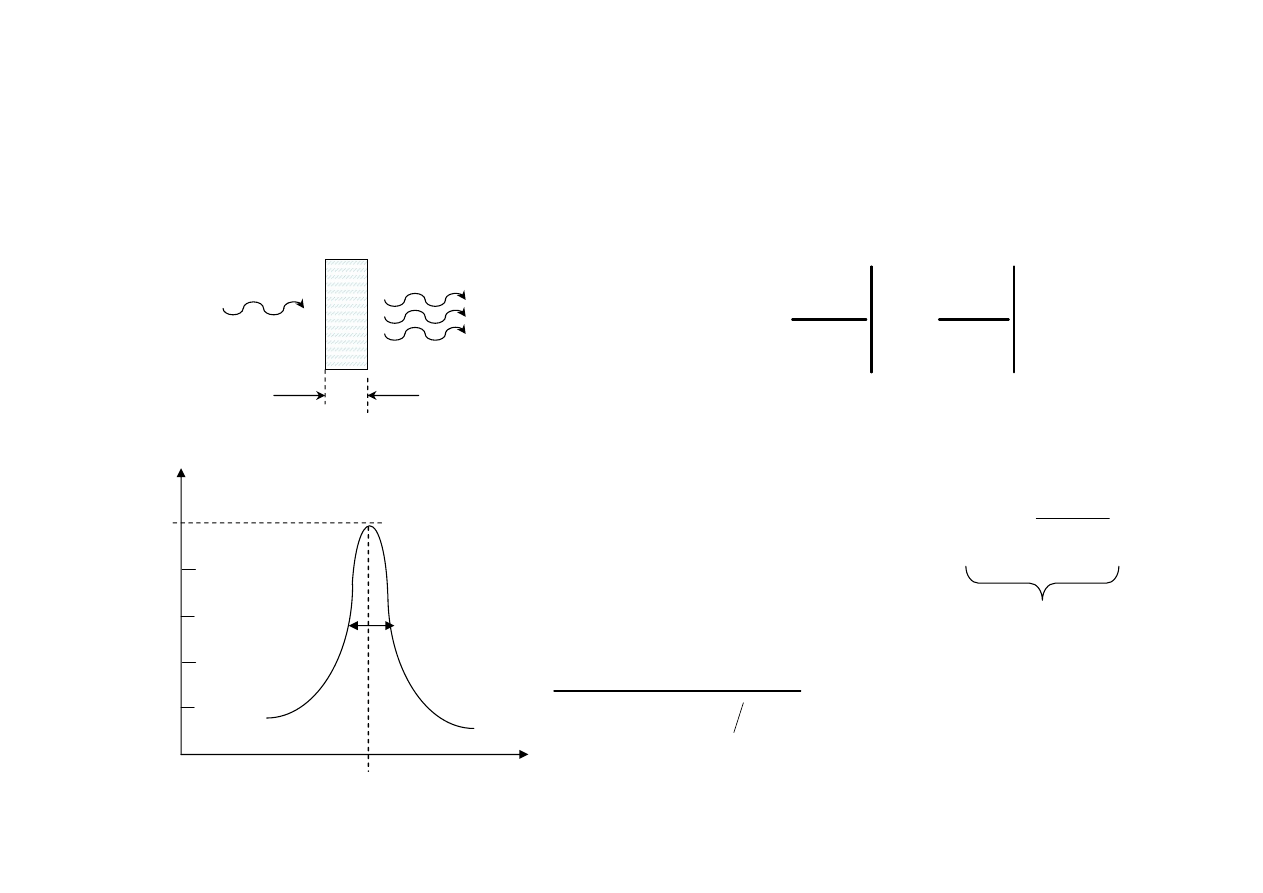
Dynamika emisji spontanicznej

i stymulowanej

2

2

2

sp

sp

dN

N

AN

dt



 

 



sp

spontaniczny czas życia [s]

2

21

2

21

2

st

dN

N

N

dt

 

 

 

R



- przekrój czynny emisji stymulowanej

– strumień fotonów



– czas życia na poziomie N

2

21

/

2

20

20

e

e

t

t

N

N

N









R



N

2

1,0

Praw

odpod

obi

e

ń

stw

o

Uwzględniając także nieradiacyjne przejścia:

stąd

21

tot

A

A





R

1

tot

A





t

Lasery

13

Skuteczność działania lasera

2

1

wy

we

st

abs

dN

dN

dz

dt

dt











 











- liczba fotonów powstałych w 1 cm

3

i 1 s.

Dlatego

2

1

21

2

12

1

21

2

1

g N

d

N

N

N

dz

g



 

 

 





















Inwersja:

<0 czyli netto absorpcja,
>0 czyli netto wzmocnienie.



we



wy

dz



wy

1,0





0





A

tot

/2

 









0

2

2

0

/ 4π

4π

tot

tot

A

A

 



 







Krzywa Lorentza

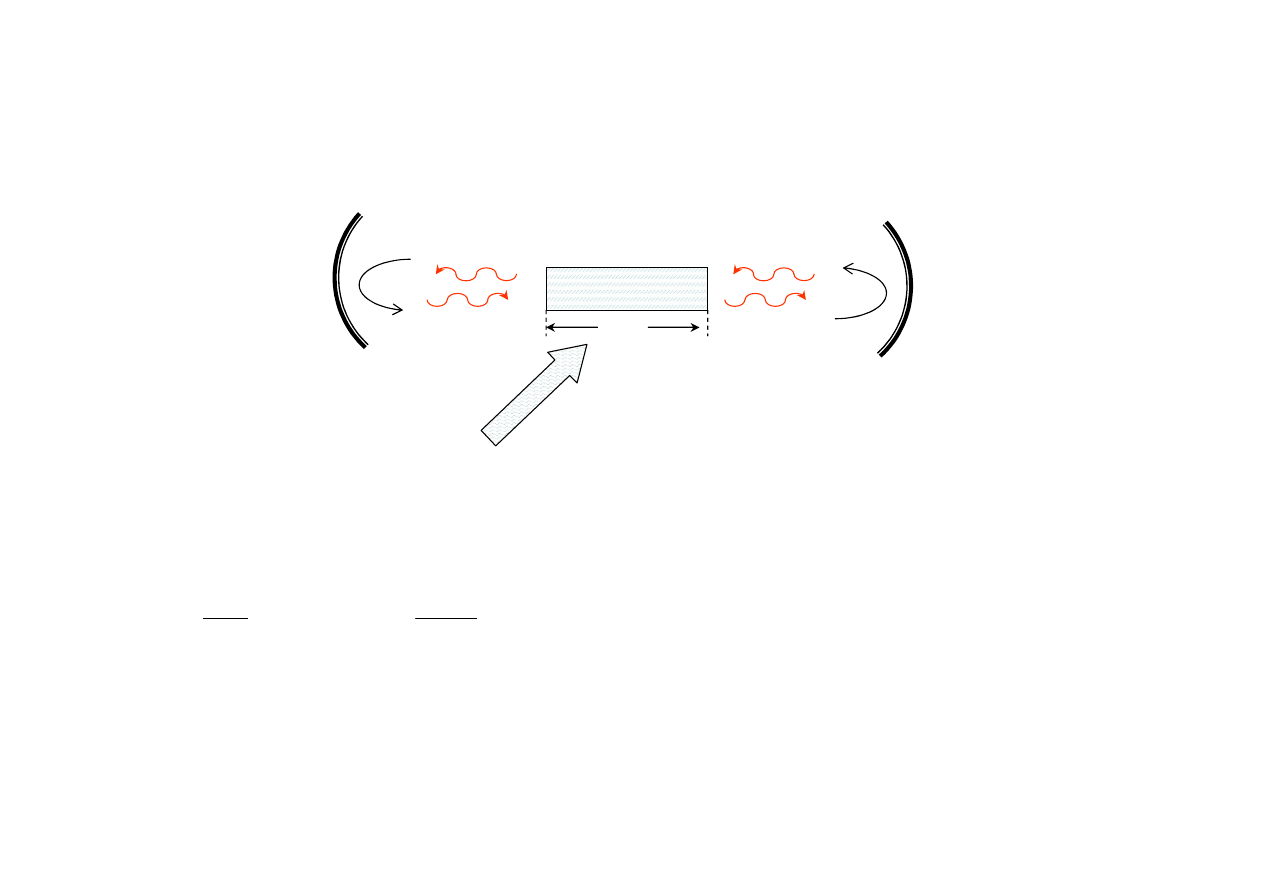
Lasery

14

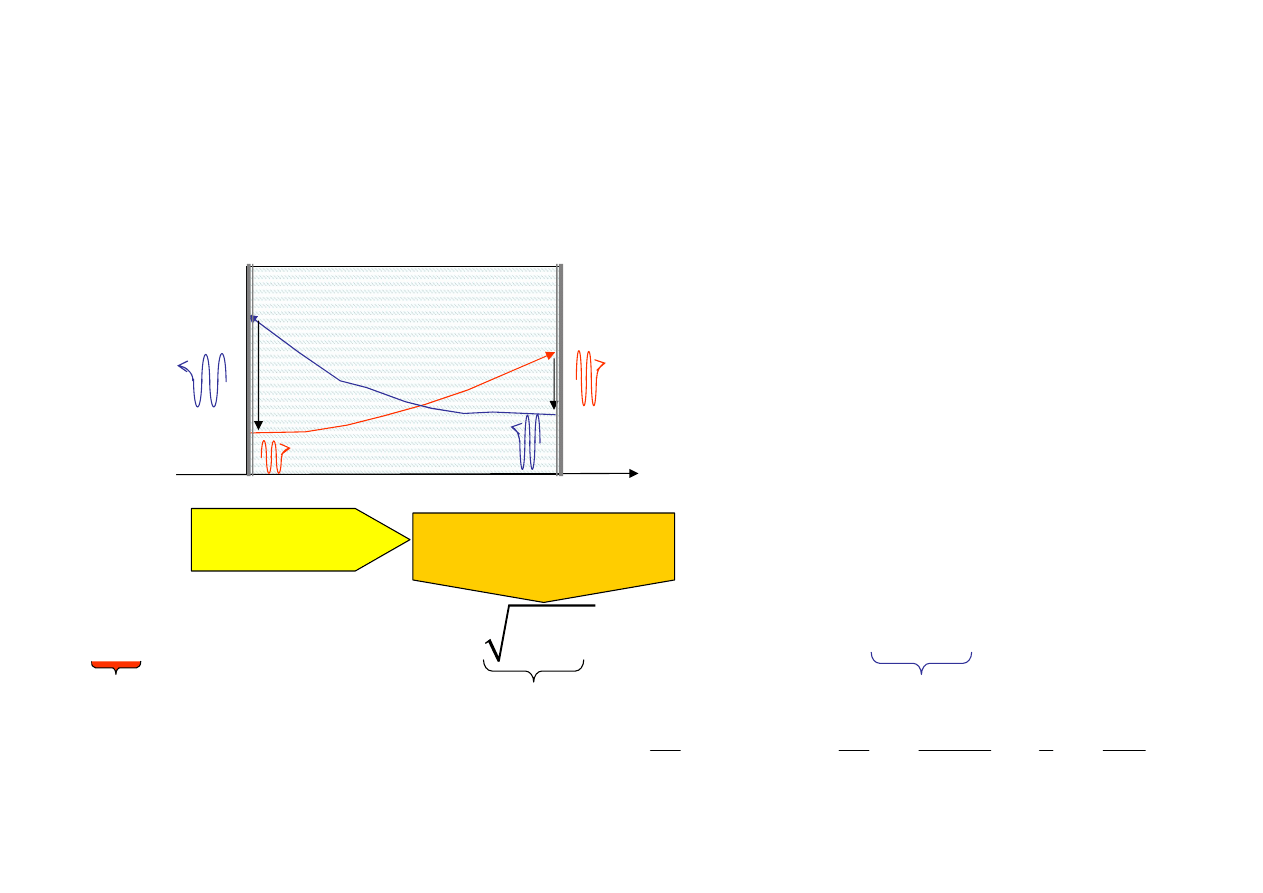
Akcja laserowa

Kiedy wzmocnienie w ośrodku wzmacniającym zbilansuje straty w zwierciadłach
oraz straty we wnęce, wtedy nastąpi akcja laserowa (lasing):

2

1

21

2

21

1

inv

g N

d

N

N

dz

g



 

 



















stąd

 

 

21

e

0

inv

N

z

z









gdzie: „wzmocnienie”

 

21

e

inv

N

z

G z





współczynnik „wzmocnienia”

[cm

-1

]

21

inv

g

N





l

Zwierciadło
z reflektancją R

1

Zwierciadło
z reflektancją R

2

„pompowanie” energii

aby wytworzyć stan nierównowagi

Wykład 3

15

Jednokrotne przejście przez wnękę

0

l z

E

+

(0)

E

+

(L)

E

-

(L)

E

-

(0)

g



WG

r

1

r

2

E

+

(0)=

r

1

E

-

(0)

 

 

 





 





 

 





 

 





 

/2

j

1

1

/2

j

1

2

/2

/2

j

j

1 2

0

0

e

e

e

e

e

e

0 e

e

WG

WG

WG

WG

l

k

l

l

k

l

l

l

k

l

k

l

E

r E

r E l

r

r E l

rr

E

 



 



 

 



























































- stąd po jednej rundzie promienia przez wnękę:





 

j2

1 2

1

e

e

WG

l

k

l

rr

 









2

I

P

E





2

pole E

moc











 





 





 

j2

j2

j2

1 2

1

2

1

e

e

R R e

e

e

e

WG

WG

WG

m

l

l

l

k

l

k

l

k

l

rr

 

 

 





























e

m

l









1

2

1

2

1 2

1

1

1

1

1

ln R R

ln

ln

2

2

R R

m

l

l

l

r r











 





















stąd

 

 

 

*

1 2

1 2

1 2

R

r

r





Transmisja mocy:

 

 

1 2

1 2

T

1 R

 



– wzmocnienie dwukierunkowe

w rezonatorze m. lustrami



WG

– straty w propagacji



m

- lokalne straty w zwierciadłach





e

WG

G

 





- net gain

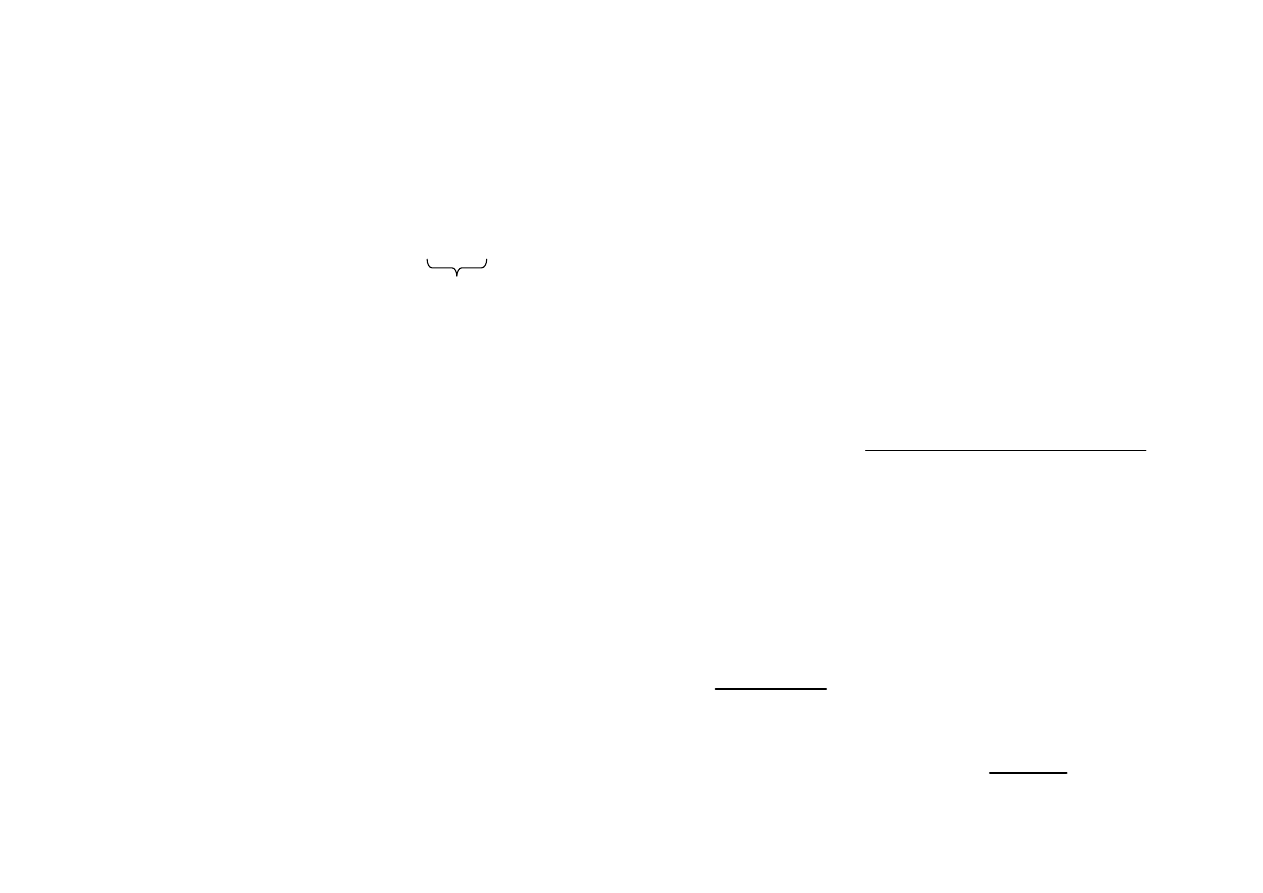
Lasery

16

Warunek „laserowania”

N

c

≡ Wartość N, dla której spełniony jest

warunek lasingu, nazywany krytyczną inwersją

"Critical Inversion„.

Często też spotykamy określenie "Logarithmic Losses"

 





1

2

2 R R 1

1

i

G

l

L





albo





2

2

1

2

e

R R 1

1

gl

i

L





albo





21

2

2

1

2

e

R R 1

1

inv

N

l

i

L







= bilans strat wzmocnienia

Straty po jednym przejściu przez wnękę









1

2

21

ln R R

2 ln 1

2

i

c

L

N

l









 









1

1

2

2

ln R

ln R

ln 1

i

i

L





















1

2

2

i















stąd

21

c

N

l







Zatem

Lasery

17

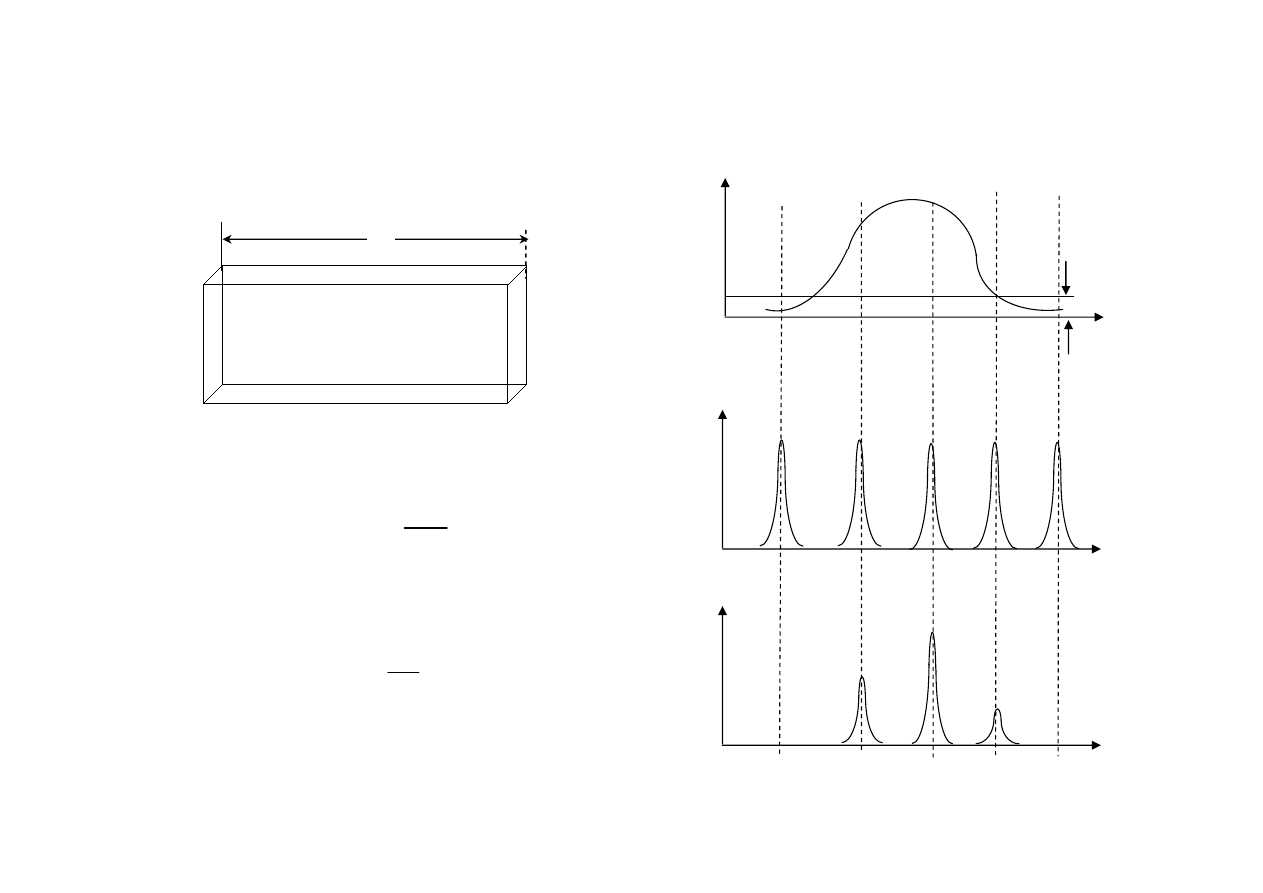
Mody wnęki rezonansowej

Wnęka

rezonansowa

l

Częstotliwości modów osiowych:

2

mc

l





odstęp między modami:

2

c

l



 

m=1, 2, ..

g

m

Straty
wnęki:

Pasm

o

w

zmacnia

cza

Refl

e

ksyjno

ść

w

n

ę

ki

Mo

c wy

jś

ciowa

lasera

Częstotliwość

Lasery

18

Warunki laserowania

1. Inwersja obsadzeń jest potrzebna, aby osiągnąć stymulowną emisję.
2. Struktura energetyczna materiału ma kilka poziomów, a najwyższy poziom ma

stan metastabilny. Długość emitowanej fali jest określona przez różnicę poziomów
energetycznych pomiędzy tym ze stanem metastabilnym i kolejnym niższym.

3. Materiał (system) powinien być przeźroczysty dla emitowanego światła.

W przeciwnym przypadku światło nie opuści materiału.

4. Odrębność (confinement) materiału i światła przez rezonator.
5. Wzmocnienie progowe musi być większe niż częściowe straty plus światło emitowane.

Lasery

19

Sprawność LED i LD

1

2

1

1

2

1

1

ln

th

zew

wew

I

l

I

R R





































 





























Zewnętrzną sprawność mocy
optycznej z kolei wyliczamy jako

.

opt

g

op

ex

e

P

E

P

eV













 







Sprawność wewnętrzną można obliczyć jako:

ilos ć emitowanych fotonów

ilos ć iniektowanych elektronów

wew









Natomiast sprawność zewnętrzną można obliczyć jako:

.

ilos ć fotonów wychodzących

ilos ć iniektowanych elektronów

opt

zew

G

P

I E













Lasery

20

Ch-ki i

D

-u

D

i i

D

-P

opt

diody laserowej

P

opt

i

D

I

TH

opt

opt

ed

D

D

P

h

dP

q

i

h

di

q











 

















 







i

D

u

D

I

TH

1

d

r



- zewnętrzna
różniczkowa sprawność
kwantowa LD

,

WY

ph WYtotal

P

h





D

TH

opt

e

i

i

I

P

h

q



 





ed

e

i



 





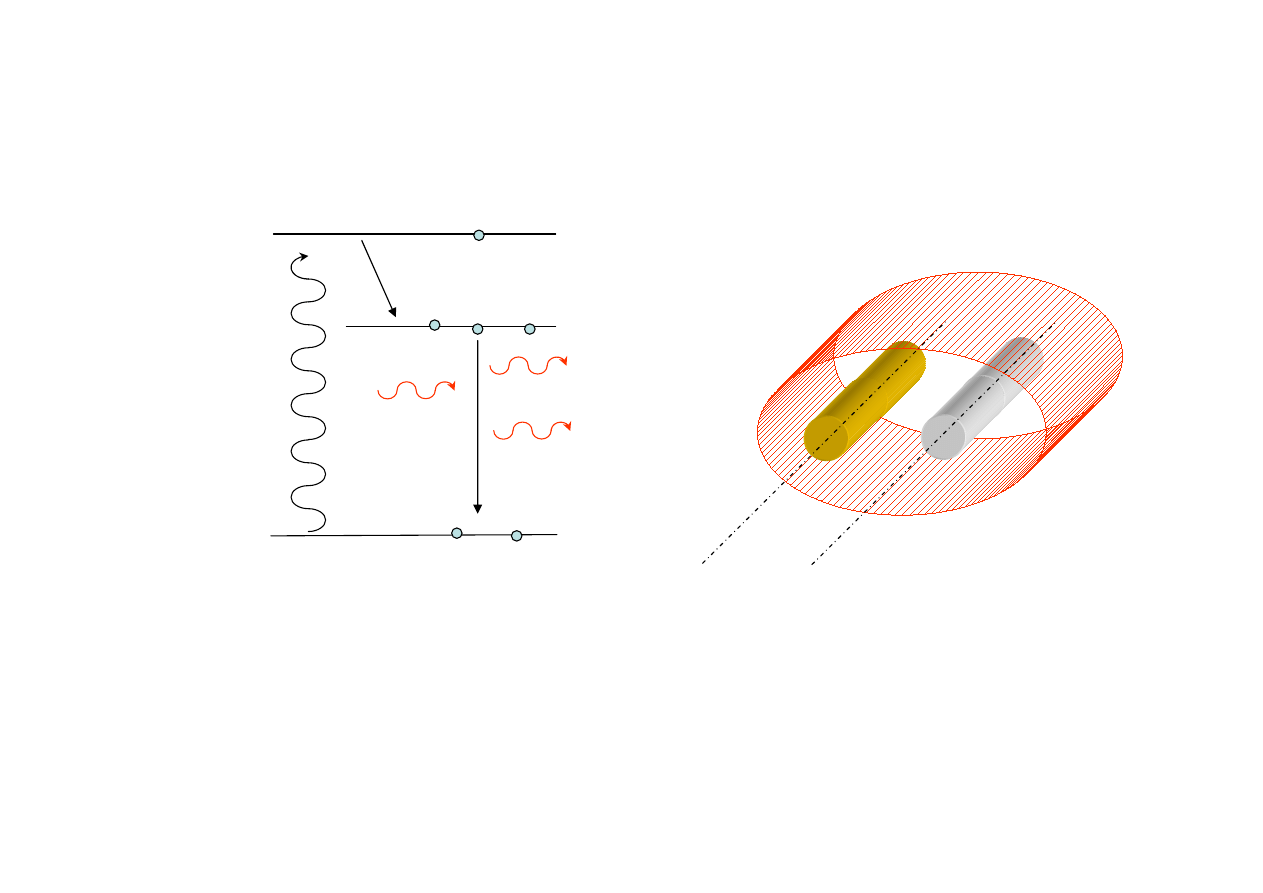
Lasery

21

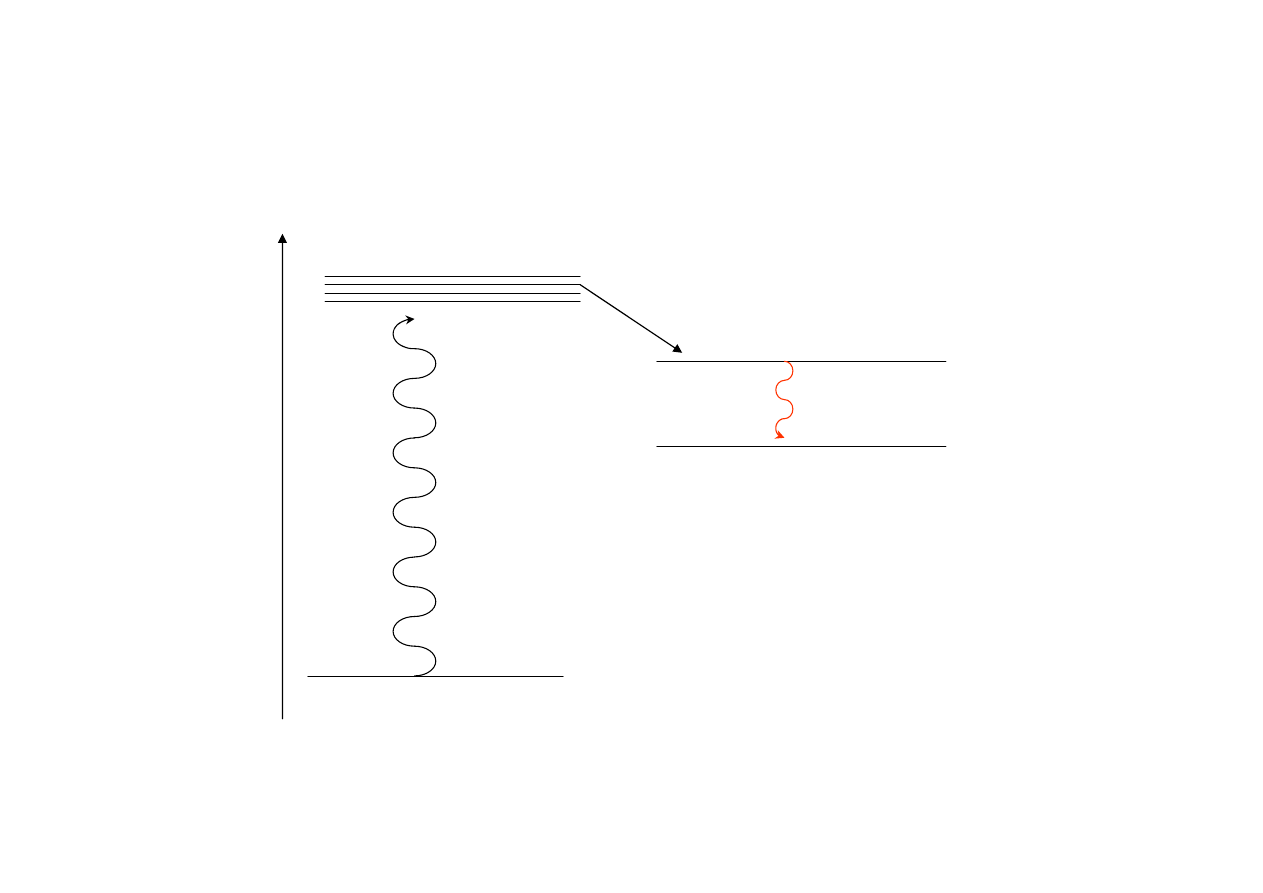
Laser rubinowy 3 poziomowy

1.

2.

3.

3

1

p

h

E

E







2

1

h

E

E







Fast decay

F

1

F

2

La

m

pa

R

dz

eń

Lasery

22

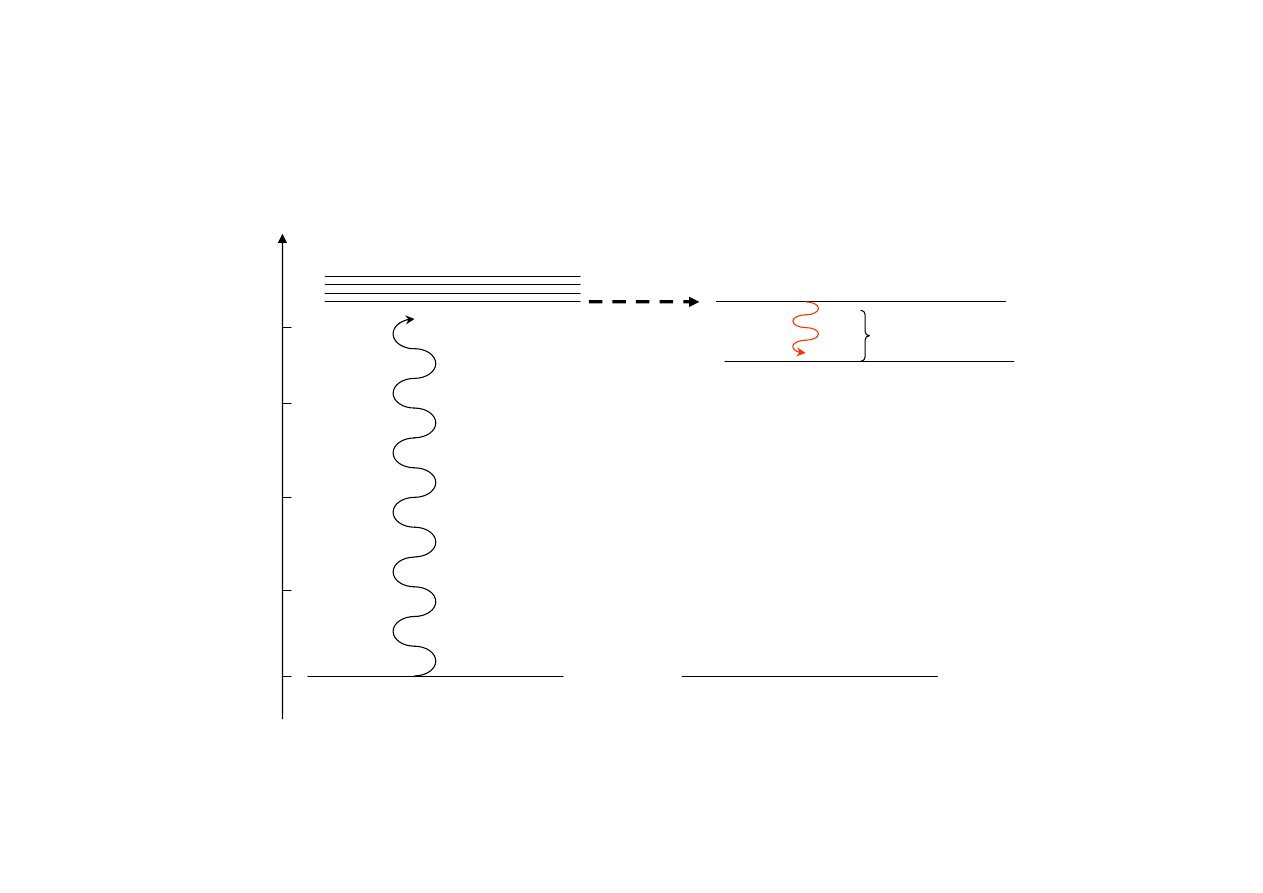
Schemat 4 poziomowego lasera

1.

2.

3.

4.

Górny poziom laserowy

Dolny poziom laserowy

„Pompow

anie

”

Przejście selektywne

Przejście laserowe

Energia

Lasery

23

Laser He-Ne

1.

2.

3.

4.

Górny poziom laserowy

Dolny poziom laserowy

„Pompow

anie 1

”

Pompowanie 2.

Energia

[eV

]

20

15

10

5

0

Hel

Neon

Poziom podstawowy

E=1,959 eV

Lasery

24

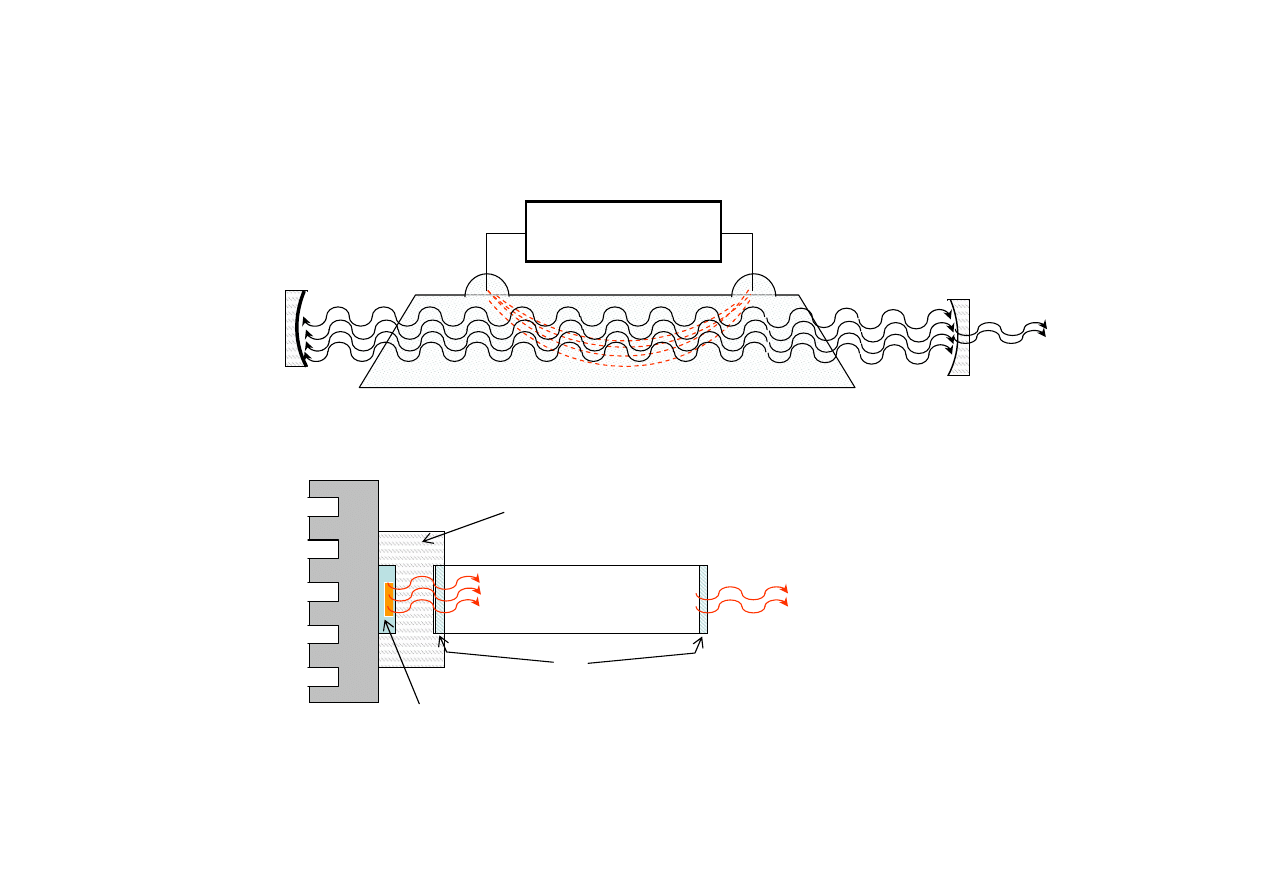
Przekrój lasera

Źródło zasilania

Mieszanina Ne-He (10:1)

Ne-He

YAG

Radiator

ciepła

Dioda LED

Sprzęgacz optyczny

Zwierciadła

Pręt YAG -rezonator

Lasery

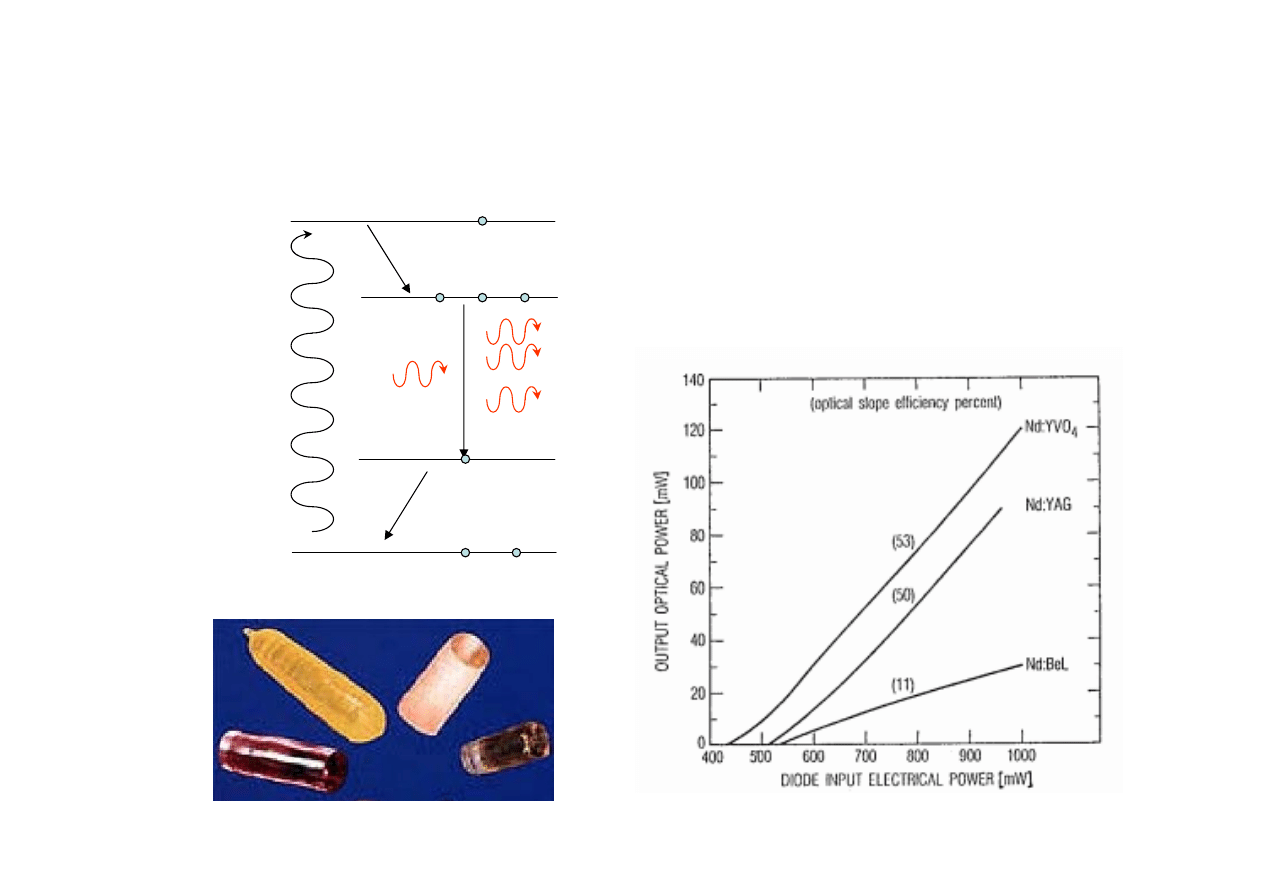
25

Laser Nd:YAG

3

0

p

h

E

E







2

1

h

E

E







0.

1.

2.

3.

Fast decay

Fast decay

Lasery

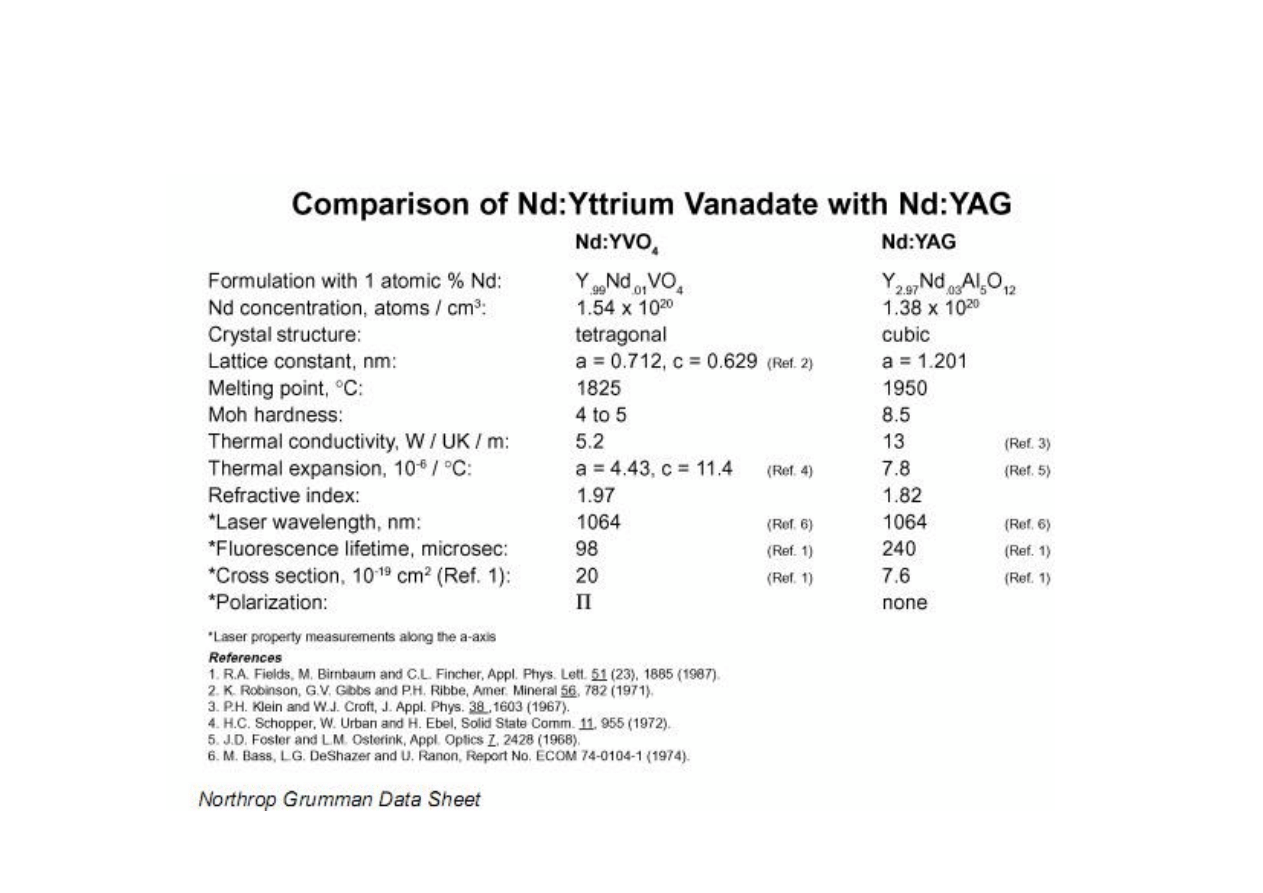
26

Porównanie właściwości Nd:YVO

4

i Nd:YAG

Lasery

27

Porównanie właściwości Nd:YVO

4

i Nd:YAG

Nd:YAG

Nd:YVO

3

Cr:LiSAF

Cr:YSO

Ti:Al

2

O

3

Nd

3+

:YAG Nd

3+

:YVO

3

Cr

3+

:LiSrAlF

6

Cr

4+

:Y

2

SiO

5

Struktura krystaliczna

romboedryczna monokliniczna

Współ. załamania n

1,41

1,8

Długość fali emisyjnej [nm] 1064 720-920 1000-1500 532
Pompowanie diodą (absorpcja) [nm] 670 808 390, 595,694, 750
Czas fluorescencji [s] 90

67 0,7

Przekrój czynny
stymulowanej emisji
[x .10

-19

cm

2

] 6. 25.

0,48.

4,6.

Lasery

28

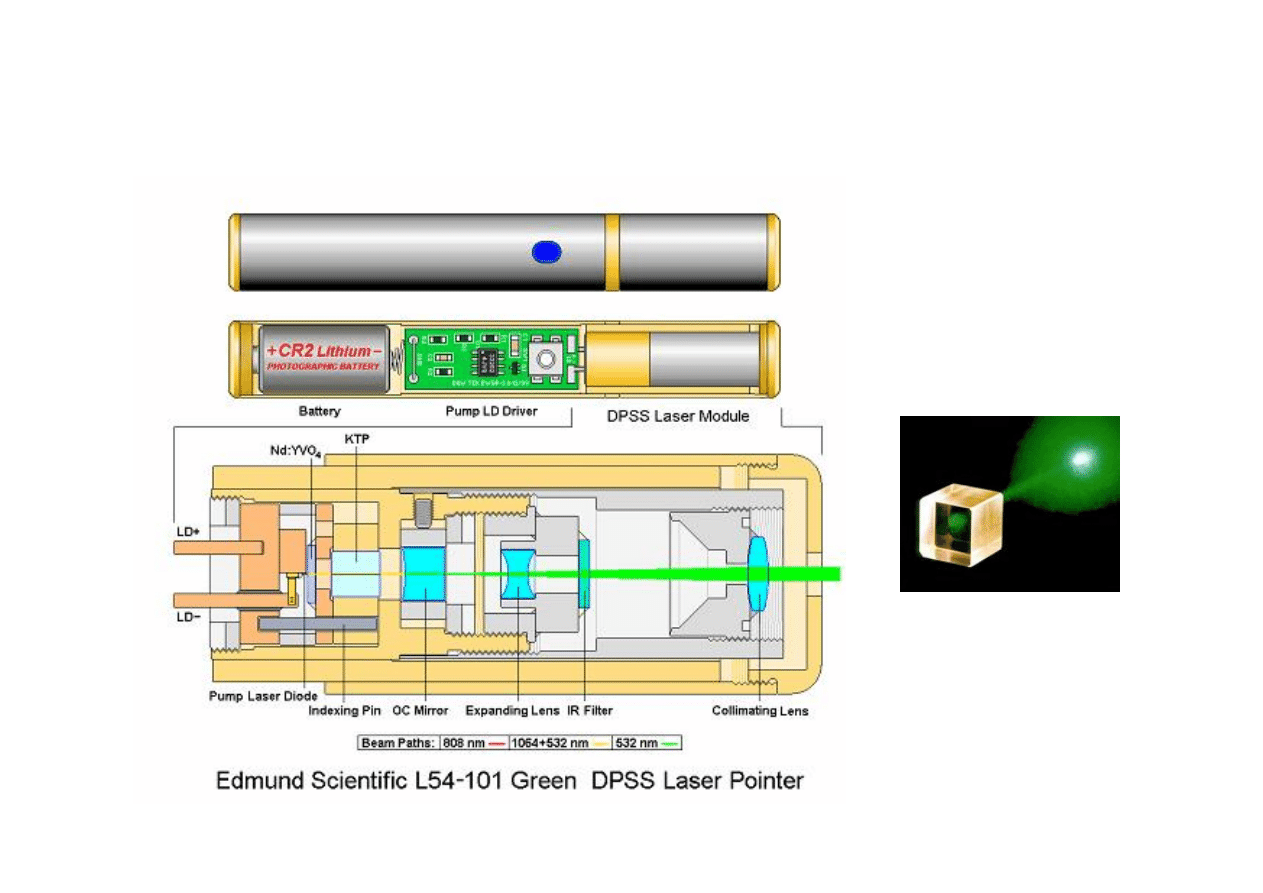
Zielony wskaźnik laserowy na Nd:YVO

4

KTP (Potassium Titanyl Phosphate),
is transparent at 1064 nm and
532 nm, has large electrooptic
coefficients, and a large damage
threshold, making it an ideal
choice for frequency doubling of a
Nd:YVO

4

laser.

Lasery

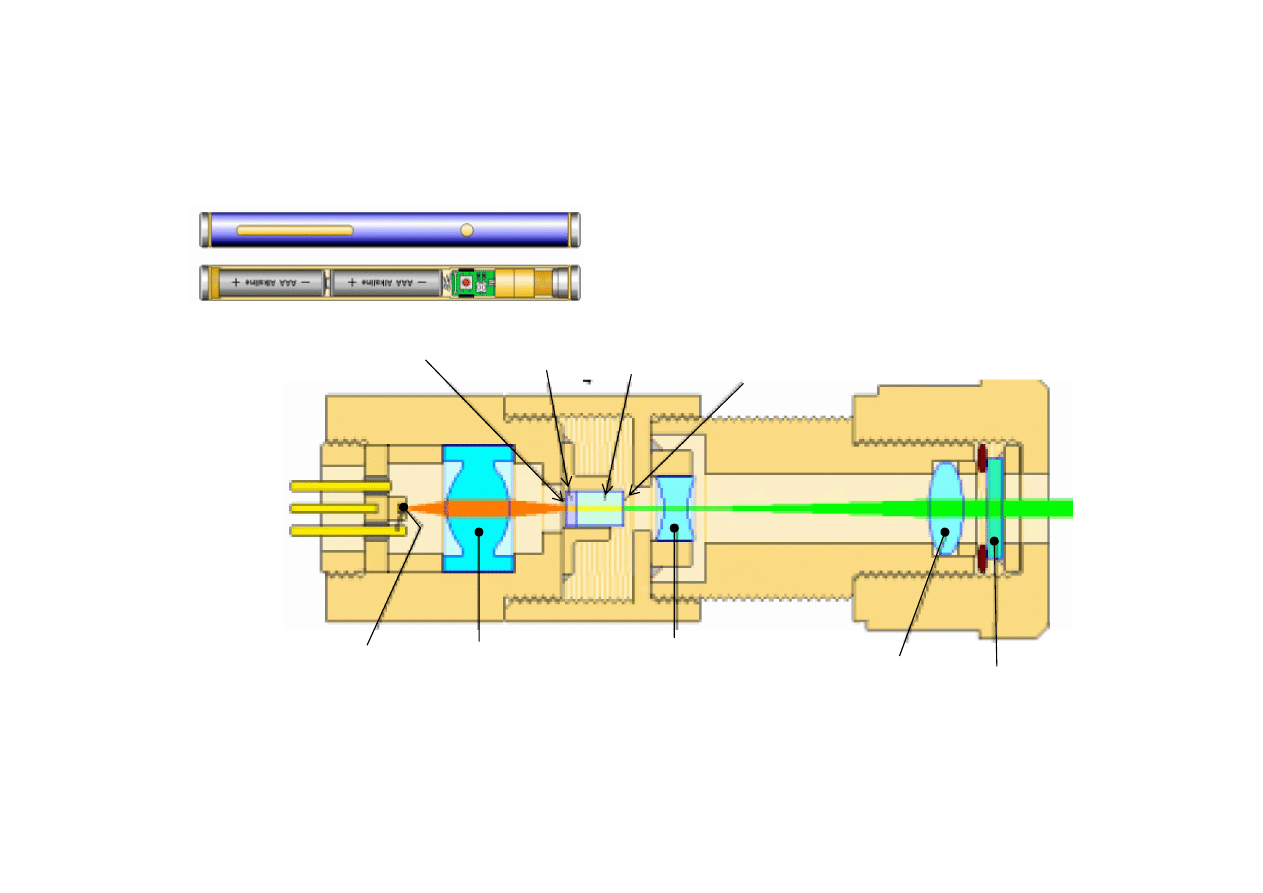
29

Schemat działania GLP

Pompująca

dioda laserowa

Pompujące

soczewki

soczewki

poszerzające

Filtr

podczerwieni

soczewki

kolimujące

Zwierciadło HR (high reflexsibility)

na tylnej powierzchni

Multiple Crystal Assembly

Nd:YVO

3

KTP

lustro OC (output coupler)

na przedniej powierzchni

Zasilanie

diody laserowej

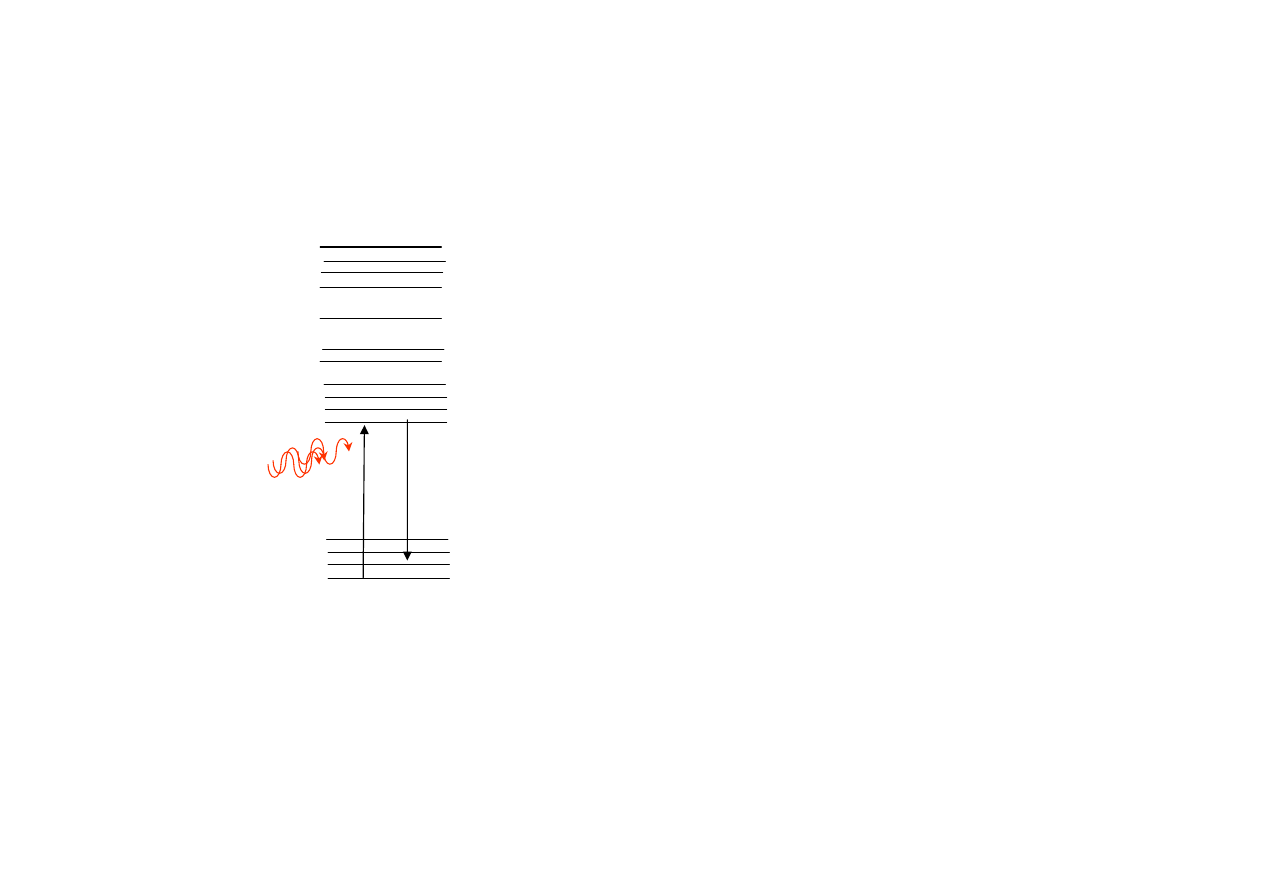
Lasery

30

The atomic energy level diagram of the

green laser pointer

4

G

4

S

2

H

4

F

4

I

4f

3

Nd

3+

w Nd:YVO

4

(Nd doped Ytrium OrthoVanadte)

Fala 808 nm
z diody laserowej

1064 nm



532 nm

KTP dublujący kryształ
KTiOPO

4

– fosforan potasowo-tytanylowy

KTP (Potassium Titanyl Phosphate) is transparent at 1064 nm and
532 nm, has large electrooptic coefficients, and a large damage
threshold, making it an ideal choice for frequency doubling of a
Nd:YVO4 laser.

Lasery

31

Generacja drugiej harmonicznej SHG

Intra-Cavity Frequency Doubling

→ Gives higher efficiency because of multiple pass geometry,
but means that a damaged KTP crystal degrades both 2nd harmonic efficiency
and Nd:YVO4 output.

Aby nastąpiła generacja fali o podwojonej częstotliwości potrzebny jest kryształ
o dużych wartościach współczynników nieliniowych w macierzy polaryzacyjnej:

0

skladniki nieliniowe

 





P

E

2

2

11

12

13

14

11

16

2

21

22

23

24

25

26

31

32

33

34

35

36

2

2

2

x

y

NL

x

z

NL

y

z

y

NL

z

z

x

x

y

E

E

P

d

d

d

d

d

d

E

P

d

d

d

d

d

d

E E

P

d

d

d

d

d

d

E E

E E



















































































Lasery

32

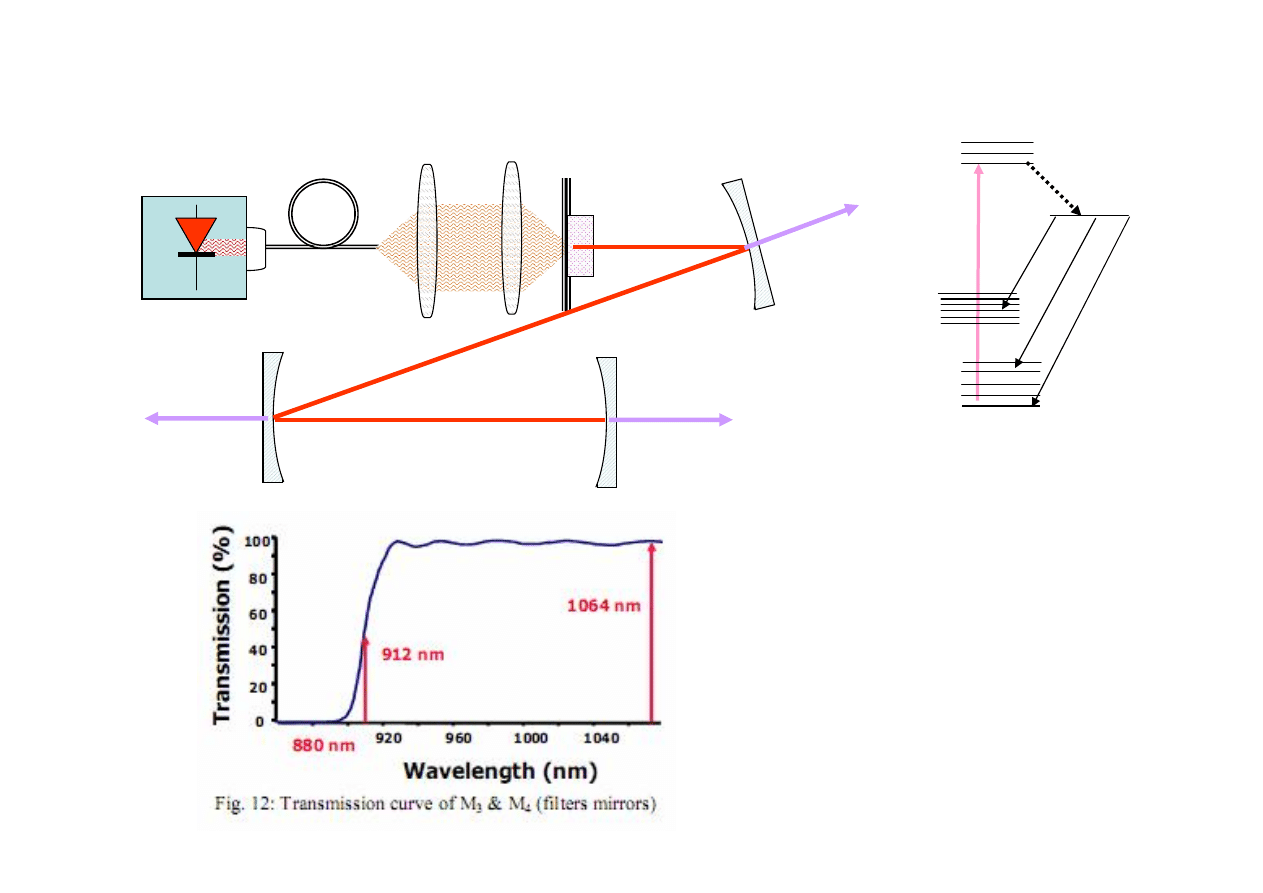
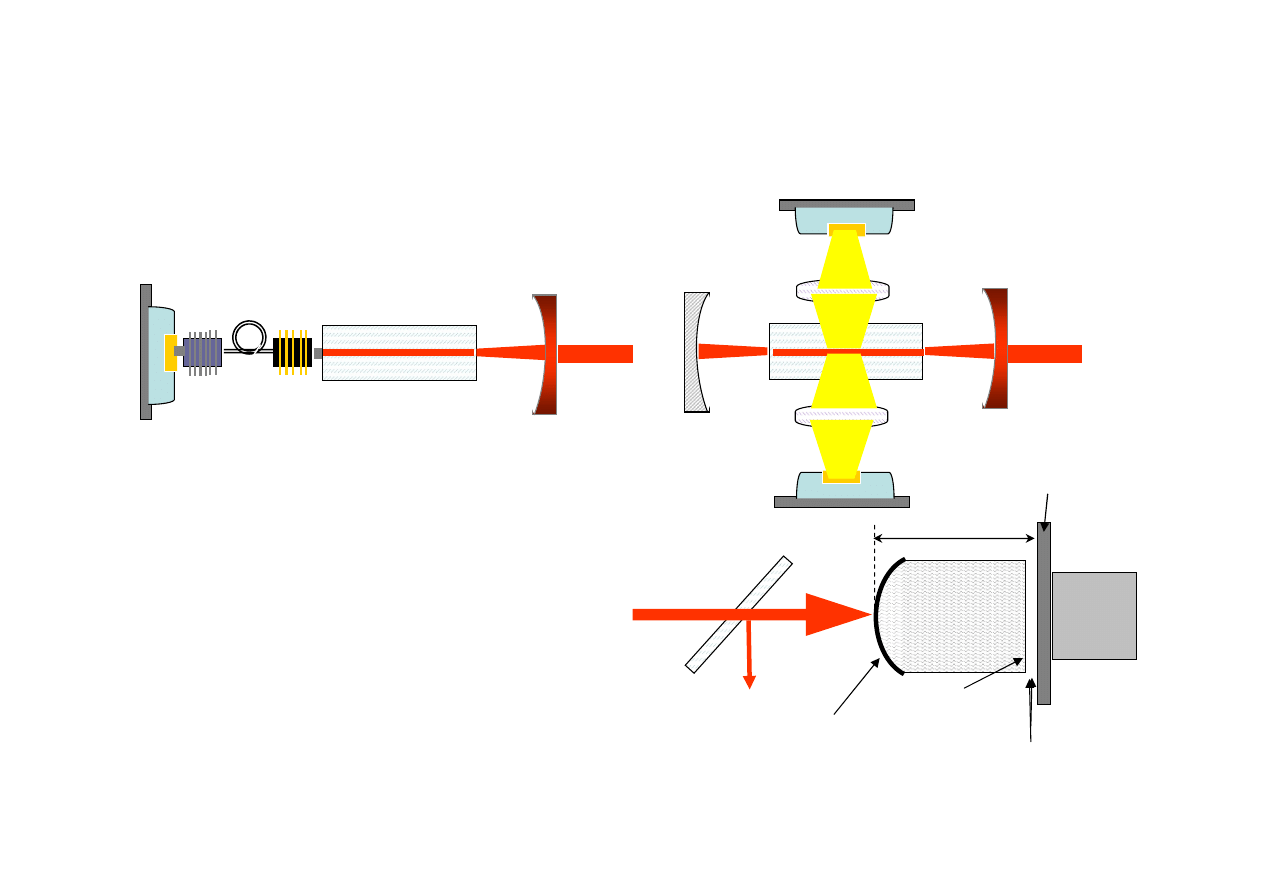
SHG

LD 25W

F=50 mm

F=100 mm

M

1

Nd:GdVO

3

5mm/0,1%

M

2

R=-200 mm



 440 nm

M

3

R= -150 mm

M

4

R= -100 mm



 440 nm



 440 nm

KNbO

3

4

F

5/2

4

F

3/2

4

I

11/2

4

I

9/2

808 nm

1063 nm

912 nm

879,4 nm

Diagram

energetyczny

Nd:GdVO

3

Lasery

33

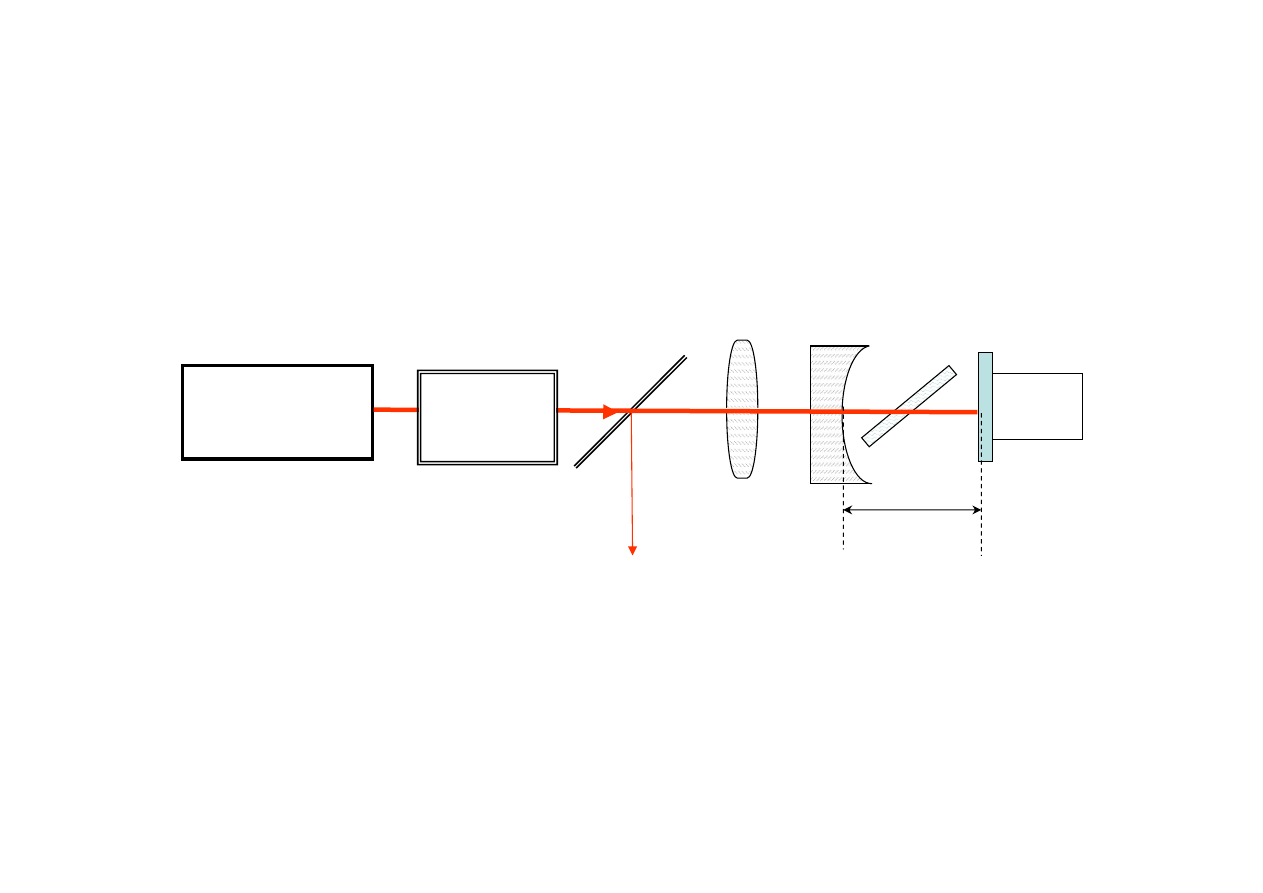
Laser pompowany diodą LED

Pompowanie od końca (end pumping)

Pompowanie boczne

(side pumping)

DPSS lasery (Diode-pumped solid state)
są optycznie pompowanymi przyrządami
monokrystalicznymi, takimi jak

Nd:YAG i Nd:YLF, wzbudzanymi przez

diodę laserową albo całą ich baterię
zamiast lampy wyładowczej albo innego źródła
o dużej intensywności.

System może być pompowany od końca

albo z boku, o typowej geometrii rdzenia.
Pompowane z boku mają zwykle większą moc.

Długość wnęki

Płaska

powierzchnia

Przerwa

powietrzna

Zwierciadło

półprzepuszczalne

Wyjście

SESAM

-Semiconductor

saturable absorber

Wypukła

i polerowana

HT@808nm

0,2%T@1064 nm

Nd:YVO

3

Pompowanie

PZT

HR zwierciadło

Kryształ lasera

Sprzęgacz
wyjściowy

Światło-

wód

LED

HR zwierciadło

Soczewki

Soczewki

Sprzęgacz
wyjściowy

Lasery

34

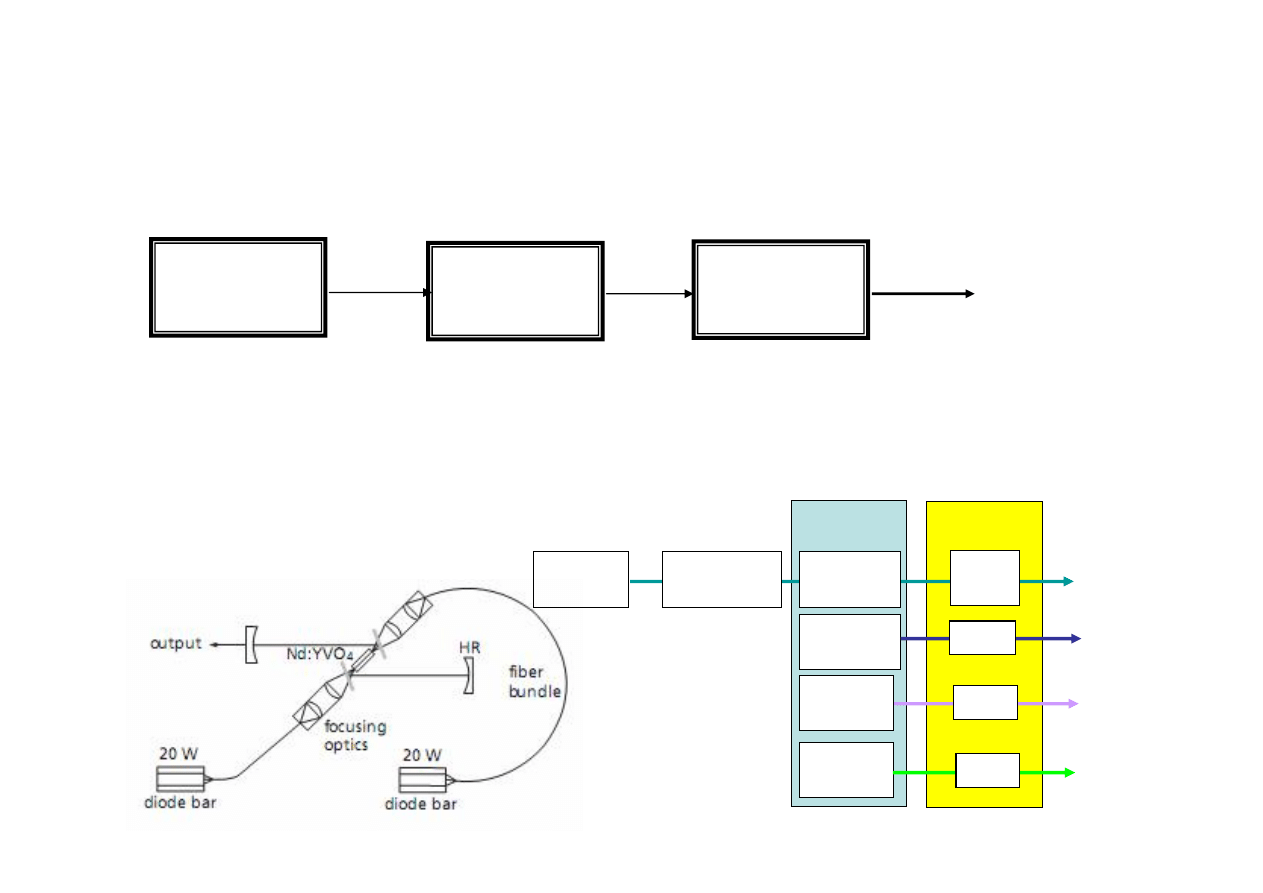
DPSS laser

Experimental setup of the 40-GHz laser with higher power.
The pump and laser wavelengths are separated with a dichroic mirror.
PZT stands for piezoelectric transducer.

Dioda pompująca

LED

2 W

Lustro

półprzepuszczalne

Sprzęgacz
wyjściowy

SESAM

PZT

Ogniskowanie

achromatyczne

Nd:YVO

3

3,11 mm

Strumień

wyjściowy

Optyka

transmisyjna

Even higher repetition rates of more than 1 THz can be reached with mode-locked edge-emitting semiconductor lasers
[11]. In general, the pulses from such laser diodes are strongly chirped, and the average output power is typically only a
few milliwatts or even below 1 mW. Optically pumped vertical-external cavity surface-emitting semiconductor lasers
(VECSELs) that are passively mode-locked with a semiconductor saturable absorber (SESAM) [12], [13], can
generate high average output powers in picosecond pulses of good quality [14], [15], and close to transform-limited
femtosecond pulses [16]. Recently, a 10-GHz device of this kind with 1.4 W average output power has been
demonstrated [17], and higher repetition rates should be possible

Lasery

35

Sprawność DPSS laserów

Melles Griot DPSS laser optical
trains for producing four different

visible output wavelengths

The visible output power, 532 nm

in the green spectrum, could break
into high-frequency chaotic
oscillations of nearly 100-percent

peak-to-peak amplitude. This

was named the “green problem”

by Tom Baer (then at

Spectra-Physics)

Pompująca

dioda laserowa

Kryształ

lasera IR

Kryształ

nieliniowy

Pierwotne

źródło światła

Konwerter

modalny

Konwerter

długości fali

Duża efektywność



p

=50%

Słaba modalność

M

2

=50

Dobra efektywność



M

=12%

Dobra modalność

M

2

=1,5

Dobra efektywność





=50%

Dobra modalność

M

2

=1



T

=



P



M





= 3%

DL pump
808 nm

Optyka

sprzęgająca

Nd:YVO

3

1064 nm

Nd:YAG

1123 nm

Nd:YVO

3

914 nm

IR laser
kryształ

Nd:YAG

946 nm

LBO/

KTP

LBO

SGH

kryształ



wy

532 nm

457 nm

473 nm

651 nm

BBO

LBO

Lasery

36

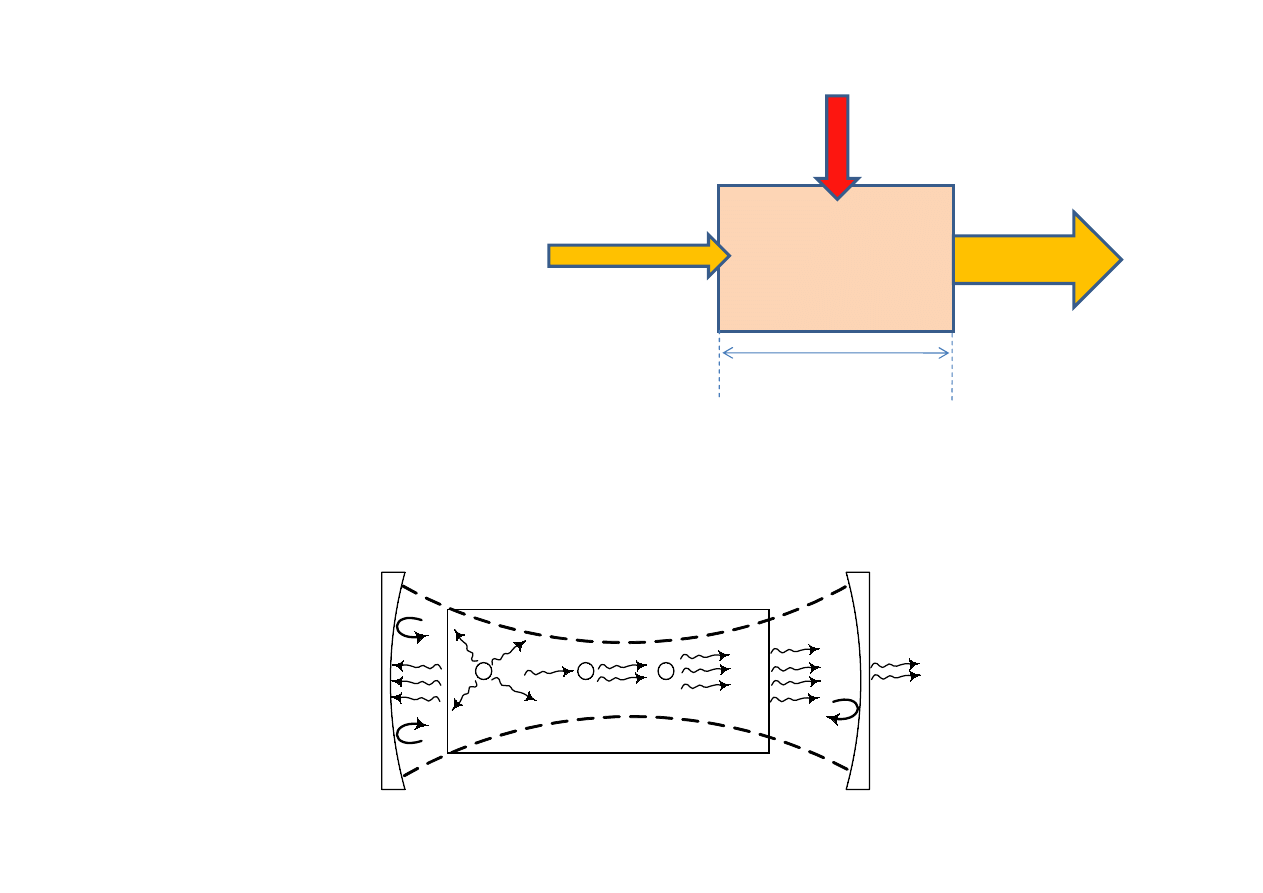
…cd

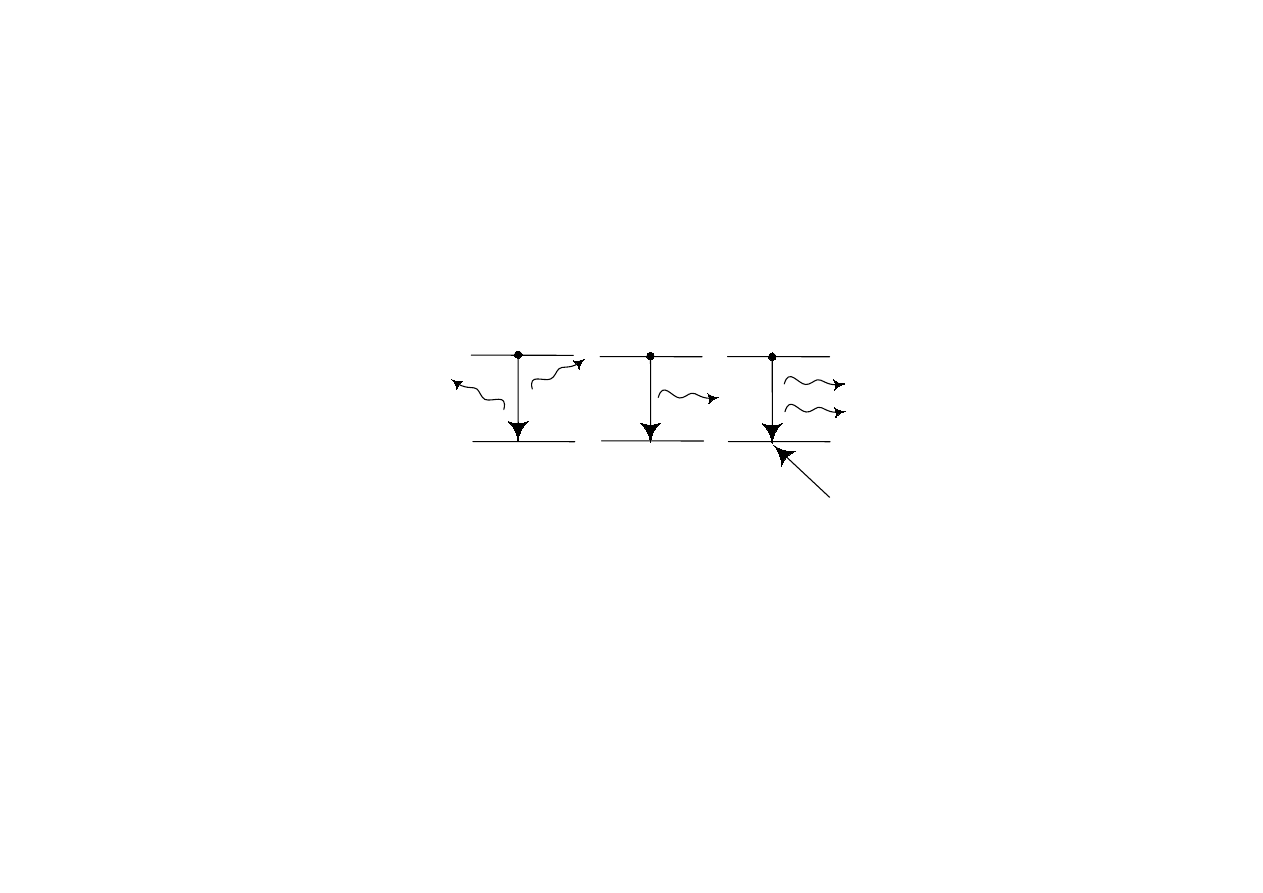
3.

“Seed” for Stimulated Emission

•

In some cases, the “seed” is supplied by spontaneous emission

•

In other cases, the “seed” can be provided in another fashion, generally

another laser. “Seeding” a laser can improve

1. Timing jitter for pulsed lasers

2. Wavelength stability

3. Spectral purity (bandwidth)

2

1



















Spontaniczna
emisja w 4 sr

Emisja stymulowana

Lasery

37

..cd

4.

Wnęka optyczna albo rezonator są niezbędne, aby

1. zapewnić sprzężenie optyczne ośrodka,

2. określić dozwolone mody przestrzenne i wzdłużne.

Zwierciadło 100%

Pompa optyczna

Sprzężenie zewnętrzne

Ośrodek wzmacniający





światło

N

p

N

p

+



N

p

g

pompowanie



z

Ośrodek
aktywny

światło

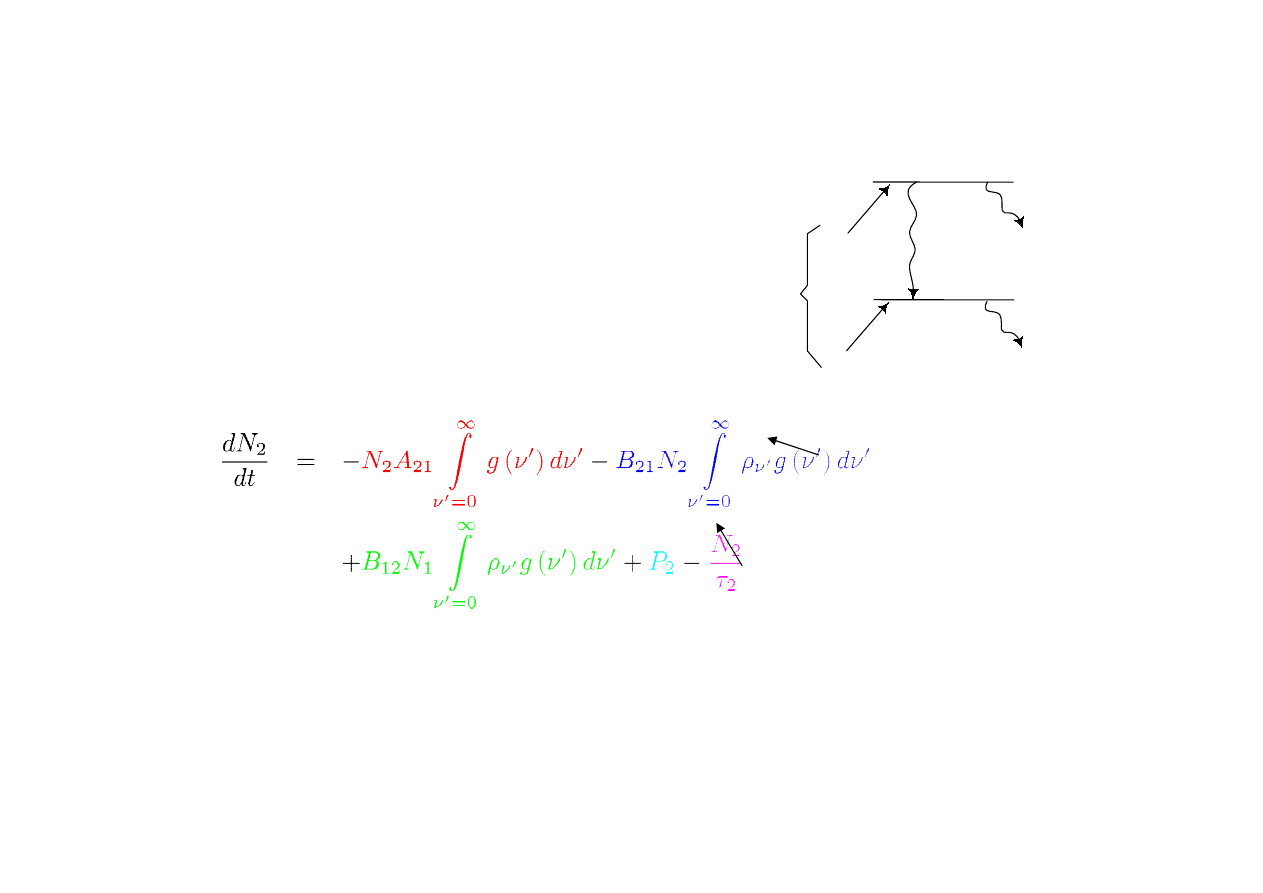
Lasery

38

…cd

• Rozważmy obsadzenia na
górnym poziomie lasera jako
funkcję czasu:

stymulowana emisja

relaksacja nieradiacyjna

Emisja spontaniczna

Absorpcja

pompowanie

gdzie



v

– spektralna gęstość energii dla v [Jcm

-3

Hz

-1

]

Szybkość
pompowania
[cm

-3

s

-1

[

(cm

-3

-s

-1

)

2

1

P

2

P

1

A

21



2



1

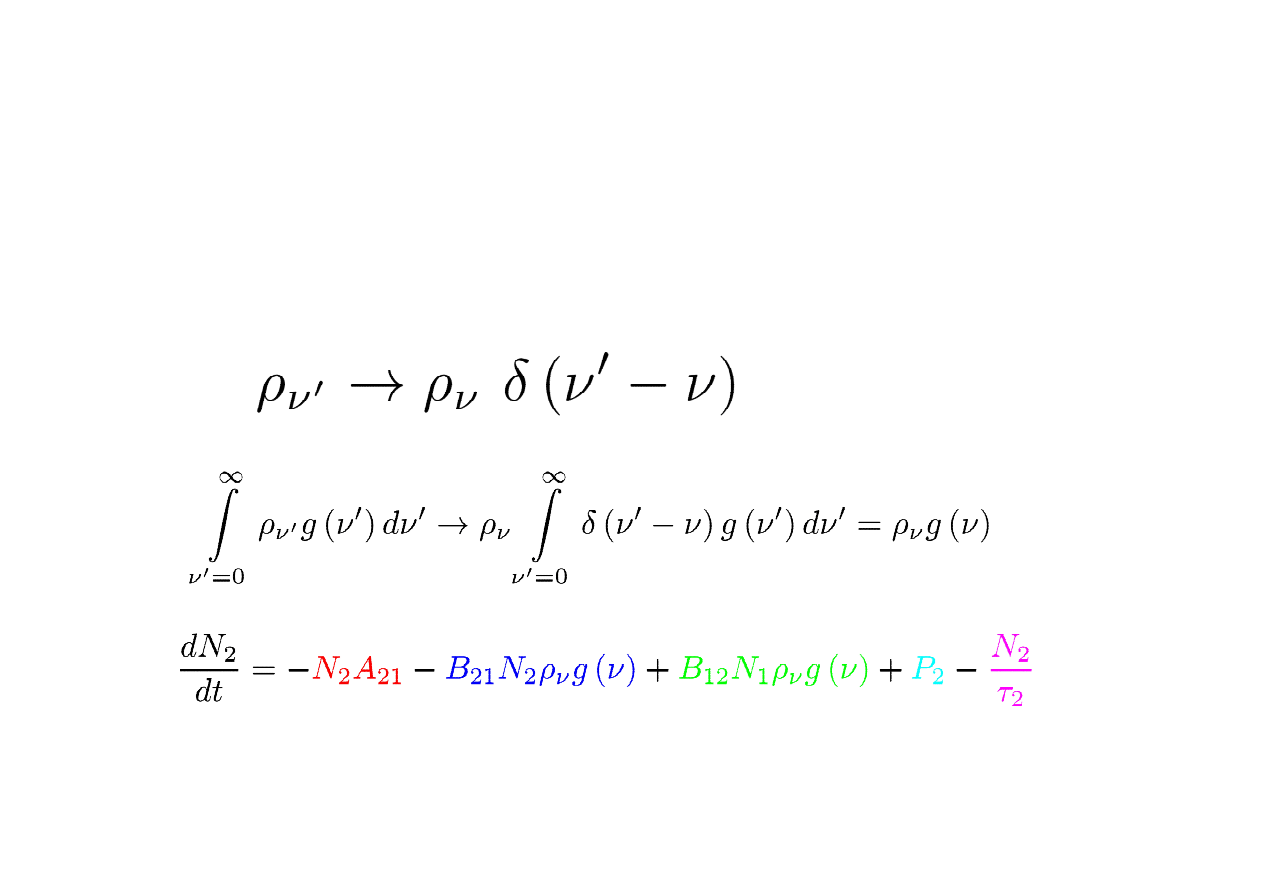
Lasery

39

..cd

•When the spectral bandwidth of the radiation field is small

• compared to the broadened transition:

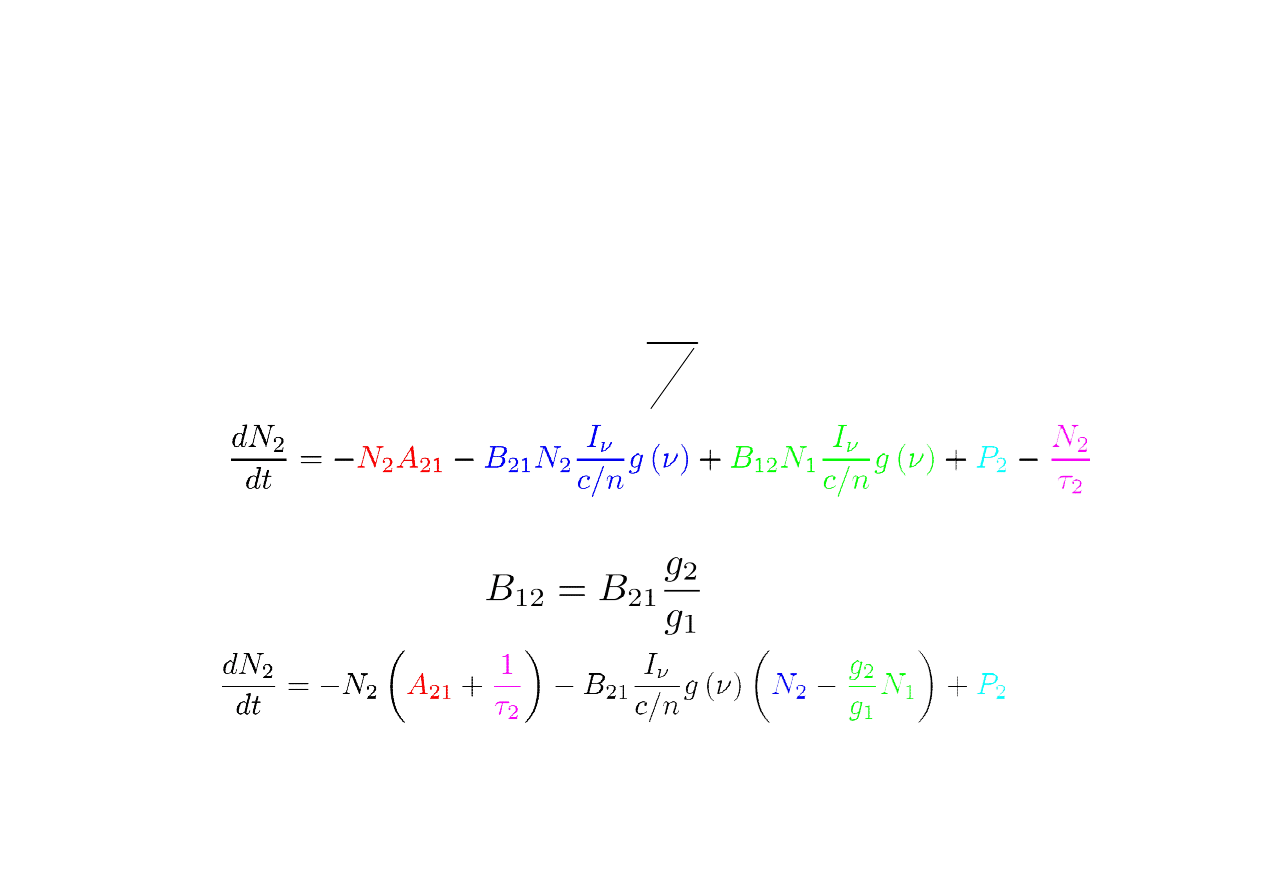
Lasery

40

Gain and Amplification

•

Wprowadzimy teraz pojęcie intensywności fotonowej

dla częstotliwości v: I

v

[W/cm

2

]:

• Now we group terms:

1

I

c

n









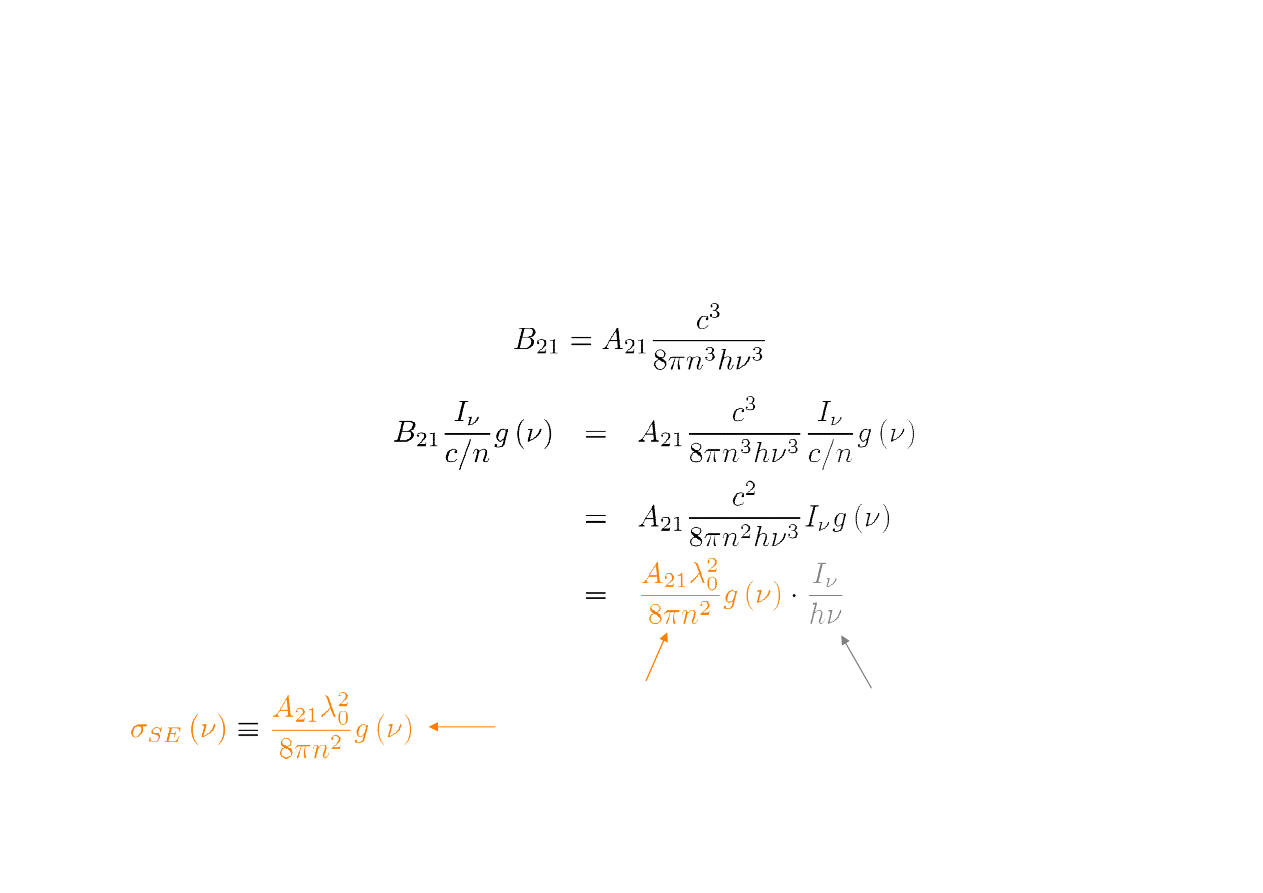
Lasery

41

Gain and Amplification

Stimulated Emission

Cross-Section

# of Photons Crossing a

unit Area per unit Time

• Lets try to regain the link to the physics in the “stimulated processes” term (2):

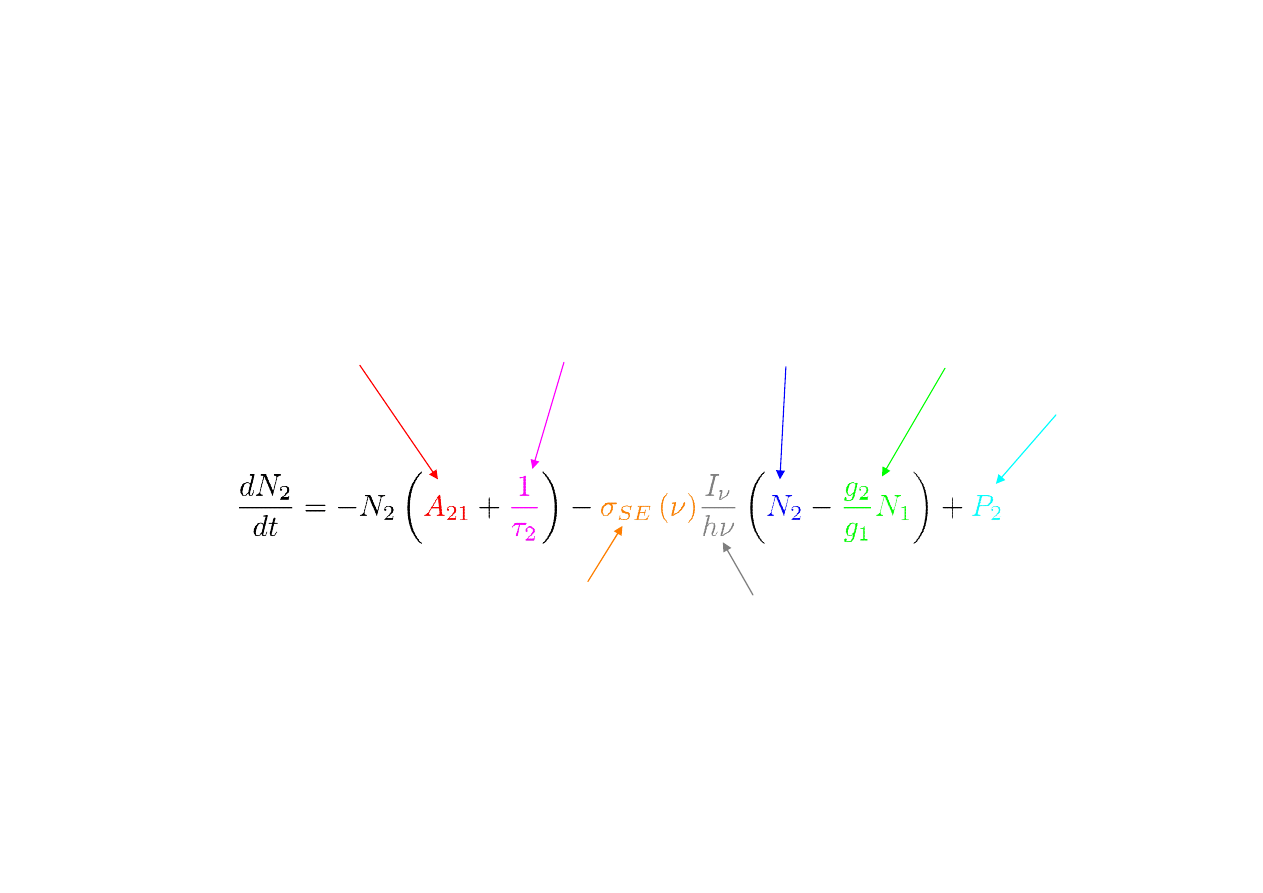
Lasery

42

Gain and Amplification

Spontaneous

Emission

Stimulated

Emission

Absorption

Pumping

Non-Radiative

Relaxation

Stimulated

Emission

Cross-Section

# of Photons Crossing a

unit Area per unit Time

•The stimulated emission cross-section is purely a property of the material

•Put it all together! THIS IS IMPORTANT!!!

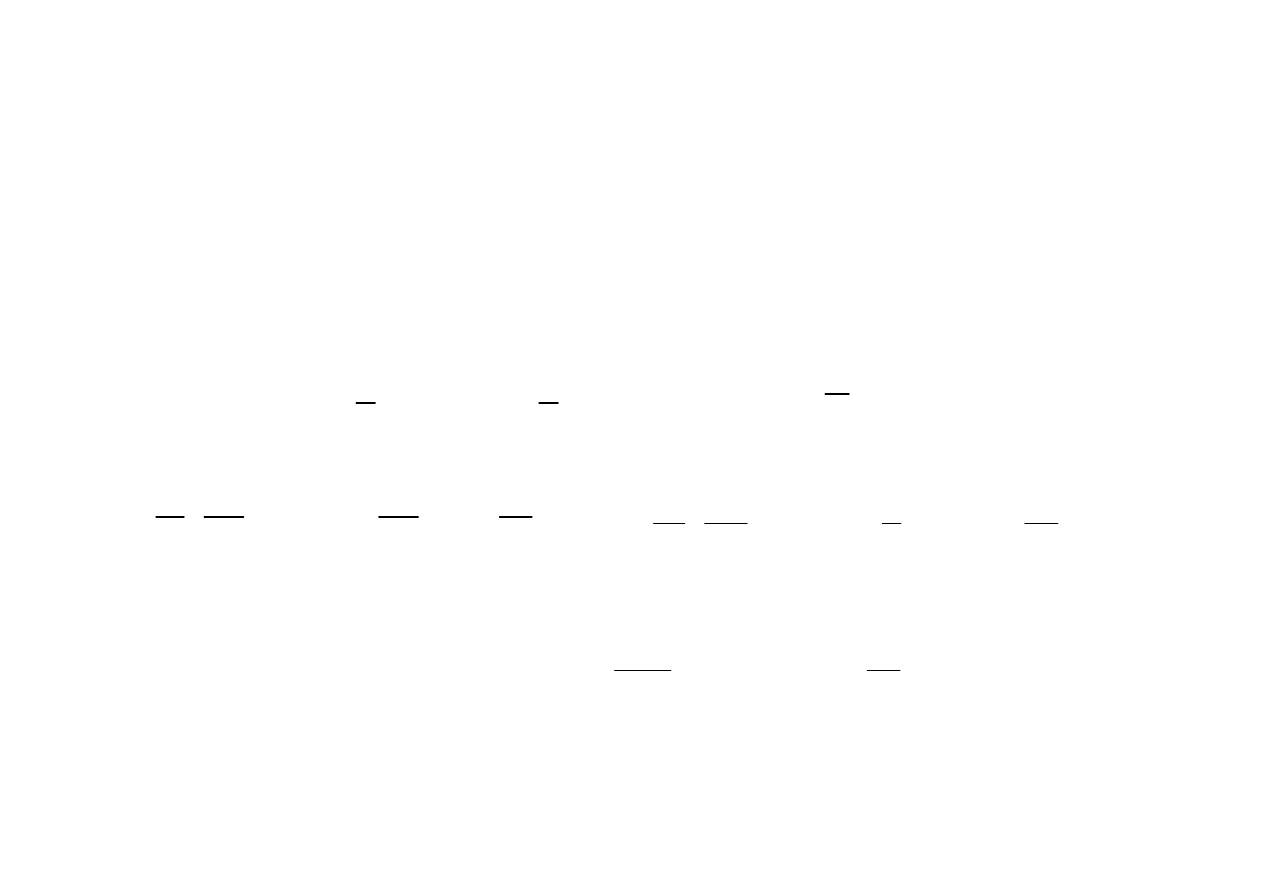
Lasery

43

Gain and Amplification

Consider the radiation field as it travels through a gain medium:

- keep in mind that this is at a single frequency,
- neglect spontaneous emission,
- propagation in the z-direction.

c

c

z

t

dz

dt

n

n







,

,

t

z

c

I

I

n







 

,

,

2

2

1

1

t

t

SE

I

I

g

d

N

N

dt

h

h

g









































 

,

2

,

2

1

1

z

SE

z

I

g

d

c

I

N

N

dz

h

n

g







































 

 

,

2

2

1

,

,

1

z

SE

z

z

dI

g

N

N

I

I

dz

g











 



















Lasery

44

Gain and Amplification

Gain Coefficient

[cm

-1

]

•The result looks suspiciously like Beer’s Law …

 

 

2

2

1

1

SE

g

N

N

g

 





















 

,

,

0

exp

z

z

I

I

z

z























Jeżeli:







, to wzmocnienie







, to absorpcja







, to transparency

Lasery

45

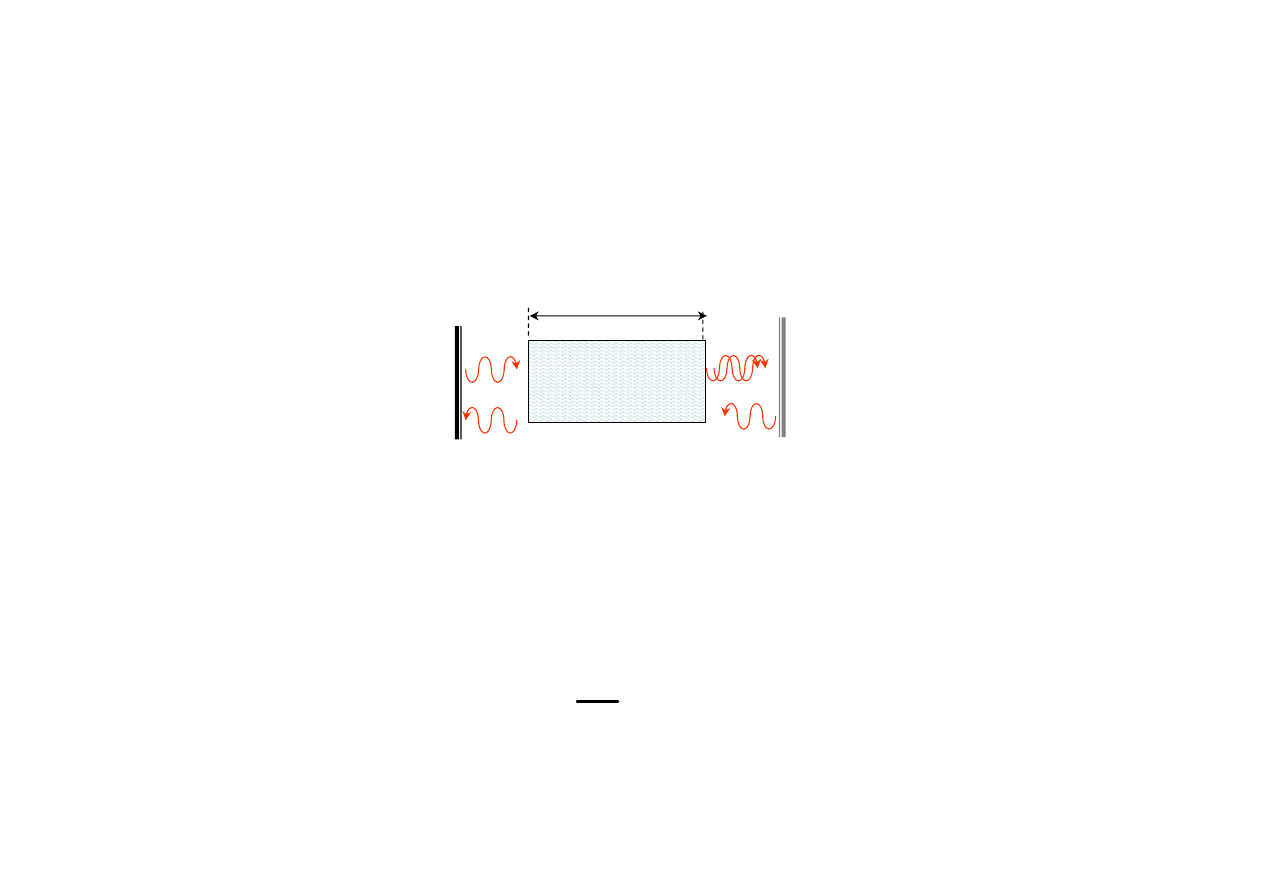
Wzmocnienie progowe

•

Jakie jest wzmocnienie progowe?

Wzmocnienie progowe jest wzmocnieniem, które zupełnie kompensuje

straty pojawiające się przy jednokrotnym przejściu przez wnękę:

Ośrodek

wzmacniający

R

1

R

2

współczynnik odbicia

1

2

1

1

ln

2

th

l

R R





















Lasery

46

Wzmocnienie progowe

Warunek progowy:

• Obserwując intensywność strumienia fotonów po jednokrotnym przejściu

przez wnękę generującą z ośrodkiem wzmacniającym:

wzmocnienie



R

1

R

2

l

I

0

e



L

I

0

R

2

e



L

I

0

I

0

R

2

e



L

0

0

2

1

e

R e

R

th

th

l

l

I

I













2

0

0

1

2

R R

e

th

l

I

I









czyli

stąd





1

2

1

ln R R

2

th

l



 

Lasery

47

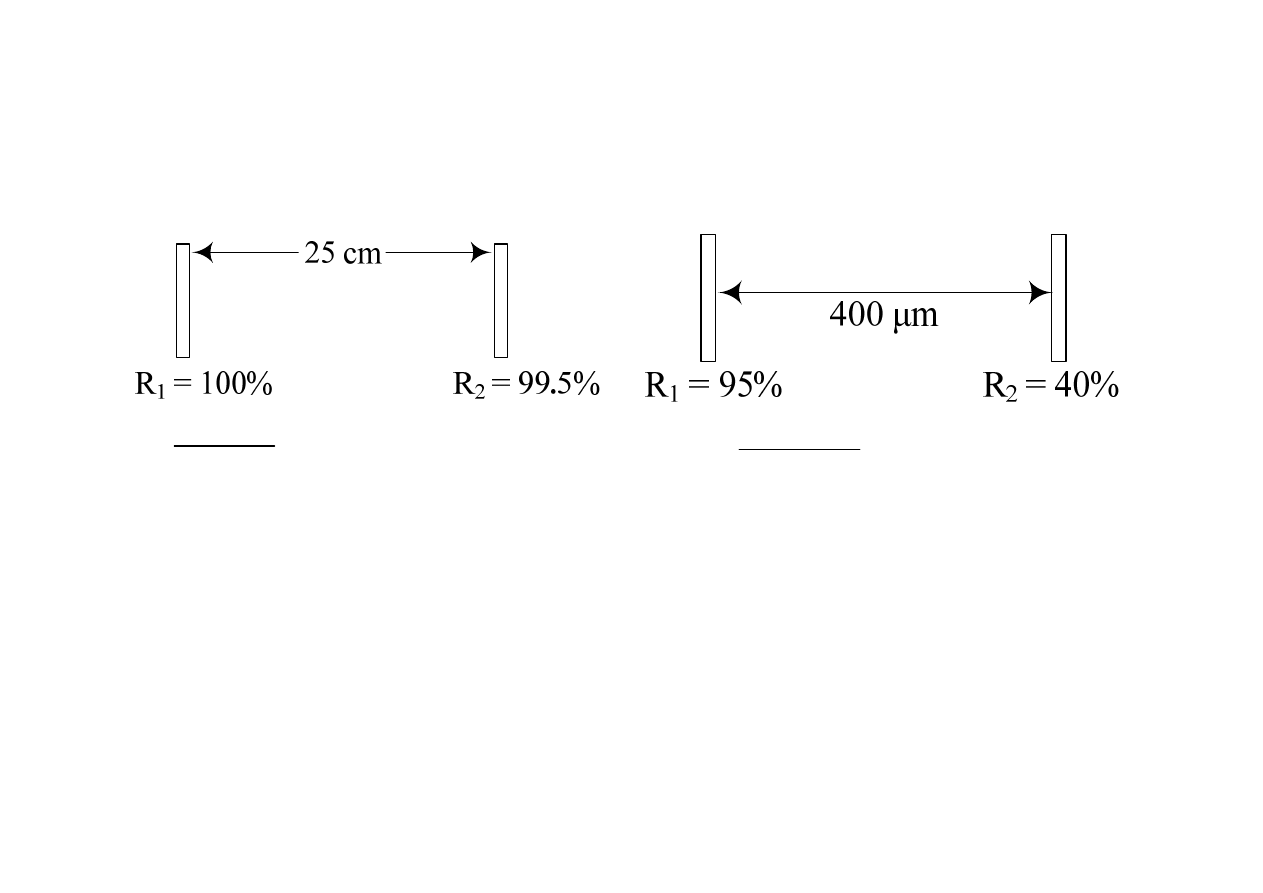
Przykłady:





5

1

1

ln 0,995

1,003.10 cm

2 25 cm

th













This is an exceedingly low threshold gain.

In general, mirror and other losses are much larger,
and the corresponding threshold gain is much

higher

.

1

0, 01% cm

th







czyli

He-Ne laser

Dioda laserowa





1

1

ln 0,95 0, 4

12,1 cm

2 400 m

th















1

1201% cm

th







czyli

This case represents the other end of the spectrum.
Threshold for diode lasers is 4 orders

of magnitude greater than the He-Ne case.

Lasery

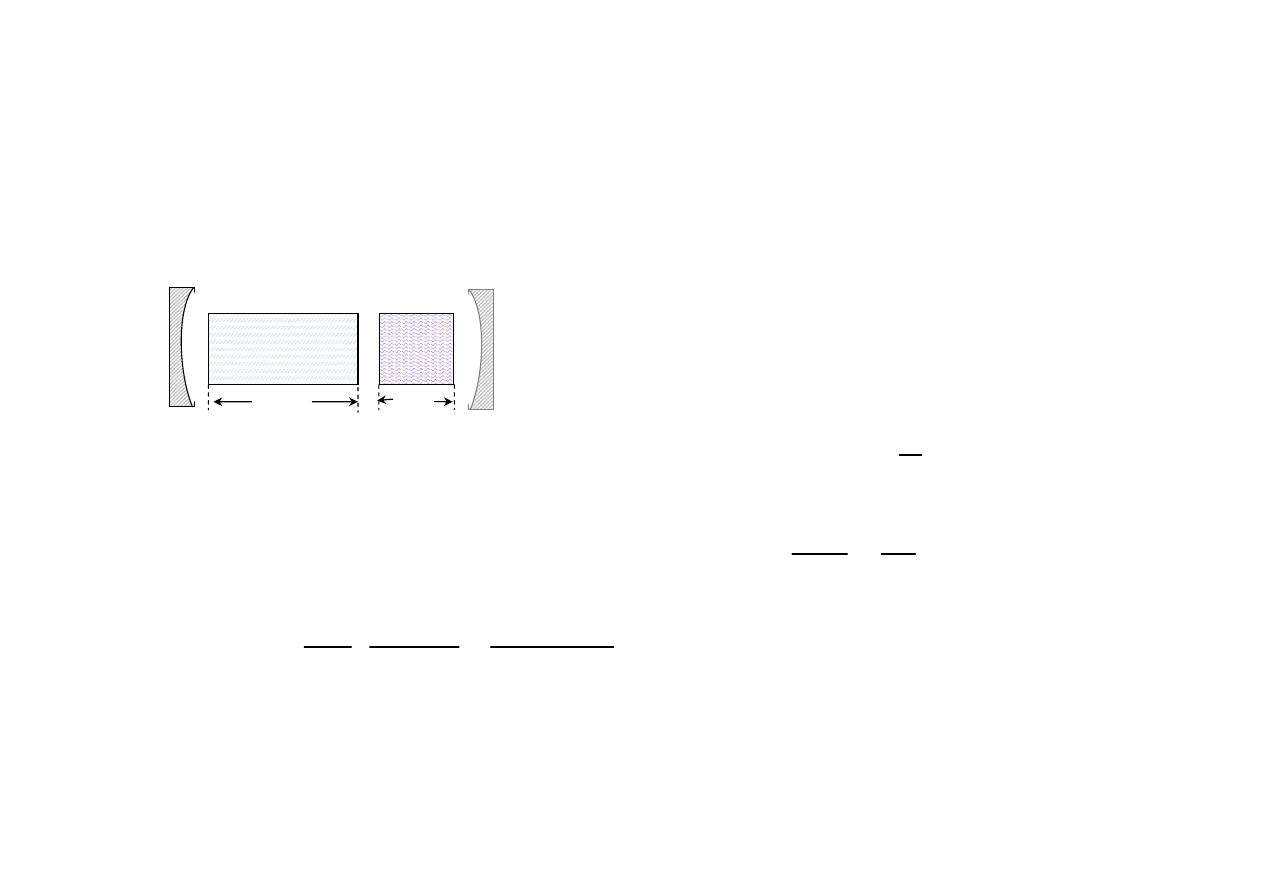
48

Przykłady wzmocnienia progowego

( Laser z komórką absorpcyjną Q-switcher)

0

0

2

1

e

e

R

e

e

R

th

th

l

l

l

l

I

I



























2

2

1

2

1

R R e

th

l

l











czyli





1

2

1

ln R R

2

th

l

l









 





1

2

1

ln R R

2

th

l

l

l















1

0, 3 4 cm

1

ln 0, 99 0, 4

0, 0146 cm

cm 40 cm

2 40 cm

th

















1

1, 46% cm

th







Rdzeń lasera
- wzmacniacz

Q-

switch

Wsp. strat



=3% cm

-1

R

1

=0,99

R

2

=0,4

40 cm

4 cm

Lasery

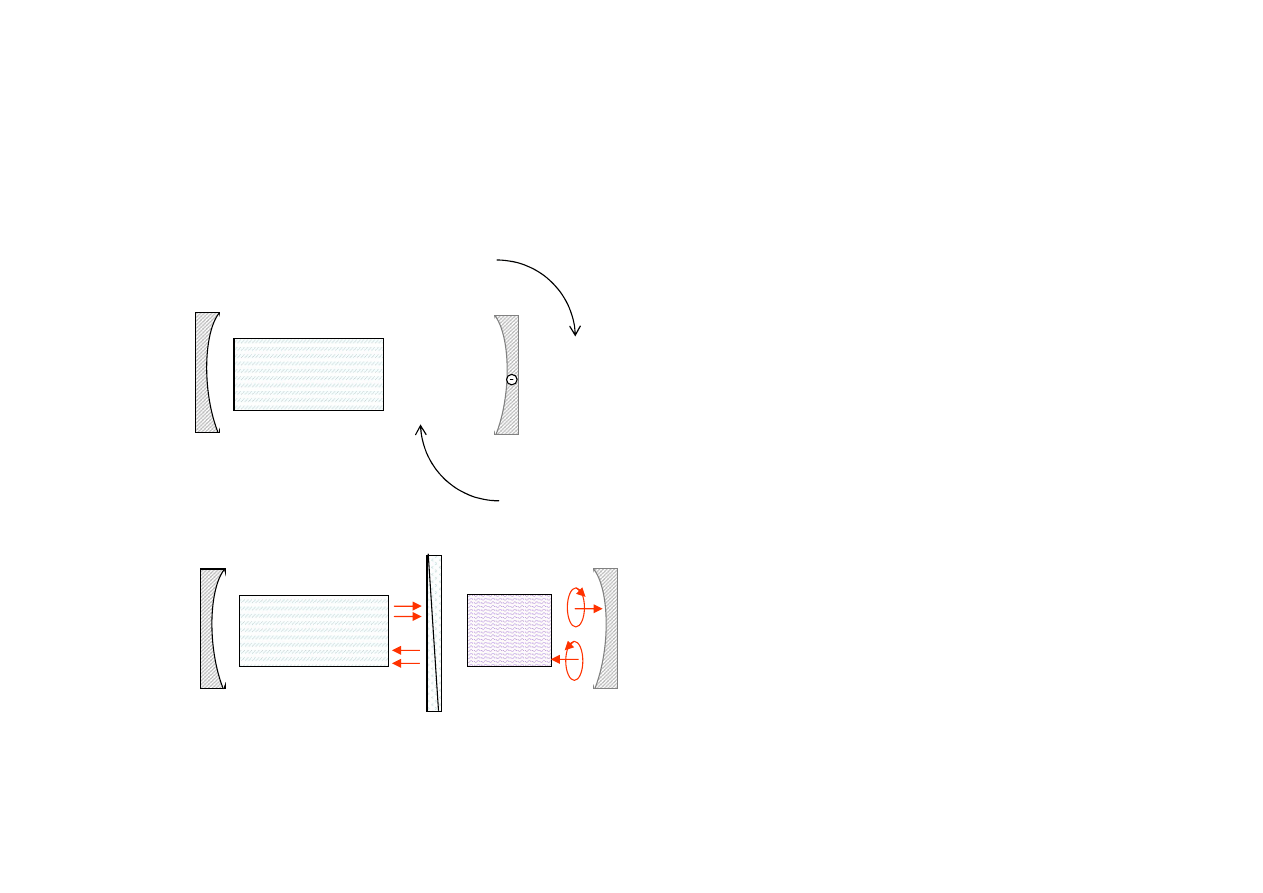
49

Metody switchingu

Rdzeń lasera
- wzmacniacz

Rdzeń lasera
- wzmacniacz

Komórka

Kerra

Obracające się

zwierciadło

Polaryzator

Ortogonalna

polaryzacja

liniowa

Polaryzacja

kołowa

Lasery

50

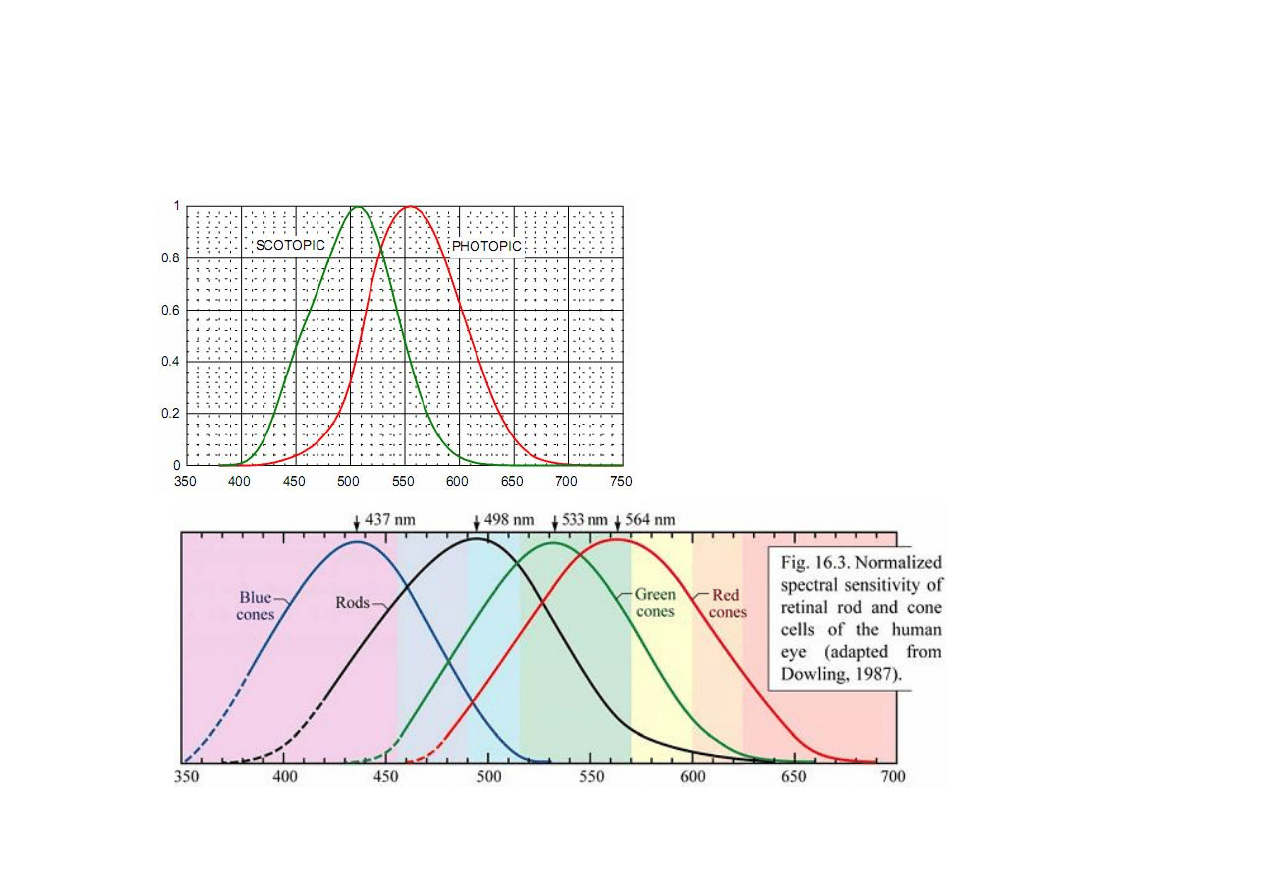
Ach, te oczy

Widzenie fototopowe (dzienne):

Próg widzenia >3 cd/m

2

 





2

321,9

0,503

0, 992 e

V













Widzenie skotopowe (nocne):

 





2

285,4

0,559

1, 019 e

V











- aktywne przy luminacji
mniejszej niż 0,01 cd/m

2

Lasery

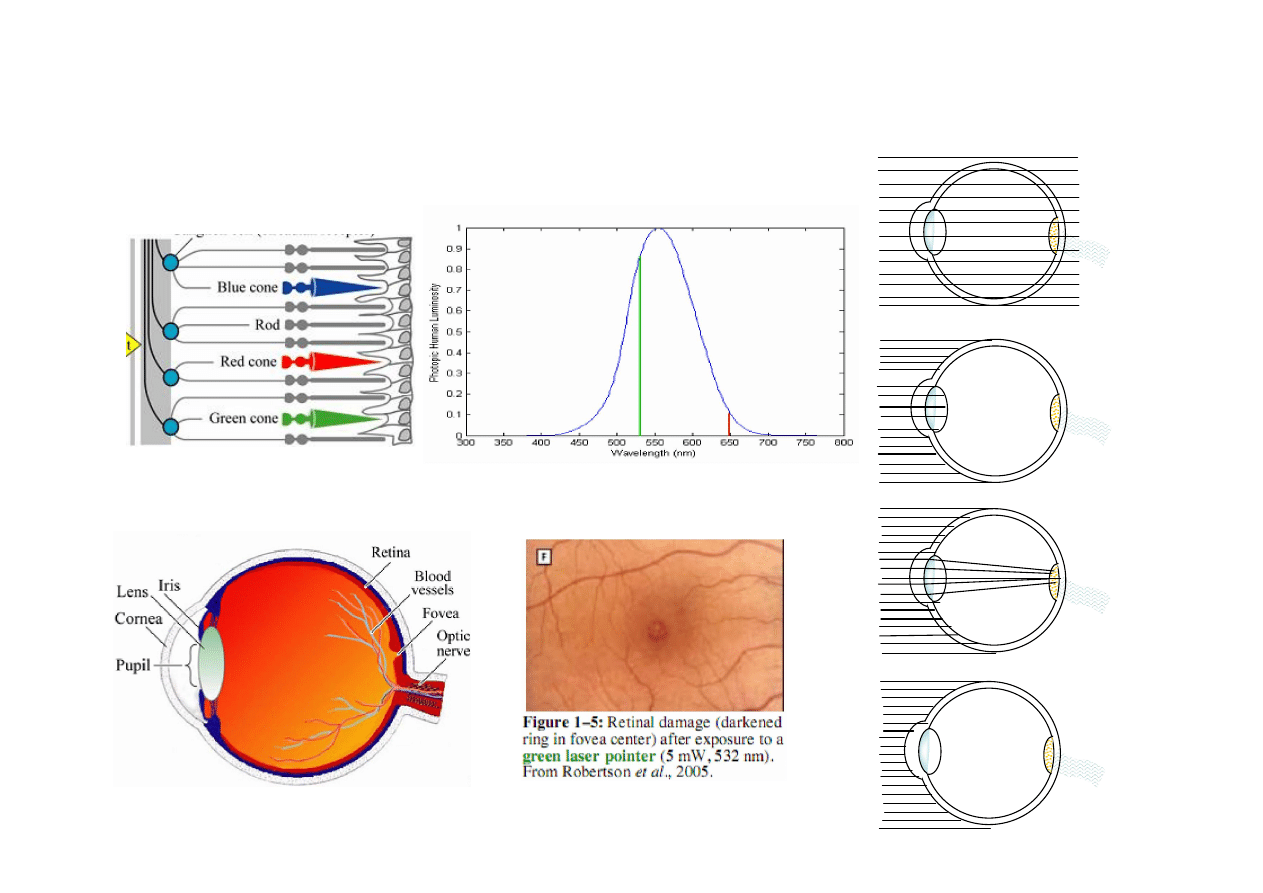
51

BHP z laserem

Diagram of human visual response showing

the wavelength of the GLP line at 532 nm

Never allow a laser beam to enter the eye!

Mikrofale, x, gamma

Ultrafiolet UVA

Widzialne,

IRA, UVA

UVB i IRB

Ligh

t pe

ne

tra

tion in

th

e hum

an

ey

e

(ad

ap

ted

from

Sline

y

and

Wolba

rsht

19

80)

.

Lasery

52

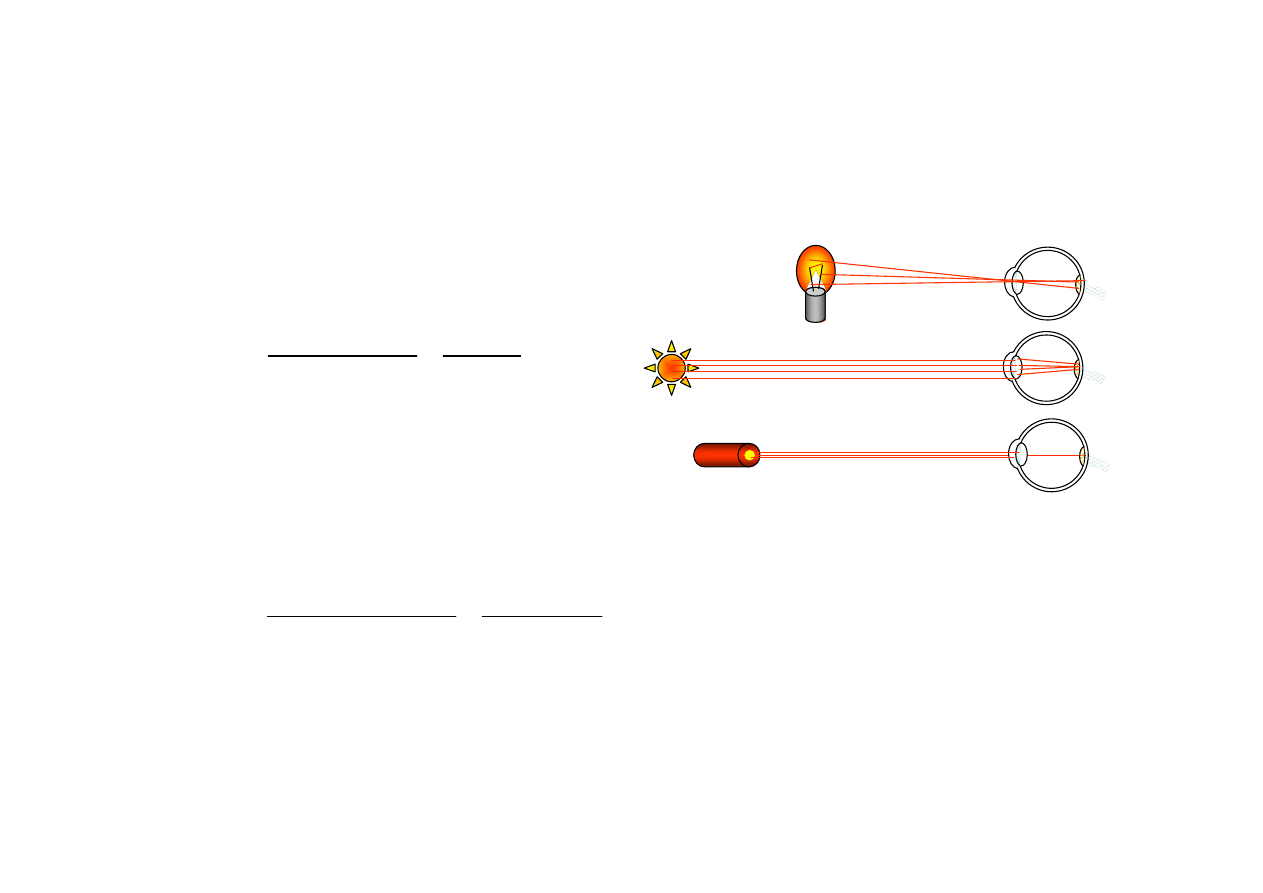
Oświetlenie siatkówki oka

przez żarówkę, Słońce i laser

Przypadek 1: Patrząc na żarówkę z odległości 1m,
W nasze oko wpada strumień świetlny, który rozprzestrzenia się

w sferę o powierzchni = 4π (1 m)

2

= 12,6 m

2

,

zatem intensywność światła wynosi

Światło wchodzi do oka przez źrenicę (ok. =2 mm).
Powierzchnia źrenicy = (1mm)

2

=3,1.10

-6

m

2

Stąd całkowita moc światła, jaka wchodzi do oka
Jest równa pow. Intensywność na rogówce x pow. źrenicy

= 1,5 × 10

–5

W (15 µW).

Soczewki oka skupiają obraz żarówki o średnicy około 300 m na siatkówce.
Zatem intensywność na niej wynosi

2

na rogówce

2

żarówki

60W

4, 5 W/m

. kuli

12, 6m

MOC

Pow













5

2

na siatkówce

2

1,5.10 W

212 W/m

. plamki żóltej

150μm

MOC

Pow













Patrząc w Słońce, którego strumień świetlny wynosi około 1000 W/m

2

, ta sama rogówka zbiera moc 3,1 mW,

a na siatkówkę pada strumień180 kW/m

2

.

Narażając się na strumień lasera o typowej średnicy 2 mm, swoją rogówkę oświetlimy strumieniem 1,6 kW/m

2

,

a siatkówkę

wypalimy

strumieniem o intensywności

64.10

6

W/m

2

.

Słońce - około 150 mln km

Żarówka

Laser

Lasery

53

Symbol ostrzegawczy

przed laserami

klasy 2 i wyższej

1 - Lasery, które są bezpieczne w racjonalnych warunkach pracy

1M - Lasery emitujące promieniowanie w zakresie długości fal do 302,5 nm do 4000 nm,
które są bezpieczne w racjonalnych warunkach pracy, ale mogą być niebezpieczne

podczas patrzenia w wiązkę przez przyrządy optyczne

2 - Lasery emitujące promieniowanie widzialne w przedziale długości fal od 700.

Ochrona oka jest zapewniona w sposób naturalny przez instynktowne reakcje obronne.

2M - Lasery emitujące promieniowanie widzialne w przedziale długości fal od 700.
Ochrona oka jest zapewniona w sposób naturalny przez instynktowne reakcje obronne,
ale mogą być niebezpieczne podczas patrzenia w wiązkę przez przyrządy optyczne.

3R - Lasery emitujące promieniowanie w zakresie długości fal do 302,5 nm do 106 nm,
dla których bezpośrednie patrzenie w wiązkę jest potencjalnie niebezpieczne.

3B - Lasery, które są niebezpieczne podczas bezpośredniej ekspozycji promieniowania.
Patrzenie na odbicia rozproszone są zwykle bezpieczne.

4 - Lasery, które wytwarzają niebezpieczne odbicia rozproszone.

Mogą one powodować uszkodzenie skóry oraz stwarzają zagrożenie pożarem.

Podczas obsługi laserów klasy 4 należy zachować szczególną ostrożność.

Klasy bezpieczeństwa laserów