
Obwody Elektryczne i Magnetyczne
®
1
Obwody elektryczne
Transformata Laplace’a oraz jej wykorzystanie w analizie
stanu nieustalonego metodą operatorową – część I
Prowadzący: dr inż. Tomasz Sikorski
Instytut Podstaw Elektrotechniki i Elektrotechnologii
Wydział Elektryczny
Politechnika Wrocławska
D-1, 205/1
tel: (071) 320 21 60
fax: (071) 320 20 06
email:

Obwody Elektryczne i Magnetyczne
®
2

Obwody Elektryczne i Magnetyczne
1. Transformata Laplace’a
1.1 Definicja
Większość spośród powszechnie stosowanych typów reprezentacji ciągłej ma postać przekształcenia
całkowego, w wyniku którego sygnałowi f(t) zostaje przyporządkowana rzeczywista lub zespolona funkcja
F(s) zmiennej rzeczywistej lub zespolonej s. Jeśli zmienna s jest określona w zbiorze
Γ
, a sygnał f(t) jest
określony w pewnym zbiorze
Ω
, to przekształcenie całkowe stanowiące ciągłą reprezentację sygnału x(t)
można zapisać w postaci ogólnej:
( )
( ) ( )
( )
( ) ( )
F s
f t
t s dt t
f t
F s
s t ds s
,
,
,
,
Ω
Γ
ϕ
Ω
ψ
Γ
=
∈
=
∈
∫
∫
Funkcja
( )
s t
,
ψ
nosi nazwę jądra przekształcenia całkowego. Funkcja
( )
t s
,
ϕ
nazywana jest jądrem
sprzężonym. Operacja całkowania przyporządkowuje sygnałowi f(t) , w sposób zależny od jądra
przekształcenia, funkcję F(s) zwaną transformatą sygnału. Funkcja F(s) jest ciągłą reprezentacją sygnału,
a znając jej postać można wyznaczyć ponownie sygnał f(t), jako transformatę odwrotną. Para funkcji f(t) –
F(s) stanowi parę transformat. W zależności od postaci jawnej jądra przekształcenia całkowego rozróżnia
się różne typy przekształceń i różne typy transformat, przy czym dobór jądra musi spełnić założenie
przekształcenia wzajemnie jednoznacznego.
®
3

Obwody Elektryczne i Magnetyczne
Dla jądra przekształcenia
( )
st
s t
e
,
ψ
=
, oraz jądra sprzężone
( )
st
t s
e
,
ϕ
−
=
otrzymujemy transformację
Laplace’a. Zmienna s należy do zbioru liczb zespolonych i może zawierać część rzeczywistą i urojoną
s
j
δ
ω
= +
.
( )
( )
{
}
( )
st
s
f t
f t e dt
F
∞
−
−∞
=
=
∫
L
W zakresie niniejszego wykładu znajdują się jedynie układy przyczynowe, a więc wszystkie sygnały w
takim obwodzie, zarówno wymuszenia, jak i napięcia i prądy, będziemy traktować jako sygnały
przyczynowe tj.
( )
f t
0
= dla t<0. Zastosowanie przekształcenia dla takiej klasy sygnałów, zostanie
ograniczone w czasie
i może być traktowane jako tzw. przekształcenie jednostronne.
0
t
< < +∞
Ostatecznie definicja jednostronnej (prawostronnej) transformaty Laplace’a przyjmie postać:
( )
( )
{
}
( )
st
0
s
f t
f t e dt
F
∞
−
=
=
∫
L
a transformata odwrotna:
( )
( )
{
}
( )
j
st
j
1
1
f t
F s
F s e ds
2 j
σ ω
σ ω
π
+
−
−
=
=
∫
L
Funkcję zespoloną
( )
s
F
argumentu zespolonego 's' nazywamy transformatą lub obrazem funkcji
( )
f t
,
natomiast funkcję
( )
f t nazywa się oryginałem przekształcenia albo przeciwobrazem.
®
4
Obwody Elektryczne i Magnetyczne
Prawostronna Transformata Laplace’a istnieje, jeśli jest zbieżna, co można wyrazić przez warunek
zbieżności w sensie modułu:
( )
( )
( )
( )
st
j
t
t
t
0
0
0
0
f t e
dt
f t e
dt
f t e
dt
f t e dt
(
)
σ ω
σ
σ
∞
∞
∞
∞
−
−
+
−
−
=
=
=
=
∫
∫
∫
∫
1
0
( )
t < 0
f t
0
,
=
∧
2
0
W każdym przedziale domkniętym spełnia tzw. warunki Dirichleta (tzn. dany przedział można
podzielić na skończoną liczbę podprzedziałów, w których funkcja jest monotoniczna
i ograniczona)
3
0
Jest funkcją typu wykładniczego, tzn. istnieją liczby rzeczywiste
i
g
M
0
σ
>
takie, że dla
dowolnego
t
0
>
( )
g
t
f t
M e
σ
≤
Istnienie transformaty Laplace’a można opisać
przez obszar zbieżności tj. zbiór zmiennej
s
j
σ
ω
= +
, dla których
( )
g
s
Re
δ
>
.
®
5
Istnieją funkcje nie będące rzędu
wykładniczego, takie jak np.
3
t
e lub
t
t
, dla
których transformata Laplace’a nie istnieje.
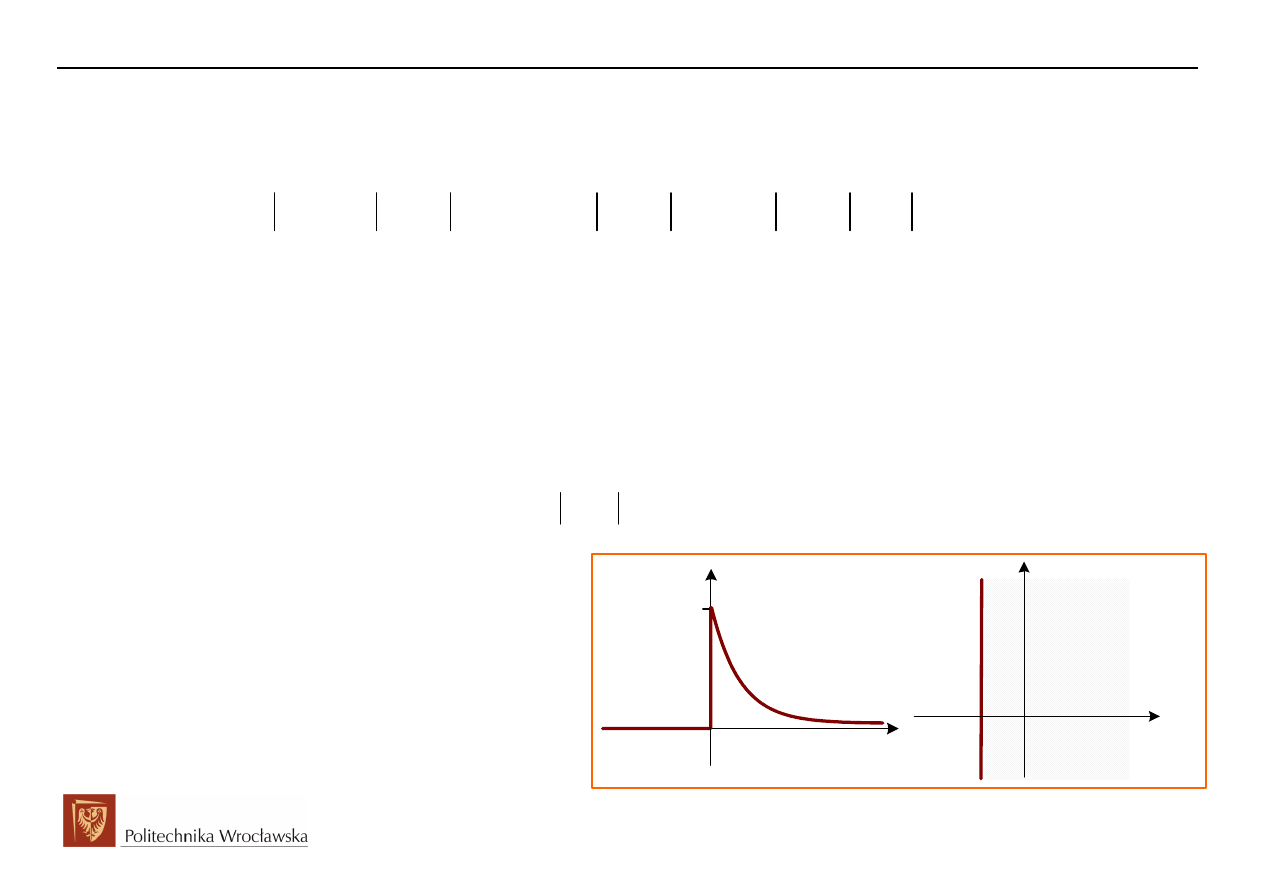
t
0
f
(t)
1
t
e
α
−
Re{s}
α
−

Obwody Elektryczne i Magnetyczne
KOMENTARZ: Pewne zakłopotanie niesie punkt t=0 w sensie precyzyjnego traktowania warunków
początkowych: czy należy traktować go jako t=0+ czy t=0-?. W analizie sygnałów, dolną granicę
całkowania w definicji prawostronnej transformaty Laplace’a przyjęto jako t=0- tak, by objąć transformacją
również specyficzne sygnały jak impuls delty Diraca czy skok jednostkowy w punkcie t=0. W innych
przypadkach, jak np. wykorzystanie transformacji Laplace’a do rozwiązywania matematycznych równań
różniczkowych, dolną granicę całkowania ustala się na t-0+.
Przykłady wyznaczania transformaty Laplace’a z definicji:
a) transformata skoku jednostkowego:
( )
{ }
st
st
0
0
s 0
1
1
t
1 e dt
e
s
s
Re
1
∞
∞
−
−
−
>
=
⋅
=
=
−
∫
L
Obszar zbieżności: Półpłaszczyzna
s
0
Re
>
b) transformata delty Diraca:
( )
{
}
( )
( )
st
0
0
t
t e dt
t
1dt
1
∞
∞
−
−
−
=
=
⋅
=
∫
∫
L
δ
δ
δ
Obszar zbieżności: Cała płaszczyzna zespolona
PYTANIE: Po co w ogóle wprowadzamy transformacje, takie jak transformacja Laplace’a, jaki jest sens
poszukiwania reprezentacji sygnału f(t) w innej dziedzinie niż dziedzina czasu? Czy postać czasowa nie
jest wystarczająca? Czy uzyskane reprezentacje wniosą „jakąś nową jakość” w dyskusji nad charakterem
sygnału f(t)? Czy ułatwią interpretację, analizę badanego sygnału?
ODPOWIEDZI NA TE PYTANIA NALEŻY SZUKAĆ WE WŁAŚCIWOŚCIACH PRZEKSZTAŁCENIA, A
ZWŁASZCZA W RELACJI NA PODSTAWOWE DZIAŁANIA MATEMATYCZNE.
®
6
Obwody Elektryczne i Magnetyczne
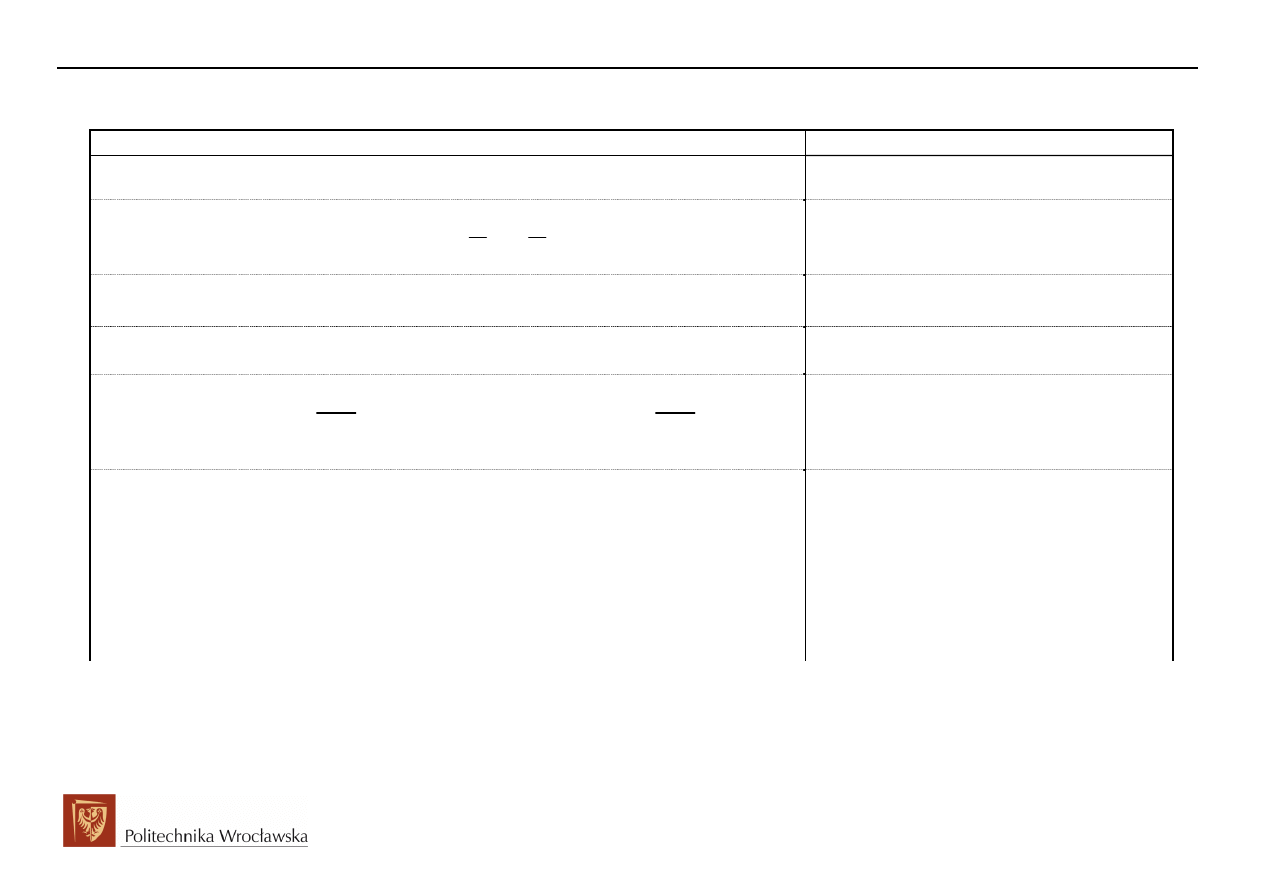
1.2 Właściwości przekształcenia Laplace’a
Właściwość Określenie
( )
( )
{
}
( )
( )
1
2
1
2
af t
bf
t
aF s
bF s
±
=
±
L
Liniowość
( )
{
}
1
s
f at
a
a
F
⎛ ⎞
=
⎜ ⎟
⎝ ⎠
L
Zmiana skali
(
)
{
}
( )
t
0
s
0
f t
t
s e
F
−
−
=
L
Przesunięcie w dziedzinie czasu
( )
{
}
(
)
at
e f t
s
a
F
=
−
L
Przesunięcie w dziedzinie zespolonej
( )
( )
{
}
( )
{
}
n
n
n
n
d
1 t f t
s
ds
F
−
=
L
,
( )
{
}
( )
( )
{
}
n
n
n
n
d
t f t
1
s
ds
F
= −
L
Pochodna transformaty
( )
( )
{
}
( )
(
)
( )
k n
n
k 1
n
n k
k 1
f
t
s
s
s
f
0
F
=
−
−
−
=
=
−
∑
L
Stąd:
( )
{
}
( )
( )
f
t
s
s
f 0
'
F
−
=
−
L
( )
{
}
( )
( ) ( )
2
f
t
s
s
sf 0
f
0
''
'
F
−
−
=
−
−
L
Transformata pochodnej
®
7
Obwody Elektryczne i Magnetyczne
( )
( )
n
1
1
2
1
2
n
n
n
0 0
0
t
1
f
d d
d
d
s
s
F
τ
τ
τ
τ τ
τ
τ
−
− −
−
⎧
⎫
⎪
⎪ =
⎨
⎬
⎪
⎪
⎩
⎭
∫ ∫ ∫
…
…
L
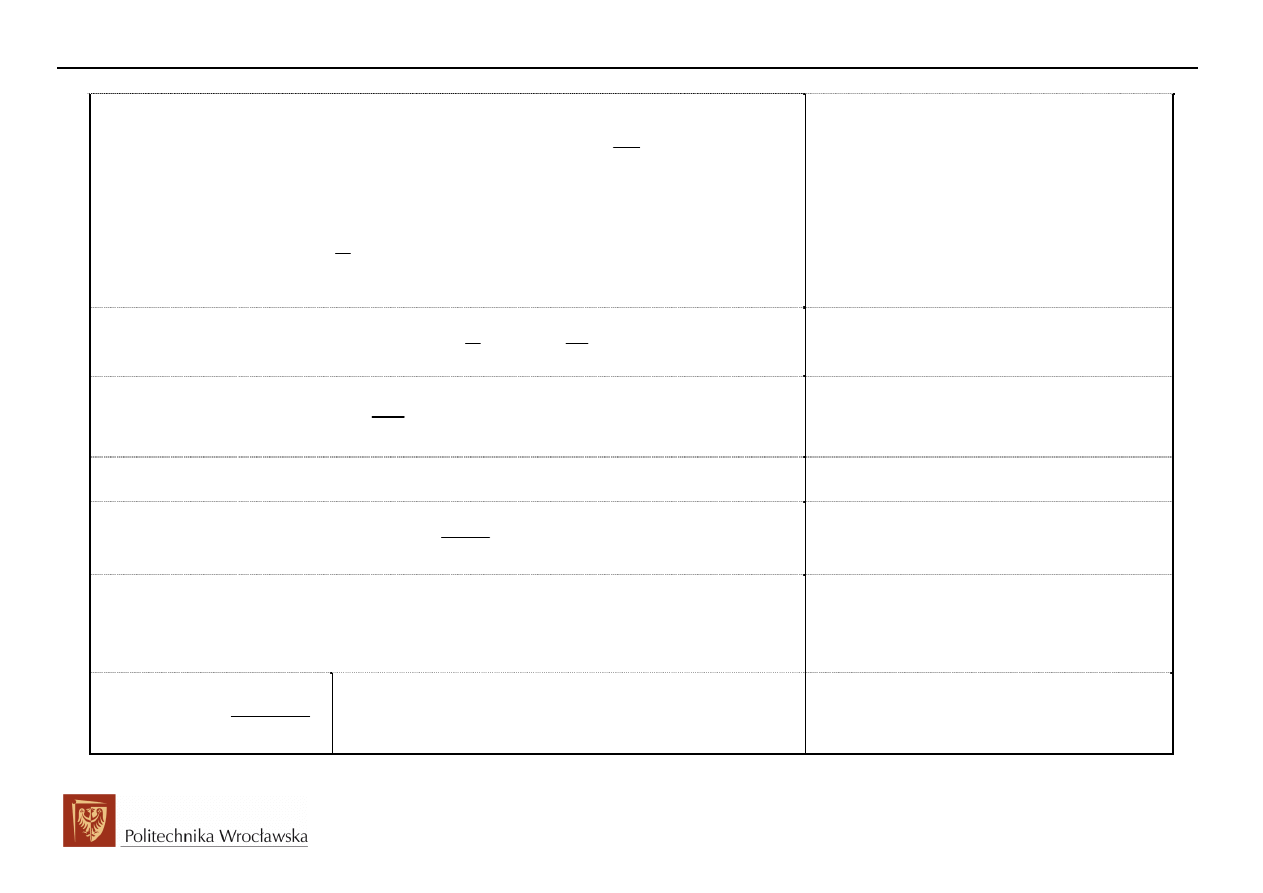
Stąd:
( )
( )
0
t
1
f
d
s
s
F
τ τ
−
⎧
⎫
⎪
⎪ =
⎨
⎬
⎪
⎪
⎩
⎭
∫
L
Transformata całki oznaczonej
( )
{
}
( )
1
C
f t dt
s
s
s
F
=
+
∫
L
Transformata całki nieoznaczonej
( )
{ }
( )
f t
t
s
d
F
λ λ
∞
=
∫
L
Całkowanie w dziedzinie zespolonej
( ) ( )
{
}
( ) ( )
f t
g t
s
s
F
G
∗
=
⋅
L
Transformata splotu
( ) ( )
{
}
( ) ( )
1
f t g t
s
s
2 j
F
G
π
=
∗
L
Splot zespolony
( )
( )
( )
t
0
s
s
s
f t
f 0
lim F
lim
→ ∞
→ +
=
=
+
;
( )
( )
0
t
s
s
s
f t
lim F
lim
→
→ ∞
=
Twierdzenia o wartości początkowej
i końcowej
( )
{ }
( )
T
sT
s
f t
1 e
F
−
=
−
L
gdzie:
( )
( )
T
T
0
st
s
f t e dt
F
−
=
∫
Transformata funkcji okresowej
®
8
Obwody Elektryczne i Magnetyczne
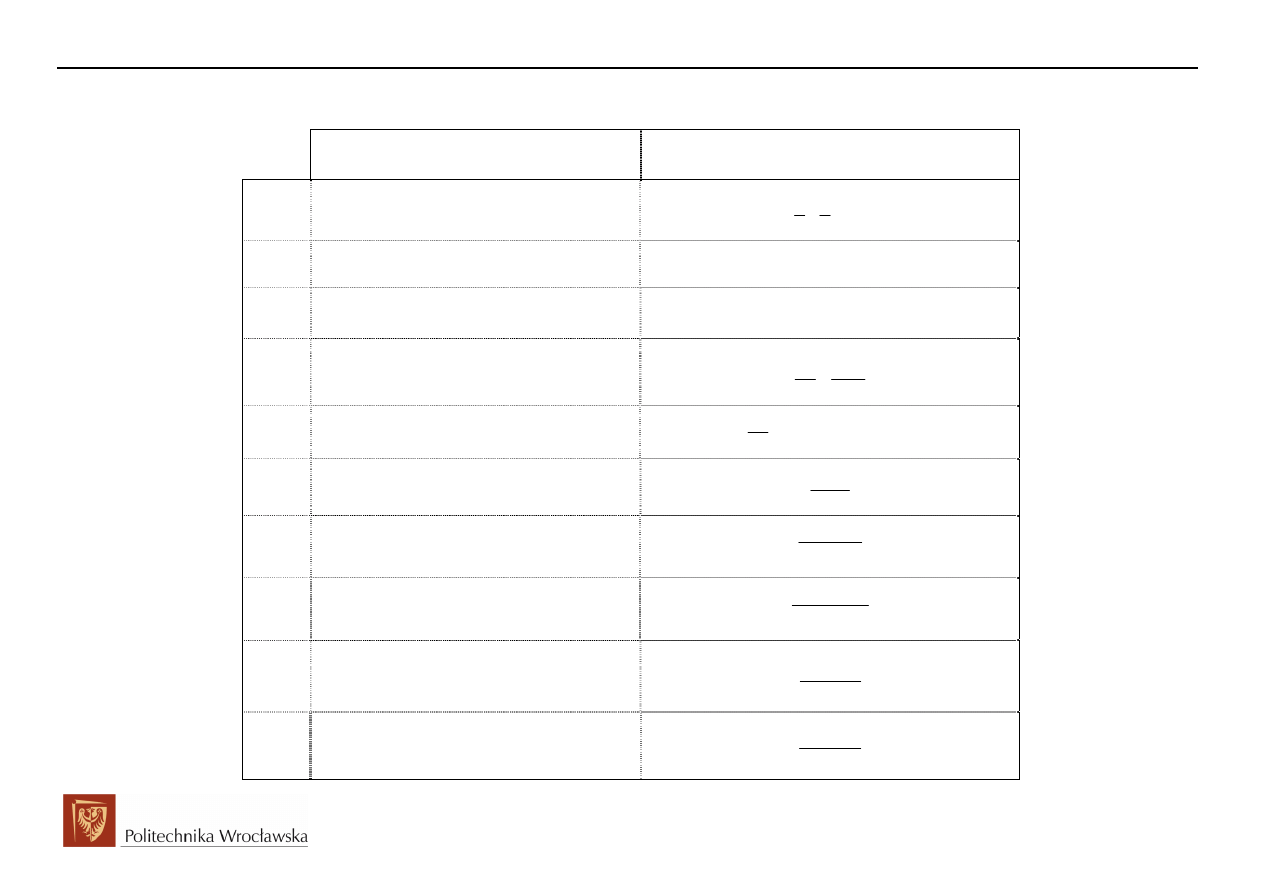
1.3 Wybrane transformaty
( )
f t
( )
( )
{ }
=
L
F s
f t
1
( )
1 t
,
(
)
1
0
t
t
−
1
s
,
0
st
1
e
s
−
2
( ) ( )
( )
( )
, ,
n
t
t
t
′
δ
δ
δ
n
1, s, s
3
(
)
0
t
t
−
δ
0
st
e
−
4
( )
1
t
t
,
( )
1
n
t
t
2
1
s
,
!
n 1
n
s
+
5
( ) (
)
1
1
0
t
t
t
t
⎡
⎤
−
−
⎣
⎦
(
)
0
0
st
2
1
1
1 t s e
s
−
⎡
⎤
− +
⎣
⎦
6
( )
1
at
e
t
1
s
a
−
7
( )
1
at
te
t
(
)
2
1
s
a
−
8
( )
1
n at
t e
t
(
)
!
n 1
n
s
a
+
−
9
( ) ( )
sin
1
0
t
t
ω
⎡
⎤
⎣
⎦
0
2
2
0
s
ω
ω
+
10
( ) ( )
cos
1
0
t
t
ω
⎡
⎤
⎣
⎦
2
2
0
s
s
ω
+
®
9
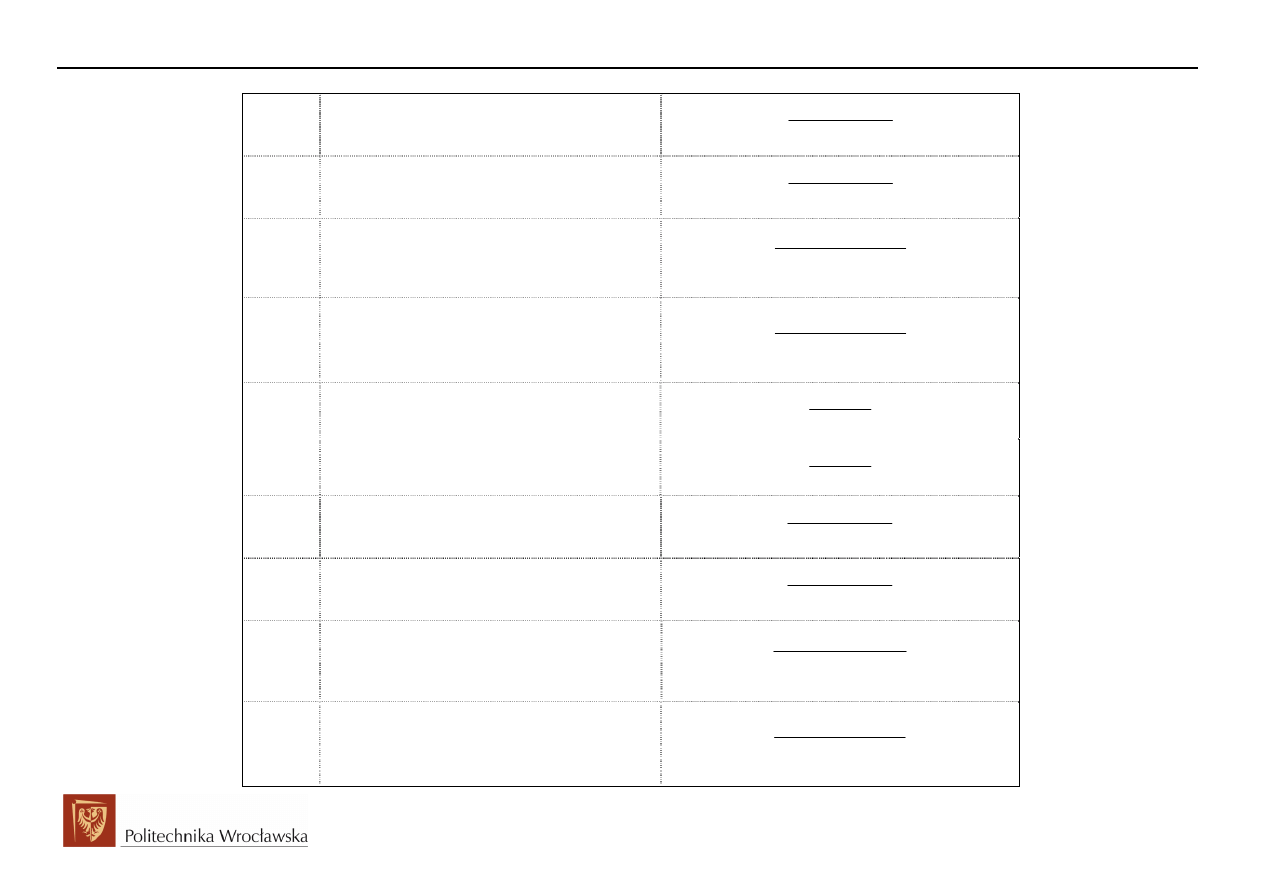
Obwody Elektryczne i Magnetyczne
11
( ) ( )
sin
1
0
at
e
t
t
ω
⎡
⎤
⎣
⎦
(
)
0
2
2
0
s
a
ω
ω
−
+
12
( ) ( )
cos
1
0
at
e
t
t
ω
⎡
⎤
⎣
⎦
(
)
2
2
0
s
a
s
a
ω
−
−
+
13
( ) ( )
sin
1
0
at
te
t
t
ω
⎡
⎤
⎣
⎦
(
)
(
)
0
2
2
2
0
2 s
a
s
a
ω
ω
−
⎡
⎤
−
+
⎣
⎦
14
( ) ( )
cos
1
0
at
te
t
t
ω
⎡
⎤
⎣
⎦
(
)
(
)
2
2
0
2
2
2
0
s
a
s
a
ω
ω
−
−
⎡
⎤
−
+
⎣
⎦
15
( ) ( )
sh
1
t
t
β
⎡
⎤
⎣
⎦
2
2
s
β
β
−
16
( ) ( )
ch
1
t
t
β
⎡
⎤
⎣
⎦
2
2
s
s
β
−
17
( ) ( )
sh
1
at
e
t
t
β
⎡
⎤
⎣
⎦
(
)
2
2
s
a
β
β
−
−
18
( ) ( )
ch
1
at
e
t
t
β
⎡
⎤
⎣
⎦
(
)
2
2
s
a
s
a
β
−
−
−
19
( ) ( )
sh
1
at
te
t
t
β
⎡
⎤
⎣
⎦
(
)
(
)
2
2
2
2 s
a
s
a
β
β
−
⎡
⎤
−
−
⎣
⎦
20
( ) ( )
ch
1
at
te
t
t
β
⎡
⎤
⎣
⎦
(
)
(
)
2
2
2
2
2
s
a
s
a
β
β
−
+
⎡
⎤
−
−
⎣
⎦
®
10

Obwody Elektryczne i Magnetyczne
Przedstawione w powyższej tabeli funkcje i ich transformaty reprezentują częste przypadki występujące w
elektrotechnice.
Możemy też zauważyć, że niektóre z podanych transformat można wyznaczyć korzystając z właściwości
przekształcenia Laplace’a. Znając transformatę funkcji 1(t) możemy wyznaczyć szereg transformat takich
funkcji jak:
( )
{
}
( )
{ }
at
s a
1
e
t
t
s
a
1
1
−
=
=
−
L
L
- wykorzystana właściwość: przesunięcie w dziedzinie zespolonej,
( )
{
}
( )
{ }
2
d
d 1
1
t
t
t
ds
ds s
s
1
1
⎡ ⎤
⎡
⎤
= −
= −
=
⎣
⎦
⎢ ⎥
⎣ ⎦
L
L
- wykorzystana właściwość: pochodna transformaty
Przez połączenie obu właściwości możemy wyznaczyć
( )
{
}
( )
{
}
(
)
at
2
s a
1
e t
t
t
t
s
a
1
1
−
=
=
−
L
L
KOMENTARZ: Warto też zwrócić uwagę na łatwość reprezentacji w dziedzinie Laplace’a funkcji
wykładniczych i ich modyfikacji. Przypomnijmy, że przecież takie funkcje stanowiły składowe
przewidywanej postaci rozwiązania ogólnego równania jednorodnego, czyli składowej przejściowej, w
zależności od wyróżnika równania charakterystycznego.
0
Δ
>
( )
( )
{
}
( )
L
p
1
2
y
t
t
t
11
21
p
11
21
p
1
2
A
A
y
t
A e
A e
Y
s
s
s
λ
λ
λ
λ
=
+
⎯⎯⎯⎯
→
=
+
−
−
( )
( )
{
}
( )
(
)
L
p
1
1
y
t
t
t
11
21
p
11
12
p
2
1
1
A
A
y
t
A e
A te
Y
s
s
s
λ
λ
λ
λ
=
+
⎯⎯⎯⎯
→
=
+
−
−
0
Δ
=
®
11
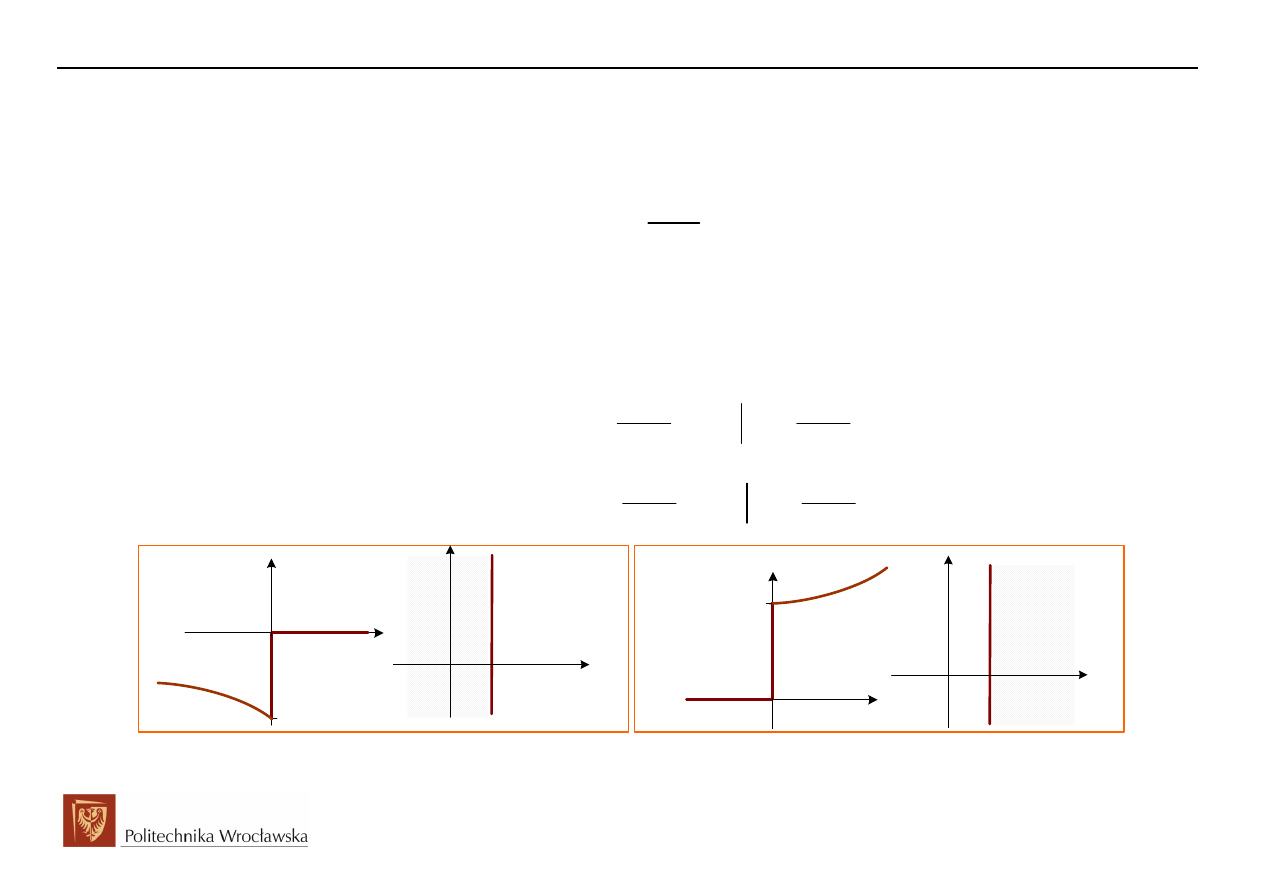
Obwody Elektryczne i Magnetyczne
1.4 Wyznaczanie transformaty odwrotnej Laplace’a
Obecnie zajmiemy się zagadnieniem poszukiwania oryginału funkcji na podstawie jej transformaty
Laplace’a. Definicyjnie musielibyśmy zrealizować operację odwrotnej transformaty Laplace’a :
( )
( )
{
}
( )
j
st
j
1
1
f t
F s
F s e ds
2 j
σ ω
σ ω
π
+
−
−
=
=
∫
L
Wymaga to określenia obszaru zbieżności, ponieważ oryginał funkcji będzie zależał nie tylko od postaci
transformaty, ale również od obszaru zbieżności.
Rozważmy na przykładzie dwie funkcje: prawostronną
( )
( )
at
1
f t
e 1 t
, oraz lewostronną
=
( )
( )
at
2
f
t
e 1
t
−
−
.
=
Ich transformaty Laplace’a wynoszą:
( )
(
)
( )
(
)
,
Re
s a t
at
st
s a t
1
0
0
0
1
1
F s
e e dt
e
dt
e
dla
s
a
s
a
s
a
+∞
+∞
− −
−
− −
+∞
−
=
=
=
=
>
−
−
∫
∫
( )
(
)
( )
(
)
,
Re
0
0
s a t
at
st
s a t
2
0
1
1
F s
e e dt
e
dt
e
dla
s
a
s
a
s
a
− −
−
− −
+∞
−∞
−
= −
=
=
=
<
−
−
∫
∫
t
0
f
(t)
1
( )
at
e 1 t
a
1
Re{s}
t
0
f
(t)
-1
( )
at
e 1
t
−
−
a
2
Re{s}
Transformaty Laplace’a obydwu funkcji są jednakowe, jednakże różne są ich obszary zbieżności i różne są
ich oryginały.
®
12
Obwody Elektryczne i Magnetyczne
UWAGA: Dla układów przyczynowych, wszystkie realizacje transformat dotyczą funkcji przyczynowych
(prawostronnych) tak, że transformaty są jednostronne. Jeżeli F(s) jest transformatą jednostronną,
wówczas znajomość obszaru zbieżności nie jest konieczna do wyznaczenia jej oryginału.
UWAGA: Liniowe systemy niezmienne w czasie o parametrach skupionych na ogół prowadzą do
transformat, które są wymiernymi funkcjami zmiennej s. tzn. transformata jest ilorazem wielomianów
zmiennej s w liczniku i mianowniku. Funkcje wymierne mogą być przedstawione w postaci sum prostszych
ułamków, których odwrotne transformaty są stabelaryzowane.
Praktyczna realizacja poszukiwania oryginału na podstawie transformaty Laplace’a w wielu przypadkach
da się sprowadzić do problemu rozkładu na ułamki proste i wykorzystania tablic transformat i oryginałów.
Znajdowanie transformaty odwrotnej metodą rozkładu na ułamki proste:
Jeśli transformata wyrażona jest w postaci funkcji wymiernej:
( )
( )
( )
( )
(
) (
)
(
)
®
13
L
L
F
M
1
0
1
1
2
r
1
0
1
m
m 1
n
n
n
n
n
n
n 1
n
1
2
r
s
s
p s
p s
p s
p
s
s
q s
q s
q
s
s
s
s
s
s
s
−
−
−
−
+
+ +
+
=
=
=
+
+ +
+
−
−
−
…
…
…
Metoda rozkładu na ułamki proste może być z powodzeniem stosowana przy następujących założeniach
stawianych postaci transformaty F(s):
1. stopień wielomianu licznika L(s) jest mniejszy od stopnia wielomianu mianownika M(s), czyli st{L(s)} <
st{M(s)} ( m < n ),
( )
2. ułamek
( )
L s
M s
jest nie skracalny, tzn. miejsca zerowe L(s) są różne od miejsc zerowych M(s).

Obwody Elektryczne i Magnetyczne
Wprowadza się dodatkowe określenia zer i biegunów transformaty F(s). Miejsca zerowe licznika, tzn.
pierwiastki równania L(s)=0 nazywamy zerami transformaty F(s), a miejsca zerowe mianownika, tzn.
pierwiastki równania M(s)=0 nazywamy biegunami transformaty F(s).
Kluczowe znaczenia dla poszukiwania oryginału transformaty mają jej bieguny. Jednocześnie możemy
rozważyć występowanie biegunów prostych (jednokrotnych) lub biegunów wielokrotnych.
Rozkład na ułamki proste jest metodą wywodzącą się z twierdzenia Heaviside’a i pozwala opisać funkcję
F(s) w oparciu o bieguny transformaty w następujący sposób:
( )
(
)
F
i
n
r
ik
k
i 1 k 1
i
A
s
s
s
=
=
=
−
∑∑
gdzie:
r – liczba biegunów, i – numeracja kolejnego bieguna i=1,2,..r,
n
i
– krotność i-tego bieguna, k – indeksowanie kolejnych elementów rozkładu pochodzących od
krotności n
i
-tego bieguna, ale w zakresie jego krotności tj. k= 1,2, ... n
i
.
Stąd A
ik
– współczynnik rozkładu skojarzony z i-tym biegunem i jego k-tym poziomem krotności
r
Dla
sprawdzenia
i
i 1
n
n
=
=
∑
Poszczególne współczynniki rozkładu A
ik
na ułamki proste możemy odnaleźć poprzez:
1. sprowadzanie do wspólnego mianownika formy rozłożonej na części proste i tożsamościowe
porównanie współczynników przy odpowiednich potęgach licznika L(s) z formą wymierną,
2. wykorzystanie metody granic
(
)
(
)
(
)
(
) ( )
{
}
lim
F
!
i
i
i
n
k
n
ik
i
n
k
i
i
s
s
1
d
A
s
s
s
n
k
ds
−
−
→
⎡
⎤
=
−
⎢
⎥
−
⎣
⎦
Ostatecznie poszczególne składniki oryginału odnajdujemy z tabel transformat i oryginałów.
®
14

Obwody Elektryczne i Magnetyczne
Znajdowanie transformaty odwrotnej metodą residuów:
Komplementarnym sposobem do metody rozkładu na ułamki proste jest wykorzystanie definicji residuum
funkcji F(s) w jej biegunie.
Założenia co do formy transformaty odwracanej są takie same, jak w przy rozkładzie na ułamki proste.
Jeśli więc transformata wyrażona jest w postaci funkcji wymiernej:
( )
( )
( )
( )
(
) (
)
(
)
®
15
L
L
F
M
1
0
1
1
2
r
1
0
1
m
m 1
n
n
n
n
n
n
n 1
n
1
2
r
s
s
p s
p s
p s
p
s
s
q s
q s
q
s
s
s
s
s
s
s
−
−
−
−
+
+ +
+
=
=
=
+
+ +
+
−
−
−
…
…
…
a ponadto F(s) spełnia poniższe warunki:
1. stopień wielomianu licznika L(s) jest mniejszy od stopnia wielomianu mianownika M(s), czyli st{L(s)} <
st{M(s)} ( m < n ),
( )
2. ułamek
( )
L s
M s
jest nie skracalny, tzn. miejsca zerowe L(s) są różne od miejsc zerowych M(s).
to prawostronny oryginał transformaty, czyli funkcję czasu f(t), możemy odnaleźć jako sumę residuów w
postaci:
( )
( )
{
}
( )
( )
i
r
1
res
st
s s
i 1
f t
F s
F s e
1 t
−
=
=
⎡
⎤
⎡
⎤
=
= ⎢
⎥
⎣
⎦
⎣
⎦
∑
L
gdzie definicja residuum uwzględnia krotność i-tego bieguna:
( )
(
)
(
)
(
)
(
)
( )
{
}
i
i
i
i
s
s
n
1
n
res
st
st
s s
i
n
1
i
i
1
d
F s e
s
s
s e
n
1
ds
lim
F
!
→
−
=
−
⎡
⎤
⎡
⎤ =
−
⎢
⎥
⎣
⎦
−
⎣
⎦
legenda oznaczeń: r – liczba biegunów, i – numeracja kolejnego bieguna i=1,2,..r,
n
i
– krotność i-tego bieguna

Obwody Elektryczne i Magnetyczne
Przykład:
Wyznacz oryginał transformaty
( )
3
2
s
2
F s
s
2s
s
+
=
+
+
Po pierwsze przygotowujemy informacje o liczniku i mianowniku danej transformaty:
( )
( )
{ }
st L s
1
=
, miejsca zerowe licznika tj. zera transformaty:
L s
0 s
2
0 s
2
,
,
=
+ =
= −
( )
{
}
st M s
3
=
, miejsca zerowe mianownika tj. bieguny transformaty:
( )
3
2
M s
0 s
2s
s
0
,
=
+
+ =
( )
(
)
(
)
2
2
M s
0 s s
2s
1
0
s s
1
0
,
=
+
+ = →
+
=
Stąd określamy bieguny i ich krotności:
1
1
s
0 n
1
,
=
=
2
2
s
1 n
2
,
= −
=
Sprawdzamy warunki:
1. stopień wielomianu licznika L(s) jest mniejszy od stopnia wielomianu mianownika M(s), czyli st{L(s)} <
st{M(s)} ( 1 < 3 ),
( )
2. ułamek
( )
L s
M s
jest nie skracalny, tzn. miejsca zerowe L(s) są różne od miejsc zerowych M(s).
( )
(
)
2
3
2
s
2
s
2
F s
s
2s
s
s s 1
+
+
=
=
+
+
+
Wykorzystanie rozkładu na ułamki proste:
( )
(
)
®
16
(
) (
) (
)
(
)
i
ik
11
21
22
11
21
22
k
1
1
2
2
i 1 k 1
i
1
2
2
A
A
A
A
s
s
s 1
s
s
s
s
s
s
s
s
s 1
F
=
=
=
=
+
+
=
+
+
+
−
−
−
−
∑∑
n
r
A
A
A
+
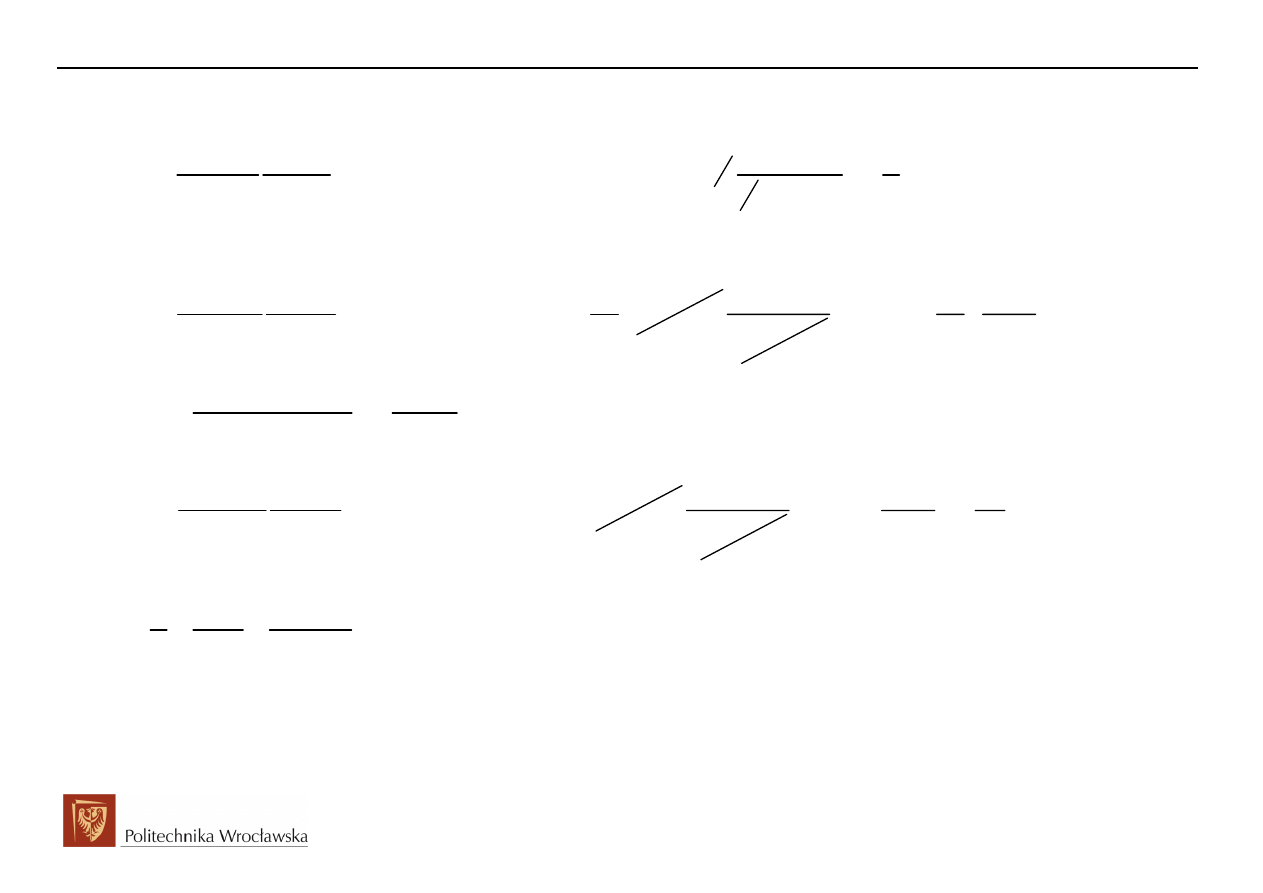
Obwody Elektryczne i Magnetyczne
Wyznaczamy współczynniki rozkładu dla pierwszego bieguna
1
1
s
0 n
1
,
=
=
(
)
( )
( )
( ) ( )
{
}
( )
1 1
1
11
1 1
s
s
s
0
0
0
1
d
A
s
s
s
s
s
1 1
ds
lim
F
lim
F
lim
!
−
−
→
→
→
⎡
⎤
⎡
⎤
=
=
=
⎢
⎥
⎣
⎦
−
⎣
⎦
s
2
s
+
(
)
2
2
2
1
s
1
⎡
⎤
= =
⎢
⎥
+
⎢
⎥
⎣
⎦
Wyznaczamy współczynniki rozkładu dla drugiego bieguna
2
2
s
1 n
2
,
= −
=
(
)
(
)
(
)
(
) ( )
{
}
(
)
2 1
2
2
21
2 1
s
s
1
1
1
d
d
A
s 1
s
s 1
2 1
ds
ds
lim
F
lim
!
−
−
→
→
−
−
⎡
⎤
=
+
=
+
⎢
⎥
−
⎣
⎦
(
)
2
s
2
s s 1
+
+
s
1
d
s
2
ds
s
lim
→−
⎡
⎤
⎧
⎫
⎡
⎤
+
⎪
⎪
⎧
⎫
⎢
⎥ =
=
⎨
⎬
⎨
⎬
⎢
⎥
⎢
⎥
⎩
⎭
⎣
⎦
⎪
⎪
⎢
⎥
⎩
⎭
⎣
⎦
(
)
2
s
1
1 s 1 s
2
1 1
2
s
1
lim
→−
⎡
⎤
⋅ − ⋅ +
− −
=
=
= −
⎢
⎥
⎣
⎦
(
)
(
)
(
)
(
) ( )
{
}
(
)
2 2
2
2
22
2 2
s
s
1
1
1
d
A
s 1
s
s 1
2
2
ds
lim
F
lim
!
−
−
→
→
−
−
⎡
⎤
=
+
=
+
⎢
⎥
−
⎣
⎦
(
)
2
s
2
s s 1
+
+
s
1
s
2
1
1
s
1
lim
→−
⎡
⎤
+
⎡
⎤
⎢
⎥ =
=
= −
⎢
⎥
⎢
⎥
−
⎣
⎦
⎣
⎦
Ostatecznie F(s) w rozkładzie na ułamki proste przyjmie postać:
( )
(
)
2
2
2
1
s
s
s 1
s 1
F
−
−
= +
+
+
+
Wykorzystując tabele transformat oraz własności odnajdujemy poszczególne składniki oryginału:
( )
( )
( )
( )
( )
t
t
t
t
f t
2 1 t
2 e 1 t
te 1 t
2
2e
te
1 t
−
−
−
−
⎡
⎤
= ⋅
− ⋅
−
=
−
−
⎣
⎦
®
17

Obwody Elektryczne i Magnetyczne
Wykorzystanie metody residuów:
Funkcja spełnia również założenia dla metody residuów, więc szukany oryginał możemy odnaleźć jako:
( )
( )
{
}
( )
( )
( )
( )
( )
i
r
1
res
st
res
st
res
st
s s
s 0
s
1
i 1
f t
F s
F s e
1 t
F s e
F s e
1 t
−
=
=
=−
=
⎡
⎤
⎡
⎤
⎡
⎤
⎡
⎤
⎡
⎤
=
=
=
+
⎢
⎥
⎣
⎦
⎣
⎦
⎣
⎦
⎣
⎦
⎣
⎦
∑
L
Residuum dla pierwszego bieguna
1
1
s
0 n
1
,
=
=
wyznaczymy jako:
( )
(
)
( )
( )
s
0
1 1
res
st
s 0
1 1
1
d
F s e
s
1 1
ds
lim
!
→
−
=
−
⎡
⎤ =
⎣
⎦
−
s
2
s
+
(
)
(
)
s
0
st
st
2
2
s
2
e
e
2
s 1
s 1
lim
→
⎡
⎤
⎧
⎫
⎡
⎤
+
⎪
⎪
⎢
⎥ =
=
⎢
⎥
⎨
⎬
⎢
⎥
+
+
⎢
⎥
⎪
⎪
⎩
⎭
⎣
⎦
⎣
⎦
Residuum dla drugiego bieguna
2
2
s
1 n
2
,
= −
=
wyznaczymy jako:
( )
(
)
(
)
(
)
(
)
s
1
2 1
2
res
st
s
1
2 1
1
d
F s e
s 1
2 1
ds
lim
!
→−
−
=−
−
⎡
⎤ =
+
⎣
⎦
−
(
)
2
s
2
s s 1
+
+
s
1
st
st
d
s
2
e
e
ds
s
lim
→−
⎡
⎤
⎧
⎫
⎡
⎤
+
⎪
⎪
⎧
⎫
⎢
⎥ =
=
⎨
⎬
⎨
⎬
⎢
⎥
⎢
⎥
⎩
⎭
⎣
⎦
⎪
⎪
⎢
⎥
⎩
⎭
⎣
⎦
(
)
s
1
st
st
t
t
2
1 s 1 s
2
s
2
e
t e
2e
te
s
s
lim
→−
−
−
⎡
⎤
⎛
⎞
⋅ − ⋅ +
+
⎛
⎞
=
+ ⋅
= −
−
⎢
⎥
⎜
⎟
⎜
⎟
⎝
⎠
⎢
⎥
⎝
⎠
⎣
⎦
Ostatecznie szukany oryginał:
( )
( )
( )
( )
( )
res
st
res
st
t
t
s 0
s
1
f t
F s e
F s e
1 t
2
2e
te
1 t
−
−
=
=−
⎡
⎤
⎡
⎤
⎡
⎤
⎡
⎤
=
+
=
−
−
⎣
⎦
⎣
⎦
⎣
⎦
⎣
⎦
®
18

Obwody Elektryczne i Magnetyczne
Wykorzystanie metody sprowadzania do wspólnego mianownika:
®
19
( )
(
)
(
)
11
21
22
2
2
3
2
s
s
2s
s
s
s 1
s s 1
s 1
F
A
A
A
s
2
s
2
+
+
=
=
=
+
+
+
+
+
+
+
(
)
(
)
(
)
(
)
(
)
(
)
2
2
2
11
21
22
11
21
22
2
2
A
s
2s
1
A
s
s
A s
A
s
1
A s s
1
A s
s s
1
s s
1
+
+ +
+ +
+
+
+ +
=
=
=
+
+
(
)
(
) (
)
(
)
2
2
2
11
21
11
21
22
11
11
11
11
21
21
22
2
2
s
A
A
s 2 A
A
A
A
A s
2 A s
A
A s
A s
A s
s s 1
s s 1
+
+
+
+
+
+
+
+
+
+
=
=
+
+
Porównując tożsamościowo współczynniki wielomianu licznika otrzymujemy układ równań:
(
) (
)
2
11
21
11
21
22
11
s
A
A
s 2 A
A
A
A
s
2
+
+
+
+
+
≡ +
2
11
21
1
11
21
22
0
11
A
A
0
s
s
2 A
A
A
1
s
A
2
+
=
→⎧
⎪
→
+
+
=
⎨
⎪
→
=
⎩
czyli
21
11
A
A
2
= −
= −
oraz
22
11
21
A
1 2 A
A
1 4
2
1
= −
−
= − + = −
Stąd
( )
(
)
2
2
2
1
s
s
s 1
s 1
F
−
−
= +
+
+
+
Wykorzystując tabele transformat oraz własności odnajdujemy poszczególne składniki oryginału:
( )
( )
( )
( )
( )
t
t
t
t
f t
2 1 t
2 e 1 t
te 1 t
2
2e
te
1 t
−
−
−
−
⎡
⎤
= ⋅
− ⋅
−
=
−
−
⎣
⎦
Wyszukiwarka
Podobne podstrony:
OEiM AiR W09 LaplaceiTransmitan Nieznany
OEiM AiR W08 LaplaceiMoperatorowa cz2
OEiM AiR W05 MetodaKlasyczna cz Nieznany
OEiM AiR W03 MetodaKlasyczna cz Nieznany
cw2 MiASC AiR id 123156 Nieznany
OEiM AiR W02 MetodaKlasyczna cz1
cw3 MiASC AiR id 123320 Nieznany
OEiM AiR W06 SLS odpowiedz
polymer at the air water interf Nieznany
OEiM AiR W01 wprowadzenie
gs w07 id 197504 Nieznany
więcej podobnych podstron