
Obwody Elektryczne i Magnetyczne
®
1
Obwody elektryczne
Wykład 5 – Metoda Klasyczna – część IV
Prowadzący: dr inż. Tomasz Sikorski
Instytut Podstaw Elektrotechniki i Elektrotechnologii
Wydział Elektryczny
Politechnika Wrocławska
D-1, 205/1
tel: (071) 320 21 60
fax: (071) 320 20 06
email:

Obwody Elektryczne i Magnetyczne
®
2
Obwody Elektryczne i Magnetyczne
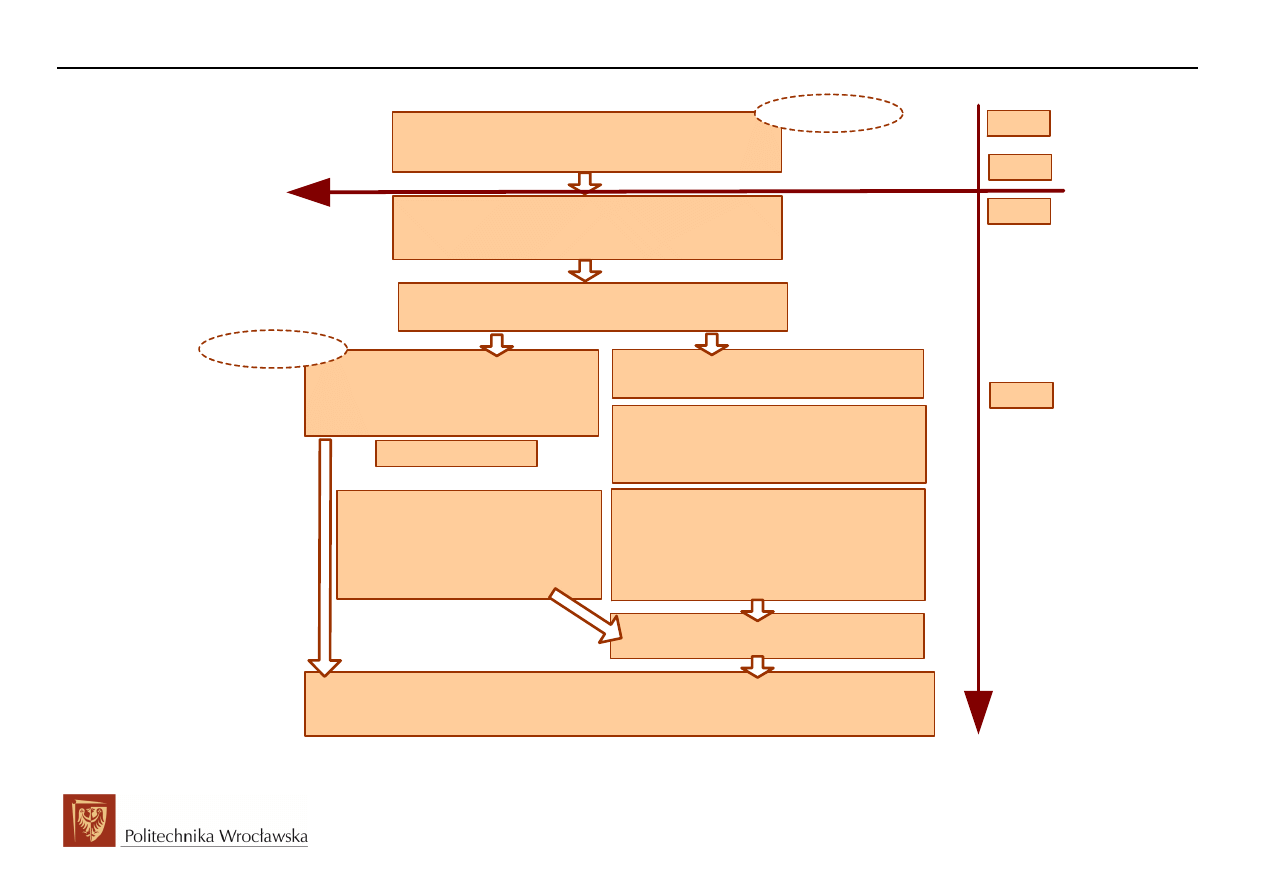
Wyznaczenie odpowiedzi całkowitej jako sumy składowej ustalonej (wymuszonej)
oraz składowej przejściowej (swobodnej)
RORN=RSRN+RORJ
Analiza obwodu w stanie ustalonym przed
komutacją
Warunek początkowy dla t=0-
Warunek początkowy dla t=0+
Dla układów wyższego rzędu warunki początkowe
dla pochodnych dla t=0+
Układ równań Kirchhoffa
Równanie różniczkowe szukanej wielkości
RSRN
składowa ustalona (wymuszona)
Analiza obwodu w stanie ustalonym
po komutacji
RORJ
składowa przejściowa (swobodna)
Wyznaczenie wartości składowej
ustalonej dla t=0+
Dla układów wyższego rzędu
wyznacznie wartości pochodnych
składowej ustalonej w chwili t=0+
Określenie przewidywanej postać
składowej przejściowej na podstawie
wielomianu charakterystycznego
Wyznaczenie wartości składowej
przejściowej w chwili to=+, oraz, dla
ukłądów wyższego rzędu, wartości
pochodnych składowej przejściowej w
chwili t=0+
Wyznaczenie stałych składowej
przejściowej
t<0
t=0-
t=0+
t>0
t->+inf
Historia obwodu
Przyszłość obwodu
®
3
Obwody Elektryczne i Magnetyczne
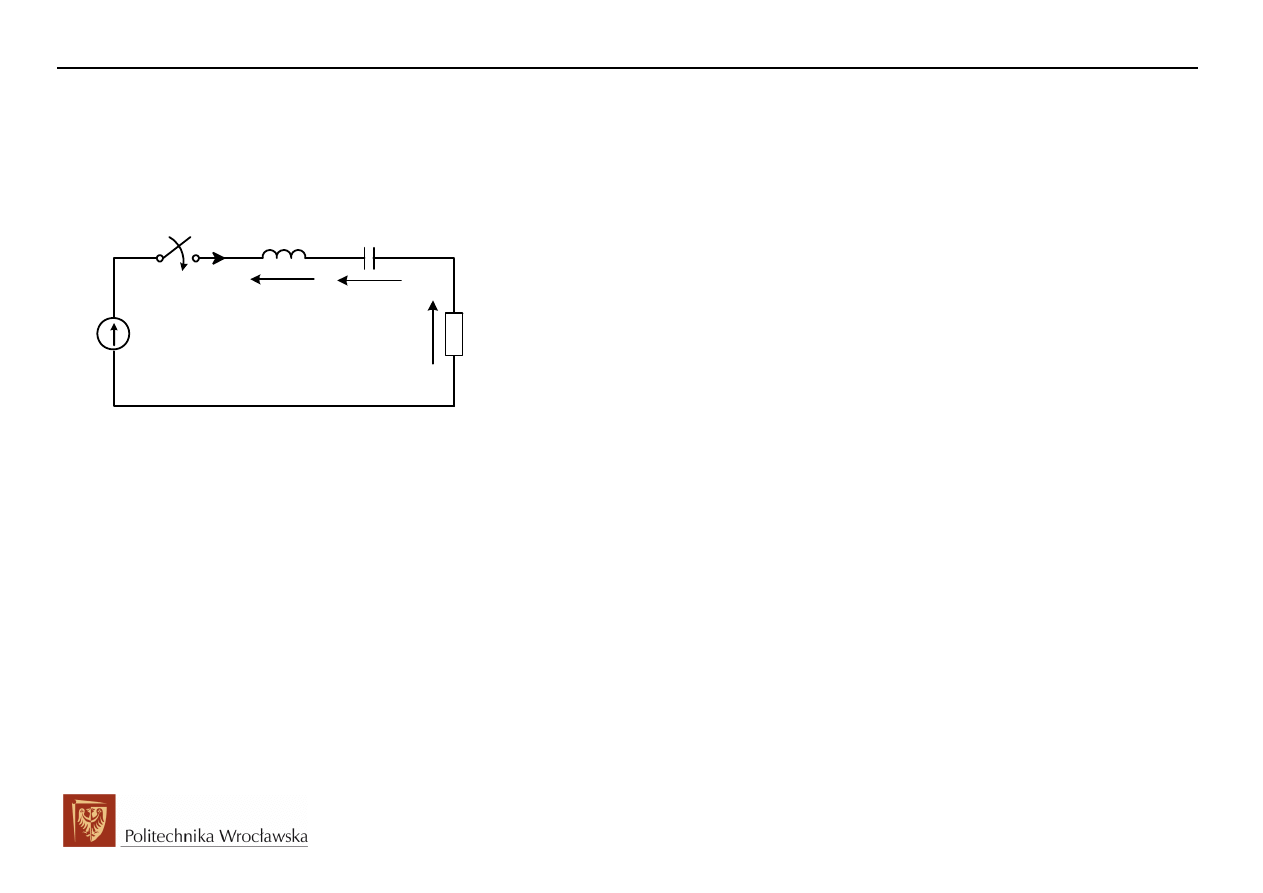
1 Stan nieustalony w gałęzi RLC
1.1 Załączanie szeregowej gałęzi RLC na napięcie sinusoidalne
Dane:
( )
(
)
m
e
®
4
e(t)
R
L
t = 0
u
L
(t)
i(t)
u
R
(t)
u
C
(t)
C
e t
E
t
R L C
sin
, ,
ω ψ
=
+
Po komutacji dwa elementy
zachowawcze różnego typu LC
Równanie różniczkowe II rzędu
oprzeć na
( )
lub
L
i t
( )
c
u t
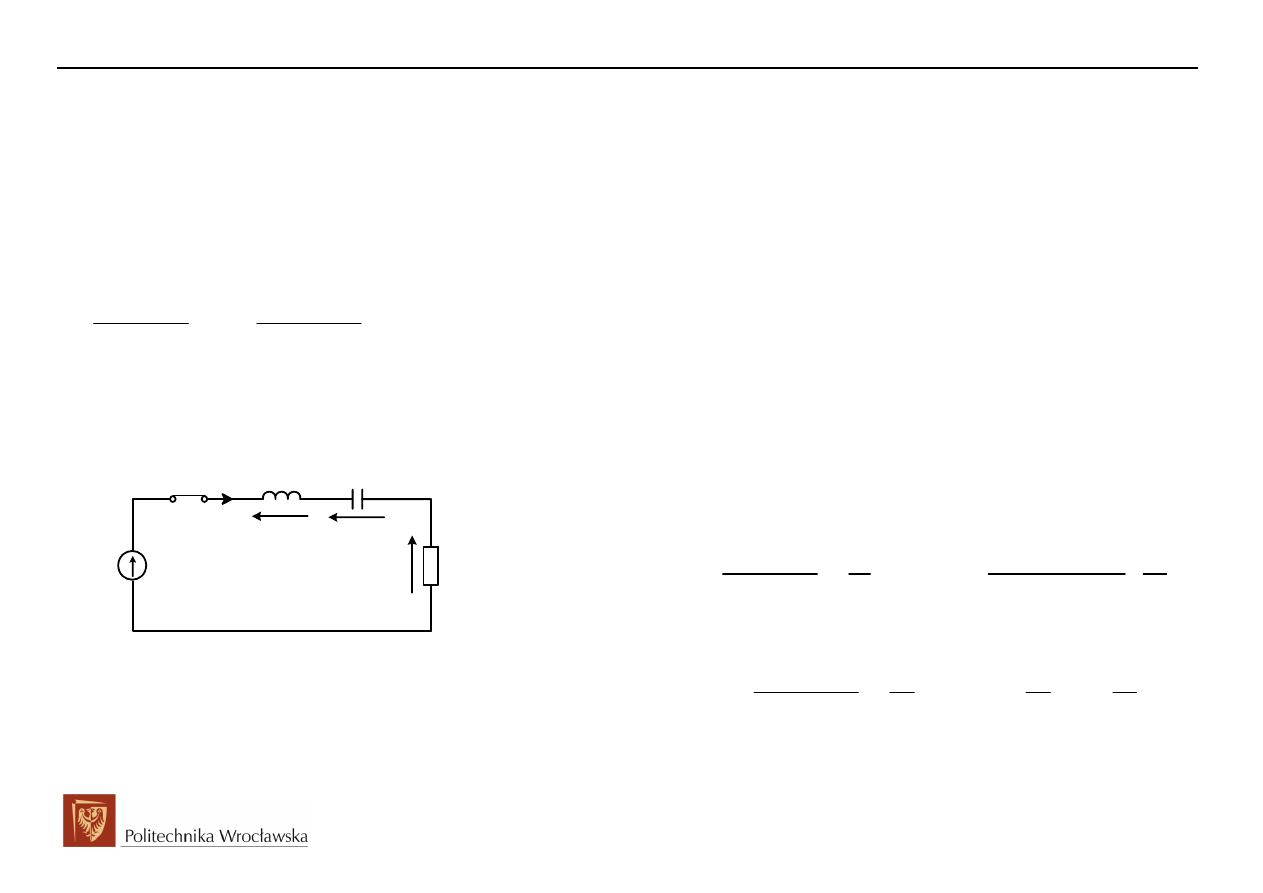
1. t<0, Analiza obwodu w stanie ustalonym przed komutacją (historia obwodu) oraz
wyznaczenie warunku początkowego dla t=0-
( )
( )
,
L
L
i
t
0 dla t
0
i 0
0
−
=
< →
=
( )
( )
,
C
C
u
t
0 dla t
0
u
0
0
−
=
< →
=
2. t=0+, wyznaczenie warunku początkowego dla t=0+
Po załączeniu łącznika nie stwierdzamy ani oczek osobliwych ani węzłów osobliwych, a zatem napięcie
na kondensatorze oraz prąd płynący przez cewkę zachowują prawa komutacji:
( ) ( )
L
L
i 0
i 0
0
+
−
=
=
( )
( )
C
C
u
0
u
0
0
+
−
=
=
Obwody Elektryczne i Magnetyczne
Ze względu na dwa różne elementy zachowawcze pozostające w obwodzie po komutacji,
wyznaczane równanie różniczkowe, czy to dla
( )
czy
L
i t
( )
c
u t
, będzie równaniem 2 rzędu i do
jego rozwiązania wymagana jest dodatkowo, tzn. oprócz
( )
L
i 0
+
oraz
( )
C
u
0
+
, znajomość
warunków początkowych dla ich pochodnych w chwili t=0
+
tj.
( )
( )
0
L
di
dt
+
oraz
0
C
du
dt
+
.
( )
( ) ( )
( )
( )
( )
( )
0
C
i
+
0
0
0
0
0
0
L
C
L
i
i
e
i
u
u
R
+
+
+
+
+
+
⎧⎪
⎨
=
+
+
=
⎪⎩
=
R
L
t = 0
u
L
( )
i( )
C
u
c
( )
u
R
( )
+
0
+
0
+
0
+
0
+
e(0
+
)
Skąd dla
( )
( )
,
L
C
i 0
0 u
0
0
+
+
=
=
otrzymujemy
( )
( )
( )
®
5
( )
( )
0
0
1
L
L
L
m
e
di
E
0
0
A
dt
L
L
e
u
u
s
sin
ψ
+
+
⎡ ⎤
=
→
=
=
⎢ ⎥
⎣ ⎦
+
+
( )
Ponadto:
( )
( )
0
+
( )
1
0
0
0
0
C
C
C
du
V
dt
C
s
i
C
+
+
+
⎡ ⎤
→
=
=
=
0
L
i
i
⎢⎣
=
⎥⎦
Obwody Elektryczne i Magnetyczne
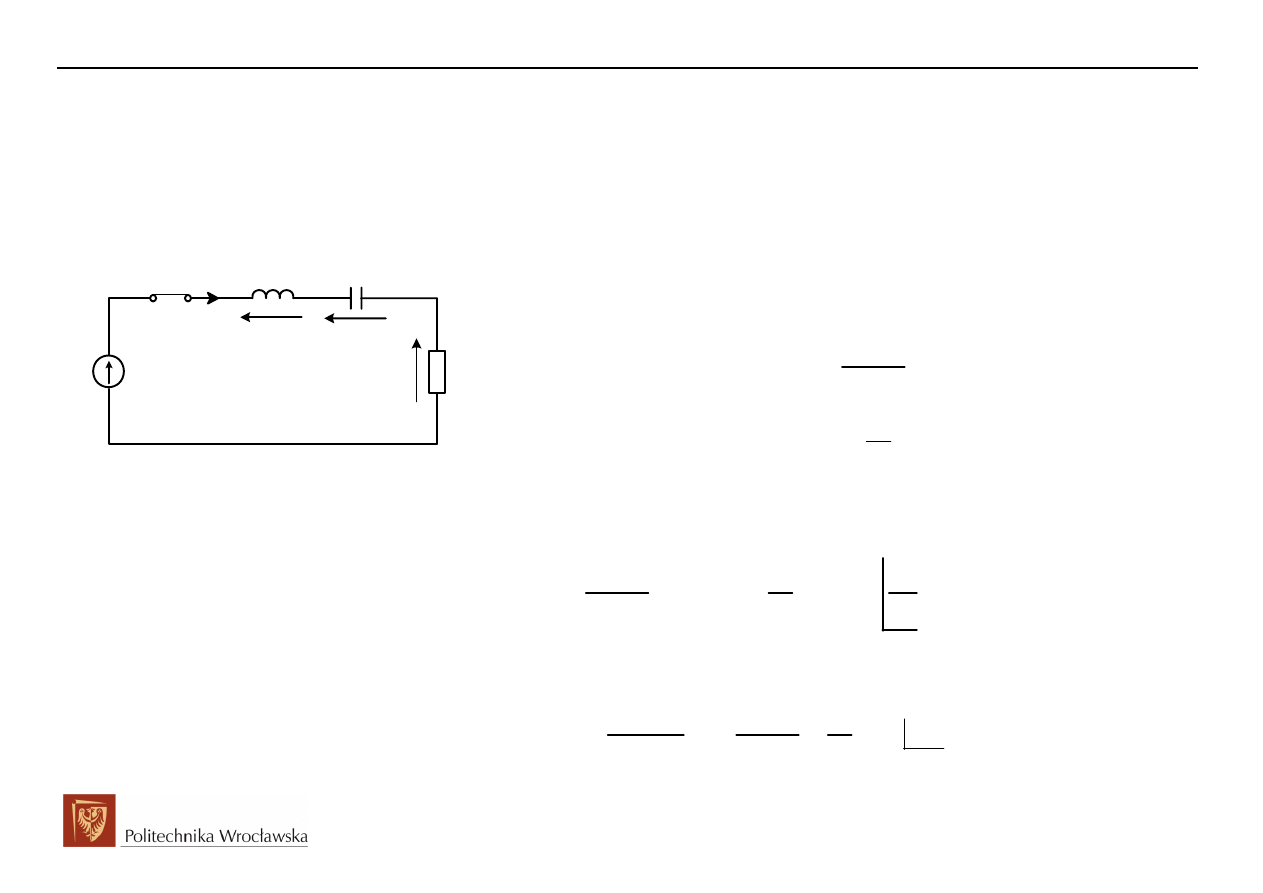
3.
, wyznaczanie równania różniczkowego
0
t
>
W przypadku dwóch i więcej elementów zachowawczych musimy podjąć decyzję, na którym z
sygnałów zachowawczych oprzeć równanie różniczkowe. W analizowanym obwodzie mamy do
dyspozycji
( )
,
(
L
i t
)
c
u t
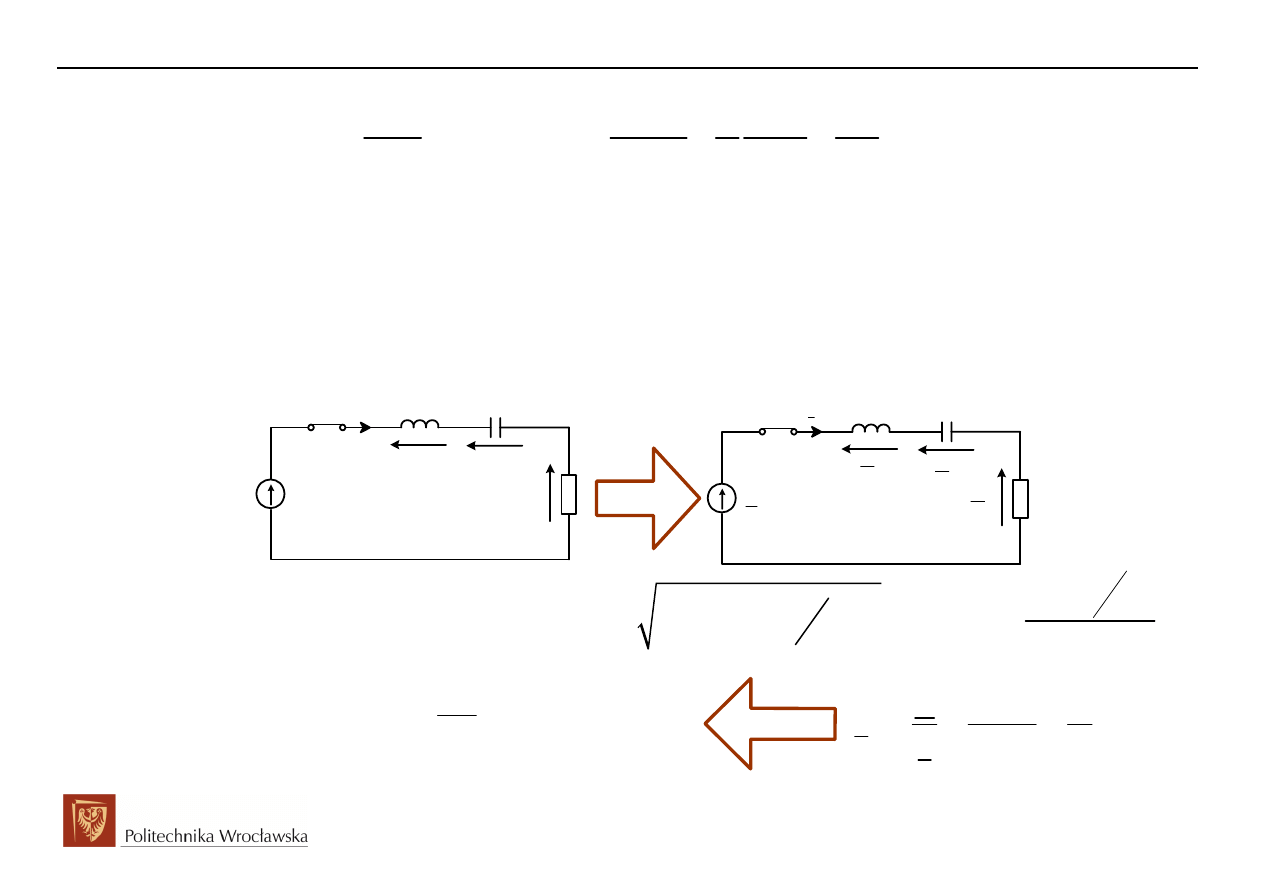
Przykład wyznaczania równania różniczkowego dla
( )
L
i t
( )
( )
( )
E
R
L
t > 0
u
L
(t)
i(t)
C
u
c
(t)
u
R
(t)
(
)
( )
( )
( )
L
C
m
e
C
i t
i t
i
t
di t
E
t
L
Ri t
u
t
dt
sin
ω ψ
⎧
=
=
⎪
⎨
+
=
+
+
⎪
⎩
.
gdzie:
( )
( )
1
C
u
t
i t dt
C
=
∫
Stąd po wyrażeniu wszystkich sygnałów biorących udział w II Prawie Kirchhoffa przez prąd płynący
przez cewkę, równanie dla
( )
L
i t
przyjmie postać różniczkowo-całkową:
(
)
( )
( )
( )
m
e
di t
1
d
E
t
L
Ri t
i t dt
dt
C
dt
sin
ω ψ
+
=
+
+
∫
Aby otrzymać szukane równanie różniczkowe możemy zróżniczkować obustronnie postać różniczkowo-
całkową:
(
)
( )
( )
( )
2
m
e
2
d i t
di t
1
E
t
L
R
i t
L
dt
dt
C
cos
ω
ω ψ
+
=
+
+
÷
®
6
Obwody Elektryczne i Magnetyczne
(
)
( )
( )
( )
2
m
e
2
d i t
di t
E
R
1
t
i t
L
dt
L dt
LC
cos
ω
ω ψ
+
=
+
+
Stwierdzamy równanie różniczkowe liniowe niejednorodne o stałych współczynnikach. Szukane
rozwiązanie tj. prąd płynący przez cewkę
( )
i t
w stanie nieustalonym zawierał będzie zarówno składową
przejściową jak i składową przejściową:
( )
( )
( )
u
p
RORN
RSRN
RORJ
i t
i t
i
t
=
+
⇒
=
+
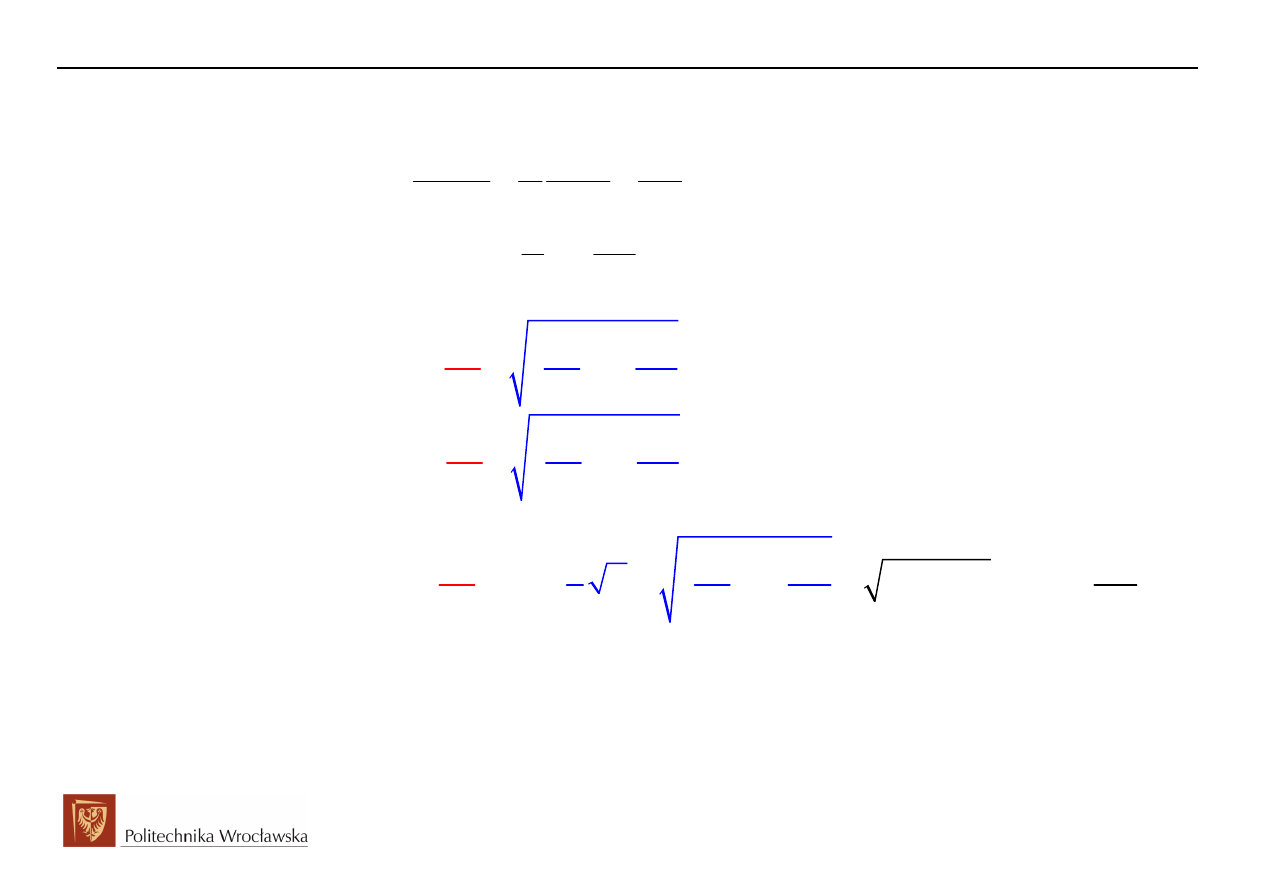
4.
, analiza obwodu w stanie ustalonym po komutacji (przyszłość obwodu) – składowa
ustalona odpowiedzi (składowa wymuszona)
t
→ +∞
( )
u
i t
Zapis
symboliczny
-jX
u
C
I
Cu
U
Ru
U
E
e(t)=E
m
sin(
ω
t+
ψ
e
)
R
L
u
Lu
(t)=0
i(t)=0
C
u
Cu
(t)=E
u
Ru
(t)=0
u
t
→ +∞
R
Lu
U
jX
L
(
)
2
2
1
1
,
L
C
z
R
L
arctg
C
R
ω
ω
ω
ϕ
ω
⎛
⎞
−
⎜
⎟
=
+
−
=
⎜
⎟
⎝
⎠
( )
(
)
(
)
m
u
um
iu
e
E
i t
I
t
t
z
sin
sin
ω ψ
ω ψ
ϕ
=
+
=
+
−
Powrót z zapisu
symbolicznego
(
)
e
e
j
j
u
j
E
Ee
E
I
e
z
ze
z
ψ
ψ ϕ
ϕ
−
=
=
=
®
7
Obwody Elektryczne i Magnetyczne
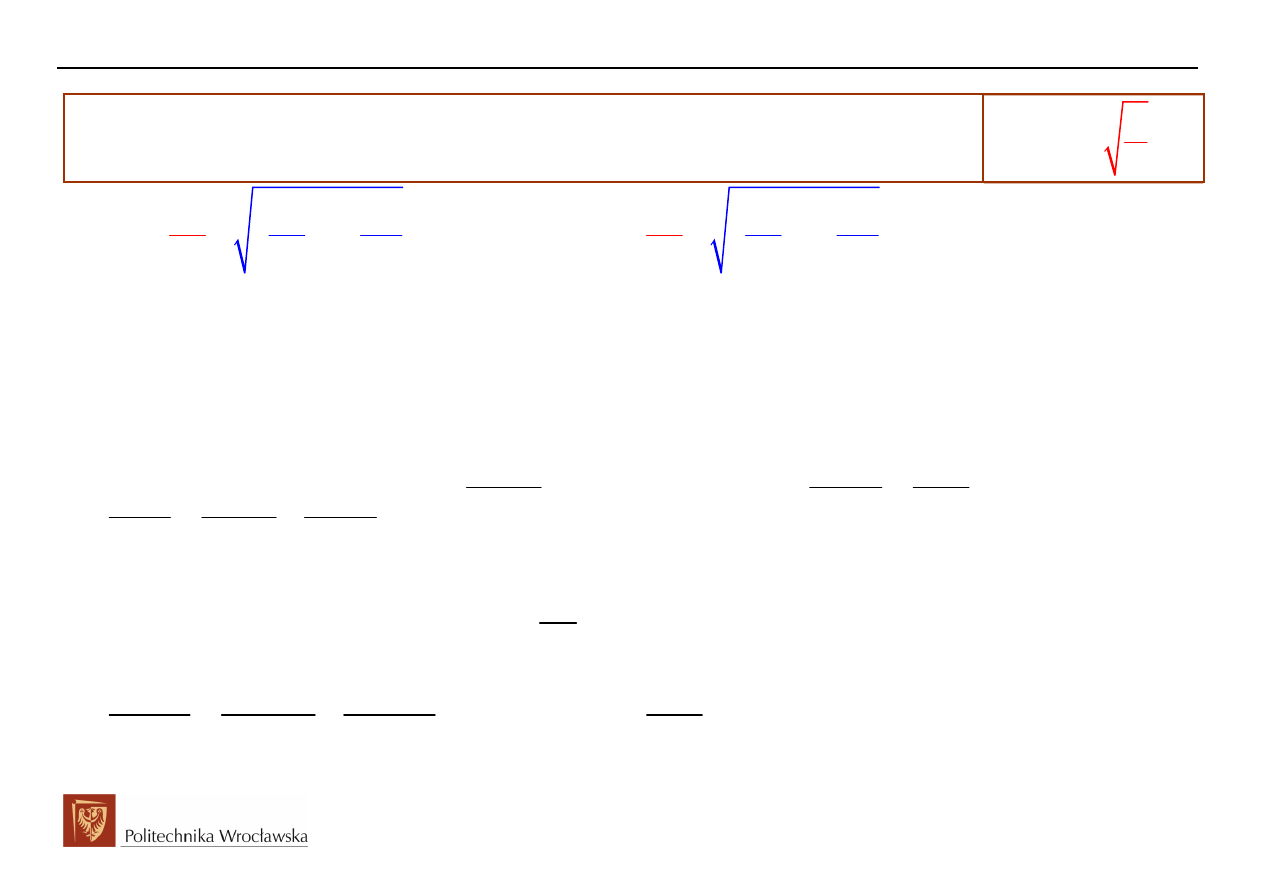
5. t>0, składowa przejściowa (swobodna)
( )
p
i
t
( )
Równanie jednorodne
( )
( )
2
2
1
0
d i t
di t
R
i t
dt
L dt
LC
=
+
+
Wielomian
charakterystyczny
( )
2
R
1
V
L
LC
λ
λ
λ
=
+
+
2
1
R
1
2L
R
2L
®
8
Pierwiastki wielomianu
charakterystycznego
C
L
α β
⎛
⎞ −
⎜
⎟
⎝
⎠
+
=
−
λ
=
+
2
2
R
1
2L
R
2L
C
L
α β
⎛
⎞ −
⎜
⎟
⎝
⎠
−
=
−
λ
=
−
gdzie:
2
2
2
r
r
2
1
1
R
1
2
2
R
L
2
C
L
LC
L
,
,
α
β
Δ
ω
ω
⎛
⎞
=
=
−
⎜
⎟
=
−
⎠
=
⎝
α
= −
Obwody Elektryczne i Magnetyczne
5.1. Przypadek 1:
, dwa różne pierwiastki rzeczywiste,
0
Δ
>
1
2
λ λ
,
®
9
Przewidywana postać składowej przejściowej
( )
1
2
t
t
p
11
21
i
t
A e
A e
t
0
,
λ
λ
=
+
>
L
R
2
C
>
2
1
R
1
2L
R
C
2L
L
α
⎛
⎞ −
⎜
⎟
⎝
⎠
+
=
−
=
+
2
2
R
1
2L
C
L
R
2L
α β
⎛
⎞ −
⎜
⎟
⎝
⎠
−
=
−
λ
β
oraz
λ
=
−
( )
(
)
(
)
t
t
p
11
21
i
t
A e
A e
t
0
,
α β
α β
+
−
=
+
>
W odróżnieniu do obwodów I rzędu do wyznaczenia są dwie stałe
11
21
A
A
,
. Nie wystarczy zatem jedno
równanie dla warunków początkowych. Drugie równanie otrzymamy adaptując równanie na warunki
początkowe w formie pochodnych.
( )
( )
( )
( )
( )
( )
p
u
p
u
i t
i
t
i t
di
t
di t
di t
dt
dt
dt
=
+
⎧
⎪
⎨
=
+
⎪
⎩
, gdzie:
( )
( )
(
)
1
2
p
t
t
u
m
11 1
21
2
e
di
t
di t
E
A
e
A
e
t
dt
dt
z
,
cos
λ
λ
ω
λ
λ
ω ψ
ϕ
=
+
=
+
−
,
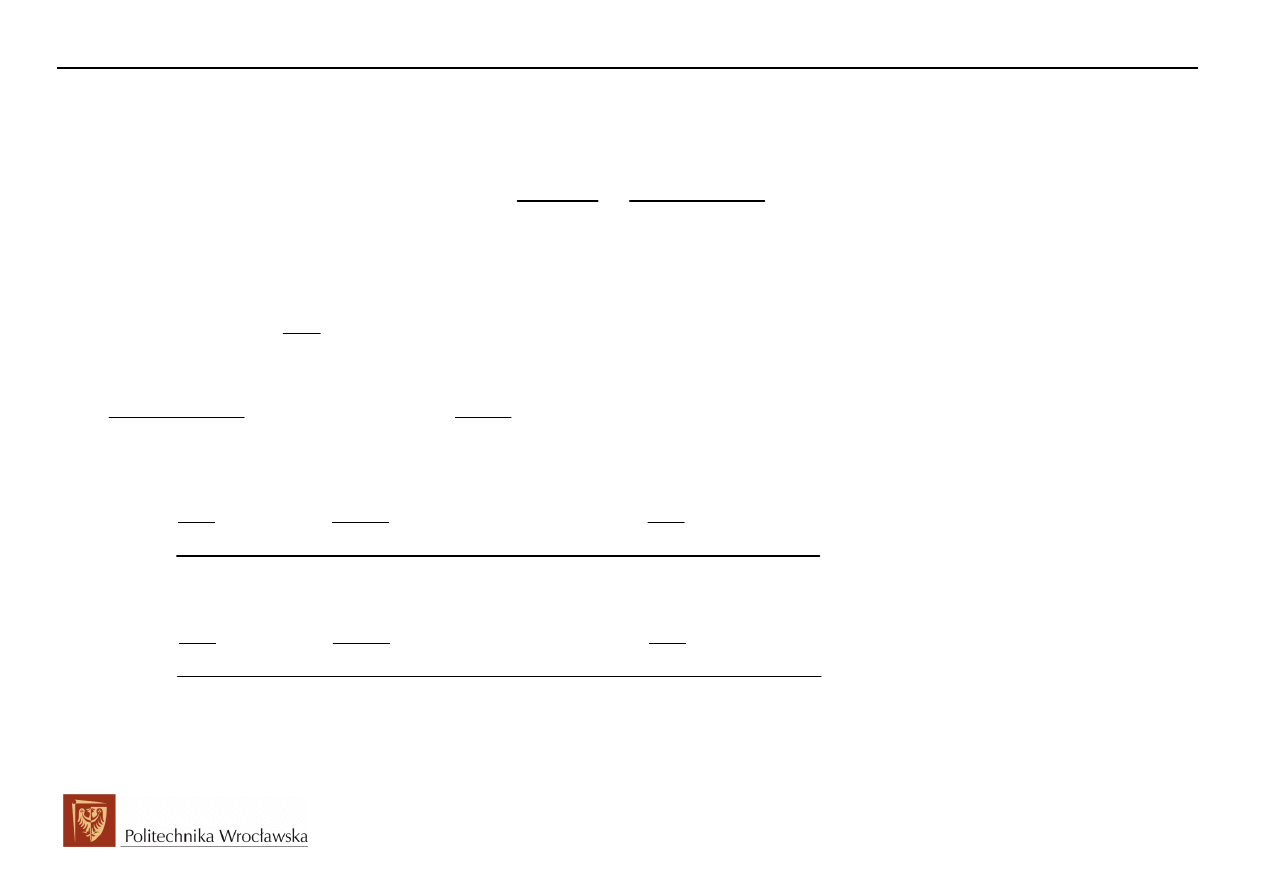
W szczególności dla t=0
+
:
( ) ( ) ( )
(
)
( )
( )
( )
(
)
m
p
u
11
21
e
p
u
m
11 1
21
2
e
E
i 0
i
0
i 0
A
A
z
di 0
di
0
di 0
E
A
A
dt
dt
dt
z
sin
cos
ψ
ϕ
ω
λ
λ
ψ
ϕ
+
+
+
+
+
+
⎧
=
+
=
+
+
−
⎪⎪
⎨
⎪
=
+
=
+
+
−
⎪⎩
Obwody Elektryczne i Magnetyczne
Przy czym z warunków początkowych
( )
( )
( )
m
e
i 0
0
di 0
E
dt
L
sin
ψ
+
+
⎧
=
⎪
⎨
⎪
=
⎩
Ostatecznie układ równań do znalezienia stałych przyjmie postać:
(
)
( )
(
)
m
11
21
e
m
e
m
11 1
21
2
e
E
0
A
A
z
E
E
A
A
L
z
sin
sin
cos
ψ
ϕ
ψ
ω
λ
λ
ψ
ϕ
⎧ = + +
−
⎪⎪
⎨
⎪
=
+
+
−
⎪⎩
Po przekształceniach szukane stałe :
( )
(
) (
)
(
)
( )
(
) (
)
(
)
m
m
m
11
m
m
m
21
E
E
E
L
z
z
A
2
E
E
E
L
z
z
A
2
sin
cos
sin
sin
cos
sin
ω
ψ
ψ ϕ
α β
ψ ϕ
β
ω
ψ
ψ ϕ
α β
ψ ϕ
β
⎧
−
−
+
−
−
⎪
=
⎪
⎪
⎨
⎪
−
−
+
+
−
⎪
=
⎪
−
⎩
®
10

Obwody Elektryczne i Magnetyczne
( )
(
) ( ) (
) ( )
1
2
t
t
t
p
12
21
21
11
11
21
i
t
A e
A e
A
A
t
A
A
t
e
sh
ch
λ
λ
α
β
β
=
+
=
−
+
+
⋅
⎡
⎤
⎣
⎦
gdzie:
2
1
R
1
2
2L
R
2L
®
11
LC
,
β
Δ
⎛
⎞
=
=
−
⎜
⎟
⎝
⎠
α
= −
( )
(
)
m
u
e
E
i t
t
z
sin
ω ψ
ϕ
=
+
−
6.1. Przypadek 1: Ostatecznie prąd w omawianym obwodzie zawiera zarówno składową
przejściową jak i ustaloną:
( )
( )
( )
p
u
i t
i
t
i t
dla t
0
,
=
+
>
Obwody Elektryczne i Magnetyczne
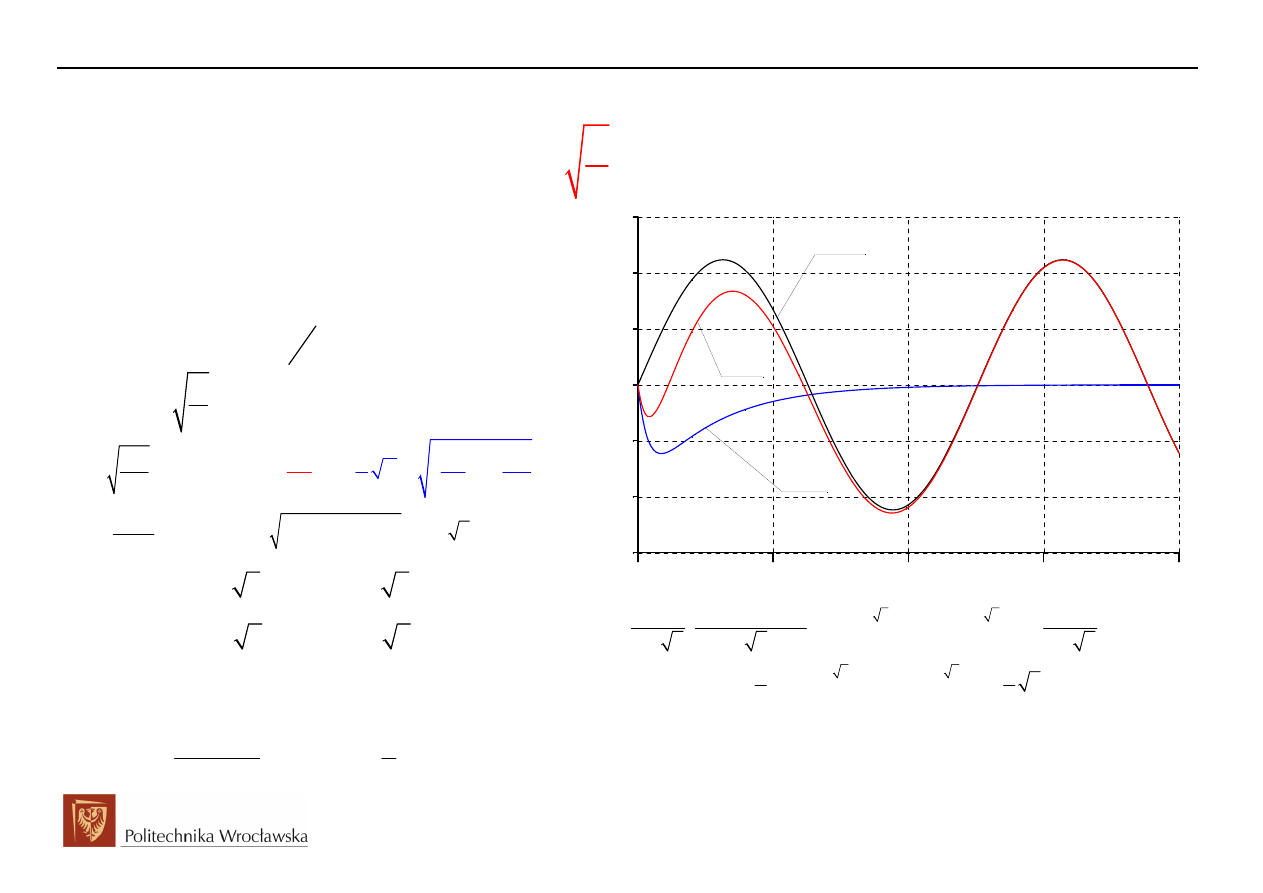
Przykład przebiegu stanu przejściowego w obwodzie RLC załączanym na napięcie sinusoidalne
dla przypadku 1,
0
Δ
>
,
L
R
2
C
>
- charakter aperiodyczny (nieokresowy)
®
12
Dane:
R = 300
Ω
, L = 0.1 H, C = 10
μ
F = 10
-5
F
ω
= 500 s
-1
,
( )
(
)
e
e t
300
500t
ψ
=
+
sin
L
C
1
X
L
50
X
200
C
ω
Ω
Ω
ω
=
=
=
=
;
czyli:
L
R
2
300
200
C
Ω
Ω
>
⎯⎯
→
>
3
1
r
1
10 s
LC
ω
−
=
=
,
2
1
R
1
2
2L
R
2L
α
= −
LC
β
Δ
⎛
⎞
=
=
−
⎜
⎟
⎝
⎠
,
(
)
2
1
3
6
1
1
300
1500 s
1 5 10
10
500 5s
1118s
2 0 1
α
β
−
−
−
= −
=
=
⋅
−
=
≈
⋅
;
.
.
(
)
(
)
1
1
1
1
1
2
1500
500 5
500 3
5 s
2618s
1500
500 5
500 3
5 s
382s
λ
λ
−
−
−
−
= −
−
= −
+
≈ −
= −
+
= −
−
≈ −
UWAGA: Dla uproszczenia obliczeń dobrano
e
ψ
ϕ
=
[ ]
L
C
rad
X
X
1
arc
arc
0 46
R
2
ϕ
−
⎛
⎞
⎛
⎞
=
=
−
≈
⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
tg
tg
.
−
0.000
0.005
0.010
0.015
0.020
t [ s ]
-1.2
-0.8
-0.4
0.0
0.4
0.8
1.2
i(t)
i (t)
u
i (t)
p
( )
(
)
(
)
(
)
(
)
(
)
(
)
sin
sin
6
500 3
5
t
500 3
5
t
500 3
5
t
500 3
5
t
300
10
300
i t
e
e
500t
150 5 2 500 5 500
150 5
4
2
e
e
5
500t
A
5
5
−
+
−
−
−
+
−
−
⎡
⎤
=
⋅
−
+
=
⎢
⎥
⋅
⋅
⎣
⎦
⎡
⎤
=
−
+
⎢
⎥
⎣
⎦
Obwody Elektryczne i Magnetyczne
5.2. Przypadek 2:
, jeden rzeczywisty pierwiastek podwójny
0
Δ
=
1
k
1 2
λ
=
,
,
®
13
Przewidywana postać składowej przejściowej
( )
1
1
t
t
p
11
12
i
t
A e
A te
t
0
,
λ
λ
=
+
>
L
R
2
C
=
2
1
R
1
0
2
2L
LC
β
Δ
⎛
⎞
=
=
−
=
⎜
⎟
⎝
⎠
1
2
R
2L
λ
λ
λ
−
=
= =
( )
R
R
t
t
t
t
2 L
2 L
p
11
12
11
12
i
t
A e
A te
A e
A te
t
0
,
λ
λ
−
−
=
+
=
+
>
Podobnie jak w przypadku pierwszym pełna postać składowej przejściowej wymaga wyznaczenia
dwóch stały
11
12
A
A
,
.
( )
( )
( )
( )
( )
( )
p
u
p
u
i t
i
t
i t
di
t
di t
di t
dt
dt
dt
=
+
⎧
⎪
⎨
=
+
⎪
⎩
, przy czym
( )
p
t
t
t
11
12
12
di
t
A
e
A e
A
te
dt
λ
λ
λ
λ
λ
=
+
+
;
( )
(
)
u
m
e
di t
E
t
dt
z
cos
ω
ω ψ
ϕ
=
+
−
Obwody Elektryczne i Magnetyczne
W szczególności dla t=0
+
:
( ) ( ) ( )
(
)
( )
( )
( )
(
)
m
p
u
11
e
p
u
m
11
12
e
E
i 0
i
0
i 0
A
z
di 0
di
0
di 0
E
A
A
dt
dt
dt
z
sin
cos
ψ
ϕ
ω
λ
λ
ψ
ϕ
+
+
+
+
+
+
⎧
=
+
=
+
−
⎪⎪
⎨
⎪
=
+
=
+
+
−
⎪⎩
gdzie
( )
( )
( )
m
e
i 0
0
di 0
E
dt
L
sin
ψ
+
+
⎧
=
⎪
⎨
⎪
=
⎩
Ostatecznie układ równań do znalezienia stałych przyjmie postać:
(
)
( )
(
)
m
11
e
m
e
m
11
12
e
E
0
A
z
E
E
A
A
L
z
sin
sin
cos
ψ
ϕ
ψ
ω
λ
ψ
ϕ
⎧ = +
−
⎪⎪
⎨
⎪
=
+
+
−
⎪⎩
(
)
( )
(
)
(
)
m
11
e
R
e
e
2
e
m
12
E
A
z
Z
L
E
A
Z
L
sin
sin
cos
sin
ψ
ϕ
ψ
ω
ψ
ϕ
ψ
ϕ
⎧
= −
−
⎪⎪
⎨
−
−
−
−
⎪
=
⎪⎩
;
( )
( )
(
)
t
t
p
11
12
m
u
e
i
t
A e
A te
t
0
E
i t
t
z
,
sin
λ
λ
ω ψ
ϕ
=
+
>
=
+
−
6.2. Przypadek 2: Ostatecznie prąd w omawianym obwodzie zawiera zarówno składową
przejściową jak i ustaloną:
( )
( )
( )
p
u
i t
i
t
i t
dla t
0
,
=
+
>
®
14
Obwody Elektryczne i Magnetyczne
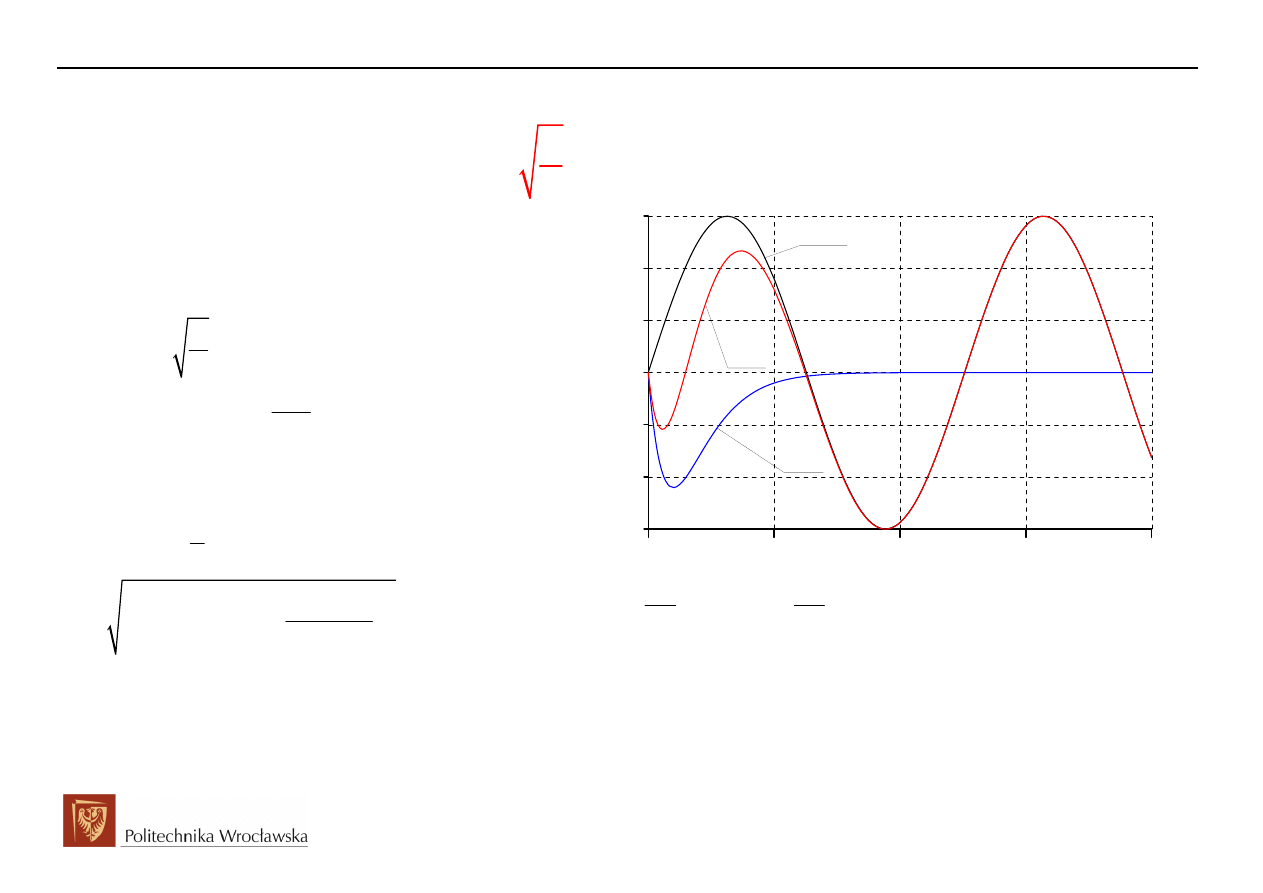
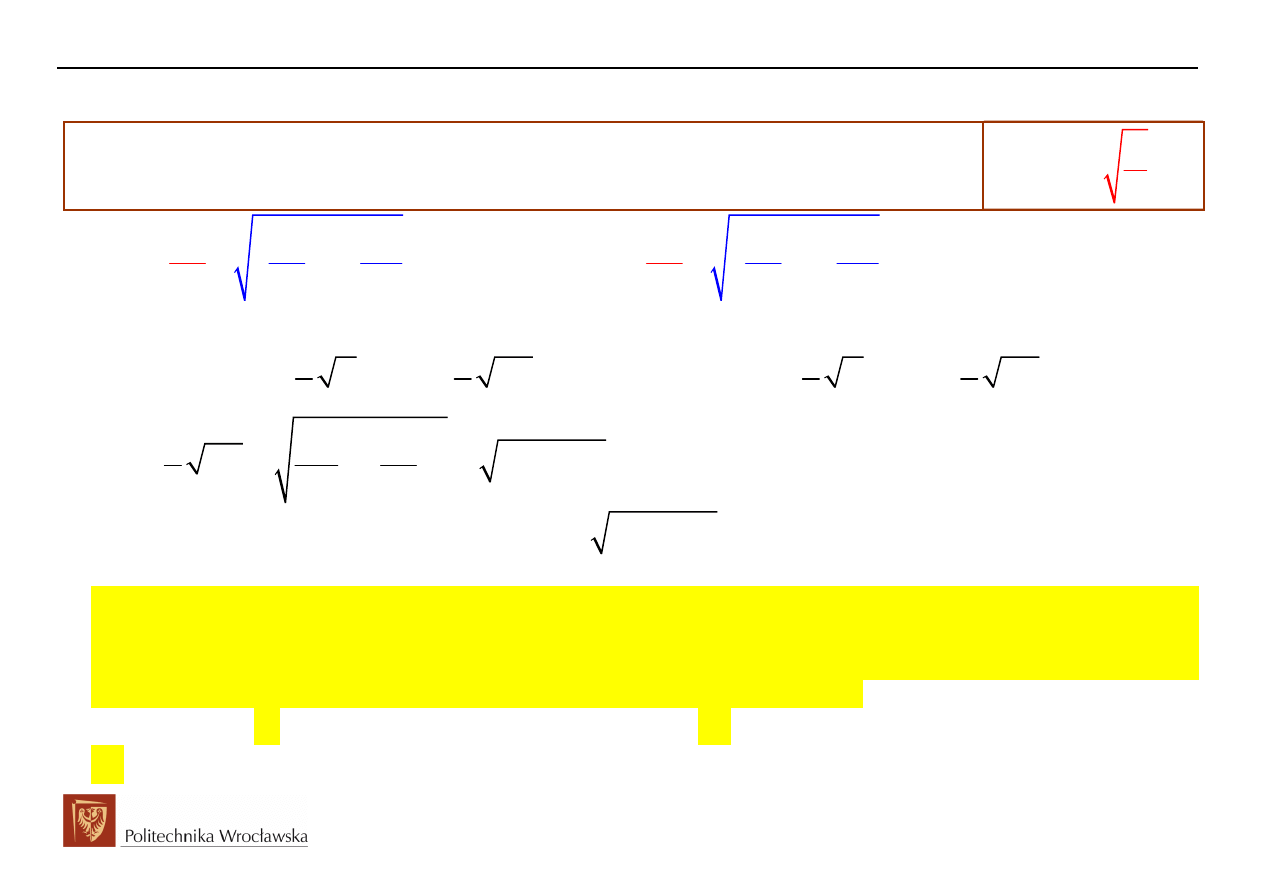
Przykład przebiegu stanu przejściowego w obwodzie RLC załączanym na napięcie sinusoidalne
dla przypadku 2,
0
Δ
=
,
L
R
2
C
=
- charakter aperiodyczny granicznie (graniczny)
Dane:
R = 200
Ω
, L = 0.1 H, C = 10
μ
F = 10
-5
F
( )
(
)
ω
= 500 s
-1
,
e
e t
300
500t
ψ
=
+
sin
czyli:
L
R
2
200
0
C
,
Ω β
=
=
=
3
1
,
r
10 s
ω
−
=
3
1
200
10 s
0 2
.
λ α
−
= = −
= −
UWAGA: Dla uproszczenia obliczeń dobrano
e
ψ
ϕ
=
[ ]
rad
3
arc
0 64
4
tg
.
ϕ
⎛
⎞
=
−
= −
⎜
⎟
⎝
⎠
2
2
5
1
Z
200
0 1 500
250
500 10
.
Ω
−
⎛
⎞
=
+
⋅
−
=
⎜
⎟
⋅
⎝
⎠
0.000
0.005
0.010
0.015
0.020
t [ s ]
-1.2
-0.8
-0.4
0.0
0.4
0.8
1.2
i(t)
i (t)
u
i (t)
p
( )
(
)
(
)
6
1000t
3
1000t
300
10
i t
500t
t
e
1 2
500t
t 2 10 e
A
250
500
sin
.
sin
−
−
⎡
⎤
⎡
⎤
=
− ⋅
⋅
=
− ⋅ ⋅
⎢
⎥
⎣
⎦
⎣
⎦
UWAGA: Porównaj z Przypadkiem 1. Rezystancja krytyczna nie uległa zmianie. Zmniejszyliśmy
rezystancję fizyczną R. Zmniejszył się współczynnik tłumienia α. Udział składowej przejściowej jest
większy.
®
15
Obwody Elektryczne i Magnetyczne
5.3. Przypadek 3:
, dwa pierwiastki zespolone sprzężone
0
Δ
<
1
2
2
1
,
;
*
λ λ λ
λ
=
®
16
Przewidywana postać składowej przejściowej
( )
1
2
t
t
p
11
21
i
t
A e
A e
t
0
,
λ
λ
=
+
>
L
R
2
C
<
2
1
R
1
2L
R
C
2L
L
α β
⎛
⎞ −
⎜
⎟
⎝
⎠
+
=
−
=
+
2
2
R
1
2L
C
L
R
2L
α β
⎛
⎞ −
⎜
⎟
⎝
⎠
−
=
−
λ
oraz
λ
=
−
,
przy czym
β
jest urojona. Jeśli zapiszemy pierwiastki w jawnej postaci zespolonej:
1
1
1
j
2
2
λ α β α
Δ α
Δ
= + = +
= +
−
oraz
2
1
1
j
2
2
λ
α β α
Δ α
Δ
= − = −
= −
−
gdzie:
0
2
2
2
r
1
1
R
2
LC
2L
Δ
ω
α
ω
⎛
⎞
− =
−
=
−
=
⎜
⎟
⎝
⎠
. , gdzie
2
2
r
0
ω
α
−
>
Stąd pierwiastki
1
0
2
0
j
j
;
λ α
ω λ
α
ω
= +
= −
,
0
2
2
r
ω
α
ω
−
=
UWAGA: Gdy rezystancja gałęzi RLC jest mniejsza od rezystancji krytycznej, przebieg prądu w gałęzi w
stanie nieustalonym od załączania napięcia stałego ma charakter aperiodyczny czyli okresowy
(oscylacyjny) o pulsacji
0
ω
. W odróżnieniu jednak od przypadku załączania na napięcie stałe, obwód
będzie dążył do ustalenia pracy z pulsacją źródła sinusoidalnego czyli
ω
.
Podsumujmy:
ω
- pulsacja źródła sinusoidalnego;
r
ω
- pulsacja rezonansowa obwodu RLC,
0
ω
- pulsacja oscylacji składowej przejściowej.

Obwody Elektryczne i Magnetyczne
Podobnie jak dla przypadku pierwszego szukamy z układu równań:
( )
( )
( )
( )
( )
( )
p
u
p
u
i t
i
t
i t
di
t
di t
di t
dt
dt
dt
=
+
⎧
⎪
⎨
=
+
⎪
⎩
, gdzie:
( )
( )
(
)
1
2
p
t
t
u
m
11 1
21
2
e
di
t
di t
E
A
e
A
e
t
dt
dt
z
,
cos
λ
λ
ω
λ
λ
ω ψ
ϕ
=
+
=
+
−
,
W szczególności dla t=0
+
:
( ) ( ) ( )
(
)
( )
( )
( )
(
)
m
p
u
11
21
e
p
u
m
11 1
21
2
e
E
i 0
i
0
i 0
A
A
z
di 0
di
0
di 0
E
A
A
dt
dt
dt
z
sin
cos
ψ
ϕ
ω
λ
λ
ψ
ϕ
+
+
+
+
+
+
⎧
=
+
=
+
+
−
⎪⎪
⎨
⎪
=
+
=
+
+
−
⎪⎩
( )
(
) (
)
(
)
( )
(
) (
)
(
)
m
m
m
11
m
m
m
21
E
E
E
L
z
z
A
2
E
E
E
L
z
z
A
2
sin
cos
sin
sin
cos
sin
ω
ψ
ψ ϕ
α β
ψ ϕ
β
ω
ψ
ψ ϕ
α β
ψ ϕ
β
⎧
−
−
+
−
−
⎪
=
⎪
⎪
⎨
⎪
−
−
+
+
−
⎪
=
⎪
−
⎩
®
17
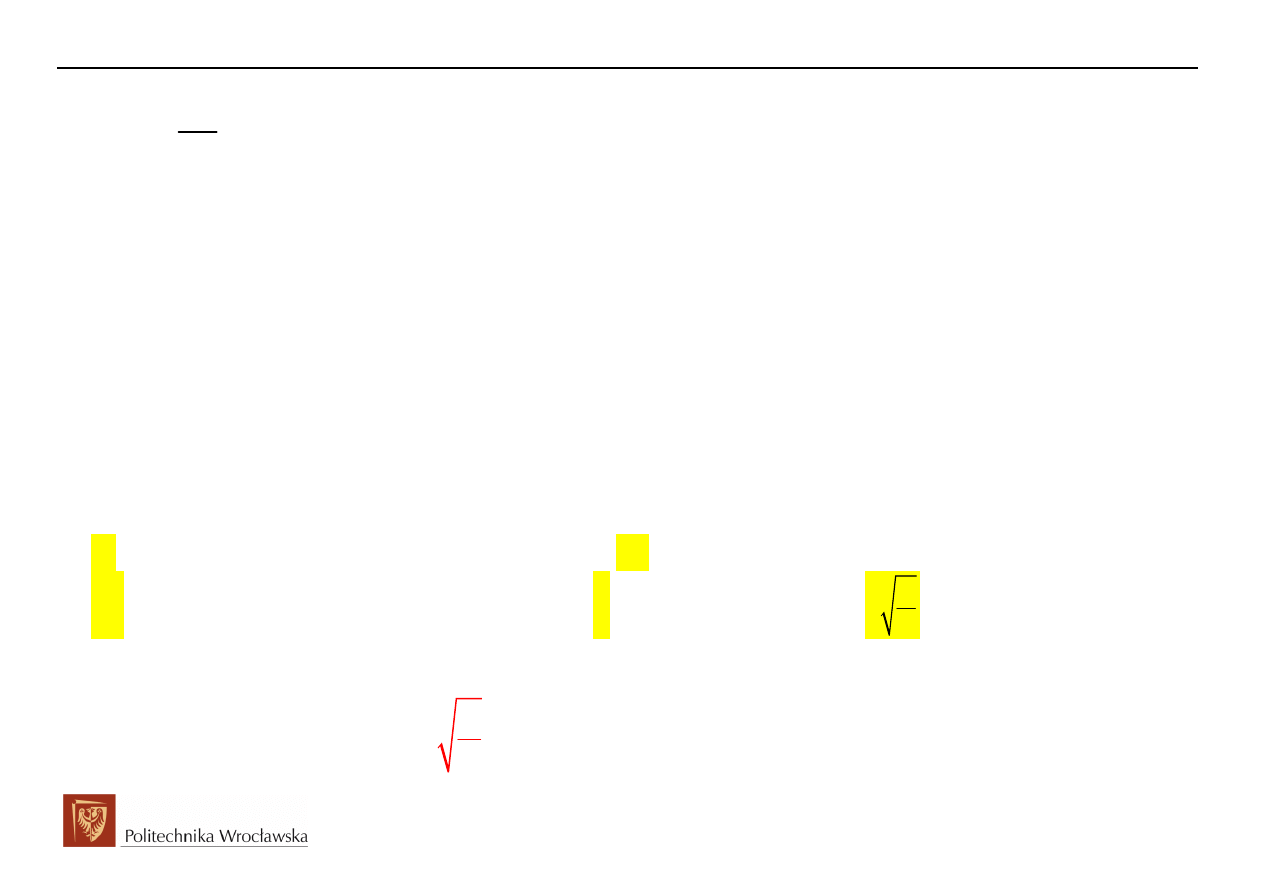
Obwody Elektryczne i Magnetyczne
( )
(
)
m
u
e
E
i t
t
z
sin
ω ψ
ϕ
=
+
−
( ) (
)
( ) (
)
( )
0
0
t
p
21
11
11
21
i
t
A
A
j
t
A
A
t
e
sin
cos
α
ω
ω
=
−
+
+
⋅
⎡
⎤
⎣
⎦
Uwaga:
21
11
A
A
−
jest liczbą urojoną i po wymnożeniu z „j” przy
( )
0
t
ω
sin
da współczynnik rzeczywisty
(
)
11
21
A
A
+
jest liczbą rzeczywistą dając rzeczywisty współczynnik przy
( )
0
t
ω
cos
6.3. Przypadek 3: Ostatecznie prąd w omawianym obwodzie zawiera zarówno składową
przejściową jak i ustaloną:
( )
( )
( )
p
u
i t
i
t
i t
dla t
0
,
=
+
>
Stan przejściowy w gałęzi RLC załączanej na napięcie sinusoidalne reprezentuje ciekawy przypadek
pracy obwodu elektrycznego gdzie do głosu dochodzą charakterystyczne cechy tego obwodu:
ω
- pulsacja źródła sinusoidalnego;
r
ω
- pulsacja rezonansowa obwodu RLC,
L
2
C
®
18
0
ω
- pulsacja oscylacji składowej przejściowej, R – rezystancja fizyczna,
- rezystancja krytyczna.
Prześledzimy teraz różnice w zachowaniu się obwodu w stanie przejściowym w zależności od relacji
przywołanych tu parametrów. Wspólną cechą rozważań jest sytuacja:
L
R
2
C
<
- charakter periodyczny (oscylacyjny)
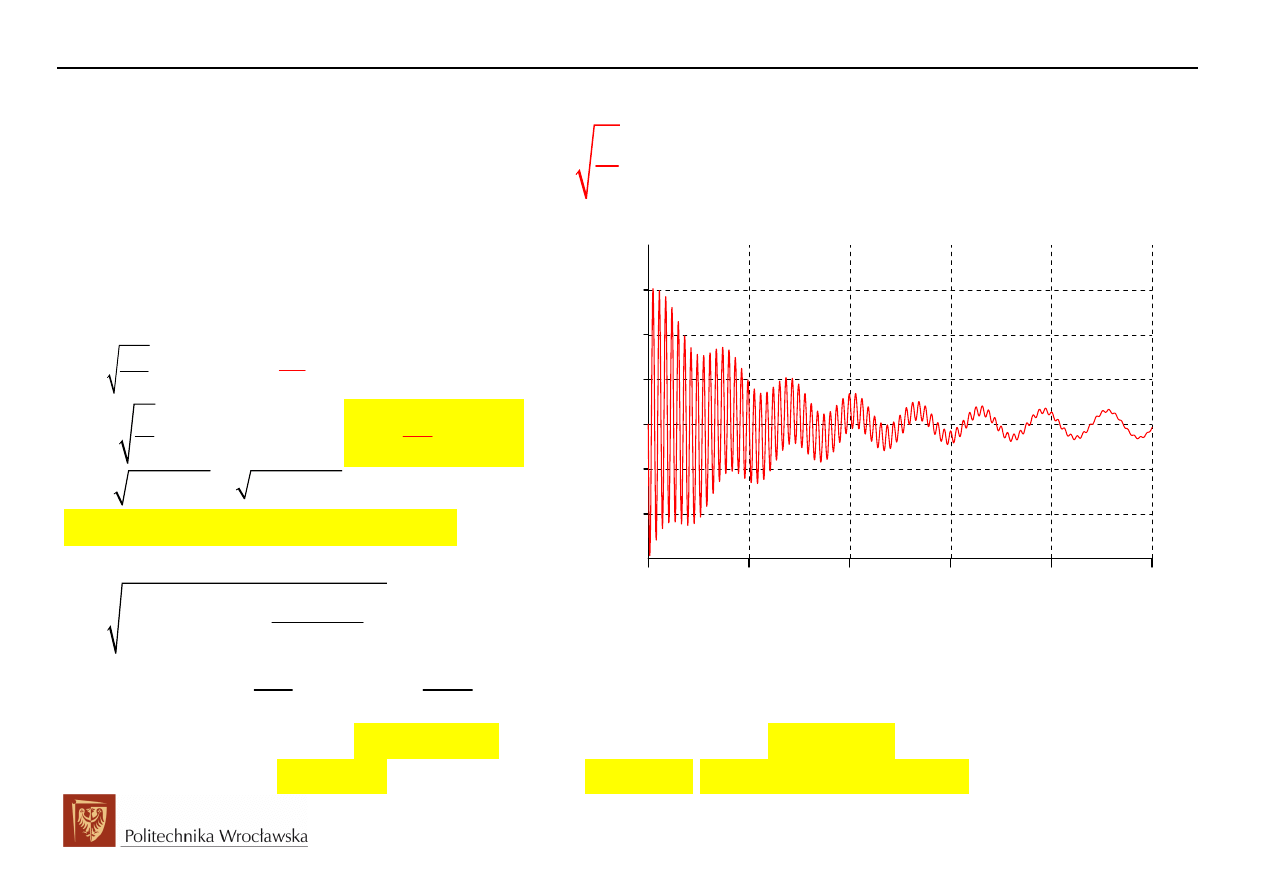
Obwody Elektryczne i Magnetyczne
Przykład przebiegu stanu przejściowego w obwodzie RLC załączanym na napięcie sinusoidalne
dla przypadku 3,
0
Δ
<
,
L
R
2
C
<
- charakter periodyczny (oscylacyjny)
®
19
DODATKOWO:
(
)
r
R
0
0 ,
α
ω
ω
≈ → ≈
<<
1
100s
ω
−
=
R = 2
Ω
, L = 0.1 H, C = 10
μ
F = 10
-5
F ,
,
( )
(
)
e
e t
300
100t
ψ
=
+
sin
;
3
1
r
1
10 s
LC
ω
−
=
=
⇒
r
10
ω
ω
≈
(
)
r
R
0 ,
;
ω
ω
≈
<<
L
R
2
2
200
C
Ω
Ω
<
⎯⎯
→
<
;
1
R
10s
2L
α
−
= −
= −
;
0
2
2
6
2
1
1
r
10
10 s
999 95s
ω
ω
α
−
−
=
−
=
−
≈
.
1
100s
ω
−
=
;
;
1
0
999 95s
ω
−
≈
.
1
r
1000s
ω
−
=
UWAGA: Dla uproszczenia obliczeń dobrano
e
ψ
ϕ
=
;
2
2
5
1
Z
2
0 1 100
990
100 10
.
Ω
−
⎛
⎞
=
+
⋅
−
≈
⎜
⎟
⋅
⎝
⎠
0.0
0.1
0.2
0.3
0.4
0.5
t [ s ]
-2.0
-1.0
0.0
1.0
2.0
3.0
i(t) = i (t) + i (t)
u
p
( )
(
)
(
)
(
)
(
)
10t
10t
300
1000
i t
100t
e
999 95t
0303
100t
10e
999 95t
A
990
100
sin
sin
.
sin
sin
.
−
−
⎡
⎤
⎡
⎤
≅
−
≈
−
⎣
⎦
⎢
⎥
⎣
⎦
Oscylacje z pulsacją
1
0
999 95s
ω
−
≈
.
1
r
1000s
ω
bliską rezonansowej
−
=
tłumione wykładniczo ze
współczynnikiem
1
10s
α
−
= −
1
100s
ω
−
=
do pulsacji źródła
dalekiej od rezonansowej
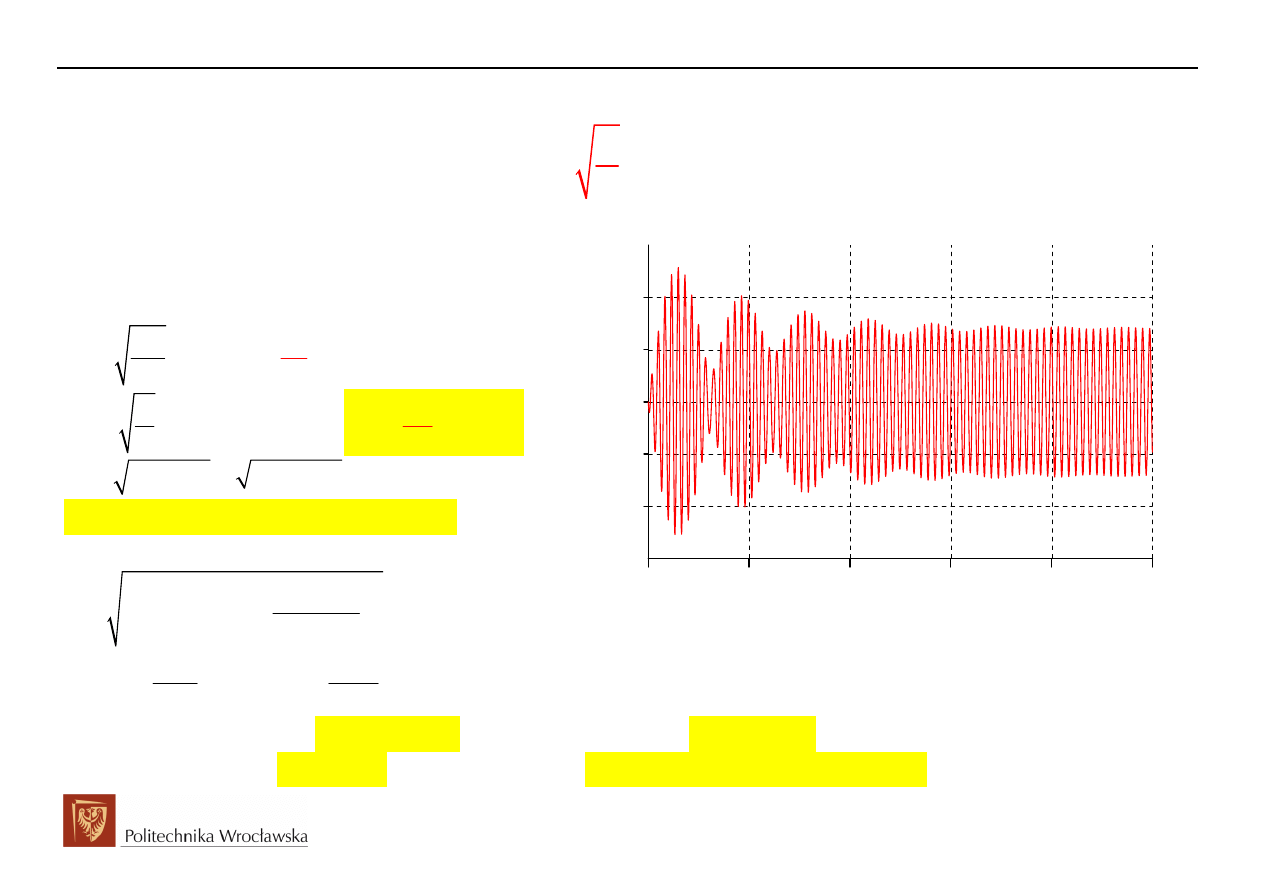
Obwody Elektryczne i Magnetyczne
Przykład przebiegu stanu przejściowego w obwodzie RLC załączanym na napięcie sinusoidalne
dla przypadku 3,
0
Δ
<
,
L
R
2
C
<
- charakter periodyczny (oscylacyjny)
DODATKOWO:
(
)
r
R
0
0,
α
ω ω
≈ → ≈
≈
1
900s
ω
−
=
R = 2
Ω
, L = 0.1 H, C = 10
μ
F = 10
-5
F ;
( )
(
)
e
e t
30
900t
ψ
=
+
sin
;
,
3
1
r
1
10 s
LC
ω
−
=
=
⇒
r
1 11
.
ω
ω
≈
(
)
r
R
0 ,
ω ω
≈
≈
;
L
R
2
2
200
C
Ω
Ω
<
⎯⎯
→
<
;
®
20
1
R
10s
2L
α
−
= −
= −
;
0
2
2
6
2
1
1
r
10
10 s
999 95s
ω
ω
α
−
−
=
−
=
−
≈
.
1
900s
ω
−
=
;
;
1
0
999 95s
ω
−
≈
.
1
r
1000s
ω
−
=
UWAGA: Dla uproszczenia obliczeń dobrano
e
ψ
ϕ
=
;
2
2
5
1
Z
2
0 1 900
21 2
900 10
.
.
Ω
−
⎛
⎞
=
+
⋅
−
≈
⎜
⎟
⋅
⎝
⎠
0.0
0.1
0.2
0.3
0.4
0.5
t [ s ]
-2.0
-1.0
0.0
1.0
2.0
i(t) = i (t) + i (t)
u
p
( )
(
)
(
)
(
)
(
)
10t
10t
30
1000
i t
900t
e
999 95t
1 42
900t
1 11e
999 95t
A
21 2
900
sin
sin
.
.
sin
.
sin
.
.
−
−
⎡
⎤
⎡
⎤
≅
−
≈
−
⎣
⎦
⎢
⎥
⎣
⎦
Oscylacje z pulsacją
1
0
999 95s
ω
−
≈
.
1
r
1000s
ω
bliską rezonansowej
−
=
tłumione wykładniczo ze
współczynnikiem
1
10s
α
−
= −
1
900s
ω
−
=
do pulsacji źródła
bliskiej rezonansowej
Obwody Elektryczne i Magnetyczne
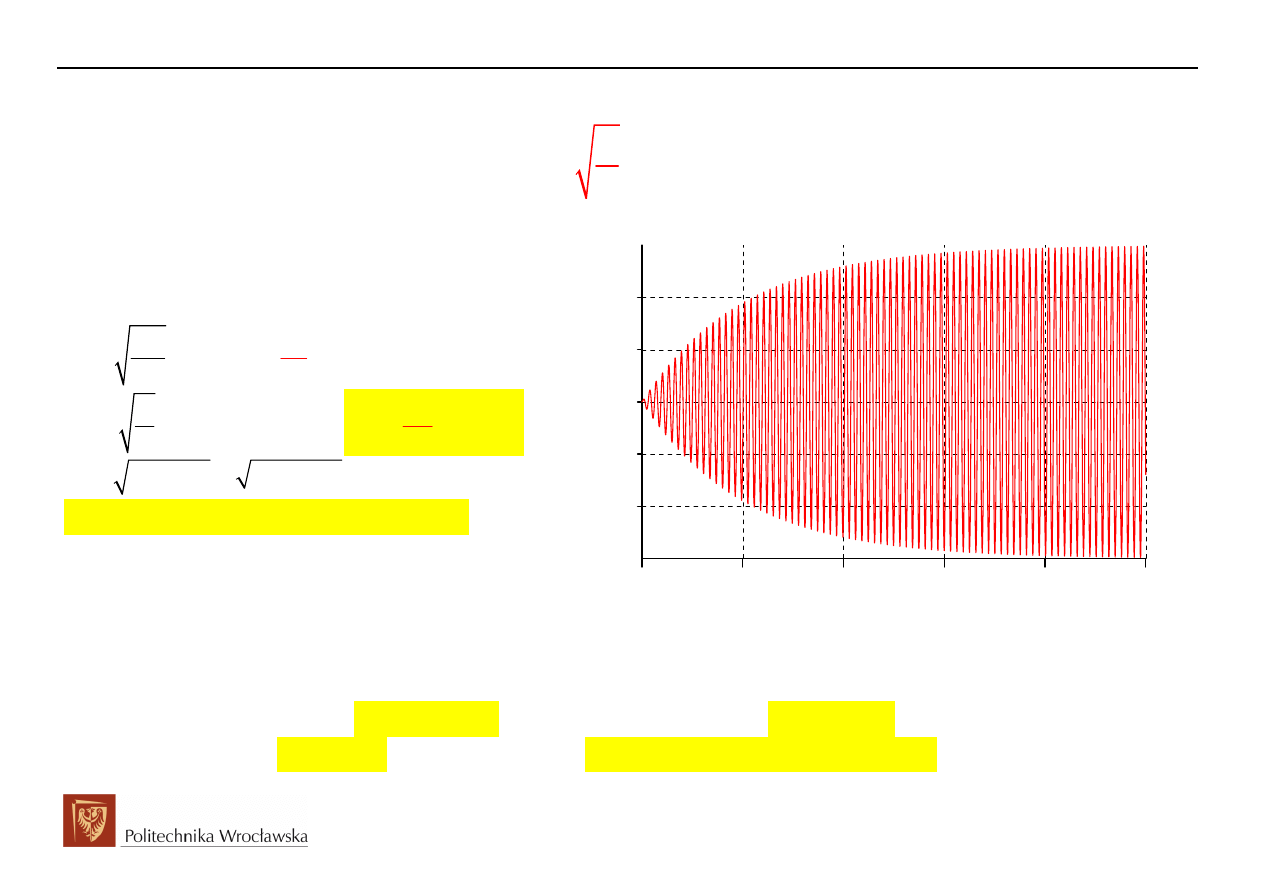
Przykład przebiegu stanu przejściowego w obwodzie RLC załączanym na napięcie sinusoidalne
dla przypadku 3,
0
Δ
<
,
L
R
2
C
<
- charakter periodyczny (oscylacyjny)
DODATKOWO:
(
)
r
R
0
0,
α
ω ω
≈ → ≈
=
1
1000s
ω
−
=
R = 2
Ω
, L = 0.1 H, C = 10
μ
F = 10
-5
F;
( )
(
)
e
e t
30
1000t
ψ
=
+
sin
;
,
3
1
r
1
10 s
LC
ω
−
=
=
⇒
r
1
ω
ω
=
(
)
r
R
0 ,
;
ω ω
≈
=
L
R
2
2
200
C
Ω
Ω
<
⎯⎯
→
<
;
®
21
1
R
10s
2L
α
−
= −
= −
;
0
2
2
6
2
1
1
r
10
10 s
999 95s
ω
ω
α
−
−
=
−
=
−
≈
.
1
1000s
ω
−
=
;
;
1
0
999 95s
ω
−
≈
.
1
r
1000s
ω
−
=
UWAGA: Dla uproszczenia obliczeń dobrano
e
0
ψ
ϕ
= =
;
Z
R
2
Ω
= =
0.0
0.1
0.2
0.3
0.4
0.5
t [ s ]
-10
-5
0
5
10
i(t) = i (t) + i (t)
u
p
( )
(
)
10t
i t
15
1 e
1000t
A
sin
−
⎡
⎤
≅
⋅ −
⋅
⎣
⎦
Oscylacje z pulsacją
1
0
999 95s
ω
−
≈
.
1
r
1000s
ω
bliską rezonansowej
−
=
tłumione wykładniczo ze
współczynnikiem
1
10s
α
−
= −
1
1000s
ω
−
=
do pulsacji źródła
równej rezonansowej.
Wyszukiwarka
Podobne podstrony:
OEiM AiR W03 MetodaKlasyczna cz Nieznany
OEiM AiR W02 MetodaKlasyczna cz1
OEiM AiR W07 LaplaceiMoperatoro Nieznany
OEiM AiR W09 LaplaceiTransmitan Nieznany
Pelnomocnictwo (do dokonania cz Nieznany
CONTROLLING JAKO METODA ZARZADZ Nieznany
Orzecznictwo lekarskie Cz 1 S Nieznany
AKADEMIA WIZAA U GOSHA cz 1 i Nieznany (2)
Kanalizacja dlaczego i po co cz Nieznany
Oznaczanie fenoli metoda z 4 am Nieznany
Orzecznictwo lekarskie Cz 2 O Nieznany
Farm klin cz 1 Nieznany
AM23 w02 Szeregi liczbowe cz 1 Nieznany
Metodologia badan naukowych cz Nieznany
diagnoza otepienia skroniowo cz Nieznany
Biologia stara matura 2004 cz 1 Nieznany
więcej podobnych podstron