Obwody Elektryczne i Magnetyczne
®
1
Obwody Elektryczne
Transformata Laplace’a oraz jej wykorzystanie w analizie
stanu nieustalonego metodą operatorową – część II
Prowadzący: dr inż. Tomasz Sikorski
Instytut Podstaw Elektrotechniki i Elektrotechnologii
Wydział Elektryczny
Politechnika Wrocławska
D-1, 205/1
tel: (071) 320 21 60
fax: (071) 320 20 06
email:
Obwody Elektryczne i Magnetyczne
®
2
Załączanie szeregowej gałęzi RL na napięcie stałe ......................................................................................................................................................... 10
Obwód rozgałęziony zawierający gałęzie aktywne, dwa oczka ...................................................................................................................................... 14
Wymuszenie sinusoidalne oraz metoda wektora wirującego .......................................................................................................................................... 24
Obwody Elektryczne i Magnetyczne
®
3
1. Metoda operatorowa
Metoda klasyczna analizy pracy obwodu elektrycznego w stanie nieustalonym bazowała na różniczkowo-
całkowych związkach prądowo-napięciowych na elementach obwodu. Pozytywnym aspektem takiego
podejścia było przede wszystkim zachowanie wszystkich kroków analizy w dziedzinie czasu i tym samym
ukłon w kierunku fizyki elementów RLC z nierozerwalnymi związkami różniczkowo-całkowymi, z prawem
zachowania energii czy ciągłości prądów płynących przez cewkę i napięć na kondensatorach. Za
negatywną stronę metody klasycznej można uznać pracochłonne i czasochłonne działania związane z
wyodrębnieniem i rozwiązaniem równania różniczkowego, zwłaszcza w przypadku obwodów wyższego
rzędu.
Wprowadzenie transformaty Laplace’a przenosi ciężar zapisu sygnału z dziedziny czasu do dziedziny
zmiennej zespolonej s, która nosi nazwę operatora s. Adaptacja tej metody w analizie obwodów
elektrycznych stwarza automatycznie dwa podstawowe pytania o wykorzystanie w:
1. zapisie równań Kirchhoffa,
2. zapisie związków prądowo-napięciowych na elementach RLC.
Czy uda się zapisać równania Kirchhoffa w zapisie operatorowym? Jak będą wyglądać związki
różniczkowo-całkowe w zapisie operatorowym i czy ich forma pozwoli na uproszczenie operacji
matematycznych potrzebnych do rozwiązania obwodu?
Odpowiedź na większość z tak stawianych pytań jest pozytywna, do tego stopnia, że reprezentacja
związków prądowo-napięciowych na elementach RLC skutkuje nawet ich operatorowymi schematami
zastępczymi, tzn. „transformacji Laplace’a” możemy poddać cały obwód, z istniejącymi w nim sygnałami
napięć i prądów, oraz elementami i gałęziami. Tak wprowadzimy pojecie schematu operatorowego.
Podobną filozofię stosowaliśmy w metodzie symbolicznej analizy obwodu w stanie ustalonym przy
wymuszeniu sinusoidalnym. Jednak w przypadku transformacji Laplace’a mamy do czynienia z pełną, nie
tylko symboliczną, reprezentacją.
Obwody Elektryczne i Magnetyczne
1.1 Prawa Kirchhoffa w zapisie operatorowym
Dla dowolnego czasu t prądy
( )
k
i t spełniają w danym przekroju (węźle) obwodu I-prawo Kirchhoffa
(algebraiczna suma prądów w przekroju (węźle) równa jest zero). Nałożenie liniowej operacji transformacji
Laplace’a pozwala zauważyć, że I-prawo Kirchhoffa jest zachowane również dla transformat prądów:
Dziedzina czas t
Dziedzina operatorowa (zespolona) s
( )
k
k
i t
0
=
∑
( )
k
k
I s
0
=
∑
Na podstawie liniowości przekształcenia Laplace’a :
{
®
4
( )
( )
}
( )
( )
1
2
1
2
af t
bf t
aF s
bF s
±
=
±
L
Identycznie możemy zaadoptować transformację Laplace’a w przypadku II prawa Kirchhoffa, gdzie
możemy powiedzieć, że algebraiczna suma transformat napięć oraz źródeł napięciowych w oczku jest
równa zero:
Dziedzina czas t
Dziedzina operatorowa (zespolona) s
( )
n
n
u t
0
=
∑
( )
n
n
U s
0
=
∑
Na podstawie liniowości przekształcenia Laplace’a :
{
( )
( )
}
( )
( )
1
2
1
2
af t
bf t
aF s
bF s
±
=
±
L
Obwody Elektryczne i Magnetyczne
1.2 Równania dla elementów RLC w zapisie operatorowym – elementy schematu
operatorowego
Adaptacja transformacji Laplace’a w opisie relacji prądowo-napięciowych na elementach RLC
wykorzystuje następujące właściwości przekształcenia:
( )
( )
{
}
( )
( )
1
2
1
2
af t
bf t
aF s
bF s
±
=
±
L
liniowość przekształcenia
( )
{
}
( )
( )
f t
s
s
f 0
'
F
−
=
−
L
transformata
pochodnej
( )
{
}
( )
1
C
f t dt
s
s
s
F
=
+
∫
L
transformata
całki
Znaczącym pozytywnym aspektem wykorzystanie transformacji Laplace’a w opisie RLC jest zastąpienie
funkcjonałów różniczkowo-całkowych przez algebraiczne relacje pomiędzy transformatami napięć i prądów
oraz parametrów obwodu. Prowadzi to do schematów operatorowych elementów obwodu.
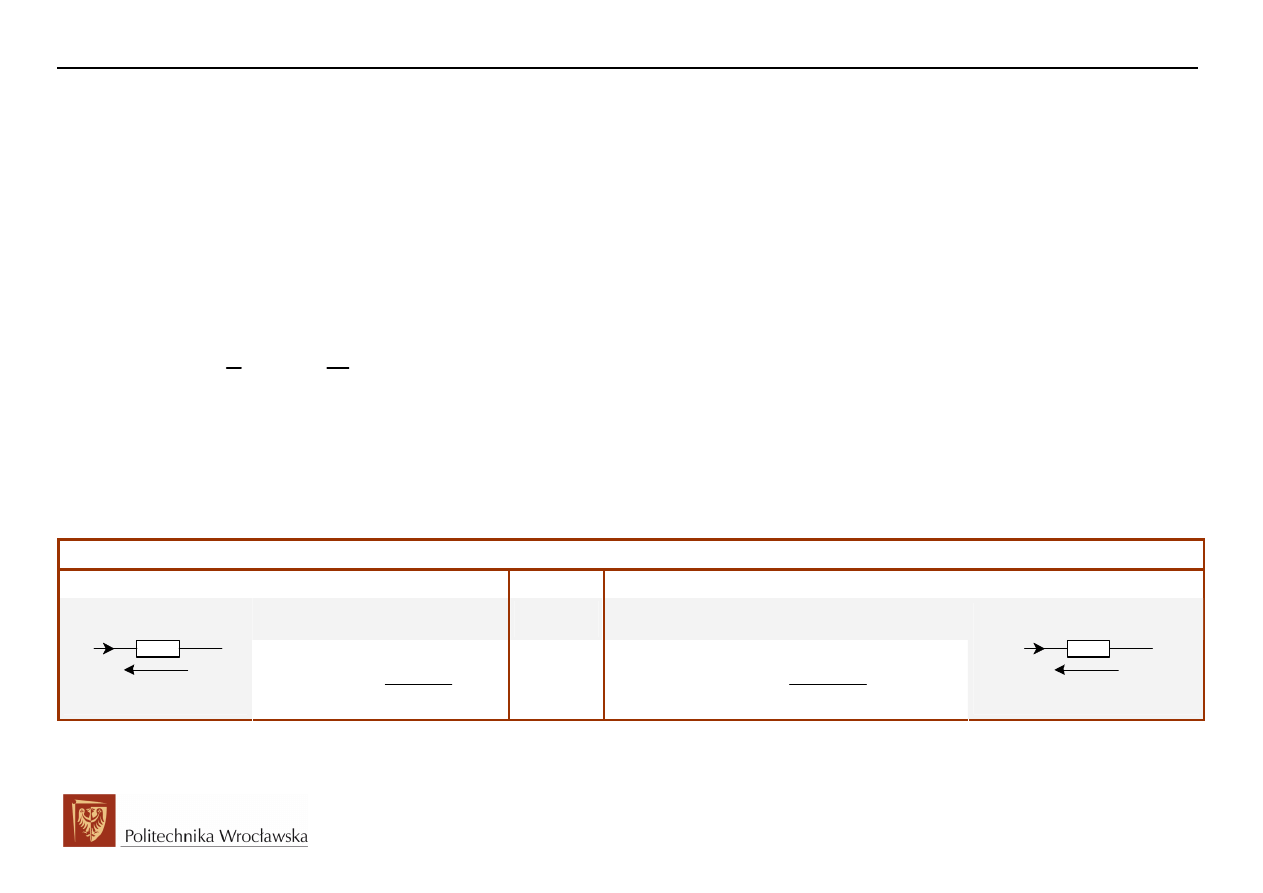
REZYSTOR:
Dziedzina czas t
Dziedzina operatorowa (zespolona) s
( )
( )
R
u t
Ri t
=
L
⎯⎯
→
( )
( )
U
I
R
s
R
s
=
R
i(t)
u
R
(t)
( )
( )
R
u t
i t
R
=
( )
( )
I
R
U s
s
R
=
R
I(s)
U
R
(s)
®
5
Obwody Elektryczne i Magnetyczne
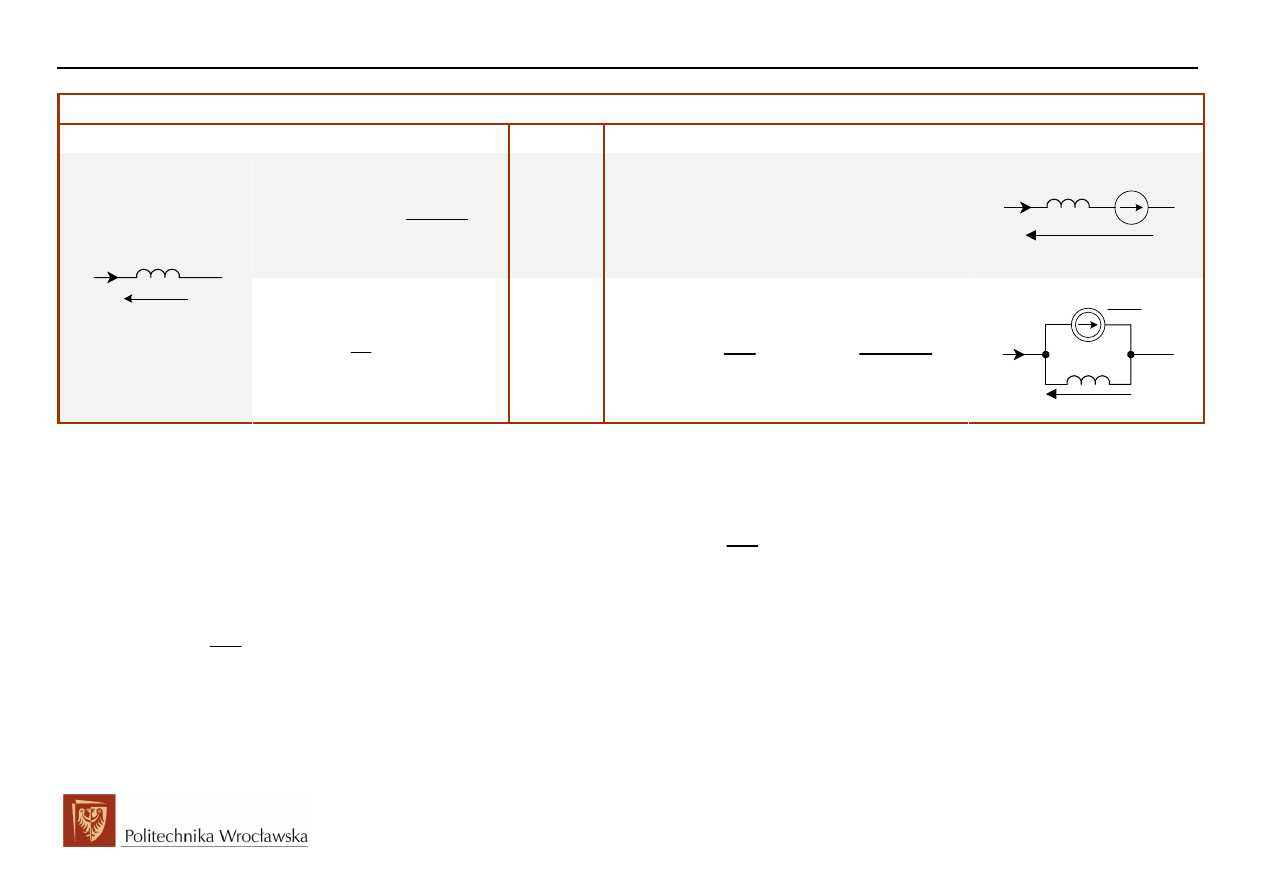
CEWKA:
Dziedzina czas t
Dziedzina operatorowa (zespolona) s
( )
( )
L
di t
u t
L
dt
=
L
⎯⎯
→
( )
( )
( )
(
)
( )
( )
U
L
s
L sI s
i 0
sLI s
Li 0
−
−
=
−
=
=
−
U
L
(s)
sL
Li(0-)
I(s)
L
i(t)
u
L
(t)
( )
( )
L
1
i t
u t dt
L
=
∫
L
⎯⎯
→
( )
( ) ( )
I
U
L
i 0
1
s
s
sL
s
−
=
+
I(s)
sL
s
i(0-)
U
L
(s)
UWAGA:
Dla zerowych warunków początkowych związek prądowo-napięciowy transformat przyjmie postać:
( )
( ) ( )
( )
U
,
U
L
L
1
s
sL I s I s
s
sL
=
⋅
=
co należy odczytywać jako prawo Ohma dla transformat lub operatorowe prawo Ohma dla cewki.
Składniki
,
1
sL
sL
można zatem traktować jako impedancje oraz admitancje operatorowe cewki.
®
6
Obwody Elektryczne i Magnetyczne
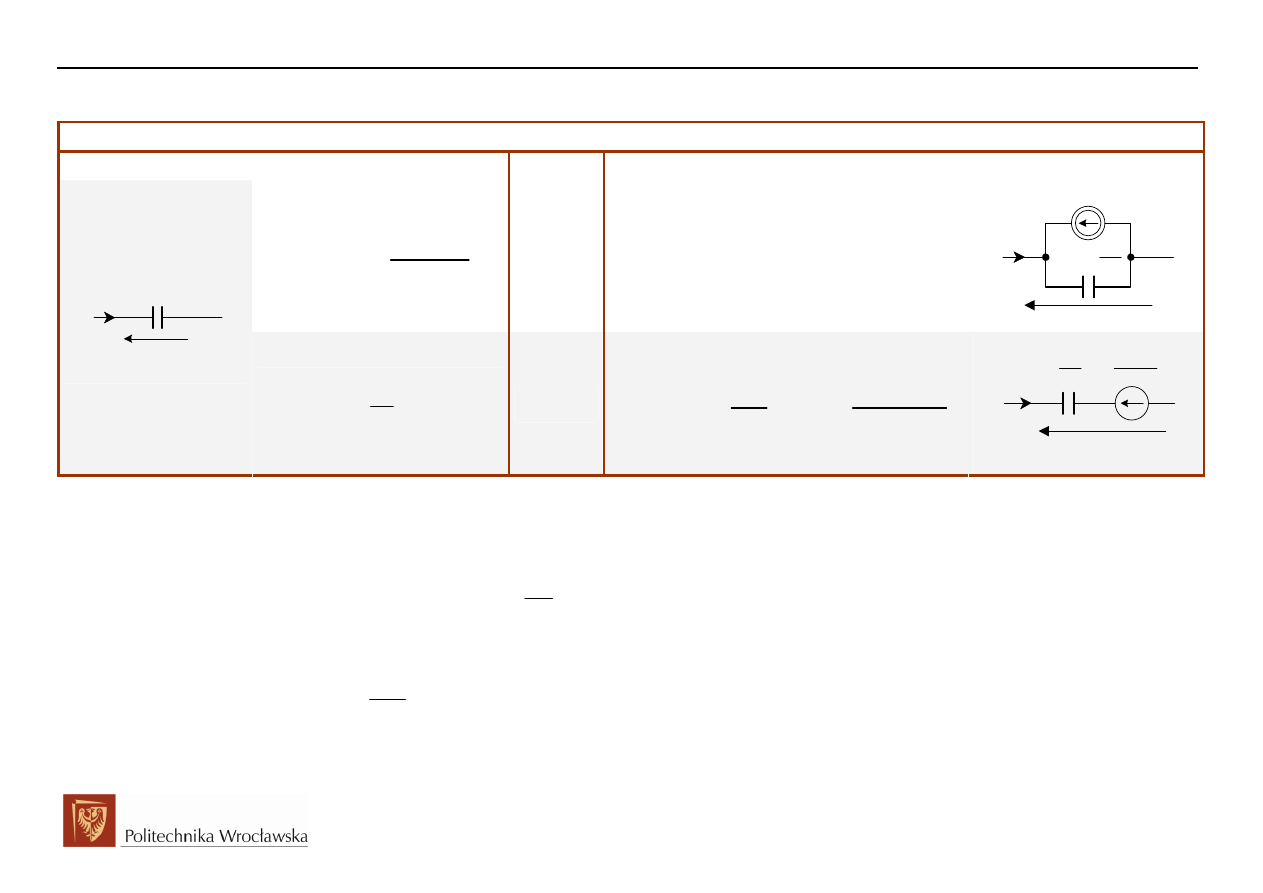
KONDENSATOR:
Dziedzina czas t
Dziedzina operatorowa (zespolona) s
( )
( )
c
du t
i t
C
dt
=
L
⎯⎯
→
( )
( )
( )
(
)
( )
( )
c
C
C
C
I s
C sU s
u 0
sCU s
Cu 0
−
−
=
−
=
=
−
Cu
c
(0-)
I(s)
sC
1
U
C
(s)
C
i(t)
u
c
(t)
( )
( )
C
1
u t
i t dt
C
=
∫
L
⎯⎯
→
( )
( )
( )
C
C
u 0
1
U s
I s
sC
s
−
=
+
I(s)
U
C
(s)
sC
1
s
u
C
(0-)
UWAGA:
Dla zerowych warunków początkowych związek prądowo-napięciowy transformat przyjmie postać:
( )
( ) ( )
( )
U
,
U
C
C
1
s
I s I s
sC
s
sc
=
⋅
=
⋅
co należy odczytywać jako prawo Ohma dla transformat lub operatorowe prawo Ohma dla
kondensatora. Składniki
,
1
sC
sC
można zatem traktować jako impedancje oraz admitancje
operatorowe kondensatora.
®
7
Obwody Elektryczne i Magnetyczne
1.3 Impedancja, admitancja operatorowa, prawo Ohma w zapisie operatorowym
Idąc dalej, dla zerowych warunków początkowych, możemy wprowadzić pojęcie impedancji
operatorowej
( )
Z s
oraz admitancji operatorowej
( )
Y
, zarówno dla gałęzi jak i zastępczych połączeń
szeregowo-równoległych.
s
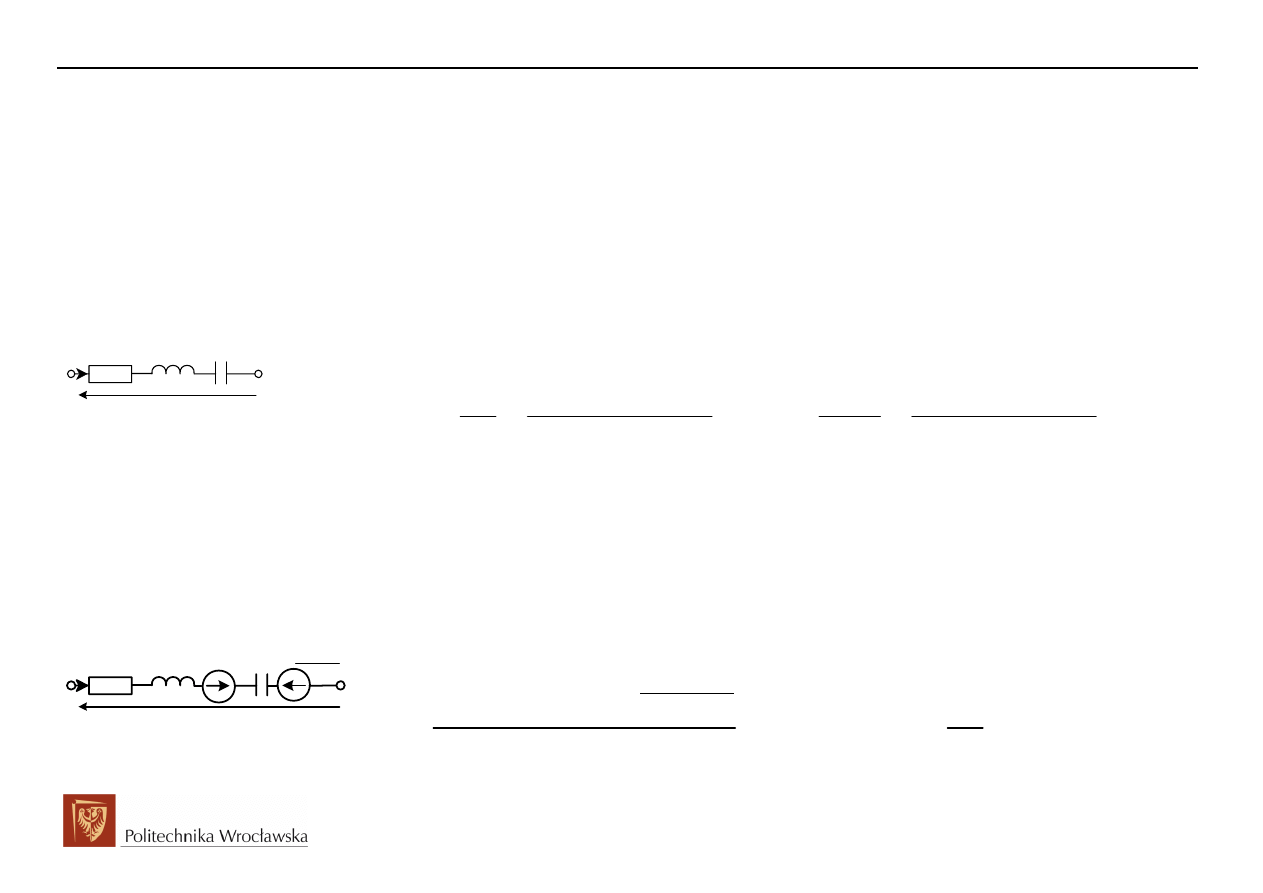
Przykład dla szeregowej pasywnej gałęzi RLC:
R
sL
1/sC
I(s)
U(s)
( )
2
1
s LC sRC 1
Z s
R sL
®
8
sC
sC
+
+
= +
+
=
,
( )
( )
2
1
sC
Y s
Z s
s LC sRC 1
=
=
+
+
Ostatecznie przy zerowych warunkach początkowych reprezentację prawa Ohma w postaci
operatorowej można zapisać jako:
( )
( ) ( ) ( )
( ) ( )
U
,
U
s
Z s I s I s
Y s
s
=
⋅
=
⋅
Przykład dla szeregowej aktywnej gałązi RLC:
R
sL
1/sC
I(s)
U(s)
( )
C
u 0
s
−
( )
Li 0
−
( )
( )
( )
( )
( )
( )
;
C
u 0
U s
Li 0
1
s
I s
Z s
R sL
Z s
sC
−
+
− −
=
= +
+
Obwody Elektryczne i Magnetyczne
PODSUMOWANIE:
Zastosowanie transformacji Laplace’a w ujęciu prądów i napięć w obwodzie zachowuje w pełni
najważniejsze prawa obwodowe tj. I-go oraz II-go prawa Kirchhoffa. Transformacji podlegają nie
tylko sygnały, ale możemy mówić o transformacji całego obwodu, łącznie z elementami. Prowadzi
to do adaptacji znanych już pojęć, lecz tym razem w znaczeniu operatorowym, takich jak.
impedancja oraz admitancja operatorowa czy operatorowe prawo Ohma.
Jeśli uda nam się przetrasformować w pełni obwód, czyli zarówno pod względem napięć, prądów,
wymuszeń, elementów, to możemy mówić o SCHEMACIE OPERATOROWYM OBWODU.
UWAGA: Do rozwiązania napięć i prądów w schemacie operatorowym możemy wykorzystać
wszystkie dostępne metody obwodowe. Stanowi to podstawę tzw. METODY OPERATOROWEJ.
Ostatecznie po rozwiązaniu obwodu metodą operatorową, szukane sygnały napięć czy prądów
możemy odnaleźć jako transformatę odwrotną.
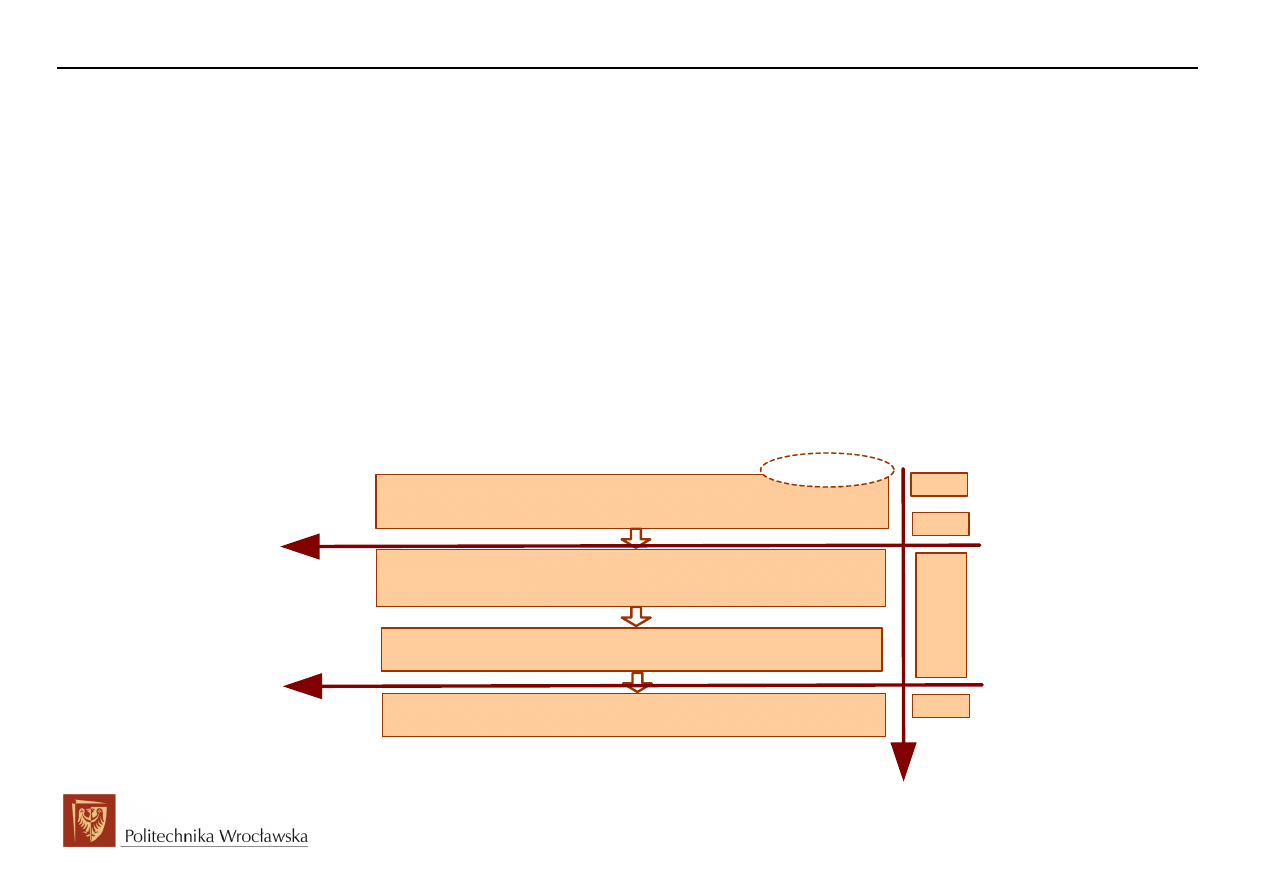
Analiza obwodu w stanie ustalonym przed komutacją
Warunek początkowy dla t=0-
Utworzenie schematu operatorowego z uwzględnieniem warunków
początkowych, źródeł
Wybór metody obwodowej oraz rozwiązanie obwodu ze względu na
szukane prądy, napięcia w postaci transformat
t<0
t=0-
Metoda
o
pe
ratorow
a
Historia obwodu
Wyznaczenie transformaty odwrotnej szukanych sygnałów napięć oraz
prądów
t>0
®
9
Obwody Elektryczne i Magnetyczne
1.4 Przykłady analizy stanu nieustalonego metodą operatorową
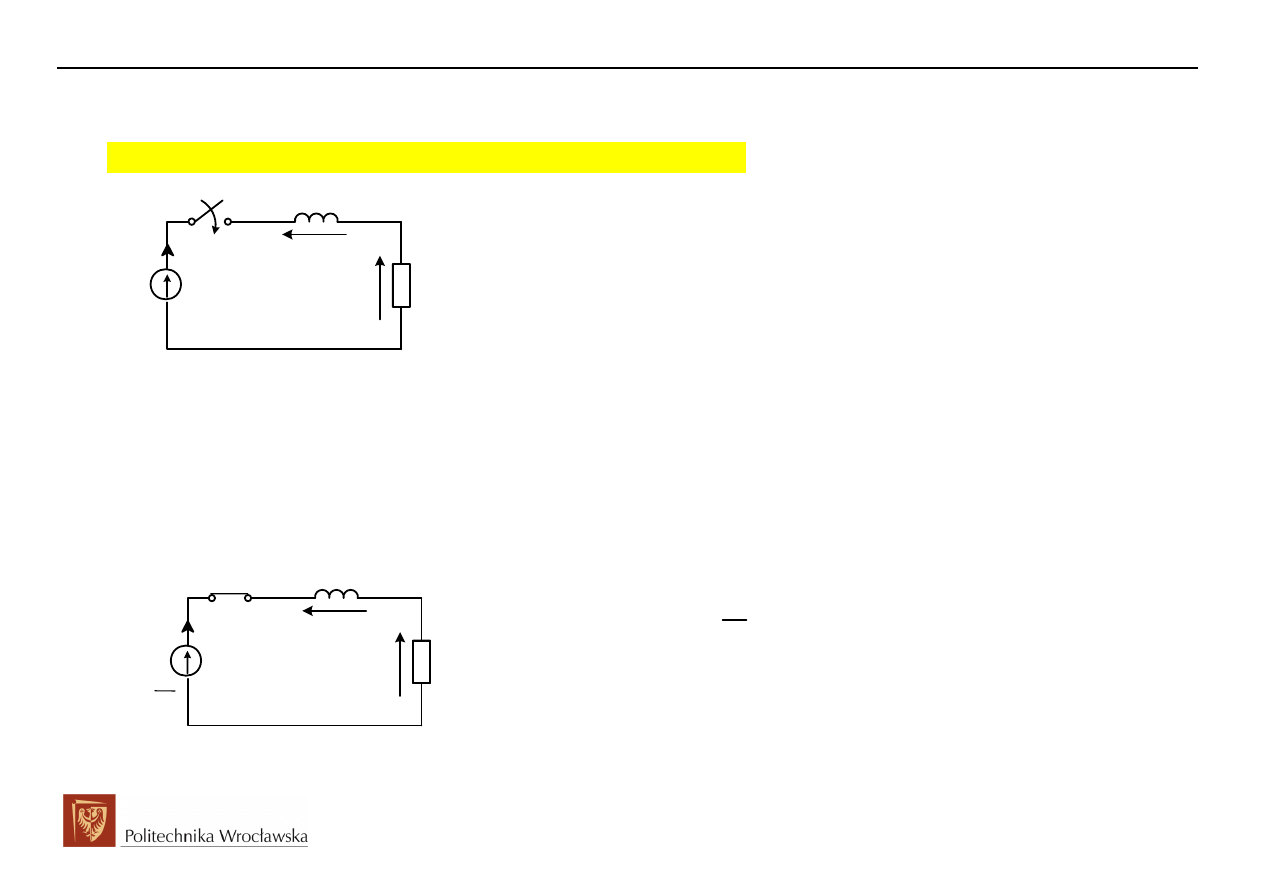
Załączanie szeregowej gałęzi RL na napięcie stałe
Dane:
( )
.
,
e t
E const
R L
= =
Szukane:
( )
i t
E
R
L
t = 0
u
L
(t)
i(t)
1. t<0, Analiza obwodu w stanie ustalonym przed komutacją (historia obwodu) oraz
wyznaczenie warunku początkowego dla t=0-
( )
i t
0 A
=
( )
i 0
0 A
−
=
2. Schemat operatorowy po komutacji
Dane:
®
10
E
R
sL
U
L
(s)
I(s)
E(s)= s
U
R
(s)
( )
( )
{ }
,
L
E
E s
e t
s
R sL
=
=
( )
0
0
Li
−
=
zerowe
warunki początkowe
Szukane:
( )
I s
Obwody Elektryczne i Magnetyczne
Ze względu na zerowe warunki początkowe obwód reprezentuje schemat z jednym
wymuszeniem operatorowym i układem połączeń impedancji operatorowych. Wykorzystamy
metodę przekształceń (redukcji obwodu).
( )
Z s
R sL
= +
Dalej prawo Ohma operatorowo:
( )
( )
( )
(
)
(
)
E s
E
E
1
I s
R
Z s
s R sL
L s s
L
=
=
=
+
+
3. Szukane
( )
i t
znajdziemy jak transformatę odwrotną
( )
I s
Po pierwsze przygotowujemy informacje o liczniku i mianowniku danej transformaty:
( )
{ }
st L s
0
=
, brak zer transformaty
( )
I s
( )
{
}
st M s
2
=
, miejsca zerowe mianownika tj. bieguny transformaty:
( )
(
)
R
M s
0
s s
0
L
= ⇒
+
=
Stąd określamy bieguny i ich krotności:
1
1
s
0 n
1
,
=
=
2
2
R
s
n
1
L
= −
=
,
Sprawdzamy warunki:
1. stopień wielomianu licznika L(s) jest mniejszy od stopnia wielomianu mianownika M(s), czyli st{L(s)} <
st{M(s)} ( 0 < 2 ),
( )
2. ułamek
( )
L s
M s
jest nie skracalny, tzn. miejsca zerowe L(s) są różne od miejsc zerowych M(s).
®
11
Obwody Elektryczne i Magnetyczne
Wykorzystanie rozkładu na ułamki proste:
( )
(
) (
) (
)
(
)
i
n
r
ik
11
21
11
21
k
1
1
i 1 k 1
i
1
2
A
A
A
A
A
I s
s
s R L
s s
s s
s s
=
=
=
=
+
=
+
+
−
−
−
∑∑
/
Wyznaczamy współczynniki rozkładu dla pierwszego bieguna
1
1
s
0 n
1
,
=
=
( )
11
s
s
0
0
E
A
s
s
s
L
→
→
⎡
⎤
=
=
⎣
⎦
lim
F
lim
1
s
(
)
E
s R L
L
⎡
⎤
=
⎢
⎥
+
⎢
⎥
⎣
⎦
/
L
E
R
R
=
Wyznaczamy współczynniki rozkładu dla drugiego bieguna
2
2
R
s
n
2
L
= −
=
,
(
)
/
/
lim
lim
/
21
s
s
R L
R L
E
A
s R L
L
→
→
−
−
=
=
+
(
)
/
1
s s R L
+
/
lim
s
R L
E 1
E
L s
L
→−
⎡
⎤
⎡
⎤
⎢
⎥ =
= −
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦
L
E
R
R
= −
Ostatecznie I(s) w rozkładzie na ułamki proste przyjmie postać:
( )
(
)
E 1 E
1
I s
R s
R s R L
=
−
+ /
Wykorzystując tabele transformat oraz własności odnajdujemy poszczególne składniki oryginału i(t):
( )
( )
( )
( )
R
R
t
t
L
L
E
E
E
i t
1 t
e 1 t
1 e
1 t
R
R
R
−
−
⎛
⎞
=
−
=
−
⎜
⎟
⎝
⎠
®
12
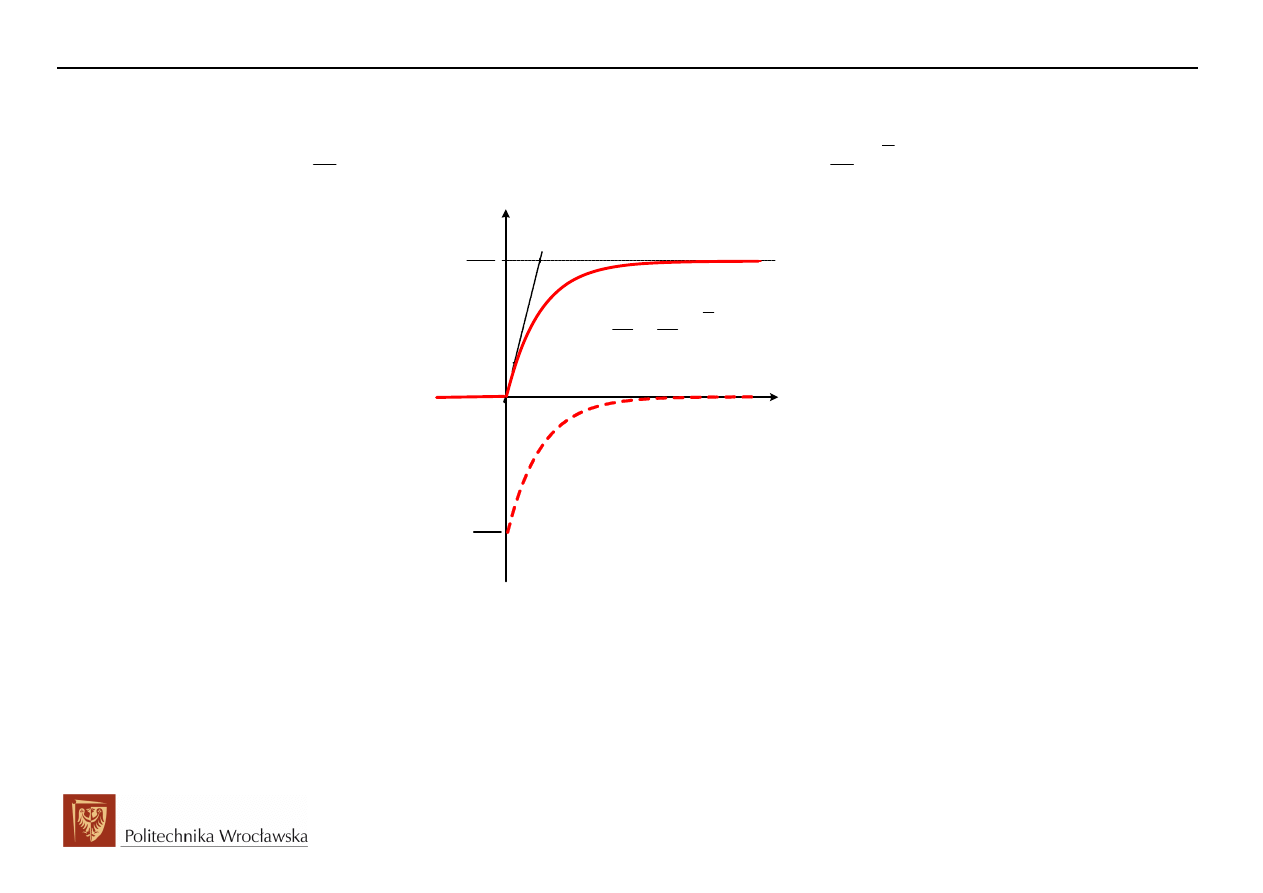
Obwody Elektryczne i Magnetyczne
W otrzymanym rozwiązaniu wyróżnić możemy składnik związany z wymuszeniem stałym, tj. składową
wymuszoną (ustaloną)
( )
E
1 t
R
, oraz składową swobodną (przejściową)
( )
R
t
L
E
e 1 t
R
−
i(t)
t
τ
E
R
t=0
( )
R
t
L
L
E E
i t
e
dla t 0
R R
−
= −
>
,
( )
Lu
i
t
( )
Lp
i
t
-E
R
L
Polecenie: proszę sprawdzić powyższe rozwiązanie metodą klasyczną – wykład 2.
®
13
Obwody Elektryczne i Magnetyczne
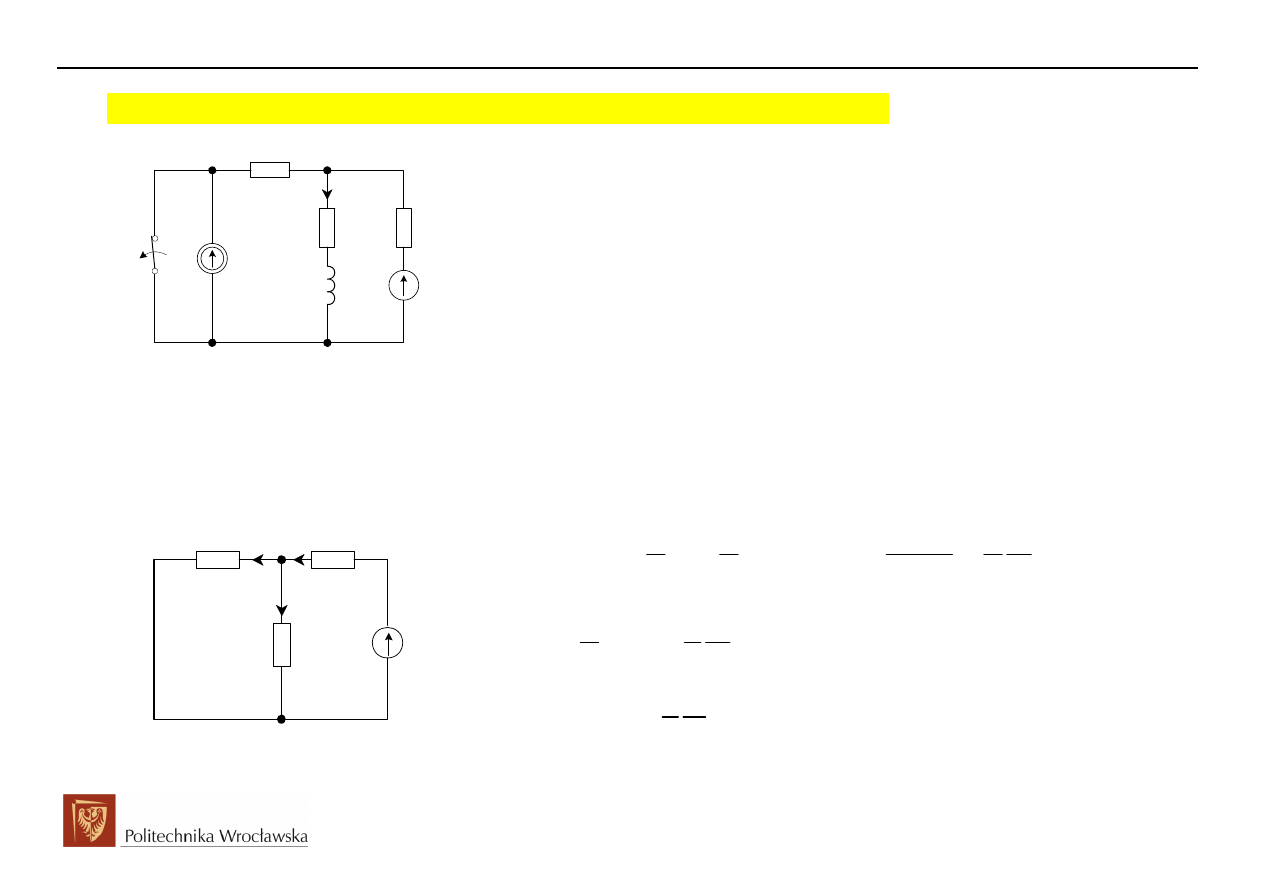
Obwód rozgałęziony zawierający gałęzie aktywne, dwa oczka
Dane:
( )
( )
.
,
źr
źr
e t
E const
i t
I
const
R L
= =
=
=
Szukane:
( )
i t
R
®
14
R
E
R
L
i
źr
(t)
t = 0
i(t)
1. t<0, analiza obwodu w stanie ustalonym przed komutacją (historia obwodu) oraz wyznaczenie
warunku początkowego dla t=0-
Przed komutacją obwód pracował ze zwartą gałęzią i
źr
(t). Jedynym aktywnym źródłem było źródło
napięcia stałego, co przy gałęziach zbudowanych z RL pozwoliło potraktować obwód przed komutacją
jako obwód czysto rezystancyjny.
( )
( )
( )
1
1
1
3
2
2
2
3
1
1
2
3
ZAST
ZAST
E
E
R
R
R
R
i t
R
R
E
i t
i t
R
= +
=
→
=
=
=
=
Stąd:
( )
1 E
i 0
3 R
−
=
R
E
i(t)
R
R
i
1
(t)
i
2
(t)
Obwody Elektryczne i Magnetyczne
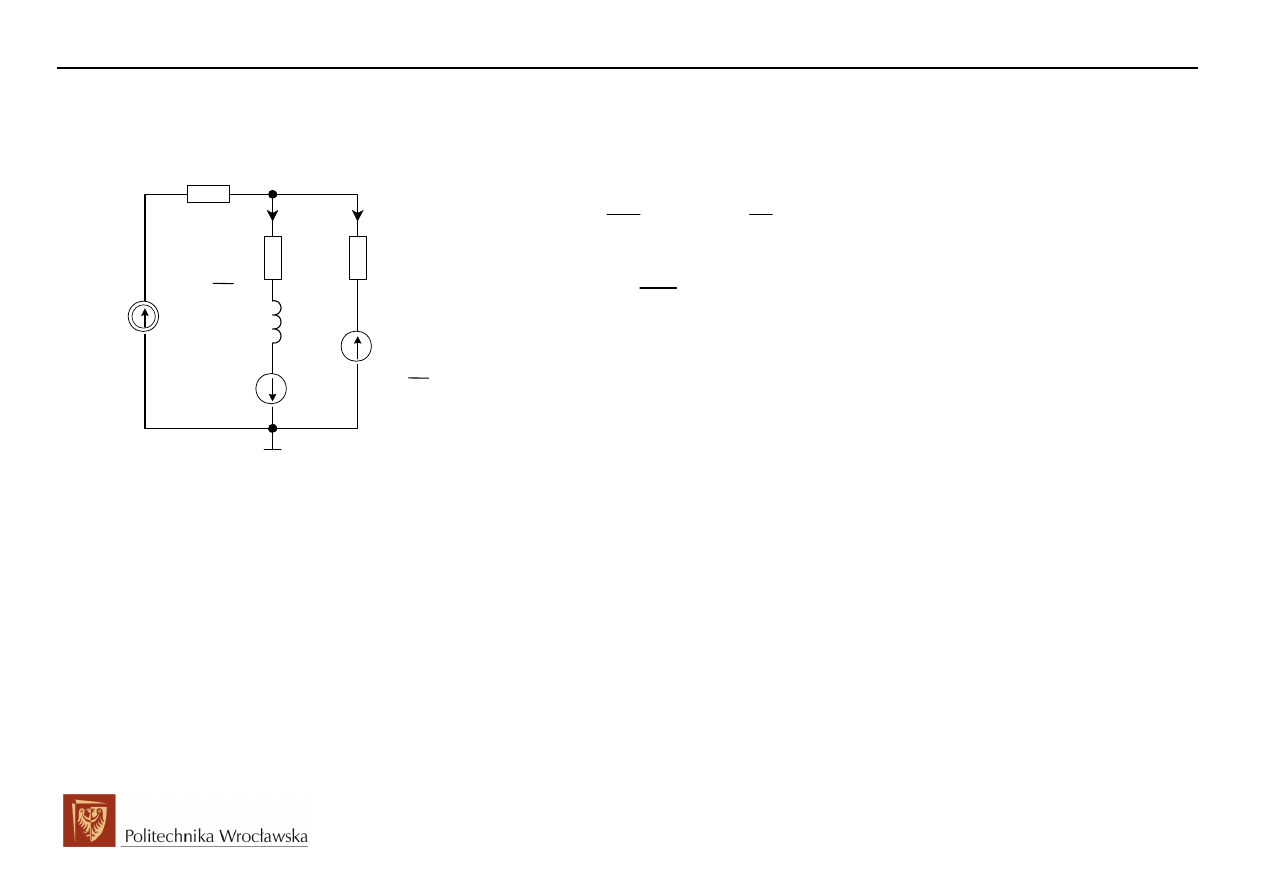
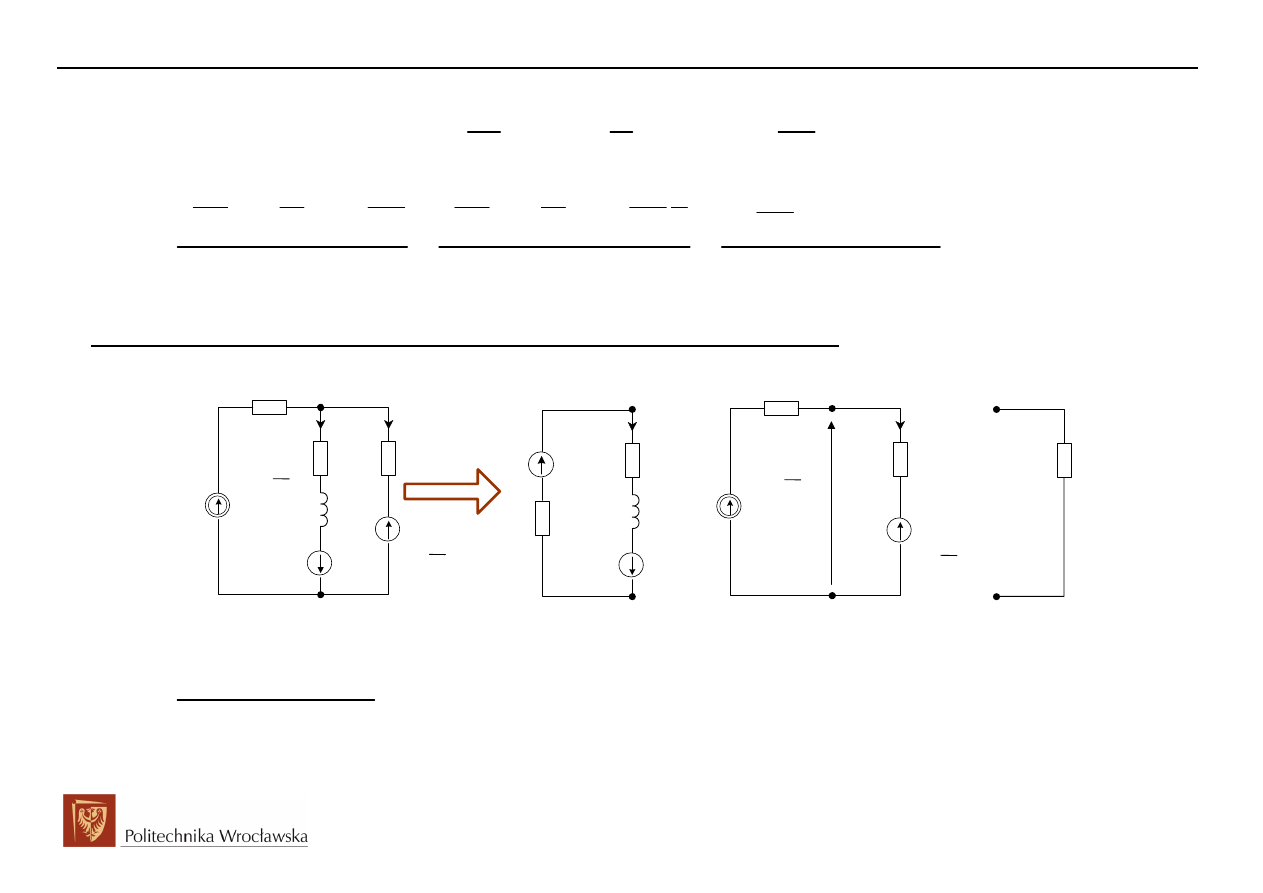
2. Schemat operatorowy po komutacji
R
R
sL
I
źr
(s)=
R
V(s)
Li(0-)
I
1
(s)
I(s)
E
E(s)= s
s
I
źr
Dane:
( )
źr
źr
I
I
s
s
=
,
( )
E
E s
s
=
( )
E
Li 0
L
3R
−
=
Szukane:
( )
( )
{ }
-1
L
i t
I s
=
Obwód reprezentuje układ dwu-oczkowy z wieloma wymuszeniami, ale o strukturze drabinkowej
(dwu-węzłowej). Decydując się na metodę rozwiązania takiego obwodu możemy zaproponować
metodę potencjałów węzłowych, metodę Thevenina czy metodę równań Kirchhoffa.
Podkreślmy jeszcze raz znaczenie operatorowej reprezentacji obwodu. Dzięki transformacji
całego obwodu do dziedziny s przenosimy ciężar poszukiwania rozwiązania na analizę obwodu
znanymi już metodami obwodowymi. Mając pewne doświadczenie możemy wybrać metodę,
która w szybki sposób pozwoli wyznaczyć transformatę szukanego sygnału. Dla porównania
wyznaczymy w zadanym przypadku I(s) trzema metodami.
Ostatnim krokiem jest wyznaczenie transformaty odwrotnej szukanej wielkości.
®
15
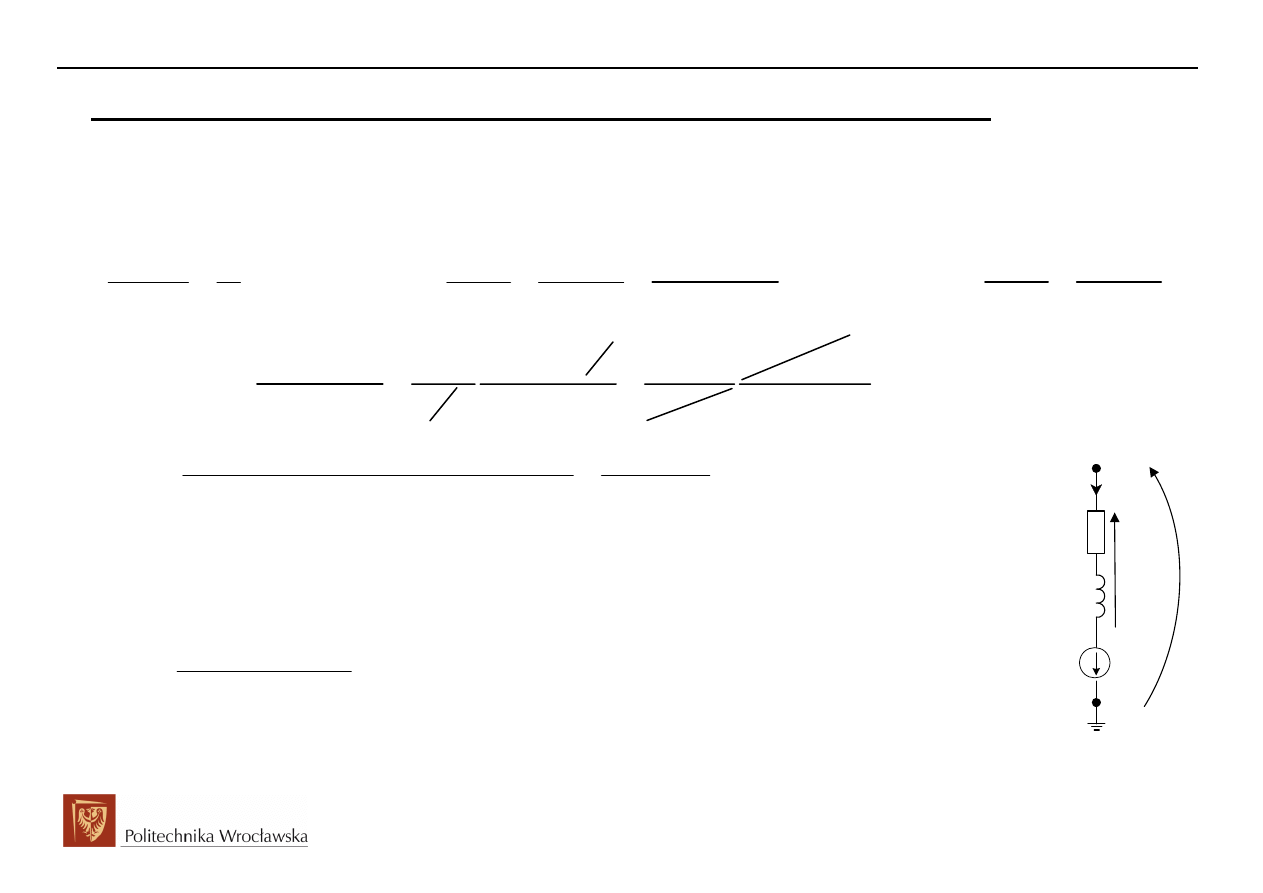
Obwody Elektryczne i Magnetyczne
Ad 2.1 Wykorzystanie metody potencjałów węzłowych w zapisie operatorowym
Dla przedstawionego obwodu w schemacie operatorowym istnieje tylko jeden węzeł niezależny i
równanie metody potencjałów węzłowych dotyczyć będzie tylko jednego potencjału V(s):
( )
( )
( )
( )
0
1
1
źr
Li
E s
V s
I
s
sL R
R
R
sL R
−
⎛
⎞
+
=
+
−
⎜
⎟
+
+
⎝
⎠
;
(
)
( )
( )
( )
( )
0
2
źr
Li
E s
sL
R
V s
I
s
sL R R
R
sL R
−
⎛
⎞
+
=
+
−
⎜
⎟
+
+
⎝
⎠
( )
( )(
)
( )
2
źr
sL R R
E s
V s
I
s
sL
R
R
+
=
+
+
(
)
sL R R
+
( )
0
2
Li
sL
R
sL R
−
−
+
+
(
)
sL R
+
2
R
sL
R
+
( ) (
) ( )
( )(
)
( )
0
2
2
źr
Li
R
sL R I
s R E s sL R
V s
sL
R
sL
R
−
+
+
+
=
−
+
+
®
16
R
sL
I
Li(0-)
(s)
V(s)
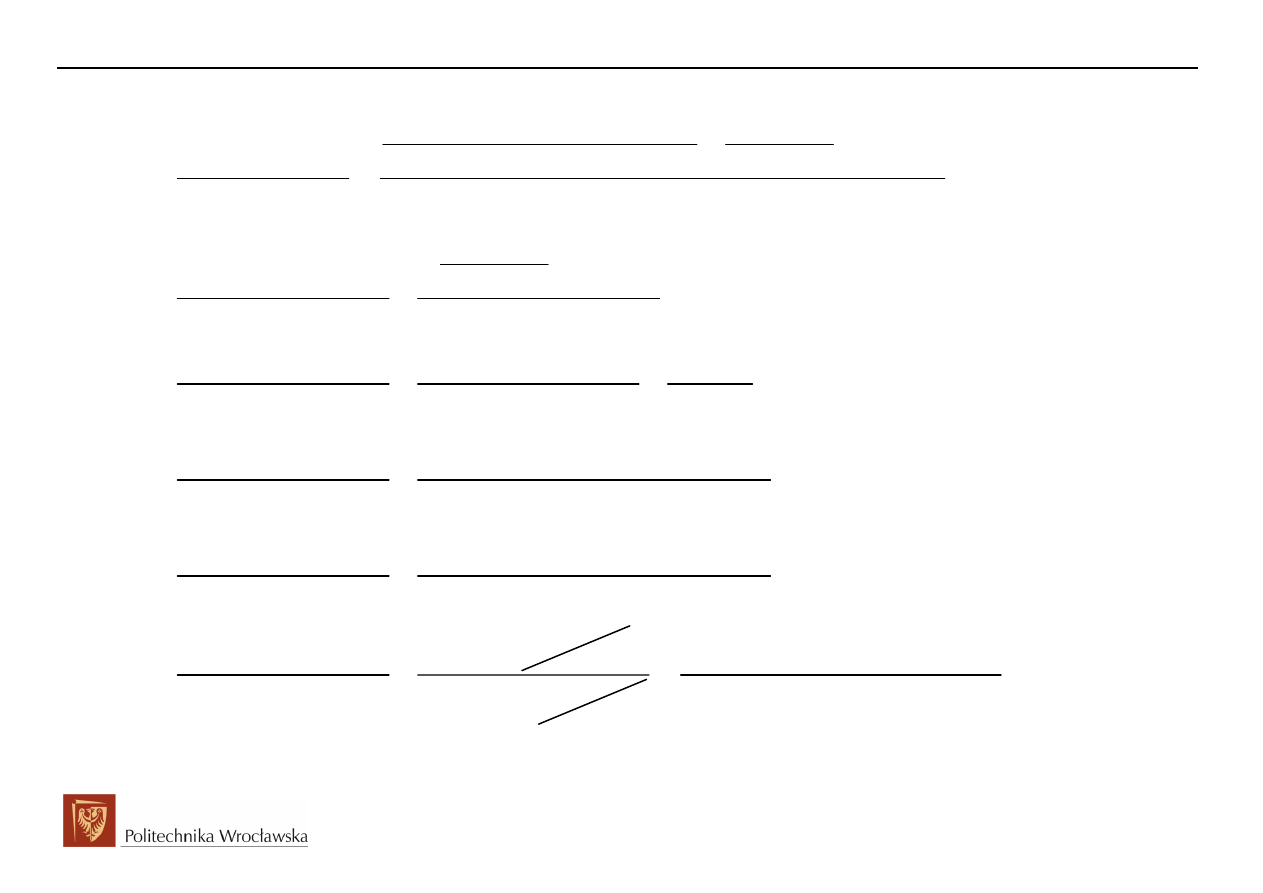
Różnica wyznaczonego potencjału i potencjału odniesienia wskazuje napięcie gałęziowe
U(s), a następnie szukaną transformatę prądu I(s) wyznaczamy z operatorowego prawa
Ohma dla tej gałęzi:
U(s)
( )
( )
( )
( )
( )
( )
( )
0
0
,
U s
Li
I s
U s
V s
V s
V s
sL R
−
+
=
=
−
=
+
Obwody Elektryczne i Magnetyczne
( )
( )
( )
(
)
( )
( )
( )
( )
0
0
0
2
2
źr
Li
R
sL R I
s R E s
Li
V s
Li
sL
R
sL
R
I s
sL R
sL R
−
−
−
⎡
⎤
+
+
⎣
⎦ −
+
+
+
+
=
=
+
+
( )
( )
( )
( )
( )
0
0
2
2
źr
Li
R
Li
I
s R E s
sL
R
I s
sL
R
sL R
−
−
−
+
⎡
⎤
+
⎣
⎦
+
=
+
=
+
+
( )
( )
( )
( )
(
)(
)
( )
0
0
2
2
źr
Li
R
Li
I
s R E s
I s
sL
R
sL
R sL R
sL R
−
−
−
⎡
⎤
+
⎣
⎦
=
+
+
+
+
+
+
( )
( )
( )
( )
( )
(
)
(
)(
)
0
0
2
2
2
źr
Li
R Li
sL
R
I
s R E s
I s
sL
R
sL
R sL R
−
−
−
+
+
⎡
⎤
+
⎣
⎦
=
+
+
+
+
( )
( )
( )
( )
( )
(
)
(
)(
)
0
0
2
2
2
źr
Li
R Li
sL
R
I
s R E s
I s
sL
R
sL
R sL R
−
−
−
+
+
⎡
⎤
+
⎣
⎦
=
+
+
+
+
( )
( )
( )
( )
(
)
0
2
źr
Li
sL R
I
s R E s
I s
sL
R
−
+
⎡
⎤
+
⎣
⎦
=
+
+
(
) (
)
2
sL
R sL R
+
+
( )
( )
( )
0
2
źr
I
s R E s
Li
sL
R
−
⎡
⎤
+
+
⎣
⎦
=
+
®
17
Obwody Elektryczne i Magnetyczne
Po podstawieniu danych:
( )
źr
źr
I
I
s
s
=
,
( )
E
E s
s
=
,
( )
E
Li 0
L
3R
−
=
( )
[
]
(
)
3
3
3
2
2
2
źr
źr
źr
I
I
E
E
E
E s
E
R
L
R
L
sL
I R E
s
s
R
s
s
R s
R
I s
sL
R
sL
R
s sL
R
⎡
⎤
⎡
⎤
+
+
+
+
+
+
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦
=
=
=
+
+
+
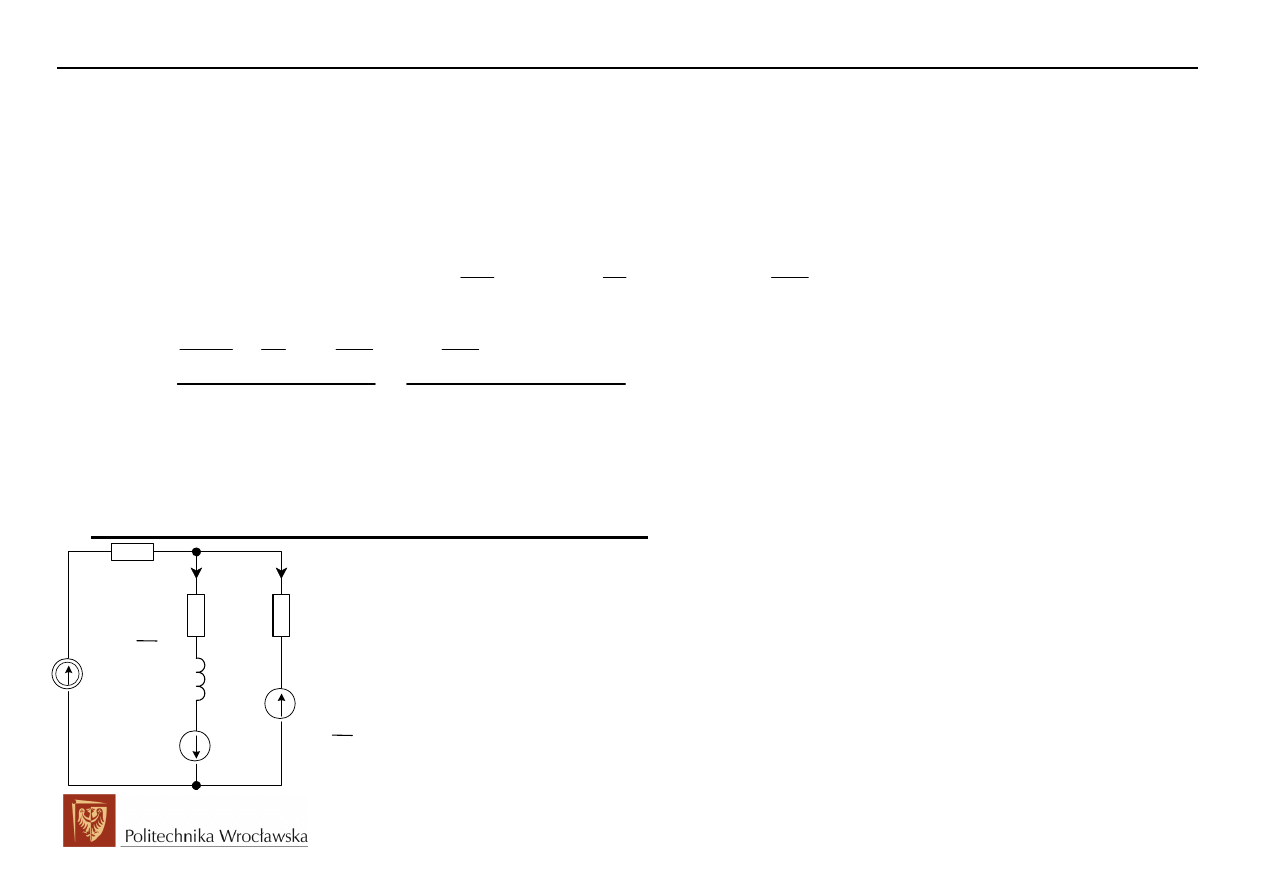
Ad 2.2 Wykorzystanie metody Thevenina w zapisie operatorowym
R
R
sL
I
źr
(s)=
R
Li(0-)
I
1
(s)
I(s)
E
E(s)= s
s
I
źr
a
b
R
I
źr
(s)=
R
I’
1
(s)
E
E(s)= s
s
I
źr
a
b
U (s)=
ab
=E (s)
TH
R
a
b
Z (s)=
ab
=Z (s)
TH
R
sL
I(s)
a
b
Li(0-)
E (s)
TH
Z (s)
TH
Thevenin
Z metody Thevenina szukany I(s) wyznaczymy jako:
( )
( )
( )
( )
0
TH
TH
E
s
Li
I s
Z
s
sL R
−
+
=
+
+
®
18
Obwody Elektryczne i Magnetyczne
Poszczególne składniki metody zastępczego źródła Thevenina potrzebne do wypełnienia powyższego
wyrażenia wskazują powyższe obwody pomocnicze: U
AB
(s)=E
TH
(s), Z
AB
(s)=Z
TH
(s)
( )
( )
( )
( )
( )
( )
1
1
'
,
: '
AB
TH
źr
U
s
E
s
RI s
E s gdzie I s
I
s
=
=
+
=
( )
( )
AB
TH
Z
s
Z
s
R
=
=
Po podstawieniu danych
( )
źr
źr
I
I
s
s
=
,
( )
E
E s
s
=
,
( )
E
Li 0
L
3R
−
=
:
( )
[
]
(
)
3
3
2
źr
źr
RI
E
E
E
L
sL
I R E
s
s
R
R
I s
R sL R
s sL
R
+ +
+
+
=
=
+
+
+
*Porównaj efektywność wyznaczenia I(s) z metodą potencjałów węzłowych.
Ad 2.3 Wykorzystanie metody równań Kirchhoffa
®
19
Układ równań Kirchhoffa przyjmie postać:
( )
( ) ( )
(
) ( )
( )
( )
( )
1
1
0
0
źr
I
s
I s
I s
sL R I s
I s R E s
Li
−
⎧
=
+
⎪
⎨
+
−
−
−
=
⎪⎩
R
R
sL
I
źr
(s)=
I
1
(s)
I(s)
E
s
I
źr
E(s)= s
Li(0-)
Obwody Elektryczne i Magnetyczne
Podstawiając
( )
( ) ( )
1
źr
I s
I
s
I s
=
−
(
) ( )
( )
( )
( )
( )
0
0
źr
sL R I s
I
s R I s R E s
Li
−
+
−
+
−
−
=
(
) ( )
( )
( )
( )
2
0
źr
sL
R I s
I
s R E s
Li
−
+
=
+
+
( )
( )
( )
( )
(
)
0
2
źr
I
s R E s
Li
I s
sL
R
−
+
+
=
+
Po podstawieniu danych
( )
źr
źr
I
I
s
s
=
,
( )
E
E s
s
=
,
( )
E
Li 0
L
3R
−
=
:
( )
(
)
[
]
(
)
3
3
2
2
źr
źr
I
E
E s
E
R
L
sL
I R E
s
s
R s
R
I s
sL
R
s sL
R
+ +
+
+
=
=
+
+
*Porównaj efektywność wyznaczenia I(s) z metodą Thevenina oraz z metodą potencjałów
węzłowych.
®
20
Obwody Elektryczne i Magnetyczne
3. Wyznaczenie oryginału szukanego i(t) jako transformaty odwrotnej I(s)
( )
( )
{ }
1
i t
I s
−
=
L
Właściwą odpowiedź uzyskamy przez realizację transformaty odwrotnej
Do tego celu możemy wykorzystać: metodę granic, metodę residuów oraz metodę sprowadzania do
wspólnego mianownika.
Jako przykład wyznaczymy i(t) z metody residuów. Polecam sprawdzenie uzyskanego wyniku stosując
rozkład na ułamki proste z wykorzystaniem metody granic i metody sprowadzania do wspólnego
mianownika.
( )
( )
{ }
( )
( )
i
r
1
res
st
s s
i 1
i t
I s
I s e
1 t
−
=
=
⎡
⎤
⎡
⎤
=
= ⎢
⎥
⎣
⎦
⎣
⎦
∑
L
,
( )
[
]
(
)
[
]
1
3
3
2
2
źr
źr
E
E
sL
I R E
s
I R E
R
R
L
I s
R
s sL
R
s s
L
+
+
+
+
=
=
+
⎛
⎞
+
⎜
⎟
⎝
⎠
1. stopień wielomianu licznika L(s) jest mniejszy od stopnia wielomianu mianownika M(s), czyli st{L(s)} <
st{M(s)} ( 1 < 2 ),
( )
2. ułamek
( )
L s
M s
jest nie skracalny, tzn. miejsca zerowe L(s) są różne od miejsc zerowych M(s).
®
21
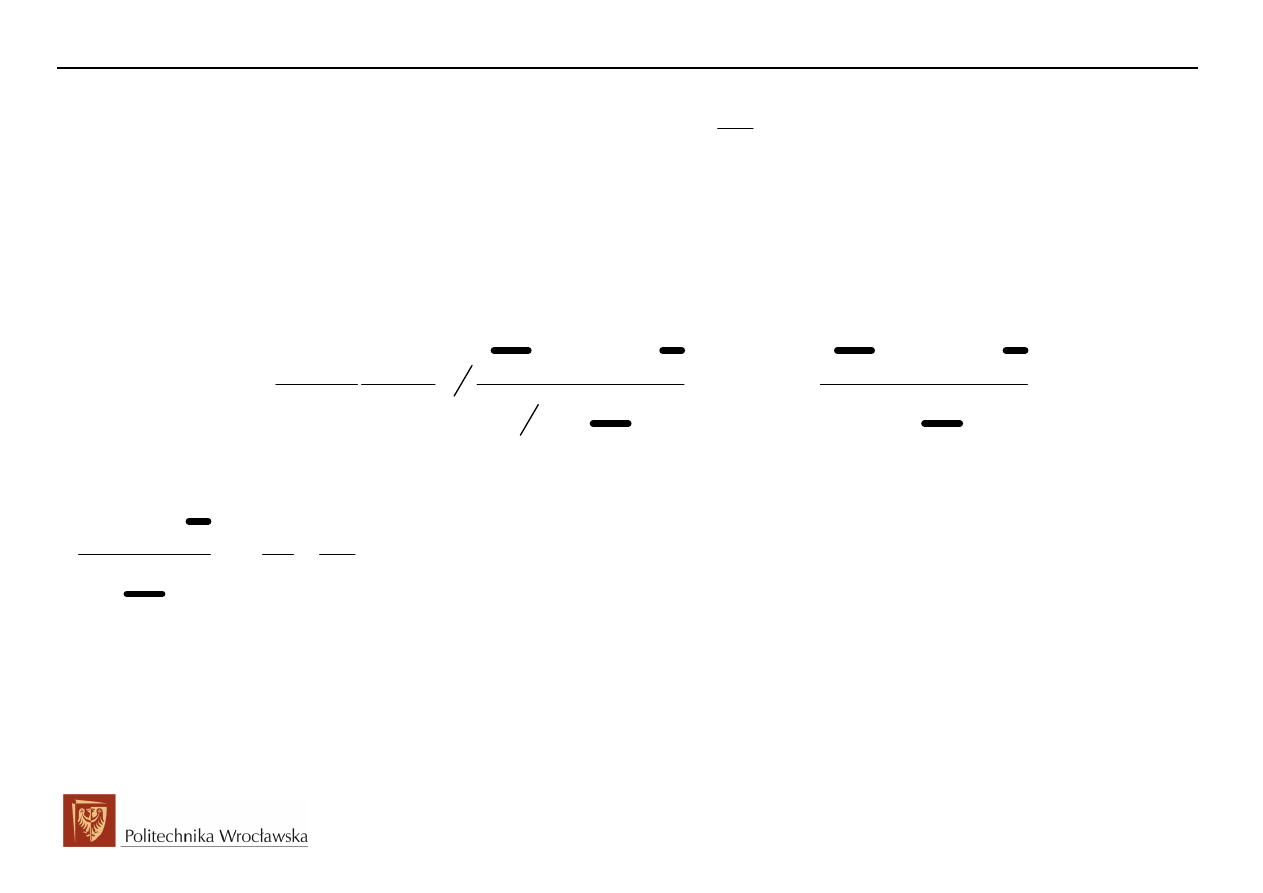
Obwody Elektryczne i Magnetyczne
Dalej określamy bieguny i ich krotności:
1
1
s
0 n
1
,
=
=
2
2
2R
s
n
1
L
= −
=
,
( )
( )
{ }
( )
( )
( )
( )
( )
i
r
1
res
st
res
st
res
st
s s
s 0
s
2 R L
i 1
i t
I s
I s e
1 t
I s e
I s e
1 t
−
=
=
=−
=
⎡
⎤
⎡
⎤
⎡
⎤
⎡
⎤
⎡
⎤
=
=
=
+
⎢
⎥
⎣
⎦
⎣
⎦
⎣
⎦
⎣
⎦
⎣
⎦
∑
L
/
Residuum dla pierwszego bieguna
1
1
s
0 n
1
,
=
=
wyznaczymy jako:
( )
(
)
( )
( )
s 0
1 1
res
st
s 0
1 1
1
d
I s e
s
1 1 ds
→
−
=
−
⎡
⎤ =
⎣
⎦
−
lim
!
[
]
źr
E
1
s
I R E
3R
L
s
+
+
[
]
[
]
s 0
źr
st
st
źr
źr
E
1
s
I R E
3R
L
e
e
2R
2R
s
s
L
L
1
I R E
I
E
L
2R
2
2R
L
→
⎡
⎤
⎧
⎫
⎡
⎤
⎢
⎥
+
+
⎪
⎪
⎢
⎥
⎪
⎪
⎢
⎥
⎢
⎥
=
=
⎨
⎬
⎢
⎥
⎢
⎥
⎛
⎞
⎛
⎞
⎪
⎪
+
+
⎢
⎥
⎢
⎥
⎜
⎟
⎜
⎟
⎪
⎪
⎢
⎥
⎝
⎠
⎝
⎠
⎩
⎭
⎣
⎦
⎣
⎦
⎡
⎤
+
⎢
⎥
⎡
⎤
⎢
⎥ =
+
⎢
⎥
⎢
⎥
⎛
⎞
⎣
⎦
⎢
⎥
⎜
⎟
⎝
⎠
⎣
⎦
lim
®
22
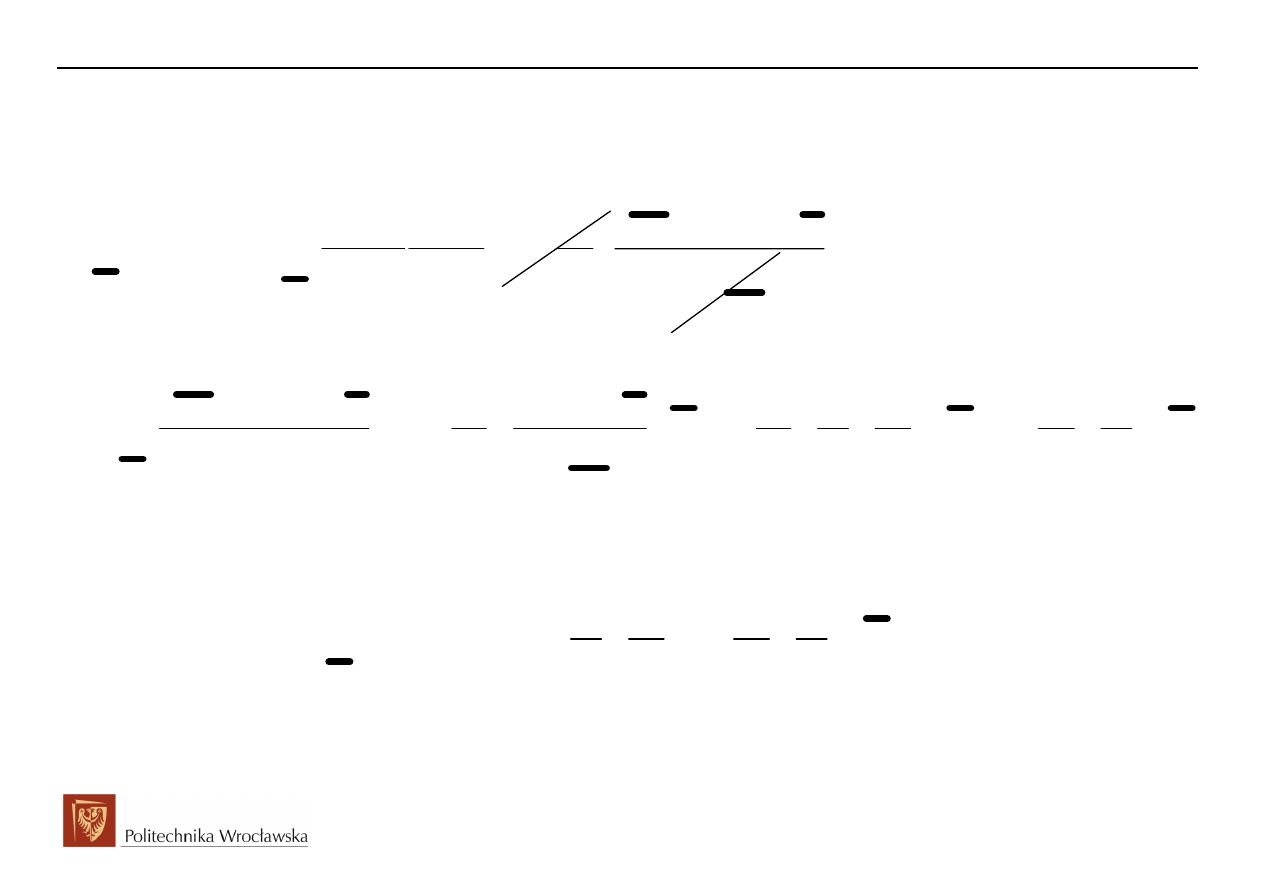
Obwody Elektryczne i Magnetyczne
®
23
s
R 2L n
Residuum dla drugiego bieguna
2
1
2
− /
,
=
wyznaczymy jako:
=
( )
(
)
(
)
(
)
s
1 1
res
st
2 R
1 1
2 R
s
L
L
1
d
2R
I s e
s
1 1
L
ds
→
−
−
=−
−
⎛
⎞
⎡
⎤ =
+
⎜
⎟
⎣
⎦
−
⎝
⎠
lim
!
[
]
źr
E
1
s
I R E
3R
L
2R
s s
L
+
+
⎛
⎞
+
⎜
⎟
⎝
⎠
[
]
[
]
s
st
2 R
2 R
2 R
źr
źr
t
t
t
st
źr
źr
L
L
L
2 R
L
e
E
1
1
s
I R E
I R E
I
I
E
E
E
E
3R
L
L
e
e
e
e
2R
s
3R
3R
2
2R
6 R
2
L
→
−
−
−
−
⎡
⎤
⎧
⎫
⎢
⎥
⎪
⎪
⎢
⎥
⎪
⎪
⎨
⎬
⎢
⎥
⎪
⎪
⎢
⎥
⎪
⎪
⎢
⎥
⎩
⎭
⎣
⎦
⎡
⎤
⎡
⎤
+
+
+
⎢
⎥
⎢
⎥
⎡
⎤
⎡
⎤
⎢
⎥
=
=
+
=
−
−
= −
−
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎛
⎞
⎣
⎦
⎣
⎦
⎢
⎥
−
⎢
⎥
⎜
⎟
⎢
⎥
⎣
⎦
⎝
⎠
⎣
⎦
lim
Ostatecznie szukany oryginał:
( )
( )
( )
( )
( )
2 R
t
res
st
res
st
źr
źr
L
s 0
2 R
s
L
I
I
E
E
i t
I s e
I s e
1 t
e
1 t
2
2R
6 R
2
−
=
=−
⎡
⎤
⎡
⎤
⎡
⎤ ⎡
⎤
⎡
⎤
⎡
⎤
=
+
=
+
+ −
−
⎢
⎥
⎢
⎥
⎢
⎥ ⎢
⎥
⎣
⎦
⎣
⎦
⎣
⎦ ⎣
⎦
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦
Obwody Elektryczne i Magnetyczne
Wymuszenie sinusoidalne oraz metoda wektora wirującego
Niejednokrotnie powtarzaliśmy, że w przypadku stanu nieustalonego przy wymuszeniu sinusoidalnym,
nie możemy stosować metody symbolicznej, tj. zastąpienia sygnałów sinusoidalnych ich statyczną
reprezentacją wektorową (wskazową), a elementów RLC obwodu impedancją zespoloną. Takie
postępowanie było możliwe tylko w stanie ustalonym przy wymuszeniu sinusoidalnym. W trakcie stanu
przejściowego mamy do czynienia z sygnałami, które różnią się od sinusoidy, np. sygnały wykładnicze,
czy oscylacje zanikające lub rosnące, dla których reprezentacja za pomocą statycznego wektora jest
niewystarczająca.
Jeśli jednak spojrzymy na wymuszenie sinusoidalne jak część urojoną funkcji zespolonej, czyli
wirującego wektora, wtedy możemy zaadoptować zapis wektora wirującego do analizy stanu
nieustalonego. Jest to bardzo efektywne narzędzie zwłaszcza w przypadku stosowania metody
operatorowej.
Przypomnijmy relacje pomiędzy funkcją zespoloną a sygnałem sinusoidalnym:
( )
(
)
( )
{ }
(
)
{
}
( )
{
}
sin
Im
Im
Im
f
f
j t
j
j t
m
f
m
m
f t
F
t
f t
F e
F e e
ω ψ
ψ
ω
ω ψ
+
=
+
=
=
=
Korzyści w zastosowaniu zapisu wektora wirującego w metodzie operatorowej upatruje się w „wygodnej”
formie transformaty Laplace’a w porównaniu do bezpośredniej transformaty Laplace’a samego sygnału
sinusoidalnego.
®
24
Obwody Elektryczne i Magnetyczne
Bezpośrednia transformata Laplace’a
Transformata Laplace’a wektora wirującego
®
25
( )
{
}
2
2
L
sin
m
F
t
ω
s
ω
ω
=
+
( )
{
}
0
1
L
m
j
t
j
m
m
F e
F e
F
s
j
s
ω
j
ω
ω
⎧
⎫
⎧
⎫
=
=
⎨
⎬ ⎨
−
−
⎩
⎭ ⎩
⎭
⎬
(
)
{
}
( )
( )
( )
( )
{
}
( )
( )
2
2
2
2
L
L
sin
sin
cos
cos
sin
cos
sin
m
f
m
f
f
f
f
m
m
F
t
F
t
t
s
F
F
s
s
ω ψ
ω
ψ
ω
ψ
ω
ψ
ψ
ω
ω
+
=
=
+
=
⋅
⋅
=
+
( )
{
}
1
L
f
f
j
j
j t
m
m
m
F e e
F e
s j
F
s j
ψ
ψ
ω
ω
ω
⎧
⎫
=
=
⎨
⎬
−
⎩
⎭
⎧
⎫
= ⎨
⎬
−
⎩
⎭
+
+
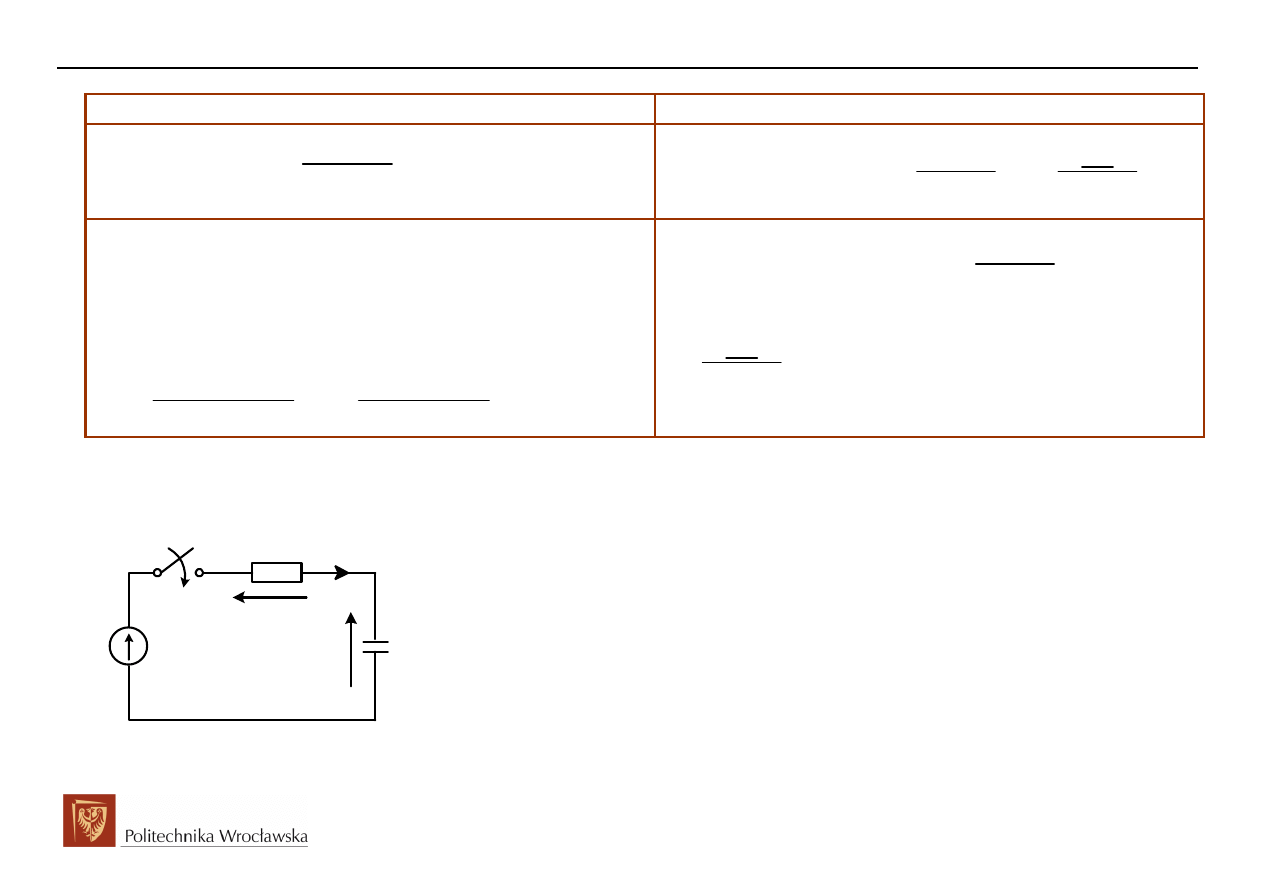
Spróbujmy wykorzystać transformatę wektora wirującego w analizie obwodu RC załączanego na
napięcie sinusoidalne:
Dane:
( )
(
)
sin
,
m
e
e t
E
t
R C
ω ψ
=
+
Szukane
( )
c
u t
R
C
t = 0
u
C
(t)
i(t)
u
R
(t)
e(t)=E
m
sin(
ω
t+
ψ
e
)
e(t)
Obwody Elektryczne i Magnetyczne
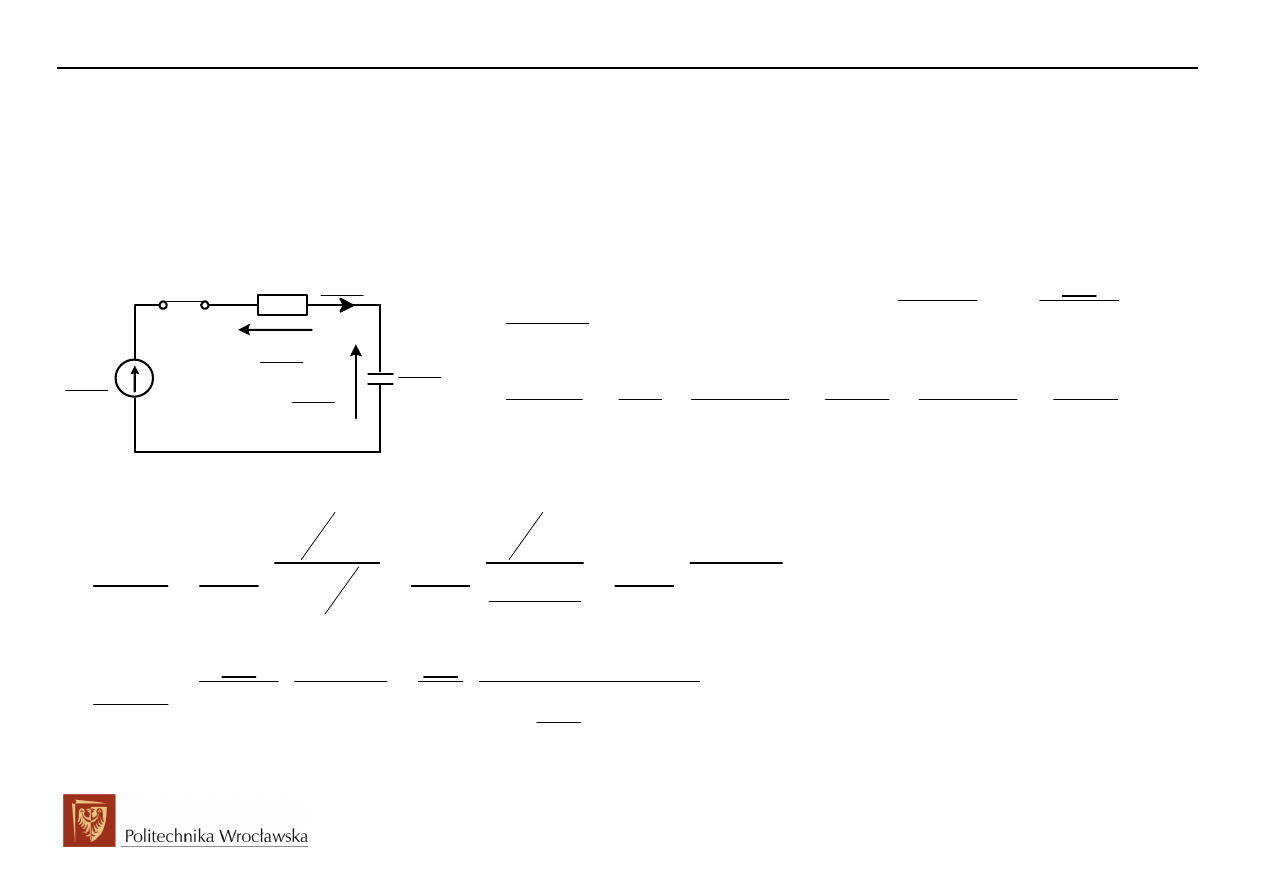
1. t<0, analiza obwodu w stanie ustalonym przed komutacją (historia obwodu) oraz wyznaczenie
warunku początkowego dla t=0-
Obwód przed komutacją pracował bezenergetycznie, czyli
( )
0
0
c
u
V
−
=
2. Schemat operatorowy po komutacji z wykorzystaniem transformaty Laplace’a wektora
wirującego:
( )
( )
{
}
1
L
e
e
m
j
t
j
j
m
m
E
E s
E e e
E e
s
j
s
j
ω
ψ
ψ
ω
ω
⎧
⎫
⎧
⎫
=
=
=
⎨
⎬ ⎨
⎬
R
sC
U
C
(s)
I(s)
U
R
(s)
E(s)
1
−
−
⎩
⎭ ⎩
⎭
( )
( )
{ }
( )
( )
{ }
( )
( )
{ }
L
L
L
;
;
R
R
C
C
I s
i t
U s
u t
U
s
u t
=
=
=
Korzystając z dzielnika napięcia:
( )
( )
( )
( )
1
1
1
1
1
1
C
sC
sC
U s
E s
E s
E s
sRC
sRC
R
sC
sC
=
⋅
=
⋅
=
⋅
+
+
+
( )
(
)
1
1
1
1
m
m
C
E
E
U s
s
j
sRC
RC
s
s
j
RC
ω
ω
=
⋅
=
⋅
−
+
⎛
⎞
+
−
⎜
⎟
⎝
⎠
®
26
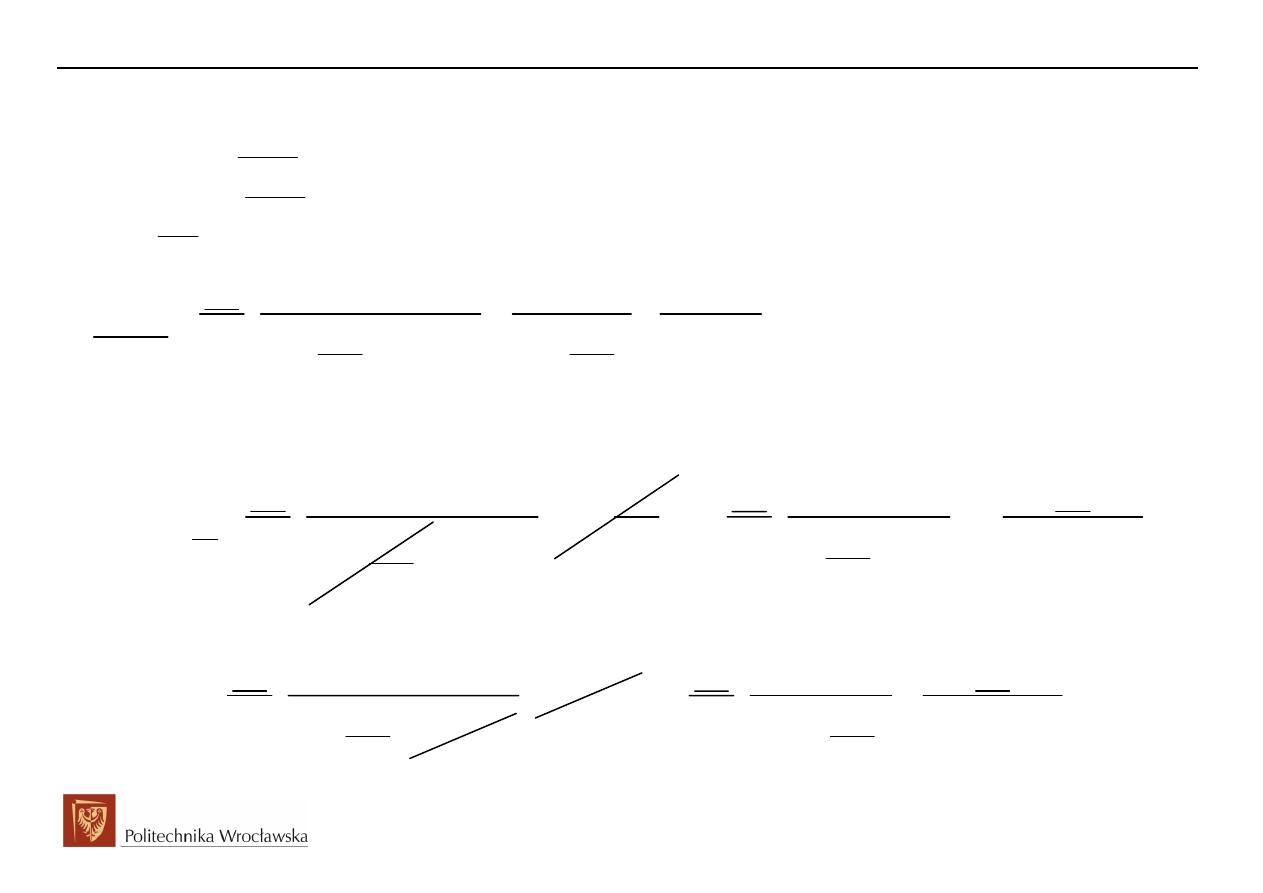
Obwody Elektryczne i Magnetyczne
3. Wyznaczenie oryginału szukanego uc(t) z wykorzystaniem transformaty Laplace’a wektora
wirującego
( )
C
U s
:
Przygotujemy
( )
C
U
s
w formie rozkładu na ułamki proste względem biegunów:
,
1
1
1
s
n
1
RC
= −
=
,
2
2
s
j n
1
ω
=
=
( )
(
)
(
)
11
21
1
1
1
m
C
E
A
A
U s
RC
s
j
s
s
j
s
RC
RC
ω
ω
=
⋅
=
+
−
⎛
⎞
⎛
⎞
+
−
+
⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
Współczynniki rozkładu znajdziemy wykorzystując metodę granic:
11
1
1
1
lim
m
s
RC
E
A
RC
s
RC
→−
=
⋅
⎛
⎞
+
⎜
⎟
⎝
⎠
(
)
1
s
RC
s j
ω
⎛
⎞
⋅
+
⎜
⎟
⎝
⎠
−
(
)
1
1
1
m
m
E
E
RC
j RC
j
RC
ω
ω
⎧
⎫
⎪
⎪
⎪
⎪ =
⋅
= −
⎨
⎬
+
⎛
⎞
⎪
⎪
−
−
⎜
⎟
⎪
⎪
⎝
⎠
⎩
⎭
(
)
21
1
1
lim
m
s
j
E
A
RC
s
s
j
RC
ω
ω
→
=
⋅
⎛
⎞
+
−
⎜
⎟
⎝
⎠
(
)
s
j
ω
⋅
−
(
)
1
1
1
m
m
E
E
RC
j RC
j
RC
ω
ω
⎧
⎫
⎪
⎪
⎪
⎪ =
⋅
=
⎨
⎬
+
⎛
⎞
⎪
⎪
+
⎜
⎟
⎪
⎪
⎝
⎠
⎩
⎭
®
27
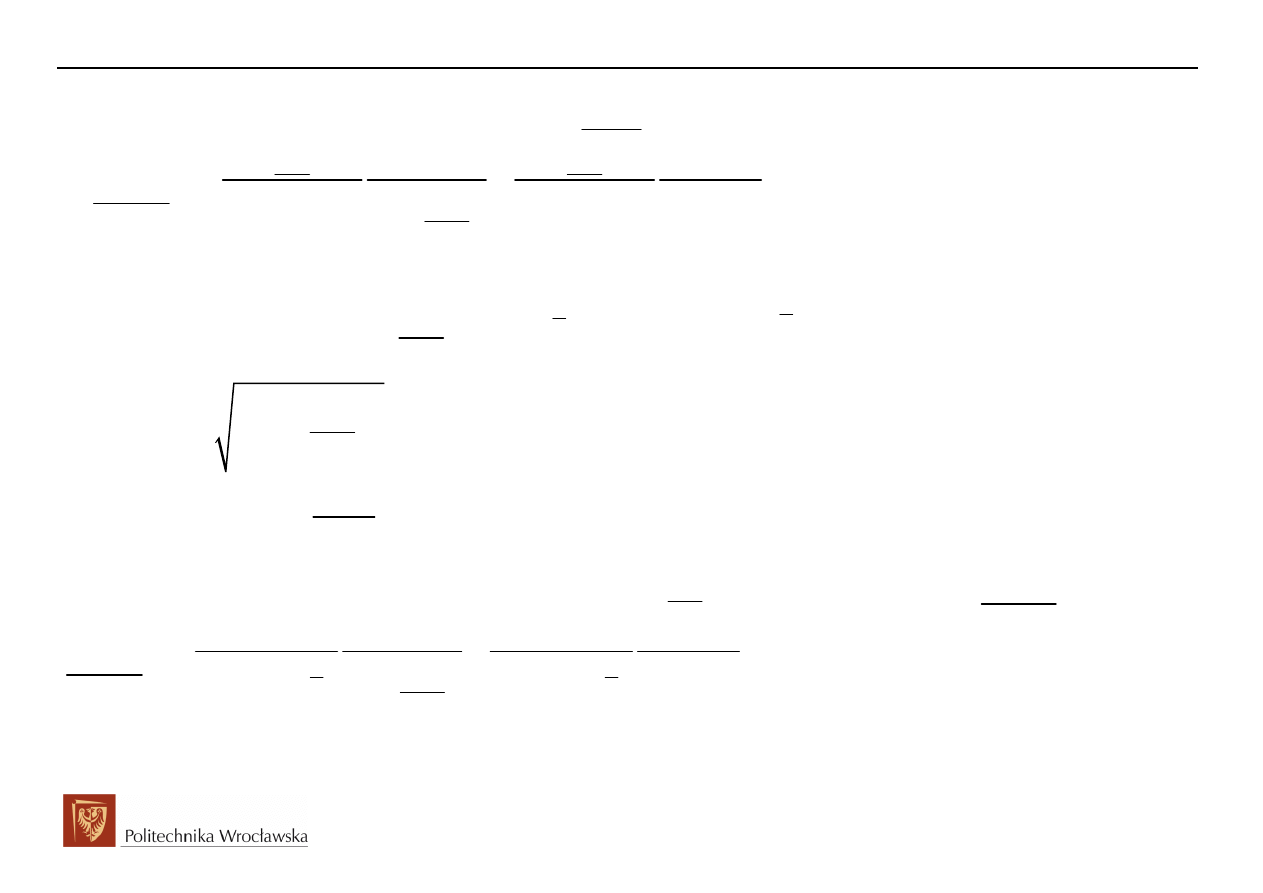
Obwody Elektryczne i Magnetyczne
Rozkład na ułamki proste wektora wirującego
( )
C
U
s
przyjmie postać:
( )
(
)
(
) (
)
1
1
1
1
1
m
m
C
E
E
U
s
j RC
j RC
s
j
s
RC
ω
ω
ω
= −
+
+
+
−
⎛
⎞
+
⎜
⎟
⎝
⎠
Dodatkowo wprowadźmy następujące przekształcenie:
(
)
2
2
1
1
j
j
j
j RC
j C R j
Ce
Ze
CZe
C
π
π
ϕ
ϕ
ω
ω
ω
ω
ω
⎛
⎞
+
⎜
⎟
⎝
⎠
⎛
⎞
+
=
−
=
⋅
=
⎜
⎟
⎝
⎠
gdzie:
2
2
1
Z
R
C
ω
⎛
⎞
=
+ ⎜
⎟
- moduł impedancji zespolonej w stanie ustalonym,
⎝
⎠
1
actg
CR
ϕ
ω
⎛
⎞
=
−
⎜
⎟
- argument impedancji zespolonej w stanie ustalonym.
⎝
⎠
Pamiętając, że amplituda zespolona rozwija się w formę
e
j
m
m
E
E e
ψ
=
, można opisać
( )
C
U
s
formą:
( )
(
)
2
2
1
1
1
e
e
j
j
m
m
C
j
j
E e
E e
U
s
s
j
s
CZe
CZe
RC
ψ
ψ
π
π
ϕ
ϕ
ω
ω
ω
⎛
⎞
⎛
⎞
+
+
⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
= −
+
−
⎛
⎞
+
⎜
⎟
⎝
⎠
®
28
Obwody Elektryczne i Magnetyczne
( )
(
)
2
2
1
1
1
e
e
j
j
m
m
C
E
E
U s
e
e
CZ
CZ
s
j
s
RC
π
π
ψ ϕ
ψ ϕ
ω
ω
ω
−
⎛
⎞
⎛
⎞
−
− −
⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
= −
+
−
⎛
⎞
+
⎜
⎟
⎝
⎠
Wyznaczenie oryginał szukanego napięcia
( )
C
u t
odbędzie się w dwóch krokach:
( )
( )
C
C
- wyznaczenie oryginału wektora wirującego
U
s
u t
→
( )
( )
{
}
1
L
C
C
u t
U
s
−
=
( )
( )
C
C
u t
u t
→
- wyznaczenie sygnału szukanego napięcia z postaci wektora wirującego
( )
( )
{ }
Im
C
C
u t
u t
=
A zatem oryginał wektora wirującego (funkcja zespolona):
( )
( )
{
}
1
1
2
2
L
e
e
j
j
t
j t
m
m
RC
C
C
E
E
u t
U s
e
e
e
e
CZ
CZ
π
π
ψ ϕ
ψ ϕ
ω
ω
ω
−
⎛
⎞
⎛
⎞
−
− −
−
⎜
⎟
⎜
⎟
−
⎝
⎠
⎝
⎠
=
= −
+
1
2
2
2
2
cos
sin
cos
sin
t
m
RC
e
e
m
e
e
E
e
j
CZ
E
t
j
t
CZ
π
π
ψ
ϕ
ψ
ϕ
ω
π
π
ω ψ
ϕ
ω ψ
ϕ
ω
−
⎡
⎤
⎛
⎞
⎛
⎞
= −
− −
+
− −
+
⎜
⎟
⎜
⎟
⎢
⎥
⎝
⎠
⎝
⎠
⎣
⎦
⎡
⎤
⎛
⎞
⎛
⎞
+
+
− −
+
+
− −
⎜
⎟
⎜
⎟
⎢
⎥
⎝
⎠
⎝
⎠
⎣
⎦
®
29
Obwody Elektryczne i Magnetyczne
Ostatecznie szukane napięcie na kondensatorze:
( )
( )
{ }
1
2
2
Im
sin
sin
t
m
m
RC
C
C
e
e
E
E
u t
u t
e
t
CZ
CZ
π
π
ψ
ϕ
ω ψ
ϕ
ω
ω
−
⎡
⎤
⎡
⎤
⎛
⎞
⎛
⎞
=
= −
− −
+
+
− −
=
⎜
⎟
⎜
⎟
⎢
⎥
⎢
⎥
⎝
⎠
⎝
⎠
⎣
⎦
⎣
⎦
(
)
(
)
1
cos
cos
t
m
m
RC
e
e
E
E
e
t
CZ
CZ
ψ
ϕ
ω ψ
ϕ
ω
ω
−
⎡
⎤
⎡
⎤
=
−
−
+
−
⎣
⎦
⎣
⎦
Wykorzystano:
( )
2
sin
cos
π
α
α
⎛
⎞
−
= −
⎜
⎟
⎝
⎠
®
30