Opracowanie danych pomiarowych

1. Pomiar wartości serii oporników

Do wykonania pomiaru potrzebny jest omomierz cyfrowy, mierzący oporność z dokładnością

do czterech lub więcej cyfr po przecinku. Do dyspozycji są przemysłowo wytwarzane oporniki o
wartościach znamionowych 5 i 10 kiloomów i tolerancji 1%, połączone w listki po 10 sztuk
Do zbadania statystyki wartości oporności należy wykonać pomiar min. 20 sztuk oporników i
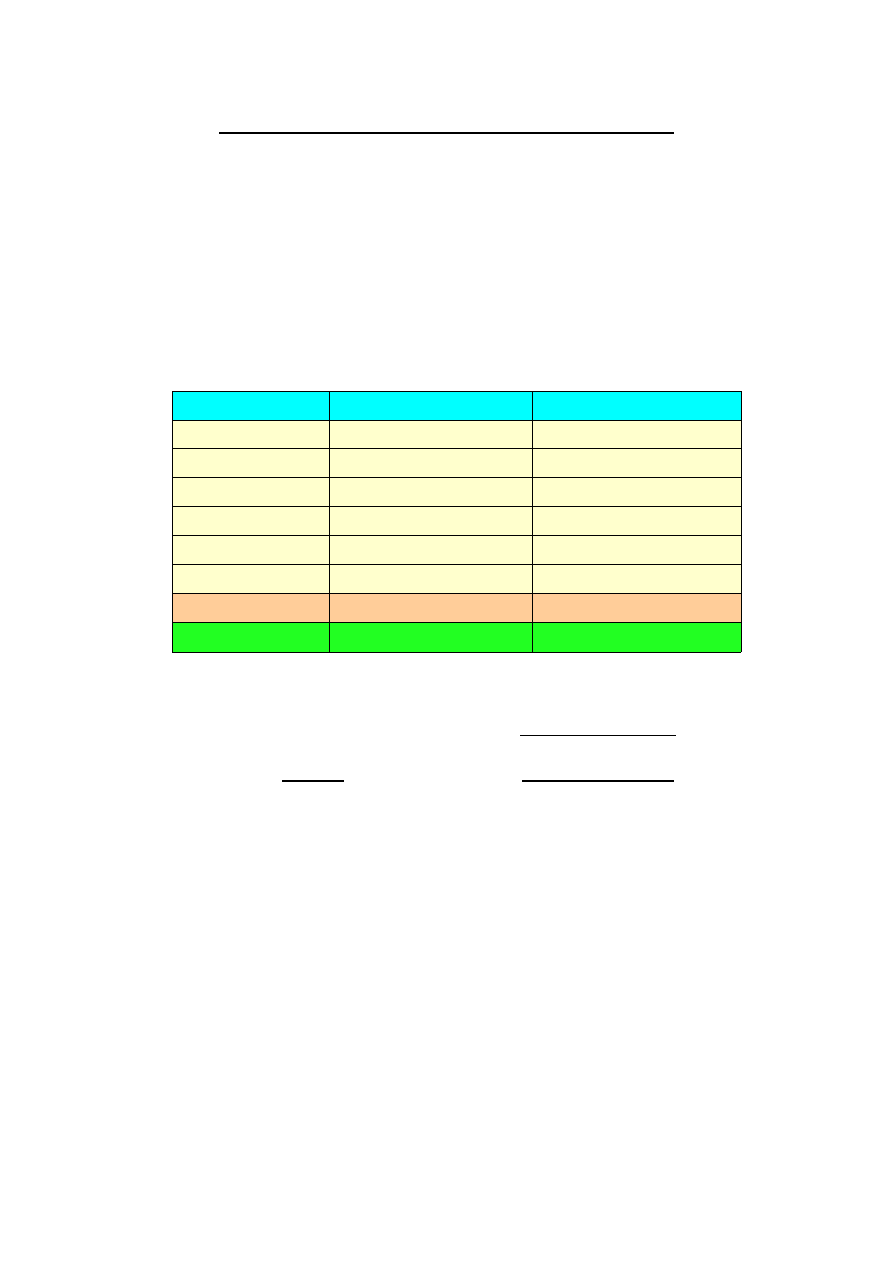
zapisać wartości ich oporności. Wyniki zapisujemy w poniższej tabeli:

I

R

i

(R

i

- <R>)

2

1

9.889

0.000676

2

9.912

0.000009

...

...

...

...

...

...

19

9.936

0.000441

20

9.886

0.000841

SUMA:

198.30

0.073036

Parametry:

<R>=9.915 k

Ω

U

R

=0.062 k

Ω

Wzory wykorzystane do obliczenia parametrów rozkładu mają postać:

〈

R〉=

∑

R

i

N

U

R

=



∑



R

i

−〈

R〉

2

N −1

Obliczone parametry charakteryzujące średnią wartość i rozrzut serii można wykorzystać do

sprawdzenia czy oporniki mieszczą się w normie. Różnica między otrzymaną średnią serii a
wartością nominalną (10 k

Ω)

powinna być mniejsza niż deklarowana tolerancja czyli 1%. W

naszym przypadku oznacza to, że dopuszczalne jest odstępstwo mniejsze niż 0.1 k

Ω ,

co jest

spełnione dla badanej serii, gdyż otrzymane w pomiarze

∆

R=0.085 k

Ω

spełnia tą relację. Również

otrzymany rozrzut wartości oporności (niepewność pomiaru) jest mniejszy niż deklarowana
tolerancja, gdyż U

R

= 0.062 k

Ω

odpowiada 0.6% i jest mniejsze niż 1%.

Jest to jedyna analiza jaką można wykonać dla tego pomiaru, gdyż kolejność otrzymywania

poszczególnych wartości w żaden dodatkowy sposób nie charakteryzuje badanej serii wyników.

2. Pomiar czasu odliczania

Do wykonania tego eksperymentu wystarcza jakikolwiek stoper mierzący czas z dokładnością do
0.05 sekundy. Pomiary polegają na dwudziestokrotnym zmierzeniu czasu odliczania od jeden do
dwudziestu na ślepo, tzn. bez patrzenia na zegarek. Ćwiczenie można wykonywać z zamkniętymi
lub skupiając wzrok na jakimkolwiek przedmiocie innym niż zegarek. Należy się starać aby
utrzymywać jednakowe tempo odliczania w czasie każdego pomiaru. Każda bardziej lub mniej
świadoma decyzja o zmianie sposobu liczenia (szybciej, wolniej, co sekundę itp.) zakłóca
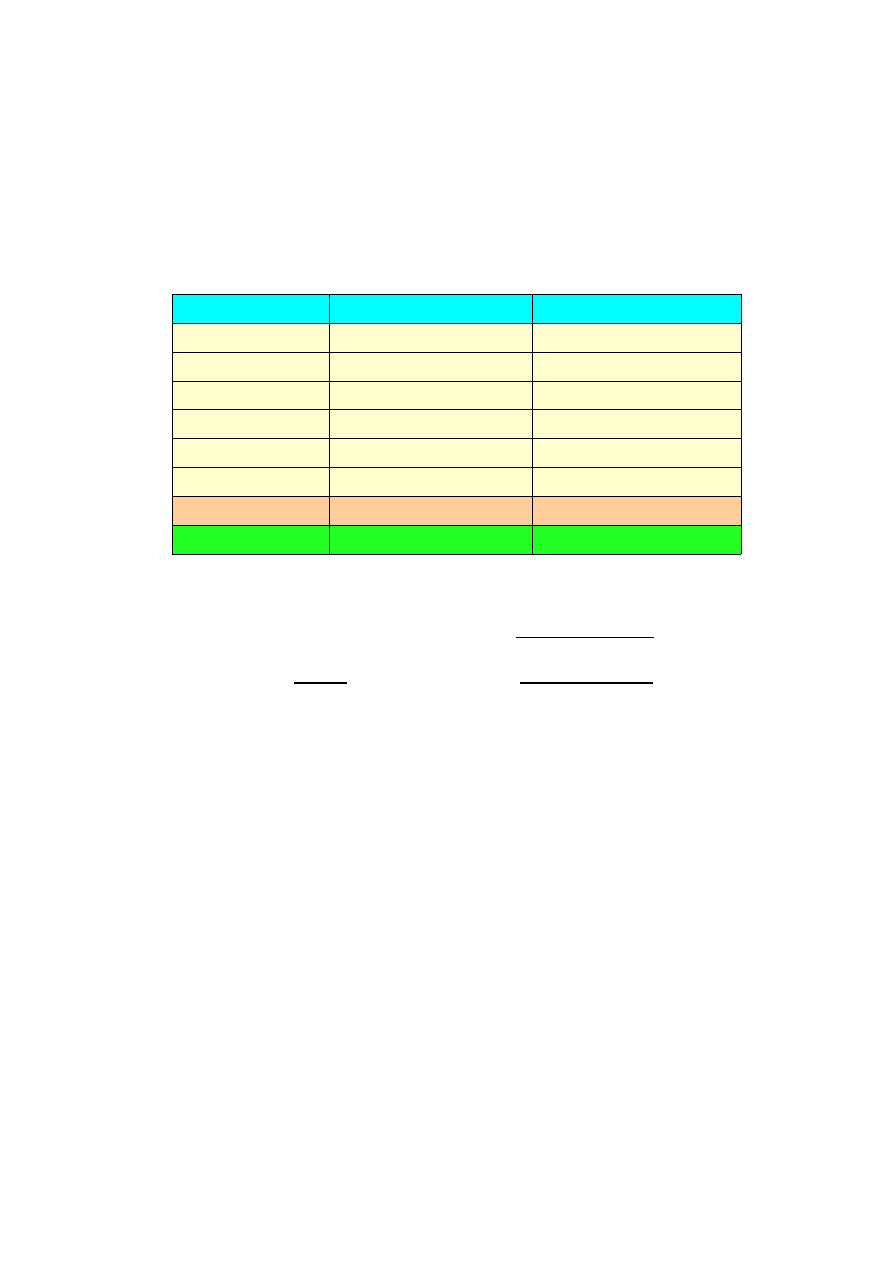
jednorodność próbki statystycznej. Pomiary zapisujemy w tabeli podobnej do tej z punktu 1:

I

t

i

(t

i

- <t>)

2

1

14.85

0.16

2

16.95

2.89

...

...

...

...

...

...

19

16.25

1.00

20

15.05

0.04

SUMA:

305.00

8.027

Parametry:

<t>=15.25 s

U

t

=0.65 s

Tak jak w poprzednim przypadku parametry rozkładu obliczamy ze wzorów:

〈

t 〉=

∑

t

i

N

U

t

=



∑



t

i

−〈

t 〉

2

N −1

W przypadku tego eksperymentu nie ma żadnej „wartości nominalnej” czy „dokładnej”, która
powinna odpowiadać centrum rozkładu. Otrzymana średnia zależy nie tylko od wybranej osoby, ale
nawet od jej chwilowego nastawienia, stanu zdrowia nastroju itp. Z tego właśnie powodu te
pomiary wykonywane są osobno dla każdego z członków zespołu.

Dużo więcej informacji niesie w tym przypadku rozrzut, czyli niepewność wartości tego

czasu gdyż jest to parametr dużo bardziej powtarzalny dla danej osoby. Stwierdzenie umiejętności
powtarzalnego odliczania czasu dostarcza cennej informacji o stabilności zegara biologicznego.
Znaczy to, że objawami pozytywnymi będą mała wartość stosunku niepewności standardowej do
wartości średniej i charakterystyki zbliżone do rozkładu normalnego (około 67% pomiarów w
przedziale o odchyleniu jednej niepewności wokół wartości średniej).

W tak otrzymanej serii wyników dużo informacji niesie również sekwencja otrzymanych

wyników, gdyż stwierdzenie systematycznego wzrostu czy spadku wartości (trendu) może dać
dodatkowe informacje o reakcji na zniecierpliwienie, niemożność dłuższego utrzymania skupienia
uwagi itp. Dlatego też w przypadku tego pomiaru warto zrobić wykres wartości t

i

od numeru

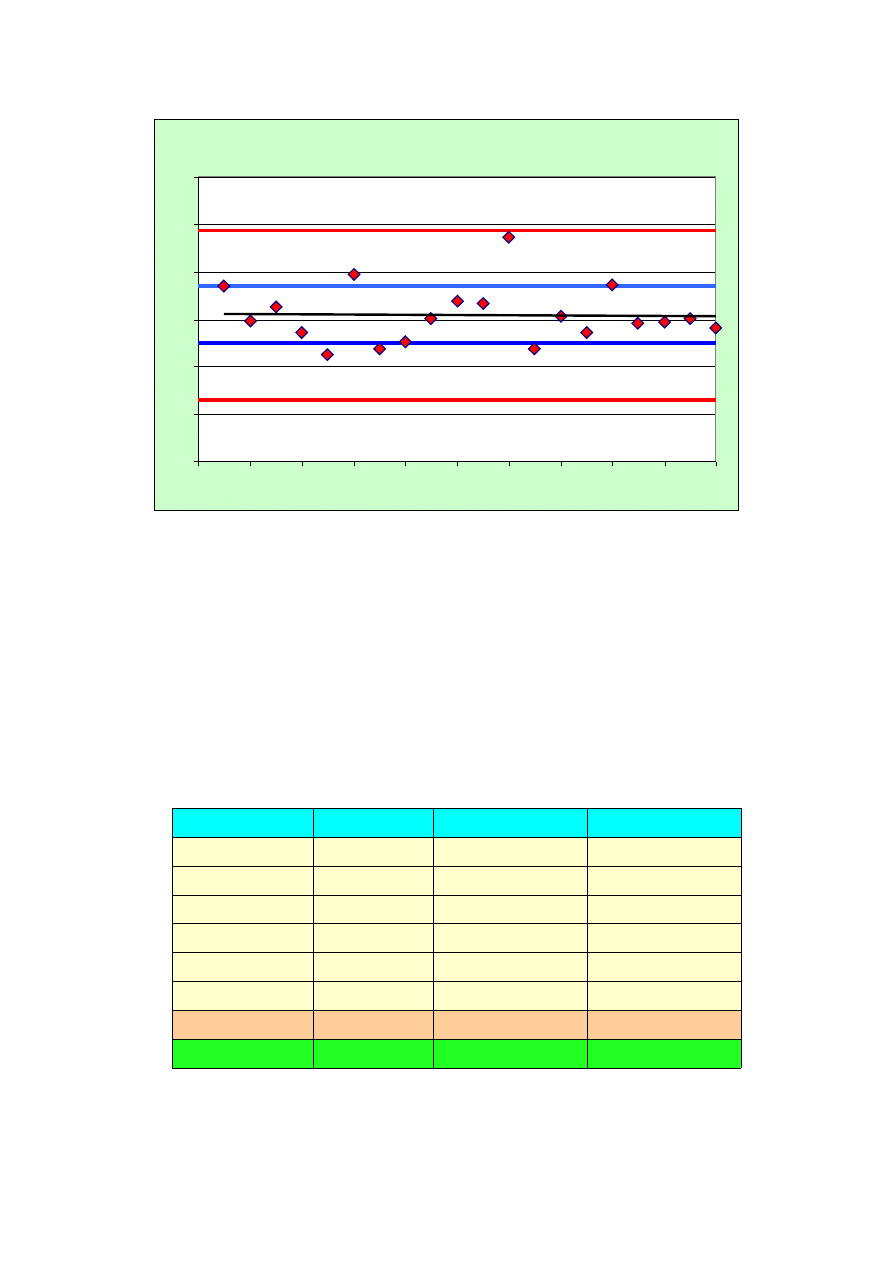
pomiaru. Przykład takiego wykresu zamieszczony poniżej zawiera serię pomiarów, tzw. linię trendu
oraz cztery dodatkowe linie na poziomach: dwie linie <t> ± u

t

i dwie linie <t> ± 3u

t.

. Można

zauważyć, że w przedziale o odchyleniu jednej niepewności (linie niebieskie) mieści się ok połowy
pomiarów, co jest już dość bliskie rozkładowi normalnemu. Dodatkową zaletą jest to, że żaden z
wyników nie wyskakuje poza przedział o odchyleniu potrojonej niepewności (linie czerwone)

Linia trendu też nie wykazuje jakichś systematycznych zmian w trakcie trwania pomiaru,

wystawiając dobre świadectwo zegarowi biologicznemu osoby mierzącej.

3. Rzuty kostkami

Zestaw eksperymentalny składa się z kubka i pięciu kostek do gry. Po wykonaniu każdego rzutu
pięcioma kostkami sumujemy liczbę oczek na wszystkich kostkach i zapisujemy w postaci tzw.
histogramu. Jest to zapis 25 wierszy oznaczonych możliwymi wartościami sumy oczek, tzn od 5 do
30. Po wypadnięciu danej liczby oczek w odpowiednim wierszu w pierwszej wolnej kratce
stawiamy krzyżyk, w ten sposób ilość kratek zaznaczonych w danym wierszu oznacza ilość
wystąpień danej sumy oczek n(X

i

) . Dla uzyskania sensownej próbki statystycznej należy wykonać

minimum 80 – 100 rzutów. Po zakończeniu rzucania uzyskane wyniki zapisujemy w tabeli:

X

i

n(X

i

)

X

i

n(X

i

)

n(X

i

) (X

i

- <X>)

2

5

0

0

0

6

2

12

268.19

...

...

...

...

...

...

...

...

29

1

29

130.42

30

1

20

154.26

SUMA:

N=100

1758

1490.38

Parametry:

<X>=17.58

Ux=3.88

Wzory wykorzystane do obliczenia parametrów rozkładu mają postać:

Sekwencja wartości czasu

y = -0.0027x + 15.116

12

13

14

15

16

17

18

0

2

4

6

8

10

12

14

16

18

20

〈

X 〉=

∑

n X

i



X

i

N

U

x

=



∑

n  X

i



X

i

−〈

X 〉

2

N −1

Rozkład Gaussa (normalny)

Opis teoretyczny pokazuje, że wygenerowany przez nas rozkład powinien być zbliżony do

tzw. rozkładu normalnego, nazywanego też rozkładem Gaussa.

n X

i

=

Aexp

[

−

X

i

−

2

2

2

]

A=

N



2

Wzór ten przewiduje jaka jest oczekiwana ilość wystąpień danej sumy oczek, przy założeniu że cała
statystyka zachowuje się jak rozkład normalny o zadanych dwóch wymaganych parametrach. Jeden
z nich

µ

stanowi informację o położeniu centrum rozkładu (wartości najbardziej prawdopodobnych)

zaś drugi

σ

stanowi informacje o rozrzucie oczekiwanych wartości wokół wartości centralnej.

Jak łatwo zauważyć parametry te są prawie dokładnymi odpowiednikami parametrów,

którymi charakteryzowane były serie pomiarów w ćwiczeniach 1 i 2. Oznacza to, że otrzymywana
wcześniej wartość <X> powinna być pewnym oszacowaniem (estymatorem) wartości

µ

, zaś

wartość niepewności U

x

, oddająca szerokość rozkładu, powinna być przybliżeniem

σ

. Można

wyliczyć, żę dla idealnie wyważonych kości odpowiednie wartości teoretyczne powinny wynosić:

=

3.5

=

3.8

Jak widać z tabeli otrzymane wartości rzeczywiste nie odbiegają szczególnie od oczekiwanych. W
szczególności otrzymane odchylenie średniej <X> od wartości oczekiwanej

µ

mieści się przedziale

o szerokości równej niepewności podzielonej przez pierwiastek z liczby pomiarów N, jak to
przewiduje statystyka.

Obliczenia ilości wystąpień n(X

i

) , oczekiwanych z faktycznego rozkładu (dla danych konkretnych

kości) można wykonać obliczając odpowiednie n(X

i

) z rozkładu Gaussa o parametrach

µ

= <X>

oraz

σ

= Ux. Przykład takiego obliczenia pokazany jest w tabeli na następnej stronie. Wartości

n(X

i

) można wyliczyć na dwa sposoby:

●

dodając do używanej tabeli dwie dodatkowe kolumny: jedną zawierającą kwadrat
odchylenia X

i

od wartości średniej: DX = X

i

- <X> , podzielony przez podwojony kwadrat

niepewności U

x

i drugą zawierającą odpowiednią eksponentę z tej wartości pomnożoną

przez stałą normalizacyjną A

●

używając zdefiniowanej funkcji bibliotecznej arkusza kalkulacyjnego MS Excel:
N*ROZKŁAD.NORMALNY (X

i

, <X>, Ux, FAŁSZ), gdzie ostatnia zmienna określa

rodzaj prezentacji rozkładu normalnego (kumulatywny bądź nie)

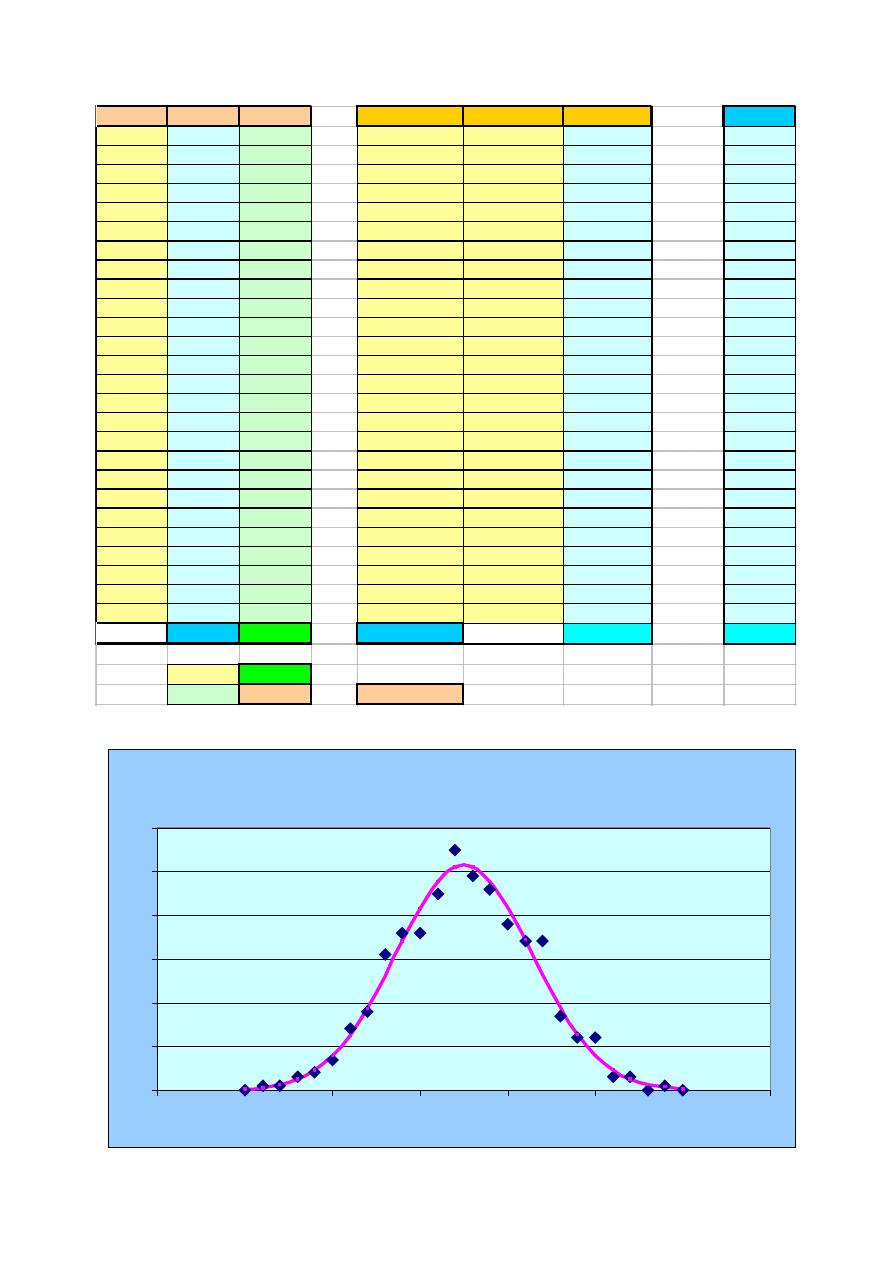
Poniższa tabelka i wykres zostały wytworzone z użyciem MS Excel i pokazuje oba te sposoby.

Xi

n(Xi)

Xi*n(Xi)

n*DX^2

0.5*(DX/Ux)^2

Gauss

R.NORM.

5

0

0

0

5.214722947 0.27941276

0.282342

6

1

6

132.7104 4.414967797 0.62169228

0.626341

7

1

7

110.6704 3.681748017 1.29422201

1.302326

8

3

24

271.8912 3.015063608

2.520845

2.533844

9

4

36

290.3616 2.414914569 4.59396369

4.613091

10

7

70

395.8528

1.8813009 7.83308844

7.85879

11

14

154

595.1456 1.414222601 12.4963321

12.52769

12

18

216

548.4672 1.013679672

18.652461

18.68694

13

31

403

633.3424 0.679672114 26.0491635

26.08295

14

36

504

446.0544 0.412199925 34.0373293

34.06647

15

36

540

228.6144 0.211263107 41.6122528

41.63409

16

45

720

103.968

0.07686166 47.5982554

47.61269

17

55

935

14.872 0.008995582 50.9406988

50.95045

18

49

882

11.2896 0.007664875 51.0085311

51.01819

19

46

874

100.7584 0.072869537 47.7886532

47.80283

20

38

760

233.7152

0.20460957 41.8900445

41.91157

21

34

714

411.7536 0.402884974 34.3558667

34.38475

22

34

748

682.3936 0.667695747 26.3630134

26.39669

23

17

391

510.5168 0.999041891 18.9274998

18.96203

24

12

288

503.8848 1.396923404 12.7143893

12.74593

25

12

300

671.4048 1.861340288 7.99101256

8.016969

26

3

78

215.7312 2.392292543 4.69907286

4.718462

27

3

81

269.6112 2.989780167 2.58539319

2.598617

28

0

0

0

3.653803162 1.33089894

1.33917

29

1

29

131.7904 4.384361527 0.64101414

0.645775

30

0

0

0

5.181455262 0.28886452

0.291392

500

17.52

7514.8

499.113971

499.6104

<X>=

17.52

Ux =

3.88

3.877

Oczekiwane ilości wystąpień sumy oczek

0

10

20

30

40

50

60

0

5

10

15

20

25

30

35