
KOD ZDAJĄCEGO
MMA-R2G1P-021
EGZAMIN MATURALNY
Z MATEMATYKI
POZIOM ROZSZERZONY
Arkusz II
Czas pracy 150 minut
Instrukcja dla zdającego
1. Proszę sprawdzić, czy arkusz egzaminacyjny zawiera 10 stron.
Ewentualny brak należy zgłosić przewodniczącemu zespołu
nadzorującego egzamin.
2. Rozwiązania i odpowiedzi należy zapisać czytelnie w miejscu
na to przeznaczonym przy każdym zadaniu.
3. Proszę pisać tylko w kolorze niebieskim lub czarnym; nie pisać
ołówkiem.
4. W rozwiązaniach zadań trzeba przedstawić tok rozumowania
prowadzący do ostatecznego wyniku.
5. Nie wolno używać korektora.
6. Błędne zapisy trzeba wyraźnie przekreślić.
7. Brudnopis nie będzie oceniany.
8. Obok każdego zadania podana jest maksymalna liczba punktów,
którą można uzyskać za jego poprawne rozwiązanie.
9. Podczas egzaminu można korzystać z tablic matematycznych,
cyrkla i linijki oraz kalkulatora. Nie można korzystać
z kalkulatora graficznego.
10. Do ostatniej kartki arkusza dołączona jest karta odpowiedzi,
którą wypełnia egzaminator.
Życzymy powodzenia!
ARKUSZ II
MAJ
ROK 2003
Za rozwiązanie
wszystkich zadań
można otrzymać
łącznie 60 punktów
(Wpisuje zdający przed rozpoczęciem pracy)
PESEL ZDAJĄCEGO
(Wpisuje zdający przed
rozpoczęciem pracy)
Miejsce
na naklejkę
z kodem
Egzamin maturalny z matematyki
Arkusz II
2
Zadanie 12. (5 pkt )
Sprawdź, czy funkcja f określona wzorem
=
=
≠
≠
+
−
−
−
=
2
3
1
1
2
1
2
3
)
2
)(
1
(
)
(
2
x
dla
x
dla
x
i
x
dla
x
x
x
x
x
x
f
jest ciągła w punktach
i
. Sformułuj odpowiedź.
1
=
x
2
=
x
Odpowiedź. ...........................................................................................................................
Zadanie 13. (3 pkt )
Niech
będzie zbiorem wszystkich zdarzeń elementarnych i
,
. Oblicz
wiedząc, że
Ω
)
B
Ω
⊂
A
Ω
⊂
B
( A
P
∩
8
5
)
(
=
∪ B
A
P
,
2
1
)
(
=
A
P
,
4
3
)
(
=
′
B
P
. Sprawdź, czy zdarzenia A i B są
zdarzeniami niezależnymi ?
Odpowiedź.
) =.................... Zdarzenia A i B .................................................
(
B
A
P
∩

Egzamin maturalny z matematyki
Arkusz
II
3
Zadanie 14. (4 pkt )
Odcinek CD jest obrazem odcinka AB w jednokładności o skali
. Wiedząc, że
, , , wyznacz:
0
<
k
)
0
,
2
(
−
A
)
2
,
0
(
−
B
)
4
,
3
(
C
)
0
,
7
(
D
a) równanie prostej przechodzącej przez punkt i jego obraz w tej jednokładności,
A
b) równanie prostej przechodzącej przez punkt B i jego obraz w tej jednokładności,
c) współrzędne środka tej jednokładności.
Odpowiedź. a) Równania prostych mają postać ......................................................................
b) Środek jednokładności ma współrzędne .........................................................
Zadanie 15. (5 pkt )
Dane są funkcje f, g i h określone wzorami :
,
2
h
, x
∈R.
x
x
f
2
)
(
=
x
x
g
−
=
)
(
,
)
(
−
= x
x
a) Naszkicuj wykres funkcji f.
b) Wyznacz wzór i naszkicuj wykres funkcji
.
g
f D
c) Wyznacz wzór i naszkicuj wykres funkcji h
.
g
f D
D
-6
-6
2
1
-3
-2
-1
0
4
y
-4
-5
-3
-2
-1
-4
-5
5
1
2
3
x
6
5
4
3
-6
-6
2
1
-3
-2
-1
0
4
y
-4
-5
-3
-2
-1
-4
-5
5
1
2
3
x
6
5
4
3
-6
-6
2
1
-3
-2
-1
0
4
y
-4
-5
-3
-2
-1
-4
-5
5
1
2
3
x
6
5
4
3
Wykres funkcji f.
Wykres funkcji
.
g
f D
Wykres
funkcji .
g
f
h
D
D
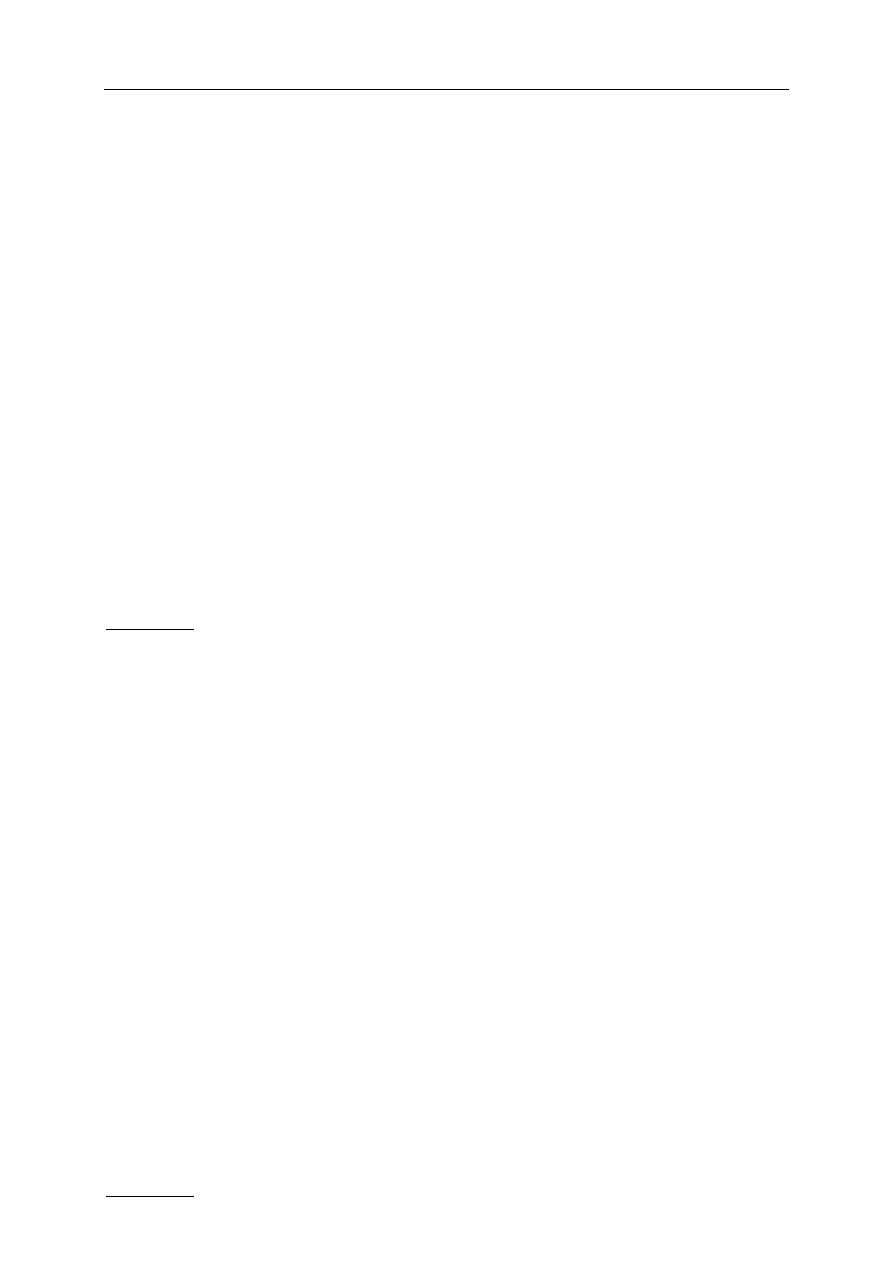
Egzamin maturalny z matematyki
Arkusz II
4
Zadanie 16. (5 pkt )
Zawierając w kolekturze Toto-Lotka jeden zakład w grze „Expres-Lotek” zakreślamy
5 spośród 42 liczb. Oblicz prawdopodobieństwo trafienia co najmniej 4 spośród
5 wylosowanych liczb. Wynik podaj w zaokrągleniu do 0,00001.
Odpowiedź. Prawdopodobieństwo jest równe ..................................................
Zadanie 17. (5 pkt )
Rozwiąż równanie
.
0
4
sin
5
cos
2
2
=
−
+
x
x
Odpowiedź. ................................................................................................................................
Egzamin maturalny z matematyki
Arkusz
II
5
Zadanie 18. (5 pkt )
W tabeli podane są wartości funkcji
dla trzech argumentów.
(
)
ℜ
→
− 4
,
3
:
f
x
-2 0 3
)
(x
f
8
5
3
8
5
-1
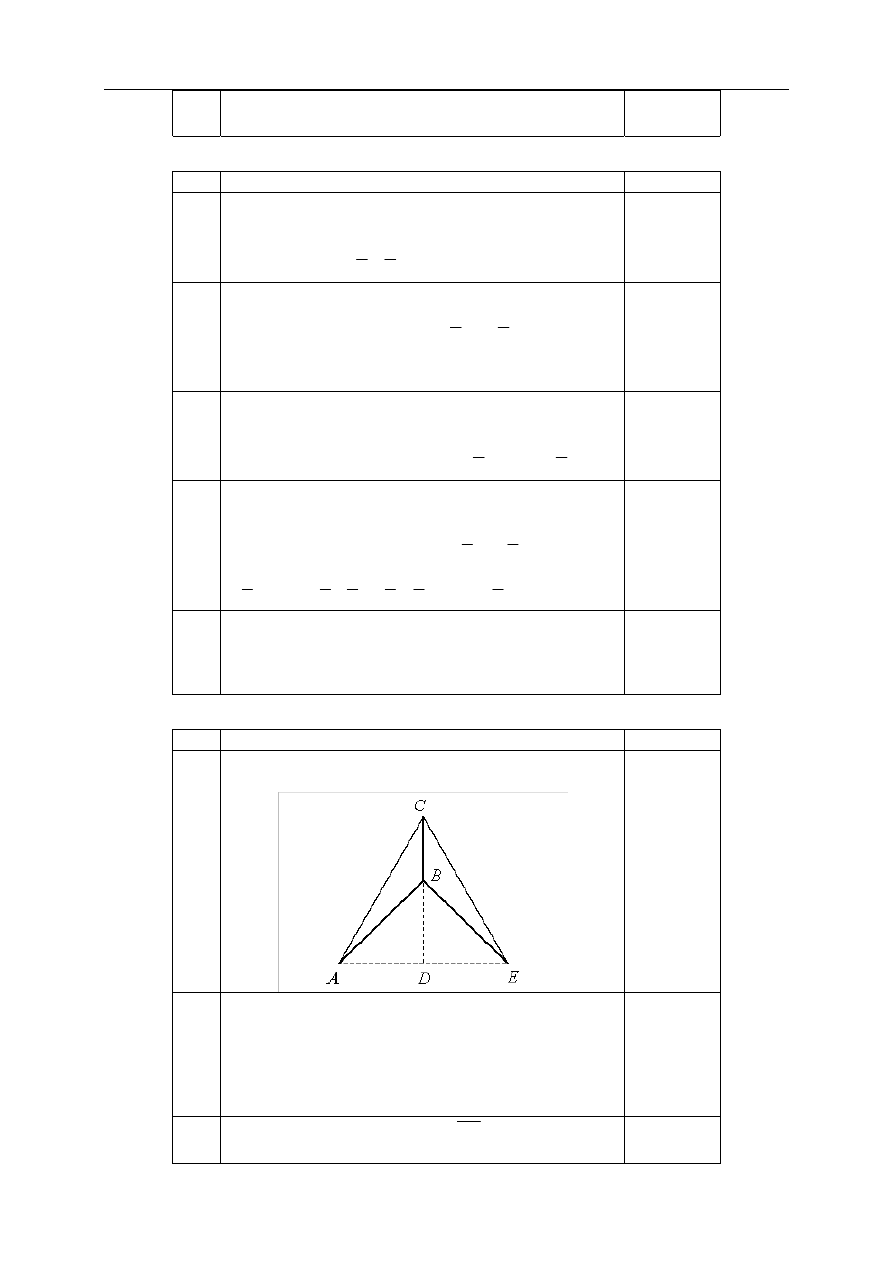
Rysunek przedstawia wykres pochodnej funkcji f.
a) Wyznacz równanie stycznej do wykresu
funkcji f w punkcie o odciętej .
0
=
x
b)
Wyznacz ekstremum funkcji f. Podaj
argument, dla którego funkcja f osiąga
ekstremum.
c) Podaj najmniejszą wartość funkcji f.
Odpowiedź. a) Równanie stycznej ma postać ............................................................................
b) Funkcja f osiąga ............................. równe ...................... dla ..........................
c) Najmniejsza wartość funkcji f jest równa ..........................................................

Egzamin maturalny z matematyki
Arkusz II
6
Zadanie 19. (4 pkt )
Funkcja f jest funkcją wykładniczą. Określ liczbę rozwiązań równania
w zależności od wartości parametru m. Odpowiedź uzasadnij.
m
x
f
=
− )
1
(
Zadanie 20. (6 pkt )
Udowodnij stosując zasadę indukcji matematycznej, że dla każdego całkowitego,
dodatniego n zachodzi równość:
n
n
n
2
1
2
3
)
1
3
(
...
8
5
2
+
=
−
+
+
+
+
2
.

Egzamin maturalny z matematyki
Arkusz
II
7
Zadanie 21. (8 pkt )
W trójkącie ABC dane są :
8
=
AC
,
3
=
BC
,
0
60
=
∠ACB
. Oblicz objętość i pole
powierzchni całkowitej bryły powstałej po obrocie trójkąta ABC dookoła boku BC .

Egzamin maturalny z matematyki
Arkusz II
8
Zadanie 22. (10 pkt )
Rozwiąż równanie
.
(
)
(
x
x
3
9
9
3
log
log
log
log
=
)

Egzamin maturalny z matematyki
Arkusz egzaminacyjny II
1
Schematy punktowania zadań do Arkusza II
Zadanie 12.
L. p.
Wykonana czynność L.
punktów
1.
Zapisanie wyrażenia
2
3
)
2
)(
1
(
2
+
−
−
−
x
x
x
x
x
w prostszej
postaci.
Odp. .
x
1
2.
Obliczenie granicy funkcji f w punkcie
.
1
=
x
Odp. 1.
1
3.
Obliczenie granicy funkcji f w punkcie
.
2
=
x
Odp. 2
1
4.
Sformułowanie odpowiedzi.
Odp. Funkcja f jest ciągła w punkcie
; funkcja f
nie jest ciągła w punkcie
.
1
=
x
2
=
x
Za każdą część odpowiedzi – 1 punkt.
2
Zadanie 13.
L. p.
Wykonana czynność L.
punktów
1.
Obliczenie .
)
(B
P
Odp.
4
1
)
(
=
B
P
.
1
2.
Obliczenie .
)
(
B
A
P
∩
)
(
)
(
)
(
)
(
B
A
P
B
P
A
P
B
A
P
∩
−
+
=
∪
Odp.
8
1
)
(
=
∩ B
A
P
.
1
3.
Porównanie liczb
oraz
i
zapisanie odpowiedzi, że zdarzenia A i B są
niezależne.
(
)
P A B
∩
( )
( )
P A P B
⋅
1
Zadanie 14.
L. p.
Wykonana czynność L.
punktów
1.
Ustalenie, że punkt D jest obrazem punktu A oraz
punkt C jest obrazem punktu B.
Fakt ten może być opisany słownie, przedstawiony
rysunkiem lub wykorzystany podczas rozwiązania.
1
2.
Wyznaczenie równania prostej AD.
Odp. .
0
=
y
1
3.
Wyznaczenie równania prostej BC.
Odp. .
2
2
−
= x
y
1
4.
Wyznaczenie współrzędnych środka jednokładności.
Odp.
(
.
)
0
,
1
1
Egzamin maturalny z matematyki
Arkusz egzaminacyjny II
2
Zadanie 15.
L. p.
Wykonana czynność L.
punktów
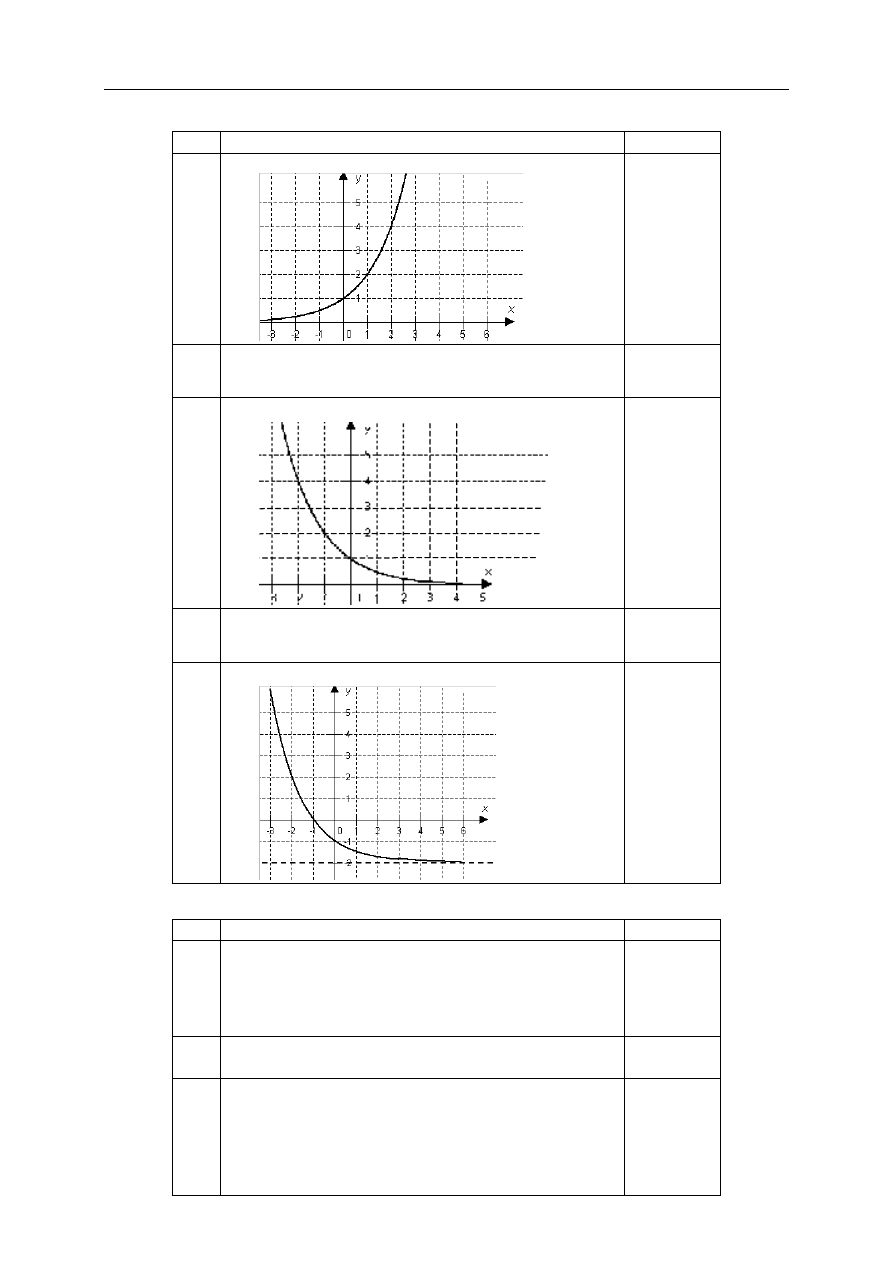
1.
Naszkicowanie wykresu funkcji f.
Odp.
1
2.
Wyznaczenie wzoru funkcji
.
g
f D
Odp.
(
)
.
( )
x
x
g
f
−
= 2
D
1
3.
Naszkicowanie wykresu funkcji
.
g
f D
Odp.
1
4.
Wyznaczenie wzoru funkcji h
.
g
f D
D
Odp.
(
)
.
( )
2
2
−
=
−x
x
g
f
h
D
D
1
5.
Naszkicowanie wykresu funkcji
.
g
f
h
D
D
Odp.
1
Zadanie 16.
L. p.
Wykonana czynność L.
punktów
1.
Zapisanie liczby wszystkich zdarzeń elementarnych
za pomocą symbolu Newtona.
Odp.
.
5
42
1
2.
Obliczenie liczby wszystkich zdarzeń elementarnych.
Odp. 850668.
1
3.
Zapisanie liczby zdarzeń sprzyjających trafieniu co
najmniej 4 spośród 5 liczb z wykorzystaniem symbolu
Newtona.
Odp.
.
1
1
37
4
5
+
1

Egzamin maturalny z matematyki
Arkusz egzaminacyjny II
3
4.
Obliczenie liczby zdarzeń sprzyjających.
Odp. 186.
1
5.
Obliczenie prawdopodobieństwa trafienia co najmniej
4 spośród 5 liczb.
0002186
,
0
850668
186 ≈
Odp. 0,00022.
1
Zadanie 17.
L. p.
Wykonana czynność L.
punktów
1. Zapisanie równania w postaci
.
0
2
sin
5
sin
2
2
=
+
−
x
x
1
2.
Zapisanie równania z niewiadomą
.
x
t sin
=
Odp.
2
.
0
2
5
2
=
+
− t
t
1
3.
Wyznaczenie rozwiązań równania 2
.
0
2
5
2
=
+
− t
t
Odp.
t
,
2
=
2
1
=
t
.
1
4. Zapisanie, że równanie
nie ma rozwiązań.
2
sin
=
x
1
5.
Zapisanie rozwiązań równania
.
0
4
sin
5
cos
2
2
=
−
+
x
x
Odp.
2
,
6
x
k k
π
π
= +
∈C lub
5
2
,
6
x
k k
π
π
=
+
∈C .
(Uznajemy też wynik zapisany w postaci.
, gdzie
lub
,
gdzie
).
0
0
360
30
⋅
+
=
k
x
C
k
∈
C
k
∈
0
0
360
150
⋅
+
=
k
x
1
Zadanie 18.
L. p.
Wykonana czynność L.
punktów
1.
Wykonanie polecenia a).
Odp.
8
5
=
y
.
Za podanie współczynnika kierunkowego stycznej lub
wartości pochodnej funkcji f dla x=0 przyznajemy 1
punkt.
2
2.
Podanie argumentu, dla którego funkcja f osiąga
minimum.
Odp. .
3
=
x
1
3.
Podanie minimum funkcji f.
Odp. .
1
)
3
(
min
−
=
f
1
4.
Wykonanie polecenia c).
Odp. Najmniejsza wartość funkcji f jest równa – 1.
1
Zadanie 19.
L. p.
Wykonana czynność L.
punktów
1.
Wykonanie polecenia zadania.
Odp. Równanie nie ma rozwiązań dla
(
0
,
∞
−
∈
(
)
∞
+
,
m
;
równanie ma 1 rozwiązanie dla
.
∈ 0
m
Po 1 punkcie za każdy z rozważonych przypadków.
2
2.
Uzasadnienie odpowiedzi.
Odp. Funkcja g określona wzorem
)
1
(
)
(
−
=
x
f
x
g
jest funkcją różnowartościową. Zbiorem wartości
2
Egzamin maturalny z matematyki
Arkusz egzaminacyjny II
4
funkcji g jest przedział (
.
)
,
0 ∞
+
Po 1 punkcie za każdy element uzasadnienia.
1
=
2
=
k
2
3
)
1
=
−
)
2
3
(
+
k
(
2
3
)
2
3
(
+
=
=
+
k
k
Zadanie 20.
L. p.
Wykonana czynność L.
punktów
1.
Sprawdzenie, czy dla
zachodzi dana równość.
n
Odp. Lewa strona równości jest równa 2. Prawa
strona jest równa
2
1
2
3 +
.
1
2.
Zapisanie założenia indukcyjnego.
Odp.
k
k
2
1
3
(
...
8
5
2
+
+
+
+
+
2
, gdzie k
jest dowolną ustaloną liczbą naturalną większą lub
równą 1.
1
3.
Zapisanie tezy indukcyjnej.
Odp.
)
1
(
2
1
)
1
(
2
3
)
1
3
(
...
8
5
2
2
+
+
+
=
+
−
+
+
+
+
k
k
k
1
4.
Przeprowadzenie dowodu tezy indukcyjnej.
Odp.
)
1
(
2
1
)
1
2
1
2
1
2
3
3
2
3
)
2
3
(
2
1
2
3
)
1
3
(
...
8
5
2
2
2
2
+
+
+
+
+
+
=
=
+
+
+
+
−
+
+
+
+
k
k
k
k
k
k
k
k
2
5.
Sformułowanie odpowiedzi.
Odp. Na mocy zasady indukcji matematycznej dana
równość jest prawdziwa dla każdej liczby całkowitej,
dodatniej n.
1
Zadanie 21.
L. p.
Wykonana czynność L.
punktów
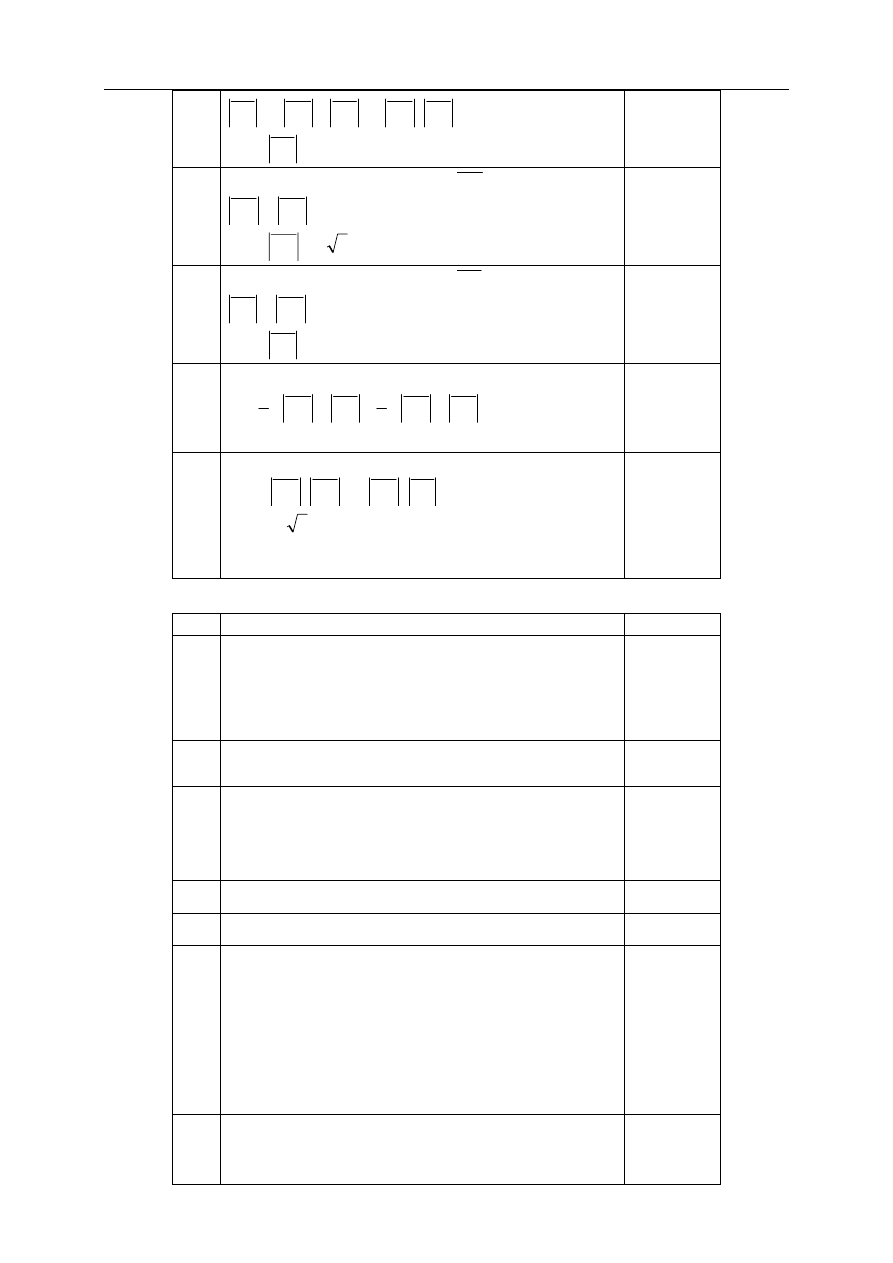
1.
Wykonanie rysunku i wprowadzenie oznaczeń.
Odp.
1
2.
Zapisanie jaką bryłą jest bryła po obrocie danego
trójkąta.
Odp. Powstała bryła jest stożkiem z wyciętym
stożkiem o tej samej podstawie.
Punkt przyznajemy także jeśli zaznaczony jest stożek
na rysunku.
1
3. Wyznaczenie długości odcinka AB .
Z twierdzenia kosinusów
1
Egzamin maturalny z matematyki
Arkusz egzaminacyjny II
5
ACB
BC
AC
BC
AC
AB
∠
⋅
−
+
=
cos
2
2
.
Odp.
7
=
AB
.
4.
Wyznaczenie długości odcinka AD .
ACB
AC
AD
∠
⋅
=
sin
Odp.
3
4
=
AD
.
1
5.
Wyznaczenie długości odcinka CD .
ACB
AC
CD
∠
⋅
=
cos
Odp.
4
=
CD
.
1
6.
Obliczenie objętości powstałej bryły.
BD
AD
CD
AD
V
⋅
−
⋅
=
2
2
3
1
3
1
π
π
Odp. 48 .
π
1
7.
Obliczenie pola powierzchni całkowitej.
AB
AD
AC
AD
P
⋅
+
⋅
=
π
π
Odp.
π
3
60
.
Jeśli wyznaczone zostało pole powierzchni bocznej
tylko jednego stożka przyznajemy 1 punkt.
2
Zadanie 22.
L. p.
Wykonana czynność L.
punktów
1.
Zapisanie warunku jaki musi spełniać niewiadoma x.
Odp.
>
>
>
0
log
0
log
0
9
3
x
x
x
1
2.
Wyznaczenie dziedziny równania.
Odp. .
)
,
1
(
∞
+
∈
x
1
3.
Zapisanie równania w postaci
.
(
)
(
x
x
3
9
2
9
9
log
log
log
log
=
)
Za zastosowanie twierdzenia o zamianie podstaw –
1 punkt.
2
4. Zapisanie równania w postaci
.
(
)
0
log
log
3
2
9
=
−
x
x
1
5. Zapisanie równania w postaci
.
(
)
0
log
2
log
9
2
9
=
−
x
x
1
6.
Wyznaczenie rozwiązań równania
.
(
)
0
log
2
log
9
2
9
=
−
x
x
Odp. lub
.
1
=
x
81
=
x
Zapisanie w postaci
- 1 punkt.
(
)
0
log
2
log
9
9
=
−
x
x
Zapisanie alternatywy:
lub log
1 punkt.
0
log
9
=
x
2
9
=
x
-
Wyznaczenie rozwiązań równania - 1 punkt.
3
7.
Wyznaczenie rozwiązań równania
.
(
)
(
x
x
3
9
9
3
log
log
log
log
=
)
Odp.
.
81
=
x
1
Wyszukiwarka
Podobne podstrony:
Matematyka Matura Maj 2003 Arkusz 1
Matematyka Matura Maj 2003 Arkusz 2
Matematyka Matura Maj 2003 Arkusz 1
Matematyka Matura Maj 2002 Arkusz 1
Matematyka Matura Maj 2002 Arkusz 2
Matematyka Matura Maj 2005 Arkusz 1
Matematyka Matura Maj 2005 Arkusz 2
Matematyka Matura Maj 2002 Arkusz 1
Matematyka Matura Maj 2002 Arkusz 2
matematyka-gazeta wyborcza-matura-maj 2003, mazowsze
matematyka gazeta wyborcza matura maj 2003 mazowsze 2C74OVWZKEBVMJZHFAG5NW3RX54OH67YEEOYHNA
fizyka matura styczen 2003 arkusz 1 YNEIP4Z27B573GY22RTYTQ
Matematyka Matura Styczen 2003 poziom rozszerzony
chemia matura styczen 2003 arkusz 1 7NL7HMDRBPQUD5O26HUGWX
chemia matura maj 2005 arkusz 2 56UX3BDIJHTIJZIJ3U3GBS
Fizyka Matura Maj 2002 Arkusz 2 (2)
więcej podobnych podstron