T.3.

BŁĘDY

PRZY

POMIARACH

PRZYRZĄDAMI

CYFROWYMI

Wstęp teoretyczny

Cel: Nauczyć wykorzystania podstawowych przyrządów pomiarowych. Zapoznać z zasadami łączenia
obwodów elektrycznych, metodami zapisu wyniku pomiaru, wyznaczaniem błędu granicznego oraz
dokładności przy pomiarach bezpośrednich i pośrednich przyrządami cyfrowymi.

1. Odczyt wartości mierzonej z przyrządów cyfrowych

Przyrządy cyfrowe są wygodniejsze w użyciu. Dzięki zastosowaniu wyświetlacza cyfrowego nie ma

konieczności stosowania wzoru (2) lub (3), nie popełnia się także subiektywnych błędów związanych z
odczytem wskazań. Niestety zastosowanie tego rozwiązania może doprowadzić do powstania błędów
grubych. Na wyświetlaczu oprócz cyfr składających się na wynik wyświetlany jest także przecinek lub
kropka dziesiętna. Wyświetlacze szczególnie typu LED charakteryzują się dość sporą zawodnością i
bardzo często zdarza się, że przecinek znak ten nie jest wyświetlany ze względu na uszkodzenie
wyświetlacza. Warto także przyjrzeć się jak skonstruowany jest wyświetlacz pojedynczej cyfry. Jego
wygląd przedstawiono na rys.4.

6

2

1

4

3

7

5

Rys.4. Wyświetlacz siedmiosegmentowy

Łatwo zauważyć, że uszkodzenie segmentu 7 spowoduje nie rozróżnianie cyfr 8 i 0. Natomiast
uszkodzenie segmentu czwartego uniemożliwi rozróżnienie cyfr 6 i 8. Zanim użytkownik zorientuje się o
takim uszkodzeniu może minąć sporo czasu a pomiary będą niewłaściwe.

2. Błąd graniczny pomiaru przyrządów cyfrowych

Dla cyfrowych przyrządów pomiarowych klasa dokładności nie jest zdefiniowana. Właściwości

dokładnościowe są opisywane za pomocą błędu bezwzględnego wyrażanego najczęściej w postaci (7) lub
(8).

)

(

%

n

X

a

X

m

g









(8)

gdzie n – liczba cyfr na najmniej znaczącej pozycji wyświetlacza.

Znając zakres pomiarowy oraz rozdzielczość cyfrowego przyrządu pomiarowego można wyznaczyć

przedział kwantowania q wyrażany w jednostkach wielkości mierzonej. Następnie liczbę q mnoży się
przez liczbę n podaną w wyrażeniu (10). W ten sposób otrzymuje się składową błędu proporcjonalną do
wartości nominalnej podzakresu. Wyrażenie (10) jest innym sposobem wyrażenia zależności (9). W tych
wyrażeniach stałe a i b mogą być wyrażone w procentach lub nie.

W przypadku cyfrowych przyrządów pomiarowych popełniany jest jeszcze błąd dyskretyzacji

wynoszący



1 cyfra na najmniej znaczącej pozycji wyświetlacza. W prawidłowo skonstruowanym

mierniku błąd ten nie ma większego znaczenia, ponieważ jest mniejszy od błędu analogowego 2 do 5 razy
a nawet więcej. Zasada ta nie dotyczy częstościomierzy-czasomierzy cyfrowych, które konstruuje się tak,
aby właśnie błąd dyskretyzacji decydował o dokładności pomiaru.

2

3. Budowa i działanie przyrządów pomiarowych wykorzystywanych w ćwiczeniu

3.1. Woltomierz cyfrowy

Woltomierze cyfrowe są przeznaczone do pomiaru napięcia stałego lub zmiennego.

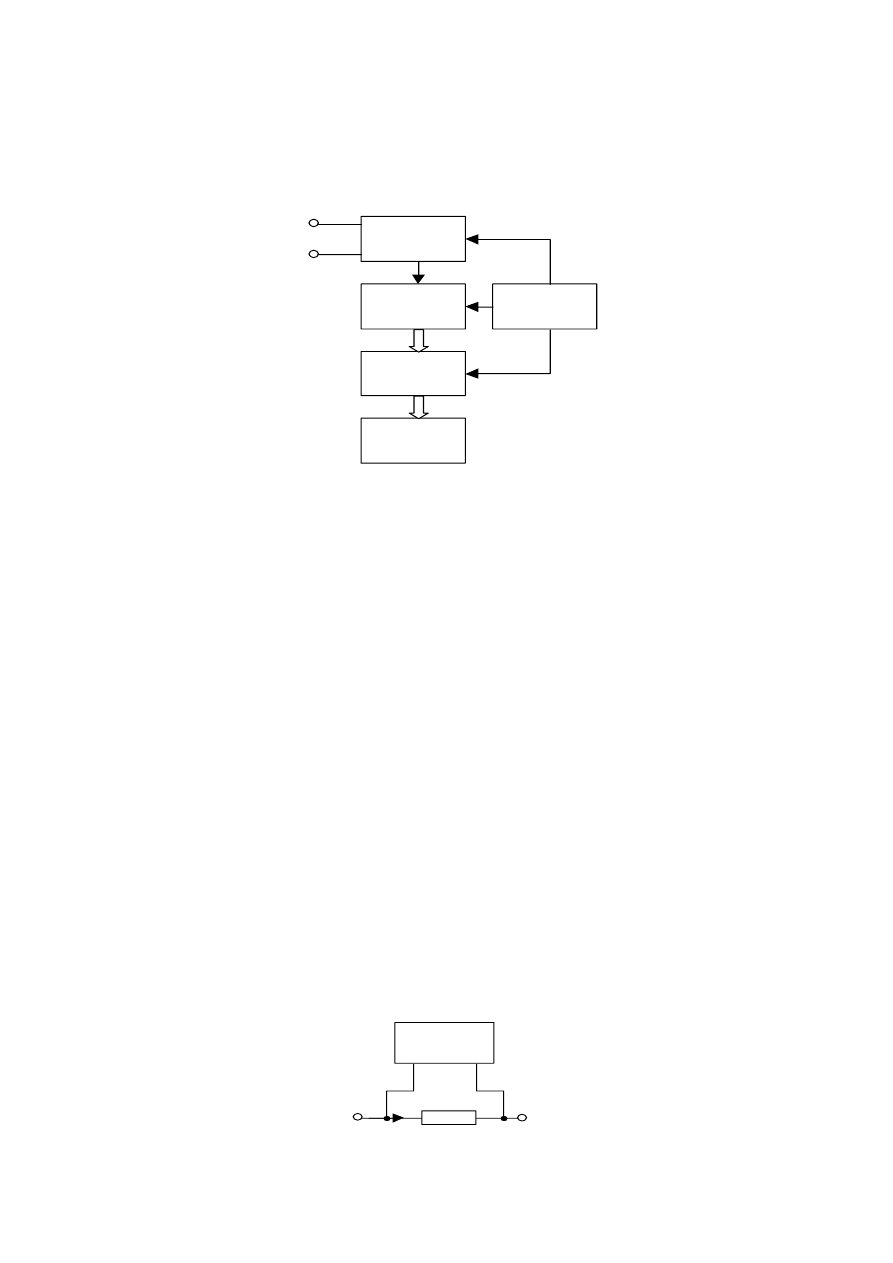
Na rys.12 przedstawiono schemat blokowy woltomierza napięcia stałego. Składa się on z bloków układu
wejściowego, przetwornika A/C, dekodera, wskaźnika cyfrowego oraz układu sterującego.

Uk ład

wejściowy

Przet wornik

A/C

Dek oder

Wsk aźnik

Uk ład

sterujący

U

Rys.12. Schemat funkcjonalny woltomierza cyfrowego

Zadaniem układu wejściowego jest wzmocnienie zbyt słabych sygnałów lub stłumienie zbyt

silnych. Przetwornik A/C służy do zamiany napięcia o postaci ciągłej na sygnał cyfrowy. Sygnał ten jest
przetwarzany do postaci zrozumiałej dla wyświetlacza cyfrowego. Z pojęciem sygnału cyfrowego wiąże
się pojęcie kodu, za pomocą którego sygnał analogowy jest zapisany cyfrowo. Na ogół kod sygnału na
wyjściu przetwornika A/C jest inny niż kod, który jest zrozumiały przez wyświetlacz cyfrowy. Dekoder
jest urządzeniem zmieniającym rodzaj kodu, w którym jest zapisywany sygnał analogowy. Całością pracy
urządzenia steruje układ sterujący. Za pomocą tego układu zmienia się zakres pomiarowy woltomierza
(przez wybór odpowiedniego tłumienia lub wzmocnienia w układzie wejściowym). Układ steruje także
pracą przetwornika A/C zmieniając jego rozdzielczość oraz czas przetwarzania, itd.

Podstawowym blokiem woltomierza jest przetwornik A/C. Obecnie wykorzystuje się przetworniki

wielokrotnego całkowania i przetworniki kompensacyjne. Woltomierze cyfrowe osiągają większe
dokładności niż woltomierze analogowe. Jednak dokładność tych mierników jest nadal ograniczona
przede wszystkim przez część analogową przyrządu.

3.2 Amperomierz cyfrowy

Amperomierze cyfrowe wykonuje się na ogół w oparciu o woltomierze cyfrowe mierząc napięcie na

wzorcowym rezystorze o niewielkiej wartości (np. 1



), przez który płynie mierzony prąd. Rezystor

wzorcowy jest oczywiścię integralną częścią przyrządu.

Zgodnie z prawem Ohma napięcie na rezystorze jest wprost proporcjonalne do przepływającego

przez niego prądu. Dokładność amperomierzy cyfrowych jest nieco gorsza (rząd lub dwa rzędy) od
dokładności woltomierzy cyfrowych, ponieważ zgodnie z prawem przenoszenia błędów dokładność
pomiaru prądu jest sumą dokładności woltomierza cyfrowego i dokładności użytego rezystora
wzorcowego.

Woltomierz

cyfrowy

R

I

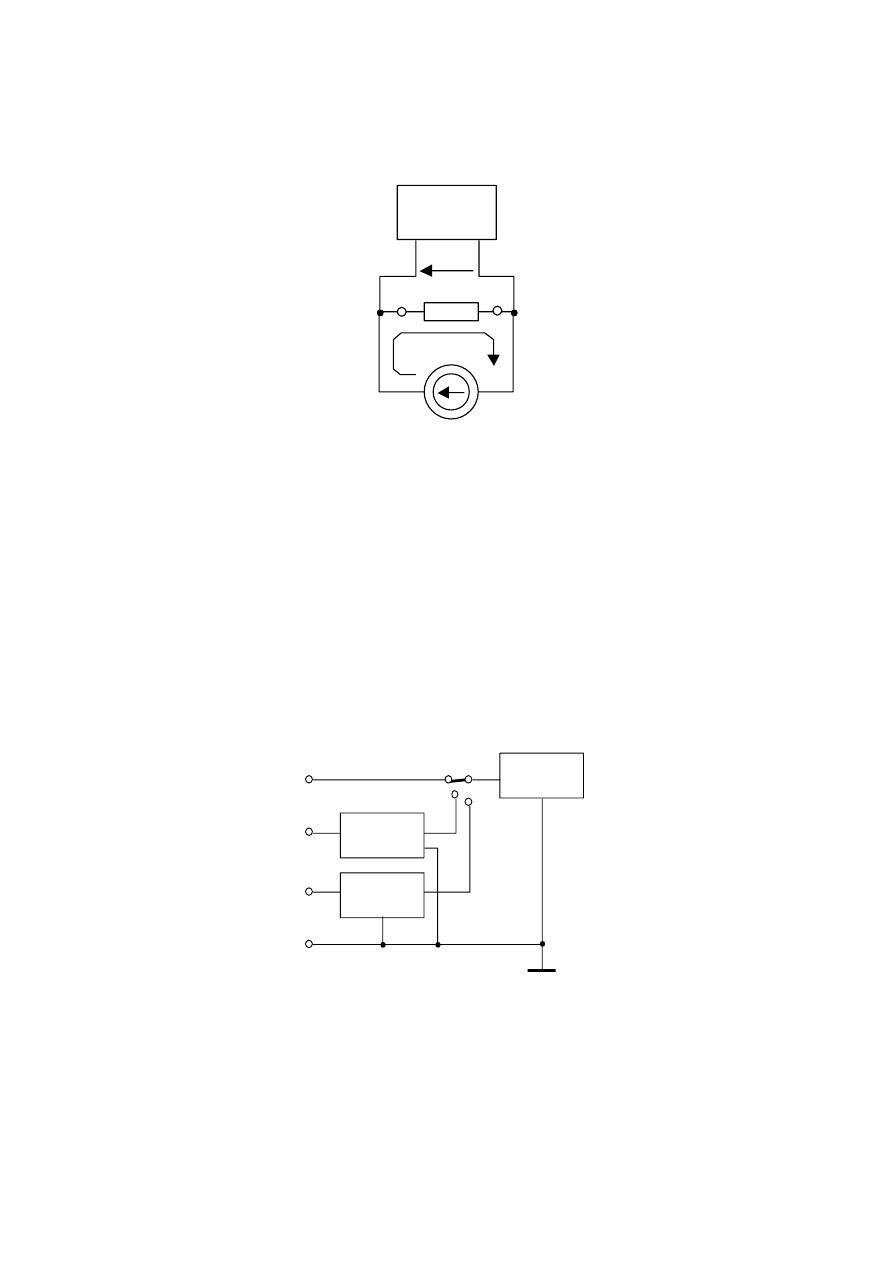
Rys.13. Amperomierz cyfrowy

3

3.3. Omomierz cyfrowy

Omomierze cyfrowe wykonuje w różny sposób. Najpopularniejsze metody polegają na

przetwarzaniu rezystancji w napięcie lub w przedział czasu. Na rys. 14 przedstawiono to pierwsze
rozwiązanie.

Woltomierz

cyfrowy

R

I

U

Rys.14. Omomierz cyfrowy z przetwarzaniem R/U

Omomierz cyfrowy składa się z woltomierza cyfrowego oraz wzorcowego źródła prądowego o

stałej i znanej wydajności. Prąd z tego źródła płynie przez rezystor o rezystancji mierzonej. Podobnie jak
w przypadku amperomierza cyfrowego wykorzystywane jest prawo Ohma. Omomierze cyfrowe są
znacznie dokładniejsze od analogowych i osiągają dokładność rzędu części procenta i lepiej. Wadą tych
mierników jest to, że rezystancja mierzona musi być znacznie mniejsza od rezystancji wewnętrznej
woltomierza. W innym wypadku zależność wskazań przyrządu od rezystancji mierzonej przestaje być
liniowa, ponieważ rzeczywisty woltomierz ma skończoną rezystancję, która jest równolegle połączona z
rezystancją badanego rezystora.


3.4. Multimetr cyfrowy

Przetwornik

R/U

Woltomierz

cyfrowy

Przetwornik

I/U

U

I

R

masa

P

Rys.15. Schemat blokowy multimetru cyfrowego

Multimetry cyfrowe mierzą na ogół znacznie więcej wielkości niż multimetry analogowe. Ich

budowa oparta jest o woltomierz cyfrowy. Ich idea polega na tym, że każdą z mierzonych wielkości
przetwarza się w napięcie stałe, a to napięcie mierzy się woltomierzem cyfrowym.

.

4

Objaśnienia:
Okre

ślanie błędów wskazań przyrządów analogowych (wskazówkowych) i cyfrowych różni

si

ę w zasadniczy sposób. W przypadku przyrządów cyfrowych błędy wykonywanych nimi

pomiarów oblicza się w odmienny sposób. Przede wszystkim nie występuje tu pojęcie klasy
dokładności, a informacje dotyczące dokładności podawane przez producentów, są dość
obszernym zbiorem różnorakich liczb. Dzieje się tak dlatego, że produkowane przyrządy
cyfrowe skupiaj

ą w sobie wiele różnych funkcji pomiarowych – stąd ich nazwa – multimetry.

Przeci

ętny multimetr pozwala na pomiar napięć i prądów stałych i zmiennych oraz

rezystancji. Bardziej złożone przyrządy tego rodzaju mierzą dodatkowo indukcyjność,
pojemno

ść elektryczną, częstotliwość, temperaturę, itp.

Dokładność cyfrowych przyrządów pomiarowych określana jest w sposób bardziej złożony

niż elektrycznych mierników wskazówkowych. Nie istnieje tu pojęcie klasy dokładności, tak
charakterystycznej dla przyrz

ądów wskazówkowych. Poza tym brak jest jednolitego sposobu

podawania przez różnych wytwórców granicznych błędów wskazań charakteryzujących
dokładność ich wyrobów. Sposób określania błędów jest w dodatku różny dla poszczególnych
funkcji pomiarowych w ramach tego samego przyrz

ądu (np. inny dla pomiaru napięć stałych,

a inny dla napi

ęć zmiennych).

Należy dodać, że renomowane firmy produkujące aparaturę pomiarową najwyższej klasy

(np. ameryka

ńska firma KITHLEY), podają wartości błędów wskazań swoich produktów,

zastrzegaj

ąc jednocześnie, że wartości te gwarantowane są tylko w określonym przedziale

czasu, po upływie którego powinny być ponownie poddane sprawdzeniu u wytwórcy.

Niżej zaprezentowano kilka charakterystycznych sposobów określania przez wytwórców,

zarówno krajowych jak i zagranicznych dokładności wskazań produkowanych przez nich
multimetrów cyfrowych. Podane przykłady, powinny w dostatecznym stopniu wyjaśnić sposoby
korzystania przez u

żytkowników z informacji podawanych w instrukcjach fabrycznych cyfrowych

przyrz

ądów pomiarowych.

Multimetr cyfrowy typu V561

Jest

to

produkt

warszawskiego Zakładu Elektronicznej Aparatury Pomiarowej

MERATRONIK. Zwróćmy uwagę, że multimetr jest wielofunkcyjnym przyrządem pomiarowym,
dlatego jego dokładność określona jest nie w postaci jednej liczby, tak jak ma to miejsce w
przypadku przyrz

ądów wskazówkowych, ale stanowi zwykle stosunkowo obszerny zbiór

informacji, podaj

ący różne dokładności wskazań dla poszczególnych funkcji pomiarowych

(pomiar napi

ęcia, natężenia prądu, rezystancji, itp.), poszczególnych rodzajów mierzonych

wielko

ści (prąd stały, prąd zmienny), a także dla poszczególnych przedziałów mierzonych

warto

ści i poszczególnych przedziałów częstotliwości mierzonych wielkości zmiennoprądowych.

1. Błąd pomiaru napięć stałych (DC)

Na wstępie przytaczamy dosłownie informację podaną przez wytwórcę:

Błąd pomiaru:

0,5% w.m. ± 1 cyfra

co oznacza, że graniczny (maksymalny) błąd bezwzględny wskazań

x

U



wyra

ża się

nast

ępująco:

x

U



= 0,5% warto

ści zmierzonej ± wartość napięcia odpowiadająca ostatniej cyfrze

maksymalnego wskazania

max

W

na nastawionym zakresie pomiarowym gdzie

1 cyfra zwi

ązana jest z tzw. błędem dyskretyzacji.

Dla omawianego multimetru wytwórca podaje jako maksymalne następujące wskazanie:

max

W

= 1999

(3,5 cyfry)

To maksymalne wskazanie odpowiada różnym wartościom napięcia dla różnych zakresów

pomiarowych, a wi

ęc także różnym wartościom napięcia odpowiadającym ostatniej cyfrze

wy

świetlanego wyniku pomiaru. Przedstawia to pokazana niżej Tabela.

5

Zakres

pomiarowy Un

Warto

ść napięcia

odpowiadaj

ąca

maksymalnemu wskazaniu

(zakresowi pomiarowemu)

Warto

ść napięcia

odpowiadaj

ąca ostatniej

cyfrze wy

świetlanego

wyniku

200 mV

2 V

20 V

200 V

1000 V

199,9 mV

1,999 V
19,99 V
199,9 V

1999 V (teoretycznie)

0,1 mV

0,001 V

0,01 V

0,1 V
1,0 V

Przykład 1.

Oblicz wzgl

ędny błąd maksymalny (graniczny), z jakim mierzone jest napięcie

x

U

= 12 V na

zakresie pomiarowym

N

U

= 20 V.

Rozwi

ązanie:

Bior

ąc pod uwagę dane producenta, napiszemy:

x

U



= 0,

5 % w.m. ± 1 cyfra

U nas: w.m. = 12 V
1 cyfra odpowiada 0,01 V, st

ąd:

x

U



= 0,5 % *

12 V ± 0,01 V =

= 0,005 *

12 V ± 0,01 V =

= 0,

06 V ± 0, 01 V

Zakładając skrajnie niekorzystny z punktu widzenia dokładności pomiaru przypadek,

przyjmiemy,

że błąd dyskretyzacji 0,01 V ma znak dodatni, skąd ostatecznie:

x

U



= 0,07 V.

Znajomo

ść tego błędu pozwala na określenie przedziału, w którym z wysoką ufnością

(P = 0,9973) zawiera si

ę wartość rzeczywista mierzonego napięcia:

12 [V] - 0, 07 [V]

≤

x

U

≤ 12 [V] + 0, 07 [V]

albo:

11,93 [V]

≤

x

U

≤ 12,07 [V]

Poszukiwany błąd względny natomiast wyniesie:

Uwaga:

W

ścisłej (teoretycznej) definicji błędu względnego w mianowniku powinna znaleźć się

warto

ść rzeczywista wielkości mierzonej. Jak wiadomo, nigdy jej nie znamy, dlatego wartość

rzeczywist

ą zstępuje się wartością, która najlepiej ją przybliża. Najczęściej jest to średnia

arytmetycz

na wyników wielokrotnie powtórzonego pomiaru. W szczególnym przypadku, gdy

dysponujemy jednym tylko wynikiem pomiaru (jak to ma miejsce w powy

ższym przykładzie),

wynik ten uznajemy za przybli

żoną wartości rzeczywistą wielkości mierzonej.

Łatwo sprawdzić, że gdyby na zakresie 20 V mierzone było napięcie

x

U

= 1 V,

błąd

wzgl

ędny wyniósłby 7 %. Widzimy więc, że w przyrządach cyfrowych, podobnie jak w

analogowych (wskazówkowych), błąd względny pomiaru zależy od stosunku wskazań do
zakresu pomiarowego. Mierz

ąc przy pomocy przyrządu cyfrowego należy więc zadbać o to, by

jego zakres pomiarowy jak najmniej

różnił się od wartości mierzonej wielkości.

%

58

,

0

%

100

]

[

12

]

[

7

,

0

%

100













V

V

U

U

U

X

X

x



6

Multimetr cyfrowy typu V-560

Jest to produkt warszawskich Zakładów Elektronicznej Aparatury Pomiarowej MERATRONIK.
Błąd pomiaru napięć stałych (DC):
Wytwórca podaje w tym wypadku następującą informację:

Uchyby pomiaru (oryginalna terminologia

wytwórcy)

a) dla podzakresów 100 mV i 1 V:

± 0,1 % w.m. ± 0,05 % w.z.

b) dla podzakresów 10 V, 100 V, 1000 V: ± 0,2 % w.m. ± 0,05 % w.z.

co oznacza,

że graniczny (maksymalny) błąd bezwzględny wskazań

x

U



wyra

ża się

nast

ępująco, (np. dla podzakresu

N

U

= 10 V):

x

U



= ± 0,2 % wartości mierzonej ± 0,05 % wartości zakresu

Przykład.
Oblicz wzgl

ędny błąd maksymalny (graniczny), z jakim mierzone jest napięcie

x

U = 8 V na

zakresie pomiarowym

N

U

= 10 V.

R

ozwiązanie

x

U



= ± 0,2 % x 8 V ± 0,05 % x 10 V =

= ± 0,002 × 8 V ± 0,0005 × 10 V =
= ± 0,016 V ± 0,005 V = ± 0,021 V

Założono tu skrajnie niekorzystny przypadek, gdy oba składniki błędu mają ten sam znak.

Znajomo

ść tego błędu pozwala na określenie przedziału, w którym z wysoką ufnością (P =

0,9973) zawiera si

ę wartość rzeczywista mierzonego napięcia:

8 [V] - 0,021 [V]

≤

x

U ≤ 8 [V] + 0,021 [V]

albo:

7,979 [V]

≤

x

U ≤ 8,021 [V]

Poszukiwany błąd względny natomiast wyniesie:

Multimetr cyfrowy firmy KITHLEY MODEL 2000

Błąd pomiaru napięć stałych (DC):

Rozpatrywany przyrz

ąd jest najwyższej klasy multimetrem cyfrowym o wielu

skomplikowanych funkcjach pomiarowych. Przykładowo obliczymy tu błąd pomiaru napięcia
stałego (DC) na zakresie 10 V. Dla zakresu 10 V (DC) producent podaje dokładność wskazań
multimetru w nast

ępującej formie:

Accuracy = ± (30 ppm of reading + 5 ppm of range)

co oznacza,

że graniczny (maksymalny) błąd bezwzględny wskazań

x

U



wyra

ża się

nast

ępująco:

x

U



= ± (30 ppm wartości odczytanej ± 5 ppm zakresu pomiarowego)

Wyja

śnimy na wstępie znaczenie skrótu ppm.

ppm - parts per million (cz

ęści na milion)

1 ppm = 0,000 001 = 0,0001% (jedna milionowa cz

ęść)

10 ppm = 0,000 010 = 0,001% (dziesi

ęć milionowych części)

%

26

,

0

%

2625

,

0

%

100

]

[

*

8

]

[

*

021

,

0

%

100















V

V

U

U

U

X

X

x



7

Przykład.

Oblicz wzgl

ędny błąd maksymalny (graniczny), z jakim multimetr mierzy napięcie

x

U

= 5 V

na zakresie pomiarowym

N

U

= 10 V.

Rozwiązanie

Bior

ąc pod uwagę dane producenta, napiszemy:

x

U



= ± (30 ppm * 5 V + 5 ppm * 10 V) =

= ± (0,000 030 × 5 V + 0,000 005 × 10 V) =
= ± (0,000 150 V + 0,000 050 V) =
= ± (150 µV + 50 µV) = ± 200 µV = ± 0,0002 V

Znajomo

ść tego błędu pozwala na określenie przedziału, w którym z wysoką ufnością (P =

0,9973) zawiera si

ę wartość rzeczywista mierzonego napięcia:

5 [V] - 0,0002 [V]

≤

x

U

≤ 5 [V] + 0,0002 [V]

albo:

4,9998 [V]

≤

x

U

≤ 5,0002[V]

Poszukiwany błąd względny natomiast wyniesie:

Otrzymana w przykładzie wartość granicznego (maksymalnego) błędu wskazań świadczy o

rzeczywi

ście wysokiej klasie rozpatrywanego przyrządu.

onego

%

004

,

0

%

100

]

[

*

5

]

[

*

10

*

200

%

100

6















V

V

U

U

U

X

X

x

